1. Introduction

Classical epidemic models provide essential frames in studying the dynamics of disease transmission in the filed of theoretical epidemiology. An interesting topic in the research of infectious diseases is to understand how intervention strategies affect the relationships between individual-level processes and ecological dynamics via the ordinary differential equations(ODEs) [19,3,41,44,4,32].

When an infectious disease appears and starts to spread in a region, the departments for disease control and prevention will do everything possible to prevent the disease spreading. The effects of intervention strategies, such as border screening, mask wearing, quarantine, isolation, or communications through the mass media (to communicate to the public the existence of an outbreak and possibly risk-reducing behavior), play an important role in administering efficient interventions to control disease spread and hopefully eliminate epidemic diseases [39,10,11,34]. Under intervention policies, for a very large number of infective individuals the infection force may decrease as the number of infective individuals increases, because in the presence of large number of infectious the population may tend to reduce the number of contacts per unit time. Individual's response to the threat of disease is dependent on their perception of risk, which is influenced by public and private information disseminated widely by the media [35,21]. Human behavior change consequently leads to reduction in number of real susceptible individuals or effective contact rates [43]. This has been interpreted as the "psychological" effect [41]. For instances, during the outbreak of SARS in 2003 [16] and the outbreak of H1N1 influenza pandemic in 2009 [43,33,42], intervention strategies such as closing schools/ restaurants, postponing conferences, isolating infectives, etc., were taken by the Chinese government. These strategies greatly reduced the contact number per unit time, and therefore, decreased the incidence rate. This demonstrated the importance of considering the infection forces that include the adaptation of individuals to infection risks under intervention strategies [5]. Hence, to curb the spread of infectious diseases, it is then crucial to examine the role of intervention strategies on disease outbreaks.

The studies by Cui et al. [10,11] suggested that the population have done better to prevent the spreading of the disease with more preventive knowledge, which suggests that media coverage was critical in disease eradication. Khanam [19] showed that acquired immunodeficiency syndrome (AIDS) awareness among married couples, media and education play a tremendous role in mounting AIDS awareness among the residents. Tang and Xiao [43,33] indicated that strict interventions (e.g., campus quarantine) were taken in mainland China to slow down the initial spread of the disease, and awareness through media and education plays a tremendous role in changing behaviors or contact patterns, and hence in limiting the spread of infectious disease. In particular, Wang [39] formulated and analyzed an SIRS model to study the impact of intervention strategies on the spread of an infectious disease and found that intervention strategies decrease endemic levels and tend to make the dynamical behavior of a disease evolution simpler. Cai et al. [5] extended a classical SIRS epidemic model with the infectious forces under intervention strategies from a deterministic framework to a stochastic differential equation one through introducing random fluctuations and found that random fluctuations can suppress disease outbreak.

It's worthy to note that the environment factors considered in ODEs is homogeneous, while spatial variation is usually neglected. Therefore, the spatial spread of infectious and what drives it is less well understood [29]. And the spatial component of ecological interactions has been identified as an important factor [22,30]. Spatial diffusion and environmental heterogeneity have been recognized as important factors to affect the persistence and eradication of infectious diseases such as measles, tuberculosis, flu, etc., especially for vector-borne diseases, such as malaria, dengue fever, West Nile virus, etc. More importantly, it is shown that the spatial transmission and environ-mental heterogeneity can decide the speed and pattern of the spatial spread of infectious diseases [15,13,14,1,2,18,24,25,26,27,40,36,6,8,7,38,20]. Therefore, it is essential to investigate the role of diffusion in the transmission and control of diseases in a heterogeneous environment [15].

In particularly, Fitzgibbon et al. [13,14] were the first to propose a family of SIR (Susceptible-Infected-Recovered) models that can include spatially-dependent terms for diffusion, convection, disease transmission, and population demography. After assuming that rates of both transmission $\beta(x)$ and recovery $\gamma(x)$ of the disease depend on spatial variables, and characterizing the habitat as high (low) risk if the average of the transmission rates is greater (less) than the average of the recovery rates, Allen et al. [2] proposed a basic SIS model

$\left\{\begin{array}{ll} \dfrac{\partial S}{\partial t}=d_S\Delta S-\dfrac{\beta(x)SI}{S+I}+\gamma(x) I, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial I}{\partial t}=d_I\Delta I+\dfrac{\beta(x)SI}{S+I}-\gamma(x) I, & x\in \Omega,\, t>0,\\[2ex] \end{array}\right.$

(1)

with a no-flux boundary condition (or Neumann boundary condition)

$\dfrac{\partial S}{\partial \mathbf{n}}=\dfrac{\partial I}{\partial \mathbf{n}}=0, x\in \partial\Omega,\, t>0.$

(2)

For the sake of establishing the theoretical results, the authors in [2] introduced the basic reproduction number as

$\widetilde{R_0}=\displaystyle\sup\limits_{\varphi\in H^1(\Omega),\,\varphi\neq 0} \left\{\dfrac{\displaystyle\int_\Omega {\beta}\varphi^2} {\displaystyle\int_\Omega d_I|\nabla \varphi|^2+\gamma\varphi^2}\right\},$

(3)

and showed that, if $\widetilde{R_0} <1$, the disease-free equilibrium is globally asymptotically stable, while $\widetilde{R_0}>1$, the disease-free equilibrium (DFE) is unstable, and there exists a unique endemic equilibrium (EE). Unfortunately, due to the difficulties caused by the mathematical analysis, they did not derive any stability result (even the local linear stability) for the EE. However, they conjectured that if such a unique EE exists, it should be globally asymptotically stable. Peng and Liu [25] confirmed that the conjecture is true in two special cases: (1) the diffusion rate $d_S$ of the susceptible individuals is equal to the diffusion rate $d_I$ of the infected individuals: if $\Omega$ is a high-risk domain, the EE is globally asymptotically stable, and if $\Omega$ is a low-risk domain, the DFE is globally asymptotically stable; (2) $\beta(x)=r\gamma(x)$ for any fixed constant $r\in(0,\infty)$: if $r\leq1$, the DFE is globally asymptotically stable, and if $r>1$, the EE is globally attractive.

And recently, Cai and Wang [6] investigated the dynamics of a parasite-host epidemiological model in a spatially heterogeneous environment and gave the existence of the endemic equilibrium and the global stability of the endemic equilibrium in the case of the death rate a constant. Kuniya and Wang [20] constructed Lyapunov functions for the global stability analysis of equilibria of a spatially diffusive SIR epidemic model for two special cases, that is, the case of no diffusive susceptible individuals and that of no diffusive infective individuals. Furthermore, Huang et al. [18] studied two modified SIS diffusion models with the Dirichlet boundary condition $S(x,t)=I(x,t)=0,\, (x\in\Omega,\, t>0)$ and defined the reproductive number for both models to govern the stability of disease free equilibrium steady state and the existence of an endemic equilibrium, and showed partial result on the global stability of the EE in the case of the diffusion coefficients are equal.

Based on the discussions above, in this paper, we will focus on the global stability analysis of the steady states for a general SIS epidemiological model with infection force under intervention strategies in a spatially heterogeneous environment. The rest of this article is organized as follows: In Section 2, we establish an SIS epidemic model in a spatially heterogeneous environment. In Section 3, we give some preliminaries. In Section 4, we accomplish our main results. In Section 5, we give some numerical results to show the relation between basic reproduction number with the diffusion and spatial heterogeneity. And in the last section, Section 6, we provide a brief discussion and the summary of our main results.

---

2. Model derivations

Suppose that the total population ($N$) is divided into two groups, susceptible ($S$) and infectious ($I$), i.e., $N = S+I$. For modelling the adaption of individual's behavior under intervention policies, the infection force may decrease as the number of infective individuals increases due to the fact that the population may tend to reduce the number of contacts per unit time under intervention policies. This has been interpreted as the "psychological effect" [41,43]. Mathematically, this phenomenon can be modeled as the infection force is increasing when $I$ is small while it is decreasing when $I$ is large. For simplicity in notations, we suppose that the incidence rate (the contact number per unit time) can be factorized into ${\beta I/f(x,I)}$, where ${1/f(x,I)}$ represents the effect of intervention strategies on the reduction of valid contact coefficient $\beta$ [39]. It's worthy to note that, in the absence of intervention strategies, i.e., ${f(x,I)=1}$, the incidence rate becomes the well-known bilinear transmission rate $\beta SI$. To ensure a nonmonotonic infection force, we make the following assumptions:

(H1) $f(x,0)>0$ and $f_I'(x,I)>0$ for $I>0$.

(H2) There is a $\xi> 0$ such that $(I/f(x,I))_I' > 0$ for $0 < I \leq\xi$ and $(I/f(x,I))_I' < 0$ for $I > \xi$.

In epidemiology, these assumptions describe the effect of intervention strategies determining by a critical level of invectives $\xi$: if $0<I\leq\xi$, the incidence rate is increasing; while $I>\xi$, the incidence rate decreasing. And our general results can be used in some specific forms for the incidence rate that have been commonly used, for example:

Example 1. Saturated incidence rate: $f(x,I)= 1+p I+q I^2$ [39]. Especially, if $p=0,$ then $f(x,I)= 1+\alpha I^2$ [41].

Example 2. Incidence rates with "media coverage"[11]: $f(x,I)=\exp(\alpha I)$, where $\alpha$ is a positive constant.

Let $\Omega$ be a bounded domain in $\mathbb{R}^m$ ($m\geq1$) with smooth boundary $\partial\Omega$. Spatial heterogeneity is taken into account via the assumption that recruitment rate $\Lambda(x)$, mortality rate $\mu(x)$, recovery rate $\gamma(x)$ and incidence term $\dfrac{\beta (x)I}{f(x,I)}$ are spatially dependent. Such a two-component SIS reaction-diffusion epidemiological model is as follows:

$\left\{\begin{array}{ll} \dfrac{\partial S}{\partial t}=d\Delta S+\Lambda(x)-\dfrac{\beta(x)I}{f(x,I)}S-\mu(x) S+\gamma(x) I, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial I}{\partial t}=d\Delta I+\dfrac{\beta(x)I}{f(x,I)}S -\mu(x) I-\gamma(x) I, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial S}{\partial \mathbf{n}}=\dfrac{\partial I}{\partial \mathbf{n}}=0, & x\in \partial\Omega,\, t>0,\\[2ex] S(x,0)=S_0(x)\geq0, I(x,0)=I_0(x)\geq0,&x\in\Omega. \end{array}\right.$

(4)

where $S(x, t)$ and $I(x, t)$ are the density of susceptible and infected individuals at location $x\in \Omega$ and time $t$, respectively. $d$ is a positive diffusion coefficient for the population. $\mathbf{n}$ is the outward unit normal vector on $\partial \Omega$. The symbol $\Delta$ is the Laplacian operator. The homogeneous Neumann boundary condition implies that the above system is self-contained and there is no infection across the boundary. Specifically, we require that:

(ⅰ) $S_0(\cdot),I_0(\cdot)\in C^1(\bar{\Omega})$ and there are initially a positive number of infected individuals, i.e.,

$\displaystyle\int_{\bar{\Omega}}I_0(x)dx>0 \,\,\,\mathrm{with}\,\,\, S_0(x)\geq0\,\,\, \mathrm{and}\,\,\, I_0(x)\geq0\,\,\, \mathrm{for}\,\,\, x\in\Omega.$

(ⅱ) $\Lambda(\cdot),\mu(\cdot),\beta(\cdot),\gamma(\cdot)\in C^1(\bar{\Omega}).$ And there exist a positive constant $\nu>0$ such that $\nu<\min\{\zeta(x),x\in\Omega\}$ for $\zeta=\Lambda,\beta,\mu,\gamma$.

(ⅲ) $f(x,0)=0$}, $f(\cdot,\cdot)\in C^1(\bar{\Omega}\times \mathbb{R}_+)$ and $f(\cdot,\cdot)> 0$ on $\bar{\Omega}\times \mathbb{R}_+$.

We are interested in the steady state solutions of model (4). Thus we will concentrate on the following strongly coupled elliptic system

$\left\{\begin{array}{ll} d\Delta S+\Lambda(x)-\dfrac{\beta(x)I}{f(x,I)}S-\mu(x) S+\gamma(x) I=0, & x\in \Omega,\\[2ex] d\Delta I+\dfrac{\beta(x)I}{f(x,I)}S -\mu(x) I-\gamma(x) I=0, & x\in \Omega,\\[2ex] \dfrac{\partial S}{\partial \mathbf{n}}=\dfrac{\partial I}{\partial \mathbf{n}}=0, & x\in \partial\Omega.\\[2ex] \end{array}\right.$

(5)

Next, we introduce some related definitions:

A disease-free equilibrium (DFE) of model (4) is a solution of (5) in which $I(x)$ vanish at every $x\in \Omega$, i.e., $I(x)=0$. We denote the DFE as $E_0=(S_*(x), 0)$.

An endemic equilibrium (EE) of model (4) is a solution in which $I(x)$ exist, i.e., $I(x)>0$ for some $x\in \Omega$. We denote the EE as $E^*=(S^*(x), I^*(x))$.

The habitat $\Omega$ is characterized as low-risk domain (or high-risk domain) if the spatial average of transmission rate $\dfrac{1}{|\Omega|}\displaystyle\int_\Omega \dfrac{\beta(x)S_*(x)}{f(x,0)}dx$ less than (or greater than) the spatial average of mortality and recovery rate $\dfrac{1}{|\Omega|}\displaystyle\int_\Omega (\mu(x)+\gamma(x))dx$. See [15,2,24] for more details.

---

3. Preliminaries

In this section, we collect some basic results concerning elliptic eigenvalue problems and linear parabolic equations, which will be used in the proofs of our main results.

For a closed linear operator $A: D(A)\subset L^2\rightarrow L^2$, where $D(A)$ denotes the domain of $A$, and the spectral bound of $A$ is defined by

$\mathbf{s}(A)=\sup\{\mathfrak{Re}(\lambda)|\lambda\in\sigma(A)\},$

where $\sigma(A)$ denotes the spectrum of $A$. For a given positive constant $d$ and a given real function $q\in C(\overline{\Omega})$, let $d\Delta +q$ be the following unbounded linear operator in $L^2(\Omega)$:

$\begin{array}{l}D(d\Delta +q)=H_{\mathbf{n}}^2(\Omega):=\left\{\phi\in H^2(\Omega)\big|\; {\dfrac{\partial \phi}{\partial\mathbf{n}}=0}\;\mbox{on}\;\partial\Omega\right\},\\ (d\Delta +q)\phi(x)=d\Delta \phi(x)+q(x)\phi(x)\,\, (x\in\Omega) \mbox{for}\;\; \phi\in H_{\mathbf{n}}^2(\Omega), \end{array}$

where $H^2(\Omega)$ denotes the usual $L^2$-type Sobolev space on $\Omega$ of order $2$. This is a densely defined closed sectorial operator in $L^2(\Omega)$, so it generates an analytic semigroup $T(t)=e^{t(d\Delta +q)}$ ($t\geq 0$) in $L^2(\Omega)$.

Concerning the spectral bound of the operator $d\Delta +q$, we have the following result:

Lemma 3.1. [9,31] Let

$\lambda^*=\displaystyle-\inf \left\{\displaystyle\int_\Omega d|\nabla\phi|^2-q\phi^2|\; \,\,\phi\in H^1(\Omega),\;\displaystyle\int_\Omega\phi^2=1\right\},$

(6)

then $\mathbf{s}(d\Delta+q)=\lambda^*$. Moreover, $\lambda^*$ is a dominant eigenvalue of the operator $d\Delta +q$ and the corresponding eigenfunction is strictly positive. In particular, if $q=0$ then $\mathbf{s}(d\Delta)=0$.

As an immediate consequence of Lemma 3.1, we have the following result (see [23]):

Corollary 1. Let $T(t)=e^{t(d\Delta +q)}$ $(t\geq 0)$ be a semigroup in $L^2(\Omega)$ generated by the operator $d\Delta +q$ and let $\lambda^*=\mathbf{s}(d\Delta+q)$, then for any $\lambda>\lambda^*$, there exists a corresponding constant $C>0$ such that

$\|T(t)\|_{\mathcal{L}(L^2(\Omega))}\leq Ce^{\lambda t},\,\,\,\,t\geq 0.$

In what follows, we only prove the convergence in $L^2(\Omega)$. By regularity theory and the Sobolev embedding theorem, actually, we are able to show that the convergence is uniform. For the convenience of notation, we write

$\|m\|=\|m\|_{L^2(\Omega)}, \|m\|_\infty=\displaystyle\max\limits_{x\in\bar{\Omega}}m(x), \underline{m}=\displaystyle\min\limits_{x\in\bar{\Omega}}m(x).$

---

4. Global disease dynamics analysis

---

4.1. Global existence of the solutions

In this subsection, we prove the global existence of solutions to model (4). We first give the following Lemma.

Lemma 4.1. Consider the following system

$\left\{\begin{array}{ll} \dfrac{\partial N}{\partial t}=d\Delta N+\Lambda(x)-\mu(x) N, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial N}{\partial \mathbf{n}}=0, & x\in \partial\Omega,\, t>0,\\[2ex] N(x,0)=N_0(x)\geq0,&x\in\Omega, \end{array}\right.$

(7)

then model (7) admits a unique positive steady state $S_*(x)$, which is globally asymptotically stable in $C(\bar{\Omega},\mathbb{R})$, where $S_*$ satisfies

$\left\{\begin{array}{ll} d\Delta S_*+\Lambda(x)-\mu(x) S_*=0, & x\in \Omega,\\ \dfrac{\partial S_*}{\partial \mathbf{n}}=0, & x\in \partial\Omega. \end{array}\right.$

(8)

Proof. The proof of the existence and uniqueness of positive steady state is based upon the super-solution [9]. Now let us prove global stability. Set $\hat{N}=N-S_*$. Notice that $d\Delta S_*+\Lambda(x)-\mu(x) S_*=0$. Thus we can rewrite (7) as

$\left\{\begin{array}{ll} \dfrac{\partial\hat{N}}{\partial t}-d\Delta \hat{N}=-\mu(x)\hat{N},& x\in\Omega,t>0,\\ \dfrac{\partial \hat{N}}{\partial \mathbf{n}}=0,& x\in\partial\Omega,t>0,\\ \hat{N}(x,0)=N_0(x)-S_*,& x\in\Omega. \end{array}\right.$

Let $U(t)$ be the semigroup generated by the operator $d\Delta-\mu$. Since $-\lambda_1=\mathbf{s}(d\Delta-\mu)<0.$ Choose $0<\lambda<\lambda_1$ and fix it. It follows from [23] that there is a constant $C>0$ such that

$\|\hat{N}(\cdot,t)\|= \|U(t)\hat{N}(\cdot,0)\|\leq Ce^{-\lambda t}\|\hat{N}(\cdot,0)\|\rightarrow 0,\,\,\mathrm{as}\,\,t\rightarrow \infty.$

It follows that $N(\cdot,t)\rightarrow S_*$ as $t\rightarrow \infty$.

Next, we give the results about the existence and uniqueness of the global solutions of model (4).

Theorem 4.2. For every initial value function, model (4) has a unique positive solution $(S(\cdot,t), I(\cdot,t))$ on $[0,\infty)$.

Proof. By the maximum principle [28], the populations $S(x, t)$ and $I(x, t)$ are positive for $x\in \bar{\Omega}$ and $t\in(0,T_{\max})$, where $T_{\max}$ is the maximal existence time for solutions of model (4). It follows from Lemma 4.1 that $N(x,t)=S(x,t)+I(x,t)$ is bounded on $t\in(0,T_{\max})$. Hence, both $S(x, t)$ and $I(x, t)$ are bounded on $\bar{\Omega}\times (0,T_{\max})$. Hence, it follows from the standard theory for semilinear parabolic systems (see, [17]) that $T_{\max}=\infty$ and so model (4) admits a unique classical solution $(S(x, t), I(x, t))$ for all time.

---

4.2. Disease-free dynamics

In this subsection, we first identify the basic reproduction number and then study the stability of DFE of model (4).

It follows from Lemma 4.1 that $E_0=(S_*,0)$ is the DFE of model (4), where $S_*$ satisfies (8).We linearize model (4) around DFE and obtain the following system of perturbation equations

$\left\{\begin{array}{ll} \dfrac{\partial S}{\partial t}=d\Delta S-\mu(x) S+\left(\gamma(x)-\dfrac{\beta(x)S_*}{f(x,0)}\right)I, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial I}{\partial t}=d\Delta I+\left(\dfrac{\beta(x)S_*}{f(x,0)}-\mu(x)-\gamma(x)\right)I, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial S}{\partial \mathbf{n}}=\dfrac{\partial I}{\partial \mathbf{n}} =0, & x\in \partial\Omega,\, t>0. \end{array}\right.$

(9)

Then we get the following linear eigenvalue problem

$\left\{\begin{array}{ll} \lambda\varphi=d\Delta \varphi-\mu(x)\varphi+\left(\gamma(x)-\dfrac{\beta(x)S_*}{f(0)}\right)\psi, & x\in \Omega,\\[2ex] \lambda\psi=d\Delta \psi+\left(\dfrac{\beta(x)S_*}{f(x,0)}-\mu(x)-\gamma(x)\right)\psi, & x\in \Omega,\\[2ex] \dfrac{\partial \varphi}{\partial \mathbf{n}}=\dfrac{\partial \psi}{\partial \mathbf{n}}=0, & x\in \partial\Omega. \end{array}\right.$

(10)

Let $\lambda^*$ denote the principal eigenvalue of the second equation of model (10), which is given by the following variational characterization

$\lambda^*=-\displaystyle\inf\limits_{\omega\in H^1(\Omega)} \left\{\displaystyle\int_\Omega d|\nabla \omega|^2-\left(\dfrac{\beta(x)S_*}{f(x,0)}-\mu(x)-\gamma(x)\right)\omega^2, \,\,\displaystyle\int_\Omega \omega^2=1\right\}.$

(11)

By using the next generation approach for heterogenous populations [12,37] and spatial heterogenous populations [2,26,40], we define the basic reproduction number $\mathcal{R}_0$ for model (4) as follows:

$\mathcal{R}_0=\displaystyle\sup\limits_{\omega\in H^1(\Omega),\,\omega\neq 0} \left\{\dfrac{\displaystyle\int_\Omega \dfrac{\beta(x)S_*}{f(x,0)}\omega^2} {\displaystyle\int_\Omega d|\nabla \omega|^2+(\mu(x)+\gamma(x))\omega^2}\right\}.$

(12)

In the spatially homogeneous case, i.e., $\Lambda, \mu, \beta, \delta, \gamma$ are all positive constants and $f(x,I)=f(I)$, we can obtain the basic reproduction number

$\mathcal{R}_0=\dfrac{\Lambda \beta}{\mu f(0)(\mu+\gamma)}.$

By Lemma 2.2, 2.3 in [2] and Lemma 3.1, we have:

Theorem 4.3. The following statements are true:

(ⅰ) $\mathrm{sign}(\mathcal{R}_0-1)=\mathrm{sign}(\lambda^*)=\mathrm{sign}\left(\mathbf{s}\left(d\Delta +\dfrac{\beta S_*}{f(x,0)}-\mu-\gamma\right)\right)$;

(ⅱ) $\mathcal{R}_0$ is a strictly monotone decreasing function of $d>0$ with

$\mathcal{R}_0\rightarrow \max\limits_{x\in\bar{\Omega}}\left\{\dfrac{\beta(x) S_*}{f(x,0)(\mu(x)+\gamma(x))}\right\} \,\,\,\mathrm{as}\,\,\,d \rightarrow 0,$

and

$\mathcal{R}_0\rightarrow \dfrac{\displaystyle\int_\Omega\left(\dfrac{\beta(x) S_*}{f(x,0)}\right)dx} {\displaystyle\int_\Omega(\mu(x)+\gamma(x))dx} \,\,\,\mathrm{as}\,\,\,d \rightarrow \infty;$

(ⅲ) In a high-risk domain, $\mathcal{R}_0>1$ for all $d>0;$

(ⅳ) In a low-risk domain, then the equation $\mathcal{R}_0=1$ has a unique positive root denoted by $d^*$. Furthermore, if $0<d<d^*$ then $\mathcal{R}_0>1$, and if $d>d^*$ then $\mathcal{R}_0<1$.

The proof is similar to that in [15,2,24] and hence we omit it here. Following, we show properties of the disease-free equilibrium (DFE), including existence, uniqueness, and stability.

Theorem 4.4. For model (4), there exists a unique DFE $(S_*,0)$, where $S_*$ is a positive solution of

$\left\{\begin{array}{ll} -d\Delta S=\Lambda(x)-\mu(x) S=0, & x\in \Omega,\\ \dfrac{\partial S}{\partial \mathbf{n}}=0, & x\in \partial\Omega, \end{array}\right.$

(13)

if $\mathcal{R}_0<1$, DFE $(S_*, 0)$ is globally asymptotically stable; while $\mathcal{R}_0>1$, it is unstable.

Proof. Suppose that $\mathcal{R}_0<1$. We will use the comparison principle to show that $I(\cdot,t)\rightarrow 0$ as $t\rightarrow\infty$. By virtue of Lemma 4.1, for any small $\epsilon>0$, we can find a large $T>0$ such that

$S(x,t)\leq N(x,t)<S_*(x)+\epsilon, \,\,\,\mathrm{for\,\,all} \,\,\,x\in\bar{\Omega}\,\,\,\mathrm{and}\,\,\,t\geq T.$

Obviously, $I$ satisfies

$\left\{\begin{array}{ll} \dfrac{\partial I}{\partial t}-d\Delta I\leq \left(\dfrac{\beta(x)(S_*+\varepsilon)}{f(x,0)}-\mu(x)-\gamma(x)\right)I, & x\in \Omega,\, t>T,\\[1ex] \dfrac{\partial I}{\partial\mathbf{n}}=0, & x\in \partial\Omega,\, t>T,\\[1ex] I(x,T)\geq0,& x\in \partial\Omega. \end{array}\right.$

(14)

Let $Z(x,t)$ with $Z(x,T)=I(x,T)$ be the solution of the following linear system

$\left\{\begin{array}{ll} \dfrac{\partial Z}{\partial t} = d\Delta Z+\left(\dfrac{\beta(x)(S_*+\varepsilon)}{f(x,0)}-\mu(x)-\gamma(x)\right)Z,& x\in\Omega, t\geq T,\\[1ex] \dfrac{\partial Z}{\partial\mathbf{n}}=0,& x\in\partial\Omega, t\geq T. \end{array}\right.$

(15)

By the comparison principle, $0\leq I(x,t)\leq Z(x,t)$ for all $t>T$ and $x\in\Omega$. Let $U_1(t)$ be the semigroup in $L^2(\Omega)$ generated by the operator $d\Delta +\dfrac{\beta(S_*+\varepsilon)}{f(0)}-\mu-\gamma$. By Theorem 4.3, we have that $\mathcal{R}_0<1$ implies that $\mathbf{s}\left(d\Delta +\dfrac{\beta S_*}{f(0)}-\mu-\gamma\right)<0$. By the continuity, there is a $\varepsilon> 0$ such that $-\lambda_2:= \mathbf{s}\left(d\Delta +\dfrac{\beta(S_*+\varepsilon)}{f(0)}-\mu-\gamma\right)<0.$ Choose $0<\lambda<\lambda_2$ and fix it. It follows from Corollary 1 that there is a constant $C>0$ such that

$\|I(\cdot,t)\|\leq \|Z(\cdot,t)\|=\|U_2(t)Z(\cdot,0)\| \leq Ce^{-\lambda t}\|I(\cdot,0)\|\rightarrow 0,\,\,\mathrm{as}\,\,t\rightarrow \infty,$

(16)

which implies that $I(x,t)\rightarrow 0$ as $t\rightarrow \infty$ in $\|\cdot\|$ and

$\left\|\left(\gamma(x)-\dfrac{\beta(x)S}{f(I)}\right)I\right\|\leq Ce^{-\lambda t},\,\,t>0,$

for some positive constants $C$. We now show that $S(\cdot,t)$ tends to $S_*(x)$ as $t\rightarrow \infty$. Set $\hat{S}=S-S_*$, then $\hat{S}$ satisfies

$\left\{\begin{array}{ll} \dfrac{\partial\hat{S}}{\partial t}-d\Delta \hat{S}=-\mu\hat{S}+\left(\gamma(x)-\dfrac{\beta(x)(\hat{S}+S_*)}{f(I)}\right)I,& x\in\Omega,\\ \dfrac{\partial \hat{S}}{\partial \mathbf{n}}=0,& x\in\partial\Omega,\\[2ex] \hat{S}(x,0)=S_0(x)-S_*,& x\in\Omega. \end{array}\right.$

(17)

Applying the formula of variation of constants [23] to the first equation of (17) and the above results, we obtain

$\begin{array}{ll} \|\hat{S}(\cdot,t)\| &\leq \|U(t)\hat{S}(\cdot,0)\|+\displaystyle\int_0^t \left\|U(t-s)\left(\gamma-\dfrac{\beta\hat{S}(\cdot,t)} {f(I(\cdot,t))}\right)I(\cdot,t)\right\|ds\\[1ex] &\leq Ce^{-\lambda t}\|\hat{S}(\cdot,0)\|+Cte^{-\lambda t}\\[1ex] &\rightarrow 0,\,\,\mathrm{as}\,\,t\rightarrow \infty. \end{array}$

Hence $S(\cdot,t)\rightarrow S_*$ as $t\rightarrow\infty$. With the use of the regularity theorem, we are able to show that $(S(x,t),I(x,t))$ tend to uniformly $(S_*,0)$ on $\Omega$ as $t\rightarrow\infty$.

Next, suppose that $\mathcal{R}_0>1$. It follows from Theorem 4.3 that there is a $\lambda_0 > 0$ and $\psi_0\neq0$ such that

$d\Delta \psi_0+\left(\dfrac{\beta(x)S_*}{f(0)}-\mu(x)-\gamma(x)\right)\psi_0=\lambda_0\psi_0.$

Rewrite the first equation in (10) with $\lambda=\lambda_0$ as

$d\Delta \varphi-(\mu(x)+\lambda_0)\varphi=\left(\dfrac{\beta(x)S_*}{f(0)}-\mu(x)-\gamma(x)\right)\psi_0.$

(18)

It follows that (18) has a unique solution $\varphi_0$ satisfying $\dfrac{\partial\varphi_0}{\partial \mathbf{n}}= 0$ for $x\in\partial\Omega$. That is, $\lambda_0> 0$ is an eigenvalue. Therefore the DFE is linearly unstable. Instability of the DFE follows from its linear instability (see [17]).

---

4.3. Endemic dynamics

In this subsection, we study the existence and global stability of EE for model (4), namely to prove Theorem 4.10.

Let $N(x,t)=S(x,t)+I(x,t)$. Then $N(x,t)$ and $I(x,t)$ satisfy the following system

$\left\{\begin{array}{ll} \dfrac{\partial N}{\partial t}=d\Delta N+\Lambda(x)-\mu(x) N, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial I}{\partial t}=d\Delta I+\left(\dfrac{\beta(x)N}{f(x,I)}-\mu(x)-\gamma(x)-\dfrac{\beta(x)}{f(x,I)}I \right) I, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial N}{\partial \mathbf{n}}=\dfrac{\partial I}{\partial \mathbf{n}}=0 & x\in \partial\Omega,\, t>0,\\[2ex] N(x,0)=N_0(x)=S_0(x)+I_0(x)\geq0, I(x,0)=I_0(x)\geq0,&x\in\Omega. \end{array}\right.$

(19)

If $(N(x,t), I(x,t))$ is a solution of the model (19) with $0\leq I_0(\cdot)\leq N(\cdot,0)$, then $0<I(x,t)\leq I(x,t)+S(x,t)=N(x,t)$ for all $t>0$ and $x\in\Omega$. Now, proving that the existence and global stability of EE for model (19) will immediately give the existence and global stability of EE for model (4). And we first consider the following lemmas.

Lemma 4.5. Assume that $\mathcal{R}_0>1$. Then there is a small $\varepsilon^*>0$ such that for each $\varepsilon$ with $|\varepsilon|<\varepsilon^*$, the equation

$\left\{\begin{array}{ll} G(I):=d\Delta I+g(x,I)I=0, & x\in \Omega,\\[1ex] \dfrac{\partial I}{\partial \mathbf{n}}=0, & x\in \partial\Omega. \end{array}\right.$

(20)

has a unique positive solution $I_*^\varepsilon$, where

$g(x,I)=\dfrac{\beta(x)(S_*+\varepsilon)}{f(x,I)}-\mu(x)-\gamma(x)-\dfrac{\beta(x) }{f(x,I)}I.$

Proof. By Theorem 4.3 (ⅰ), $\mathcal{R}_0>1$ implies that $\lambda^*=\mathbf{s}\left(d\Delta+\dfrac{\beta S_*}{f(x,0)}-\mu-\gamma\right)>0$. By the continuity, there is an $\varepsilon$ with $|\varepsilon|< \varepsilon^*$ such that $\tilde{\lambda}=\mathbf{s}\left(d\Delta+\dfrac{\beta (S_*+\varepsilon)}{f(x,0)}-\right. \left.\mu-\gamma\right)>0.$ We first claim that $\underline{I}=\rho \psi^*$ and $\bar{I}=S_*$ are sub-and super-solutions of model (20), respectively, if $\rho$ is chosen to be positive and sufficiently small, where $\psi^*>0$ be an eigenfunction to $\tilde{\lambda}$, that is $\psi^*$ satisfies $d\Delta\psi^*+\left(\dfrac{\beta(x)(S_*+\varepsilon)}{f(x,0)}-\mu(x)\right.$ $\left.-\gamma(x) \right) \psi^*=\tilde{\lambda}\psi^*$ and $\dfrac{\partial \psi^*}{\partial \mathbf{n}}=0$ on $\partial\Omega$. Upon a direct substitution we obtain

$\begin{align*} G(\underline{I})&=d\Delta (\rho \psi^*)+\rho \psi^*g(x,\rho \psi^*)\\[2ex] &=\rho\left(d\Delta \psi^*+ \psi^*\left(g(x,0)+\dfrac{\partial g}{\partial I}(x,0)\rho \psi^*+O((\rho\psi^*)^{2})\right)\right)\\[2ex] \end{align*}$

$\begin{array}{ll} &=\rho\left(d\Delta\psi^*+ \left(\dfrac{\beta(x)(S_*+\varepsilon)}{f(0)}-\mu-\gamma\right)\psi^*+\dfrac{\partial g}{\partial I}(x,0)\rho \psi^*{^2}+O(\rho^2\psi^*{^3})\right)\\[2ex] &=\rho\left(\tilde{\lambda}-\dfrac{\rho \psi^*{^2}\beta(x)(f(x,0)+(S_*+\varepsilon)f'(x,0))}{f^2(0)}+O(\rho^2\psi^*{^3})\right). \end{array}$

$\tilde{\lambda}>0$ immediately implies that $G(\underline{I})>0$ if $\rho$ is small enough. Also, $\dfrac{\partial \underline{I}}{\partial \mathbf{n}}=0$ on $\partial\Omega$. Therefore, $\underline{I}=\rho \psi^*$ is a sub-solution of (20). Now, for $\varepsilon>0$ with $|\varepsilon|< \varepsilon^*$, since

$\begin{array}{ll} G(\bar{I})&=d\Delta S_*+S_*g(x,S_*)=d\Delta S_*-\mu(x)S_*+S_*\left(\dfrac{\varepsilon\beta(x)}{f(I)}-\gamma(x)\right)\\[2ex] &=-\Lambda(x)+S_*\left(\dfrac{\varepsilon\beta(x)}{f(I)}-\gamma(x)\right)<0, \end{array}$

and $\dfrac{\partial \bar{I}}{\partial \mathbf{n}}=0$ on $\partial\Omega$, it follows that $\bar{I}$ is a super-solution of model (20). It is obvious that $\underline{I}\leq \bar{I}$ on $\Omega$ if $\rho$ is sufficiently small. We hence infer that there must be a $I_\varepsilon(x)\in [\underline{I},\bar{I}]$ satisfying model (20). That is, there exist some $I_\varepsilon(x)\in C^2(\bar{\Omega})$ satisfying model (20) with $0<I_\varepsilon\leq S_*$ for $x\in \Omega$. We argue by contraction to show that $I_\varepsilon\neq S_*$ on $\Omega$. Suppose that $I_\varepsilon=S_*$ on $\Omega$. As $I$ achieves its maximum on $\Omega$ at $x$, it must be that $\Delta I(x)\leq 0$. But for fixed $\varepsilon$ then $G(I(x))<0$, a contradiction. We conclude that $0<I_\varepsilon< S_*$ for $x\in\Omega$. This prove the existence of positive solution $(S^*(x),I^*(x))$ of model (4).

In order to prove the uniqueness, we argue by contradiction. Suppose that model (20) has two positive solutions $I_1(x)$ and $I_2(x)$ with $I_1(x)\not\equiv I_2(x)$ on $\Omega$. It follows from above that we may choose $\rho$ small enough so that $\underline{I}< I_1(x),I_2(x)<S_*$ on $\bar{\Omega}$. Let $I_m$ and $I^m$ denote the minimal and maximal solutions of model (20), respectively, within the set $[\underline{I}, \bar{I}]$. Since $I_1(x)\not\equiv I_2(x)$, we have $I_m\leq I^m$ and $I_m(x)\not\equiv I^m(x)$. The maximum principle now implies that $I_m<I^m$ on $\bar{\Omega}$. We substitute $I_m$ and $I^m$ individually into model (20) to get

$\left\{\begin{array}{ll} d\Delta I_m+I_m g(x,I_m)=0, & x\in \Omega,\\[2ex] d\Delta I^m+I^m g(x,I^m)=0 & x\in \Omega,\\[2ex] \dfrac{\partial I_m}{\partial \mathbf{n}}=\dfrac{\partial I^m}{\partial \mathbf{n}} =0,& x\in \partial\Omega. \end{array}\right.$

(21)

Multiplying the first equation of (21) by $I^m$ and the second equation of (21) by $I_m$, subtracting the resulting equations, and then integrating by parts over $\Omega$ gives

$\displaystyle\int_\Omega I_mI^mF(I_m,I^m)dx=0,$

(22)

where

$\begin{array}{ll}F(I_m,I^m)&=\dfrac{\beta(x)(S_*+\varepsilon-I_m)}{f(I_m)} -\dfrac{\beta(x)(S_*+\varepsilon-I^m)}{f(I^m)}\\[2ex] &=\dfrac{\beta(x)}{f(I_m)f(I^m)}\Bigl((S_*+\varepsilon-I_m) (f(I^m)-f(I_m))+f(I_m)(I^m-I_m)\Bigr)\\[2ex] &=\dfrac{\beta(x)\Bigl(f(I^m)-f(I_m)\Bigr)}{f(I_m)f(I^m)}\left(S_*+\varepsilon-I_m+\dfrac{f(I_m)(I^m-I_m)}{f(I^m) -f(I_m)}\right). \end{array}$

Hence, we can choose sufficiently small $|\varepsilon|$ such that $F(I_m,I^m)>0$ on $\Omega$. But this result contradicts (22) because $0<I_m<I^m\leq S_*$. We conclude that model (20) has a unique positive solution $I_\varepsilon^*(x)$ on $\Omega$.

From the comparison principle we infer that the following Lemma.

Lemma 4.6. Let $(N(x,t),I(x,t))$ be a positive solution of model (19) such that $S_*-\varepsilon\leq N(x,t)\leq S_*+\varepsilon$ for all $t\geq 0$. Let $(N_\varepsilon(\cdot,t),I_\varepsilon(\cdot,t))$ be a nonnegative solution of the following system

$\left\{\begin{array}{ll} \dfrac{\partial N}{\partial t}=d\Delta N+\Lambda(x)-\mu(x) N, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial I}{\partial t}=d\Delta I+\left(\dfrac{1}{f(I)}\beta(x)((S_*+\varepsilon)-I)-\mu(x)-\gamma(x) \right) I, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial N}{\partial \mathbf{n}}=\dfrac{\partial I}{\partial \mathbf{n}}=0 & x\in \partial\Omega,\, t>0, \end{array}\right.$

(23)

If $\varepsilon<0$ and $(N_\varepsilon(\cdot,0),I_\varepsilon(\cdot,0))\leq (N(\cdot,0), I(\cdot,0))$, then $(N_\varepsilon(\cdot,t),I_\varepsilon(\cdot,t))\leq (N(\cdot,t), I(\cdot,t));$ and if $\varepsilon>0$ and $(N_\varepsilon(\cdot,0),I_\varepsilon(\cdot,0))\geq (N(\cdot,0), I(\cdot,0))$, then $(N_\varepsilon(\cdot,t),I_\varepsilon(\cdot,t)) \geq (N(\cdot,t),I(\cdot,t)).$

Lemma 4.7. ([18]) Consider the equation

$\left\{\begin{array}{ll} {\dfrac{\partial u}{\partial t}}-d\Delta u=c(x)u+h_1(x,t),& x\in \Omega,\, t>0,\\[1ex] {\dfrac{\partial u}{\partial\mathbf{n}}=0}, & x\in \partial\Omega,\, t>0. \end{array}\right.$

(24)

where $c(x)\in C(\bar{\Omega})$, $h(x,t) \in C([0, t_0],C(\bar{\Omega}))$ for some $t_0>0$. Suppose that $\mathbf{s}(d\Delta +c)=0$ and let $\phi^*$ be the strictly positive eigenfunction corresponding to the zero eigenvalue of the operator $d\Delta +c$. If $h(x,t) \geq0$ for $t\in[0, t_0]$ and $x\in\Omega$ and $u(x, t)$ is a solution of (24) with $u(\cdot,t)=\phi^*$, then

$u(\cdot, t) \geq u(\cdot,0), \,\,t\in[0, t_0].$

Recall that $\mathcal{R}_0>1$ implies that $\mathbf{s}\left(d\Delta+\dfrac{\beta S_*}{f(0)}-\mu-\gamma\right)>0$. Moreover, we have $\mathbf{s}(d\Delta-\mu)<0$. Hence, there are two positive constant $\alpha_1$ and $\alpha_2$ such that

$\mathbf{s}(d\Delta+\alpha_1-\mu)=0,\,\, \mathbf{s}\left(d\Delta+\dfrac{\beta S_*}{f(0)}-\mu-\gamma-\alpha_2\right)=0.$

(25)

We let $\phi_1^*$ and $\phi_2^*$ be strictly positive eigenfunctions corresponding to the zero eigenvalue of the operator $d\Delta+\alpha_1-\mu$ and $d\Delta+\dfrac{\beta S_*}{f(0)}-\mu-\gamma-\alpha_2$, respectively. That is,

$d\Delta \phi_1^*+(\alpha_1-\mu)\phi_1^*=0,\,d\Delta \phi_2^* + \left(\dfrac{\beta S_*}{f(0)}-\mu-\gamma-\alpha_2\right)\phi_2^*=0,$

and $\dfrac{\partial \phi_1^*}{\partial\mathbf{n}}=\dfrac{\partial \phi_2^*}{\partial\mathbf{n}}=0$ on $\partial \Omega$.

Lemma 4.8. For each fixed $\varepsilon<0$ with $|\varepsilon|<\varepsilon^*$, there is a $\delta^*>0$ such that for sufficient small $\delta\in(0,\delta^*)$, the solution $(N_\varepsilon^\delta(t, x), I_\varepsilon^\delta(t, x))$ of model (23) with the initial condition

$N_\varepsilon^\delta(\cdot,0)=\delta\phi_1^*,\,\, I_\varepsilon^\delta(\cdot,0)=\delta\phi_2^*$

is monotone increasing with respect to $t$.

Proof. Let $\alpha_i, i = 1, 2$, be the positive numbers defined in (25). Then $\mathbf{s}\left(d\Delta+\dfrac{\beta S_*}{f(0)}\right. \left.-\mu-\gamma\right)> 0$ and $\mathbf{s}\left(d\Delta+\dfrac{\beta S_*}{f(0)}-\mu-\gamma-\alpha_2\right)=0$ imply that $\alpha_2+\dfrac{\beta(x)\varepsilon}{f(0)}> 0$. Hence there are positive constants $\delta^*$ and $\eta$ such that

$\begin{array}{ll} \Lambda(x)-\alpha_1\delta^*\phi_1^*(x)>\eta,\\[2ex] \alpha_2+\dfrac{\beta(x)\varepsilon}{f(0)}- \dfrac{(\beta(x)(S_*+\varepsilon))(\delta^*\phi_2^*(x)f'(0) +O((\delta^*\phi_2^*)^2)}{f(0)f(\delta^*\phi_2^*(x))} -\dfrac{\beta(x)\delta^*\phi_2^*(x)}{f(\delta^*\phi_2^*(x))}>\eta \end{array}$

(26)

for $x\in\Omega$. Now let $\delta\in[0,\delta^*]$ and $(N_\varepsilon^\delta(x,t), I_\varepsilon^\delta(x,t))$ be defined as above. Since $\phi_i^*\in C_0^2(\bar{\Omega})\, (i=1,2),$ then,

$(N_\varepsilon^\delta(x,t), I_\varepsilon^\delta(x,t))\rightarrow(\delta\phi_1^*,\delta\phi_2^*),\,\, \mathrm{as}\,\,\,t\rightarrow0$

uniformly for $x\in\Omega$. Hence from the continuity and the inequality (26), it follows that there is a $t_1>0$ such that

$\begin{array}{ll} &\Lambda(x)-\alpha_1N_\varepsilon^\delta(x,t)>\eta_1, (x,t)\in[0,t_1]\times \Omega,\\[1ex] &\alpha_2+\dfrac{\beta(x)\varepsilon}{f(0)}-\dfrac{(\beta(x)(S_*+\varepsilon)) (f(I_\varepsilon^\delta(x,t))-f(0))} {f(0)f(I_\varepsilon^\delta(x,t))} -\dfrac{\beta(x)I_\varepsilon^\delta(x,t)}{f(I_\varepsilon^\delta(x,t))}>\eta_1,\\&(x,t)\in[0,t_1]\times \Omega \end{array}$

(27)

for some positive constants $\eta_1$. Considering (23) again, we can check that $(N_\varepsilon^\delta(x,t), I_\varepsilon^\delta(x,t))$ satisfies the system

$\left\{\begin{array}{ll} {\dfrac{\partial N}{\partial t}}-d\Delta N=(\alpha_1-\mu(x))N+h_1(x,t),& x\in \Omega,\, t>0,\\[1ex] {\dfrac{\partial I}{\partial t}}-d\Delta I=\left(\dfrac{\beta(x)S_*}{f(0)}-\mu(x)-\gamma(x)-\alpha_2 \right) I+h_2(x,t), & x\in \Omega,\, t>0,\\ {\dfrac{\partial N}{\partial \mathbf{n}}=\dfrac{\partial I}{\partial \mathbf{n}}}=0, & x\in \partial\Omega,\, t>0. \end{array}\right.$

(28)

where

$h_1(x,t)=\Lambda(x)-\alpha_1N,\,\,$

$h_2(x,t)=I\left(\alpha_2+\dfrac{\beta(x)\varepsilon}{f(0)} -\dfrac{(\beta(x)(S_*+\varepsilon)) (f(I)-f(0))} {f(0)f(I)} -\dfrac{I}{f(I)}\right).$

It follows from (27) that $h_1(x,t)$ and $h_2(x,t)$ are positive for $(x,t)\in\Omega\times [0,t_1]$. And Lemma 4.7 implies that

$(N_\varepsilon^\delta(x,t),I_\varepsilon^\delta(x,t))>(N_\varepsilon^\delta(0, \cdot),I_\varepsilon^\delta(0, \cdot)),\,\,t\in[0,t_1].$

(29)

It is clear that model (23) is a monotone system. Suppose that the semiflow $\Psi_t$ generated by model (23) is defined by

$\Psi_t(\varphi)=(N_\varepsilon(\cdot,t, \varphi_1),I_\varepsilon( \cdot,t,\varphi_2))$

with $(N_\varepsilon(\cdot,0, \varphi_1),I_\varepsilon(\cdot,0, \varphi_2))=\varphi=(N_0(\cdot),I_0(\cdot))$. Set $\varphi^\delta=(N_\varepsilon^\delta(\cdot,0, \varphi_1^\delta),I_\varepsilon^\delta(\cdot,0,$ $\varphi_2^\delta))=(N_\varepsilon^\delta(\cdot,0),I_\varepsilon^\delta(\cdot,0))$, then

$(N_\varepsilon^\delta(\cdot,t, \varphi_1^\delta),I_\varepsilon^\delta(\cdot,t, \varphi_2^\delta))=\Psi_t(\varphi^\delta).$

Fix $t_1>0$ and rewrite $t=k t_1+s$ with $k\in\mathbb{N}, s\in[0, t_1)$. From (29), we can obtain $\Psi_s(\varphi^\delta)>\varphi^\delta$. Hence the monotonicity of the semiflow yields that

$\Psi_{t_1+s}(\varphi^\delta)=\Psi_s(\Psi_{t_1}(\varphi^\delta))\geq\Psi_s(\varphi^\delta),$

then

$\begin{array}{ll} \Psi_t(\varphi^\delta)=\Psi_{s+kt_1}(\varphi^\delta)>\Psi_{s+(k-1)t_1}(\varphi^\delta) \geq\cdot\cdot\cdot\geq \Psi_s(\varphi^\delta). \end{array}$

So $(N_\varepsilon(\cdot,t),I_\varepsilon(\cdot,t))$ is monotone increasing.

Lemma 4.9. Let $\varepsilon>0$ be fixed. For ang $\sigma>1$ with $\varepsilon <\sigma\|\Lambda\|_\infty$, let $(N_\varepsilon^\sigma(\cdot,t), I_\varepsilon^\sigma(\cdot,$ $t))$ be a solution of model (23) with

$(N_\varepsilon^\sigma(\cdot,0), I_\varepsilon^\sigma(\cdot,0))\equiv \left(\dfrac{\sigma\|\Lambda\|_\infty}{\underline{\mu}}, \dfrac{\sigma\|\Lambda\|_\infty}{\underline{\mu}}\right),$

then $(N_\varepsilon^\sigma(\cdot,t), I_\varepsilon^\sigma(\cdot,t))$ is decreasing with respect to $t$.

Proof. Then maximum principle enables us to infer that

$(N_\varepsilon^\sigma(\cdot,t), I_\varepsilon^\sigma(\cdot,t))\leq\left(\dfrac{\sigma\|\Lambda\|_\infty}{\underline{\mu}}, \dfrac{\sigma\|\Lambda\|_\infty}{\underline{\mu}}\right)$

for $t>0$ and $x\in\Omega$. The monotone decreasing property of $(N_\varepsilon^\sigma(\cdot,t), I_\varepsilon^\sigma(\cdot,t))$ therefore follows the same argument used in the proof of Lemma 4.8.

Next, we show the existence, uniqueness and stability of the endemic equilibrium (EE).

Theorem 4.10. If $\mathcal{R}_0>1$, then model (4) has a unique EE $(S^*(x),I^*(x))$. Moreover, all positive solutions $(S(x,t),I(x,t))$ of model (4) tend to $(S^*(x),I^*(x))$ uniformly as $t\rightarrow \infty$ for $x\in\bar{\Omega}$. That is, the EE is globally asymptotically stable.

Proof. Let $(N(x,t), I(x,t))$ be a solution of model (19) with the initial conditions satisfying $0<I(\cdot,0)\leq N(\cdot,0)$. Then $(N(x,t), I(x,t))$ is strictly positive for $t>0$. Since $N(\cdot,t) \rightarrow S_*$ as $t\rightarrow\infty$, for any $\varepsilon<0$ with $|\varepsilon| <\varepsilon^*$, there is a $t_*>0$ such that $N(\cdot,t)\geq S_*+\varepsilon$ for all $t\geq t_*$. Hence, for sufficiently small $\delta\in(0,\delta^*)$, there is a $\delta^*>0$ such that $(N(t_*, \cdot), I(t_*, \cdot))\geq (\delta\phi_1^*,\delta\phi_2^*)$. Let $(N_\varepsilon^\delta(\cdot,t), I_\varepsilon^\delta(\cdot,t))$ be a monotone increasing solution of model (23). Lemma 4.6 yields that

$(N_\varepsilon^\delta(\cdot,t), I_\varepsilon^\delta(\cdot,t))\leq(N_\varepsilon^\delta(\cdot,t+t_*), I_\varepsilon^\delta(\cdot,t+t_*))\leq(N(\cdot,t+t_*), I(\cdot,t+t_*)),\,\,t\geq0.$

Hence the monotonicity of the $((N_\varepsilon^\delta(\cdot,t), I_\varepsilon^\delta(\cdot,t))$ and the uniqueness of positive equilibrium $(S_*, I_*^\varepsilon)$ of model (23) imply that

$I_*^\varepsilon\leq \displaystyle\liminf I(\cdot,t).$

(30)

Next we pick $\sigma> 1$ and sufficiently large $t^*$ such that

$(N(\cdot,t^*), I(\cdot,t^*))\leq \left(\dfrac{\sigma\|\Lambda\|_\infty}{\underline{\mu}}, \dfrac{\sigma\|\Lambda\|_\infty}{\underline{\mu}}\right),$

then

$(N(\cdot,t+t^*), I(\cdot,t+t^*))\leq(N_{|\varepsilon|}^\sigma(\cdot,t+t^*), I_{|\varepsilon|}^\sigma(\cdot,t+t^*))\leq(N_{|\varepsilon|}^\sigma(\cdot,t), I_{|\varepsilon|}^\sigma(\cdot,t)),\,\,t\geq0,$

where $(N_{|\varepsilon|}^\sigma(\cdot,t), I_{|\varepsilon|}^\sigma(\cdot,t))$ is a monotone decreasing solution of model (23) with $\varepsilon=|\varepsilon|$. It follows that

$\displaystyle\limsup I(\cdot,t)\leq I_*^{|\varepsilon|}.$

(31)

It is obvious that

$I_*^{\varepsilon}\rightarrow I^*, I_*^{|\varepsilon|}\rightarrow I^*,\,\,\mathrm{as}\,\,\,\varepsilon\rightarrow0.$

(32)

It follows from (30), (31) and (32) that $I(\cdot,t)\rightarrow I^*$, as $t\rightarrow\infty$. Hence, we immediately deduce that

$(S(\cdot,t), I(\cdot,t))=(N(\cdot,t)-I(\cdot,t), I(\cdot,t))\rightarrow \left(S_*-I^*,I^*\right),\,\,\mathrm{as}\,\,\,t\rightarrow\infty,$

which is completed the proof.

---

5. Numerical example

For the sake of learning the threshold dynamics of model (4) further, in this section, as an example, we adopt $f(x,I)=1+\alpha(x) I^2$ [41], and take the parameters as follows:

$\Lambda=1,\mu= 0.2,\alpha=4,\gamma= 0.15,\beta(x)=\beta_0(1+c\cos(\pi x)),$

(33)

where $0\leq c\leq 1$ is the magnitude of spatially heterogeneous transmission rate. The spatially homogeneous case occurs at $c=0$ and the higher $c$ means the more heterogeneity of spatial transmission rate. In this case, $f(x,0)=1$ and $S_*=\Lambda/\mu$. Thus, we can obtain the basic reproduction number $\mathcal{R}_0$ as

$\mathcal{R}_0=\displaystyle\sup\limits_{\omega\in H^1(\Omega),\,\omega\neq 0} \left\{\dfrac{\displaystyle\int_\Omega {\Lambda\beta(x)}/{\mu}\omega^2} {\displaystyle\int_\Omega d|\nabla \omega|^2+(\mu+\gamma)\omega^2}\right\}.$

(34)

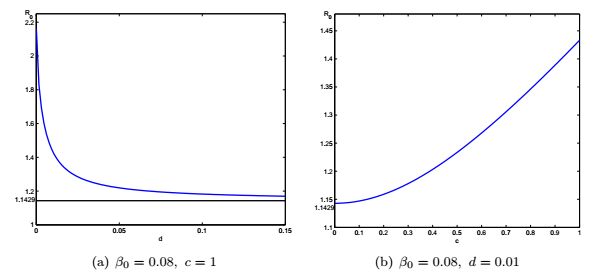
In the low-risk domain, Fig. 1(a) indicates that $\mathcal{R}_0$ is a decreasing function of $d$ and undergoes the transition from $\mathcal{R}_0>1$ to $\mathcal{R}_0<1$ as $d$ increases, and equals $1$ at $d=d^*\approx1.77\times 10^{-2}$. It would be noted that as $d \rightarrow\infty$, $\mathcal{R}_0\rightarrow0.8571$, which equals that in the case of spatially homogeneous, i.e., $c=0$ (the black line). Hence, with spatial heterogeneity, the larger the diffusion coefficient $d$ of individuals, the smaller the basic reproduction number $\mathcal{R}_0$. Hence, as the infected individuals move very fast, the disease tends to be extinct when $d>d^*$ (cf., Theorem 4.3 (ⅳ), ). Fig. 1(b) shows that $\mathcal{R}_0$ is an increasing function of $c$ and equals $1$ at $c=c^*\approx 0.7677$. Hence, the larger the magnitude of spatially heterogeneous transmission rate, the larger the basic reproduction number $\mathcal{R}_0$. Hence, the spatial heterogeneity can enhance the spread of disease and lead to the endemic when $c>c^*$.

In the high-risk domain, Fig. 2(a) indicates that $\mathcal{R}_0$ is a decreasing function of $d$ and greater than 1 identically as $d$ increases. It would be noted that as $d \rightarrow\infty$, $\mathcal{R}_0\rightarrow1.1429$, which equals that in the case of spatially homogeneous, i.e., $c=0$. Fig. 2(b) shows that $\mathcal{R}_0$ is an increasing function of $c$ and greater than 1 identically as $c$ increases. In these cases, no matter diffusion or heterogeneity has no influence on control of the disease. This high-risk domain is an endemic region (cf., Theorem 4.3 (ⅲ)).

---

6. Conclusion and discussions

In this paper, we investigate the global stability of the steady states of an SIS epidemiological model with a general infection force under intervention strategies in a spatially heterogeneous environment. We introduce the basic reproduction number $\mathcal{R}_0$, which exhibit the effects of spatiotemporal factors on the extinction and persistence of the disease.

In a nutshell, we summarize our main findings as well as their related biological implications. Theorem 4.4 provides us with a full picture of disease-free dynamics of model (4). If the basic reproduction number $\mathcal{R}_0<1$, model (4) has a unique globally asymptotically stable DFE, that is, the disease goes extinct. And Theorem 4.10 shows that model (4) can have an outbreak of disease. If $\mathcal{R}_0>1$, model (4) has at least one EE, which is globally asymptotically stable EE, that is, the disease will break out in the domain. Furthermore, we give the asymptotic behavior of $\mathcal{R}_0$ with respect to the diffusion coefficient $d$ (cf., Theorem 4.3).

Our results are different from the results in [39,10,11] with homogenous environment (i.e., $d=0$ in model (4)), as a consequence, our results suggest that the combination of the diffusion and the spatial heterogeneity tend to enhance the outbreak of the infectious for the SIS model (4), these may be the useful supplements of the disease dynamics of epidemic models. Simply say, our results may provide some potential applications in disease control. In fact, Theorems 4.4 and 4.10 suggest that, to effectively control the spread of the epidemic disease, it seems very necessary to create a low-risk habitat for the population.

It's worthy to point out that, in contrast with [25] and [20], in this paper, the mathematical analysis method of the global stability of the EE is the super-sub solution method. While in [25] and [20], they studied the global stability of the EE in some special cases by using the Lyapunov functional method.

In addition, it should be indicated that, in this paper, due to the difficulties caused by the mathematical analysis, we only focus on the global stability of model (4) in a special case, that is, the diffusion coefficients of $S$ and $I$ are equal to $d$. If their diffusion coefficients are not identical, then model (4) can be rewritten as:

$\left\{\begin{array}{ll} \dfrac{\partial S}{\partial t}=d_S\Delta S+\Lambda(x)-\dfrac{\beta(x)I}{f(x,I)}S-\mu(x) S+\gamma(x) I, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial I}{\partial t}=d_I\Delta I+\dfrac{\beta(x)I}{f(x,I)}S -\mu(x) I-\gamma(x) I, & x\in \Omega,\, t>0,\\[2ex] \dfrac{\partial S}{\partial \mathbf{n}}=\dfrac{\partial I}{\partial \mathbf{n}}=0 & x\in \partial\Omega,\, t>0,\\[2ex] S(x,0)=S_0(x)\geq0, I(x,0)=I_0(x)\geq0,&x\in\Omega. \end{array}\right.$

(35)

For model (35), it is interesting to study whether the reproduction number ${\mathcal{R}_0}$ for model (35) can be used to govern the disease dynamics or not. More precisely, if ${\mathcal{R}_0}<1$, is the DFE of model (35) globally stable? If ${\mathcal{R}_0}>1$, does there exist an EE of model (35), and is the EE globally stable? These are desirable in future studies.

---