A calibration of E-field probe based on tissue-equivalent liquid waveguide and evaluation of uncertainty

1.   Introduction

SAR testing is a measure, applied to the wireless communication devices, to quantify the exposure to radiofrequency (RF) fields ^[1,2,3], and the peak spatial-average SAR is commonly used for safety compliance of the RF exposure. The core component of the current SAR measurement system is the Dosimetric E-field Probe that allows to be read when immersed in the tissue-equivalent liquid. In order to confirm its reliability, the E-field probe needs to be calibrated regularly, and the calibration is usually required to be performed with the E-field probe as a whole (such complexity is because of its encapsulation). IEC 62209-1 has introduced the easier way to calibrate the probe, but there is no detail given. The method in this paper managed to simplify the calibration process while maintaining precision.

More specifically, for the liquid waveguide with a known E-filed, there will be a change in its E-field distribution if the dosimetric E-field probe inserts into the waveguide. By analyzing the difference between these distributions, the conversion factor can be gained effectively.

2.   Theory fundamentals for the calibration

An E-field probe generally consists of three orthogonally arranged dipoles directly loaded with a detector diode and connected with resistive lines to the readout electronics. Probe robustness and protection of the components are achieved by mounting the sensors on a core and encapsulating the entire probe.

The total electrical field can be evaluated by the root sum square (RSS) of the three E-field components. In the square-law region of the diode response, the sensor output voltage is proportional to the mean square of the corresponding field component. Also, linearization is required within the dynamic region, as the output voltage will be compressed beyond this square-law region. Manufacturing tolerances between the sensors and diodes may produce different sensitivities for each sensor ^[3], therefore, for the purpose of having accurate measurement data, it is necessary to have the sensitivities evaluation during calibration.

The total field shall be evaluated according to the Eq. (1).

Where f_i(V_i) is the linearization function of the rectified sensor signal V_i, η_i is the absolute sensitivities [μV/(v/m)²] of the dipole sensors in free space, ϒ_iis the ratios of the sensitivities of the probe sensors in media to their sensitivities in free space.

The separation of the E-field probe sensitivity into two factors (ηi and ϒi) allows the probe to be calibrated in free-space and tissue-equivalent liquid, respectively. That is, the frequency response and linearity can be estimated in free space, while it is able to make the assessment of conversion factor (ConvF), isotropy and boundary compensation in the tissue-equivalent liquid. In this way, the complexity of calibration can be considerably reduced.

3.   Calibration platform description

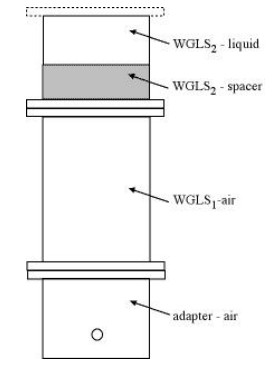
According to the IEC 62209-1, the liquid waveguide was used as the calibration platform in this paper (see table 1). The liquid waveguide is a self-contained system in which the cross-sectional field distributions are not dependent upon reflections.

A dielectric spacer should be of low-loss material (δ < 0.02) with low water absorption characteristics (<0.1%). The dielectric spacer is placed at a distance > λ from the feeding coupler in order to provide a good impedance match (>10 dB return loss) (see Figure 1). The dimensions of the spacer block should be adjusted to the dimensions of the actual waveguide used and the edges sealed after placing it in the final location (e.g. with silicon). The medium depth must be three times larger than skin depths in order to have negligible reflections at the upper surface of the liquid.

For accurate power assessments (i.e. high-end power meter and sensors), the most critical parameter in the calibration procedure is the assessment of the net RF power dissipated into the waveguide. This implies the precise measurement of the incident power (P_f), adaptor loss (trans_loss) and return loss at the waveguide input port (γ). The net power inside the lossy liquid can then be calculated as the Eq. (2):

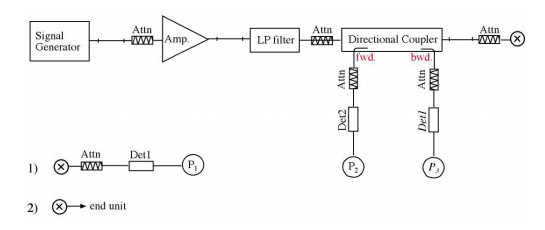
Figure 2 shows the recommended setup. The P1 and attenuator placed in front of the P1 sensor head measure the forward power at the location of the system check dipole connector. The signal generator is adjusted for the desired forward power at the dipole connector and the power meter P2 is read at that level. After connecting the cable to the dipole, the signal generator is readjusted for the same reading at power meter P2. If the signal generator does not allow a setting in 0.01 dB steps, the remaining dierence at P2 must be noted and considered in the normalization of the system check results. Power meter P3 is optional. If available, it will provide a constant monitoring of the backward power.

4.   Evaluation of conversion factor and boundary compensation

The total power absorbed by the lossy liquid can be accurately determined by measurement of the forward and reflected powers. Because of the low cutoff frequency in the lossy media, the wave is almost a TEM wave such that the decay in the liquid can be assessed by measuring along a vertical axis from the liquid surface and exponential curve fitting. As all power entering the lossy liquid is absorbed by the liquid, the SAR along the vertical z-axis can be determined as the Eq. (3):

where a, b is the cross-sectional area of the waveguide, P_fw and P_bw the forward and backward (reflected) powers inside the waveguide, δ the penetration depth inside the lossy liquid, and ρ the density of the lossy liquid conventionally assumed to be 1000 kg/m³.

Filling the liquid waveguide with tissue-equivalent liquid at the calibrated frequency and inserting the E-field probe vertically in the center of the waveguide. The probe shall be rotated around its axis from 0° to 360° by the probe positioner and measurement data (E_θ) is recorded in steps of 10°. After the rotation, the probe is moved to the max data of the angle, then along with the Z-axis, the measurement data is recorded in steps of 1mm ^[4].

By comparing the measurement data from the Z-scan and the target value SAR_cal by every step, it was getting the minimum of SAR values (eq 4):

In the liquid waveguide, as the waveguide dimensions (a, b) and the net power absorbed in the liquid (P_net) are known, Eq. (4) can be reformulated using the carrier frequency (f) and the dielectric (l) parameters of the medium. ConF_i(f, l) and δ(f, l) then are expressed as Eq. (5):

Moreover, the maximum values are below the linearized range and that lowest values are sufficiently above the noise floor, e.g., > 20 dB. As the measured values close to the waveguide layer are distorted by the boundary effect, only values that were measured at positions larger than twice the probe tip diameter from the surface of the waveguide spacer should be considered. The boundary parameters β(f, l) and α(f, l) are determined by the Eq.6:

5.   Calibration data analysis

A dosimetric E-field probe is chosen to perform calibration. The calibration frequency is 900MHz by the head liquid, so the liquid waveguide filled with 900 MHz head tissue-equivalent liquid, which conforms to the standard requirements. According to Table 1, the waveguide chosen in this paper is R9LS.

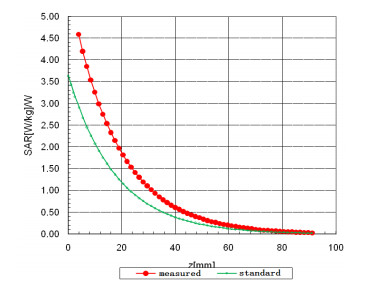
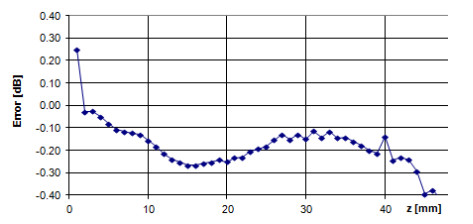
In conformity with the calibration procedure, after the E-field probe inserted into R9LS, the Z-scan job retracts the probe from the waveguide and acquires the voltage at each step. Since the reference filed of the waveguide is known, its relation to the measured field showing in figure 3 can be drawn. it is straightforward to find a considerable deviation between them.

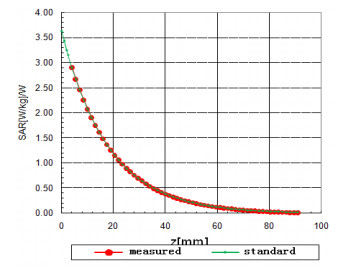
According to chapter Ⅳ, the ConvF is imported to the measured field, then the deviation is shown in figure 4.

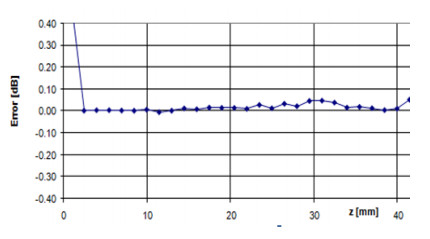
For the Z-scan, after the measurement data had been compensated by ConvF, the error of the E-field will be less than ± 0.1 dB, which meets the standard requirements. Hence, as shown in figure 5, it has been proved that this procedure is feasible and practicable.

6.   Uncertainty analysis

In accordance with the procedures in IEEE 1528, IEC 62209-1 and the uncertainty under the actual circumstance, the uncertainty components of the ConvF in this calibration please see table 2.

6.1.   Uncertainty component introduced by the RF power

1) According to the calibration certificate of the power meter, the uncertainty u_1a = 3.4% (k = 2), so the standard uncertainty u_1a' = 1.7% (k = 1).

2) The mismatch error between the power meter and cable is smaller than 0.05 dB, so the uncertainty introduced by mismatch error α₁ = 1.2%, U-shape distribution, the coverage factor $k = \sqrt{2}$,

3) The uncertainty of net power delivered to the waveguide, the maximum allowable drift is 0.20 dB, so the uncertainty introduced by mismatch error α₃ = 4.7%, U-shape distribution, the coverage factor $k = \sqrt{2}$,

4) Due to the u_1a', u_1b and u_1c are uncorrelated, so uncertainty introduced by the RF power:

6.2.   Uncertainty component introduced by the Repeatability

For this source, the calibration system has been repeated 10 times for the ConvF at 900 MHz. The data please see table 3. According to table 3, the u2 = 0.3%

6.3.   Uncertainty component introduced by the Probe mechanical positioning

The mechanical tolerance of the field probe positioner can introduce probe positioning uncertainty. The resulting SAR uncertainty is assessed by comparing the SAR obtained according to the specifications of the probe positioner with respect to the actual position defined by the geometric center of the probe sensors. According to the standard IEC 602209-1, The tolerance is determined as:

The specified repeatability of the Staubli robot arm used in DASY system is ±25 μm. The absolute accuracy for short distance movements is better than ±0.1 mm, i.e., below 3 GHz the ErrorSAR(%) is better than 0.4%, rectangular distribution, coverage factor, $k = \sqrt{3}$,

6.4.   Uncertainty component introduced by the Field uniformity

At the geometric center of the R9LS waveguide, along with the vertical and horizontal respectively, the field data are recorded in steps of 1mm, and they can be seen in table 4. According to table 4, the average is 1631.8 mV/m, the standard deviation is 4.045, so the u₄ = 0.3%

6.5.   Uncertainty component introduced by the Probe linearity

According to the manufacturing characteristic of the E-field probe, the maximum deviation is ± 0.2 dB, rectangular distribution, coverage factor, $k = \sqrt{3}$,

6.6.   Uncertainty component introduced by the Tissue-equivalent liquid

According to the IEC 62209-1, the maximum allowable drift of conductivity is 5 %, rectangular distribution, coverage factor $k = \sqrt{3}$, so u_6a = 2.9 %.

Likewise, the maximum allowable drift of permittivity is 5 %, rectangular distribution, coverage factor $k = \sqrt{3}$, so u_6b = 2.9 %.

The u_6a and u_6b are uncorrelated, so uncertainty introduced by the Tissue-equivalent liquid:

6.7.   Combined and expanded uncertainties

Concluding the contents of the chapters 6.1 to 6.7, the standard combined uncertainties of ConvF is:

So the expanded uncertainties of ConvF are:

7.   Conclusion

The convF of E-filed probe has been obtained through the method proposed in this paper. In addition, the result values show no excess of the standard requirement. The calibration procedure, therefore, is achievable and practicable.

However, the calibration of the E-field probe involves numerous parameters. Further studies and researches will be necessary.

Conflict of interest

The authors declare no conflict of interest in this paper.