Mathematical analysis for an age-structured SIRS epidemic model

1.   Introduction

In a seminal series of papers published during the 1920s and the 1930s, Kermack and McKendrick proposed infection–age structured epidemic models that take into account demography of the host population, the waning immunity and reinfection of recovered individuals (^[1,2]). In their models, the total population is decomposed into three compartments, the susceptibles, the infectious and the recovered populations (SIR model), and it is assumed that reinfection occurs for the recovered population depending on the time since recovery (recovery-age). Recently the concept of reinfection is recognized as more and more important in understanding emerging and reemerging infectious diseases, since it makes the control of infectious diseases difficult, and a waning immunity is widely observed among many infectious diseases. In fact, the recovered individuals or vaccinated individuals could be reinfected as time passes owing to the natural decay of host immunity, or a genetic change in the circulating virus. The Kermack–McKendrick infection-age dependent reinfection model has been reinvestigated by several authors (^[3,4,5,6,7]), and it was shown that a backward bifurcation of endemic steady states is possible to occur.

On the other hand, we can formulate another type of reinfection model such that recovered individuals can return to the full susceptible class due to the loss of immunity, which model is simply called a SIRS model. So far SIRS epidemic models have been studied by several authors. Hethcote ^[8] first examined an ODE model for SIRS epidemic and shown that there exists a unique globally stable endemic steady state if and only if $R_0 > 1$, where $R_0$ denotes the basic reproduction number (although Hethcote did not use this notation at 1976). Aron (^[9,10,11]) developed an SIRS model with recovery-age for malaria epidemic by which we can take into account the boosting of immunity. If we consider the recovery-age independent case, Aron's SIRS model has a globally stable endemic steady state ^[12]. Although in many cases, the host population is assumed to be in a demographic steady state, Busenberg and Hadeler ^[13] and Busenberg and van den Driessche ^[14] considered a homogeneous SIRS epidemic model in a changing host population. Recently Nakata et al. ^[15] developed an infection-age structured SIRS epidemic model and studied global stability of the endemic equilibrium by using the Lyapunov method. It is noted that the infection-age structured SIRS model can be formulated by a scalar nonlinear renewal integral equation (^[16,6]).

Different from the above-mentioned existing SIRS models, we here investigate a SIRS epidemic model with chronological age structure, which kind of model was proposed by Tudor ^[17] in 1985. As the age-structured SIRS model is an extension of the well-known age-structured SIR epidemic model ^[18], we can make use of many ideas developed for the SIR model, but we have to develop new technique to deal with problems arising from the reversion of susceptibility for recovered individuals. For application purpose, it is important to clear the implication of reinfection on $R_0$ and the critical coverage of immunization, because the reinfection phenomena would make disease control more difficult and complex. In fact, quantitative threshold results of the SIRS epidemic are similar to those of the SIR epidemic, but its controllability is very much different from the SIR epidemic. An important effect of vaccination policy is reduction of the effective size of the susceptible population, however in the reinfection model, there is a possibility that a disease can invade a fully vaccinated population, and we are naturally led to the idea of the reinfection threshold (^[6,7]). In other words, for the SIRS reinfection model, mass-vaccination policy is not necessarily almighty.

For simplicity, in this paper we only treat the case that the host population is assumed to be in a demographic steady state, so the force of infection is given by the pseudo mass-action type ^[19]. The reader may refer to ^[20] and ^[21] for more complex model formulation to take into account subclinical infection. Moreover, it is noted that our explicit bifurcation and persistence calculations are based on the separable mixing assumption for the transmission coefficient (Assumption 3.8). The separable mixing assumption implies that there is no correlation between the age of the infecteds and the age of susceptibles when their contacts occur. Further, we neglect vertical transmission because our analysis is sufficiently complex even without vertical transmission and also its essential features of reversion phenomena could be well understood by considering horizontal transmission.

In the following, we first give a standard proof for the well-posedness of the normalized age-structured SIRS model. Next we examine existence of endemic steady states by fixed point arguments and bifurcation method, where we introduce the next generation operator and the basic reproduction number $R_0$ to formulate endemic threshold results. Thirdly we investigate stability of steady states by bifurcation calculation and comparative method, and we show existence of a compact attractor and discuss the global behavior based on the population persistence theory ^[22]. Finally we give some numerical examples and discuss the effect of mass-vaccination.

2.   Model formulation

2.1.   The basic model

We here consider an infectious disease in a closed age-structured host population and assume that the disease confers temporary immunity on the recovered individuals. For simplicity, we neglect the disease-induced death rate, the effect of infection on fertility, the latent period and the infection-age dependency of the parameters. Let $S(t, a)$ be the age density of susceptible individuals at time $t$, $I(t, a)$ be the age density of infected individuals at time $t$ and $R(t, a)$ be the age density of recovered individuals at time $t$. The basic age-structured SIRS model is then formulated by the following system of McKendrick equations:

where $0 < \omega < \infty$ is the maximum attainable chronological age of the host population, $m(a)$ and $\mu(a)$ are the age-specific birth rate and death rate respectively, $\gamma(a)$ and $\delta(a)$ are the age-dependent recovery rate and the loss-of-immunity rate respectively. Let $\beta(a, \sigma)$ be the transmission coefficient between susceptibles with age $a$ and infecteds with age $\sigma$. The age-density function of the host population is $N(t, a) = S(t, a)+I(t, a)+R(t, a)$ and the force of infection is given by

Then the host population satisfies the stable population model ^[7]:

Define the survival function by

We assume that the net reproduction rate (demographic basic reproduction number) of the host population is unity:

Without loss of generality, we can assume that the host population has already reached the demographic steady state:

where $N(a)$ is the demographic stationary host population and $B > 0$ denotes its number of birth per unit time.

From technical reasons, we assume that $m, \gamma, \delta \in L_+^\infty(0, \omega)$, $\beta \in L_+^\infty((0, \omega)\times(0, \omega))$ and $\mu \in L_{loc, +}^1(0, \omega)$ with $\int_0^\omega \mu(\sigma) d\sigma = \infty$, which implies $\ell(\omega) = 0$. Let $\beta^\infty$, $\gamma^\infty$ and $\delta^\infty$ be the essential supremum of $\beta$, $\gamma$ and $\delta$ respectively.

2.2.   The normalized system and its semiflow

Let

Then the basic system (2.1) can be written as the normalized system:

where $\lambda[a \mid \psi], \; \psi \in L^{1}(0, \omega)$ is the mapping on $E: = L^{1}(0, \omega)$ defined by

and

In what follows, we mainly investigate the normalized SIRS epidemic model (2.7).

Since $s = 1-i-r$, the state space for $(i, r)$-system is a convex closed set in $E^2: = L^1(0, \omega) \times L^1(0, \omega)$ given as

Let $\phi = (\phi_1(a), \phi_2(a))^{\rm T} \in E^2$ and let us introduce operators $\mathcal A$ and $\mathcal F$ on $E^2$ as

where $AC[0, \omega]$ is the set of real-valued absolutely continuous functions on $[0, \omega]$. Then $(i, r)$-system can be formulated as a semilinear Cauchy problem on $E^2$:

The linear operator $\mathcal A$, which is called population operator, generates the $C_0$-semigroup $\{\mathcal T(t) \}_{t\geq 0}$ on $E = L^2(0, \omega)$:

Then the state space $C$ is positively invariant with respect to the semiflow defined by $\{e^{t\mathcal A}\}_{t\geq 0}$, that is,

Lemma 2.1. The operator $\mathcal F$ is Lipschitz continuous. Moreover, there exists a constant $\alpha \in (0, 1)$ such that

Proof. Lipschitz continuity is obvious. Observe that

Thus it is easy to see that $u+\alpha \mathcal F(u) \ge 0$ if $u \in C$, $1-\alpha \delta^\infty > 0$ and $1-\alpha \gamma^\infty > 0$. Furthermore, it follows that if $u \in C$, then

Hence we have proved that $(I+\alpha \mathcal F)(C) \subset C$.

By using the method in ^[23], we obtain the following proposition.

Proposition 2.2. Let $u_0 \in C$. Then the Cauchy problem (2.13) has a unique mild solution in C. The mild solution $u(t)$ is given by the following variation of constants formula:

Proof. First we choose $\alpha$ such that (2.16) holds. Define the series $\{u^n\}_{n\geq 1}$ iteratively as

Since (2.15) and (2.16) hold, if $u^n\in C$, then $u^{n+1}\in C$. In fact, $u^{n+1}$ is a convex linear combination of $e^{t\mathcal A}u_0$ and $[u^n(s)+\alpha \mathcal F(u(s))]$ with $e^{-\frac{1}{\alpha}t}+\frac{1}{\alpha}\int_0^t e^{-\frac{1}{\alpha}(t-s)}ds$ = 1. Because of the Lipschitz continuity of $\mathcal F$, $u^n(t)$ converges to the mild solution $u(t) \in C$ uniformly as $n\rightarrow \infty$.

3.   Existence of steady states

We now consider the existence of endemic steady states. First note that the endemic steady state $(s^*(a), i^*(a), r^*(a))^{\rm T}$ satisfies the following ODE system:

where

Formally solving the above ODEs, we have the following expressions:

Inserting the above expression into (3.3), we obtain

Let $b^*(a): = \lambda^*(a)s^*(a)$ be the density of newly infecteds at steady state and define a nonlinear operator $f$ given by

Moreover we define

which denotes the transition probability that individuals recovered at age $\zeta$ become susceptible again at age $\sigma$. Then for all $\zeta \in [0, \omega]$ it holds that

In fact, we can observe that

which shows (3.9).

From (3.6), we have

where $T[\lambda^*]$ is a linear operator in $E = L^1(0, \omega)$ defined as:

Lemma 3.1. There exists a number $k \in (0, 1)$ such that $\|T[\lambda^*]\| \le k$ uniformly for $\lambda^* \in E_+$.

Proof. For a given $\lambda^* \in E_+$, it follows from (3.9) that

which shows that $\|T[\lambda^*]\| \le k < 1$ with $k: = (1-e^{-\|\delta \|_E}) (1-e^{-\|\gamma\|_E})$. Thus we have our conclusion.

If $\lambda^* \in E_+ = L^1_+(0, \omega)$ is given, (3.10) is a Volterra integral equation with respect to $b^*$. As the Volterra operator has the spectral radius zero, (3.10) is solved as following:

Therefore, we obtain a fixed point equation for the force of infection $\lambda^*$:

where $\Psi$ is a nonlinear operator from $E_+$ into itself defined by the right hand side of (3.13).

Then the Fréchet derivative of $\Psi$ at zero is given by

For simplicity, we call $K = \Psi'[0]$ the next generation operator (NGO) and its spectral radius ${\cal R}_0 : = r(K)$ the basic reproduction number for the normalized system, although $K$ is a similar operator of the next generation operator for the original system (2.1) (Chapter 9, ^[7]). If $K$ and ${\cal R}_0$ are defined for the original system (2.1), for given age distribution $\phi$ of primary cases, $K\phi$ represents the age distribution of secondary cases, and the number ${\cal R}_0$ means the expected number of secondary cases produced by an infected individual during its entire period of infectiousness in a completely susceptible population. The reader may refer to ^[24,25,26,7] for the original implications of ${\cal R}_0$. See also ^[27] for a practical approach to the computation of ${\cal R}_0$.

In order to solve the fixed point problem $\lambda^* = \Psi \lambda^*$ in $E: = L^1(0, \omega)$, we use a corollary of the well-known theorem by Krasnoselskii (^[28,7]):

Theorem 3.2. Suppose that $E$ is a real Banach space and $E_+$ is a positive cone of E. Let $\Psi$ is a positive operator on $E_+$ which has a strong Fréchet derivative at the origin $K = \Psi'[0]$, satisfies $\Psi(0) = 0$ and $\Psi(E_+)$ is bounded. Moreover, K has a positive eigenvector $v_0 \in E_+$ associated with eigenvalue $\lambda_0 > 1$, but has no eigenvector in $E_+$ with unity. Then, $\Psi$ has at least one nonzero fixed point in $\Psi(E_+)$.

According to ^[18], we adopt the following technical assumptions for the transmission coefficient $\beta(a, \sigma)$, which is a natural assumption to make the next generation operator becomes nonsupporting and compact.

Assumption 3.3. 1. There exist numbers $\delta_0 \in (0, \omega)$ and $\underline{\beta} > 0$ such that

2. $\beta \in L^\infty_+ ((0, \omega)\times (0, \omega))$ is extended into $L^\infty_+(\mathbb R ^2)$ by $\beta(a, \sigma) = 0$ for $(a, \sigma) \not\in (0, \omega)\times (0, \omega)$ and satisfies

Here we summarize basic definitions from positive operator theory ^[7]. Let $E$ be a real or complex Banach space and let $E^*$ be its dual space. Then, $E^*$ is a space of all linear functionals on $E$. In the following, we write the value of $f \in E^*$ at $\psi \in E$ as $\langle f, \psi \rangle$. A closed subset $C \subset E$ is called the cone (or positive cone) if the following conditions hold: (1) $C + C \subset C$, (2) $\lambda \ge 0 \Rightarrow \lambda C \subset C$, (3) $C \cap (-C) = \{0\}$ and (4) $C \neq \{0\}$. With respect to the cone $C$, we write $x \le y$ if $y-x \in C$ and $x < y$ if $y-x \in C \setminus \{0\}$. If the set $\{\psi-\phi \mid \psi, \phi \in C\}$ is dense in $E$, the cone $C$ is said to be total. If $E = C-C$, $C$ is called a reproducing cone. Let $B(E)$ be a set of bounded linear operators from $E$ into itself. Let $r(T)$ be the spectral radius of $T \in B(E)$ and let $P_\sigma(T)$ be the point spectrum of $T$. The dual cone $C^*$ is a subset of $E^*$ composed of all positive linear functionals. $f \in C^*$ is called a positive linear functional if $\langle f, \psi \rangle \ge 0$ for all $\psi \in C$. $\psi \in C$ is called a quasi-interior point or nonsupporting point if $\langle f, \psi \rangle > 0$ for all $f \in C^* \setminus \{0\}$. A positive linear functional $f \in C^*$ is called strictly positive if $\langle f, \psi \rangle > 0$ for all $\psi \in C^+$. A nonzero operator $T \in B(E)$ is called positive if $T(C) \subset C$. If $(T-S)(C) \subset C$ for $T, S \in B(E)$, we write $S \le T$. A positive operator $T \in B(E)$ is called semi-nonsupporting if, for any $\psi \in C^+$ and $f \in C^* \setminus \{0\}$, there exists an integer $p = p(\psi, f)$ such that $\langle f, T^p\psi \rangle > 0$. A positive operator $T \in B(E)$ is called nonsupporting if, for any $\psi \in C^+$ and $f \in C^* \setminus \{0\}$, there exists an integer $p = p(\psi, f)$ such that $\langle f, T^n\psi \rangle > 0$ for all $n \ge p$. A positive operator $T \in B(E)$ is called strictly nonsupporting if, for any $\psi \in C^+$, there exists a positive integer $p = p(\psi)$ such that $T^n\psi$ is a quasi-interior point of $C$ for all $n \ge p$.

Lemma 3.3. The next generation operator $K$ is nonsupporting and compact.

Proof. Define the positive linear functional $f_0 \in E_+^*$ by

where

Then $K\psi \geq \langle f_0, \psi \rangle e$ for all $\psi \in E_+$, where $e = 1 \in E_+$, which implies

Thus for arbitrary $F\in E_+^* \setminus \{0\}$, $\psi\in E_+ \setminus \{0\}$ and $n\geq 1$,

This shows $K$ is nonsupporting. Next we show the compactness of $K$. Let $\mathcal C$ be an arbitrary bounded subset in $L^1_+(0, \omega)$, and take $M > 0$ such that $\sup_{\phi\in \mathcal C} \| \phi \|_{E} \leq M$. For all $\phi \in \mathcal C$, using Assumption 1.1,

By the Fréchet-Kolmogorov criterion for the compactness of sets in $L^p({\mathbb R})$ (^[29,22]), $\Psi(\mathcal C)$ is relatively compact. This shows that $K$ is compact.

Lemma 3.5. Let $E_+ = L^1_+(0, \omega)$ and $\Omega_M: = \{\phi \in E_+: \|\phi \|_E \le M\}$. There exists a number $M > 0$ such that $\Psi(E_+) \subset \Omega_M$.

Proof. Define the nonlinear operator $\mathcal G: \lambda^* \to b^*$ in $E_+$ by $\mathcal G\phi = (I-T[\phi])^{-1}f[\phi](\cdot, 0)$. From Lemma 3.1, it follows that

Let

Then it is easy to see that $\|\Psi \lambda^*\|_E \le M$, from which we have $\Psi(E_+) \subset \Omega_M$.

From the well-known Krein-Rutman's Theorem, we know that $r(K)$ is a positive eigenvalue if $r(K) > 0$, and it is a pole of the resolvent because $K$ is compact. Then we can apply Sawashima's results for nonsupporting operator to obtain the following properties (see ^[30,31]):

Proposition 3.6. Suppose that the cone $E_+$ is total, $K$ is compact, nonsupporting with respect to $E_+$ and $r(K) > 0$. Then the following holds:

1. $r(K) \in P_\sigma(K) \setminus \{0\}$ and $r(K)$ is a simple pole of the resolvent $(\lambda I-K)^{-1}$.

2. The eigenspace corresponding to $r(K)$ is one-dimensional and its eigenvector $v_0 \in E_+$ is a quasi-interior point. Any eigenvector in $E_+$ is proportional to $v_0$.

3. The adjoint eigenspace corresponding to $r(K)$ is one-dimensional and its eigenfunctional $f\in E^* \setminus \{0\}$ is strictly positive.

As is seen above, the idea of being nonsupporting for positive operator is an infinite-dimensional extension of the primitivity of nonnegative matrices in the finite-dimensional case.

Using the above facts, we can show the main theorem in this section:

Theorem 3.7. If ${\cal R}_0 > 1$, there exists at least one endemic steady state, while there is no endemic steady state if ${\cal R}_0 \le 1$.

Proof. If ${\cal R}_0 > 1$, thanks to the Lemma 3.4 and above Proposition 3.6, there is no eigenvector of $K$ which is corresponding to unity in $E_+$. Then by Lemma 3.5 and Theorem 3.2, we can show the first half of statement. Next suppose that ${\cal R}_0 \le 1$ and there exists an endemic steady state and the force of infection at the endemic steady state is given by $\lambda^* > 0$. From (3.10), it follows that

Then we know that $\lambda^* = \Psi\lambda^* < \Psi'[0]\lambda^*$, which implies that ${\cal R}_0 = r(\Psi'[0]) > 1$. This contradicts our assumption. Then there is no endemic steady state if ${\cal R}_0 \le 1$.

Next we show that an endemic steady state bifurcates forwardly at ${\cal R}_0 = 1$. For this purpose, we adopt the following assumption called separable mixing assumption which means that there is no correlation between the age of the infected individuals and that of the susceptible individuals.

Assumption 3.8. There exist $\beta_1, \beta_2 \in L_+^\infty(0, \omega)$ such that $\beta(a, \sigma) = \beta_1(a)\beta_2(\sigma)$.

Then the next generation operator $K$ is represented as follows:

So the range of $K$ is one-dimensional and $\beta_1$ becomes a positive eigenvector as

which shows that the basic reproduction number is given by

Let us introduce a bifurcation parameter $\epsilon > 0$ and suppose that $\beta_1 = \epsilon \beta_{10}$, where the standard susceptibility $\beta_{10}$ is chosen such as ${\cal R}_0 = 1$ if $\epsilon = 1$. Then the basic reproduction number is equal to $\epsilon$ and it holds that

Then the infection force at the endemic steady state is $\lambda^*(a) = c\epsilon \beta_{10}(a)$ for some $c > 0$. Hence the fixed point problem (3.13) is rewritten as

where

Then it follows from (3.22) that $\Theta(0, 1) = 0$. Observe that

where

Then it follows that

from which we can conclude that

From the Implicit Function Theorem, $\Theta(c, \epsilon) = 0$ can be solved as $c = c(\epsilon)$ with $c(1) = 0$ at the neighborhood of $(c, \epsilon) = (0, 1)$. Corresponding to a positive root $c > 0$ of $\Theta(c, \epsilon) = 0$, there exists an endemic steady state. Moreover it follows from (3.22) that

and so

which implies that $c(\epsilon) > 0$ if $\epsilon > 0$ and $|\epsilon-1|$ is small enough. Then a positive steady state forwardly bifurcates at $\epsilon = {\cal R}_0 = 1$. Then we have the following bifurcation result:

Proposition 3.9. For the separable mixing case, an endemic steady state forwardly bifurcates from the disease-free steady state when ${\cal R}_0$ crosses unity.

4.   Stability of steady states

Next we consider the stability of steady states of the system (2.7).

4.1.   Disease-free steady state

The system (2.7) has a unique disease-free steady state: $(s^0(a), i^0(a), r^0(a))^{\rm T} = (1, 0, 0)^{\rm T}$. In order to consider the dynamics around the disease-free steady state, we introduce the small perturbation terms:

where $x(t, 0) = y(t, 0) = z(t, 0) = 0$. Then the second equation in (2.7) is rewritten as

Neglecting the second order term of small perturbation, we obtain the linearized equation of (4.1):

This equation describes the dynamics of the initial invasion phase of the infected population. Define two linear operators $A_0$ and $F_0$ on $E$ as the following:

Then the equation (4.2) is transformed into the following linear Cauchy problem

Note that from Assumption 3.3, $F_0\in B(E)$ is a compact operator. Define the linear operator $S_\zeta$ for given $\zeta \in \rho(A_0)$ as follows:

where $R(\zeta, A_0) = (\zeta-A_0)^{-1}$. Equation (4.3) has been well studied and the following statement can be proved as Lemma 4.7 of this paper (^[18], ^[32]):

Lemma 4.1. $A_0+F_0$ has a compact resolvent and it holds that

So we are going to investigate the properties of the operator $S_\zeta$ instead of $A_0+F_0$, which determines the location of eigenvalues of the linearized generator $A_0+F_0$.

Lemma 4.2. The operator $S_\zeta$ is compact and nonsupporting for all $\zeta\in\mathbb R$.

Proof. The operator $S_\zeta$ is the composition of the compact operator $F_0$ and the bounded operator $R(\zeta; A_0)$ on $E$, so $S_\zeta$ is compact.

Define the strictly positive linear functional $f_\zeta \in E_+^*$ by

then $S_\zeta \psi \geq \langle f_\zeta, \psi \rangle e$ for all $\psi\in E_+$ and $\zeta\in\mathbb R$. Therefore, we obtain

Thus for arbitrary $F\in E_+^* \setminus \{0\}$, $\psi\in E_+ \setminus \{0\}$ and $n\geq 1$,

which implies $S_\zeta$ is nonsupporting.

Lemma 4.3. There is a unique $\zeta_0 \in\mathbb R$ such that $r(S_{\zeta_0}) = 1$ and the sign relation holds:

Moreover, $\zeta_0$ is the dominant characteristic root, that is, $\Re \zeta < \zeta_0$ for any $\zeta\in\Sigma\setminus\{\zeta_0\}.$

To prove Lemma 4.3 we need the following theorem on the monotone property of spectral radius.

Theorem 4.4 (^[31]). Let $E$ be a Banach lattice. Suppose that $S, T \in B(E)$ are positive operators. Then, the following holds:

1. If $S\leq T$, then $r(S)\leq r(T)$.

2. If $S, T$ are semi-nonsupporting and compact, $S\leq T, S\neq T$ and $r(T)\neq 0$, then $r(S) < r(T)$.

Proof of Lemma 4.3. To prove the first half we will show that

and that the mapping $\mathbb R \ni \zeta \rightarrow r(S_\zeta)$ is strictly decreasing and continuous. Applying Proposition 3.5, $r(S_\zeta)$ is an eigenvalue of $S_\zeta^*$ and its corresponding eigenfunctional $F_\zeta\in E_+^*$ is strictly positive. Then we have

Because of the strict positivity of $F_\zeta$, we can divide the both sides of the above inequality by $\langle F_\zeta, e \rangle > 0$ to obtain $r(S_\zeta)\geq \langle f_\zeta, e \rangle$. Since

holds, it follows that $\liminf_{\zeta\rightarrow -\infty} r(S_\zeta) = \infty$ by the Fatou's lemma. Furthermore, we define a strictly positive functional $g_\zeta \in E_+^*$ by

Using the same argument as above, we obtain

By the reverse Fatou's lemma, $\limsup_{\zeta\rightarrow +\infty} r(S_\zeta) = 0$. Consequently, (4.7) holds. Note that if $\zeta > \mu$, then we have $S_\zeta\leq S_\mu$ and $S_\zeta\neq S_\mu$, so it follows from Theorem 4.4 that $r(S_\zeta) > r(S_\mu)$. As $S_\zeta$ is a compact operator for any $\zeta \in \mathbb R$ and $r(S_\zeta) > 0$, it follows from the Krein-Rutman's theorem that its spectral radius $r(S_\zeta)$ is a positive eigenvalue, so it is a continuous function of $\zeta$. Then $r(S_\zeta) = 1$ has a unique real root $\zeta_0$ such that ${\rm sign}(\zeta_0) = {\rm sign}(r(S_{0})-1)$. Since $r(S_{0}) = r(K) = {\cal R}_0$, we have the sign relation (4.6).

Next we show the latter half. If we take $\zeta\in\Sigma$, there exists an eigenfunction $y_\zeta\in E \setminus \{ 0 \}$ such that $S_\zeta y_\zeta = y_\zeta$. If we use the notation $|y_\zeta|(a): = |y_\zeta(a)|$, it follows that

In short, $|y_\zeta|\leq|S_\zeta y_\zeta|\leq S_{\Re\zeta} |y_\zeta|$. Let $F_{\Re\zeta}$ be an eigenfunctional of $S_{\Re\zeta}^*$ corresponding to the eigenvalue $r(S_{\Re\zeta})$. By Proposition 3.5, it is strictly positive. Then we have

and dividing the both sides by $\langle F_{\Re\zeta}, |y_\zeta| \rangle > 0$, we obtain $r(S_{\Re\zeta})\geq 1$. This implies $\Re \zeta\leq\zeta_0$ for all $\zeta \in \Sigma$ by the sign relation. Let us show that $\zeta = \zeta_0$ if $\Re \zeta = \zeta_0$. In this case, we have $|y_\zeta|\leq S_{\Re\zeta} |y_\zeta| = S_{\zeta_0} |y_\zeta|$. In particular $|y_\zeta| = S_{\zeta_0} |y_\zeta|$ holds. In fact, if we assume $|y_\zeta| < S_{\zeta_0} |y_\zeta|$ then

which is a contradiction. Let $y_0$ be the eigenfunction of $S_{\zeta_0}$ corresponding to $1 = r(S_{\zeta_0})$. Since $|y_\zeta|$ is a positive eigenfunction of the nonsupporting operator $S_{\zeta_0}$, it follows from Proposition 3.6 that there exists $c > 0$ such that $|y_\zeta| = c y_0$ and, without loss of generality, we can assume that $c = 1$. Hence the function $y_\zeta$ is represented as $y_\zeta(a) = e^{iv(a)} y_0(a)$ for some real valued function $v \colon (0, \omega) \rightarrow \mathbb R$. From the relation $|S_\zeta y_\zeta| = S_{\zeta_0} y_0$ with $\zeta = \zeta_0+\Im \zeta$, we have

Applying Lemma 6.12 in ^[33], it follows that $-\Im \zeta(\sigma-\eta)+v(\eta) = \kappa$ for some constant $\kappa$. Inserting $y_\zeta = e^{iv(a)}y_0$ into the relation $S_\zeta y_\zeta = y_\zeta$, we have $e^{i\kappa}S_{\zeta_0}y_0 = e^{iv(a)}y_0$, so $\kappa = v(a)$ and $\Im \zeta = 0$. Then $\zeta_0$ is the strictly dominant eigenvalue.

Finally we can conclude the following stability theorem.

Theorem 4.5. If ${\cal R}_0 < 1$, the disease-free steady state is locally asymptotically stable whereas unstable if ${\cal R}_0 > 1$.

Proof. The $C_0$-semigroup $\{ e^{t A_0} \}$ is zero for $t \ge \omega$, so it is eventually norm continuous. Since $F_0$ is compact, $\{ e^{t(A_0+F_0)} \}_{t\geq 0}$ is also eventually norm continuous ^[34]. Then applying the spectral mapping theorem, $e^{t \omega_0(A_0+F_0)} = e^{t s(A_0+F_0)}$ for all $t\geq 0$. Then it holds that

where $\omega(A)$ denotes the growth bound of the semigroup $e^{tA}$. Then it follows that

Thus by the principle of linearized stability, the disease-free steady state is locally asymptotically stable if ${\cal R}_0 < 1$, while it is unstable if ${\cal R}_0 > 1$.

Theorem 4.6. If ${\cal R}_0 < 1$, the disease-free steady state is globally asymptotically stable.

Proof. Let $U(t)$ and $V(t)$ be the semiflows induced by the mild solution of (2.13) and the mild solution $v(t)$ of

Since $\mathcal F (u) \le \mathcal F'[0]u$ for $u \in C$, by using iterative argument, it is easily seen that $U(t) \le V(t)$ in $C$. For the asymptotic behavior of the linearized equation, it is shown above that if ${\cal R}_0 = r(K) < 1$, then

which implies the global stability of the disease-free steady state.

4.2.   Endemic steady states

Next we consider the local stability of endemic steady states. Throughout this subsection, we again adopt the separable mixing assumption. As is shown in the previous section, the endemic steady state exists if and only if ${\cal R}_0 > 1$, so we assume this supercriticality condition to consider the stability of the endemic steady state. Let $(s^*(a), i^*(a), r^*(a))^{\rm T} \in E_+^3 = (L_+^1(0, \omega))^3$ be an endemic steady state. Again let us introduce the small perturbation terms:

Then the system (2.7) is rewritten as

Since $x(t, a)+y(t, a)+z(t, a) = 0$, (4.10) is reduced to $(y, z)$-system, so it can be formulated as an abstract linear problem on the Banach space $E^2$:

where $A$ is defined as the same as $\mathcal A$ in Section 2, and

Now let us consider the resolvent equation for $A+F$:

By the definition of the operators $A$ and $F$, $v_1$ satisfies

Once $v_1$ is determined by (4.14), $v_2$ is calculated as

Define an operator $V_\zeta$ on $E$ by

Moreover, define an operator $g$ and a given function $h$ as

Thus if we suppose $\lambda = \lambda[\cdot\mid v_1]$ is given, the equation (4.14) with respect to $v_1$ is rewritten as

Since $V_\zeta$ is Volterra type operator, $R(1;V_\zeta): = (I-V_\zeta)^{-1}$ exists and (4.19) is solved as:

Then we have

where $W_\zeta$ is an integral operator from $L^1(0, \omega)$ into itself defined by

Roughly speaking, if $(I-W_\zeta)^{-1}$ exists, $\lambda$ can be calculated as $(I-W_\zeta)^{-1}\xi$ and the resolvent $(\zeta-(A+F))^{-1}$ exists.

Lemma 4.7. For the linearized generator $A+F$ at the steady state, it holds that

where $\sigma(A)$ denotes the spectrum of $A$.

Proof. From the expression (4.20) and (4.15), we know that $A+F$ has a compact resolvent, so it holds that $\sigma(A+F) = P_\sigma(A+F)$ (Theorem 6.29, ^[35]). Let $\mathcal S: = \{\zeta\in\mathbb C: 1 \in \sigma(W_\zeta)\}$. From the above argument, it follows that $\mathbb C \setminus \mathcal S \subset \rho(A+F)$, where $\rho(A)$ denotes the resolvent set of $A$. Thus $\mathcal S \supset \sigma(A+F) = P_\sigma(A+F)$. Since $W_\zeta$ is a compact operator, its spectrum different from zero is an eigenvalue (Theorem 6.26, ^[35]), so there exists an eigenfunction $\phi_\zeta$ such that $W_\zeta\phi_\zeta = \phi_\zeta$ if $\zeta \in \mathcal S$. In this case,

becomes an eigenfunction of $A+F$ associated with eigenvalue $\zeta$. Hence we have $\mathcal S \subset P_\sigma(A+F)$. Then we have (4.23).

In the following, we again adopt the separable mixing assumption that

in order to simply make use of bifurcation arguments explicitly, although our argument could be applied to the model with the general transmission coefficient as is observed in ^[18].

In the separable mixing case, we can observe that

which shows that $\beta_1$ is a positive eigenvector of $W_\zeta$.

As is shown in section 3, if we introduce a bifurcation parameter $\epsilon > 0$ such that $\beta_1 = \epsilon \beta_{10}$ and ${\cal R}_0 = 1$ when $\epsilon = 1$, we have $\lambda^* = c(\epsilon) \epsilon \beta_{10}$ for a right neighborhood at $\epsilon = 1$, $c(1) = 0$ and $c'(1) > 0$. Then the parametrized model has the basic reproduction number $\epsilon$. Now we define a two parameter function $\Lambda$ as

where

Then the operator $I-W_\zeta$ is not invertible if and only if $\Lambda(\zeta, \epsilon) = 0$.

Since $V_\zeta = 0$ for $\epsilon = 1$, we have $\Lambda(0, 1) = 1-R_0 = 0$. Observe that

Therefore it follows from the Implicit Function Theorem that $\Lambda(\zeta, \epsilon) = 0$ can be solved as $\zeta = \zeta(\epsilon)$ with $\zeta(1) = 0$ in the neighborhood of $(\zeta, \epsilon) = (1, 0)$. From Lemma 4.1, we know that $\zeta(1) = 0$ is the dominant real eigenvalue of the linearized generator $A+F$ when $\epsilon = 1$.

Theorem 4.8. For the separable mixing case, the endemic steady state bifurcated from the disease-free steady state is locally asymptotically stable, if ${\cal R}_0 > 1$ and $|{\cal R}_0-1|$ is sufficiently small.

Proof. Observe that

On the first term of the summation in (4.29),

where $s^*(\cdot; \epsilon)$ is the prevalence of susceptibles in the bifurcated endemic steady state with the bifurcation parameter $\epsilon$. Since $\lambda^*(a)s^*(a) = b^*(a)$ and (3.12), we have

Therefore we obtain

where

From our assumption, we have $J_3 = -{\cal R}_0 = -1$. Moreover, it follows from (3.27) and (3.30) that

On the second term of the summation in (4.29),

The third and the subsequent term in (4.29) is equal to zero, hence we obtain

Therefore we conclude that

which shows that the dominant real eigenvalue moves to the left when $\epsilon$ crosses the unity. Using the Rouché theorem (^[36,37]), we can show that another eigenvalues stays in the left half plane if $|\epsilon-1|$ is small enough. Then we conclude that the forwardly bifurcated small endemic steady state is locally asymptotically stable.

5.   Global behavior

In this section, we again adopt the separable mixing assumption 3.8 to discuss the persistence threshold result of the SIRS model. The reader may find elementary ideas and techniques in ^[22,38,39]. A key idea is that the weak persistence could imply the strong persistence if there exists a compact attractor for the semiflow defined by the basic dynamical system.

5.1.   Weak persistence

First we consider the weak persistence of the semiflow induced from our SIRS epidemic model. The persistence can be seen as a mathematical formulation of the disease endemicity.

Definition 5.1. Let X be an arbitrary nonempty set and $\rho \colon X \rightarrow \mathbb R_+$. A semiflow $\Phi \colon [0, \infty) \times X \rightarrow X$ is called uniformly weakly $\rho$-persistent, if there exists some $\epsilon > 0$ such that

and is called uniformly strongly $\rho$-persistent, if there exists some $\epsilon > 0$ such that

Now we set the state space $X = \{(x_1, x_2, x_3)^{\rm T} \in E^3_+ \; |\; x_1+x_2+x_3 = 1\}$ and the continuous semiflow $\Phi(t, x_0) = u(t; x_0)$, which is the solution of (2.7) with the initial value $x_0$. Let us consider the persistence of the system (2.7) under the separable mixing assumption 3.8. Then the force of infection $\lambda$ is represented as the form of separation of variables:

where

Integrating along the characteristic line, for $t > a$, we have an expression

Lemma 5.2. If $\|i_0\|_E > 0$, then $\|i(t)\|_E > 0$ for all $t > 0$, where $i(t): = i(t, \cdot) \in L^1(0, \omega)$.

Proof. Let $t_0 = \inf\{t \in \mathbb R_+: \|i(t)\|_E = 0\}$ and suppose that $t_0 < \infty$. As $\|i(t)\|_E$ is continuous with respect to $t$, our assumption implies that $t_0 > 0$ and $i(t_0, a) = 0$ for almost all $a \in (0, \omega)$. Let us fix a positive number $0 < h < t_0 \wedge \delta_0$, where $\delta_0$ is defined in Assumption 3.3. From (2.7), we have

which shows that $i(t_0-h, a) = 0$ for almost all $a \in (0, \omega-h)$. Using (5.5), we obtain for almost all $a \in (0, t_0 \wedge \omega)$,

From the Assumption 3.3 and the separable mixing assumption, we have $\beta_1(a) > 0$ for all $a \in (0, \omega)$ and $s(t_0-a+\eta, \eta) > 0$ for all $\eta > 0$ because $s(t, 0) = 1$ for $t \ge 0$. Then we have $\phi(t_0-a+\eta) = 0$ for almost all $\eta \in (0, a)$ and $a \in (0, t_0 \wedge \omega)$. Hence we have $\phi(t) = 0$ for all $t \in (0 \vee (t_0-\omega), t_0)$. Observe that

Then $i(t, a) = 0$ for almost all $a \in (\omega-\delta_0, \omega)$ and $t \in (0 \vee (t_0-\omega), t_0)$. Since $\omega-\delta_0 < \omega-h$ and $t_0-h \in (0 \vee (t_0-\omega), t_0)$, we have $i(t_0-h, a) = 0$ for almost all $a \in (0, \omega)$, so $\|i(t_0-h)\|_E = 0$, which contradicts the definition of $t_0$. Then we have $t_0 = \infty$ and our conclusion.

Define the function $\rho \colon X \rightarrow \mathbb R_+$ as

We decompose the state space $X$ into two disjoint subsets:

Then we obtain

Lemma 5.3. If $\rho(s_0, i_0, r_0) > 0$, then $\rho(\Psi(t, (s_0, i_0, r_0)) > 0$ for all $t > 0$.

Proof. If $\rho(s_0, i_0, r_0) > 0$, then $\| i_0 \|_E > 0$. From of Lemma 5.2, $\| i(t, \cdot) \|_E > 0$ for all $t > 0$. Thus we obtain $\rho(\Psi(t, (s_0, i_0, r_0)) = \int_0^\omega N(\sigma)i(t, \sigma)d\sigma > 0$ for all $t > 0$.

Theorem 5.4. Suppose that the separable mixing assumption 3.8 holds. If ${\cal R}_0 > 1$, then the semiflow $\Phi$ is uniformly weak $\rho$-persistent. That is, there exists a number $\epsilon > 0$ such that

for all $(s_0, i_0, r_0)^{\rm T}\in X$ with $\rho((s_0, i_0, r_0)) > 0$

Proof. Substituting (5.5) into the definition (5.4), we have

For given $b\geq 0$, define $\phi_b(t): = \phi(t+b)$. Here we adopt a convention that $N(a) = 0$ for $a > \omega$. For $t > \omega$, we can observe that

Since

then $s$ is estimated as

Thus we obtain

Now we are going to prove (5.11) by contradiction. Assume that for all $\epsilon > 0$, there exist a time $T_0 > 0$ and an initial data $x_0 = (s_0, i_0, r_0)^{\rm T} \in X$ such that $\rho(\Phi(t, x_0))\leq\epsilon$ for all $t\geq T_0$. We set $T_0 > \omega$ without loss of generality. By (5.15), we obtain

where $\beta_2^\infty = \sup_{a \in [0, \omega]} \beta_2(a)$. For sufficiently large $T > \omega$ and $t > T_0$,

Since $\phi$ is a bounded function, it is Laplace transformable on $\{ \lambda > 0 \}$. By (5.17), we obtain

where

In particular, note that

Because of the continuity of $F(\cdot, \cdot, \cdot)$, there are small positive number $\epsilon, \lambda$, and large positive number $T > \omega$ such that $F(\epsilon, \lambda, T) > 1$ which implies $\widehat{\phi}_{b+T} (\lambda) = 0$ by (5.18). Then for sufficiently large $T > \omega$, ${\phi}_{b+T}(t) = 0$ for all $t\in (0, \infty)$. If we take sufficiently large $T_1$ such that $T_1 > b+T$,

which implies $i(T_1, a) = 0$ for almost all $a\in (\omega-\delta_0, \omega)$. Let us take positive numbers $p$ and $q$ such that $0 < p < q < \omega-\delta_0$ with $q-p < \delta_0$, then $(p+\tau, q+\tau) \subset (\omega-\delta_0, \omega)$ for $\omega-\delta_0-p < \tau < \omega-q$. Hence $i(T_1+\tau, a) = 0$ for almost all $a \in (p+\tau, q+\tau)$, that is, $i(T_1, a) = 0$ for almost all $a \in (p, q)$. Repeating to choose $p$ and $q$ finitely many times, we obtain $i(T_1, a) = 0$ for almost all $a \in (0, \omega-\delta_0)$. Consequently $i(T_1, a) = 0$ for almost all $a \in (0, \omega)$, so $\int_0^\omega N(\sigma)i(T_1, \sigma)d\sigma = 0$, which contradicts Lemma 5.3.

5.2.   The existence of global compact attractor

Let $\Phi \colon \mathbb R \times X \rightarrow X$ be the semiflow induced by the mild solution of the system (2.7). Then it is easy to see that $\Phi$ is state-continuous, i.e., all maps $\Phi(t, \cdot): X \to X$, $t \ge 0$ is continuous. According to ^[22], here we summarize some basic definitions for a semiflow $\Phi$ in a metric space $X$. A nonempty, compact, invariant set $K \subset X$ is called a compact attractor of bounded sets if $K$ attracts all bounded sets of $X$. The state-continuous semiflow $\Phi$ is called point-dissipative if there exists a bounded subset $\mathcal B$ of $X$ which attracts all points in $X$. $\Phi$ is called asymptotically smooth if $\Phi$ is asymptotically compact on every forward invariant bounded closed set. $\Phi$ is called eventually bounded on a set $M \subset X$ if $\Phi([r, \infty) \times M)$ is bounded for some $r > 0$.

Theorem 5.5. Suppose the Assumption 3.8. There exists a compact attractor $\mathcal B$ of bounded sets in $X$.

Proof. From Theorem 2.33 of ^[22], the statement is proved if we can check that the semiflow $\Phi$ is point-dissipative, eventually bounded on every bounded sets in $X$ and asymptotically smooth. The first and the second conditions hold trivially, because $X$ itself is a bounded set. We are going to prove the eventual smoothness. As $X$ itself is forward invariant bounded closed set, it is sufficient to show that $\Phi(t, \cdot)X$ is compact. In order to check the Fréchet-Kolmogolov criterion for the compactness of sets in $L^p({\mathbb R})$ (Theorem B.1, ^[22]; ^[29]), it is sufficient to show the equi-continuity in $L^1$ of $\Phi(t, \cdot)X$ for a large $t > 0$. By Assumption 3.3, for any $\epsilon > 0$ there exists some $\kappa \in (0, \epsilon)$ such that

whenever $|h| < \kappa$. For sufficiently large $T_0 > \omega$, let $\mathcal B = \{ \Phi(T_0; (s_0, i_0, r_0)) \mid (s_0, i_0, r_0)^{\rm T} \in X \}$. Integrating $s$, $i$ and $r$ in (2.7) along the characteristic line, for $t > \omega > a$ and $|h| < \kappa$,

By the same kind of calculation, we have

Thus for all $t > 3\omega$,

where

Define a function

Then $h'$ satisfies

Therefore we know that $h(b)\leq c_1 (1-e^{-c_2 b})\epsilon$ holds. Then we have

which shows that

Thus each $P_i B$ ($i = 1, 2, 3$) is relatively compact subsets of $E$, where each $P_i\colon X\rightarrow E$ is the projection to the $i$-th component. This implies the set $\mathcal B$ is relatively compact set in $X$.

Theorem 5.6. Suppose the Assumption 3.8. If ${\cal R}_0 > 1$, then the semiflow $\Phi$ is uniformly strongly $\rho$-persistent.

Proof. To show this, it is needed to show that there is no total trajectory $\phi \colon \mathbb R \rightarrow \mathcal B$ such that $\rho(\phi(0)) = 0$ and $\rho(\phi(t)) > 0$ for all $t\in \mathbb R \setminus \{0\}$ (see ^[22] Theorem 5.2.). Assume $\rho(\phi(0)) = 0$. Then we obtain $i_0 = 0 \in E$. For $t\in [0, \omega]$, $I(t): = \int_0^\omega N(\sigma)i(t, \sigma)d\sigma$ is estimated as

From the Gronwall inequality, we conclude that $I(t) = 0$ for all $t \in [0, \omega]$, which shows that there is no trajectory such as mentioned at the beginning.

6.   Numerical simulation

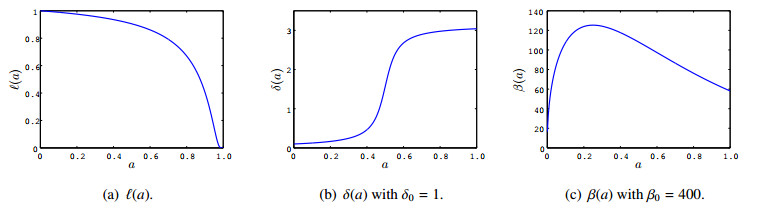
In this section, we provide numerical examples that support our theoretical results. Let $\omega : = 1$ to normalize the age interval as $[0, 1]$. Fix the age-specific death rate as $\mu(a) : = [10(1-a)^2]^{-1}$, $a \in [0, 1)$. We then see that $\mu \in L_{loc, +}^1(0, 1)$, $\int_0^1 \mu(\sigma)d\sigma = \infty$ and $\ell(a) = \exp \left(-\int_0^a \mu(\sigma)d\sigma \right) = \exp (-a/[10(1-a)])$, $a \in [0, 1)$ (see Figure 1 (a)). Let $B : = 1/\int_0^1 \ell(a) da \approx 1.2527$, and thus, the total population is normalized as $\int_0^1 N(a) da = \int_0^1 B \ell(a) da = 1$. We fix the following parameter functions:

where $\beta_0 > 0$ and $\delta_0 > 0$ are positive constants. The choice of these functions is based on the following biological assumptions: the average infectious period $1/\gamma(a) = 1/100$ is age-independent and $100$ times smaller than the maximum attainable age; the loss-of-immunity rate $\delta(a)$ is high in the elderly people (see Figure 1 (b)); the transmission coefficient $\beta(a, \sigma) = \beta(a)$ depends only on the age of susceptibles and the youth people are more likely to be infected (see Figure 1 (c)). We can easily check that all necessary assumptions on the parameter functions stated in the previous sections are satisfied. In particular, the basic reproduction number ${\cal R}_0$ is explicitly calculated as

In what follows, we fix the following initial data $x_0 = (s_0, i_0, r_0)$:

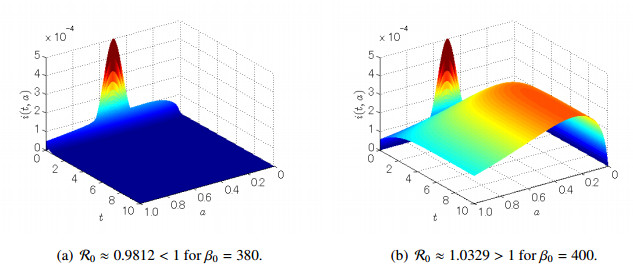
We first verify the threshold property of ${\cal R}_0$ under the fixed $\delta_0 = 1$. For $\beta_0 = 380$, we obtain ${\cal R}_0 \approx 0.9812 < 1$. Hence, by Theorem 4.6, we can expect that the disease-free steady state is globally asymptotically stable. In fact, Figure 2 (a) exhibits that the age distribution of infected population converges to zero as time evolves. On the other hand, for $\beta_0 = 400$, we obtain ${\cal R}_0 \approx 1.0329 > 1$. Hence, by Theorems 3.6, 4.5, 4.8 and 5.6, we can expect that the disease-free steady state is unstable, there exists a locally asymptotically stable endemic steady state and the semiflow $\Phi$ is uniformly strongly $\rho$-persistent. In fact, Figure 2 (b) exhibits that the age distribution of infected population converges to a positive distribution as time evolves. This example suggests that the endemic steady state is not only locally but also globally asymptotically stable in this case.

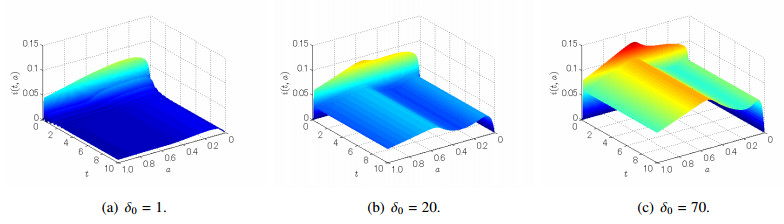
We next observe the effect of loss of immunity $\delta_0$ under the fixed $\beta_0 = 600$. Note that ${\cal R}_0$ is independent of $\delta_0$ and fixed to $1.5493 > 1$ in this case. In Figure 3, we see that the infected population increases in particular in the elderly age class as the effect of loss of immunity $\delta_0$ increases. Specifically, the total number of infected population $\int_0^1 N(\sigma) i(t, \sigma) d\sigma$ converges to $0.0095$, $0.0338$ and $0.0747$ as time evolves for $\delta_0 = 1$, $20$ and $70$, respectively. This implies that ${\cal R}_0$ for the SIRS epidemic model does not reflect the intensity of the disease endemicity but it is the threshold for the eradication or persistence of the disease.

7.   Vaccination

We here briefly consider a mass-vaccination effect on the basic system (2.1) to clear the implication of reinfection on ${\cal R}_0$ and the threshold results, because it has practically important implications that the reinfection phenomena would make disease control more difficult and complex. In fact, threshold results of the SIRS epidemic are similar to those of the SIR epidemic, but its controllability is very much different from the SIR epidemic. An important effect of vaccination policy is reduction of the effective size of the susceptible population, however in the reinfection model, there is a possibility that a disease can invade a fully vaccinated population, and we are naturally led to the idea of the reinfection threshold (^[6,7]). In other words, for the SIRS reinfection model, mass-vaccination policy is not necessarily almighty.

Suppose that newborns in the virgin population are mass vaccinated with coverage $\epsilon \in [0, 1]$ and the immunological status of newly vaccinated individuals is identical with that of the newly recovered individuals. Then it is easy to see that the boundary condition in (2.1) is replaced by $s(t, 0) = 1-\epsilon$, $i(t, 0) = 0$ and $r(t, 0) = \epsilon$. Then it is easy to see that the disease-free steady state is a partially immunized state given by $(s^\dagger, i^\dagger, r^\dagger) = (1-\epsilon \Delta(a), 0, \epsilon \Delta(a))$. Here let us introduce the effective next generation operator $K_\epsilon$ as

Then the effective reproduction number ${\cal R}_\epsilon$ is given by its spectral radius $r(K_\epsilon)$. From the monotonicity of the spectral radius, we have ${\cal R}_\epsilon \le {\cal R}_0$. Let $\sigma: = {\cal R}_1/{\cal R}_0$, where ${\cal R}_1$ is the effective reproduction number for the fully vaccinated population. Given that the qualitative change in the epidemiological implication occurs for the prevalence and controllability at ${\cal R}_0 = 1/\sigma$, Gomes et al. (^[40,41]) referred to $1/\sigma$ as the reinfection threshold of ${\cal R}_0$. As seen above, the reinfection threshold of ${\cal R}_0$ corresponds to the fact that $\sigma {\cal R}_0 = {\cal R}_1 = 1$, i.e., ${\cal R}_0 = 1/\sigma$ does not imply a bifurcation point of the basic system (2.1), but the threshold condition ${\cal R}_1 = 1$ of the fully vaccinated system. The disease is uncontrollable by the mass vaccination if ${\cal R}_1 = \sigma {\cal R}_0 > 1$, because the fully vaccinated population can be invaded by the disease.

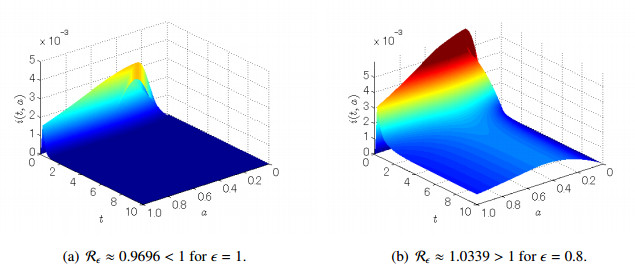
As an example, we consider the same parameter functions as in Section 6 with $\beta_0 = 500$ and $\delta_0 = 30$. In this case, we have ${\cal R}_0 \approx 1.2911$, and thus, the disease will persist without vaccination. For $\epsilon = 1$, we obtain ${\cal R}_1 \approx 0.9696 < 1$, and hence, the reinfection threshold is $\sigma^{-1} = {\cal R}_0/{\cal R}_1 \approx 1.33 > {\cal R}_0$, the complete mass-vaccination policy is successful and the disease will be eradicated in this case (see Figure 4 (a)). On the other hand, for $\epsilon = 0.8$, we obtain ${\cal R}_\epsilon \approx 1.0339 > 1$. This implies that the disease will persist even if $80$ percent of newborns are successfully immunized by vaccination in this case (see Figure 4 (b)). In fact, as in (6.2), we can calculate ${\cal R}_\epsilon$ as

and hence, ${\cal R}_\epsilon < 1$ is equivalent to

That is, more than $90$ percent of newborns should be immunized to control the disease in this case, and (7.3) is a much severe criterion than the usual critical coverage of immunization $\epsilon > 1-1/{\cal R}_0$ calculated for the SIR disease with permanent immunity.

8.   Discussion

In this paper, we have rigorously established the threshold property of ${\cal R}_0$ in the age-structured SIRS model that the disease will be naturally eradicated if ${\cal R}_0 < 1$, while it is strongly persistent and endemic steady states exists if ${\cal R}_0 > 1$. It is noted that different from the SIR model, we have not yet known whether the endemic steady state is unique or not even in the separable mixing case, because the characteristic equation satisfied by the force of infection at the endemic steady state is complex, and not monotone. The number of endemic steady states and their stability should be investigated in future. Although our main analysis depends on the separable mixing assumption, it is limited and could be relaxed to obtain the same kind of results.

Using numerical calculations, we have shown that the loss of immunity has a drastic effect on the critical coverage of immunization. In fact, if the basic reproduction number is grater than the reinfection threshold, we cannot control the disease by the mass vaccination to newborns. We have shown the critical coverage of immunization for the separable mixing case.

For future extension of our model and real-world applications, it is noted that if the vaccination effect is incomplete, the vaccinated individuals could be partially susceptible and their infection would lead partial infectivity. If the secondary infection will lead a longer infective period, the reproductivity enhancement would occur and we could expect that there exist subcritical endemic steady states ^[7]. In such a case, even the subcriticality ${\cal R}_0 < 1$ does not guarantee the eradication of the disease.

Another possible extension would be realized if we introduce the class age structure of recovered individuals, because the loss of immunity depends on the time since recovery. It is a future challenge to develop age-structured epidemic models that can describe more realistic, complex dynamics of susceptibility, infectivity and immunity within host individuals.

Acknowledgements

H. Inaba and K. Okuwa were supported by the Japan Society for the Promotion of Science (JSPS), Grant-in-Aid for Scientific Research (C) (No.16K05266) and T. Kuniya was supported by JSPS, Grant-in-Aid for Early-Career Scientists (No.19K14594).

Conflict of interest

The authors declare there is no conflict of interest.