Steganographic coding scheme based on dither convolutional trellis under resampling mechanism

1.   Introduction

As an important branch of data hiding, steganography aims to establish covert communication by embedding the secret messages in the inconspicuously perceptive cover materials, such as text, audio, image, etc. In recent years, the traffic in mobile social networking and media sharing software have become the main traffic in mobile network while the technologies of mobile Internet, cloud computing and so on are developing rapidly and the intelligent mobile terminals are widely popularized. The massive digital media files in the traffic have become the important carriers of steganography. Due to the constraint of mobile network bandwidth and differences of various mobile terminals' displays, these digital media files may commonly be resampled by the media server when being pushed to the intelligent mobile terminals. The resampling is a transformation which enlarges or shrinks digital media files by a scale factor that is the same in all dimensions. For example, the audio resampling and image scaling are the common one-dimensional and two-dimensional resampling. The steganographic coding scheme which can reduce embedding distortion while ensuring the correct extraction of secret messages under resampling mechanism is worthy of more attentions.

To our best knowledge, there are some works on digital watermarking which are proposed to resist the resampling of media files. The watermarking messages were embedded in some domains which are insensitive to the resampling of media files, for example, non-subsampled contourlet transform (NSCT) domain^[1], discrete wavelet transform domain^{[2,3,4,5,6,7]}, lifting wavelet transform domain^[8], quaternion wavelet transform domain^[9], and three dimensional discrete cosine transform domain of sub block^[10]. To resist the resampling, the watermarking schemes based on geometric center and image mass centroid^[11], the phase spectrum of the frequency domain signal^[12,13], the invariant moment constructed by utilizing Radon and Fourier-Mellin transform^[14] and Zernike moment^[15] are presented. However, the capacities of the messages embedded in watermarking are small when the stego media files are distorted significantly and distinguished by some forensics scheme^[16] in these watermarking schemes. Consequently, it is necessary to conduct a research on the steganographic coding scheme under resampling mechanism which can minimize embedding distortion and combine with current typical steganographic schemes in the context of the current mobile internet applications.

In this paper, a steganographic coding scheme based on dither convolutional trellis is proposed. The approximate linear relation of the resampling mapping is analyzed so that the resampling mapping is estimated with finite sample pairs. The resampling stego media files with secret messages embedded are generated from the estimated resampling cover media files by syndrome-trellis codes (STCs)^[17,18]. Then the dither convolutional trellis (DCT) in one dimensional resampling is constructed. The source stego media files are generated from estimated resampling mapping, resampling stego media files and source cover media files by DCT embedding. The proposed scheme is also extended to the circumstance of two dimensional resampling such as image scaling. The proposed scheme can ensure the integrity of extracted messages and minimize embedding distortion under multi-dimensional resampling mechanism.

The rest of the paper is organized as follows. In the next section, some preliminaries including steganography under resampling mechanism, interpolation mapping in resampling, and the estimation of the resampling mapping are derived. In Section 3, some works on digital watermarking of media files to resist the resampling process are introduced. In Section 4, we propose the steganographic coding scheme based on dither convolutional trellis which includes the construction of dither convolutional trellis under one dimensional resampling mechanism and extensions of the proposed scheme to two dimensional resampling. Section 5 gives experimental results on embedding efficiency of the proposed scheme in one-dimensional resampling and steganalysis result of the proposed scheme applied in image scaling. Finally, Section 6 concludes the whole paper.

2.   Preliminaries

2.1.   Steganography under resampling mechanism

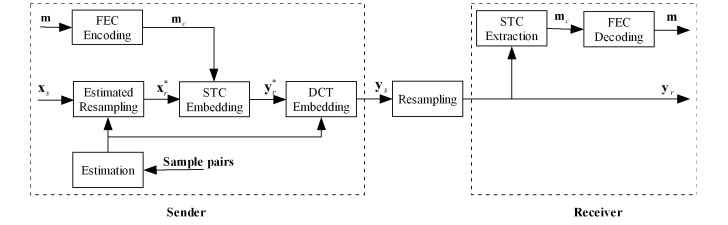
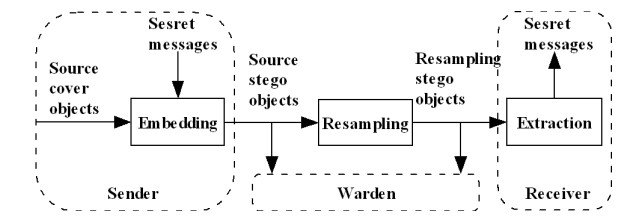
The generic communication system of steganography under resampling mechanism is shown in Figure 1. The sender and receiver are two end-points of the system. The digital media files employed to embed the secret messages are defined as source cover objects. The secret messages are embedded in source cover objects to generate the stego digital media files which are defined as source stego objects. Then the transmitted stego digital media files are resampled by the media server. The practical resampling of digital media files is the process of generating the new media files with different sizes by one or two dimensional interpolation, such as audio resampling and image scaling ^[19,20,21]. The resampling stego digital media files are defined as the resampling stego objects. The resampling module in this system is not disregarded, which means that the sender can not communicate with receiver directly. At the receiver, the secret messages are extracted from the resampling stego objects.

Figure 1.  Generic communication system of steganography under resampling mechanism.

DownLoad: Full-Size Img PowerPoint

In the steganography under resampling mechanism, we assume that the resampling strategy of media server is stable which means that a resampling media file is certain for the corresponding source media file. Not only generating the source stego objects to ensure the receiver extract secret messages from the corresponding resampling stego objects correctly, but the security of the system is significant which means that the warden cannot reveal the existence of the steganography by steganalysis. In this paper, we assume that the warden has full administrative authority over the whole communication system. This implies that the warden has access to both the source and resampling stego objects and has the knowledge of the steganography schemes, which is also shown in Figure 1.

2.2.   Interpolation mapping in resampling

The interpolations in resampling can be classified by target objects. The one-dimensional (1D) media files are resampled by 1D interpolation, and the two-dimensional (2D) interpolation is employed in resampling the 2D media files which is extended from the 1D interpolation. In the common 1D or 2D nearest-neighbor interpolation^[22], each resampling element is equal to the nearest neighbor source element. The resampling objects are the impaired versions of the source objects. The steganographic coding scheme for this case has been proposed in the related work^[23] which is omitted in the rest of the paper.

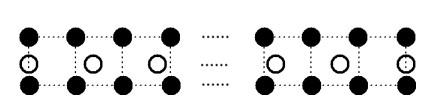
In 1D interpolation, the source and resampling objects with sizes ${N_s}$ and ${N_r}$ are denoted as ${\bf{s}} = \left({{s_1}, \ldots, {s_{{N_s}}}} \right)$ and ${\bf{t}} = \left({{t_1}, \ldots, {t_{{N_r}}}} \right)$. For a resampling element ${t_u}, u = 1, \ldots, {N_r}$, the interpolation coordinate which is defined as the relative coordinate in the corresponding source objects is obtained as (2.1).

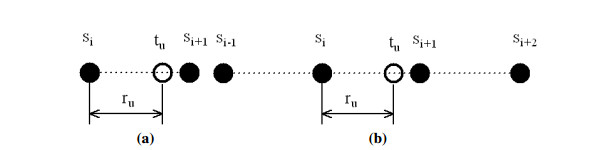
On the basis of the interpolation coordinate and window size $\delta$ of chosen interpolation strategy, the interpolation window of ${t_u}$ is determined which denotes the set of the neighbor source elements involved in the interpolation. The common 1D interpolation strategies are linear and cubic interpolations. The interpolation windows of a resampling element in linear and bilinear interpolation are denoted as ${{\bf{w}}_{2, u}} = \left({{s_i}, {s_{i + 1}}} \right)$ and ${{\bf{w}}_{4, u}} = \left({{s_{i - 1}}, {s_i}, {s_{i + 1}}, {s_{i + 2}}} \right)$ respectively, which are shown in Figure 2. The coordinate of the source element is got by $i = \left\lfloor {L\left(u \right)} \right\rfloor$ where the symbol $\left\lfloor {} \right\rfloor$ represents the process of rounding down. The decimal part of interpolation coordinate is obtained by ${r_u} = L\left(u \right) - \left\lfloor {L\left(u \right)} \right\rfloor$. The coefficients of the source elements in linear and cubic interpolation windows are denoted as ${{\bf{c}}_{2, u}} = \left({1 - {r_u}, {r_u}} \right)$ and ${{\bf{c}}_{4, u}} = \left({{c_1}\left({{r_u}} \right), {c_2}\left({{r_u}} \right), {c_3}\left({{r_u}} \right), {c_4}\left({{r_u}} \right)} \right)$ respectively.The coefficients of the source elements in cubic interpolation are determined by the specific interpolation strategy which are related to the decimal part of interpolation coordinate ${r_u}$. The mappings of the source and resampling elements in linear and cubic interpolation windows are given in (2.2) and (2.3).

Figure 2.  Interpolation windows in (a) linear interpolation and (b) cubic interpolation.

DownLoad: Full-Size Img PowerPoint

As the common 2D interpolations, the bilinear and bicubic interpolations are the extensions of linear and cubic interpolations^[22]. The interpolation windows of a resampling element in bilinear and bicubic interpolations are shown in Figure 3. The mappings of the source and resampling elements in bilinear and bicubic interpolations are given in (2.4) and (2.5). The decimal parts of interpolation coordinates in horizontal and vertical directions are represented by ${r_u}$ and ${r_v}$. Consequently, the mappings in bilinear and bicubic interpolations have the similar linear forms as those in linear and cubic interpolations by (2.2)-(2.5).

Figure 3.  Interpolation windows in (a) bilinear interpolation and (b) bicubic interpolation.

DownLoad: Full-Size Img PowerPoint

2.3.   Estimation of resampling mapping

Given that the elements in resampling digital media files are always integers, the resampling elements are rounded after the linear mapping of interpolations. The function of resampling for a resampling element $t$ can be denoted as (2.6)

Where $\left[\kern-0.15em\left[{} \right]\kern-0.15em\right]$ means rounding the values got by the linear mapping of interpolations, $\delta$ denotes the size of interpolation window and ${c_k}$ is corresponding coefficients of source element ${s_k}$ in the interpolation window.

However, it is difficult to directly get the detailed function of resampling under normal circumstances. We assume that the sender can collect some sample pairs which has the same sizes as those for steganography. Because the coefficients in interpolation window of the resampling element with the same interpolation coordinate keep unchanged, the resampling mapping in a interpolation window can be represented as (2.7) with ${N_p}$ pairs of source and resampling objects:

Where ${\bf{t}} = {\left({{t_1}, \ldots, {t_{{N_p}}}} \right)^{\rm{T}}}$ denotes a set of the resampling elements, ${{\bf{s}}_k} = {\left({{s_{k, 1}}, \ldots, {s_{k, {N_p}}}} \right)^{\rm{T}}}$ denotes a set of the source elements in interpolation window, and ${c_k}$ denotes the corresponding interpolation coefficients of source elements, ${\bf{\Delta }} = {\left({{\Delta _1}, \ldots, {\Delta _{{N_p}}}} \right)^{\rm{T}}}$ are the errors due to the rounding process. To estimate the coefficients of source elements ${c_k}$ with statistical stability, the equation (2.7) is solved by covariance. The errors ${\bf{\Delta }}$ have little relationship with the source elements, the covariance of the errors ${\bf{\Delta }}$ and the source elements is negligible^[24,25]. With ${\mathop{\rm cov}} \left({{\bf{\Delta }}, {{\bf{s}}_l}} \right) = 0, l = 1, \ldots, \delta$, the equation (2.7) is converted to (2.8)

The $\delta$ coefficients of source elements in (2.7) can obtained from the $\delta$ equations generated by (2.8). With estimated coefficients $c_k^ *$ in interpolation windows, the function of the estimated resampling mapping can be represented by (2.9)

3.   Related work

There are some works on digital watermarking of media files to resist the resampling process which is a type of geometric attacks.

The watermarking messages were embedded in some transform domains which are insensitive to the resampling of media files. In ^[1], two rotation invariant watermark embedding schemes in the non-subsampled contourlet transform (NSCT) domain based on the scale-adapted local regions are presented which can efficiently resist both signal processing attacks and geometric attacks. A novel scaling watermarking scheme is proposed in ^[2] which embedded the watermark in the low-frequency wavelet coefficients to achieve improved robustness. ^[3] presents a secure, robust, and blind adaptive audio watermarking algorithm based on singular value decomposition (SVD) in the discrete wavelet transform domain using synchronization code. The watermark data embedded by applying a quantization-index-modulation process on the singular values in the SVD of the wavelet domain blocks is robust to additive noise, resampling, low-pass filtering, requantization, MP3 compression, cropping, echo addition, and de-noising. In ^[4], in order to resist both traditional signal processing attacks and geometric attacks, the watermark image is embedded in a content-based manner by modifying the wavelet transform coefficients. In ^[5], a blind and adaptive audio watermarking algorithm is proposed by combining the robustness of vector norm with that of the approximation Components after the discrete wavelet transform (DWT). This algorithm is able to tolerate a wide class of common attacks such as additive white Gaussian noise (AWGN), Gaussian Low-pass filter, Kaiser Low-pass filter, resampling, requantizing, cutting, MP3 compression and echo. In ^[6], the data is embedded in high pass filter coefficients of Discrete Wavelet Transform by LSB method. A blind digital speech watermarking technique based on Eigen-value quantization in Discrete Wavelet Transform is presented in ^[7] which is robust against different attacks such as filtering, additive noise, resampling, and cropping. In ^[8], a watermarking scheme for breath sounds, combining lifting wavelet transform (LWT), discrete cosine transform (DCT), singular value decomposition (SVD) and dither modulation (DM) quantization is proposed to insert encrypted source and identity information in breath sounds. The watermarking scheme obtains good robustness against common manipulation attacks and preserves imperceptivity. A audio watermarking scheme based on self-adaptive particles warm optimization (SAPSO) and quaternion wavelet transform (QWT) is proposed in ^[9]. The scheme is not only robust against de-synchronization attack, but also typical signal manipulations and StirMark attack. In order to improve the ability of resisting geometric attacks, a watermarking algorithm for medical volume data in sub-block three-dimensional discrete cosine transform domain is presented in ^[10].

The data can be embedded in some other domains to resist the resampling attack. An anti-geometric attack SVD digital watermark algorithm based on geometric center and image mass centroid is proposed in ^[11] to resist large scale geometric deformation. In ^[12,13], the data is embedded in the phase spectrum of the frequency domain signal of audio files by the phase coding technique which can resist signal processing operations like noise addition, cropping and resampling. In ^[14], a watermarking algorithm based on constructing invariant moments by the analytic Fourier–Mellin transform is proposed which was robust to usually image processing operation and geometrical attacks. In ^[15], a spatial image adaptive steganography algorithm based on Zernike moment is proposed to resist scaling attack and statistic detection.

However, in these watermarking schemes, the cover media files may be distorted significantly which may be distinguished by some forensics scheme^[16], and the capacities of the messages embedded are small. It is necessary to conduct a steganographic coding scheme under resampling mechanism which can minimize embedding distortion in the context of the current mobile internet applications.

4.   Steganographic coding scheme based on dither convolutional trellis

In this section, we propose a steganographic coding scheme based on dither convolutional trellis under the resampling mechanism. The framework of the proposed steganographic coding scheme is shown in Figure 4. Due to the errors resulting from the estimation of resampling mapping, forward error corrections (FECs) are employed in the framework to reduce the influence on the transmission of the secret messages. Convolutional code is selected as the FEC in this paper. The parity check matrix of convolutional code and the extraction matrix in STCs have the similar structures. The joint parity check matrix generated from them also has the similar structure as that of convolutional code^[23].

Figure 4.  Framework of steganographic coding scheme based on dither convolutional trellis.

DownLoad: Full-Size Img PowerPoint

At the sender, the secret messages ${\bf{m}}$ are encoded to coded secret messages ${{\bf{m}}_c}$ by FEC encoding. Meanwhile the estimated resampling cover objects ${\bf{x}}_r^ *$ are generated by estimated resampling mapping and source cover objects ${{\bf{x}}_s}$. The coded secret messages ${{\bf{m}}_c}$ are embedded in the estimated resampling cover objects ${\bf{x}}_r^ *$ by STC embedding. The estimated resampling stego objects with the least distortion are generated which are denoted as ${\bf{y}}_r^ *$. Then the dither convolutional trellis (DCT) is constructed by source cover objects ${{\bf{x}}_s}$, estimated resampling stego objects ${\bf{y}}_r^ *$ and estimated resampling mapping. The corresponding source stego objects ${{\bf{y}}_s}$ with the least distortion are got by dither convolutional trellis (DCT) embedding. At the receiver, the resampling stego object ${{\bf{y}}_r}$ are obtained after the processing of the media server. Then the coded secret messages ${{\bf{m}}_c}$ are got by extraction matrix in STC schemes, and the secret messages ${\bf{m}}$ are got by FEC decoding. The proposed scheme is not reversible where the receiver can not reconstructed the source cover objects ${{\bf{x}}_s}$ from the resampling stego objects ${{\bf{y}}_r}$.

Owing to that the source and resampling stego objects ${{\bf{y}}_s}$ and ${{\bf{y}}_r}$ can be captured by warden, minimizing the distortion of the steganographic coding scheme under resampling mechanism can be converted to two steps. Firstly, with distortion profiles and the estimated resampling cover objects ${\bf{x}}_r^ *$ which are got from estimated resampling mapping and source cover objects ${{\bf{x}}_s}$, the distortions of the resampling stego objects ${\bf{y}}_r^ *$ with secret messages embedded are minimized by STC embedding. Secondly, according to the estimated resampling mapping, distortion profiles and the resampling stego objects ${\bf{y}}_r^ *$, the distortions of the source stego objects ${{\bf{y}}_s}$ are minimized by DCT embedding. The function of the DCT embedding is represented by (4.1):

Where ${R^ * }\left({} \right)$ denotes the function of estimated resampling mapping and ${D_s}\left({} \right)$ denotes the function of the distortions in source objects.

In the following subsection, the construction of the dither convolutional trellis under 1D resampling mechanism is described. Then the extension of the proposed scheme to 2D resampling is demonstrated.

4.1.   Dither convolutional trellis under 1D resampling mechanism

The dither convolutional trellis under 1D resampling mechanism is constructed by source cover objects and estimated resampling stego objects. The source cover objects are denoted as ${{\bf{x}}_s} = \left({{x_{s, 1}}, \ldots, {x_{s, {N_s}}}} \right)$ with size ${N_s}$, and the estimated resampling stego objects are denoted as ${\bf{y}}_r^ * = \left({y_{r, 1}^ *, \ldots, y_{r, {N_r}}^ * } \right)$ with size ${N_r}$. So the equation (4.1) can furtherly be written as (4.2).

Where the distortion profile in $\pm 1$ embedding of the source cover objects is denoted as $\rho = \left({{\rho _1}\left({{\omega _1} - {x_{s, 1}}} \right), } \right.\left. { \ldots, {\rho _{{N_s}}}\left({{\omega _{{N_s}}} - {x_{s, {N_s}}}} \right)} \right)$. The source stego objects ${{\bf{y}}_s}$ satisfying ${\bf{y}}_r^ * = {R^ * }\left({{{\bf{y}}_s}} \right)$ are got by dither convolutional trellis and distortion profiles.

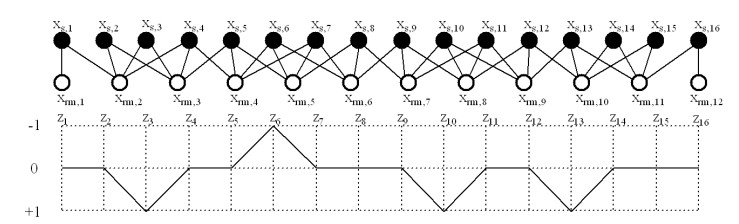
The dither convolutional trellis is a graph consisting of $3{N_s}$ nodes which is organized in a grid of ${N_s}$ columns and 3 rows. The node in $ith$ column and $jth$ row means that the source cover element ${x_{s, i}}$ is possibly modified by the value ${n_{i, j}} = j - 2$. The edges connecting two nodes in adjacent columns represent the combinations of the modifications to adjacent source elements. The paths which start in the leftmost column and extend to the rightmost column in the trellis represent the modification choices of all source cover elements. The path can be denoted as ${\bf{z}} = \left({{z_1}, \ldots, {z_{{N_s}}}} \right)$ in which each element satisfies ${z_i} = {n_{i, j}} \in \left\{ { - 1, 0, + 1} \right\}$. The feasible source stego objects can be got by ${{\bf{y}}_s} = {{\bf{x}}_s} + {\bf{z}}$ when the modified resampling objects satisfy ${{\bf{x}}_{rm}} = {R^ * }\left({{{\bf{x}}_s} + {\bf{z}}} \right) = {\bf{y}}_r^ *$. To find the source stego objects with the least embedding distortion, we assign distortion weights to all trellis nodes and thus convert the equation (4.2) to the problem of finding the feasible path with the least distortion weights through the trellis. The distortion weights of the nodes with label ${\rho _i}({n_{i, j}})$ in the trellis depend on the input of distortion profiles. The path through a node ${n_{i, 2}} = 0$ increases a distortion weight of 0 and the path through a node satisfying ${n_{i, 2}} = 1$ or ${n_{i, 2}} = -1$ increases a distortion weight of ${\rho _i}(1)$ or ${\rho _i}(-1)$. The dither convolutional trellis of cubic interpolation with the sizes of the source and resampling objects ${N_s} = 16, {N_r} = 12$ is shown in Figure 5. In Figure 5, the feasible path kept with the least distortion of the source cover object is shown as ${\bf{z}} = \left({0, 0, 1, 0, 0, - 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0} \right)$.

Figure 5.  Example of a path in dither convolutional trellis of cubic interpolation.

DownLoad: Full-Size Img PowerPoint

Then the dither convolutional trellis embedding is described. Because the modifications of the source cover objects ${{\bf{x}}_s}$ are restricted by the resampling stego objects ${\bf{y}}_r^ *$, the DCT embedding is conducted with the interpolation window moving. There are ${N_r}$ steps in DCT embedding. It is observed that the modifications of the first and last source elements are only determined by the corresponding resampling elements in 1D interpolation. As a result, the modification in the first column of trellis is ${z_1} = y_{r, 1}^ * - {x_{s, 1}}$. The modification in the last column of trellis is ${z_{{N_s}}} = y_{r, {N_r}}^ * - {x_{s, {N_s}}}$. In the embedding of the other resampling elements, the interpolation windows of adjacent resampling elements may be overlapped. The number of the overlapped source elements between the interpolation windows of resampling stego elements $y_{r, u - 1}^ *$ and $y_{r, u}^ *$ is represented by ${w_u}, u = 2, \ldots, {N_r}$. We assume that the resampling is downsampling in which the resampling rate satisfies $\beta = {N_r}/{N_s} \in (0, 1)$. The interpolation windows of adjacent resampling elements will never be completely overlapped. With window size $\delta = 2$ in linear interpolation, the number of the overlapped source elements is ${w_u} \in \left\{ {0, 1} \right\}$. The number of the overlapped source elements is satisfying ${w_u} \in \left\{ {0, 1, 2, 3} \right\}$ with window size $\delta = 4$ in cubic interpolation.

Take the DCT embedding of the resampling stego element $y_{r, u}^ *$ for example, the interpolation windows and dither convolutional trellis in cubic interpolation are described in Figure 6. Here the window size of cubic interpolation is $\delta = 4$, the coefficients of interpolation window are denoted as ${{\bf{c}}_u} = \left({{c_1}, {c_2}, {c_3}, {c_4}} \right)$, and the source cover elements in interpolation window are denoted as ${{\bf{w}}_u} = \left({{x_{s, i - 1}}, {x_{s, i}}, {x_{s, i + 1}}, {x_{s, i + 2}}} \right)$. Before the embedding of the resampling stego element $y_{r, u}^ *$, the number of the overlapped source elements between the interpolation windows of resampling stego elements $y_{r, u-1}^ *$ and $y_{r, u}^ *$ is ${w_u} = 2$. In the embedding of the resampling stego element $y_{r, u-1}^ *$, the paths have been extended to the source element ${x_{s, i}}$. The number of paths with all combinations of $\left({{z_{i - 1}}, {z_i}} \right)$ which are kept with the least distortion weights is not more than ${3^{{w_u}}} = 9$. Then all the paths extend to the rightmost source cover element ${x_{s, i + 2}}$ in interpolation window of resampling stego elements $y_{r, u}^ *$. There are $\delta - {w_u} = 2$ source elements are newly involved in the embedding. All modified combination of the $\delta - {w_u} = 2$ source elements which are denoted as $\left({{z_{i + 1}}, {z_{i + 2}}} \right) \in {\left\{ { - 1, 0, + 1} \right\}^2}$ are represented by red lines in Figure 6. The dither modification of the interpolation window is represented as ${{\bf{z}}_u} = \left({{z_{i - 1}}, {z_i}, {z_{i + 1}}, {z_{i + 2}}} \right)$. The modified resampling element is got by (4.3)

Figure 6.  DCT embedding of a resampling stego element in cubic interpolation.

DownLoad: Full-Size Img PowerPoint

Each modified resampling cover element is checked whether that is equal to the resampling stego element $y_{r, u}^ *$. The path is kept if the modified resampling cover element satisfies ${x_{rm, u}} = y_{r, u}^ *$. After finding all feasible paths, the number of the overlapped source elements between the interpolation windows of resampling stego elements $y_{r, u}^ *$ and $y_{r, u+1}^ *$ is ${w_{u + 1}} = 3$. The distortion weight of all paths with all the combinations of $\left({{z_i}, {z_{i + 1}}, {z_{i + 2}}} \right)$ are calculated and the path with the least weight in each combination is kept. The complexity of DCT embedding in this steganographic coding scheme is related to the length of resampling stego objects and number of the overlapped source elements between the adjacent interpolation windows.

In the case of upsampling, the interpolation windows of the adjacent resampling elements may be completely overlapped. That means it may be impossible to embed the secret message bits into the adjacent resampling elements at the same time. Thus part of the resampling cover elements are chosen for embedding secret messages in which interpolation windows of all resampling elements are not completely overlapped. Then the steganographic coding scheme under upsampling mechanism is converted to that under downsampling mechanism.

4.2.   Extension of the proposed scheme to 2D resampling

In conventional steganographic coding schemes, the cover objects with one dimension are transformed from 2D digital media files which are the common carriers of steganography. The steganographic coding scheme based on dither convolutional are extended to the case of 2D resampling by some additional processes.

According to the dither convolutional trellis under 1D resampling mechanism, the computational complexity of the DCT embedding depends on the number of the overlapped source elements between the adjacent interpolation windows. In 2D resampling, the source elements between the adjacent interpolation windows are overlapped complicatedly. So too many paths in each step of the DCT embedding has to be kept if the secret messages are embedded in all resampling cover objects. To reduce the computational complexity and embed the secret messages as much as possible, we choose some rows (columns) of the resampling objects for embedding in which interpolation windows of resampling elements are not overlapped in column (row) direction. Take the rows for example, the source elements between the adjacent interpolation windows in the same row are overlapped like that in 1D resampling, but the source elements between any interpolation windows in the different rows are never overlapped. If the ${u_1}th$ row of the resampling objects in bilinear interpolation are chosen for embedding, the last row coordinate of the source elements in interpolation windows is $\left\lfloor {L\left({{u_1}} \right)} \right\rfloor + 1$. In the next ${u_2}th$ row for embedding, the first row coordinate of the source elements in interpolation windows must satisfy $\left\lfloor {L\left({{u_2}} \right)} \right\rfloor > \left\lfloor {L\left({{u_1}} \right)} \right\rfloor + 1$ which can be further written as $\left\lfloor {L\left({{u_2}} \right)} \right\rfloor - \left\lfloor {L\left({{u_1}} \right)} \right\rfloor > 1$. In bicubic interpolation, the last row coordinate of interpolation windows of the chosen ${u_1}th$ row is $\left\lfloor {L\left({{u_1}} \right)} \right\rfloor + 2$, the first row coordinate of interpolation windows of the chosen ${u_2}th$ row must satisfy $\left\lfloor {L\left({{u_2}} \right)} \right\rfloor - 1 > \left\lfloor {L\left({{u_1}} \right)} \right\rfloor + 2$ which can be further written as $\left\lfloor {L\left({{u_2}} \right)} \right\rfloor - \left\lfloor {L\left({{u_1}} \right)} \right\rfloor > 3$.

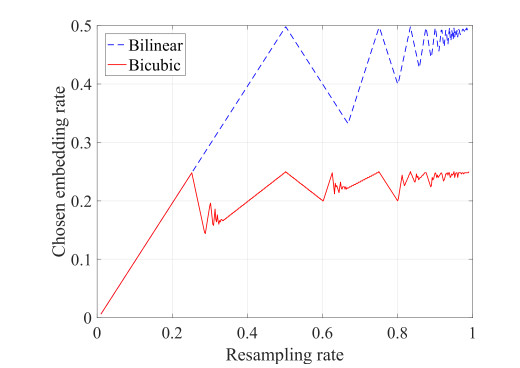
Assumed that the sizes of the source objects and resampling objects are ${N_s} \times {N_s}$ and ${N_r} \times {N_r}$ respectively, the resampling rates in row and column directions are $\beta = {N_r}/{N_s}$. The chosen embedding rate $\gamma$ is defined as the rate of the maximum number of the chosen rows in resampling objects to the number of the rows in source objects. The chosen embedding rate with ${N_s} = 512$ are shown in Figure 7 in different interpolations. In Figure 7, the chosen embedding rate raises with the resampling rate increasing when the resampling rate is small, then the chosen embedding rate is stabilizing with the resampling rate increasing. The chosen embedding rate are not more than 1/2 in bilinear interpolation, which are not more than 1/4 in bicubic interpolation.

Figure 7.  Chosen embedding rates with different resampling rates in bilinear and bicubic interpolation.

DownLoad: Full-Size Img PowerPoint

Take a source image with the size $512 \times 512$ for example, the resampling rate is set to be $\beta = 0.7$ in linear interpolations, the most resampling elements and the corresponding source elements chosen for embedding are presented in Figure 8. In Figure 8, the partly rows of resampling elements are chosen for embedding, and partly rows of source elements are involved in embedding. It should be noted that the other resampling elements may be modified although they are not selected for embedding.

Figure 8.  Resampling elements and the corresponding source elements chosen for embedding.

DownLoad: Full-Size Img PowerPoint

The dither convolutional Trellis of each row in 2D resampling is similar to that in 1D resampling. There are some differences in DCT embedding of the resampling elements. The first and last resampling elements are related to the two or four source elements in corresponding columns. If the resampling rate is $\beta \in \left({0, 1} \right)$, the interpolation windows of adjacent resampling elements in the same row may be partly overlapped. The number of the overlapped source elements between the interpolation windows of resampling stego elements is represented by ${w_{u, v}}$. With window size $\delta = 4$ in bilinear interpolation, the number of the overlapped source elements is satisfying ${w_{u, v}} \in \left\{ {0, 2} \right\}$. The number of the overlapped source elements is satisfying ${w_{u, v}} \in \left\{ {0, 4, 8, 12} \right\}$ with window size $\delta = 16$ in bicubic interpolation. The interpolation windows of a row of the resampling elements in bilinear interpolation is shown in Figure 9.

Figure 9.  Interpolation windows of a row of resampling elements in bilinear interpolation.

DownLoad: Full-Size Img PowerPoint

5.   Experimental results

The experiments of the proposed steganographic coding scheme are presented in this section. The proposed coding scheme is evaluated by embedding efficiency in 1D resampling. Then the security of the proposed scheme applied in image scaling (2D resampling) is benchmarked. The convolutional code with the code rate $1/2$ is employed in the proposed scheme as the FEC. The secret messages can be extracted correctly in the proposed steganographic coding scheme in 1D resampling and image scaling.

5.1.   Evaluation of the proposed coding scheme

The source cover objects and the secret messages are both provide by a pseudo-random bits generator. Three distortion profiles are used for benchmarking security of the steganographic coding scheme which are similar to ^[17,18]. They are the constant profile ${\rho _i} = 1$, the linear profile ${\rho _i} = 2i/{N_s}$ and the square profile ${\rho _i} = 3{\left({i/{N_s}} \right)^2}$. We assume that the profiles of the resampling cover objects are got from those of the source cover objects and the estimated resampling mapping. The embedding efficiency is employed to evaluate the proposed scheme. The embedding efficiencies of source and resampling objects for three distortion profiles are calculated. Each embedding efficiency is obtained as an average over 2000 samples.

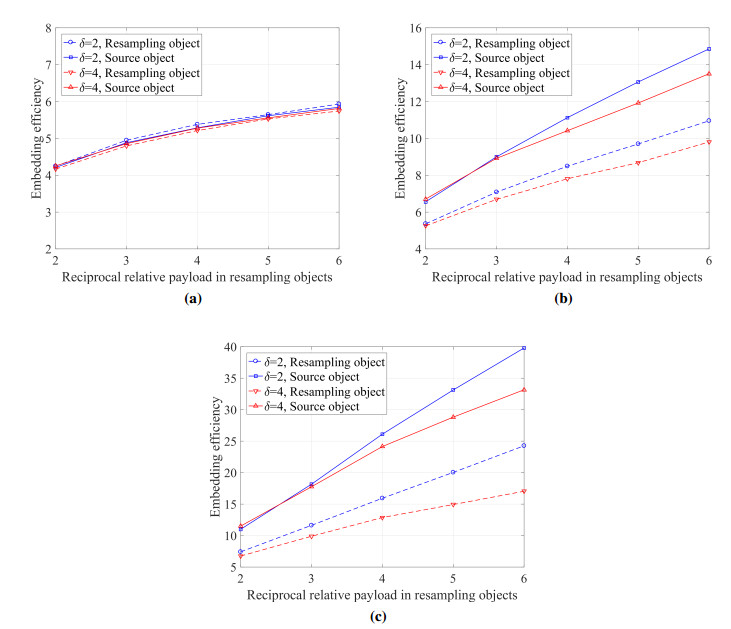
The embedding efficiencies of source and resampling objects with different relative payloads for three distortion profiles are performed in Figure 10. The size of source cover objects is set to be ${N_s} = 2000$, the resampling rate is set to be $\beta = 0.75$. The relative payloads in resampling objects are set to be $\alpha = 1 / 2, 1 / 3, 1 / 4, 1 / 5, 1 / 6$. In Figure 10, the embedding efficiency of the source and resampling objects arise with relative payload decreasing. In Figure 10a, the embedding efficiency of the source and resampling objects with different window sizes are almost the same for constant profiles. In Figure 10b and 10c, for linear and square profiles, the embedding efficiencies of the source object are better than those of the estimated resampling objects, and the embedding efficiencies of the source and resampling objects decrease slightly with window size increasing.

Figure 10.  Embedding efficiencies of source and resampling objects with different relative payloads for (a) the constant profile (b) the linear profile (c) the square profile.

DownLoad: Full-Size Img PowerPoint

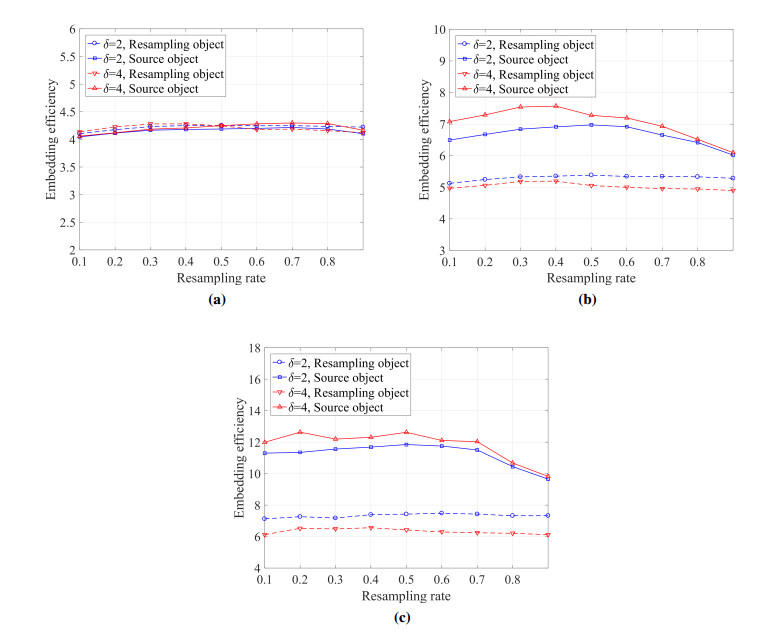
Then the embedding efficiencies of source and resampling objects with different resampling rates for three distortion profiles are shown in Figure 11. The size of source objects is set to be ${N_s} = 2000$, the relative payload in resampling objects is set to be $\alpha = 1/2$. The resampling rates are set to be $\beta = 0.1, 0.2, \ldots, 0.9$. In Figure 11, the embedding efficiencies of the resampling objects almost keep unchanged with resampling rate increasing for three distortion profiles. In Figure 11a, the embedding efficiencies of the source objects for constant profile are almost the same with the resampling rate increasing. In Figure 11b and 11c, the embedding efficiencies of the source objects for linear and square profiles will keep unchanged with resampling rate $\beta < 0.5$ and decrease with resampling rate $\beta > 0.5$. With window size increasing, the embedding efficiencies of the source objects arise slightly, and the embedding efficiencies of the resampling objects decrease slightly.

Figure 11.  Embedding efficiencies of source and resampling objects with different resampling rates for (a) the constant profile (b) the linear profile (c) the square profile.

DownLoad: Full-Size Img PowerPoint

It is proved that the proposed steganographic coding scheme under 1D resampling mechanism minimizes the embedding distortion while ensuring the accuracy of secret messages extraction for different distortion profiles.

5.2.   Security of the proposed scheme in image scaling

The experiments in image scaling are carried out on the BOSSbass ver.1.01^[26], which contains 10000 uncompressed grayscale images sized $512 \times 512$. The relative payloads in the resampling pixels in a row are set to be $\alpha = 0.2, 0.4$. The bilinear interpolation is chosen as the interpolation strategy in image scaling. The resampling rates are set to be $\beta = 0.25, 0.5, 0.75$. The steganographic method S-UNIWARD^[27] is employed to generate the distortion profiles of source and resampling images. In the phase of steganalysis, the feature sets maxSRM^[28] are employed in source and resampling images. The ensemble classifier^[29] is used to measure the property of feature sets. In detail, half of the cover and stego feature sets are used as the training set while the remaining half are used as testing set. The criterion to evaluate the performance of feature sets is the minimal detection error ${p_E}$ under equal priors achieved on the testing set^[29]:

Where ${p_{FA}}$ is the false alarm rate, and ${p_{MD}}$ is the missed detection rate. The performance is evaluated using the average value of ${p_E}$ over ten random tests. As the closest methods, the detection error rates of image steganography based on Zernike moment (ISZM) are present for comparison.

The detection error rates of source and resampling images with different relative payloads and resampling rates are demonstrated in Table 1. In Table 1, all the detection errors decrease with the relative payload and resampling rate arising. The detection errors of resampling images are larger than those of source images.Then the detection error rates of the source images in the proposed scheme and ISZM with different resampling rates are presented in Table 2 when the lengths of the secret message bits embedded in each image are given in Table 3. From Table 2 and 3, the detection error rates of the proposed scheme in which more secret messages are embedded are larger than those of ISZM. It is proved that the proposed steganographic coding scheme applied in image scaling performs better security than existing methods.

Table 1.  Detection error rates of resampling and source images.

	$\beta=0.25$	$\beta=0.5$	$\beta=0.75$
$\alpha=0.2$, Source images	0.4796	0.4526	0.4363
$\alpha=0.2$, Resampling images	0.4803	0.471	0.4558
$\alpha=0.4$, Source images	0.4439	0.3586	0.3383
$\alpha=0.4$, Resampling images	0.4452	0.4199	0.3709

---

 | Show Table

DownLoad: CSV

Table 2.  Detection error rate of the proposed scheme and ISZM.

	$\beta=0.25$	$\beta=0.5$	$\beta=0.75$
$\alpha=0.2$	0.4796	0.4526	0.4363
$\alpha=0.4$	0.4439	0.3586	0.3383
ISZM	0.2988	0.2845	0.2979

---

 | Show Table

DownLoad: CSV

Table 3.  Lengths of the secret message bits per image in the proposed scheme and ISZM.

	$\beta=0.25$	$\beta=0.5$	$\beta=0.75$
$\alpha=0.2$	1613	6502	9753
$\alpha=0.4$	3226	13004	19506
ISZM	128	128	128

---

 | Show Table

DownLoad: CSV

6.   Conclusion

In this paper, we propose the steganographic coding scheme based on dither convolutional trellis under resampling mechanism. The dither convolutional trellis under 1D resampling mechanism is constructed by utilizing common linear mapping in resampling. The source stego objects are generated from source cover objects and resampling stego objects by dither convolutional trellis embedding. The proposed scheme is also extended to 2D resampling such as image scaling. The experimental results show that the proposed scheme can achieve less embedding distortion while ensuring the covert communication under multi-dimensional resampling mechanism.

Even if the steganographic coding scheme based on dither convolutional trellis can achieve high security, the computational complexity of the scheme is high. Part of the resampling elements are discarded in the embedding under 2D resampling mechanism. In the future work, we will reduce the computational complexity of steganographic coding scheme and try to make use of all resampling elements for secret messages embedding.

Acknowledgments

This work was supported by The National Natural Science Foundation of China(Grant No. 61602247, 61702235, U1836104, U1636117), Natural Science Foundation of Jiangsu Province(Grant No. BK20160840) and Fundamental Research Funds for the Central Universities (30918012204).

Conflict of interest

All authors declare no conflicts of interest in this paper.