1. Background
Tuberculosis (TB) is an infectious disease caused by the bacterium Mycobacterium Tuberculosis, which typically affects lungs (known as pulmonary TB of PTB) and that mostly occurs in adults, i.e. in individuals above 14 years of age, but could also affect other parts of body (known as extra-pulmonary TB or EPTB). Tuberculosis is one of the leading causes of death worldwide after HIV and remains a major public threat in many countries. An estimate shows that globally about one-third of the population is infected with TB bacteria. The global incidence of all forms of TB cases during 2008 was estimated to be 9.4 million, at the rate of 139/100,000 population and in 2014 there were an estimated 9.6 million incident cases of TB, which is equivalent to 130/100,000 population.
In this paper we present a model for the disease situation in India, one of the countries in which the disease is endemic. This work is an extension of previous results, [3,15,18] and in particular of the work in progress [19], in that we account for the diagnostic system to be partioned into the public and private sectors, contrary to what was assumed in the earlier works.
2. Motivation
In India, the tuberculosis situation is characterized by high prevalence (total number of TB cases over a period of one year) and incidence (new TB cases over a period of one year) of disease or active TB (when the individual is infectious and transmits bacteria to others) and high rate of transmission of infection (the latent TB-individual is infected with TB bacteria but cannot transmit them to others; also, in this situation, bacteria remain in the dormant state). Primary surveys show that about 30% -50% of India population is latently infected. This means that people have been infected by TB bacteria but are not ill with the disease and do not transmit it but may become infectious in the future.
The countrywide National Tuberculosis Program (NTP) to control TB was originally undertaken in 1962, but it did not achieve the goal of disease burden reduction. The Government of India has intensified anti-tuberculosis activities by implementing the DOTS strategy under the Revised National Tuberculosis Control Program (RNTCP) since 1998. DOTS is the WHO recommended treatment strategy to cure TB. The 2015 TB statistics show that the incidence rate is 217 [112-315] per thousand individuals in the population [16] and the prevalence rate estimate for the year 2014 is 195 [131-271] per 100,000 individuals in the population, [17]. The implementation of DOTS across the world has shown a decline of 1.5% in incidence over the past decade. In the new 2016-2020 Global Plan to end TB, "The Paradigm Shift", one of the targets is to achieve a 10% annual decline in TB incidence. The question of resistance to treatment and reactivation has been addressed in [13,14].
By formulating a model and analysing it, the objective of this paper is to give some estimates of the crucial parameters so that acting on these parameters may help in achieving the eradication of TB. These results could help in defining polices to bring down the TB burden in India. To achieve these goals the need for modelling is evident.
As it will become clear in the following sections, there is a discrepancy between the rates at which TB is diagnosed between the public and the private sectors. While one would expect the latter to be more efficient, and therefore to achieve a higher diagnosis rate, in fact exactly the opposite occurs. One highly improbable possibility is that the equipment or the doctors in the private sector is less efficient than in the public one. Another alternative considers instead psychologic reasons: doctors would be reluctant to notify paying patients that they have been exposed to the disease or maybe are even asymptomatic disease-carriers. At this point, independently of the reason, the question arises whether this diagnosis failure rate contributes in a substantial way to the endemicity of the disease.
On the basis of the above discussion, we would like then to address two main questions: namely whether the somewhat surprising difference in the diagnosis rates of the public and private sector makes a relevant difference for the disease eradication, and whether this eradication is at all possible.
3. The model assumptions
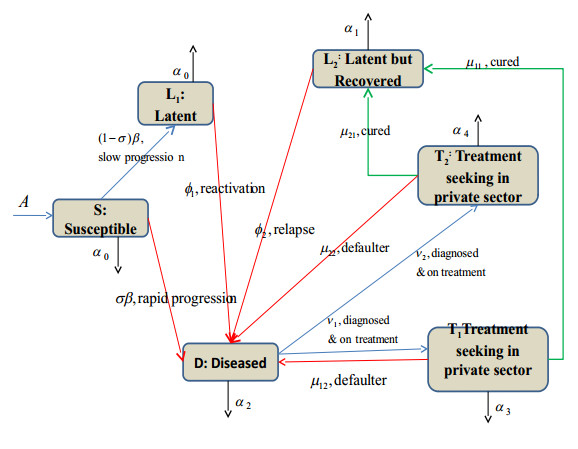
The flow diagram in Figure 1 below corresponds to the understanding among epidemiologists in India of how a susceptible person in a population may become infected and infectious, move through treatment, recover and then possibly become infectious again. This provides the road map for writing the mathematical model for TB. In India, the healthcare sector is segregated into two sectors: the public one (i.e. government run hospitals) and the private one (clinics and/or hospitals run by private practitioners). Research shows that diagnosis and treatment in the public sector has a larger success rate in comparison to seeking care in the private sector. But, unfortunately, due to different reasons TB patients tend to seek care in private sector clinics/hospitals. TB spread is determined largely by the nature of interaction of patients with active TB with the rest of the population.
We assume that the total human population is N(t). This population is divided into six classes consisting of susceptible S(t), latently-infected L1(t), latent but recovered L2(t), the infectious or diseased population D(t), population treated in public sector T1(t) and lastly the population treated in private sector T2(t). Note that the L2 individuals are cured (recovered) after completing six-months of anti-TB treatment (ATT). These cured individuals remain latent as TB bacteria may remain dormant in the host body. Thus
|
N(t)=S(t)+L1(t)+L2(t)+D(t)+T1(t)+T2(t).
|
(1)
|
For convenience we omit the explicit dependence on time in these population classes.
The model, given by equations (2) below, assumes standard incidence between the diseased and susceptible population and mass action interaction between the latent but recovered L2 individuals and diseased populations. A fraction σ of the latent persons exposed to infection L1 rapidly moves to the infectious/diseased state D, because the disease progresses spontaneously to the virulent form. The rest (1−σ) remain latently infected (L1) for a long period of time. In the model we have considered only endogenous reactivation which means that the TB bacteria which remain dormant have now become active and thus the individual becomes infectious. Thus an L1 individual becomes diseased only by reactivation. Also, it is known that the relapse to the infectious state (D) from the latent state (L2) is enabled by contact with an infectious individual. Thus recovered individuals, L2, become diseased by re-infection. This can only happen after interacting with the diseased population, D. Therefore, we have considered mass-action of L2 and D individuals to model these interactions and thus to represent the re-infection process of the L2 class.
Further, note that the individuals under treatment cannot infect the suceptibles and recovered populations, since the TB bacterium becomes inactive already in the first few weeks of the treatment. Also, other safety measures, like wearing masks, reduce the chances of transmitting disease early in the treatment. Therefore, in the model we have not assumed transmission of disease from individuals undergoing treatment i.e. T1 and T2.
The parameter β is reported by epidemiologists as the number of people infected by one infected person per year. Usually people who are in class D show symptoms and seek treatment. The rate at which treatment is sought from public clinics is ν1 and from private clinics is ν2. Not all diseased individuals are successfully treated. Those seeking treatment from the public and the private sectors remain diseased at rates μ12 and μ22 respectively. This happens for several reasons including noncompliance of drug regimen, drug resistance or other health complications. Recovery after treatment occurs at rates μ11 and μ21 from the public and the private sector, respectively. Recovered individuals are considered latently infected as the TB bacilli remain in their lungs. So these fall into the class L2 and are more likely to relapse into the diseased (D) class than those in class L1. The progression to diseased state from the L1 class occurs at rate ϕ1. The progression rate to the diseased state from the L2 class is ϕ2 with ϕ2>ϕ1. In India 40% of the population lies in classes L1 and L2, with 1% of the population being added every year.
4. The mathematical model
Recalling (1) and using standard incidence for modeling the disease spread among susceptibles and diseased, as explained in the previous section, we have
|
dSdt=A−βSDN−α0SdL1dt=(1−σ)βSDN−α0L1−ϕ1L1dDdt=σβSDN−α2D+ϕ1L1+ϕ2L2D+(μ12T1+μ22T2)−(ν1+ν2)DdT1dt=ν1D−(α3+μ11+μ12)T1dT2dt=ν2D−(α4+μ21+μ22)T2dL2dt=μ11T1+μ21T2−α1L2−ϕ2L2D
|
(2)
|
For later purposes, we give here the Jacobian of (2)
|
J=(J11βSDN2βSN(DN−1)βSDN2βSDN2βSDN2J21J22J23J24J25J26J31J32J33J34J35J3600ν1J440000ν20J55000−ϕ2Dμ11μ21J66)
|
(3)
|
with
|
J11=βDN(SN−1)−α0,J21=(1−σ)βDN(1−SN),J22=−(1−σ)βSDN2−(α0+ϕ1),J23=J24=J25=J26=−(1−σ)βSDN2,J31=σβDN(1−SN),J32=ϕ1−σβSDN2,J33=σβSN(1−DN)+ϕ2L2−(ν1+ν2+α2),J34=μ12−σβSDN2,J35=μ22−σβSDN2,J36=ϕ2D−σβSDN2,J44=−(α3+μ11+μ12),J55=−(α4+μ21+μ22),J66=−(α1+ϕ2D).
|
5. Basic reproduction number
It is easily seen that there are only two possible equilibria, as all other combinations of population values lead to some inconsistency in the solution of the equilibrium system.
The disease-free equilibrium (DFE) E0=(S0,0,0,0,0,0) is easily assessed, the value of susceptibles coming from the first equilibrium equation of (2), S0=Aα−10, with all other populations vanishing. Then there is possibly the coexistence equilibrium E∗=(S∗,L∗1,D∗,T∗1,T∗2,L∗2), which will be discussed later.
Note that presently there are no available data on the value of R0 for TB in India. We thus calculate the basic reproduction number R0 as the spectral radius of next generation matrix [30].
There are two infected classes L1 and D, so evaluating the gains and losses of each such compartment, we have:
|
[New infections, i.e. Gains to L1New infections, i.e. Gains to DLosses from L1Losses from D]=[(1−σ)βSDNσβSDN+ϕ2L2D+ϕ1L1(α0+ϕ1)L1(α2+ν1+ν2)D−(μ12T1+μ22T2)]
|
By suitably taking partial derivatives, we find
|
F=[∂∂L1[(1−σ)βSDN]∂∂D[(1−σ)βSDN]∂∂L1(σβSDN+ϕ2L2D)∂∂D(σβSDN+ϕ2L2D)] =[−(1−σ)βSDN2(1−σ)βSN−(1−σ)βSDN2ϕ1−σβSDN2σβSN−σβSDN2+ϕ2L2],V=[∂∂L1((α0+ϕ1)L1)∂∂D((α0+ϕ1)L1)V21V22]=[α0+α100α2+ν1+ν2],
|
with
|
V21=∂∂L1((α2+ν1+ν2)D−(μ12T1+μ22T2))V22=∂∂D((α2+ν1+ν2)D−(μ12T1+μ22T2)).
|
Evaluation at E0 then gives
|
FE0=[0(1−σ)βϕ1σβ],VE0=[α0+α100α2+ν1+ν2]
|
so that
|
V−1E0=[1α0+ϕ1001α2+ν1+ν2],G=FE0V−1E0=[0(1−σ)βα2+ν1+ν2 ϕ1α0+ϕ1σβα2+ν1+ν2].
|
It follows that the dominant eigenvalue of G gives the value of the basic reproduction number
|
R0=12{σβα2+ν1+ν2+[σ2β2(α2+ν1+ν2)2+4(1−σ)βϕ1(α0+ϕ1)(α2+ν1+ν2)]12}.
|
With the values reported in Table 1, it appears that R0≈1.8414, a value that indicates that the disease is endemic, and this value of the basic reproduction number is also not too close to the eradication threshold.
Table 1. Model parameters.
| Description |
Symbol |
Value |
Unit |
Reference |
| Immigration rate |
A |
30 |
|
[21] |
| transmission rate |
β |
5.31 |
|
[1,4,5,7,8]
[11,24,25,31] |
| Proportion of infectious rapidly progressing to active disease |
σ |
0.015 |
pure number |
[6] |
| Progression from latent to diseased class |
ϕ1 |
0.02284 |
year−1 |
[9] |
| Diagnosis and treatment rate in the public sector |
ν1 |
0.49 |
year−1 |
[16,17,22] |
| Diagnosis and treatment rate in the private sector |
ν2 |
0.41 |
year−1 |
[16,17,22] |
| Recovery (cure) rate after treatment in the public sector |
μ11 |
0.89 |
year−1 |
[16] |
| Recovery (cure) rate after treatment in the public sector |
μ21 |
0.51 |
year−1 |
[10,27,28] |
| Failure rate after treatment in the private sector |
μ12 |
0.064 |
year−1 |
[16] |
| Failure rate after treatment in the private sector |
μ22 |
0.32 |
year−1 |
[27] |
| Relapse from treatment |
ϕ2 |
0.11 |
year−1 |
[23,26] |
| Natural death rate |
α0 |
0.0071 |
person−1 year−1 |
[21] |
| Latently infected population L2 death rate |
α1 |
0.016 |
year−1 |
[23] |
| Diseased population death rate (Case fatality rate in untreated) |
α2 |
0.32 |
year−1 |
[17] |
| Population under treatment death rate in public sector |
α3 |
0.074 |
year−1 |
[16] |
| Population under treatment death rate in private sector |
α4 |
0.32 |
year−1 |
[27] |
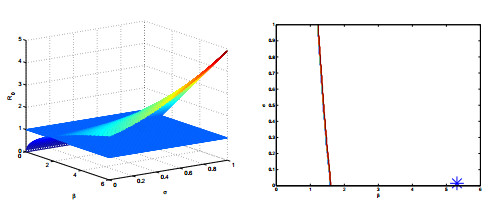
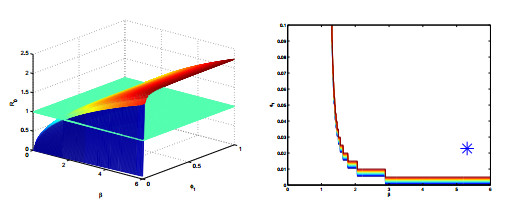
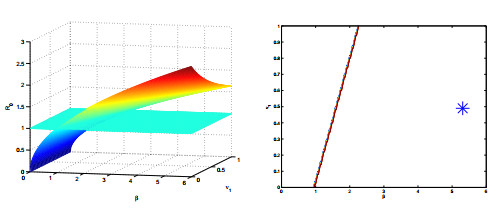
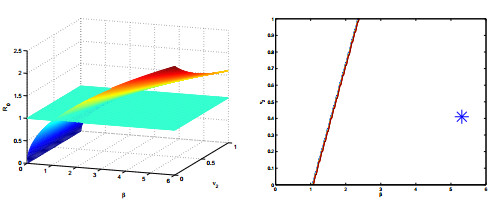
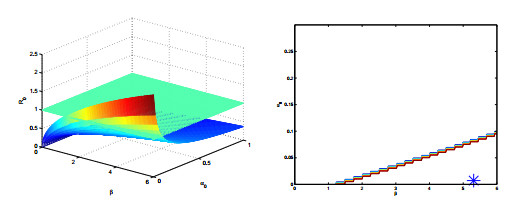
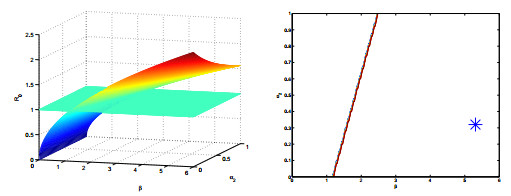
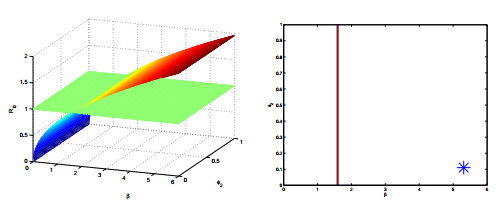
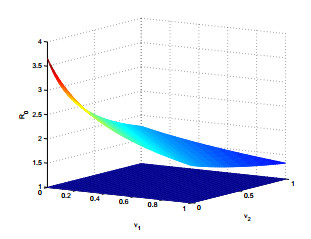
To gain more insight, we provide a sensitivity analysis of R0 in terms of the most important parameters of the model. Since the basic reproduction number depends on six them, we choose to fix β as a reference. In each parameter space given by β coupled with one of the remaining parameters, namely σ, ϕ1, α0, α2, ν1 and above all ν2, we plot the surface R0 and the contour line corresponding to the threshold R0=1. The resulting surfaces and contour curves are plotted in Figures 2-7.
Recall that to achieve disease eradication, a value of R0<1 must necessarily be attained. We thus concentrate now on possible means to achieve this goal. The following discussion aims at ascertaining whether acting on each parameter that appears in the expression for R0, a sufficient reduction of this threshold can at all be obtained. This could perhaps lead to indications for suitable policies to be pursued by the authorities in order to curb the burden of this endemic and pernicious disease.
From Figure 2 it appears that from the current situation, variations in σ will not lead to any improvement, in fact if this parameter is enlarged, the endemicity of the disease will be more pronounced, while even if it is reduced to values very close to zero, the disease is not going to disappear, without a simultaneous reduction of the transmission rate β. A similar situation appears from Figure 3. The system behavior is sensitive to the parameter ϕ1, in that a relatively small reduction of the latter induces disease eradication. But this parameter is an intrinsic parameter of the disease, the spontaneous progression to the active form from an unknown latently infected individual. It therefore appears that acting on this parameter in practice is extremely difficult if at all possible.
Sensitivity with respect to the diagnosis and treatment rates is shown in Figures 4 and 5. The same result is obtained in Figure 7, by an increased diseased-related mortality, which however goes in the opposite direction of the goal of saving lives. Incidentally, this is an example of what in ecology and epidemiology is sometimes found, that something harmful at the individual level is beneficial for the community, and vice versa. Such an observation is found for instance in beehives, [2]. It appears that an increase in the identification of the cases and their cure will help in reducing the endemicity range of the disease. Clearly Figure 6 shows that an increase in the natural death rate will contribute also to disease eradication, but this is certainly not a practical recommendation to follow.
In Figure 8 we observe that changes in ϕ2 are irrelevant on the value of the basic reproduction number. This however is to be expected, in that ϕ2 does not appear in the definition of R0.
Finally, in Figure 9 we plot the value of the basic reproduction number as function of the treatment rates in both public and private sectors. The findings indicate that the difference in the public and private sectors diagnosis rate is not essential for eradicating the disease. In fact, even if they were 100%, the plot indicates that the surface for R0 would still be above the critical threshold 1, so that the disease could not be eradicated.
6. Nonlinear stability of the disease-free equilibrium
We can assess the asymptotic stability of the disease-free equilibrium E0 by means of a suitable nonlinear Lyapunov function. As candidate, choose:
|
L1=aS0[S−S0S0−ln(1+S−S0S0)]+bL1+cD+eT1+fT2+gL2.
|
Note that L1 is nonnegative and L1(E0)=0. Differentiation with respect to time and use of (2), with N0=S0, leads to
|
L′1=−aA(S−S0)2SS0+β(S−S0)DN[b(1−σ)−a+cσ]+βDN(N−N0)S0[b(1−σ)+cσ]+L1[cϕ1−b(α0+ϕ1)]+DL2(c−g)ϕ2+D[βS0N0[b(1−σ)+cσ]+eν1+fν2−c(α2+ν1+ν2)]−α1gL2+T1[cμ12−e(α3+μ11+μ12)+gμ11]+T2[cμ22−f(α4+μ21+μ12)+gμ21].
|
Taking then c=g and a=b(1−σ)+cσ, since N−N0≤N, we find the upper bound
|
L′1≤−aA(S−S0)2SS0+L1[cϕ1−b(α0+ϕ1)] +D[aβS0+aβS0N0+eν1+fν2−c(α2+ν1+ν2)]−α1cL2+T1[cμ12−e(α3+μ11+μ12)+cμ11]+T2[cμ22−f(α4+μ21+μ12)+cμ21].
|
Finally imposing the following inequalities
|
cϕ1<b(α0+ϕ1),aβS0(1+1N0)+eν1+fν2<c(α2+ν1+ν2),c(μ12+μ11)<e(α3+μ11+μ12),c(μ22+μ21)<f(α4+μ21+μ22),
|
it follows that
|
L′1≤−aA(S−S0)2SS0−α1cL2≤0
|
showing that it is nonpositive definite. This is not enough to ensure global stability. Rather, it could be the starting point to assess the largest domain of attraction of the DFE. Following [20], one can search for the largest invariant subset in R6 for which L′1=0, i.e. S=˜S and L2=0. In principle it can be obtained by making such substitutions into the right hand side of (2) and solving the resulting system. This appears to be rather complicated, so that we will only investigate the situation via numerical methods below.
7. Local stability of the disease-free equilibrium and backward bifurcation
At the disease-free equilibrium the Jacobian (3) has immediately three easy eigenvalues −α0<0, −(α0+ϕ1)<0, −α1<0. The remaining ones, that characterize the stability of this equilibrium, are those of the submatrix
|
J0=J(E0)=(σβ−(ν1+ν2+α2)μ12μ22ν1−(α3+μ11+μ12)0ν20−(α4+μ21+μ22))
|
(4)
|
We now investigate numerically the disease-free equilibrium and the endemic one. Departing from the Table values only for the new individuals recruitment rate, setting it to the value A=100, for which the susceptibles at disease-free equilibrium would attain the value S0=14085.50704 we find that R0=1.8414>1, so that the disease is endemic. However, the computation of the eigenvalues shows that they are negative, −1.5390, −0.7265, −1.0528 and this is further convalidated by the Routh-Hurwitz conditions at the DFE. Denoting by M2 the sum of the principal minors of order 2 of J0, they are
|
−tr(J0)=3.3184>0, −det(J0)=1.1772>0,−tr(J0)M2(J0)−det(J0)=10.4481>0.
|
This shows that the DFE is stable, therefore giving rise to a bistability situation and to a backward, or subcritical, bifurcation, see [29] and [12] page 28. We investigated numerically the possibility of attaining the DFE, searching the initial values space for values that upon integration would lead to the DFE. In fact, this occurs, but for unrealistically small values of the diseased classes, namely L1(0)=D(0)=10−15, but the value for the susceptibles can be large, reasonably far away from the equilibrium value, S(0)=S0+9950, while the remaining initial conditions have always been chosen as
|
T1(0)=0.49D(0), T2(0)=0.41D(0), L2(0)=0.85T1(0)+0.51T2(0).
|
Any increase in the values of L1(0), D(0) or S(0) given above would instead make the system tend to the endemic equilibrium.
We then tried to study this situation as β decreases. For β=2.3, we find R0=1.2044 but the eigenvalues at DFE are still negative, −1.5623, −0.7476, −1.0535, so that this equilibrium is stable. The initial conditions leading to the DFE can now be chosen a bit larger, namely L1(0)=D(0)=10−12 while the choice for the susceptibles is now much wider, up to S(0)=S0+179000.
A further decrease, β=1.5, gives now R0=0.97045, for which apparently the disease would be eradicated. But again, in view of the backward bifurcation, the endemic equilibrium persists and is attained for the following choice of initial conditions
|
S(0)=S0+180000=194084.5070, D(0)=0.3S(0)=58225.3521,T1(0)=28530.4225, T2(0)=23872.3944,L2(0)=36425.7803, L1(0)=.8S(0)=155267.6056.
|
(5)
|
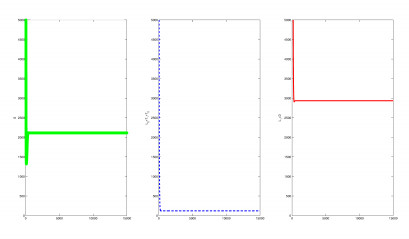
It is plotted in Figure 10.
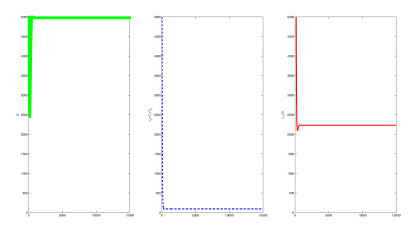
A similar situation arises for β=0.9, giving R0=0.7501, but the endemic equilibrium is found for the same initial conditions (5), see Figure 11. Here susceptibles more than double the value of Fig 10, latently infected do not change sensibly, infected are found at a smaller steady level.
For β=0.6, we find R0=0.6116, in this case using the initial conditions (5), the endemic equilibrium seems now to have disappeared, and the same holds for β=0.4, for which R0=0.4988.
8. Coexistence equilibrium analysis
Although the result of the previous section indicates that the disease could in principle be eradicated, in addition, we could now pursue an alternative road for trying to curb it.
First of all, we investigate whether the the coexistence equilibrium can be assessed analytically. We solve the fourth and the fifth equilibrium equations in terms of D and solve the sixth one for L2, to get T1=Dη1, T2=Dη2 with
|
η1=ν1α3+μ11+μ12, η2=ν2α4+μ21+μ22, L2=μ11T1+μ21T2α1+ϕ2D.
|
(6)
|
Using the first two above equations in the last one, we find L2 in terms of D,
|
L2=Dα1+ϕ2D[μ11ν1α3+μ11+μ12+μ21ν2α4+μ21+μ22]=D(μ11η1+μ21η2)α1+ϕ2D.
|
(7)
|
Taking the linear combination of the first two equilibrium equations with weights 1−σ and 1 respectively, we find
Adding the first, with weight σ, and the third equilibrium equations, setting Ω=μ12η1+μ22η2−α2−ν1−ν2∈R and using (7), we obtain
|
σA−α0σS+ϕ1L1+ϕ2D2μ11η1+μ21η2α1+ϕ2D+DΩ=0.
|
(9)
|
Rearranging (9) and letting
|
W=Ω+μ11η1+μ21η2∈R, θ=σα0+ϕ1α0+ϕ1>0,
|
leads to
|
σAα1+ϕ1α1L1+D(σAϕ2+Ωα1)+ϕ1ϕ2L1D+ϕ2D2W=α0σS(α1+ϕ2D).
|
(10)
|
Use of (8) into (10) gives
|
Φ(S,D):=θAα1−α0α1θS+D(θAϕ2+Ωα1)−α0ϕ2θSD+ϕ2D2W=0.
|
(11)
|
Finally, the first equilibrium equation can be rewritten as (A−α0S)[S+L1+D+T1+T2+L2]−βSD=0 from which, substituting into it (6), (8) and (7), we obtain
|
Ψ(S,D):=−βSD+(A−α0S)[S+(1−σ)A−α0Sα0+ϕ1+D(η1+η2+1)+Dμ11η1+μ21η2α1+ϕ2D]=0.
|
(12)
|
The curve obtained by taking the common denominator in (12) and setting the numerator to zero is a third order implicit function and therefore very difficult to study, even numerically. The values of the diseased and susceptible populations at the coexistence equilibrium would be obtained by the intersection of Φ and Ψ in the first quadrant of the S−D plane, while the remaining populations would come from (6), (7) and (8).
The mathematical problem appears to be a hard task. For this reason, in order to gain anyway some insight into the actual situation, we make a very strong simplifying assumption. The mathematical difficulty arises from the denominator in the last fraction of (12). To simplify it, we assume ϕ2=0, which implies that there are no relapses after treatment. As said, this is very unlikely, but we use it as a probe into the problem.
In view of the simplification, the equations for Φ and Ψ become easier to handle, in fact the first one is a straight line and the second one a conic section, namely:
|
Φs(S,D):=θA−α0θS+DΩ=0,
|
(13)
|
|
Ψs(S,D):=ρA2+νAS+πAD−(α0π+β)SD−α0θS2=0,
|
(14)
|
where
|
ρ=1−σα0+ϕ1>0, ν=2α0σ−α0+ϕ1α0+ϕ1∈R, π=η1+η2+1+μ11η1+μ21η2α1>0.
|
Note that the straight line Φs(S,D) in the S−D plane has slope and height at the origin of uncertain signs, α0θΩ−1∈R, AθΩ−1∈R. But its intercept with the D axis is positive, S0=Aα−10>0. Now Ψs(S,D) is a nondegenerate curve if its first invariant does not vanish, a condition that in fact we assume:
|
14A2[α0θπ2−(α0π+β)πν−(α0π+β)2ρ]≠0.
|
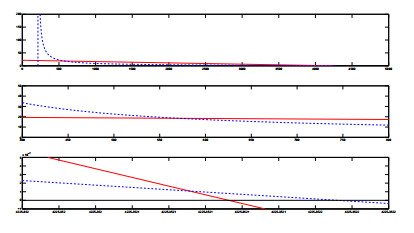
In particular it is a hyperbola, since its second invariant is negative, −4−1(α0π+β)2<0. We study it by intersecting it with vertical lines, S=k. Its intersections with these lines are the points
|
D=α0θk2−kνA−ρA2Aπ−(α0π+β)k.
|
The latter are feasible when positive, which shows that there is a feasible branch of Ψs(S,D) in between the values S∗ and ˆS=ˆk=Aπ(α0π+β)−1. Here S∗=S±=k±=A(2α0θ)−1[ν±(ν2+4α0ρθ)12], where the plus sign is taken when ν>0 since then S∗=S+>0>S− and the minus sign whenever ν<0, since in such case S∗=S−>0>S+. This situation leads to two possible configurations. Thus, depending on whether S∗>ˆS or ˆS>S∗, Ψs(S,D) has a branch raising up to +∞ at S=ˆS from the zero at S=S∗, in the former case, or conversely decaying from +∞ at S=ˆS to zero at S=S∗ in the second one. An intersection with Φs(S,D) cannot occur for sure if the zero S0 of this straight line, whenever its slope is positive, lies beyond the zero of Ψs(S,D), or conversely if the slope is negative, namely either for S0>max{S∗,ˆS}, Ω>0 or for S0<min{S∗,ˆS}, Ω<0. In our case, taking again A=30, we find Ω=−1.0754<0, S∗=4225.352112676057 ˆS=213.0447, S0=4225.352112676056<S∗. We would need S0<213.0447 which is not true, indicating that the intersection exists. In fact, in Figure 12 we plot the situation and discover that in fact there are 2 intersections. In order to eradicate the disease, one could try to make them vanish, through a saddle-node bifurcation, by influencing the slope of the straight line m=α0θΩ−1<0, but that cannot certainly be achieved by reducing the natural mortality rate α0. An increase of m is then necessary so that the intersections do not occur. The same result can be achieved by lowering the height at the origin, Aθ(−Ω)−1>0. A decrease in the recruitment rate A could be viable, but highly improbable. One can try then to reduce θ or to increase −Ω. For the former, one could try to reduce σ, but that at most gives θ|σ=0=ϕ1(α0+ϕ1)−2, which might not be enough; on the other hand, observe that
implying that we must reduce ϕ1. The second alternative it to increase −Ω=α2+ν1+ν2−μ12η1−μ22η2, the maximum being of course −Ω=2+α2, if the diagnosis rates achieve 100% of precision and the failure rates after treatment vanish altogether.
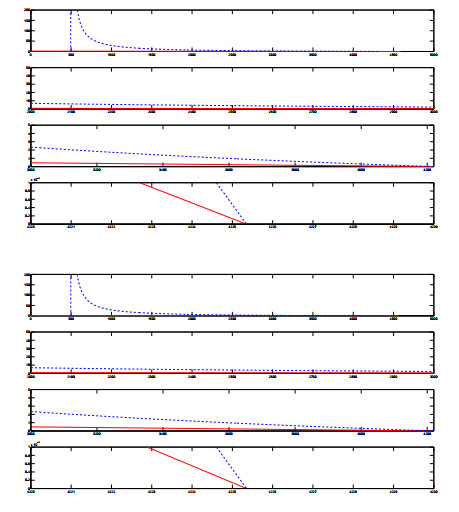
Disease eradication can in fact be achieved for an almost extreme case, taking ϕ1=0.001, ϕ2=0, σ=0, μ12=0, μ22=0, ν1=1, ν2=1 and in this case Ω=−2.320, see left column of Figure 13. In the right column, a similar situation occurs, for the following parameters that do not achieve the extreme values, but are really quite close to them: ϕ1=0.001, ϕ2=0, σ=0.01, μ12=0.001, μ22=0.001, ν1=.999, ν2=.999 for which Ω=−2.316. In any case these considerations would hold only for ϕ2=0, which is a very restrictive situation.
9. Discussion
The model that has been introduced here was meant to compare the TB treatments performed in the public and private sectors of health care in India. The bottom line of the results of our investigation are the considerations that can be inferred from Fig. 9, namely that the low rate of diagnosis actually found in the private sector, whether it be due to malpractice, poorer diagnostic means or simply ascribed to the fact that doctors may be reluctant to let paying patients know that they are infected, seems not to constitute the main problem in the disease endemicity. It appears thus that even achieving 100% correct diagnosis in both sectors would not help in eradicating the disease.
From the extensive simulations that we ran, see Figures 2-8, it appears that apart from the disease contact rate, the effect of the other parameters affecting R0 is rather thin and essentially negligible in the disease eradication issue. At most, changing some of them might render the set in the parameter space where R0<1 smaller, but without a corresponding substantial change in the disease contact rate β the critical threshold cannot be crossed. On the other hand, by drastically reducing this parameter, the basic reproduction number can be reduced to values less than one. In this case, however, another unexpected and unpleasant phenomenon occurs, the onset of a backward, or subcritical, bifurcation, for which, in spite of the theoretical result assessing the possibility of achieving disease eradication, because the system is coming from an endemic equilibrium, it will continue on this manifold, even if the disease-free equilibrium exists. This happens until really low values of β are achieved, which might be unrealistic in practice.
Alternatively, for values of β that bring R0 below the critical threshold, or even larger values of β, one could try to achieve the disease-free equilibrium by acting on the initial conditions of the system, drastically and suddenly reducing them, so that this change brings the system into the domain of attraction of the disease-free equilibrium. But our experiments indicate that in order to fall into the domain of attraction of this equilibrium, the number of infected must be so small to be essentially unreacheable in ordinary life.
A different approach has also been attempted, namely to try to render the endemic equilibrium unfeasible. This approach appears to be analytically untractable, except for the unrealistic case of no disease relapses, i.e. ϕ2=0, from the class L2 of latent and cured individuals, and also difficult to address numerically. In principle however this approach indicates an alternative way of fighting the disease, namely to render the coexistence equilibrium unfeasible.
For the particular case ϕ2=0, a highly improbable situation to achieve, since in practice it is nearly impossible to prevent relapses, the system is reduced to the intersections of the curves (11) and (12), i.e. Φs and Ψs. The point at which they meet provides the population values for susceptibles and diseased at the endemic equilibrium. To attain this situation some means of rendering disease relapses after cure impossible or negligible enough should be devised, to keep ϕ2 at zero or at a very low level. Although we did not perform on this an exhaustive investigation, nevertheless some information can be gathered. Our simulations in the previous section indicate that disease eradication is possible but for values of the some of the parameters that are almost extreme. This entails for instance that ϕ1 must be reduced. However, this is an almost impossible task, as this parameter models the intrinsic progress from the latently infected individuals to active disease outbreak. In other words, even if a drug would be discovered to slow down this progression, it would need to be administered to a set of unknown individuals, the latently infected, or it could be given to the same set of people after their identification, following a suitable screening, which is probably a measure that has enourmous economical costs. The other relevant parameters are the disease diagnosis rates νi, in both public and private sectors. These should achieve almost 100% certainty. Further, μ1i, the relapse rates after treatment, should drop almost to zero and the proportion of the primary latently infected progressing to the active disease stage should be lowered too, but not that dramatically. However this last task is rather difficult, as σ is an intrinsic disease parameter and it is difficult to act on it, even if some drug to this effect were discovered, as this parameter pertains also to the unknown population of the latently infected as mentioned above. Hence, also this approach unfortunately does not appear to be viable in practice.
The rater sad conclusion that we must draw from all these considerations is therefore that eradicating the disease in the present state of affairs is rather difficult if not at all impossible.
Acknowledgments
This work was undertaken when the first author visited the University of Torino, with a WWS2 grant, which is thankfully acknowledged. The research has also been partially supported by the project "Metodi numerici nelle scienze applicate" of the Dipartimento di Matematica "Giuseppe Peano". EV gratefully acknowledges very useful discussions with Antoine Perasso and Rafael Bravo de la Parra and the referees for their constructive comments.









 DownLoad:
DownLoad: