1. Introduction
In DNA, ionizing radiations produce clustered DNA damages defined as two or more lesions occurring within one helical turn of DNA. They are known to be more challenging for the repair machinery than individual and widely dispersed lesions [reviewed in 1-5]. In consequence, they may have cellular deleterious effects such as mutations, DNA double strand breaks or even lethality. The most frequent lesions found in clustered DNA damages are oxidized nucleobases and their radical degradation products, single strand breaks and abasic sites (AP sites) [6,7,8]. Such lesions are mainly repaired by the base excision repair (BER) pathway [9,10], the efficiency of which is compromised when the lesions are in a context of clusters [11,12,13]. For example, it has been shown in vitro that the repair of clustered DNA damage sites containing the 2'-deoxyribose abasic site (AP site) and 8-oxoguanine lesions (Figure 1) is delayed [14] and the mutation frequency occurring at clustered lesions is increased compared to isolated ones [3,15,16]. In some cases, their processing may also lead to the formation of complex and highly cytotoxic DNA double strand breaks (DSBs) [5,17] repaired by either homologous recombination (HR) or non-homologous end joining (NHEJ).
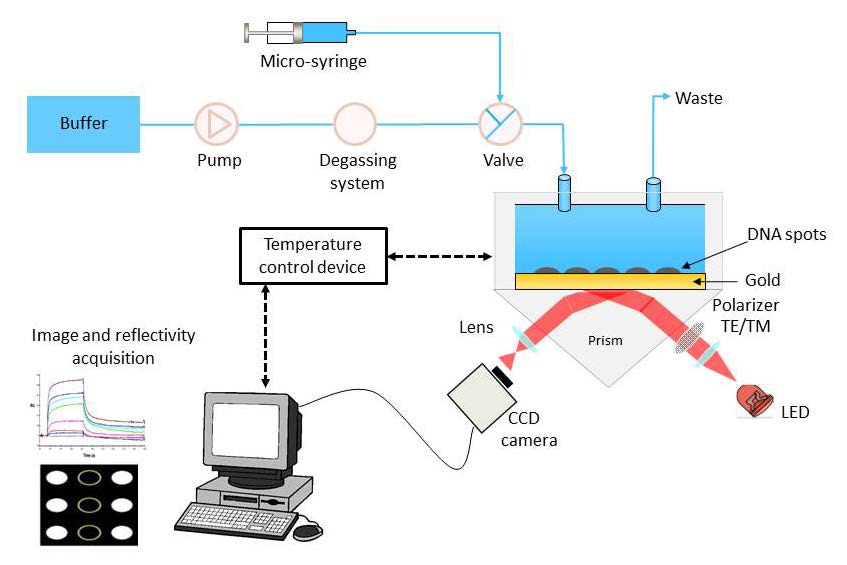
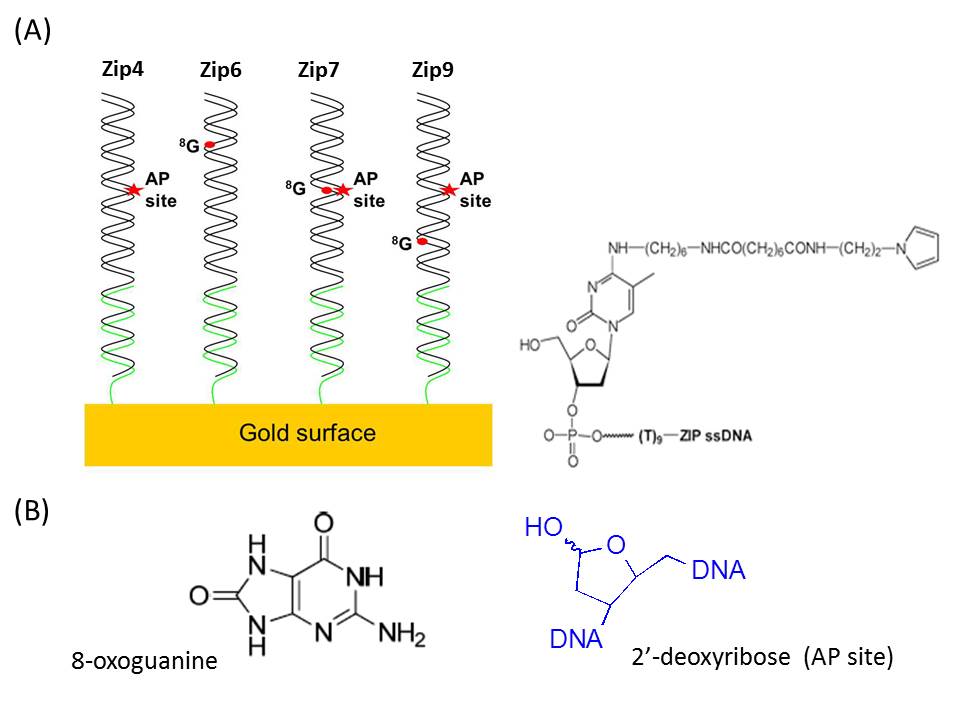
In previous studies, T. Livache and co-workers have designed a multiplexed technique based on DNA-biochips and Surface Plasmon Resonance imaging (SPRi) to simultaneously detect and analyze the recognition of DNA probes containing single damages by specific DNA glycosylase repair enzymes [18] (Figure 2). In the present study, we report the use of a SPRi-based assay to monitor the repair activity of the Fpg protein on 2’-deoxyribose AP site and 8-oxoguanine damages (Figure 1 and 2) located at various positions in DNA strands, either as single lesions or in a context of clusters. Fpg is a bi-functional DNA glycosylase for which the mechanism of action has been extensively documented and can be divided into three steps: 1. DNA binding, 2. 8-oxoguanine recognition and excision (N-glycosylase activity), which generates an abasic site intermediate (AP site), 3. cleavage at AP site (AP lyase activity) via successive b-and d-elimination reactions forming a single nucleotide gap flanked by 3’ and 5’ phosphate extremities. We used the already optimized approach cited above [18] to design a DNA biochip with four different DNA duplexes containing single lesions and groups of lesions and one control. The main interest in SPR imaging resides in its rapid, miniaturized and multiplexed format (up to 64 spots) giving the possibility of detecting and analyzing simultaneously the Fpg enzyme activity toward several different DNA damage targets. In the present study 20 samples were spotted, each DNA being spotted 5 times to measure reproducibility whereas classical SPR is limited to the detection of 4 tracks only. In a first step, four oligonucleotides functionalized with a pyrrole residue (named ZipPy, Figure 1) are grafted electrochemically on the chip gold surface. These functionalized spots can then be used to hybridize complementary DNA strand bearing a double stranded part containing specific lesions. The complete immobilized DNA duplexes are named Zipn (n=4,6, 7 and 9, Figure 1).
The choice and design of the double-stranded clusters containing an 8-oxoguanine and an AP site is based on abundant literature results demonstrating the influence of the distance separating the lesions and their relative orientation (3' or 5' to each other) on the cleavage efficiency of Fpg at both lesions sites [14,15,17,19,20,21]. SPRi is a label free, non-destructive, optical method, which appears quite suitable to investigate the different steps of Fpg action (DNA binding, lesion recognition and cleavage) and to establish the hierarchy of Fpg incision at 8-oxoguanine and AP site positions either as single lesions or included in clusters. Depending on the sequence context and the lesion incision efficiency by Fpg the SPRi signal for the different steps is expected to vary. Prior to SPRi experiments, we performed in vitro studies of five different duplexes containing an AP site in a central position on one strand and an 8-oxoguanine on the other strand positioned at 0 to 5 nucleotides distance, either on the 3' or the 5' side of the abasic lesion (31mer, see Table 1). The same DNA sequences were used for both in vitro studies and SPRi.
Table 1. Sequence of oligonucleotides used for enzymatic cleavage assays.
| Strand 1 : 5’G ATG AAT TCA CGC TCX CAC GCA TCG CTG GTA3’ |
| Strand 2 : |
| (-5) 3’C TAC TTA AGT GCG AGC GTG C8GT AGC GAC CAT5’ |
| (-3) 3’C TAC TTA AGT GCG AGC GT8G CGT AGC GAC CAT5’ |
| (-1) 3’C TAC TTA AGT GCG AGC 8G TG CGT AGC GAC CAT5’ |
| (0) 3’C TAC TTA AGT GCG AG8G GTG CGT AGC GAC CAT5’ |
| (+1) 3’C TAC TTA AGT GCG A8G C GTG CGT AGC GAC CAT5’ |
| (+3) 3’C TAC TTA AGT GC8G AGC GTG CGT AGC GAC CAT5’ |
| (+5) 3’C TAC TTA AGT 8G CG AGC GTG CGT AGC GAC CAT5’ |
Strand 1 is annealed with Strand 2 to form the DNA duplexes containing the cluster of lesions. X: 2’-deoxyribose (or AP site) or cytosine (C). (+1) to (+5) = position of the 8-oxoguanine base 5’ from the X position on the complementary strand. (−1) to (−5) = position of the 8-oxoguanine base 3’ from the X position on the complementary strand. X: 2’-deoxyribose (or AP site) or cytosine (C). 8G: 8-oxoguanine.
2. Materials and Method
2.1. Oligonucleotides
All oligonucleotides were synthesized in the laboratory and purified by polyacrylamide gel electrophoresis (PAGE). Uracil was used as a precursor of AP sites obtained after enzymatic treatment with E. coli uracil-DNA glycosylase (UDG, New England Biolabs, Ipswich, USA).
DNA hybridization: The four DNA strands (Zip4c, Zip6c, Zip7c, Zip9c) containing the abasic sequence were first hybridized with their complementary strand containing 8-oxoguanine (CompZip4, CompZip6, CompZip7, CompZip9; Table 2) in the reaction buffer (10 mM BisTris HCl pH 7,10 mM MgCl2, 1 mM DTT, 100 mM KCl) by heating at 80°C for 10 minutes and allowing to cool down slowly to room temperature. A sample (250 pmoles) of all duplexes (including Zip6c) was then treated with E. coli UDG (500 fmoles). The reaction was performed in 1 mL reaction buffer at 37°C for one hour. All solutions were filtered with a 0.22 mm filter prior to their injection in the SPRi reaction chamber.
Table 2. Oligodeoxyribonucleotide sequences and sandwich constructs grafted on the SPRi chip.
| Zip4Py: 5' Py - (TTTTTTTTTT) - TGC.GGG.TAC.AGC.ACC.TAC.CTT.GCG 3' |
| Zip6Py: 5' Py - (TTTTTTTTTT) - GAC.CGG.TAT.GCG.ACC.TGG.TAT.GCG 3' |
| Zip7Py: 5' Py - (TTTTTTTTTT) - TGC.GAT.CGC.AGC.GGT.AAC.CTG.ACC 3' |
| Zip9Py: 5' Py - (TTTTTTTTTT) - GAC.CAT.CGT.GCG.GGT.AGG.TAG.ACC 3' |
| Zip4c 5' G.ATG.AAT.TCA.CGC.TCU .CAC.GCA.TCG.CTG.GTA. CGCCGT CGC.AAG.GTA.GGT.GCT.GTA.CCC.GCA 3' |
| CompZip4 3’ C.TAC. TTA.AGT.GCG.AGC.GTG.CGT.AGC.GAC.CAT GCGGCA |
| Zip6c 5’ G.ATG.AAT.TCA.CGC. TCG .CAC.GCA.TCG.CTG.GTA.CGCCGT CGC.ATA.CCA.GGT.CGC.ATA.CCG.GTC 3' |
| CompZip6 3’ C.TAC.TTA.AGT.GC8G.AGC.GTG.CGT.AGC.GAC.CAT.GCGGCA |
| Zip7c 5' G.ATG.AAT.TCA.CGC.TCU. C AC.GCA.TCG.CTG.GTA. CGCCGT GGT.CAG.GTT.ACC.GCT.GCG.ATC.GCA 3' |
| CompZip7 3’ C.TAC.TTA.AGT.GCG.AG8G. GTG.CGT.AGC.GAC.CAT GCGGCA |
| Zip9c 5' G.ATG.AAT.TCA.CGC.TCU .CAC.GCA. TCG. CTG.GTA.CGCCGT GGT CTA CCT ACC CGC ACG ATG GTC |
| CompZip9 3’ C.TAC.TTA.AGT.GCG.AGC.GTG.C8GT.AGC.GAC.CAT GCGGCA |
| The uracil is used as a precursor of the 2’-deoxyribose AP site (see Material and Methods). |
2.2. SPRi
2.2.1. Spotting
The DNA chips were prepared as previously described on a glass prism coated with a gold layer purchased from Genoptics [18]. The single strand DNA sequences (Zip4Py, Zip6Py, Zip7Py and Zip9Py, Table 2) bearing a pyrrole residue on the 5’-end position and a deca-thymine spacer (Figure 1A) were immobilized by electrochemical copolymerization process using a homemade electro spotter according to a previously described protocol [18]. For each sequence, the electro polymerization solution contained 20 mM of pyrrole and 10 mM of ZipPy DNA in spotting buffer (30% acetonitrile, 20% dimethylsulfoxide, 0.5% glycerol, 0.1 M lithium perchlorate). A 20 mM solution of pyrrole was used to generate polypyrrole spots (Ppy) used as negative control. For each sequence grafted, five independent spots were deposited in order to control the reproducibility. The DNA chips were then dried under argon and could be stored at 4 °C for several weeks. The SPRi experiments were repeated at least in triplicate.
2.2.2. SPRi apparatus
The SPRi experiments were carried out on a homemade SPRi system with integrated temperature regulation [18] (Figure 2). The LabView software from Genoptics (France) was used for the real-time monitoring of the reflectivity for each spot of the chip captured by a CCD camera.
2.2.3. SPRi experiments
All SPRi experiments were performed according to previously described protocols [18] at 37 °C in the reaction buffer. After treatment with UDG, the DNA duplexes were immediately injected onto the chip via a 500 mL sample loop injection at a flow rate of 1 mL s−1. The specific hybridization of the DNA targets on the gold surface was controlled by examining the spots lightning up in the CCD images and measuring the reflectivity changes. To prevent non-specific interactions with the Fpg protein, the gold surface was coated with cytochrome C (1 mM, two successive injections of 1 mL). The Fpg solution (50 nM) protein was injected on the chip for 8 minutes at a flow rate of 1 mL s−1 followed by a rinsing period of 9 minutes at a flow rate of 1 mL s−1 according to previously described optimized conditions [18]. The reflectivity change for each spot was monitored during this period. The E. coli Fpg protein was a generous gift from Dr. M. Saparbaev (Institute Gustave Roussy, Villejuif, France).
2.3. Enzyme cleavage assay
Oligonucleotides were 5’-end labeled by T4 polynucleotide kinase (New England Biolabs, Ipswich, USA) in thepresence of [g-32P] ATP (3000 Ci/mmol, Perkin Elmer, Waltham, USA)
The 2’-deoxyribose lesion was obtained by incubating the dU containing oligonucleotide (strand 1,10 pmoles) with 16 fmoles of E. coli UDG at 37 °C for 60 min in 10 mL reaction buffer. The conversion efficiency of dU into abasic site was controlled by alkali treatment in 0.5 M NaOH solution for 20 min at 37°C. Under these conditions more than 90% conversion was obtained. The duplexes were prepared by hybridizing the 32P-labeled oligonucleotides with 10% molar excess of the non-radio labeled complementary strand at 50 °C for 5 min and then slowly cooled down to room temperature. To prevent degradation, the abasic site containing duplexes where hybridized at room temperature. For double-kinetics experiments, the two 32P-DNA strands were hybridized at an equimolar ratio.
The enzymatic activity of Fpg was measured by monitoring the conversion of oligonucleotide duplexes containing the 8-oxoguanine at defined positions (see Table 1) into cleavage products. The assay (10 mL) contained 0.25 pmoles of 5’-[32P]-end labeled oligonucleotide duplex and 0.165 pmoles of Fpg. Incubations were carried out at 37 °C for 20 min and quenched by adding 10 mL of stop solution (95% formamide, 20 mM EDTA pH 7,0.025% xylene cyanol, 0.025% bromophenol blue). The reaction products were separated by PAGE in denaturing conditions (7 M urea, (19:1) acrylamide:bisacrylamide, HEPES 100 mM, pH 7), 50 W for 1.5 hour. The gels were analyzed using a Typhoon 9410 (GE HealthCare) and the incision products were quantified with the Image Quant TL software. The percentage of enzymatic cleavage corresponds to the ratio of the cleaved DNA strand over the sum of the intact DNA strand and cleaved strand. All experiments were repeated thrice.
2.4. Double kinetics assay
In the double kinetics assay, the duplex was prepared by annealing at room temperature equimolar amounts of the two 32P 5’-end labeled complementary strands as described above. The assay (200 mL) contained 5 pmoles of DNA and 3.3 pmoles of Fpg in the reaction buffer at 37 °C. Aliquots of 10 mL were taken out at different periods of time (from 30 seconds to 20 minutes) and the reaction was quenched by adding 10 mL denaturing stop solution. The reaction products were analyzed as described above.
3. Results and Discussion
3.1. In vitro activity of Fpg on single and clustered lesions
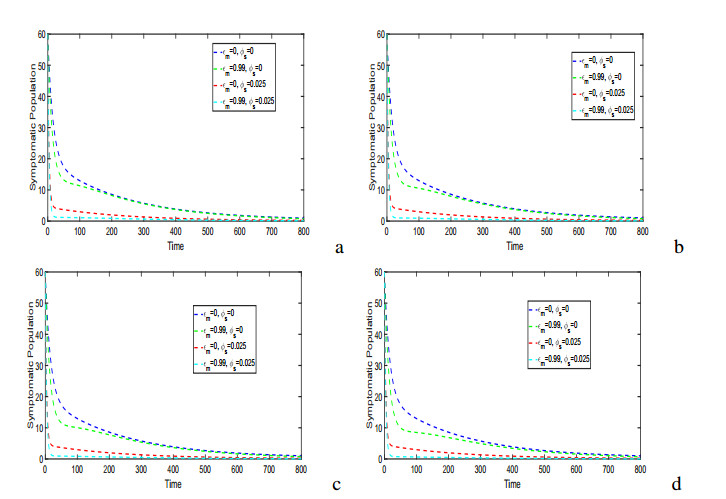
In vitro enzymatic cleavage assays of the oligonucleotides sequences described in Table 1 were performed with the E. coli Fpg protein in reaction buffer. In a typical experiment, the abasic site-containing strand 1 was hybridized with 32P labeled strand 2 containing an 8-oxoguanine at various positions. As shown in Figure 3A, the enzyme activity is comparable for the different 8-oxoguanine positions when the complementary strand is undamaged. In contrast, the presence of an AP site on the complementary strand alters significantly the 8-oxoguanine incision profile (Figure 3B). A significant inhibition is observed when 8-oxoguanine is facing AP site (0 position) or located at positions −3, −1 and +1. For position +5 the cleavage at 8-oxoguanine occurs but is significantly reduced. Further, cleavage is quite efficient for positions +3 and −5.
Interestingly, the Fpg excision of 8-oxoguanine located at two "symmetrical" positions +3 and −3 gave opposite results. For +3 position, the cleavage is quite efficient whereas a markedly inhibition is observed for −3 position. Assuming that conformational differences between the two clusters might alter the enzyme binding and partly explain these results, we performed a structural study by high field NMR of undecamer duplexes containing these clusters. We notably showed that both clusters induced a higher local flexibility but had no effect on the global DNA conformation [22] suggesting that alteration of Fpg cleavage is not driven by the DNA conformation but rather by the reaction products.
As mentioned above, AP site incision by Fpg in vitro is very efficient and almost quantitative during the first minute of the reaction. Thus, the dramatic effect on 8-oxoguanine excision most likely comes from the conversion of abasic sites into highly destabilizing single strand breaks. Furthermore, if both lesions are efficiently excised, the Fpg action will convert a cluster of usually non-lethal lesions into a double strand break. To demonstrate this possibility, we performed a qualitative double-kinetics experiment on duplexes containing the cluster −5 32P labeled on both strands. In Figure 4, a typical gel electrophoresis experiment shows the cleavage efficiency of Fpg on both lesions as a function of time (from 30 sec to 20 min). If the cleavage at abasic sites is almost complete after 2 min (production of the corresponding 15 mer cleavage product), the 8-oxoguanine incisions begins only after 2 minutes and takes less than 10 min for completion (production of the corresponding 10 mer cleavage product). This simple experiment clearly and unambiguously demonstrates that in vitro action of Fpg may rapidly convert a cluster of lesions into a potentially lethal double strand break.
3.2. In situ cleavage kinetics monitored by SPRi
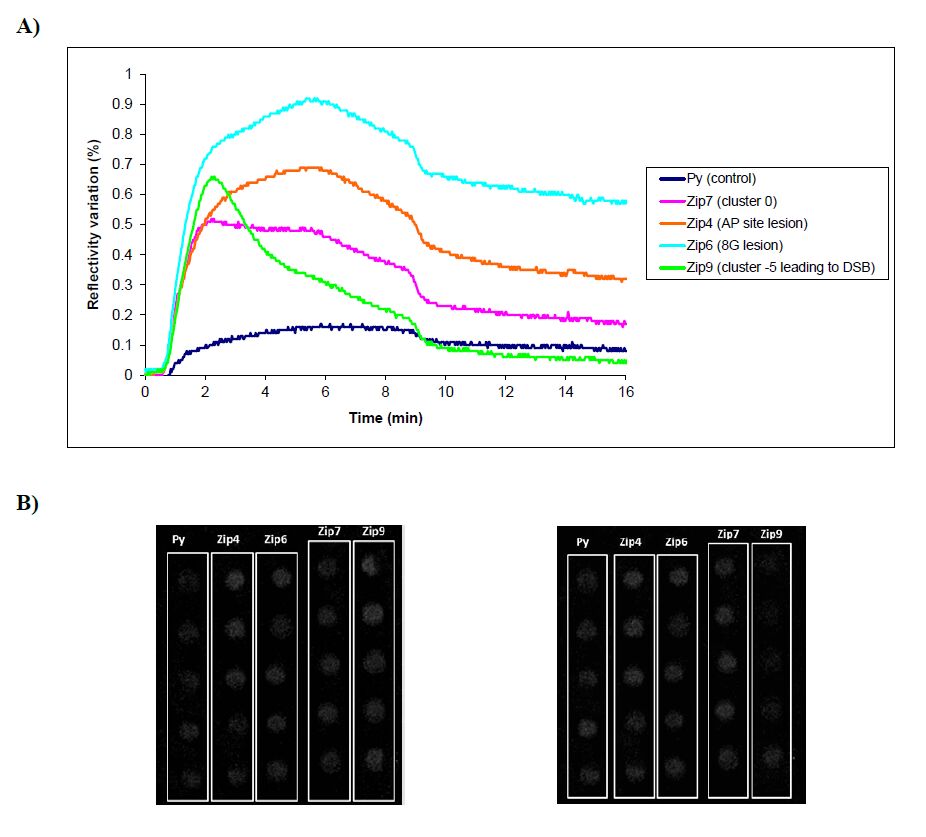
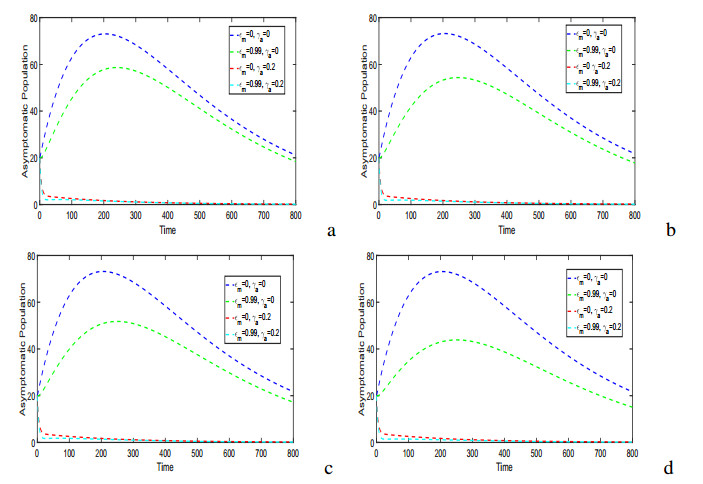
The DNA duplexes grafted on the biochip surface contain the sequences used for the in vitro experiments: Zip7 and Zip9 bear the clusters 0 and −5 respectively, Zip4 and Zip6 bear a single AP site and a single 8-oxoguanine located in the middle of the sequence, respectively (Figure 1 and Table 2). Each Zip duplex is injected separately at 37 °C on the chip functionalized with the four different complementary ZipPysequences. For a better comparison and to minimize the non-specific UDG binding contribution, the four Zip duplexes were treated with the same amount of UDG and injected as such. UDG affinity for DNA is rather low (KD in the micromolar range) [23] and it is reasonable to assume that the protein is eliminated during the rinsing period prior to Fpg injection. The set of SPRi curves obtained after the injection of Fpg is displayed in Figure 5 and their shape can be correlated to Fpg action (binding to DNA and cleavage at the lesion sites). A significant increase of reflectivity is observed for the four damaged DNA sequences whereas a weaker signal is observed for the polypyrrole control (Py), composed of a small reflectivity change due to buffer change (as seen at onset of rinsing period) and a small unspecific signal. This provides evidence for a strong interaction of Fpg with all DNA sequences. For the single lesion containing sequences (Zip4 and Zip6), a slight decrease of reflectivity occurs after 5 min, which has been correlated with a partial release of enzyme products. The incision at lesion positions generates shorter hybridized sequences of 15 base pairs with estimated Tm of 72 °C. Partial denaturation occurring at 37 °C can lead to strand loss due to the continuous flow of buffer. The reflectivity signal for Zip7, which contains a cluster of lesions cleaved mainly at the abasic site position increased rapidly but leveled off faster than the signal corresponding to isolated lesions. This suggests a weaker association of Fpg with this cluster. The Fpg is released from DNA very rapidly, as revealed by the diminution of the signal occurring in less than 3 minutes after the injection. However, the rinsing period (starting at 8 minutes) reveals that some Fpg still binds to DNA spots as reflected by a significant persistence of the signal, which was also observed for Zip6 and Zip4.
The case of Zip9, which contains the cluster of lesions leading rapidly to double strand break gives rise to a completely different sensorgram. The in vitro experiment revealed that the abasic site is almost quantitatively cleaved after 1 min of reaction with Fpg and that the second incision at the 8-oxoguanine position starts 2 min later. This suggests that during the SPRi experiment, the formation of DSB might occur rapidly and most likely during the first minutes of Fpg injection. As a matter of fact, the maximum of reflectivity is reached 3 minutes after the injection of the protein and then the signal rapidly and sharply decreases. This is consistent with a strong binding of Fpg to DNA and a rapid cleavage of DNA at both lesion sites soon after the beginning of the protein injection.
Cleavage at both lesion sites generates a short duplex (4 nucleotides) that dissociates immediately to produce a double strand break (DSB). DSB formation is accompanied with the release of a big DNA fragment containing 34 nucleotides (representing 30% of the grafted duplex constituted of 98 nucleotides). This DNA fragmentation favors the enzyme dissociation as revealed by the sharpness and amplitude of the signal decrease. In the corresponding differential images, the Zip 9 spots light off (Figure 5B). After the rinsing period, the signal becomes lower than the negative control signal. This can be explained by the massive degradation of the DNA substrate due to DSB formation.
4. Conclusion
In summary, we used SPR imaging to simultaneously investigate the processing steps (protein binding and excision steps) of different clustered DNA damages by the repair enzyme Fpg. Our findings clearly demonstrate that Fpg binds strongly to all damaged DNA duplexes and is able to perform more or less efficiently strand incision at damage positions. We notably observed Fpg double strand cleavage for cluster −5 as evidenced by a specific signal shape revealing a rapid and massive release of incision products. We believe that SPRi is a powerful non-denaturing and label free technique particularly suited for the study of many other aspects of DNA repair.
Acknowledgments
The authors acknowledge support from ICMG FR 2607. We thank also the French Agency of National Recherche through the LABEX ARCANE (ANR-11-LABX-0003-01).
Conflict of Interest
All authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: