1. Introduction
Intrinsic fluorescence emission in the near ultraviolet (300-350 nm) is a peculiar characteristic of protein biopolymers because of the presence in most of them of the three aromatics, ultraviolet absorbing and emitting, amino acids tryptophan, tyrosine and phenylalanine. Protein fluorescence is widely used to provide sensitive information about the native conformation of proteins as well as the conformational transitions induced by denaturing agents, ligands, and interactions with other proteins [1,2,3]. In the last two decades, several papers reported that proteins and synthetic peptides in the solid-state as well as in concentrated solutions exhibit a new type of intrinsic fluorescence in the blue-green range of emission wavelength when excited at wavelengths higher than 350 nm [4,5,6,7]. In many cases, under appropriate experimental conditions, the examined peptides were also able to form amyloid fibrils closely resembling those formed by proteins associated to misfolding diseases. Recent studies performed on a wider range of polypeptides, including some human disease-related peptides such as Aβ (1-40) and Aβ (1-42), lysozyme and tau protein showed that, irrespective of the presence of aromatic amino acids, the appearance of the intrinsic blue-green fluorescence is strictly associated to the amyloid fibril formation [8,9].
So far, a comprehensive assessment of the origin of blue-green fluorescence exhibited by proteins in either solid state and concentrated solutions or fibril (amyloid) state is still far from being fully understood. The major complexity arises from the observation that the recorded fluorescence properties, i.e., excitation and emission maximum, are different for proteins and peptides so far examined (Table 1). Probably, this is due to differences in the local environmental structures surrounding the amyloid fluorophore that might somewhat affect the intrinsic emission.
The employment of a specific, structure-related fluorophore in amyloid aggregates opens a wide range of possible applications because of the implications of fibrils in the physio-pathology of neurodegenerative diseases and other aggregation-related diseases. Recently, novel methods based on nanopore technology have been successfully applied to the characterization of amyloid aggregates [10]. Although these approaches have been shown to specifically detect amyloid species in vitro, they cannot be applied for the in vivo detection of amyloid aggregates in living cells or tissues. Differently, the appearance of blue-green fluorescence could be used as an alternative method for the investigation and the detection of the aggregation state without using external probes both in basic research and in the development of aggregation-inhibiting drugs [9,11,12]. Moreover, it has been shown to be particularly useful for biophysical studies involving the effect of natural compounds on amyloid aggregation, as most of them are known to interfere with the commonly used methods based on the employment of Congo red absorption and ThT fluorescence [13].
In this study we report, for the first time, an overview of the experimental evidences provided for the blue-green fluorescence in amyloid aggregates for several protein models. In addition, we critically review the different hypothesis suggested for the different protein models in order to rationalize the molecular origin of the intrinsic blue-green fluorescence in amyloid aggregates.
2. Protein aggregation and amyloid formation
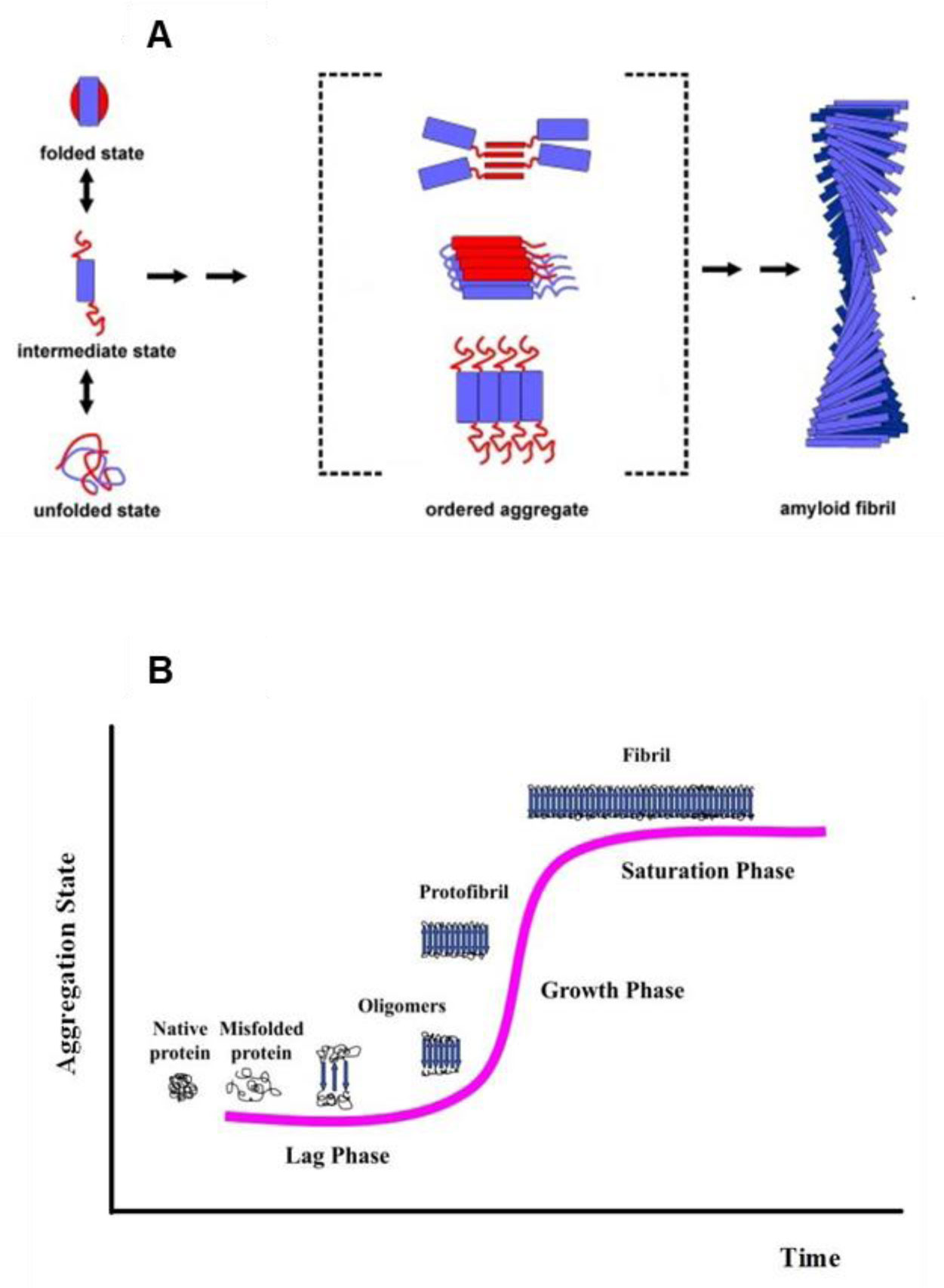
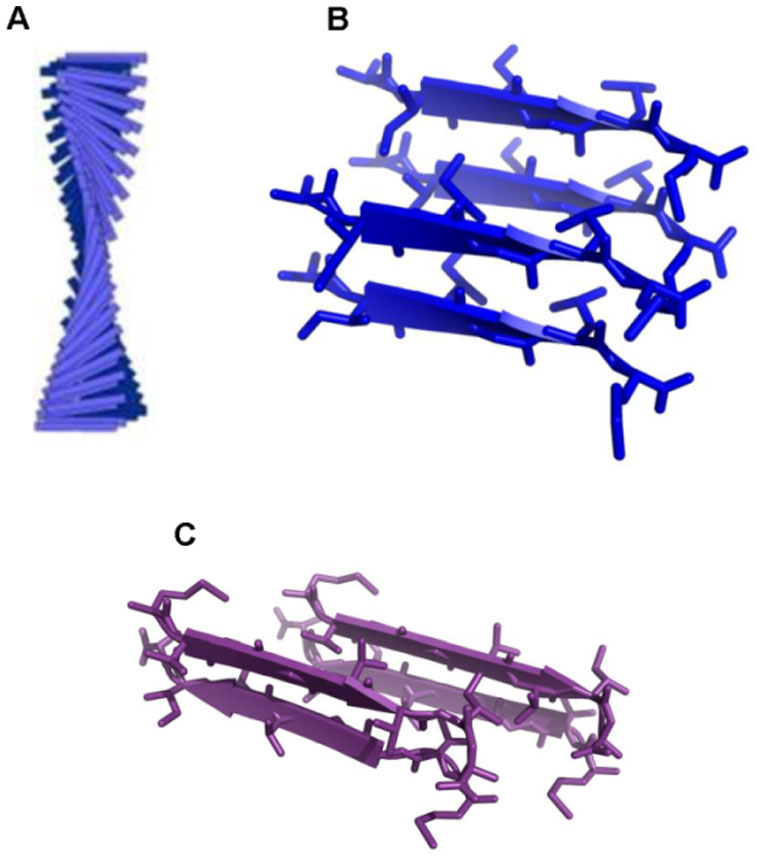
Protein misfolding diseases are characterized by tissue accumulation of well-ordered fibril aggregates, called amyloid [14]. Currently, about 20 different syndromes are associated with the formation of amyloid deposits such as Alzheimer's disease, immunoglobulin-light-chain disease, reactive amyloid disease and the familial amyloid polyneuropathies [15]. The ability of polypeptide chains to form amyloid structures is not restricted to the relatively small number of proteins associated with recognized clinical disorders, but it now seems to be a generic feature of polypeptide chains. Indeed, the intrinsic tendency to aggregate into amyloid assemblies of proteins/peptides is only marginally related to the specific amino acid sequence; rather, it is a general property of the peptide backbone arising from the intrinsic tendency of the latter to self-organize into ordered polymeric assemblies [14,16,17,18]. Amyloid fibrils show similar biophysical and ultrastructural characteristics irrespectively of the protein involved. Despite major differences in the sequences and three-dimensional structures of the peptides and proteins involved, the fibrillar forms of the aggregates share a similar ultrastructure [19,20]. In particular, amyloid fibrils are characterized by a common structural motif, the cross-β-structure in which individual β-strands in the β-sheets run perpendicular to the long axis of the fibrils. In this structure, β-sheets can be either parallel, if the peptide strands run in the same direction, or antiparallel if in the opposite direction (Figure 1). In both cases, β-strands are held together in the β-sheets by hydrogen bonds between the amide nitrogen and carbonyl oxygen. Amyloid aggregates in their final form (fibrils) exhibit different morphologies. Generally, 2-6 proto-filaments are twisted together in a rope-like or ribbon form having a diameter of 7-15 nm [21,22]. The kinetics of amyloid formation and the amyloid content of a protein solution is usually investigated by a combination of spectroscopic methods as thioflavin T fluorescence, dynamic light scattering, Congo red absorption, far UV circular dichroism, and microscopic techniques like transmission electron microscopy or atomic force microscopy. The assembly of amyloid fibrils involves key steps common to all polypeptides. The basic conformational change is the formation of extensive arrays of ordered β-sheets that allow the formation of aggregation nuclei, whose growth is considered the rate-limiting step of the process [23,24,25]. Once a nucleus is formed, fibril growth is thought to proceed rapidly by further association of either monomers or oligomers with the nucleus through a nucleation-dependent polymerization mechanism (Figure 2).
3. Intrinsic fluorescence properties in amyloid fibrils
So far, the most accredited method to detect amyloid formation both in vitro and in vivo is based on the fluorescence of an extrinsic fluorophore, the Tioflavin T, able to selectively bind the cross-β structure of amyloid fibrils [26,27]. Although ThT fluorescence is highly specific for amyloid aggregates, the employment of an extrinsic probe has some disadvantages both for clinical diagnostics and also for biophysical studies involving the effect of natural compounds in amyloid aggregation as most of them are known to interfere with ThT fluorescence [12].
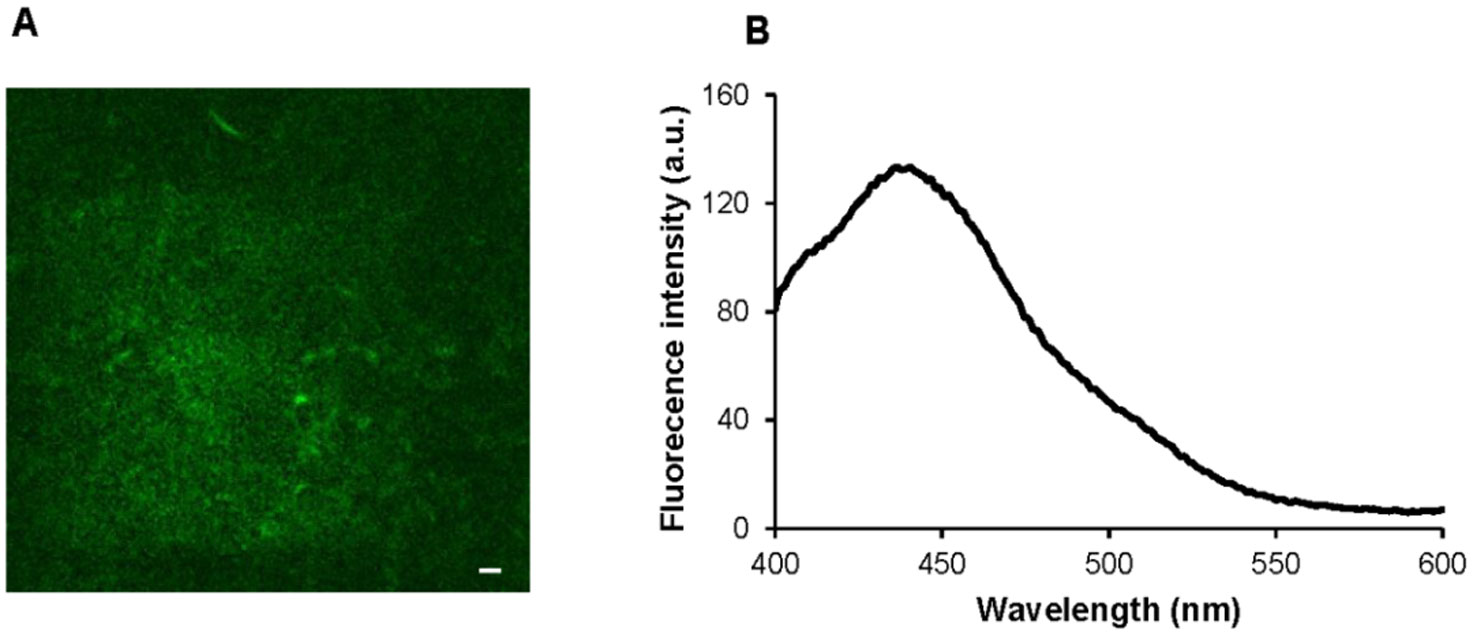
Recently, proteins and polypeptides containing a high proportion of β-sheets have been reported to exhibit, in their amyloid aggregated states, a fluorescence emission in the blue-green visible range when excited at 350 nm, which was also observed for proteins free of aromatic residues (Figure 3). As the discovery of a specific, structure-related fluorophore in amyloid aggregates would open a wide range of diagnostic applications, much attention is now payed to the characterization of this intrinsic property in different amyloidogenic proteins. The blue-green fluorescence for amyloid aggregates was first observed for gamma-II crystalline aggregates that showed a visible blue-green emission with a maximum at 466 nm upon excitation at 354 nm [4]. Similarly, the blue-green fluorescence was then observed also for amyloid aggregates formed by α-synuclein and lysozyme [28,29]. In particular, for α-synuclein, the fluorescence properties of the blue-green emission have been reported. In this study the fluorescence intensity at 440 nm (upon excitation at 350 nm) was directly related to the fibril content. For these protein models the intrinsic fluorescence was proposed to originate by a cooperative mechanism involving through-space dipolar coupling between excited states of aromatic amino acids densely packed in the fibril structure [4,28,29,30]. Further studies have directly related the intrinsic blue-green fluorescence to amyloid fibril formation. Indeed, also human lysozyme, Aβ peptide, human tau and α-synuclein have shown blue-green fluorescence in their amyloid state by fluorescence microscopy [8,9,10]. In addition, fluorescence spectroscopy studies on human lysozyme revealed a strong fluorescence intensity at 440 nm upon excitation at 355 nm that was closely associated to amyloid aggregation [8]. In these proteins, the novel fluorophore was proposed not to be related to the presence of aromatic side-chain residues within the polypeptide structure, but instead to a delocalization of the peptide electrons through intramolecular or intermolecular hydrogen bonds involved in the stabilization of secondary structure in amyloid fibrils [8,9,10].
More recently, a combination of fluorescence spectroscopy and molecular dynamic simulation studies performed for both Aβ peptide 1-42 and 33-42 allowed the identification of a structure-specific fluorophore that does not require the presence of aromatic residues or, more generally, multiple bond conjugation that characterize conventional fluorescent systems [31,32]. These studies have suggested that the phenomenon is strongly coupled to proton transfer along H-bonds formed between the N- and C-termini in protein fibrils. Thus, amyloid fibrils in either a fully protonated or deprotonated form would undergo significant changes in their optical properties. This hypothesis was supported by the experimental observation that fibrils formed for Aβ-peptide at strongly acidic or alkaline pH show a significant decrease of their intrinsic fluorescence [31,32]. Recently, this hypothesis has been supported by similar results reported for human insulin [33]. Indeed, the blue-green fluorescence observed for insulin amyloid fibrils at neutral pH was completely abolished at acidic pH.
4. Electronic transitions underlying the amyloid blue-green fluorescence
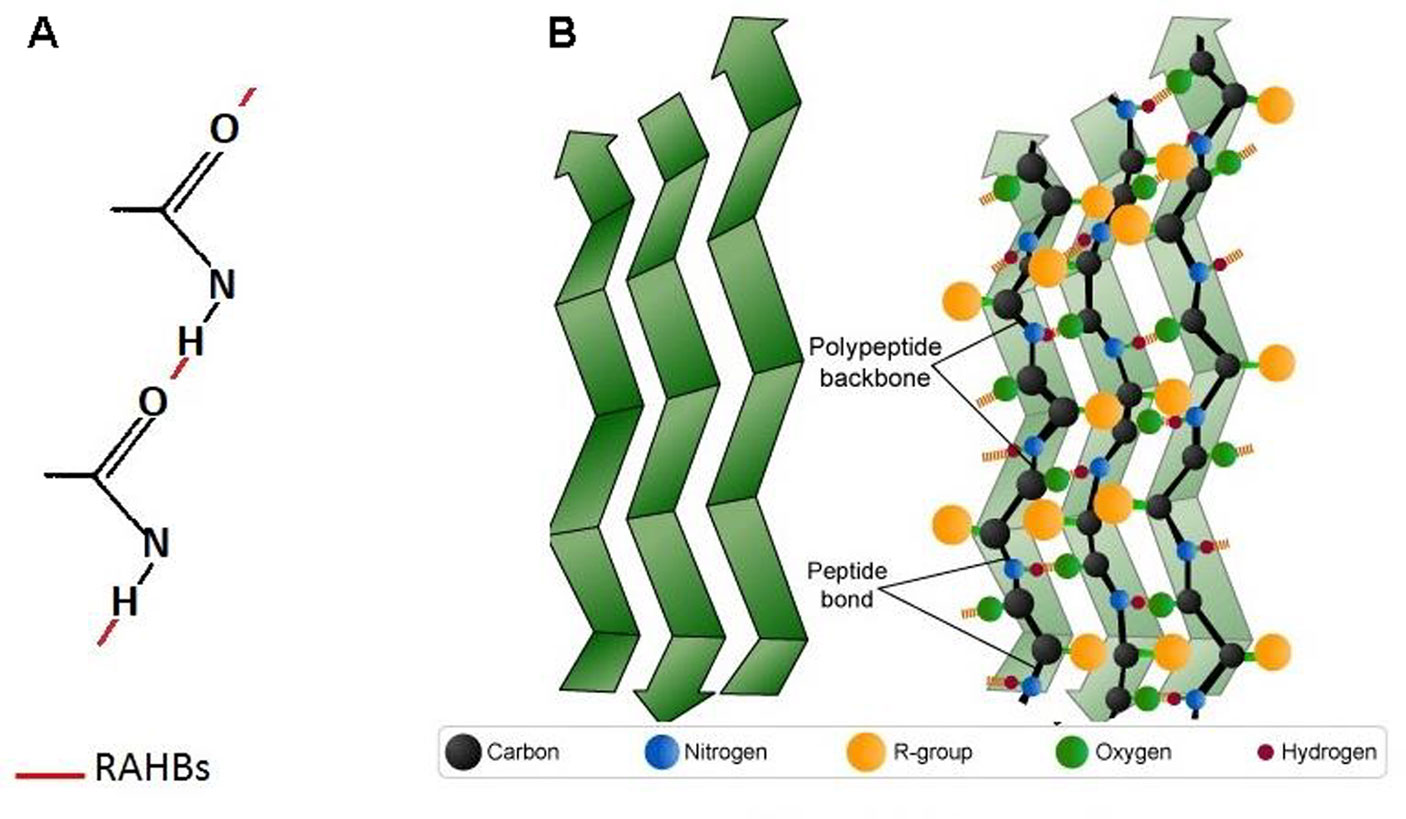
Although the appearance of the blue-green fluorescence has been described to be concomitant with the formation of fibril structure in several amyloidogenic proteins, the molecular origin of this phenomenon has not been clarified and different hypotheses have been proposed. Specifically, the intrinsic fluorescence was, at first, attributed to the dipolar coupling between the excited states of aromatic residues in the fibril structure [28,29]. However, this hypothesis has not been validated by experimental data as also fibrils free of aromatic residues showed the intrinsic blue-green fluorescence [8,9]. A more accredited hypothesis has suggested that the intrinsic fluorescence could be linked to the presence of a dense network of H-bonds in the amyloid fibrils. In this case, the intrinsic emission is supposed to be associated to an expansion of the π-electronic delocalization of the peptide bond through the backbone-to-backbone hydrogen bonds connecting the-sheets in the fibril cross-β structure [8,9,10]. When this delocalization takes place, the H-bonds are defined resonance assisted hydrogen bond (RAHBs). The broadening of the π-delocalization would induce a decrease in the excitation energy thus shifting the decay of the excited state from the UV into the visible region. Some structural considerations have raised doubts about the general validity of this hypothesis. Indeed, as the molecular orbitals involved in the peptide bond are σ and π type, its main characteristic is the delocalization of the nitrogen electron pair into the carbonyl group resulting in a significant double bond character between the carbonyl carbon and the nitrogen that allows the peptide bond to be planar and resistant to conformational changes. Thus, the extension of π-delocalization among peptide planes belonging to adjacent beta-strands mediated by CO-HN hydrogen bonds (RAHBs) requires donor and acceptor to be coplanar (Figure 4). In the antiparallel arrangement of β-sheets, the inter-strand hydrogen bonds between carbonyls and amines are planar and this would favor the conjugation of π electrons of peptide bonds of adjacent strands via RAHBs. Differently, the parallel arrangement induces a non-planarity in the inter-strand hydrogen bonding pattern thus impairing conjugation of π electrons. This would suggest that the appearance of intrinsic amyloid fluorescence could be a distinct feature of amyloid fibrils possessing antiparallel configuration although this is not supported by experimental data. Indeed, amyloid fibrils organized both in parallel and antiparallel orientation have been shown to emit in the blue-green range of wavelength (Table 1). For instance, amyloid fibrils formed by hen egg white lysozyme were found to be mainly organized in parallel β-sheet arrangement [34,35]. In addition, through a combination of ATR (attenuated total reflection) and FTIR (Fourier-transform infrared) analysis, Aβ (1-42) oligomers were found to adopt an antiparallel β-sheet structure, whereas Aβ (1-42) mature fibrils were mostly organized in highly stable parallel β-sheet configuration, in agreement with solid-state NMR models [36,37]. Only Aβ (1-42) fibrils, mainly in parallel β-sheet configuration, have shown intrinsic fluorescence while Aβ (1-42) oligomers, mostly organized in antiparallel configuration, were not fluorescent [8]. For human insulin, amyloid fibrils formed at both acidic and neutral pH were mainly organized in parallel β-sheet arrangement although only fibrils formed at neutral pH have shown the intrinsic fluorescence [33,38]. Data for β-sheet configuration in amyloid fibrils of human tau K18 protein are still contrasting [39,40]. Thus, the lack of correlation between β-sheet configuration in amyloid structure and intrinsic fluorescence raises doubts on the general validity of the hypothesis regarding the expansion of the π-electronic delocalization in the peptide bond.
Table 1. Intrinsic blue-green fluorescence properties in amyloid fibrils.
| Proteins/peptides |
Excitation maximum (nm) |
Emission maximum (nm) |
Reference |
| Henn egg white lysozyme |
355 |
440 |
[8] |
| Human α-synuclein |
350 |
440 |
[27] |
|
405 |
455 |
[9] |
| Bovine γ-II crystalline |
354 |
466 |
[4] |
| Human tau (isoform K18) |
405 |
460 |
[9] |
| Human Aβ (1-42) |
450 |
488 |
[8] |
|
405 |
455 |
[9,10] |
| Poly (VGGLG) |
405 |
465 |
[5] |
| Human insulin |
350 |
440 |
[33] |
More recently, an alternative hypothesis has suggested that the appearance of intrinsic amyloid fluorescence does not require the presence of aromatic residues or conjugated π-electron system [31,32]. Specifically, being protons along H-bonds between N-C termini in amyloid fibrils exceptionally labile, it has been hypothesized that the blue-green fluorescence could be strongly coupled to the proton transfer involving C- and N-terminus in amyloid fibrils. Indeed, the proton transfer would lower the electron excitation energies thereby decreasing the likelihood of energy dissipation associated with conventional hydrogen bonds. This conclusion was supported by the experimental observation showing that fibrils in either a fully protonated or deprotonated form would undergo significant changes in their optical properties. In particular, fibrils formed at strongly acidic or alkaline pH exhibit a significant decrease of their intrinsic fluorescence [31,32,33].
Finally, it may not be excluded that the appearance of amyloid blue-green fluorescence may have a different electronic origin. The electronic transitions allowed from the ground to the excited state responsible for the spectroscopic properties of the peptide bond namely are: n→π*, π→π*, and σ→σ*. The latter two transitions involve the excitation of a bonding electron (σ or π) to the corresponding anti-bonding orbital. The n→π* transition is typical of carbonyl compounds and it is caused by excitation of a nonbonding oxygen (or another hetero-atom) electron (n) to an anti-bonding π* molecular orbital. The σ→σ* transition requires the absorption of a high energy photon with a wavelength which does not fall in the UV-vis range, whereas π→π* and n→π* transitions require absorption of photons of lower energy and, therefore, they appear in the near UV-vis region. In particular, the energy barrier for n→π* transition is extremely low in diluted solutions (lone pair electrons are not engaged in a network of hydrogen bonds). This barrier increases moderately in the solid and amyloid state because of the involvement of the peptide bond in the network of hydrogen bonds likely causing the appearance of blue-green fluorescence and, finally, it shifts to very high values in strongly acidic conditions (lone pair electrons are engaged in a high energy covalent bond) determining the fluorescence disappearance. Although this hypothesis could provide a rationale for the pH dependence of intrinsic fluorescence observed for in insulin and Aβ-peptide, it does not explain data published for amyloid aggregation of lysozyme [8,9]. Indeed, for this protein, the amyloid fibrils show the blue-green fluorescence even at strongly acidic pH, i.e., 2.0. However, it should be considered that lysozyme has a very high isoelectric point, which could not allow the protein to be fully protonated at the examined pH [41].
5. Concluding remarks
In this paper, we have thoroughly analyzed the origin of the intrinsic blue green fluorescence exhibited by proteins or peptides in amyloid fibrils. This is a very tough problem, complex to assess. The complexity arises from the consideration that the fluorescence properties, i.e., excitation and emission maxima, are different for the proteins and peptides so far examined. In fact, the different local environments surrounding the fluorophore might affect the energy of the involved electronic transition thus shifting the intrinsic emission. Recently, growing interest has been paid to this intrinsic property as it may offer an alternative method for the investigation and detection of the amyloid aggregation state without using external probes. However, this possibility must be taken with great caution. In fact, as shown in this review, the appearance of the blue-green fluorescence cannot be taken as general marker for the amyloid fibril formation being strongly dependent not only on environmental factors, such as pH, but likely also on the spatial organization of the β-sheet configuration. To further clarify and rationalize the problem, it will be advisable to extend this study to a wider range of protein/peptide models.
Acknowledgements
This study has been supported by the grant “Finanziamento per Rientro dei Cervelli “Rita Levi Montalcini” from Italian Minister of University and Research (MIUR).
Conflict of interest
The authors declare no conflict of interest in this paper.









 DownLoad:
DownLoad: