Probabilistic approaches to exploring Binet's type formula for the Tribonacci sequence

1.   Introduction and main results

One of the most famous series of numbers in number theory is the Fibonacci sequence $\{F_n\}$. This sequence, comprised of integer values, was first introduced by Leonardo Fibonacci and defined by a recurrence procedure as

for all $n\ge 0$. Moreover, through countless examples, this sequence illustrates the connection between mathematics and nature. To this end, researchers have studied many generalizations of this sequence through either:

$(1)$ By preserving the original recurrence relation while modifying the initial terms: for example $F_0 = F_1 = 2$ ^[1] or $F_0 = 2$ and $F_1 = 1$ ^[2].

$(2)$ By maintaining the initial terms while introducing slight modification to the recursive relation: One can cite the $k$-Fibonacci numbers defined by Falcon and Plaza ^[3,4]. For any positive real number $k$, the $k$-Fibonacci sequence is defined recurrently by

which was intensively studied (see, for instance, ^[5,6,7]). One can also consult ^[8,9,10] when $F_{n+2} = F_{n+1}+ 2F_{n}$.

$(3)$ By changing the initial terms and introducing a modification to the recursive relation. For example, one can consider the relation.

$F_{n+2} = a F_{n+1}- b F_n,$ for any initial terms ^[11] or the $k$-bonacci sequence when each therm is the sum of $k$ previous terms ^[12] (see also ^[13,14]).

The enduring fascination with the Fibonacci sequence $\{ F_n\}$ has prompted continuous scholarly investigation into its inherent properties and practical applications. Furthermore, Makover in ^[15] stands out for shedding light on the exponential growth of $\{F_n\}_{n \geq 0}$ with respect to the golden ratio $\varphi = (1 + \sqrt{5})/2 = 1.61803398\ldots.$ The pivotal property of the Fibonacci-like sequence is encapsulated by Binet's formula: calculating the general terms of the sequence

where $\sigma$ and $\varphi$ are roots of the characteristic equation $x^2 = x + 1$ associated with the recurrence relation (1.1).

In the present work, we focus on one of the most important generalizations of the Fibonacci sequence, the Tribonacci sequence denoted by $\{ {\mathsf T}_{n}\}_{n \geq 0}$ and defined as

This sequence was originally studied by Feinberg in 1963 as ^[17], ^[16]. Since then, numerous authors have explored its properties, highlighting various interesting aspects such as generating functions, Binet's type formulas, and summation formulas. For further details, see, for example, ^[18,19,20], as well as ^[21,22,23] for studies specifically on the Tribonacci functions. For different initial values, we construct different Tribonacci sequences. In particular, the standard one is considered when ${\mathsf T}_0 = 0$ and ${\mathsf T}_1 = {\mathsf T}_2 = 1$, whereas the Tribonacci$-$Lucas sequence is given for ${\mathsf T}_0 = 3$, ${\mathsf T}_1 = 1$, and ${\mathsf T}_2 = 3$ ^[24]. Hence, the initial numbers of the Tribonacci sequence are intrinsic to establishing some properties, such as Binet's type formulas. In ^[25], with arbitrary initial values, the author gives a complete discussion, on Binet's formula, where he showed that

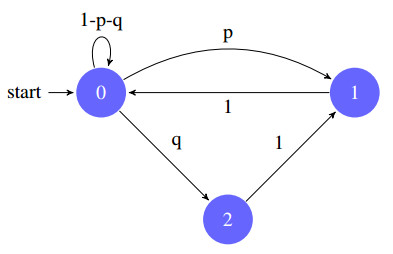
where $({\mathsf T}_0, {\mathsf T}_1, {\mathsf T}_2) = (a, b, c)$, $\phi = 1.839286$ is the real solution of the equation $x^3-x^2-x-1 = 0$, $\gamma\pi = \arccos \Big(\frac{(1-\phi)\sqrt{\phi}}{2} \Big) = 24.688997\ldots$, $\theta = 5.470354\ldots$, $\alpha = 3.857689\ldots$ and $\omega_3$ is the phase shift introduced in order to verify initial conditions. Moreover, one can use a probabilistic approach to study this recursive sequence ^[26] (see also ^[27] in the case of the Fibonacci sequence), to prove the asymptotic behavior of $\{\xi_{n}: = \frac{ {\mathsf T}_{n+1}}{ {\mathsf T}_{n}}\}_n$. We consider a Markov chain $\{X_i\}_{i\ge 1}$ defined as $X_1 = X_2 = X_3 = 0$ and $X_i\in \{0, 1, 2\}$ (see transition graph of probabilities in Figure 1). We compute how rapid the convergence to the limiting distribution is, by establishing an exact formula for ${\mathbb P}(X_{n+1} = i)$ for all $i = 0, 1, 2,$ which allows us to deduce a Binet's type formula. Let

the conjugate of $x_1$, where $p$ is the unique solution of $x+\sqrt{x}(x+1)-1 = 0$ and $q = p\sqrt{p}$. In Section 2, we will prove that $x_1$ and $x_2$ are the roots of the characteristic polynomial $P_A$ of an appropriately chosen matrix $A$, which is essential for proving Binet's type formula. We set

Our first main result is the following, which will be proved in Section 2.

Theorem 1. Let $\{ {\mathsf T}_n\}$ be the Tribonacci sequence defined by (1.3). Then, for all $n\ge 0$,

where $\Delta_1 = \big(\sqrt{p }\delta_{0}\, x_1 +\frac{\delta_1 x_2}{q} \big)$.

Let $\phi$, $\beta$ and $\bar{\beta}$ defined as

the roots of the equation $x^3-x^2-x-1 = 0$, where $\beta$ and $\bar\beta$ are conjugate. One can get a simplified version of Binet's type formula from Theorem 1.

Corollary 1. For $n\ge 0$,

One of the most well-known properties of the Fibonacci sequence is the identity $\sum_{k = 0}^n F_k = F_{n+2} - 1$. In ^[28], the authors extended this concept to prove that

where ${\mathsf T}_0 = 0$ and ${\mathsf T}_1 = {\mathsf T}_2 = 1$. A similar result will be explored in Section 4 to analyze the Tribonacci sequence of random variables (TSRV). Let $(\Omega, {\mathcal A}, {\mathbb P})$ be a probability space, and let ${\mathbb E}$ be the expectation with respect to ${\mathbb P}$. We define ${\mathsf Z}_0, {\mathsf Z}_1,$ and ${\mathsf Z}_2$ be absolutely continuous random variables, with joint probability density function (pdf) $f_{({\mathsf Z}_0, {\mathsf Z}_1, {\mathsf Z}_2)}$. For $n\ge 3$, we define

Denote by $f_{ {\mathsf Z}_0}, \; f_{ {\mathsf Z}_1},$ and $f_{ {\mathsf Z}_2}$ the marginal pdf's of ${\mathsf Z}_0, \; {\mathsf Z}_1,$ and ${\mathsf Z}_2$ respectively; we will give the pdf of ${\mathsf Z}_n$ in general setting (Theorem 4). A special and non trivial example, when ${\mathsf Z}_i, \; i = 0, 1, 2$ be mutually independent and identically distributed (i.i.d.) random variables having exponential distribution with parameter $\lambda = 1$ (${\mathsf Z}_i \sim {\mathcal E}(1)$) is given in Example 1.

In Section 3, we will delve into the concept of the color model and its application in obtaining an approximation of $T_n$ for large values of $n$. An application of Binet's type formula proved in Section 2, we obtain

Our main result in Section 3 is the following.

Theorem 2. Let $\{ {\mathsf T}_n\}$ be the Tribonacci sequence such that ${\mathsf T}_0 = 1$, ${\mathsf T}_1 = 1$ and ${\mathsf T}_2 = 2$. For all $n \geq 3,$ one has

In particular, (1.7) holds.

Our study explores how the inherent properties of the model can be leveraged to simplify complex computations and gain insights into its asymptotic behavior. Our approach is rooted in probabilistic methods, which offer a robust framework and derive an approximation that accurately reflects the behavior of ${\mathsf T}_n$ as $n$ grows large. This probabilistic perspective not only provides a pathway to approximate ${\mathsf T}_n$ but also facilitates a deeper understanding of the interplay between randomness and structure within the color model. Moreover, it gives an interesting relation, such as (1.8) and (3.1) below. First, combining Proposition 1 and (2.3), one has

where $\alpha_0$ is defined in (2.1). This implies, in particular, that (1.7) holds.

When studying sequences of random variables, it is common to encounter asymptotic (or limit) theorems. These theorems are often used to approximate the distribution of large-sample statistics with a limiting distribution, which is typically much simpler to analyze. One of the most well-known theorems in the field of asymptotic probability theory is the central limit theorem (CLT). It states that, under certain conditions (independence and same distribution), the distribution of a properly normalized sample mean converges to a standard normal distribution, even if the original variables are not normally distributed. In fact, there are various ways in which the CLT can fail, depending on which hypotheses are violated. In Section 4, we study the asymptotic distribution of the random variables $\{ {\mathsf Z}_n\}$. A crucial observation is that these random variables are neither independent nor identically distributed (i.i.d.), which introduces additional complexity into their analysis. However, we will establish specific limit results that shed light on the long-run behavior of $\{ {\mathsf Z}_n\}$. These results, presented in Theorem 5, highlight the asymptotic characteristics of $\{ {\mathsf Z}_n\}$ Specifically, define

and assume that the random variables ${\mathsf Z}_0$, ${\mathsf Z}_1$, and ${\mathsf Z}_2$ are i.i.d. Then, the sequence of random variables

where ${\mathsf L} = {\mathsf Z}_0 + \phi {\mathsf Z}_1 + \phi^2 {\mathsf Z}_2$. In particular, when ${\mathsf Z}_0$, ${\mathsf Z}_1,$ and ${\mathsf Z}_2$ are normally distributed, then the sequence $\{ {\mathsf Z}_n\}$ satisfies the CLT.

2.   A probabilistic approach to obtain Binet's type formula

2.1.   Markov chain and preliminaries results

We consider $\Gamma = (X_0, X_1, \ldots)$, a family of random variables. Then, $\Gamma$ is called a Markov chain if the variables $(X_0, X_1, \ldots, X_{k-1})$ and $(X_{k+1}, \ldots, )$ are independent of each other for any given $k$. Thus, describing the distribution of $X_{n-1}$ for each $n$ allows us to describe the entire Markov chain. We define the random variables $\{X_n\}$ by

(1) $X_1 = X_2 = X_3 = 0.$

(2) ${\mathbb P}\big(X_{i+1} = 0 | X_i = 0 \big) = 1-p-q$, ${\mathbb P}\big(X_{i+1} = 1 | X_i = 0\big) = p,$ and ${\mathbb P}\big(X_{i+1} = 2 | X_i = 0\big) = q$.

(3) ${\mathbb P}\big(X_{i+1} = 0 | X_i = 1 \big) = 1$.

(4) ${\mathbb P}\big(X_{i+1} = 1| X_i = 2 \big) = 1$.

Since the Markov chain $\{X_n\}$ is aperiodic, meaning that there exists a state with a positive probability of returning to itself, and irreducible, meaning that it is possible to transition from any state to any other state with positive probability, it follows that $\lim_{n \to \infty} {\mathbb P}(X_n = i)$ exists for $i = 0, 1, 2$.

Lemma 1. Let, for $i = 0, 1, 2$, $\alpha_i = \lim\limits_{n\to \infty} {\mathbb P}(X_n = i)$ and $p, q \in (0, 1)$ such that $1-p-q > 0$. Then

In addition $\lim_{n\to \infty} {\mathbb P}(A_n) = (1-p-q)/(2q+p+1)$, where $A_n = \big\{ X_{n+1} = X_{n+2} = 0 \big\}$.

Proof. Observe that

Therefore, we have

Letting $n$ tend to infinity to obtain

Let us consider $A_n = \big\{ X_{n+1} = X_{n+2} = 0 \big\}$. It follows that

Then, $\lim_{n\to \infty} {\mathbb P}(A_n)$ exists and depends on $p$ and $q$. It follows that

□

Lemma 2. Let, $A_n = \big\{ X_{n+1} = X_{n+2} = 0 \big\}$. Then,

Proof. Notice, for $k = 0, 1, \ldots$, that

Then

□

Remark 1. Lemma 2 shows, in particular, that the event $A_n$ is adequate to study the sequences $\{ {\mathsf T}_n\}_n$. Indeed, for any sequence $\{\Upsilon_n\}_n$ defined as $\Upsilon_n = \alpha \frac{ {\mathbb P}(A_n)}{\sqrt{p}^{n-1}}$ Tribonacci sequence, where $\alpha$ is a positive integer. Indeed,

which implies that $\{\Upsilon_n\}_n$ is Tribonacci sequence.

As a consequence of Lemma 2, one can prove Binet's type formula. More precisely, we have the following result:

Proposition 1. Let $\{ {\mathsf T}_n\}$ be the Tribonacci sequence defined by (1.3). Then, for all $n \geq 0$,

where $p$ is the unique solution of $x+\sqrt{x}(x+1)-1 = 0$ and $q = p\sqrt{p}$.

Proof. We will prove this result by induction. To do this, we calculate the first values of ${\mathbb P}(A_n)$ in Table 1.

Hence, ${\mathsf T}_0 = {\mathbb P}(A_2)/\sqrt{p} = 1$ and similarly, ${\mathsf T}_1 = 1$, ${\mathsf T}_2 = 2$ and ${\mathsf T}_3 = 4$. Then, the result follows using Remark 1. □

2.2.   Asymptotic distribution of $X_n$

In order to compute the general term of the sequence $\{ {\mathsf T}_n\}_n$, using Proposition 1 and since

it will be useful to introduce the following matrices:

where $n\ge 4$. Hence, using (2.2), $\pi_{n+1} = A \pi_{n}.$

Proposition 2. The only invariant probability measure $\pi$ of the Markov chain $\{ {\mathcal X}_n\}$ defined above is

where $v^t$ is the transpose of the vector $v$.

Proof. To get the invariant probability measure $\pi$ of the chain, we solve the equation $\pi = A \pi,$. However, for $\pi = (\alpha_{0}, \alpha_{1}, \alpha_{2})^t$ we obtain

where, we have used (2.2) and (2.1). Then, we deduce

the only invariant measure. □

Let $P_A$ (or simply $P$ when no confusion arises) denote the characteristic polynomial of the matrix $A$ then

Let $x_1$ and $x_2$ be the roots of $P_A$ distinct from $1$, that is:

Lemma 3. (1) $x_1x_2 = x_{1}\overline{x_{1}} = q$.

(2) $x_2-x_1 = i \sqrt{4 q - (p+q)^2}$.

(3) $x_1^2 = -q +(p+q)i \; \sqrt{4 q - (p+q)^2}$.

(4) $x_2^2 = -q -(p+q)i \; \sqrt{4 q - (p+q)^2}$.

In this paragraph, we will prove the following result.

Theorem 3. For $n\ge 0$,

where $\delta_0$, $\delta_1,$ and $\delta_2$ are defined in (1.4).

Proof. A simple calculation proves that the eigenvectors associated with the eigenvalues $1, \; x_{1},$ and $x_{2}$ respectively are $(1, p+q, q)^t$, $(1, \frac{p x_1+q}{x_1^2}, \frac{q}{x_1})^t$ and $(1, \frac{p x_2+q}{x_2^2}, \frac{q}{x_2})^t$. It follows that

where

and

Notice, using Lemma 3, that

Since $X_{1} = X_{2} = X_{3} = 0,$ then $\pi_{n} = A^{n-4} \pi_{4}$, for all $n\ge 4$, which implies that

It follows that

as required in Theorem 3. □

As a consequence, since $|x_1| = |x_2| = \sqrt q$, we obtain the following result.

Corollary 2. For all $n\ge 4$, one has

where $\alpha_0$ is defined by (2.1).

The previous corollary explains the convergence of the Markov chain ${\mathbb P}(X_{n} = 0)$ to $\alpha_0$. Moreover, the extra term $\frac{2\sqrt{\alpha_0 }}{ \sqrt{4 q - (p+q)^2}} \sqrt{q}^{n-1}$ tells us exactly how far away the Markov chain is from converging.

2.3.   Binet's type formula related to Tribonacci sequence

Here, we will prove our main result (Theorem 1). Recall the event $A_n$ introduced in Lemma 2.1; our result is essentially based on the following relation proved in Proposition 1:

when $p$ is the unique solution of $x+\sqrt{x}(x+1)-1 = 0$ and $q = p\sqrt{p}$. Notice that

Thus, using (2.5), we have

where

2.4.   Alternative formula: proof of Corollary 1

Recall $\phi$, $\beta$ and $\bar{\beta}$, the roots of the equation $x^3-x^2-x-1 = 0$ defined in (1.5). Before giving the proof of Corollary 1, we start by proving the following lemma.

Lemma 4. Let $\phi$, $\beta$ and $\bar{\beta}$ defined in (1.5). Then

(1) $\beta \bar \beta = \frac{1}{\phi } = \phi -2$ and $\beta +\bar \beta = 1-\phi$,

(2) $\phi = 1/\sqrt{p}$,

(3) $\beta = x_1/ \sqrt{p}$ and $\bar\beta = x_2/ \sqrt{p}$.

Proof. (1) Since

Then $\beta$ and $\bar \beta$ are the solutions of $x^2 +(\phi-1) x + \phi-2 = 0$.

(2) Observe that,

It follows that $\phi^{-2}\in (0, 1)$ is a solution of $f(x) = x+\sqrt{x}(x+1)-1 = 0,$ which implies that $p = \phi^{-2} = 0.295597\ldots$ and then $q = 0.160713\ldots.$

(3) Define $t = \frac{x_1}{\sqrt p}$ and then $t\sqrt p = x_1$. Since $P(x_1) = 0$, then we have

It follows that $t$ is the solution of $- x^{3}+ x^{2}+ x+ 1 = 0$ and $t = \beta$. Similarly, if we consider $t = \frac{x_2}{\sqrt p}$ then

Thus, we deduce that $t = \bar \beta$. □

It follows ^[25] that the Tribonacci sequence $\{ {\mathsf T}_n\}$ can be written as

Since we choose ${\mathsf T}_{0} = {\mathsf T}_{1} = 1$ and ${\mathsf T}_{2} = 2$, one has

By inverting the Vandermonde matrix, we obtain the desired result, that is,

3.   Approximation of ${\mathsf T}_n$: color model

In this section, we investigate how the intrinsic properties of the model can be utilized to streamline complex computations and reveal insights into its asymptotic behavior. Grounded in probabilistic methods, we will prove Theorem 1.2, which may give an approximation of ${\mathsf T}_n$ as $n$ becomes large. Let $\{s_n\}_{n \geq 1}$ denotes the number of sequences of 1's, 2's, and 3's that sum to $n$. It is easy to see that $s_1 = 1 = {\mathsf T}_1$, $s_2 = 2 = {\mathsf T}_2$, and $s_3 = 4 = {\mathsf T}_3$. Additionally, since

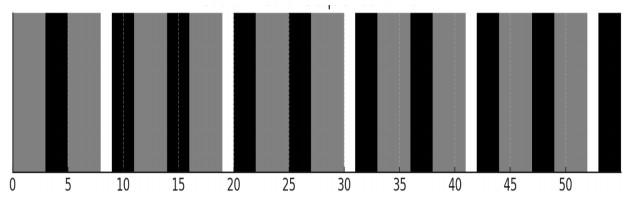
we conclude that $s_n = {\mathsf T}_n$. Therefore, for $n \geq 4$, $T_n$ can be combinatorially interpreted as the number of ways to tile a board of length $n-1$ using tiles of size 1, 2, and 3 cells. To illustrate this, consider an infinite board with cells labeled $1, 2, 3, \dots$, where each cell is independently colored black, white, or gray with probability $1/3$, as shown in Figure 2. Moreover, any coloring of the first $n$ cells has a probability of $(1/3)^n$.

An infinite tiling can be represented as alternating sequences of black, white, and gray cells of varying lengths. For instance, the tiling shown in Figure 2 consists of a gray sequence of length 3, followed by a black sequence of length 2, then another gray sequence of length 3, a white sequence of length 1, a black sequence of length 2, and so on.

Let the random variable $X$ repre sent the position of the end of the first black string that is not a multiple of two, or the first gray string that is not a multiple of three. We now ask: For $n \geq 1$, what is the probability that $X = n$? To answer this, note that $X = n$ occurs if and only if:

(1) Cell $n$ is covered by $B$ (a black cell), and cell $n+1$ is covered by $\overline{B}$ (a white or gray cell), or Cell $n$ is covered by $G$ (a gray cell), and cell $n+1$ is covered by $\overline{G}$ (a white or black cell), and

(2) cells $1$ through $n-1$ are covered using any combination of white cells, black double cells, and gray triple cells.

It follow that

(i) If tile number $n$ is black, we will have ${\mathsf T}_{n-1}$ ways from $1$ to $n-1.$

(ii) If tile number $n$ is gray and if the number of tiles has a remainder of $2$ when divided by $3,$ we will have ${\mathsf T}_{n-2}$ ways from $1$ to $n-2.$ However, if the number of last gray tiles admits a remainder of $1$ when divided by $3,$ we will have ${\mathsf T}_{n-1}$ ways from $1$ to $n-1.$

Proposition 3. Let $\{ {\mathsf T}_n\}$ be a Tribonacci sequence defined by (1.3); then

where $\{ {\mathsf T}_n\}_{n\ge 0}$ is naturally extended forward by putting ${\mathsf T}_{-1} = 0$.

Proof. Let $X$ be the random variable introduced above. Then, for all $n\ge 1$, one has

Since $X$ is finite with probability $1,$ this gives a combinatorial explanation of the identity □

Corollary 3. Let $\{ {\mathsf T}_n\}$ be a Tribonacci sequence defined by (1.3); then

Now, we tile an infinite board by independently placing cells, double cells, and triple cells with probability $\sqrt{p}, \; p$ and $q = p \sqrt{p}.$ Conveniently, $p+\sqrt{p}(p+1) = 1.$ In this model, the probability that a tiling begins with any particular length $n$ of cells, double cells and triple cells is $\sqrt{p}^{n}.$ Let $\varsigma_{n}$ be the probability that a random tiling is breakable at cell $n,$ i.e., that a cell or double cell, or triple cell begins at cell $n.$ The example in Figure 2 is breakable at cells

Since there are ${\mathsf T}_{n-1}$ different ways to tile the first $n-1$ cells,

For a tilling to be unbreakable at $n,$ it must be

(i) breakable at $n-1$ followed by a double cell or triple cell,

(i) breakable at $n-2$ followed by a triple cell.

Thus, for $n \geq 3,$ one has

which implies in particular Theorem 2. Let $\varsigma = \lim_{n \rightarrow +\infty}\varsigma_{n}.$ Taking a limit in (3.4) gives

then $\varsigma = \alpha_0 = \frac{1}{1+p+2p\sqrt{p}}$ and ${\mathsf T}_{n}\sim \alpha_{0}\sqrt{p}^{-n}.$

4.   Distribution of Tribonacci random variable

In this section we focus on the asymptotic distribution of the TSRV $\{ {\mathsf Z}_n\}$, defined by (1.6). As mentioned above, these random variables are neither independent nor identically distributed. In fact, unlike classical scenarios where i.i.d. assumptions simplify the derivation of limiting behavior, here we must account for potential dependencies and non-uniform distributional properties within the sequence. Our main result will be presented in Theorem 5. We denote, for $k = 0, 1, \ldots$,

the expectation and the variance of ${\mathsf Z}_k,$ respectively. First, observe that one can easily establish the following two lemmas.

Lemma 5. There exists a Tribonacci sequence $\{ t_n\}_{n \ge 0}$ with $t_0 = t_1 = t_2 = 1$ such that

In particular, we have $\mu_n = t_{n-2} \mu_0 + t_{n-1} \mu_1+ t_{n} \mu_2,$ and if the random variables ${\mathsf Z}_0$, ${\mathsf Z}_1,$ and ${\mathsf Z}_2$ are independent, then

for all $n\ge 3$.

Lemma 6. Let $\{t_n\}$ be a Tribonacci sequence such that $t_0 = t_1 = t_2 = 1,$ then

Proof. The result is trivial for $n = 0, 1$ and $2$. In addition, assume that (4.1) holds, then

Thus the result follows by induction. □

Remark 2. Lemma 6, will be used in the proof of the convergence of the sequence $\{ {\mathcal S}_n \}$ defined in Theorem 5.

Recall that ${\mathsf Z}_0, {\mathsf Z}_1,$ and ${\mathsf Z}_2$ are absolutely continuous random variables with joint pdf $f_{({\mathsf Z}_0, {\mathsf Z}_1, {\mathsf Z}_2)}$. In the following, we will give the pdf of the random variable ${\mathsf Z}_n$.

Theorem 4. Let $\{ {\mathsf Z}_n\}$ be a TSRV defined by (1.6),

(1) The pdf of ${\mathsf Z}_n$ is given by

Moreover, if ${\mathsf Z}_0, \; {\mathsf Z}_1$ and ${\mathsf Z}_2$ are mutually independent, then

where $f_{ {\mathsf Z}_0}, \; f_{ {\mathsf Z}_1}$ and $f_{ {\mathsf Z}_2}$ are the marginal pdf's of ${\mathsf Z}_0, \; {\mathsf Z}_1$ and ${\mathsf Z}_2$ respectively.

(2) The joint pdf of $Z_{n}$ and $Z_{n+k}$ is given by

where

Proof. $(1)$ Equations (4.2) and (4.3) are straightforward results of distributions of linear functions of random variables (see, for instance, ^[29,30,31]).

$(2)$ We can write

and let

Notice that, the Jacobian of this linear transformation is $J_{n, k},$ and the solution of the previous system of equations is given by

Therefore, the joint pdf of $Z_n$ and $Z_{n+k}$ is

□

Remark 3. Notice, with respect to squared error loss, the best unbiased predictor of $Z_{n+k}$, given $Z_{n},$ is

where $g(x)$ provides the conditional expectation of $Z_{n+k}$ given $Z_{n} = x$; that is,

Hence, Theorem 4 offers a way to obtain a good approximation of ${\mathsf Z}_n,$ as we can see in the following example.

Example 1. In this example, we will consider the case when the random variables ${\mathsf Z}_0$, ${\mathsf Z}_1,$ and ${\mathsf Z}_2$ are i.i.d. with exponential distribution with parameter $1$ ($\mathcal{E} (1)$). Under the above notation we have $f_{ {\mathsf Z}_3}(x) = \frac{x^{2}}{2} \exp (-x)I_{\{ x \geq 0\}}$ and for all $n \geq 4,$

Choose $n = 3$ and $k = 4$, so that $t_0 = t_1 = t_2 = 1, \; t_3 = 3, \; t_4 = 5, \; t_5 = 9, \; t_6 = 17,$ and $t_{n+k} = t_7 = 31.$ Using Theorem 4, since $J_{3, 4} = t_6 t_1-t_2t_5 = 8$, we obtain

Then

This gives, in particular, an estimation of ${\mathsf Z}_3$.

In the following, we will study some useful asymptotic properties of the TSRV. To this end, we define the random variable ${\mathsf L} : {\mathsf Z}_0 + \phi {\mathsf Z}_1 + \phi^2 {\mathsf Z}_2$, and, for all $n \ge 3$,

where $\phi$ is the real solution of the equation $x^3-x^2-x-1 = 0$, and $S_n = \sum_{k = 0}^n {\mathsf Z}_k$. In particular, one can expect that the sequence $\{ \chi_n\}$ converges to $\phi$. To this end, we define the event $\mathsf S = \{ \omega \in \Omega,$ such that ${\mathsf L}(\omega)\neq 0 \}$.

Theorem 5. We consider the TSRV defined by (1.6). Then

(1) The sequence of random variables $\{\chi_n \}$ converges pointwise to $\phi$ on ${\mathcal S}$.

(2) Assume that $(\sigma_0, \sigma_1, \sigma_2)\neq (0, 0, 0)$, then $Y_n$ converges pointwise to

(3) Assume that ${\mathsf Z}_0$, ${\mathsf Z}_2,$ and ${\mathsf Z}_3$ are i.i.d., then the sequence of random variables $\{ {\mathcal S}_n \}$ converges pointwise to ${\mathcal S}$.

Proof. $(1)$ Using Lemma 5, for all $\omega \in \mathsf S$, we have

where $\xi_n = \frac{t_{n+1}}{t_n}.$ It follows, since $\lim_{n\to \infty} \xi_n = \phi$, that

$(2)$ Clearly, one has

$(3)$ First, observe that

Using (4.1), we obtain that

Using Lemma 5, then

which implies that

□

Remark 4. Consider the special case when the random variable ${\mathsf Z}_0$, ${\mathsf Z}_1,$ and ${\mathsf Z}_3$ are normally distributed. Then, the CLT holds, that is ${\mathcal S}_n$ converges in law to ${\mathsf L}\sim\mathcal N(0, 1)$.

5.   Conclusions

In this work, we investigated the Tribonacci sequence $\{ {\mathsf T}_n\}$. We examined an irreducible and aperiodic Markov chain with a finite state space $\{X_n\}$. Conditioned on $X_{n+1} = X_{n+2} = 0$, the values of $(X_1, \ldots, X_n)$ are uniformly distributed. In Section 2, we derived Binet's type formula for the Tribonacci sequence. In Section 3 we explored the color model to approximate ${\mathsf T}_n$. The probabilistic perspective offers a valuable approach to achieve this approximation. Furthermore, in Section 4, we proved that the TSRV is fully determined by the initial random values ${\mathsf Z}_0$, ${\mathsf Z}_1$, and ${\mathsf Z}_2$, and satisfies certain limiting properties in comparison to the Central Limit Theorem (CLT).

Author contributions

Both authors contributed equally to the preparation of this manuscript. Both authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence tools in the creation of this article.

Funding

The authors acknowledge the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research at King Faisal University, Saudi Arabia, for financial support under the annual funding track [KFU251894].

Conflict of interest

The authors have no relevant financial or non-financial interests to disclose.