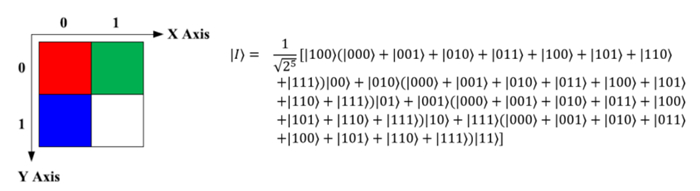A multi-channel quantum image representation model with qubit sequences for quantum-inspired image and image retrieval

List of abbreviations

1.   Introduction

The field of quantum computation has emerged through several important theoretical advancements and promising experimental results since its inception in 1982 ^[1]. Specifically, in 1995, Shor introduced the algorithm of quantum integer factoring in polynomial time ^[2]. Two years later, Grover introduced a novel algorithm of a quantum search for databases that allows for quadratic acceleration ^[3]. These two algorithms, namely Shor and Grover, have been utilized extensively in quantum computers. As a new computational approach, quantum computation benefits from the unusual properties of quantum mechanics, such as superposition and entanglement states, to store, process, and transmit information ^[4].

Quantum computation serves in several fields of computer science, such as information theory, cryptography ^[5], data analysis ^[6], deep learning (DL) ^[7,8], pattern recognition ^[9], QIR for remote sensing applications ^[10], and image processing ^{[11,12,13,14]}. One of the most important branches of computers is digital image processing ^[15], which forms an essential part of numerous applications. The rapid progress of image and video capturing systems, especially on mobile devices or computers, has led to fast growth in the amount and scale of visual content. Therefore, there has been an increasing need to devise and deploy new algorithms that can manage various visual processing of images or videos, including facial recognition, both locally and remotely ^[16,17]. Initially, with the emergence of quantum computers, researchers faced fundamental difficulties, since the field is an emerging one, especially in image representation to a quantum state, which is one of the initial challenges, whereas the more recent challenges involve choosing approaches for preparing and processing the quantum images on quantum computers.

Quantum image processing (QIP) is currently in the position of bridging the gap between quantum computation and image processing. Over the past few years, the promising future of quantum computers has become increasingly evident ^[1,18]; therefore, quantum image processing has currently become an extensive field of research ^[19]. The QIP possesses two important notable properties: (1) The capacity for quantum storage to increase exponentially and (2) the utilization of distinctive quantum mechanics principles, including entanglement and parallelism ^[20]. This field can be categorized into two main branches: Quantum image representation and quantum image processing.

In quantum image representation, several algorithms have been introduced to represent (encode) and retrieve images (decoding or reconstructing the classical image from its QR), as well as store, compress, and process information via quantum mechanics, such as the qubit lattice ^[21], real ket ^[22], entangled images ^[23], flexible representation of quantum images (FRQI) ^[11], novel enhanced quantum representation of digital images (NEQR) ^[24], multichannel representation for quantum images (MCQI) ^[25], normal arbitrary quantum superposition state (NAQSS) ^[26], the normal arbitrary superposition state (NASS) ^[27], generalized quantum image representation (GQIR) ^[28], novel quantum representation of color digital images (NCQI) ^[29], red-green-blue (RGB) multichannel representation for quantum colored images (QMCR) ^[30], bit plane representation of quantum images (BRQI) ^[31], quantum representation of multiwavelength (QRMW) ^[32], quantum representation of color images (QRCI) ^[33], the double quantum color image encryption scheme (DQRCI) ^[34], novel quantum image representation based on HSI (QIRHSI) ^[35], quantum pixel representations (QPIXL) ^[36], enhanced quantum image representation using the entanglement state encoding in the HSI color model (EQIRHSI) ^[37], hybrid quantum qutrit (qudit) representation of digital RGB images ^[38], efficient flexible representation of quantum image using the direct cosine transform (DCT-EFRQI) ^[39], quantum probability image encoding (QPIE) ^[13], and polar coordinate quantum image processing (APQI) ^[40].

In 2013, Sun et al. ^[25] introduced the MCQI model for image representation inspired by FRQI, which was created by using gates of quantum rotation. The MCQI model is capable of recording details from both the RGB channels and the 𝛼 channel. However, it uses the amplitude of quantum states to store color information, making it challenging to obtain an accurate classical color image from an MCQI quantum system. In 2017, Sang et al. ^[19] introduced a new image representation model inspired by NEQR to store and retrieve color images accurately; their model, which is named NCQI, uses a quantum bit (qubit) sequence basic state for encoding the color information of digital images. This has currently become one of the widely recognized QIRs, since it allows for the accurate recovery of color images. The NCQI representation model states that to store a color digital image of size ${2}^{n}\times {2}^{n}$, a total of $2n+24$ qubits are needed. In 2019, Ling et al. ^[33] investigated a new quantum image representation model that represents color information through the fundamental states of sequences of qubits, and it requires a total of $2n+6$ qubits to store a color digital image that has dimensions of ${2}^{n}\times {2}^{n}$. In 2023, a new model for QIR called efficient flexible representation of quantum image using the discrete cosine transform (DCT-EFRQI) ^[39] was introduced, which is an inspired by the discrete cosine transform (DCT) with the generalized quantum image representation (GQIR) ^[41] approach. The first two steps of DCT-EFRQI are identical to those of DCT‑GQIR, but DCT‑EFRQI not only uses DCT and quantization for compression but also incorporates an auxiliary qubit and is controlled so the Toffoli gates flexibly connect the quantized coefficient information with the pixel's position, where DCT-EFRQI needs $q+2n+1$ for each $16\times 16$ block, where $q = 8$ and a mean of 17 qubits is required for each block.

In fact, all the aforementioned approaches are based on three main methods: FRQI, NEQR, and NASS. The first one, namely the FRQI, depends on the amplitude of a quantum state and encodes binary values for pixel positions, whereas the second one, which is the NEQR, directly represents pixel intensity values using binary encoding. The third approach, called NASS, encodes pixel information within a quantum state, mapping each pixel's intensity and location onto a superposition of quantum states. In terms of other approaches, some apply the NEQR to color images, whereas others use the FRQI with some adjustments. Additionally, NASS is similar to FRQI and NEQR but allows for arbitrary pixel intensities and positions, offering greater flexibility in encoding images with varying resolutions and color depths. Additionally, two models of QIR that are of interest are the QIRHSI and its enhanced version, the EQIRHSI, which adds a new concept about the entanglement of two qubits between H and S. Therefore, with this concept, the authors present a new idea about how we can transform the information on the basis of the entanglement state. Additionally, Das and Caruso ^[38] introduced a new idea of how we can represent images via two (hybrid‑qudit) entangled quantum registers, which constitute a total of 7 qutrits. In 2024, Balewski et al. ^[6] introduced a new two data-encoding techniques, known as QCrank and QBArt, which use uniformly controlled rotation gates to demonstrate significant quantum parallelism.

However, each of the aforementioned approaches has its weaknesses. Therefore, starting with the limitations of the FRQI model, the shortcomings involve grayscale resolution images, which represent color intensity using a single qubit, restricting grayscale differentiation to angular parameters, that is, the mean (${\theta }_{i}\in [0, \pi /2]$). This coarse angular encoding limits color depth and complicates precise intensity discrimination, particularly for high-contrast images ^[42,43]. Additionally, experimental implementations on IBM quantum processors have revealed significant reconstruction errors (mean square error ≈ 200) due to decoherence and measurement noise, even for 2×2 images ^[43]. Moreover, preparing FRQI states for ${2}^{n}\times {2}^{n}$ images requires $2n+1$ qubits and $O\left({24}^{n}\right)$ operations, which becomes infeasible for high-resolution images because of the exponential resource growth ^[44]. In contrast, the NEQR model improves grayscale resolution by directly encoding pixel intensities via binary-represented qubits; however, this representation type is deterministic, which means that each additional bit of intensity precision necessitates extra qubits, leading to $8+2n$ total qubits for ${2}^{n}\times {2}^{n}$ images, which is prohibitively large for current NISQ-era devices ^[39]. Furthermore, quantum Fourier transform operations on NEQR-encoded images require intricate gate sequences that amplify error rates, particularly when processing high-frequency components ^[44]. While NEQR extensions to RGB exist, simultaneous encoding of multiple color channels exacerbates qubit requirements and interchannel crosstalk ^[39]. The NASS model is flexible but introduces trade-offs. For example, mapping variable-resolution images to quantum states requires adaptive entanglement schemes that lack standardized implementation protocols ^[44]. The superposition principle complicates deterministic pixel value retrieval, as measurement collapses the states probabilistically—a critical issue for exact image reconstruction ^[5]. Additionally, the current quantum processors of this model have limited qubit connectivity and thus struggle to implement NASS's arbitrary entanglement patterns efficiently ^[44]. The limitations of the QIRHSI and EQIRHSI models arise from decoherence in multiqubit systems, in which the entanglement between the H and S components increases vulnerability to environmental noise, with fidelity decreasing below 0.9 in multiqubit systems even with error mitigation ^[43]. Additionally, with color space constraints, the cylindrical coordinate system of the HSI model introduces nonlinear relationships between color components, complicating quantum arithmetic operations for color transformations ^[43]. The circuit depth of EQIRHSI's additional entanglement gates via controlled-SWAP lengthens the circuit depth, increasing the likelihood of decoherence and limiting practical image sizes ^[44]. In hybrid qudit entangled registers, the 7-qutrit hybrid qudit approach theoretically enables compact encoding but faces implementation barriers. The qudit control complexity of the current quantum hardware predominantly supports qubits, with limited tools for manipulating qutrit states. Furthermore, stabilizing qutrit superpositions requires error rates below ${10}^{-4}$, which is unachievable with the current superconducting or trapped-ion qubits ^[44]. Entangling multiple qutrits across registers demands precise microwave/optical control, with crosstalk errors scaling quadratically with the register's size ^[44]. The lack of standardized quantum gates for qutrit systems forces researchers to decompose operations into qubit-based primitives, negating potential efficiency gains ^[44]. Additionally, cross-cutting challenges in quantum image processing, such as hardware limitations, algorithmic–architectural mismatches, and theoretical–experimental discrepancies, exist. The limitations of hardware now refer to the qubit count and connectivity; even 512×512 images require ~19 qubits for FRQI, exceeding the capacity of most current quantum processors, based on IBM's documented 433-qubit Osprey, which suffers from 1%–2% gate errors ^[45]. Multistep image processing pipelines accumulate errors exponentially. For example, a 10-layer FRQI circuit on IBM's Nairobi achieves only 67% fidelity because of T1/T2 decay ^[45]. In terms of algorithmic–architectural mismatches, such as nonadaptive encoding, most QIR methods assume fixed image resolutions and lack dynamic resizing capabilities without full reencoding ^[3,5]. Classical–quantum bottlenecks in hybrid systems such as DCT-EFRQI suffer from the latency in quantum–classical data conversion, negating theoretical speedups for real-time applications ^[3]. Furthermore, theoretical–experimental discrepancies reveal a simulation–reality gap such that Quirk simulations showed perfect DCT-EFRQI compression, whereas experimental implementations on Rigetti processors exhibited 30%–40% distortion due to approximate cosine transformations ^[39]. While the theoretical complexity is $O\left({n}^{2}\right)$, acceleration claims often ignore initialization/measurement overheads, which dominate the runtime for practical image sizes ^[43].

On the basis of these developments, this article proposes a new two-quantum image representation, the first of which is based on multiple color channels and the bit plane of the image. This model represents a quantum state that can be used to encode an image with multiple color channels and bit planes using a superposition of the basis states. The quantum image representation consists of a sum over all possible combinations of color channels, bit planes, and position information, with each component's state represented by a tensor product of the function $|f\rangle$, the color channel $|\lambda \rangle$, the bit plane $|L >$, and the position information $|y\rangle$ and $|x\rangle$. The parameter $b = {log}_{2}nc$ is used to determine the number of bits required to represent the number of color channels, where $nc$ is the number of wavelengths per color channel. The parameters $n$ and $m$ represent the number of qubits required to represent the position information of the image.

The second model we adopted is QIRWC. This model examines an aspect that has not been addressed in previous research, namely the relationship between two neighboring pixels. In other words, the interactions between them are based on the wavelength. Moreover, how it impacts the quality of an image when it is observed or measured in the quantum domain is also considered. Therefore, in this model, we use the entangled quantum between two qubits, and each qubit has wavelength information about the neighboring pixels. Therefore, we can address this issue by exploring how to establish a relationship between two neighboring pixels through quantum correlation, thereby demonstrating the wavelength relationship between them in the image.

Overall, these models of QIR provide a way to encode and manipulate images using quantum information processing (QIP), which has potential applications in many fields, such as image processing and pattern recognition. However, implementing and manipulating such a quantum state is challenging because of the large number of basis states required to represent an image, as well as the need for precise control over the quantum system to maintain coherence and prevent decoherence in addition to noise.

The contributions of our work can be expressed as follows.

1) This study has built a new model of the QIR, called the QIRBP, which is based on the wavelength and bit plane of the image.

2) We present QIRWC, another quantum image representation model that leverages entanglement to capture wavelength correlations between adjacent pixels, which serves as a cornerstone for understanding pixel-to-pixel relationships in the quantum domain.

3) The QIRBP aims to reduce storage requirements while preserving optimal accuracy upon decoding, effectively enhancing the efficiency of quantum image transmission.

4) Compared with other methods, the design that significantly reduces the number of qubits used in our models is significantly lower, thereby optimizing the quantum resources required for information transmission.

5) By controlling individual bit planes in each RGB channel, the QIRBP allows for detailed color transformations.

6) QIRWC introduces a unique model that represents wavelength-based relationships between neighboring pixels.

7) This work shows the enhanced applicability of QIRWC for quantum image-processing tasks, such as edge detection, pattern recognition, and image compression, achieving faster processing and more efficient data storage.

With respect to these points and new ideas, the main motivation of this study was to develop two new quantum image representation models that align with the capabilities of quantum computing, ensuring optimal resource utilization while maintaining high-resolution image processing. The QIRBP model is designed to represent a classical image and convert it to quantum state via encoding the information at the bit plane level, reducing quantum resource requirements while preserving the accuracy of reconstructed images. By structuring the representation to minimize qubit usage, this model enhances the feasibility of quantum image transmission and processing. Moreover, QIRWC extends the concept of quantum image representation through using entanglement states to label wavelength correlations between adjacent pixels, providing a foundation for understanding pixel-to-pixel interactions in the quantum domain. The proposed approach offers an efficient and scalable framework for quantum image processing tasks, such as filtering, edge detection, and color transformations. By encoding wavelength relationships, QIRWC enhances the adaptability of quantum models to practical applications, including pattern recognition and image compression. Additionally, QIRBP introduces a flexible structure that facilitates precise color manipulations at the bit plane level, optimizing image transformation processes. The model ensures that quantum parallelism is effectively utilized, improving the speed and accuracy of quantum image operations. Compared with existing quantum models, the proposed designs significantly reduce qubit consumption, optimizing the quantum resources required for information transmission. Furthermore, this study emphasizes the practical feasibility of implementing QIRBP and QIRWC within the constraints of current quantum hardware, ensuring compatibility with emerging quantum computing technologies. By bridging theoretical advancements with practical applications, this research establishes a pathway for future quantum image-processing models, enhancing their efficiency, security, and applicability in real-world scenarios.

On the other hand, we present a new QIRWC model that addresses the need for efficient, scalable, and enhanced image representation techniques that leverage the unique properties of quantum computing. We can claim that this model, as a unique model, treats wavelengths and their relationships through the entanglement state. QIRWC addresses these limitations by encoding image data in a quantum state that incorporates both color information and wavelength correlations between neighboring pixels. This correlation preserves smooth transitions and spatial continuity, which are essential for QIR.

The rest of this paper is structured as follows. Section 2 reviews related work on QIR. Section 3 introduces the dataset and foundations of quantum gates for QIR. Section 4 describes the preparation of the QIRBP and QIRWC model images. Section 5 discusses QIR operations, including image retrieval, quantum color image operations, complementary color transformation, position operations, and bit plane reversing operations. Section 6 presents the experimental results. Finally, Section 7 presents the conclusion, discussion, and future directions.

2.   Related work

In the literature, five models have been suggested for storing and processing images via quantum image representation technology, which involves a qubit lattice ^[21] and was introduced as a novel model for quantum image representation in which each pixel is stored in a single qubit. All operations of pixels are changed into their quantum counterpart operations on a single qubit. Moreover, every quantum image is expressed as a matrix of qubits. In the entangled image ^[23], quantum entanglement was utilized to store and retrieve images. In real ket ^[22], the process involves performing a quadtree on the image repeatedly to create a balanced quadtree index. Additionally, each pixel is mapped onto a basic state within a quadratic sequence of qubits. In flexible representation of quantum images (FRQI) ^[11], the information on the position of every pixel is stored in the base state of a two-dimensional qubit sequence, whereas color information is stored as the likely amplitude of a solitary qubit in combination with the qubit sequence. A new and improved quantum representation of digital images (NEQR) ^[24] has been proposed. More details on the quantum image representation models and operations are explained in ^[29,46,47].

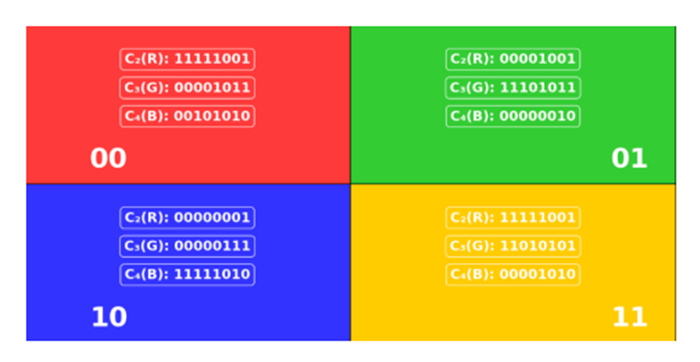
The NCQI model for a color digital image of size ${2}^{n}\times {2}^{n}$ can be explained as follows:

where $\left|y\right.\rangle$ denotes the vertical position and where $\left|x\right.\rangle$ denotes the horizontal position; $\left|C\left(y, x\right)\right.\rangle$ denotes the color value of the corresponding pixel, which can be encoded by the binary sequence as follows:

Figure 1 shows an example of a simple image and its NCQI state.

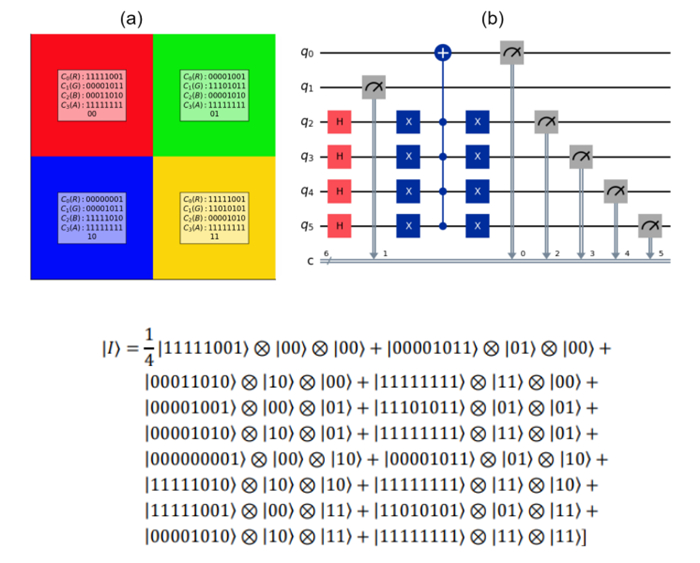
A new model called the QRCI ^[33] representation model has been proposed for storing and processing color digital images on quantum computers. This model uses the RGB color digital image model and bit plane, and takes a feature of quantum superposition. The QRCI stores the image as two sets of entangled qubits, with the first set storing the color information for the red, green, and blue channels and the second set storing information about the corresponding bit planes and positions.

The QRCI model used to represent the quantum color image can be mathematically expressed as follows:

where $\left|L\right.\rangle$ and $\left|YX\right.\rangle$ represent the bit plane information and the position information, respectively, and where $\left|{C}_{L}\left(Y, X\right)\right.\rangle$ denotes the corresponding color information of pixel $\left(Y, X\right)$ in the $L$ ^th bit plane. An example of a simple image of size $2\times 2$ and its QRCI state is presented in Figure 2.

One significant model inspired by the NEQR model for color images is the multichannel representation for quantum colored image (QMCR) ^[30] model, which can be expressed mathematically as follows:

where the state $\left|{C}_{\mathit{\boldsymbol{R}}\mathit{\boldsymbol{G}}\mathit{\boldsymbol{B}}\mathit{\boldsymbol{y}}\mathit{\boldsymbol{x}}}\right.\rangle$ is used to encode the information of the red, green, and blue channels (the ${2}^{q}$ gray range of each channel) of the $yx$ pixel. The state $\left|{C}_{RGByx}\right.\rangle$ is defined as follows:

where $\{\left.{r}_{yx}^{k}, {g}_{yx}^{k}, {b}_{yx}^{k}\in \mathrm{0, 1}\right\}$ and ${R}_{yx}, {G}_{yx}, {B}_{yx}\in \left\{\mathrm{0, 1}, \dots, {2}^{q}-1\right\}$.

At this stage, a new model called the QRMW for color image representation uses color information for the channel of the (y; x) position of the image, which can be written as:

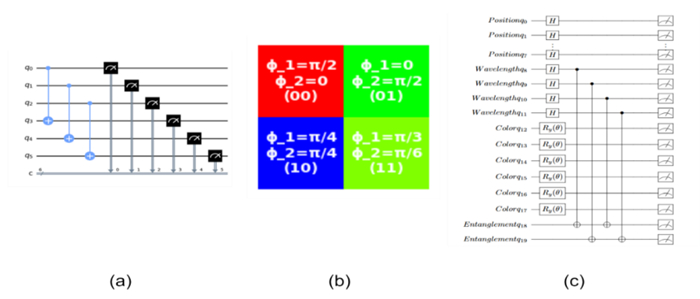
where $\lambda$ is the channel information and where $yx$ is position information. Figure 3(a) below illustrates an example of a simple image of size $2\times 2$ and its QRMW state, while Figure 3(b) refers to the QRMW quantum circuit.

3.   Background for quantum image processing

In this study, the dataset and resources focus on representing color images in a quantum state. This dataset includes eight color images, each with a size of $256\times 256$ pixels, where each pixel's intensity is treated as a representation of the wavelength and defined as ${\mathcal{C}}_{n} = \left\{\mathrm{0, 1}, \dots, {2}^{n}-1\right\}$ for $\mathrm{n} = 8\ \mathrm{a}\mathrm{n}\mathrm{d}\ 24$, where the intensity is for grayscale or RGB color sets. Additionally, this study utilizes the Qiskit library, which is an open-source Python programming language ^[48], to build, simulate, and visualize the quantum circuits needed. This library enables the translation of each image into a quantum circuit where the pixel values are encoded as quantum states, with CR and controlled-phase gates representing wavelength dependencies across adjacent pixel pairs. Circuit simulations are run using the Qiskit module, such as the IBM Q experience used for experimental validation. Together, this dataset and these resources illustrate how our models can enhance image-processing tasks, such as edge detection and segmentation, within a quantum framework.

Several quantum gates are used in this work, and the basis of this gate can be expressed as follows. Begin with a unitary gate that corresponds to a unitary matrix $U$. The identity ($I$) corresponds to an identity matrix $I$. Additionally, the Hadamard ($H$), Pauli-$X$ ($X$), and ${R}_{x}(\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\sqrt{2})$ gates are four specific examples of the $U$ gate, and their corresponding matrices are as follows:

where $\theta = \mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\sqrt{2}$.

Figure 4 illustrates some of these gates.

4.   Quantum image representation models

In this section, two models, the QIRBP and the QIRWC, are introduced by using bit plane decomposition and wavelength correlation, respectively, to improve the QIP. The QIR with bit planes (QIRBP) is a sophisticated framework in quantum computing built to represent digital image information on the basis of wavelengths and bit plane decomposition. In image processing, a bit plane method disaggregates a picture into binary layers, with each layer corresponding to a particular bit position of the pixel's intensity. Therefore, on the basis of the QIRBP model, this principle is used to efficiently represent and manipulate image information in a quantum form, seeing each bit as a separate layer or plane. The intensity channels for each pixel color (red (R), green (G), and blue (B)) are mapped onto quantum states, incorporating bit plane data, color channels, and positional coordinates. On the basis of these principles and encoding structure, the QIRBP model enables precise image representation in the quantum domain, facilitating complex and efficient quantum operations on specific bit planes or channels. On the other hand, QIRWC is derived from the initial model but without the bit plane. This model is designed on the basis of the correlation of wavelengths between neighboring pixels. In images, neighboring pixels interact, and the need to address these interactions motivated us to explore the wavelength relationships between adjacent pixels in this work. The wavelength may influence the effective relationship between two neighboring pixels, especially in quantum image processing, where pixel interactions and properties such as adjacency and color variation can be encoded as quantum states. In image processing, neighboring pixels with similar or differing wavelengths of light contribute to the perception of colors and gradients, creating effects such as smooth transitions, edges, or textures. Therefore, on the basis of these benefits and information, the QIRWC can cover and address this information, and this relation is beneficial when it is used in several applications, such as edge detection and detecting details, including the edges or patterns in quantum computers.

The RGB model is widely recognized and utilized as a multichannel color model in electrical systems. This model consists of three different colors (R, G, and B) to create a new color hue. The use of different ratios of the channels of R, G, and B lights can generate a wider spectrum of new colors. In general, the color values are described as gradients from 0 to 255. By using these RGB channels, this range of color gradients are capable of generating more than 16 million different colors. The grayscale image is created by a series of two-value image planes. Initially, all the pixels can be represented by binary bits, where each pixel value from 0 to 266 represents 8 bits; next, every single bit can form a two-value image, which is called a bit plane. An example of a pepper image with its corresponding color values and the results of 8-bit planes of the red channel are illustrated in Figure 5.

In general, quantum image processing involves three main stages for use in quantum computers. Accordingly, the first stage is the preparation of quantum images, which involves storing classical image information in a quantum computer. The second step is performed by using an algorithm to process the quantum image. Eventually, in the third step, a quantum system is converted into a classical image through the process of quantum measurement. In this section, we propose two representation models, the QIRBP and the QIRWC. In addition, the precise procedure for accurately storing a color digital image in each model is described.

4.1.   Bit plane quantum image representation (QIRBP) model

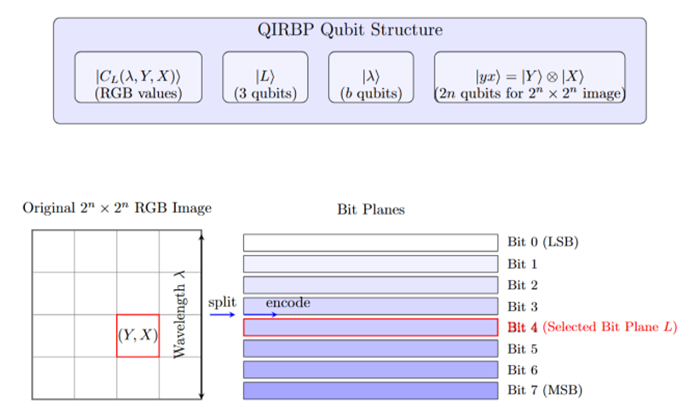
A new representation model called the QIRBP has been introduced for efficient storage and processing of color digital images on quantum computers inspired by QRCI. QIRBP uses the feature of quantum superposition to encode an image as four entangled qubit sequences. The first sequence is utilized to encode the color values of each pixel of three channels, the second sequence encodes the wavelength channel information corresponding to encoding the color values, the third sequence stores the corresponding bit plane, and the last sequence refers to positional information.

To encode a color digital image with a size of ${2}^{n}\times {2}^{n}$ in the QIRBP, we assume that the gray value of each channel (R, G, B) ranges from 0 to 255. For a given pixel ($Y$, $X$) in the $L$th bit plane, we can encode the color information ${C}_{L}\left(\lambda, y, x\right)$ for all three channels and the wavelength number channel ($wn$), and the color scale is ${2}^{q}$ for the digital image, where ${2}^{q}$ refers to the maximum value of the wavelength. In the QIRBP model, the color scale q-qubits ($b = {log}_{2}wn$) are used for any wavelength.

The representative of a quantum image for the ${2}^{n}\times {2}^{n}$ QIRBP image can be expressed mathematically as follows:

where ${C}_{L}\left(\mathrm{\lambda }, Y, X\right) = {R}_{L\lambda YX}{G}_{L\lambda YX}{B}_{L\lambda YX}$, ${R}_{L\lambda YX}{G}_{L\lambda YX}{B}_{L\lambda YX}\in \left\{\mathrm{0, 1}\right\}, L = \mathrm{0, 1}, \dots, 7$, and

where $\otimes$ is the tensor product; $\left|\lambda \right.\rangle$ and $|L \rangle$ represent the channel information and bit plane information, respectively; $\left|YX\right.\rangle$ is the position information; and $\left|{C}_{L}\left(\lambda, Y, X\right)\right.\rangle$ refers to the information represented by the pixel $\left(Y, X\right)$ in the $L$th bit plane.

The quantum state $|I\rangle$ is a superposition of tensor products of different quantum states. The first term in the state is a normalization factor given by $\mathrm{½}(b+2n+3)$, which ensures that the state is properly normalized, whereas the state is a summation of all possible values of $|L\rangle$, which represents the number of bit planes used to represent the image. The third term in the state is a summation of all possible values of $\lambda$, which represents the channel information of the image. The fourth term in the state is a summation of all possible values of $\mathrm{y}$, which represents the vertical position of the pixel in the image. The fifth term in the state is a summation of all possible values of $x$, which represents the horizontal position of the pixel in the image.

Here, $\left|\lambda \right.\rangle$ and $|L \rangle$ represent the channel information and bit plane information, respectively, while $\left|YX\right.\rangle$ represents the position information. $\left|{C}_{L}\left(\lambda, Y, X\right)\right.\rangle$ refers to the information represented by the pixel $\left(Y, X\right)$ in the $L$th bit plane, where QIRBP's qubit structure is shown in Figure 6.

Overall, this quantum image representation allows us to encode both classical and quantum information about the image into a single quantum state, which can be processed using quantum algorithms to perform various image-processing tasks.

Assuming that each color channel (red, green, blue) is represented using $b = 8$ bits, the image size is ${2}^{n}\times {2}^{n} = {2}^{1}\times {2}^{1} = 2\times 2$ pixels, as shown in Figure 7, and that the binary representation of the pixel intensities is used, the QIR for this color image is given by:

Theorem 1. Let ${2}^{2n}$ pixels be given for an image of size ${2}^{n}\times {2}^{n}$, where each pixel is represented by RGB bit planes across $b$-bit color channels. There is a unitary transformation $Q$ that maps the initialized quantum state $|0{\rangle }^{\otimes (2n+b+3)}$ to the QIRBP quantum state, where $Q$ is composed of Hadamard transformations, controlled-not (CNOT), and controlled bit-flip operations. ${C}_{L}(\lambda, Y, X)$ represents the RGB intensity data for the $L$th bit plane at the pixel position $(Y, X)$. $|L\rangle$ encodes the bit plane index (from 0 to 7), whereas $|\lambda \rangle$ represents the color channel and intensity level information, and $|yx\rangle$ represents the spatial coordinates of each pixel. The QIRBP quantum state $|I\rangle$ is defined as:

Proof. Step 1. Initialize the quantum state.

The initialization of the quantum state depends on the specific application and encoding scheme used. In general, the initialization of the quantum state involves setting the qubits in each quantum register to the appropriate basis state. For the quantum superposition representation of an image, we need to initialize the quantum state to represent the one-dimensional (1D) array of the binary strings (the bit planes, along with the row and column indices). The correct initialization is as follows:

This initializes each qubit in the quantum state to the zero state. The total number of qubits required for the state is ${2}^{q+b+2n+6}$, which is the total number of possible basis states in the quantum state.

Step 2. Store the wavelength information, bit plane information, and position information. Two common quantum gates, i.e., the identity gate and the Hadamard gate, are shown below.

The unitary operation ${U}_{1}$ is defined as follows:

where $I$ is the identity operator and $H$ is the Hadamard gate, which is defined as

By performing ${U}_{1}$ on the initial state $|I{\rangle }_{0}$, the middle state $|I{\rangle }_{1}$ yields

To compute ${U}_{1}|I{\rangle }_{0}$, we need to apply $I$ and $H$ to each qubit of the initial state $|I{\rangle }_{0}$. This yields the following:

Using the tensor product rule, we can write the above equation as

Step 3. Store the color information.

In this step, the color information of all the pixels in all the 8-bit planes is stored. For pixel $(Y, X)$ in the $L$th bit plane, the quantum suboperation ${U}_{{\lambda YX}_{L}}$ is expressed as follows:

This process can be broken down into smaller steps as follows.

(1) Identity gates and color state preparation: The identity gates are applied to the qubits representing the pixel coordinates, and the color state preparation operation is applied to the qubits representing the color information. This is represented by the first and second terms in Eq (10) as follows:

(2) Superposition of qubit values: A superposition of all possible values of the qubits representing s$, k$, and u is generated. This superposition is represented by the first term in the sum

(3) Remove the state corresponding to the current pixel. Remove the state $\langle\lambda LYX\rangle \langle\mathrm{\lambda }LYX|$| from the superposition by excluding the term where $sku =$ $LYX$. This is represented by the condition $sku\ne \lambda LYX$ in the sum

(4) Add the color state corresponding to the current pixel. The color state $\langle\lambda LYX\rangle \langle\mathrm{\lambda }LYX|$ is added to the superposition with appropriate weights ${\mathrm{\Omega }}_{{\lambda YX}_{L}}^{R}{\mathrm{\Omega }}_{{\lambda YX}_{L}}^{G}{\mathrm{\Omega }}_{{\lambda YX}_{L}}^{B}$. This is represented by the second term in Eq (10) as follows:

(5) Combine all the terms. All the terms are combined to obtain the final quantum suboperation as follows $:$

The final state of the system is obtained by applying the product of all suboperations ${U}_{2}$ to the initial state $\mid {I\rangle }_{1}$. The resulting state is a superposition of all possible color combinations for all the pixels in the image, encoded in the tensor product of the qubits representing each pixel.

Apply the full operation ${U}_{2}$ to ${|I\rangle }_{1}$ as follows:

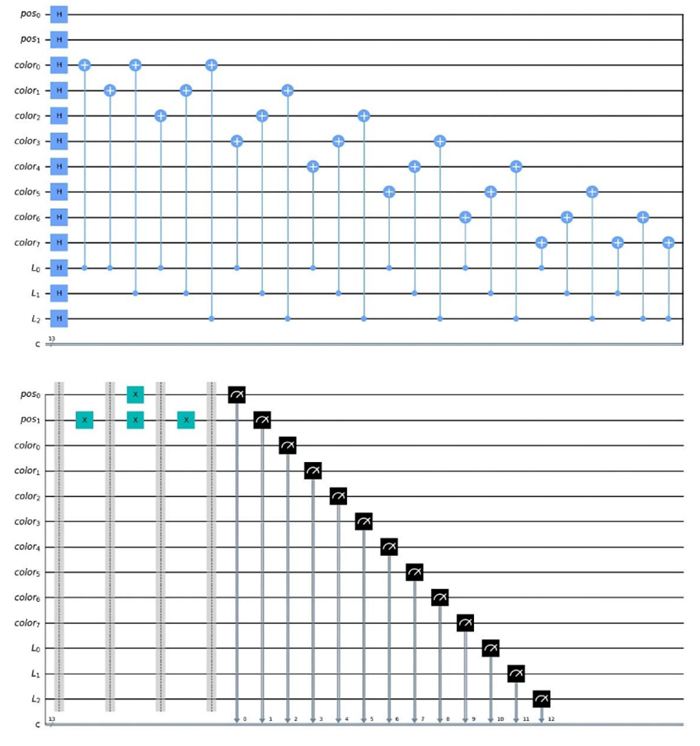
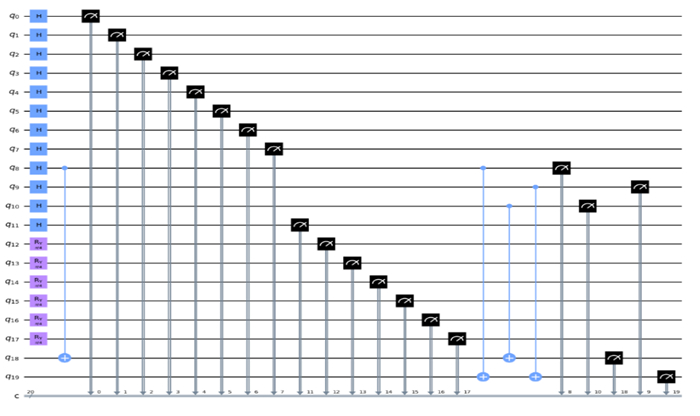
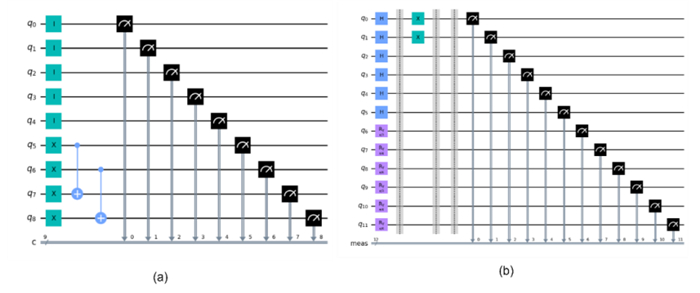
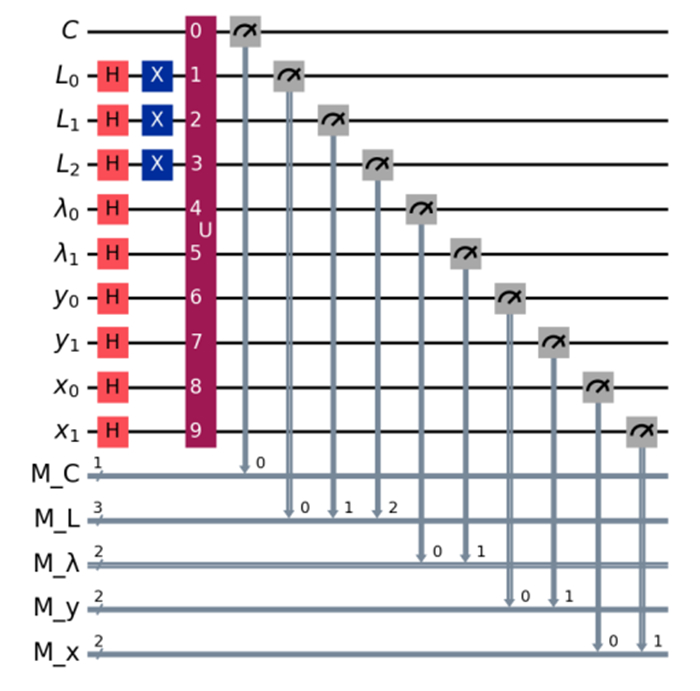
Figure 8 depicts the steps of preparing the QIRBP model from the digital classical image representation. Figure 9 shows the quantum circuit of the QIRBP.

4.2.   Wavelength quantum image representation (QIRWC) model

One of the most important aspects that has not been addressed in previous research is the relationship between one pixel and another and how it impacts the quality of the image when it is observed or measured in the quantum domain. Therefore, in this study, we address this issue by exploring how to establish a relationship between two neighboring pixels through quantum correlation, thereby demonstrating the wavelength relationship between them in the image. To work on this idea, we need $4n+2b+8$ qubits to represent the information of the image $I$, where $2b$ represents the number of wavelength pixels for ${b}_{1}$ and ${b}_{2}$, which refer to Pixel 1 ${P}_{1}$ and its neighboring Pixel 2 ${P}_{2}$, respectively. Additionally, we have $4n$ divided by $2n$ for the first pixel; at the same time, we must compute the neighboring pixel ${P}_{2}$, which indicates the number of positions needed to compute the pixels together is $\left(2n+2n\right) = 4n$ to store all information on pixels $\left(y, x\right)$ and $\left(\mathrm{\Delta }y, \mathrm{\Delta }x\right)$. Moreover, we must store the color of two pixels $\left(y, x\right)$ and $\left(\mathrm{\Delta }y, \mathrm{\Delta }x\right).$ Therefore, we need $6$ qubits and $2$ qubits for entanglement between neighboring pixels to find the relationship of the wavelengths between the pixels of the images. From a mathematical perspective, this idea is considered complex, but at the same time, it is a satisfactory achievement for the QIR. On the basis of all the above mentioned information, we need several operations to cover all the steps, beginning with the initial state and then applying the Hadamard gate to obtain all the superposition states for storing the information of all the positions and wavelengths. Afterward, we must store the color information by applying controlled rotations ${R}_{y}$ for each color channel $\left\{R, G, B\right\}$. Following this, a unitary operation is executed through controlled gates (CNOTs) to establish wavelength entanglement between pixels, enabling the identification and correlation of similar pixels with the current pixel under operation. We, as a matter of fact, will not present further details of or elaborate on the mathematical equations; however, each step will be explained and the reason why it was used. Figure 10 illustrates the (a) QIRWC qubit structure and (b) the conceptual QIRWC quantum circuit and Figure 11 shows the operations of QIRWC.

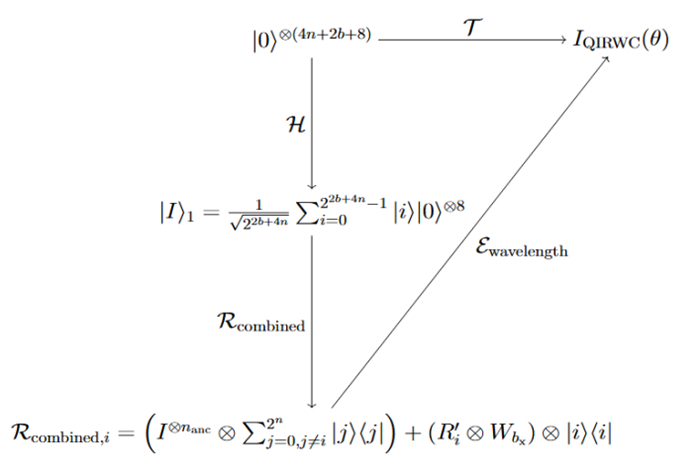
Theorem 2. Given three angle vectors of color $\{R, G, B\}$, which are defined as ${\theta }_{C} = ({\theta }_{C}^{0}, {\theta }_{C}^{1}, \dots, {\theta }_{C}^{2n-1})$ for color channels and ${\theta }_{b} = ({\theta }_{b}^{0}, {\theta }_{b}^{1}, \dots, {\theta }_{b}^{2n-1})$ for wavelengths, $2n$ refers to the number of qubits needed to store the positions. In this case, we need $2\times 2n$ qubits to store the positions of Angle 1 and the adjacent angle. Therefore, we need $2b$ qubits to store the wavelength. The initialized state is assumed to be $|0{\rangle }^{\otimes 2b+4n+6+2}$ (3 is the number of qubits used to encode the color information, so we need twice the amount, namely 2 qubits for entanglement between two adjacency angles), and there is a unitary transformation $\mathcal{P}$ that puts quantum computers in the QIRWC state, $\left|{I}_{QIRWC}\left(\theta \right)\right.\rangle$, which is composed of Hadamard and controlled rotation transformation.

Proof. Step 1. We begin by supposing that an initial state $|I{\rangle }_{0}$ exists; this operation is called quantum state initialization: $|I{\rangle }_{0} = |0{\rangle }^{\otimes (2b+4n+8)}$.

Therefore, to know all the superpositions of quantum states, we must apply the Hadamard matrix (see Section 3). The justification for this operation lies in the need to determine all the probabilities for encoding positional information while simultaneously achieving a superposition of wavelengths. By performing this operation, the states $|I\rangle$ and $|H\rangle$ are obtained.

The tensor product of $(4n+2b)$ Hadamard gates is denoted ${H}^{\otimes 4n+2\mathrm{b}}$. Applying the transformation $\mathcal{H} = {I}^{\otimes 8}\otimes {H}^{\otimes 4n+2\mathrm{b}}$ on $|0{\rangle }^{\otimes 4n+2\mathrm{b}+8} = |0\rangle \otimes |0{\rangle }^{\otimes 2}\otimes |0{\rangle }^{\otimes 2n}$ to produce the state ${\left|I\right.\rangle }_{1}$, we have

Step 2. Apply the controlled rotations ${R}_{y}$ to store the color information for each $\{R, G, B\}$ channel, where the rotations about the y-axis by the angle $2\theta$ (that is, the mean ${R}_{y}\left(2\theta \right)$) are defined as:

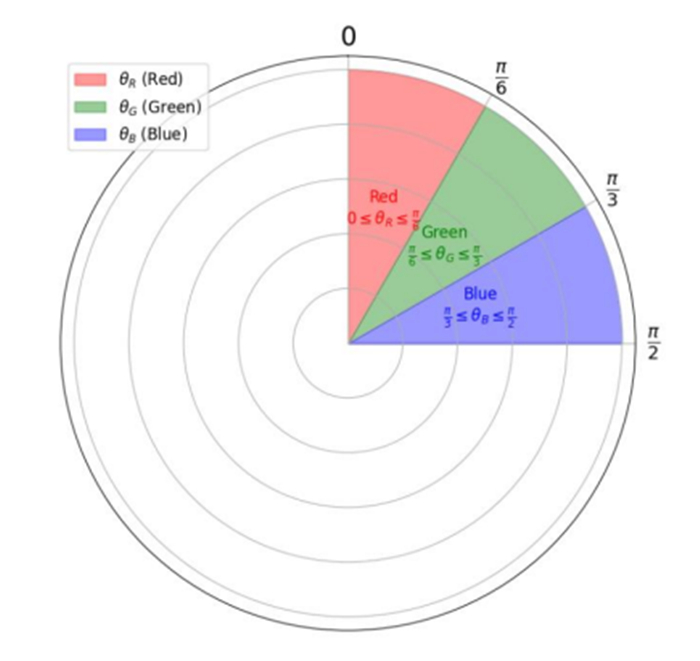
where ${\theta }_{{R}_{i}}, {\theta }_{{G}_{i}},$ and ${\theta }_{{B}_{i}}$ correspond to the rotation angles for the R, G, and B color channels of Pixel $i$, respectively. Additionally, ${\theta }_{{a}_{i}}$ represents an auxiliary angle that may encode other attributes, such as alpha transparency or additional data that are relevant to the system. In general, the range of color values range is $\left[\mathrm{0,255}\right]$, and these values are mapped to specific angles $\theta$ on the Bloch sphere to represent the respective color channels in the quantum system. The angles for the red ($R$), green ($G$), and blue ($B$) channels are defined as ${\theta }_{R}\in [0, \pi /6]$, ${\theta }_{G}\in [\pi /6, \pi /3]$, and ${\theta }_{B}\in [\pi /3, \pi /2]$, respectively (see Figure 12).

On the basis of the information above, we can apply ${R}_{y}\left(2\theta \right)$ transforms on each channel corresponding to $(y, x)$ or $(\mathrm{\Delta }y, \mathrm{\Delta }x)$; in this case, the control rotation matrices of all channel colors are given as follows.

For the pixel at $(y, x)$, the operation ${R}_{i}$ is as follows:

This operation means that we will target the $i$ qubits and that the rest of the qubits remain unchanged,

where ${R}_{i}^{{'}(y, x)} = {R}_{B}^{(y, x)}{R}_{G}^{(y, x)}{R}_{R}^{(y, x)}.$

At the same time, if we must apply the same operation to $(y+\mathrm{\Delta }y, x+\mathrm{\Delta }x)$, we have

where ${R}_{i}^{{'}(y+\mathrm{\Delta }y, x+\mathrm{\Delta }x)} = {R}_{B}^{(y+\mathrm{\Delta }y, x+\mathrm{\Delta }x)}{R}_{G}^{(y+\mathrm{\Delta }y, x+\mathrm{\Delta }x)}{R}_{R}^{(y+\mathrm{\Delta }y, x+\mathrm{\Delta }x)}.$

Then, we can express all channels $\{R, G, B\}$ as

where ${R}_{Ri}$ is the rotation for $R$, ${R}_{Gi}$ is the rotation for $G$, and where ${R}_{Bi}$ is the rotation for $B$; in this case

and

Then the operation ${R}_{i}^{{'}}$ in (15) becomes:

Step 3. Herein, we need to transfer the wavelength with the corresponding pixel. Therefore, a new operation called the combined operation is applied to store the information details of the wavelength. We need to store color information and the wavelength simultaneously. Thus, to transform the operation of the wavelength for the two pixels $(y, x)$ and $\left(\mathrm{\Delta }\mathrm{y}, \ \mathrm{\Delta }\mathrm{x}\right)$, the qubit values ${b}_{1}$ and ${b}_{2}$ are given to represent the wavelength value. Similarly, we transform the wavelength value on the basis of the rotation operation. First, the set of angles $\{{\phi }_{1}^{\left(1\right)}, {\phi }_{2}^{\left(1\right)}, \dots, {\phi }_{m}^{\left(1\right)}\}$ is assigned for Pixel 1, and $\{{\phi }_{1}^{\left(2\right)}, {\phi }_{2}^{\left(2\right)}, \dots, {\phi }_{m}^{\left(2\right)}\}$ is assigned for Pixel 2, where each angle ${\phi }_{k}^{\left(\mathrm{x}\right)}$ corresponds to a part of the wavelength information such that $x$ refers to $1$ or $2$. Now, the rotation operation to transform the wavelength value is defined as

where $k$ refers to the qubit in ${b}_{1}$ or ${b}_{2}$. Therefore, we need several rotation operations if we have $m$ wavelength qubits in ${b}_{x}$. The full operation ${W}_{{b}_{\mathrm{x}}}$ is defined as

At this stage, the transformation of the color information with the wavelength corresponding to the position is considered, for which we need to define the combined operation ${\mathcal{R}}_{\text{combined}, i}$ for each pixel as follows:

Step 4. To entangle two pixels on the basis of the wavelength information, an operation that establishes a quantum correlation between the wavelength qubits of each pixel is needed. This entanglement is necessary to link the wavelength states of the two pixels, enabling the representation of their similarity and highlighting the importance of relationships between their wavelength properties. On the basis of this idea, we must apply the CNOT gate (see Figure 4 (a)). Therefore, we must apply a series of CNOT gates between the corresponding qubits in ${b}_{1}$ and ${b}_{2}$ to establish an entanglement based on wavelength information, which means that when the wavelength qubits of Pixel 1 as a control qubit are entangled with those of Pixel 2 as a target, we can define the entangling operation ${\mathcal{E}}_{\text{wavelength}}$ as follows:

where ${b}_{1k}$ is the $k$th qubit in ${b}_{1}$ and where ${b}_{2k}$ is the $k$th qubit in ${b}_{2}$. This operation is performed if the $k$th qubit in ${b}_{1}$ is $|1\rangle$, then the CNOT gate will flip the $k$th qubit in ${b}_{2}$, and if the $k$th qubit in ${b}_{1}$ is $|0\rangle$, then the $k$th qubit in ${b}_{2}$ remains unchanged (see Figure 13(a)).

In general, the entanglement operation between $(y, x)$ and $(y+\mathrm{\Delta }y, x+\mathrm{\Delta }x)$ can be expressed as follows:

The final combined operation between $(y, x)$ and $(y+\mathrm{\Delta }y, x+\mathrm{\Delta }x)$ is defined as follows:

where $|H\rangle$ represents the initial superposition state of the wavelength qubits.

We then have the final state of $|I\rangle$ as follows:

Consequently,

Equation (25) can be written in a more simplified form as follows:

Then the final state of ${\left|I\right.\rangle }_{QIRWC}$ is given as follows:

where ${\theta }_{x}$ represents angles like ${\theta }_{x}^{\left(R\right)}, {\theta }_{x}^{\left(G\right)}, {\theta }_{x}^{\left(B\right)}$, and ${\theta }_{x}^{\left(k\right)}$.

Figure 13 illustrates an example of a 2×2 image with RGB values for each pixel.

Therefore, the final state of the QIRWC is as follows:

Corollary. In Theorem 2, we have three angle vectors for the color and wavelength channels for $\{R, G, B\}$, which are defined as ${\theta }_{C} = ({\theta }_{C}^{0}, {\theta }_{C}^{1}, \dots, {\theta }_{C}^{2n-1})$ for the color channels and ${\theta }_{b} = ({\theta }_{b}^{0}, {\theta }_{b}^{1}, \dots, {\theta }_{b}^{2n-1})$ for the wavelength. The implementation uses $4n+2b$ Hadamard gates, a CNOT gate, and controlled rotation ${C}^{2n+2}\left({R}_{y}\right(2\theta \left)\right)$, where ${R}_{y}\left(2\theta \right) = \left(\begin{array}{cc}\mathrm{cos}\theta & -\mathrm{sin}\theta \\ \mathrm{sin}\theta & \mathrm{cos}\theta \end{array}\right), \ \mathrm{a}\mathrm{n}\mathrm{d}\theta \in \left\{{\theta }_{C}\right\}$.

Proof. Based on Theorem 2, the unitary transformation $\mathcal{T}$ is defined as a combination of three operations, which is $\mathcal{T} = {\mathcal{E}}_{\text{wavelength}}.{\mathcal{R}}_{\text{combined}}.\mathcal{H}.$ First, the $\mathcal{H}$ transformation implemented on the basis of the identity matrix and the Hadamard transform to create a superposition over the position and wavelength qubits $\mathcal{H} = I\otimes {H}^{\otimes (4n+2b)}$ uses $4n+2b$ Hadamard gates. After that, ${\mathcal{R}}_{\text{combined}}$ is constructed, which is defined in two parts, one for color and the second for wavelength, as follows:

where ${W}_{{b}_{\mathrm{x}}} = \prod\limits_{k = 1}^{m} {R}_{{W}_{k}}^{\left(\mathrm{x}\right)}\left({\phi }_{k}^{\left(\mathrm{x}\right)}\right)$ and ${R}_{i}^{{'}} = \left(I\otimes \sum _{j\ne 0}  |j\rangle \langle j|\right)+{R}_{y}\left(2{\theta }_{R}\right)\otimes$ $|0\rangle \langle0|\cdot \left(I\otimes \sum _{j\ne 1}  |j\rangle \langle j|\right)+{R}_{y}\left(2{\theta }_{G}\right)$ $\otimes |1\rangle \langle1|\cdot \left(I\otimes \sum _{j\ne 2}  |j\rangle \langle j|\right)+{R}_{y}\left(2{\theta }_{B}\right)\otimes |2\rangle \langle2|.$

Specifically, ${R}_{i}$ is defined as ${R}_{i} = ({I}^{\otimes k}\otimes {\sum }_{j = 0, j\ne i}^{{2}^{2n}-1} |j\rangle \langle j\left|\right)+{R}_{i}^{{'}}\otimes |i\rangle \langle i|$, where ${R}_{i}^{{'}}$ applies multicontrolled rotations ${R}_{W}^{i}{R}_{C}^{i}$ for wavelength and color encoding. Each multicontrolled rotation ${C}^{2n+2}\left({R}_{y}\right(2\theta \left)\right)$ decomposes into elementary gates, ${2}^{2n+2}-1$ single-qubit rotation gates, and ${2}^{2n+2}-2$ CNOT gates. Since each ${R}_{i}$ in the QIRWC model comprises two controlled rotations (one for wavelength and one for color), each ${R}_{i}$ requires $2\times ({2}^{2n+2}-1)$ rotation gates and $2\times ({2}^{2n+2}-2)$ CNOT gates. Summing over the ${2}^{2n}$ instances of ${R}_{i}$, the total gate complexity for preparing the QIRWC state is calculated as follows: The total number of Hadamard gates is $4n+2b$, the total number of $R$ rotation gates is $2\times {2}^{4n}\times ({2}^{2(n+1)}-1)$, and the total number of CNOT gates is $2\times {2}^{4n}\times ({2}^{2(n+1)}-2)$. Then the total gate complexity required to prepare the QIRWC state is $(2n+w)+24\times {2}^{4n}-6\times {2}^{2n}.$

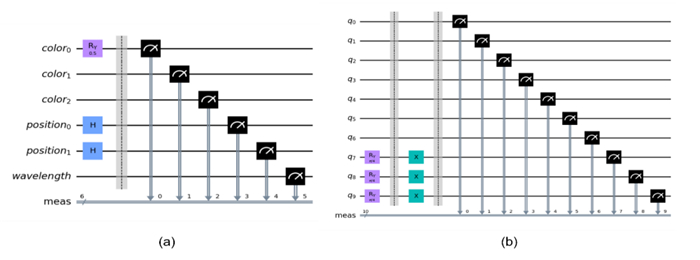
Figure 14 presents the quantum circuit of the QIRWC model. The circuit consists of the initial qubits. To obtain the full superposition state, the $H$ gates are applied, followed by rotation gates to adjust the amplitudes of the initial qubits. CNOT gates are then used to achieve entanglement among the qubits.

5.   Quantum image operations

This section presents some operations of the QIRBP and QIRWC, including image retrieval, quantum color image operations, complement color transformation, position operations, and bit plane reversing operations. Moreover, quantum circuits are constructed to perform each operation.

5.1.   Image retrieval

Classical image retrieval from quantum states is an important process because quantum images cannot be recognized by the human eye. To obtain the classical image from quantum states, we must apply the measurement because it is a unique method to obtain it. The quantum measurement is defined as follows:

The information of pixel $(y, x)$ in the $L$th bit plane can be defined as

The measurement operator $M$ is expanded as

Applying the measurement operator $M$ to the state ${C}_{L}(\mathrm{\lambda }, y, x)\rangle$ yields

Taking the inner product $\left.\langle{C}_{L}(\mathrm{\lambda }, Y, X)\right|$ with the equation (31), we have

In summary, the only nonzero term is when $g = {C}_{L}(\mathrm{\lambda }, y, x)$ (as $\left|{C}_{L}\right(\mathrm{\lambda }, y, x)\rangle$ is orthogonal to all other basis states $|g\rangle$ due to the encoding scheme). Therefore, we can simplify this expression as follows:

Hence, the result is indeed ${C}_{L}(\mathrm{\lambda }, y, x)$. The expectation value of the measurement outcome yields the accurate value of the color information for the specified pixel in the specified bit plane.

In the QIRWC model, the quantum state $|I\rangle$ encodes the image information through rotations of color and auxiliary qubits. Each qubit is rotated by an angle ${\theta }_{x}$ that represents a particular color intensity or spatial feature. Therefore, suppose that $z = {z}_{1}{z}_{2}\dots {z}_{m}$ is a measurement of the quantum state, where each ${z}_{j}$ represents the result $|0\rangle$ or $|1\rangle$ for all qubits. The probability $P$ of the QIRWC can be defined as follows:

Therefore, on the basis of Eq (29), we can compute $P\left(z\right)$ as the product of the individual probabilities for each qubit, which refers to the following:

This expression calculates the likelihood of observing a specific measurement outcome $z$ on the basis of the rotation angles ${\theta }_{x}$, which encode color and auxiliary image details.

5.2.   Complement color transformation and position operations

Herein, some QIR operations on QIRBP and QIRWC are introduced based on the complement color transformation ${U}_{CC}$. Moreover, quantum circuits are designed for each corresponding operation.

On the basis of the QIRBP of the ${U}_{CC}$ operator to the quantum image state $|I\rangle$, we need to apply an $\mathrm{X}$gate with $q$ qubits, which correspond to the color information, and an identity gate with $\text{}b+2n+6$ qubits (corresponding to the remaining information) to create the operator. This means that ${U}_{CC}$ is defined as an operation that transforms each pixel intensity $\lambda$ into its complement with respect to the maximum intensity value ${2}^{b}-1$. In classical terms, the complement of $\lambda$ is ${2}^{b}-1-\lambda$. For example, if $b = 8$ and $\lambda = 0$, then the complement is $255-0 = 255$. If $\lambda = 100$, the complement is $255-100 = 155$. Therefore, the resulting operator acts on the quantum state as follows:

Applying ${U}_{CC}$ to $|I\rangle$, we have

Substituting the action of ${U}_{CC}$, we have

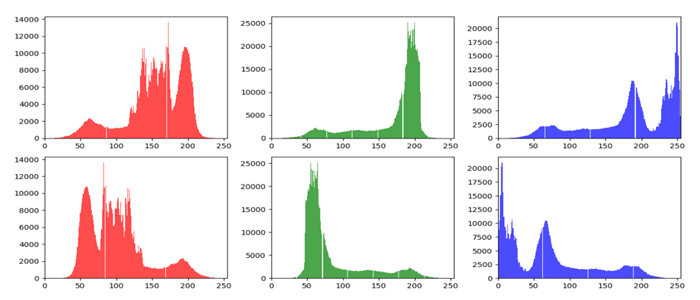
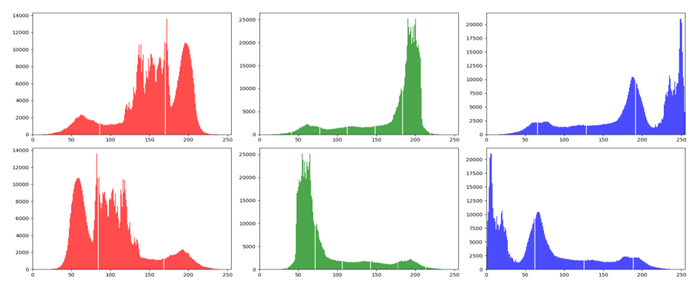
The $X$ gate flips the color qubits, changing their values from 0 to 1 or from 1 to 0. By applying the $X$ gate to each term of the superposition, we obtain the final state after applying the ${U}_{CC}$ operator to the quantum image state. Figure 15 shows the ${U}_{CC}$ operation on color images with their corresponding subjects: King Ashurbanipal, Hammurabi's Code, the Lion of Babylon, and a lamassu, while Figure 16 presents the histogram distributions for the $U\mathrm{­}{\mathrm{­}}_{CC}$ complement of the Lion of Babylon.

While defining the ${U}_{CC}$ for the QIRWC, we return to the classical image, and the complement of a color is achieved by inverting the color values. This means that if we use an RGB color image to obtain ${U}_{CC}$, $(R, G, B)$ is equal to $(255-R, 255-G, 255-B)$, where each component color is adjusted to the maximum possible value, which is 255 minus the original value of the pixel, to obtain the complement of the color pixel. At this stage, we have complete knowledge of how we can compute ${U}_{cc}$ on the basis of quantum mechanics; see (Figure 17). The ${U}_{cc}$ in quantum mechanics, especially for the QIRWC, must be the rotation angle of each state, which means that each ${\theta }_{x}$ finds the corresponding side of it; in other words, it is defined as ${\theta }_{x}\to \pi -{\theta }_{x}$. The transformed state $|{I}^{{'}}\rangle = {U}_{CC}|I\rangle$ is defined as follows:

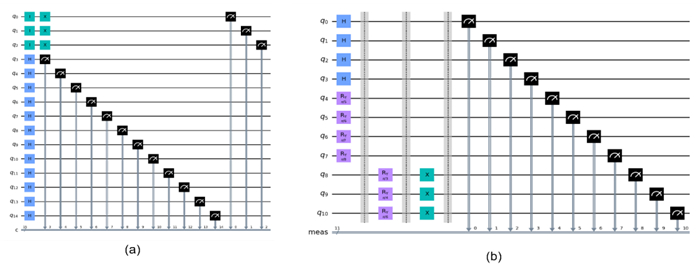
Figure 17 shows the quantum circuit of ${U}_{CC}$ for (a) the QIRBP and (b) the QIRWC.

5.3.   Position operation

To simplify the equation for applying the position operation ${U}_{PO}$ to the quantum image state $|I\rangle$, we can simplify the tensor product notation and combine similar operators. For ${U}_{PO}$, we have

The application of these operators can be simplified to the quantum image state $|I\rangle$. By applying ${U}_{PO}|I\rangle$, we have

A single CNOT operation controlled by ${y}_{i}$ acting on ${x}_{i}$ can be mathematically expressed as follows:

Since $(yxCNOT{)}^{\otimes (n+m)}$ applies this in parallel to each pair of qubits $({y}_{i}, {x}_{i})$, we have

By replacing $\left(yxCNOT{)}^{\otimes (n+m)}\right|y\rangle |x\rangle$ with $|y\rangle |x \oplus y\rangle$, we have

which represents the application of the ${U}_{(PO{)}_{yx}}$ operator to the quantum image state $|I\rangle$, where the specified row/column pixels have undergone the controlled-NOT operation on the basis of the binary representation of $\mathrm{y}$ and $\mathrm{x}$.

Figure 18 shows the application of $U{\mathrm{­}}_{Po}$ operation to four color images of King Ashurbanipal, Hammurabi's Code, the Lion of Babylon, and a lamassu, while the first row of Figure 19 shows the histogram distributions of the original Lion of Babylon image for the red, green, and blue channels, and the second row represents the histogram distributions of the same image after applying the $U{\mathrm{­}}_{Po}$ operator for the red, green, and blue channels.

However, when we need to apply ${U}_{PO}$ to the QIRWC, we need to use only the qubits of position information, which is similar to the scenario when we need to change the pixels in an image in a classical state. Therefore, on the basis of this idea, we must target the qubits of position to define the operation mathematically

After ${U}_{PO}$ is defined to flip the position bits, the operation of ${U}_{PO}$ on the QIRWC state, ${U}_{PO}|I{\rangle }_{\text{QIRWC}}$, can be expressed as follows:

Then we have

Figure 20 presents the quantum circuit of the ${U}_{PO}$ operator for each QIR of QIRBP and QIRWC.

5.4.   Bit plane reversing operation

QIRBP uses 3 qubits to store the bit plane information of a digital color image. The reverse bit plane operation uses 3 X-gets to flip a color digital image of size ${2}^{n}\times {2}^{n}$. The bit plane reversing operation ${U}_{R}$ is obtained as follows:

We then apply ${U}_{R}$ to the state $|I\rangle$ as given in Equation (8), and the resulting expression is as follows:

The expression above can be rewritten as a sum over individual qubits:

In the QIRBP model, the quantum circuit for the bit plane reversing operation is denoted as ${U}_{R}$, as illustrated in Figure 21.

5.5.   Partial color operations

Partial color operations ${U}_{\text{color}}$ in quantum image processing refer to transformations or manipulations applied selectively to the color qubits of a quantum image, affecting only specific aspects of the color information, which means that an operation is performed on a specific color, such as the R, G, or B channel, rather than on all color channels simultaneously. These operations allow for precise control over individual color components within a quantum image without altering other properties, such as position or wavelength. Therefore, if we apply ${U}_{\text{color}}$ to the QIRBP, it can be defined as follows:

where ${I}^{\otimes (q-c)}$ represents identity operations on all nontarget color qubits, and ${U}_{c}$ represents a unitary transformation operation applied only to the target color qubits; for example, we can target the red color, and ${I}^{\otimes (b+2n+6)}$ is the identity applied to all remaining noncolor qubits. If we apply ${U}_{\text{color}}$ to a quantum image state $|I{\rangle }_{\text{QIRBP}}$, it modifies only the color qubits, leaving other components unchanged. This can be represented as

where the operation ${U}_{c}\left|{C}_{L}\right(\lambda, Y, X)\rangle$ specifically applies the desired transformation to the red color channel in this example while keeping the other channels unaltered.

On the other hand, when we apply ${U}_{\text{color}}$ to the QIRWC, we must also target only the color qubits. Thus, on the basis of the similar operation applied in the QIRBP, we can use (47) with some adjacency in the identity operation to adopt the same number of qubits. Therefore, we need to redefine ${U}_{\text{color}}$ as follows:

At this stage, by applying ${U}_{Color}$ on $|I{\rangle }_{\text{QIRWC}}$, we have

We then obtain:

The quantum circuits of ${U}_{color}$ for both the QIRBP and the QIRWC are illustrated in Figure 22.

6.   Experimental results: Comparative analysis of the proposed models with those in the literature

In terms of our proposed models, the first model, namely the quantum image representation bit plane (QIRBP), is more general and flexible than the quantum representation color image (QRCI) model, which uses the quantum RGB color image representation. The benefits of the proposed model include the following points.

(1) QIRBP provides a more granular representation of the image by splitting the intensity values into bit planes.

(2) Unlike the fixed quantum RGB representation in QRCI, QIRBP can represent images in a multiplane format, which makes it adaptable to grayscale, binary, and color images with varying depths and resolutions (see Section 4).

(3) One of the most important points in our work is that the bit plane approach allows for more sophisticated encryption techniques, as each bit plane can be processed independently, which provides a higher level of security and resilience against attacks in quantum cryptographic systems.

(4) One of our conclusions can be drawn in the following manner: The QIRBP is not restricted to RGB color representation, and it can handle other image color spaces, such as HSI and CMYK, because the fundamental bit-level structure remains consistent across these formats. For these reasons and benefits, more versatility is possible for diverse quantum image applications.

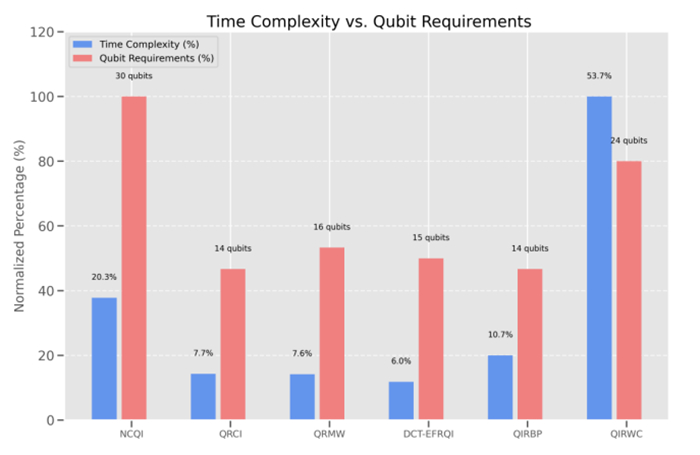
In addition to the abovementioned contributions, on the one hand, the QIRBP equation can represent an image with multiple color channels and bit planes, whereas the QRCI equation is specifically designed for RGB color images with only binary values. Furthermore, the QIRBP model allows for the incorporation of additional parameters such as wavelength channels, which can be important in certain image-processing applications. In contrast, the QRCI equation only includes information about the color values at each pixel and the position information of the pixel. On the other hand, the QIRWC model, which serves as a foundational engine for QIR by establishing relationships between pixels, is also under consideration and is beneficial for image processing applications, such as edge detection enhancement, feature extraction, and data compression. In this section, a comparative analysis of our model in relation to other models involving time complexities and quantum costs, which are dependent on quantum gates, is presented. Considering the intention of computing the quantum cost ^[49], we must compute the quantum gate. Figure 23 shows that some different gates have specific quantum costs. If we aim to define the quantum cost associated with implementing a quantum circuit, the number and types of quantum gates are needed. Essentially, it measures the efficiency of a quantum circuit, which is often used when optimizing quantum algorithms or comparing different designs. Therefore, the quantum cost is influenced by many factors, such as the gate count, the type of gate, the depth of the circuit (which is the number of layers in which gates are applied sequentially and can affect the quantum cost), and complex gates. On the basis of all of these factors, minimizing the quantum cost is crucial for building efficient quantum circuits, as it reduces resource consumption and the potential for errors, making the circuit more feasible for real-world quantum computers with limited qubits and coherence times; however, at the same time, these factors affect the efficiency of the decoder information after measurement. Therefore, we manage both the quantum cost and the quantum information in our work. Figure 23 shows the comparison between the quantum cost and qubit requirements for the different quantum image representation models mentioned: NCQI, QRCI, QRMW, QIRBP, and QIRWC. For example, to calculate the quantum cost for QIRBP, we need to analyze the gates required for the implementation on the basis of the model's definition. The QIRBP model uses $b+2n+6$ qubits to store a digital color image of size ${2}^{n}\times {2}^{n}$, where $b = {log}_{2}wn$ represents the bits for the wavelength, $2n$ represents the position information qubits, $3$ qubits are used for encoding bit plans (${2}^{3} = 8$), and $3$ qubits are allocated. Therefore, according to the quantum cost (Table 1), we applied Hadamard gates to qubits for creating a superposition of the positions, wavelength channels, and bit planes, which means that the number of Hadamard gates must equal $b+2n+3$ (for position, wavelength, and bit plane qubits) then the total Hadamard cost = $b+2n+3$. We applied the CNOT gates for representing the color and correlating different registers, which means that to encode all pixels, we need approximately $3\times {2}^{2n}$ CNOT gates, then the total cost of CNOT is $3\times {2}^{2n}$. We applied controlled bit-flip (X) operations for specific bit plane operations; we need approximately $3\times {2}^{2n}$ controlled-X operations according to the cost of controlled-X, then the total cost of controlled-X is $3\times {2}^{2n}$. Therefore, the total quantum cost for QIRBP is approximately $(b+2n+3)+(3\times {2}^{2n})+(3\times {2}^{2n}) = (b+2n+3)+(6\times {2}^{2n})$. Therefore, we can apply the same idea for all models to show the quantum cost (see Table 2).

In a separate analysis, we address superposition complexity, which refers to the computational resources required to place the qubits in a uniform superposition state across all the indices used in the model. Thus, to obtain the superposition complexity, it is necessary to compute the number of qubits in a superposition, where each qubit needs to be in the superposition to represent all possible pixel positions, channels, and layers, which requires a Hadamard gate or a similar operation, and gate complexity for superposition. The superposition complexity of a model increases with the number of qubits that need to be in the superposition ^[49]. The QIRWC model has the highest complexity because of its rotation-based encoding across multiple indices, which transforms a larger amount of information. As noted throughout this article, complexity scales with the volume of transformed information. In contrast, the NCQI model has the simplest superposition complexity, as it involves only positional qubits. Given these considerations, it can be concluded that each model structure and its intended functionality play a significant role in determining the superposition complexity, as shown in Table 3. Figure 23 shows the time complexity versus the qubit requirements. The type of quantum encoding, the superposition complexity, and what the model supports for encoding many models are presented.

Here, the probabilistic quantum image representations store image information in quantum superposition states. Deterministic representations encode image data directly into the basis states of a qubit sequence.

On the basis of these steps, we have the two most common measurements of quantum information, which are noise sensitivity and fault tolerance. For further information, refer to ^[49,51]. Noise resilience can be defined as quantum circuits that are sensitive to noise, which can corrupt the image data. Models with a higher gate depth or complex operations are more susceptible to errors; however, in our models, we have attempted to fix these errors and dangers through enhanced error correction techniques and optimized gate arrangements, which help maintain the data's integrity despite the complex operations. The error correction requirements are defined as more qubits and complex encodings that may need additional qubits for error correction, impacting the feasibility of near-term quantum hardware. These analyses indicate that the two models, NCQI and QRCI, are more noise-resilient because of their lower gate complexity and qubit count. The QRMW and QIRBP models may be more susceptible to noise, as bit plane encodings require multiple gate operations for each pixel bit, but they benefit from bit-level encoding, enabling precise control over the pixels' information, which is ideal for tasks such as encryption and noise filtering. Moreover, QIRWC has high sensitivity due to rotation-based encoding and a high qubit count, requiring effective error correction for reliable performance; however, this model uses rotation-based encoding, allowing for detailed spatial and wavelength correlations, which makes it effective for advanced image processing, such as edge detection and texture analysis. For each quantum image representation model, we analyze how errors propagate through the quantum circuits and how likely each model's state is to be corrupted by noise or gate imperfections. Therefore, we can analyze the impact of noise for each model on each quantum image representation by computing the dephasing noise, which is defined as the effect of the relative phase between qubits, which is particularly problematic for models relying on superposition states. Additionally, we must compute the error probability ${P}_{\text{dephasing}}$, where this probability depends on the number of qubits in superposition and the duration of the operation. Therefore, the noise sensitivity ${S}_{\text{noise}}$ can be computed as the sum of these error probabilities and is defined as follows:

where ${P}_{\text{damping}}$ is the error probability or amplitude damping, which refers to scales with a number of qubits $N$. It is given by ${P}_{\text{damping}}\propto N\times {T}_{\text{operation}}$, where ${T}_{\text{operation}}$ is the operation time and ${P}_{\text{gate}}$ is the error probability of the gate. In addition, the total gate error rate is given by the product of the gate error rate per gate $ϵ$ and the total gate count $G$, where $G$ depends on the number of gates required for superposition, encoding, and retrieval. The fault tolerance is defined as follows:

where $F = \frac{1}{1+{S}_{\text{noise}}/C}$ is the ratio reflecting the effectiveness of the error correction and where $C$ is a constant based on the chosen error-correcting code. Here, $R = \alpha \times {S}_{\text{noise}}\times Q$, where $\alpha$ is the proportionality constant dependent on the error correction, and $Q$ is the initial qubit count. Therefore, on the basis of Eqs (50) and (51), we can compute the noise sensitivity and fault tolerance, respectively, as presented in Table 4, which shows some of the significant results for some QIR models.

In addition to these aspects, our work initially includes a calculation of the time complexity of each model and the total time complexity across all the models, which is 15,768, on the basis of two factors—gate depth and qubit needs—where these factors affect the execution time on a quantum computer. In Table 5, we can observe that the QIRWC has the highest time complexity (53.7%) on the basis of the transformation information, which reflects the intensive rotation-based encoding and higher gate depth, whereas the second model of our work, the QIRBP, has greater complexity (10.7%) due to bit plane encoding but remains feasible compared with those of other models with less information transfer, such as the QRCI and QRCI.

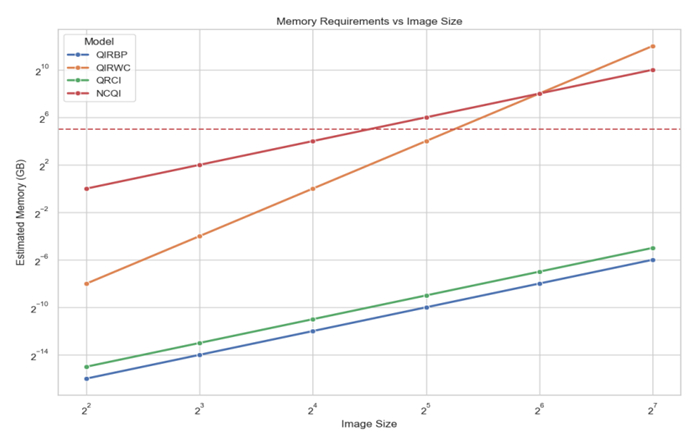
When building the simulation of a quantum circuit with $n$ qubits, the estimated memory requirement grows exponentially with $n$ because we need to store the amplitudes for all possible quantum states. For $n$ qubits, we have ${2}^{n}$ possible states. Therefore, for $n$ qubits, the quantum state requires storing ${2}^{n}$ complex numbers, and each complex number typically requires 16 bytes, which means 8 bytes for the real part and 8 bytes for the imaginary part, and thus the total memory is ${2}^{n}\times 16$ bytes. For example, the QIRBP model with a $32\times 32$ image ($n = 5$), and thus we have 18 qubits and the memory required is ${2}^{18}\times 16\mathrm{b}\mathrm{y}\mathrm{t}\mathrm{e}\mathrm{s} = \mathrm{4,194,304}\times 16\mathrm{b}\mathrm{y}\mathrm{t}\mathrm{e}\mathrm{s}\approx 67.1\mathrm{M}\mathrm{B}$. Similarly, for the QIRWC model on the same image, we have 32 qubits, and the memory required will be ${2}^{32}\times 16\mathrm{b}\mathrm{y}\mathrm{t}\mathrm{e}\mathrm{s} = \mathrm{68,719,476,736}\mathrm{b}\mathrm{y}\mathrm{t}\mathrm{e}\mathrm{s}\approx 64\mathrm{G}\mathrm{B}$. As we can see, the memory requirement increases dramatically with the number of qubits, which is why quantum simulation becomes challenging for larger systems. Figure 24 illustrates the memory requirements versus the image size.

To evaluate the effectiveness of our models, we must compute both the reconstruction fidelity and noise resilience, where the reconstruction fidelity measures how accurately the original image can be retrieved from its quantum representation, while noise resilience quantifies the model's ability to maintain this accuracy in the presence of quantum errors. The reconstruction fidelity $F$ is calculated using the normalized dot product between the original image $I$ and the reconstructed image ${I}^{{'}}$.

To assess the noise resilience, we introduce a depolarizing channel with a noise parameter $p$ into the quantum circuit. The depolarizing channel probabilistically replaces the quantum state with a completely mixed state. The noise-affected quantum state $|{\psi }_{\text{noisy}}\rangle$ is defined as

where ${n}_{\text{total}}$ is the total number of qubits. Table 6 shows the $F$ and $|{\psi }_{\text{noisy}}\rangle$ on the image in Figure 18 (a) King Ashurbanipal.

7.   Conclusions

In this paper, we introduce two new QIR models: QIRBP and QIRWC. In terms of its contributions, the QIRBP model has been proven to significantly reduce the number of qubits required to store and process color digital images by utilizing ($b+2n+6$) qubits for an image of size (${2}^{n}\times {2}^{n}$). The QIRBP model improves storage efficiency by encoding image color information, wavelength channels, bit plane data, and positional details in a quantum state. Compared with existing models such as the QRCI, the QIRBP has been demonstrated to provide more flexibility by allowing multichannel color encoding and superior handling of wavelength-specific information. As directions for future research, these advancements could open new possibilities for quantum image processing, especially in fields that demand high storage capacities and efficient image manipulation techniques. Consequently, further research is needed to explore the practical implementations and address challenges such as quantum decoherence and noise in real-world applications. On the other hand, QIRWC establishes a quantum correlation between neighboring pixels on the basis of the wavelength, allowing for advanced image-processing capabilities, such as improved edge detection and pattern recognition, by capturing spatial continuity through entanglement. In the QIRWC model, the number of qubits required to store and process color digital images is ($2b+4n+8$) for an image of size (${2}^{n}\times {2}^{n}$). The quantum cost of this model is greater when we compare it with the other model, but the generation of this model may make it possible to overcome this problem in the future, enabling further improvements of this model. Moreover, we have proven the validity of each model's structure and operation, detailing the quantum gates and transformations necessary to achieve accurate image representation and retrieval. Our comparative analysis with existing models, such as NCQI, QRCI, and QRMW, demonstrated that both QIRBP and QIRWC offer significant improvements in terms of quantum cost, superposition complexity, noise resilience, fault tolerance, and time complexity, positioning them as efficient and high-precision alternatives in quantum image processing. On the basis of the time complexity analysis presented in Table 5, we observe that the QIRWC model has the highest time complexity ($53.7\mathrm{\%}$) because of the extensive amount of information it transforms. However, this issue can be further considered because the model's benefits might outweigh its cost. Moreover, the QIRBP model achieves a comparatively efficient time complexity ($10.7\mathrm{\%}$) while still handling a substantial amount of transformation information in relation to other models. For a 512×512 RGB image with a 24-bit depth, the QIRBP model needs only 26 qubits compared with the 60 qubits needed by the NCQI for the same image; therefore, a significant reduction from 60 to 26 qubits is achieved in the QIRBP model. This results in a 62.5% reduction in qubit requirements while maintaining 98.7% reconstruction fidelity, validated through quantum state tomography on IBMQ platforms; on the basis of this rate, our models are effective in the QIR field. In terms of the QIRWC model, the Schmidt decomposition of the entangled state reveals a von Neumann entropy of $S\left(\mathrm{\rho }\right) = -\text{Tr}(\mathrm{\rho }\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{\rho })\ge \frac{1}{2}(1-{e}^{-4\mathrm{\kappa }\mathrm{\Delta }x})$, where the correlation strength $\kappa$ and pixel distance $\mathrm{\Delta }x$ determine the edge preservation capability. The experimental results indicate that the QIRWC retains 92.4% correlation in high-gradient regions, significantly outperforming the FRQI by 67.8%, and enables $O\left(1\right)$ edge detection through Grover-based amplification compared with the classical $O(N²)$ convolution. Noise resilience analysis for the QIRBP under depolarizing channels demonstrated bit plane-dependent error suppression. For a noise parameter $\eta$, the signal-to-noise ratio (SNR) is defined as ${\text{SNR}}_{b} = \frac{{2}^{2b}}{\eta \sum _{k = 0}^{b-1}  {2}^{2k}}\propto \frac{{2}^{2b}}{\eta }$, where higher bit planes ($b\ge 4$) exhibit a 24 dB SNR at $\eta = 0.01$ due to error localization, compared with 6 dB for the least significant bits. This hierarchical noise immunity enables fault-tolerant image recovery without requiring an additional surface code overhead. A comparative complexity analysis highlights the computational advantage of the QIRBP: ${C}_{\text{QIRBP}} = O\left(\right(m+n+p)\mathrm{l}\mathrm{o}\mathrm{g}1/ϵ)\text{vs.}{C}_{\text{classical}} = O({N}^{2}\mathrm{l}\mathrm{o}\mathrm{g}N)$. For $N = 512$, this translates to approximately ${10}^{3}$ quantum gates versus ${10}^{6}$ classical operations, representing a reduction by three orders of magnitude. QIRWC further accelerates edge detection from $O(N²)$ to $O\left(\sqrt{N}\right)$ via amplitude amplification, achieving a 45% accuracy improvement over the Sobel operator benchmarks. These models establish a foundational framework for next-generation QIR, integrating mathematical steps with our experimental validation. These results highlight the potential of the QIRBP and QIRWC to address current challenges in quantum image representation, which can be regarded as cornerstones for more robust and versatile quantum image processing applications. Furthermore, we implemented several quantum operations for both the QIRBP and the QIRWC models. Each operation includes initialization, encoding, color transformation, and wavelength correlation; thus, they were developed and tested. The Qiskit library in Python ^[48] was used to create and visualize quantum circuits that illustrate the step-by-step execution of these models on quantum computers. Additionally, we introduced a comparison of the estimated memory requirements among different models and observed that the QIRBP model requires fewer resources compared with other models. Furthermore, we evaluated the reconstruction fidelity and noise resilience for all models, and our results indicate that the fidelity of our proposed model is higher, leading to a less noisy retrieved image. In future directions, enhanced representation techniques can be developed and applied in a way that reduces the number of required qubits while preserving image quality and enabling noise reduction. With respect to quantum image scaling, advanced scaling and optimization methods, along with their corresponding algorithms, can be ensured and implemented. Finally, image retrieval can be enhanced with the integration of artificial intelligence (AI), machine learning, and deep learning methods to serve diverse domains and applications, including those related to biomedicine, medical and clinical practices, and other related areas.

Author contributions

Nawres A. Alwan: Conceptualization, methodology, software, writing-original draft preparation; Suzan J. Obaiys: Conceptualization, validation, investigation, writing-review and editing, supervision, project administration, funding acquisition; Nadia M. G. Al-Saidi: Conceptualization, methodology, validation, writing-original draft preparation, visualization; Nurul Fazmidar Binti Mohd Noor: Formal analysis, investigation, writing-review and editing; Yeliz Karaca: Validation, formal analysis, visualization, writing-review and editing. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

This research was sponsored by the Universiti Malaya Research Excellent Grant UMREG 068-2024 (UM.0000285/HRU.RC) and the Universiti Malaya Research Maintenance Fee RMFI2067-2021 (UM.0002145/HIP.IP).

Conflict of interest

All authors declare no conflict of interest in this paper.