Search Advanced

AIMS Mathematics

2025, Volume 10, Issue 5: 10976-10993. doi: 10.3934/math.2025498
Previous Article Next Article
Research article

The pattern dynamics of interneuronal networks with inhibitory synaptic coupling

  • School of Mathematics and Statistics, Shandong Normal University, Ji'nan, 250014, China
  • Received: 27 March 2025 Revised: 26 April 2025 Accepted: 30 April 2025 Published: 13 May 2025

  • MSC : 62M10, 92C15

  • Interneurons modulate the excitability of neural networks and maintain neural activity balance via inhibitory or excitatory synaptic connections. Here, we studied the formation of patterns of interneuronal networks with inhibitory synaptic coupling. We found that both electrical synaptic coupling and inhibitory synaptic coupling play a crucial role in the formation of neural network patterns. In addition, delayed inhibitory synapses can also affect the transition of target waves to chaotic states. As the strength of electrical synaptic coupling increases, the firing behavior of neurons gradually becomes highly ordered. When the inhibitory synaptic delay reaches a critical value, we observe a transition in oscillatory patterns from an ordered state to a synchronized state. We further investigated how inhibitory synaptic conductance influences the formation of oscillatory patterns in the network. The study reveals that increasing synaptic conductance disrupts the structure of target waves, inducing chaotic states such as spiral wave fragmentation, while simultaneously elevating neuronal firing rates.

    Citation: Ying Xu, Xiaodi Li. The pattern dynamics of interneuronal networks with inhibitory synaptic coupling[J]. AIMS Mathematics, 2025, 10(5): 10976-10993. doi: 10.3934/math.2025498

    Related Papers:

    [1] Loïs Naudin . Biological emergent properties in non-spiking neural networks. AIMS Mathematics, 2022, 7(10): 19415-19439. doi: 10.3934/math.20221066
    [2] Nehad Abduallah Alhajaji, Afrah Ahmad Noman Abdou, Jamshaid Ahmad . Application of fixed point theory to synaptic delay differential equations in neural networks. AIMS Mathematics, 2024, 9(11): 30989-31009. doi: 10.3934/math.20241495
    [3] Xiaojun Xie, Saratha Sathasivam, Hong Ma . Modeling of 3 SAT discrete Hopfield neural network optimization using genetic algorithm optimized K-modes clustering. AIMS Mathematics, 2024, 9(10): 28100-28129. doi: 10.3934/math.20241363
    [4] Pablo Fernández-López, Patricio García Báez, Ylermi Cabrera-León, Aleš Procházka, Carmen Paz Suárez-Araujo . Modeling the implications of nitric oxide dynamics on information transmission: An automata networks approach. AIMS Mathematics, 2023, 8(12): 30142-30181. doi: 10.3934/math.20231541
    [5] Canhong Long, Zuozhi Liu, Can Ma . Synchronization dynamics in fractional-order FitzHugh–Nagumo neural networks with time-delayed coupling. AIMS Mathematics, 2025, 10(4): 8673-8687. doi: 10.3934/math.2025397
    [6] Aziz Belmiloudi . Cardiac memory phenomenon, time-fractional order nonlinear system and bidomain-torso type model in electrocardiology. AIMS Mathematics, 2021, 6(1): 821-867. doi: 10.3934/math.2021050
    [7] Naseem Abbas, Amjad Hussain, Mohsen Bakouri, Thoraya N. Alharthi, Ilyas Khan . A study of dynamical features and novel soliton structures of complex-coupled Maccari's system. AIMS Mathematics, 2025, 10(2): 3025-3040. doi: 10.3934/math.2025141
    [8] Pratap Anbalagan, Evren Hincal, Raja Ramachandran, Dumitru Baleanu, Jinde Cao, Chuangxia Huang, Michal Niezabitowski . Delay-coupled fractional order complex Cohen-Grossberg neural networks under parameter uncertainty: Synchronization stability criteria. AIMS Mathematics, 2021, 6(3): 2844-2873. doi: 10.3934/math.2021172
    [9] Chengbo Yi, Rui Guo, Jiayi Cai, Xiaohu Yan . Pinning synchronization of dynamical neural networks with hybrid delays via event-triggered impulsive control. AIMS Mathematics, 2023, 8(10): 25060-25078. doi: 10.3934/math.20231279
    [10] Guillaume Cantin, Cristiana J. Silva . Influence of the topology on the dynamics of a complex network of HIV/AIDS epidemic models. AIMS Mathematics, 2019, 4(4): 1145-1169. doi: 10.3934/math.2019.4.1145

  • Interneurons modulate the excitability of neural networks and maintain neural activity balance via inhibitory or excitatory synaptic connections. Here, we studied the formation of patterns of interneuronal networks with inhibitory synaptic coupling. We found that both electrical synaptic coupling and inhibitory synaptic coupling play a crucial role in the formation of neural network patterns. In addition, delayed inhibitory synapses can also affect the transition of target waves to chaotic states. As the strength of electrical synaptic coupling increases, the firing behavior of neurons gradually becomes highly ordered. When the inhibitory synaptic delay reaches a critical value, we observe a transition in oscillatory patterns from an ordered state to a synchronized state. We further investigated how inhibitory synaptic conductance influences the formation of oscillatory patterns in the network. The study reveals that increasing synaptic conductance disrupts the structure of target waves, inducing chaotic states such as spiral wave fragmentation, while simultaneously elevating neuronal firing rates.



    1.   Introduction

    As a fundamental spatiotemporal ordered pattern in neural networks, target waves can serve as persistent pacemakers that precisely regulate the spatial distribution of neuronal activity and maintain global rhythmic synchronization [1,2,3]. This wave-dynamic phenomenon can be initiated by local electrical stimulation and propagate across the neural network [4]. Research demonstrates that the formation and propagation of target waves are critically dependent on the network's coupling strength and topological connectivity [5]. Under optimized parameters, target waves can fully dominate the network space, driving highly synchronized electrical activity in neuronal populations [6,7,8]. Remarkably, target waves exhibit exceptional noise robustness, maintaining stable propagation even under significant noise interference while effectively suppressing pathological patterns like spiral waves and spatiotemporal chaos [9]. Physiologically, this process bears a striking similarity to the cardiac conduction system, where pacemaker signals from the sinoatrial node propagate as target waves through myocardial tissue to coordinate rhythmic contraction-relaxation cycles [10,11]. In-depth investigation of target wave mechanisms not only provides novel insights into neural network dynamics but also holds translational potential, and the targeted induction of target waves to intervene in abnormal neural activities such as epileptic seizures may pioneer new therapeutic approaches for neurological disorders [12,13,14,15].

    In recent years, significant progress has been made in the study of intermediate neural networks, particularly in their role in regulating neural rhythms and network dynamics [16,17,18]. Research demonstrates that interneurons can modulate the synchrony and periodicity of neural activity not only through intricate network architectures but also via inhibitory chemical synapses and electrical synapses [19,20]. For instance, cutting-edge studies have identified that specific interneuron subtypes play pivotal roles in generating high-frequency gamma oscillations [21]. Furthermore, computational modeling and experimental evidence indicate that dynamic modifications in synaptic plasticity and connection strength within interneuron networks can substantially impact the stability of neural oscillations and information processing efficiency [22,23,24]. Notably, emerging research has uncovered the crucial involvement of interneuron networks in neurodevelopmental disorders. Functional abnormalities in these networks may underlie rhythm disturbances and cognitive impairments observed in autism spectrum disorders and schizophrenia [25]. These findings collectively highlight how interneurons serve as master regulators of network synchronization and rhythmic activities through their diverse connectivity patterns and dynamic regulatory mechanisms [26].

    The delay in information transmission is a fundamental characteristic of neuronal dynamics, primarily arising from the physical constraints of conduction velocity in neural electrical signals and the inherent temporal delays during dendritic integration and synaptic transmission [27]. Research indicates that electrical synapses, due to their direct electrical coupling properties, typically exhibit shorter synaptic delays [28,29,30]. Moreover, the functional synergy between electrical and chemical synapses can significantly enhance the synchronization efficiency of neural networks and achieve sub-millisecond precision in temporal coding [31,32]. This dual-synaptic cooperative mechanism plays a critical role in neural circuits requiring rapid information processing. From the perspective of information processing, synaptic delay is not merely a simple conduction lag but also a crucial parameter for spatiotemporal encoding of neural information [33]. Hybrid synapse modeling uncovers their joint control over neural synchronization and complexity. [34,35]. Experimental evidence demonstrates that synaptic delay dynamically regulates synaptic weights by precisely modulating the window of spike-timing-dependent plasticity. This mechanism is considered the foundational neural basis for working memory formation and associative learning [36]. Under pathological conditions, abnormalities in synaptic delay are closely associated with various neuropsychiatric disorders. Recent studies have found that the dispersion of synaptic delays in the prefrontal cortex of autism patients increases by approximately 40%, impairing gamma oscillation synchronization, which may underlie their executive dysfunction [37]. Similarly, abnormal fluctuations in synaptic delays have been observed in the hippocampal-prefrontal circuits of schizophrenia patients. Notably, the dynamic regulation of synaptic delays during development—particularly during critical periods—is essential for the functional optimization of neural networks. Dysregulation of this process may contribute to neurodevelopmental disorders [38].

    Although the pivotal role of interneuron networks in generating rhythmic activity has been extensively studied, the impact of delays in inhibitory coupling on synchronization properties, wave propagation, and network stability remains unclear. Investigating how these delays govern the generation and modulation of rhythmic oscillations is thus critical, providing insights into both normal brain function and pathological states such as epilepsy. Therefore, we investigated the pattern dynamics in a two-dimensional interneuron network coupled by delayed inhibitory synapses and fast electrical synapses, with a particular focus on how inhibitory synaptic delays affect the propagation of target waves in the network. In our research, we discovered that when the delay time of inhibitory synapses reaches a certain threshold, the neural network abruptly transitions from a resting state to a highly ordered state, accompanied by the emergence of target waves. Further analysis revealed that both the synaptic conductance strength and delay time of inhibitory synapses play crucial roles in the formation of this ordered network state. This finding not only provides compelling evidence once again for the central role of time delays in the dynamic behavior of neural networks but also highlights the key driving function of synaptic mechanisms in the generation of target waves.

    2.   Materials and methods

    The dynamics of fast-spiking interneurons is described by the Wang-Buzsaki (WB) model [39]. It has a form similar to the classical Hodgkin–Huxley model [40,41], with details as follows:

    {CdVdt=−gNam3∞(V)h(V−ENa)−gKn4(V−EK)−gL(V−EL)+Iext,dhdt=ϕ[αh(V)(1−h)−βh(V)h],dndt=ϕ[αn(V)(1−n)−βn(V)n]. (1)

    The system variables include membrane potential (V), sodium current inactivation parameter (h), and potassium current activation parameter (n). The six kinetic equations governing channel gating dynamics are defined as:

    {m∞(V)=αm(V)/[αm(V)+βm(V)],αm(V)=0.1(V−35)/{1−exp[−0.1(V+35)]},βm(V)=4exp[−(V+60)/18],αh(V)=0.07exp[−(V+58)/20],βh(V)=1/{exp[−0.1(V+28)]+1},αn(V)=0.01(V+34)/{1−exp(V+34)},βn(V)=0.125exp[−(V+44)/80]. (2)

    The parameter C denotes the membrane capacitance. The parameters gNa, gK, and gL are the maximum conductances for sodium, potassium, and leak ion channels, respectively. Meanwhile, ENa, EK, and EL denote Nernst equilibrium potentials for respective ionic species. The parameters are set as follows: C = 1 μF/cm2, gNa = 35 mS/cm2, gK = 9 mS/cm2, gL = 0.1 mS/cm2, ENa = 55 mV, EK = −90 mV, EL = −65 mV, and φ = 5. The parameter Iext represents an external stimulus current.

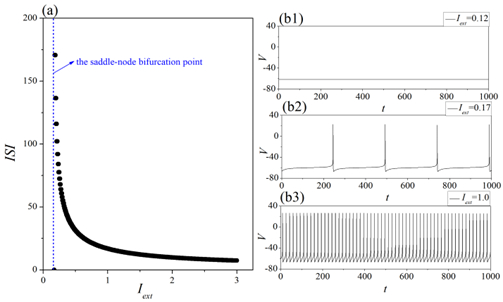
    The WB model has a saddle-node bifurcation on an invariant cycle at Iext ≈ 0.16 μA/cm2. From the bifurcation diagram in Figure 1(a), it can be clearly observed that as the external stimulus current gradually increases, neurons transition from a resting state to a state of periodic firing. Meanwhile, the interspike intervals become progressively shorter. This indicates that external stimuli can significantly promote neuronal firing, and the firing frequency is positively correlated with the intensity of the external stimulus current. From the time series diagram, it can be observed that when the stimulation current is 0.12 μA/cm2, the neuron remains in a resting state [Figure 1(b1)]; however, when the current increases above 0.16 μA/cm2, the neuron begins to enter a firing state, as shown in Figure 1(b2). Previous studies have shown that when the stimulus current approaches 1.0 μA/cm2, as shown in Figure 1(b3), the firing frequency of neurons reaches 60 Hz within the gamma range [39].

    Figure 1.  Dynamics of the WB model versus the external stimulus current Iext. (a) The bifurcation diagram. Time series of membrane potential: (b1) Iext = 0.12 μA/cm2; (b2) Iext = 0.17 μA/cm2; (b3) Iext = 1.0 μA/cm2. As the stimulus current increases, the neuron transitions from a resting state to periodic firing, with progressively shorter interspike intervals, indicating that external current significantly enhances neuronal activity, and firing frequency is positively correlated with current intensity.
    DownLoad: Full-Size Img PowerPoint

    We constructed a neural network model consisting of N×N fast-spiking interneurons with nearest-neighbor coupling. For simplicity, neurons are interconnected via inhibitory synapses and electrical synapses. All synapses are bidirectionally conductive, and self-connections of neurons are excluded. Building on the instantaneous transmission properties of electrical synapses, while specifically considering signal latency effects in inhibitory pathways, the network employs the WB model (Eq 1) to describe neuronal dynamics. This model inherits the theoretical framework of the classical Hodgkin–Huxley model [40], and the specific dynamical equations are as follows:

    {CdVijdt=−gNam3∞,ij(Vij)hij(V−ENa)−gKn4ij(Vij−EK)−gL(Vij−EL)+Iext,ij+Iel,ij+Iche,ij,dhijdt=φ[αh,ij(Vij)(1−hij)−βh,ij(Vij)hij],dnijdt=φ[αn,ij(Vij)(1−nij)−βn,ij(Vij)nij]. (3)

    where the subscript i, j stands for the (i, j)th neuron in the networks. In the present paper, the total number of neurons is N = 100. The three variables of the (i, j) neuron correspond to the three variables in Eq 1. In particular, Iel, ij and Iche, ij denote the electrical coupling current and the inhibitory synaptic current received by the neuron at position (i, j), respectively. These currents are characterized as follows:

    {Iel,ij=D∑(k,l∈N(i,j))(Vkl−Vij),Iche,ij=−gche14∑(k,l∈N(i,j))sche,kl(Vij−Eche),N(i,j)={(i+1,j),(i−1,j),(i,j+1),(i,j−1)}. (4)

    In this equation, D is the electrical synaptic strength from neuron (k, l) to neuron (i, j). gche and Eche are the synaptic conductance and the reversal potential, respectively. In this study, the reversal potential is Eche = −75 mV, to make sure that the synaptic current is inhibitory. The factor of 1/4 in the expression for Iche, ij is due to the two-dimensional regular network structure, where each node has four nearest neighbors. The variables sche, kl in Eq (4) represent the fractions of open synaptic channels, and are modeled as follows:

    dsche,kldt=α11+exp[−0.5(Vkl−θ)](1−sche,kl)−1τsche,kl. (5)

    Where α is the opening rate of the synaptic channel, and θ represents the synaptic threshold. In the study, α and θ are set to 12 ms-1 and 0 mV. To measure the formation of patterns in neuronal networks, we have introduced synchronization factors that statistically characterize collective dynamical behaviors. These factors aim to quantify the coordinated activity of neuronal networks and their spatiotemporal dynamical properties, thereby revealing the mechanisms and principles underlying pattern formation.

    R=⟨F2⟩−⟨F⟩21/1N2N∑j=1N∑i=1(⟨V2ij⟩−⟨Vij⟩2)N2N∑j=1N∑i=1(⟨V2ij⟩−⟨Vij⟩2),F=1N2N∑j=1N∑i=1Vij=⟨Vij⟩. (6)

    By calculating the mean field activity of the neuronal network, we assess the overall synchronization. The mean field synchronization factor reflects the consistency of collective behavior among neurons in the network, with higher values indicating stronger synchronization.

    3.   Results

    The study employs the Euler difference method for numerical simulation of differential equations, with a time step of 0.02 ms. The network adopts no-flux boundary conditions, and for simplicity, the initial values of the network nodes are set to 0.1. For target wave generation in neuronal networks, we applied 1.0 μA/cm2 to the central [48,52]×[48,52] region versus 0.12 μA/cm2 peripherally, exploiting symmetric stimulation for controlled pattern formation. This setup aims to induce neuronal activity in specific areas through localized high stimulation currents, thereby observing the formation and propagation mechanisms of patterns within the network. We first present the fundamental simulation results, analyzing the impact of fast electrical synaptic coupling on the generation and propagation of target waves in intermediate neuronal networks in the absence of delayed inhibitory synaptic coupling.

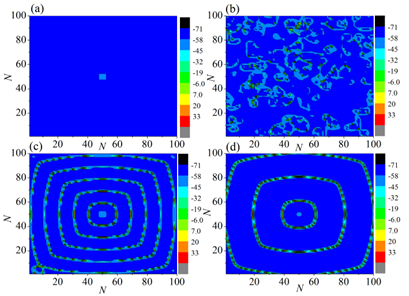
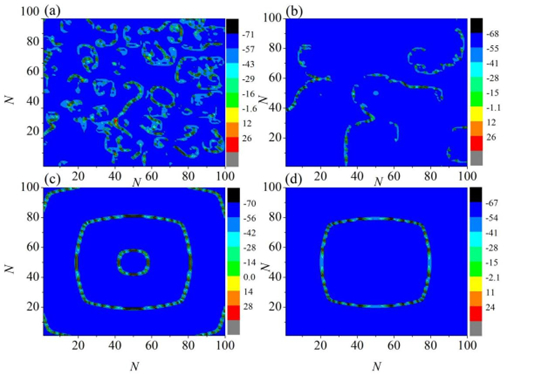
    In Figure 2, typical patterns of neuronal networks are plotted under different electrical coupling strengths in the absence of chemical synaptic coupling (gche = 0). The results clearly demonstrate that electrical synaptic coupling plays a significant role in the pattern formation process within the neuronal network. In the absence of fast electrical synaptic coupling in Figure 2(a), when D = 0, due to the heterogeneity in externally applied currents across different regions of the network, only neurons within the region (i, j)∈(48, 52)×(48, 52) exhibit firing activity, while neurons in other regions remain in a resting state. As the strength of electrical coupling increases, the neuronal network begins to display disordered patterns. This phenomenon arises because the electrical coupling strength within the network is weak, and the interactions between neurons are insufficient to establish an ordered activity pattern. However, when the electrical coupling strength reaches a certain threshold [e.g., D = 0.2 ms/cm2 in Figure 2(c)], regular target waves emerge in the neuronal network. Further increasing the coupling strength to 0.3 does not cause the target waves to break up during propagation; instead, their propagation speed significantly increases.

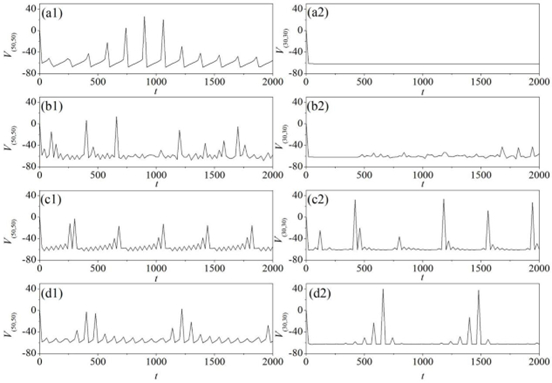
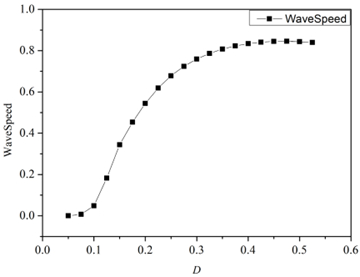
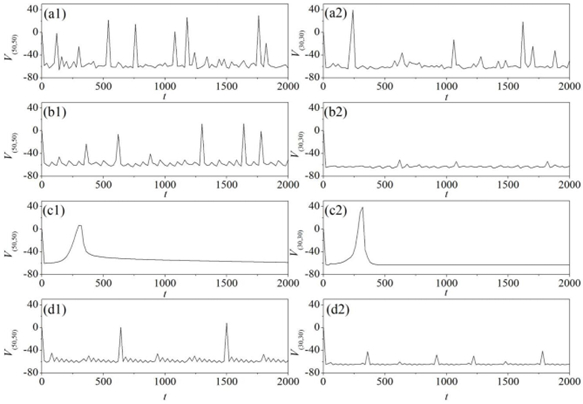
    Figure 2.  Time evolution of spatial patterns is calculated at gche = 0. For electrical coupling strength (a) D = 0, localized neuronal firing only; (b) D = 0.1 ms/cm2, disorganized firing pattern; (c) D = 0.2 ms/cm2, emergence of regular target waves; (d) D = 0.3 ms/cm2, target wave accelerates propagation and maintains stability.
    DownLoad: Full-Size Img PowerPoint

    In Figure 3, we present the membrane potential firing sequences of two sampling points, (30, 30) and (50, 50), in the neuronal network. An external current of 1.0 μA/cm2 is applied at the position (50, 50). The numerical simulation results indicate that, in addition to the influence of the external current, electrical coupling also significantly affects the firing states of the neurons. When the coupling strength is weak, target waves do not emerge in the neuronal network, meaning that the membrane potential firing of neurons at the network center is insufficient to drive the firing of surrounding neurons. This is corroborated by the resting state of the sequence at the (30, 30) sampling point, as shown in Figure 3 (a2). As the coupling strength D increases to 0.1 ms/cm2, the propagating target wave undergoes rupture, driving the network into a chaotic state [Figure 2 (b)]. This chaotic state further influences the firing behavior of neurons [Figure 3(b1),(b2)], which may be attributed to the bidirectional nature of electrical coupling. In other words, neurons interact with and alter each other's dynamical properties through mutual influence. As the electrical coupling strength further increases, a regular target wave pattern gradually forms in the neural network, leading to a highly ordered state in the entire system. The discharge behavior of neurons also exhibits almost periodic oscillation characteristics [see Figure 3 (c1), (c2)]. When the coupling strength increases from 0.2 ms/cm2 to 0.3 ms/cm2 [Figure 3(d1),(d2)], the waveform of target waves in the system gradually becomes sparse. From the time series of sampling points, it can be observed that the firing frequency of neurons has undergone significant changes, and the distance traveled by waves per unit time has significantly increased. This phenomenon indicates that the enhancement of electrical coupling strength can significantly accelerate the propagation of target waves in the system. In addition, the results in Figure 3 indicate that electrical synaptic coupling provides strong mechanistic support for promoting the formation of ordered states in the network. To validate this mechanism, the dependence of target wave dynamics on the strength of electrical coupling was quantitatively analyzed. The wave speed was calculated as follows: the propagation time required for the wavefront to reach different radial distances was measured from the network center (50, 50), and the speed was computed using speed = distance/propagation time. Finally, the average speed was determined across four principal directions (up, down, left, right) to obtain a robust estimate. The results are shown in Figure 4.

    Figure 3.  Time series of sampling point (50, 50) and (30, 30) positions in neural networks at gche = 0. For electrical coupling strength (a1)(a2) D = 0; (b1)(b2) D = 0.1 ms/cm2; (c1)(c2) D = 0.2 ms/cm2; (d1)(d2) D = 0.3 ms/cm2. Electrical coupling governs wave formation and propagation efficiency, and ordered patterns require critical coupling strength.
    DownLoad: Full-Size Img PowerPoint
    Figure 4.  Dependence of target wave propagation speed on electrical coupling strength. The data demonstrate a significant increase in wave speed with enhanced coupling strength.
    DownLoad: Full-Size Img PowerPoint

    As demonstrated in Figure 4, the propagation speed of target waves in the system was observed to increase significantly with enhanced electrical coupling strength, which is consistent with the conclusion drawn from Figure 3 that electrical synaptic coupling facilitates the formation of ordered states. Next, we focused on analyzing the impact of inhibitory synapses on pattern formation in neuronal networks and the underlying mechanisms. The results are shown in Figure 5.

    Figure 5.  Time evolution of spatial patterns and time series of sampling points in neural networks at τ = 10 ms and electrical coupling strength D = 0. For the synaptic conductance (a) gche = 0.02 ms/cm2; (b) gche = 0.1 ms/cm2; (c) time series of sampling point (30, 30) and gche = 0.02 ms/cm2; (d) time series of sampling point (50, 50) and gche = 0.02 ms/cm2; (e) time series of sampling point (30, 30) and gche = 0.1 ms/cm2; (f) time series of sampling point (50, 50) and gche = 0.1 ms/cm2. Target wave modes cannot be generated in the absence of electrical coupling, and the network consequently loses its spatiotemporal self-organization capability.
    DownLoad: Full-Size Img PowerPoint

    Figure 5 illustrates the pattern dynamics in the neuronal network with only inhibitory synaptic coupling. For simplicity, the delay of inhibitory synaptic coupling was set to a fixed value of 10 ms. The results indicate that, in the absence of electrical synaptic coupling, the neuronal network fails to form target wave patterns. When electrical synaptic coupling is activated, high-quality target wave patterns can still be observed even under the condition of gche = 0. As the strength of electrical synaptic coupling increases, the firing behavior of neurons gradually becomes highly ordered. In fact, existing studies have shown that electrical synaptic coupling is more effective than chemical coupling in achieving ordered states in the system [42]. A possible mechanism for this phenomenon is that chemical synapses only function when the presynaptic neuron fires, whereas electrical synapses can continuously and efficiently transmit the membrane potential of presynaptic neurons to postsynaptic neurons, thereby more effectively regulating the overall dynamical behavior of the network. Therefore, we comprehensively considered the combined effects of electrical synaptic coupling and inhibitory coupling on pattern formation in the neuronal networks; the results are shown in Figures 6 and 7.

    Figure 6.  Time evolution of spatial patterns is calculated at τ = 10 ms. For (a) D = 0.2 ms/cm2, gche = 0.02 ms/cm2; (b) D = 0.2 ms/cm2, gche = 0.1 ms/cm2; (c) D = 0.3 ms/cm2, gche = 0.02 ms/cm2; (d) D = 0.3 ms/cm2, gche = 0.1 ms/cm2. The network can only maintain stable target wave patterns when the electrical coupling strength reaches 0.3 ms/cm2, and increased inhibitory conductance accelerates target wave propagation.
    DownLoad: Full-Size Img PowerPoint
    Figure 7.  Time series of sampling points (50, 50) in panels (a1), (b1), (c1), (d1), and (30, 30) in panels (a2), (b2), (c2), (d2) within neural networks at τ = 10 ms. (a1)(a2) D = 0.2 ms/cm2, gche = 0.02 ms/cm2; (b1)(b2) D = 0.2 ms/cm2, gche = 0.1 ms/cm2; (c1) (c2) D = 0.3 ms/cm2, gche = 0.02 ms/cm2; (d1)(d2) D = 0.3 ms/cm2, gche = 0.1 ms/cm2. Inhibitory synapses reduce neuronal firing amplitude but increase firing frequency during target wave states.
    DownLoad: Full-Size Img PowerPoint

    In the presence of only electrical synaptic coupling, when the coupling strength is 0.2 ms/cm2, the system can form perfect target wave patterns. However, when inhibitory chemical synaptic coupling is introduced, this ordered state is disrupted. Under the influence of inhibitory synaptic coupling, the target waves break during propagation, leading the system into a chaotic state, as shown in Figure 6(a). In this state, as the inhibitory synaptic conductance increases, the system further exhibits dynamic behaviors characterized by spiral wave fragments [see Figure 6(b)]. Electrical synaptic coupling tends to promote synchronization and ordered states in the neuronal network, while inhibitory chemical synaptic coupling disrupts this order through its delayed and nonlinear effects, resulting in the breakdown of target waves and the emergence of chaotic states. With the increase in inhibitory conductance, the system's dynamics become more complex, ultimately manifesting as the formation of spiral wave fragments. This phenomenon reveals the intricate mechanisms of competition and synergy between electrical and chemical synapses in neuronal networks. Furthermore, by comparing Figures 2 and 6(c) and (d), it can be observed that the introduction of inhibitory synaptic coupling significantly enhances the propagation speed of the original target waves. As the inhibitory synaptic conductance increases from 0 to 0.02 ms/cm2 and further to 0.1 ms/cm2, the wave rings of the target waves gradually become sparser.

    Similarly, we calculated and analyzed the membrane potential time series of the sampling points (30, 30) and (50, 50) in the neuronal network. Figure 7 indicates that inhibitory synapses significantly suppress the firing behavior of neurons, manifested as a reduction in the amplitude of membrane potentials. However, when the system is in the ordered state of target wave patterns, an increase in inhibitory synaptic conductance promotes a rise in neuronal firing frequency. This finding is consistent with the aforementioned results, suggesting that an increase in inhibitory synaptic conductance can accelerate the propagation speed of target waves in the neuronal network. The research results indicate that inhibitory synaptic conductance significantly enhances the synchronicity of neuronal firing activity in neural networks. Building upon this discovery, we further conducted a quantitative analysis of the dependency between the synchronization factor R and gche with different electrical synaptic coupling strength D; the results are shown in Figure 8.

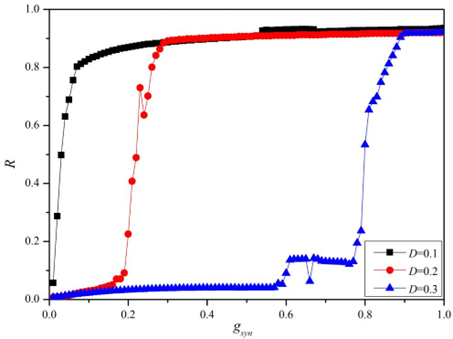
    Figure 8.  Dependence of the synchronization factor R of the coupled network at τ = 10 ms. The black, red, and blue line segments correspond to the coupling strengths D = 0.1 ms/cm2, D = 0.2 ms/cm2, and D = 0.3 ms/cm2, respectively.
    DownLoad: Full-Size Img PowerPoint

    As gche increases from 0 to 1.0 mS/cm2, under different electrical coupling strengths, the value of the synchronization factor R exhibits a trend of sharply rising from a minimal value to near 1 before stabilizing (Figure 8). It is noteworthy that the critical value of gche (inflection point) required for the system to achieve complete synchronization is closely related to the electrical synaptic coupling strength D: the larger the D value, the greater the gche value needed for the system to attain complete synchronization. This phenomenon further confirms the enhancing effect of synaptic conductance on the synchronization of neuronal networks. When the synchronization factor of the system is at a low value, it indicates that the system may be in a chaotic state or an ordered state dominated by target waves; when the synchronization factor increases to 1, it signifies that the neuronal firing activities within the system have reached a high degree of synchronization, at which point the target wave patterns will no longer emerge in the system. Previous studies have demonstrated that the oscillatory patterns of neural networks are significantly modulated by inhibitory synaptic delays [43]. Building upon this foundation, the present research further investigates the regulatory mechanisms and the underlying principles of how synaptic delays influence the pattern dynamics in neuronal networks. The results are shown in Figure 9.

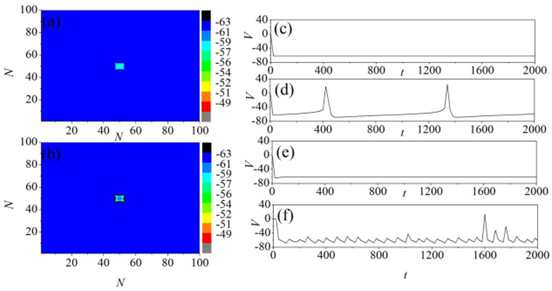
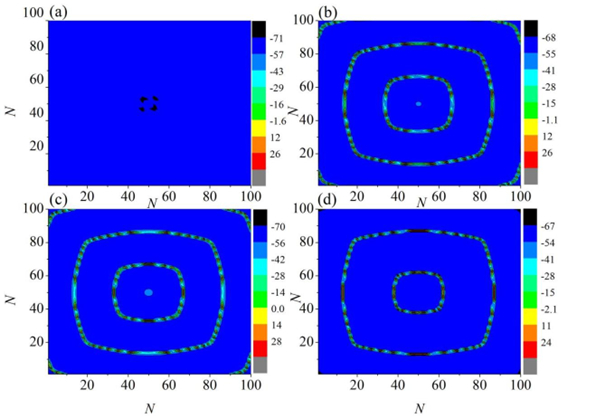
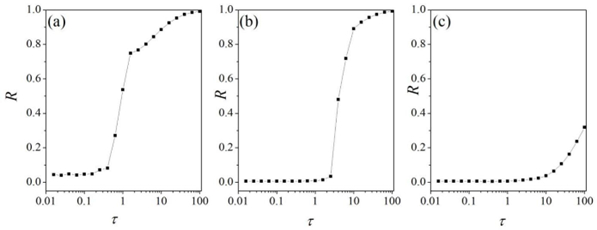
    Figure 9.  Time evolution of spatial patterns is calculated at D = 0.3 ms/cm2, gche = 0.02 ms/cm2. (a) τ = 0.01 ms (no target wave formation); (b) τ = 0.05 ms (target wave patterns emerge); (c) τ = 0.4 ms (well-defined target waves appear); (d) τ = 20 ms (large waveform interval).
    DownLoad: Full-Size Img PowerPoint

    The results depicted in Figure 9 elucidate that the oscillatory pattern is significantly influenced by the inhibitory synaptic delay. For appropriate values of τ, a well-ordered oscillatory pattern can be discerned. However, if the delay τ is sufficiently small, we can observe the absence of target waves in the network, which implies that the neurons within the system are in a state of quiescence, and a sufficiently large external stimulus current does not induce oscillations in the neuronal membrane potential. It is only when the delay increases to a certain extent that perfect target waves emerge in the network, and the system enters an ordered state at this point. Numerical simulation results further indicate that the greater the delay, the faster the propagation speed of the target waves, that is, the smaller the oscillation period of the neuronal membrane potential.

    Theoretically, the emergence of target wave patterns in the network occurs only when the inhibitory synaptic delay is sufficiently long. Under these conditions, the firing frequency of neurons within the network increases. It is evident that the longer the inhibitory synaptic delay τ, the shorter the firing period of each neuron becomes. Furthermore, once the inhibitory synaptic currents induced by the first neuron begin to take effect, these currents tend to reduce the membrane potential of the neurons and prolong their firing cycle. During the course of numerical simulations, we observed that in the absence of robust synaptic coupling strength, even with adjustments to the inhibitory synaptic delay, the oscillatory modes within the neuronal network are unlikely to undergo significant abrupt changes (see Figure 10).

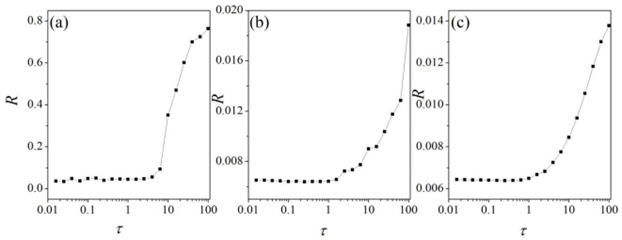
    Figure 10.  Dependence of the synchronization factor R of the coupled network at gche = 0.02 ms/cm2 for the coupling strengths (a) D = 0.1 ms/cm2; (b) D = 0.2 ms/cm2; (c) D = 0.3 ms/cm2.
    DownLoad: Full-Size Img PowerPoint

    When the inhibitory synaptic parameter gche is small, the system exhibits a characteristic weak synchronization. As shown in Figure 11(b) and (c), with increasing synaptic delay time (D = 0.3 ms/cm2), the synchronization factor R remains within a low range (0.006~0.014), indicating that neuronal clusters fail to establish effective synchronous firing patterns. When gche increases to 0.3 ms/cm2, the system demonstrates significant synchronization enhancement. Numerical results in Figure 11 reveal a three-stage transition in R values with progressive delay time: rapid progression from weak (R ≈ 0.1) through intermediate (R ≈ 0.5) to strong synchronization (R = 1). Notably, the system maintains stable R values under prolonged delays after achieving strong synchronization, demonstrating robust behavior. These results demonstrate the dual regulatory function of inhibitory synaptic delays as a critical parameter for oscillation mode selection; their temporal characteristics directly determine network synchronization states, and sustained inhibitory delays establish stable phase-locking mechanisms that provide the necessary dynamical foundation for spatiotemporal pattern formation, particularly target waves. This discovery offers new theoretical insights into pattern selection mechanisms in neural information encoding.

    Figure 11.  Dependence of the synchronization factor R of the coupled network at gche = 0.3 ms/cm2. Coupling strengths (a) D = 0.1 ms/cm2; (b) D = 0.2 ms/cm2; (c) D = 0.3 ms/cm2.
    DownLoad: Full-Size Img PowerPoint

    4.   Discussion

    This study employs numerical simulations to elucidate the synergistic regulatory mechanisms of electrical synaptic coupling and inhibitory chemical synaptic coupling in the formation of spatiotemporal patterns in neuronal networks. Electrical synaptic coupling strength is a critical factor in target wave formation. When the coupling strength reaches 0.2 ms/cm2, the network generates regular target wave patterns, with wave propagation speed significantly increasing as D rises. This demonstrates that electrical synapses, through continuous and efficient membrane potential transmission, effectively promote the emergence of ordered network states. Increasing the time delay τ markedly accelerates target wave propagation, with the system transitioning to an ordered state when τ > 0.4 ms. Enhancing synaptic conductance disrupts target wave structures, inducing chaotic states such as spiral wave fragments, while simultaneously increasing neuronal firing frequency. As the coupling strength D increases, the system undergoes a distinct three-stage phase transition in synchronization: evolving from an initially desynchronized state (R ≈ 0) to a critical transition regime before reaching complete synchronization (R ≈ 1). Electrical synaptic coupling establishes rapid phase synchronization as the foundational framework for pattern formation, while inhibitory synapses enable plasticity-driven pattern modulation through spatiotemporal tuning. This regulatory paradigm may underpin dynamic information processing in neural computations.

    This study employed computational neuroscience modeling to systematically investigate the regulatory mechanisms of inhibitory chemical and electrical synaptic coupling on spatiotemporal pattern formation in interneuron networks. By constructing a biophysical neural network based on the WB model, we demonstrated that inhibitory synapses can induce diverse firing patterns—from synchronous oscillations to traveling wave propagation—through modulation of postsynaptic current dynamics. Notably, our results elucidate the synergistic regulation of inhibitory synaptic strength and temporal delay in selecting network dynamic patterns. These findings not only advance our understanding of neural information–encoding mechanisms but, more importantly, establish a novel theoretical framework for explaining abnormal neural oscillations in epilepsy and other brain disorders. This work provides important insights for developing targeted synaptic modulation strategies in neurological disease treatment.

    Author contributions

    Ying Xu: Writing-original draft, Writing-final version, Numerical calculation. Xiaodi Li: Methodology, Supervision, Numerical calculation.

    Acknowledgments

    The authors gratefully acknowledge Prof. Jun Ma from Lanzhou University of Technology for the constructive suggestions. This research is supported by the National Natural Science Foundation of China (12402061).

    Use of Generative-AI tools declaration

    The authors declare that no Artificial Intelligence (AI) tools were used in the creation of this article.

    Conflict of interest

    Xiaodi Li is an editorial board member for AIMS Mathematics and was not involved in the editorial review or the decision to publish this article. All authors declare that there are no competing interests.



    [1] Y. Qian, X. Huang, G. Hu, X. Liao, Structure and control of self-sustained target waves in excitable small-world networks, Phys. Rev. E, 81 (2010), 036101. https://doi.org/10.1103/PhysRevE.81.036101 doi: 10.1103/PhysRevE.81.036101
    [2] Z. Rostami, V. T. Pham, S. Jafari, F. Hadaeghi, J. Ma, Taking control of initiated propagating wave in a neuronal network using magnetic radiation, Appl. Math. Comput., 338 (2018), 141–151. https://doi.org/10.1016/j.amc.2018.06.004 doi: 10.1016/j.amc.2018.06.004
    [3] C. Wang, M. Lv, A. Alsaedi, J. Ma, Synchronization stability and pattern selection in a memristive neuronal network, Chaos, 27 (2017), 113108. https://doi.org/10.1063/1.5004234 doi: 10.1063/1.5004234
    [4] H. Qin, C. Wang, N. Cai, X. An, F. Alzahrani, Field coupling-induced pattern formation in two-layer neuronal network, Physica A, 501 (2018), 141–152. https://doi.org/10.1016/j.physa.2018.02.063 doi: 10.1016/j.physa.2018.02.063
    [5] J. Ma, Y. Xu, G. Ren, C. Wang, Prediction for breakup of spiral wave in a regular neuronal network, Nonlinear Dyn., 84 (2016), 497–509. https://doi.org/10.1007/s11071-015-2502-6 doi: 10.1007/s11071-015-2502-6
    [6] Y. Wu, Q. Ding, W. Huang, T. Li, D. Yu, Y. Jia, Dynamic learning of synchronization in coupled nonlinear systems, Nonlinear Dyn., 112 (2024), 21945–21967. https://doi.org/10.1007/s11071-024-10192-y doi: 10.1007/s11071-024-10192-y
    [7] J. Ma, J. Tang, A review for dynamics in neuron and neuronal network, Nonlinear Dyn, 89 (2017), 1569–1578. https://doi.org/10.1007/s11071-017-3565-3 doi: 10.1007/s11071-017-3565-3
    [8] Q. Ding, Y. Wu, W. Huang, Y. Jia, A dynamic learning method for phase synchronization control in Hodgkin–Huxley neuronal networks, Eur. Phys. J. Spec. Top., (2024). https://doi.org/10.1140/epjs/s11734-024-01171-w
    [9] M. C. Deo, S. S. Jagdale, Prediction of breaking waves with neural networks, Ocean Eng., 30 (2003), 1163–1178. https://doi.org/10.1016/S0029-8018(02)00086-0 doi: 10.1016/S0029-8018(02)00086-0
    [10] D. Yu, X. Li, X. Wang, W. Huang, X. Hu, Y. Jia, Community modularity structure promotes the evolution of phase clusters and chimeralike states, Phys. Rev. E, 111 (2025). https://doi.org/10.1103/PhysRevE.111.034311
    [11] Y. Xu, J. Ma, Pattern formation in a thermosensitive neural network, Commun. Nonlinear Sci. Numer. Simul., 111 (2022), 106426. https://doi.org/10.1016/j.cnsns.2022.106426 doi: 10.1016/j.cnsns.2022.106426
    [12] R. Wang, J. Li, M. Du, J. Lei, Y. Wu, Transition of spatiotemporal patterns in neuronal networks with chemical synapses, Commun. Nonlinear Sci. Numer. Simul. 40 (2016), 80–88. https://doi.org/10.1016/j.cnsns.2016.04.018 doi: 10.1016/j.cnsns.2016.04.018
    [13] J. Ma, J. Tang, A review for dynamics of collective behaviors of network of neurons, Sci. China Inf. Sci., 58 (2015), 2038–2045. https://doi.org/10.1007/s11431-015-5961-6 doi: 10.1007/s11431-015-5961-6
    [14] X. Liu, Y. Yu, Q. Wang, Dynamic epileptic seizure propagation based on multiscale synaptic plasticity, Nonlinear Dyn., 113 (2025), 10445–10459. https://doi.org/10.1007/s11071-024-10590-2 doi: 10.1007/s11071-024-10590-2
    [15] Y. Yu, H. Wang, X. Liu, Q. Wang, Closed-loop transcranial electrical stimulation for inhibiting epileptic activity propagation: A whole-brain model study, Nonlinear Dyn., 112 (2024), 21369–21387. https://doi.org/10.1007/s11071-024-10132-w doi: 10.1007/s11071-024-10132-w
    [16] A. E. Pereda, Electrical synapses and their functional interactions with chemical synapses, Nat. Rev. Neurosci., 15 (2014), 250–263. https://doi.org/10.1038/nrn3708 doi: 10.1038/nrn3708
    [17] N. Kopell, B. Ermentrout, Chemical and electrical synapses perform complementary roles in the synchronization of interneuronal networks, Proc. Natl. Acad. Sci. U. S. A., 101 (2004), 15482–15487. https://doi.org/10.1073/pnas.040634310 doi: 10.1073/pnas.040634310
    [18] P. Ge, H. Cao, Synchronization of Rulkov neuron networks coupled by excitatory and inhibitory chemical synapses, Chaos, 29 (2019), 023129. https://doi.org/10.1063/1.5053908 doi: 10.1063/1.5053908
    [19] R. Harris-Warrick, Synaptic chemistry in single neurons: GABA is identified as an inhibitory neurotransmitter, J. Neurophysiol., 93 (2005), 3029–3031. https://doi.org/10.1152/classicessays.00026.2005 doi: 10.1152/classicessays.00026.2005
    [20] D. Guo, Q. Wang, M. Perc, Complex synchronous behavior in interneuronal networks with delayed inhibitory and fast electrical synapses, Phys. Rev. E, 85 (2012), 061905. https://doi.org/10.1103/PhysRevE.85.061905 doi: 10.1103/PhysRevE.85.061905
    [21] Y. Shao, F. Wu, Q. Wang, Synchronization and complex dynamics in locally active threshold memristive neurons with chemical synapses, Nonlinear Dyn., 112 (2024), 13483–13502. https://doi.org/10.1007/s11071-024-09747-w doi: 10.1007/s11071-024-09747-w
    [22] Y. Jia, H. Gu, X. Wang, Nonlinear mechanisms for enhanced and synchronized post-inhibitory rebound spiking associated with seizures in an inhibitory–excitatory neuronal network, Chaos, 35 (2025), 033104. https://doi.org/10.1063/5.0232718 doi: 10.1063/5.0232718
    [23] R. Wang, H. Gu, Y. Li, Nonlinear mechanism for paradoxical facilitation of spike induced by inhibitory synapse in auditory nervous system for sound localization, Nonlinear Dyn., 112 (2024), 19393–19419. https://doi.org/10.1007/s11071-024-10008-z doi: 10.1007/s11071-024-10008-z
    [24] P. Zhou, Y. Xu, J. Ma, Dynamical and coherence resonance in a photoelectric neuron under autaptic regulation, Physica A, 620 (2023), 128746. https://doi.org/10.1016/j.physa.2023.128746 doi: 10.1016/j.physa.2023.128746
    [25] X. Li, Y. Xu, How lights affect the circadian rhythm in sleep-awake circle, Chin. J. Phys., 91 (2024), 719–733. https://doi.org/10.1016/j.cjph.2024.08.016 doi: 10.1016/j.cjph.2024.08.016
    [26] X. Li, Y. Xu, Energy level transition and mode transition in a neuron, Nonlinear Dyn., 112 (2024), 2253–2263. https://doi.org/10.1007/s11071-023-09147-6 doi: 10.1007/s11071-023-09147-6
    [27] F. Yang, J. Ma, G. Ren, A Josephson junction-coupled neuron with double capacitive membranes, J. Theor. Biol., 578 (2024), 111686. https://doi.org/10.1016/j.jtbi.2023.111686 doi: 10.1016/j.jtbi.2023.111686
    [28] Y. Guo, Y. Xie, J. Ma, Nonlinear responses in a neural network under spatial electromagnetic radiation, Physica A, 626 (2023), 129120. https://doi.org/10.1016/j.physa.2023.129120 doi: 10.1016/j.physa.2023.129120
    [29] Y. Wu, Q. Ding, W. Huang, X. Hu, Z. Ye, Y. Jia, Dynamic modulation of external excitation enhance synchronization in complex neuronal network, Chaos Soliton. Fract., 183 (2024), 114896. https://doi.org/10.1016/j.chaos.2024.114896 doi: 10.1016/j.chaos.2024.114896
    [30] W. Huang, Y. Wu, Q. Ding, Y. Jia, Effects of potassium channel blockage on chimera-like states in the excitatory–inhibitory neuronal network, Eur. Phys. J. Spec. Top., (2025)https://doi.org/10.1140/epjs/s11734-025-01529-8
    [31] T. Obut, E. Cimen, M. Cakir, A novel numerical approach for solving delay differential equations arising in population dynamics, Math. Modell. Control, 3 (2023), 233–243. https://doi.org/10.3934/mmc.2023020 doi: 10.3934/mmc.2023020
    [32] Y. Jia, H. Gu, Y. Li, Influence of inhibitory autapses on synchronization of inhibitory network gamma oscillations, Cognitive Neurodyn., 17 (2023), 1131–1152. https://doi.org/10.1007/s11571-022-09856-5 doi: 10.1007/s11571-022-09856-5
    [33] Q. Wang, M. Perc, Z. Duan, G. Chen, Delay-induced multiple stochastic resonances on scale-free neuronal networks, Chaos, 19 (2009), 325407. https://doi.org/10.1063/1.3133126 doi: 10.1063/1.3133126
    [34] K. Xu, J. P. Maidana, P. Orio, Diversity of neuronal activity is provided by hybrid synapses, Nonlinear Dyn., 105 (2021), 2693–2710. https://doi.org/10.1007/s11071-021-06704-9 doi: 10.1007/s11071-021-06704-9
    [35] J. T. Fossi, Z. T. Njitacke, W. N. Tankeu, J. M. Mendimi, J. Awrejcewicz, J. Atangana, Phase synchronization and coexisting attractors in a model of three different neurons coupled via hybrid synapses, Chaos Soliton. Fract., 177 (2023), 114202. https://doi.org/10.1016/j.chaos.2023.114202 doi: 10.1016/j.chaos.2023.114202
    [36] D. Yu, X. Zhou, G. Wang, Q. Ding, T. Li, Y. Jia, Effects of chaotic activity and time delay on signal transmission in FitzHugh-Nagumo neuronal system, Cognitive Neurodyn., 16 (2022), 887–897. https://doi.org/10.1007/s11571-021-09743-5 doi: 10.1007/s11571-021-09743-5
    [37] F. Yang, J. Ma, F. Wu, Review on memristor application in neural circuit and network, Chaos Soliton. Fract., 187 (2024), 115361. https://doi.org/10.1016/j.chaos.2024.115361 doi: 10.1016/j.chaos.2024.115361
    [38] M. Sainz-Trapaga, C. Masoller, H. A. Braun, M. T. Huber, Influence of time-delayed feedback in the firing pattern of thermally sensitive neurons, Physical Review E, 70 (2004), 031904. https://doi.org/10.1103/PHYSREVE.70.031904 doi: 10.1103/PHYSREVE.70.031904
    [39] X. J. Wang, G. Buzsáki, Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model, J. Neurosci., 16 (1996), 6402–6413. https://doi.org/10.1186/1471-2202-12-S1-P264 doi: 10.1186/1471-2202-12-S1-P264
    [40] A. L. Hodgkin, A. F. Huxley, Propagation of electrical signals along giant nerve fibres, Proc. R. Soc. B, 140 (1952), 177–183. https://doi.org/10.1098/rspb.1952.0054 doi: 10.1098/rspb.1952.0054
    [41] A. L. Hodgkin, The Croonian Lecture-Ionic movements and electrical activity in giant nerve fibres. Proceedings of the Royal Society of London, Proc. R. Soc. B, 148 (1958), 1–37. https://doi.org/10.1098/rspb.1958.0001 doi: 10.1098/rspb.1958.0001
    [42] R. D. Traub, N. Kopell, A. Bibbig, E. H. Buhl, F. E. LeBeau, M. A. Whittington, Gap junctions between interneuron dendrites can enhance synchrony of gamma oscillations in distributed networks, J. Neurosci., 21 (2001), 9478–9486. https://doi.org/10.1523/JNEUROSCI.21-23-09478.2001 doi: 10.1523/JNEUROSCI.21-23-09478.2001
    [43] M. Bartos, I. Vida, M. Frotscher, A. Meyer, H. Monyer, J. R. Geiger, et al., Fast synaptic inhibition promotes synchronized gamma oscillations in hippocampal interneuron networks, Proc. Natl. Acad. Sci. U. S. A., 99 (2002), 13222–13227. https://doi.org/10.1073/pnas.192233099 doi: 10.1073/pnas.192233099
  • Reader Comments
  • © 2025 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索
AIMS Mathematics
1.8 3.4

Metrics

Article views(175) PDF downloads(41) Cited by(0)

Preview PDF
Download XML
Export Citation
Article outline
Abstract
   Introduction
   Materials and methods
   Results
   Discussion
Author contributions
Acknowledgments
Use of Generative-AI tools declaration
Conflict of interest
References

Figures and Tables

Figures(11)

Other Articles By Authors

Related pages

Tools

Copyright © AIMS Press

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return

Catalog