Finitely generated classes of multi-argument logic functions excluding majority and choice functions

1.   Introduction

The study of closed classes of functions is among the central topics in mathematical logic and algebra ^[1,2,3,4]. Recall that closed classes of functions in logic are sets of functions that remain closed under certain operations ^[5], such as superposition ^[6], and include all functions obtainable from the given class by these operations.

Let $P_k$ be the set of all $k$-valued functions of $n$ variables, where $k \in \mathbb{N}$ and $k \ll \infty$. A closed class $F \subseteq P_k$ is a set of $k$-valued functions with the following property: if $f_1, f_2, \ldots, f_m \in F$, then any function obtained by superposing these functions also belongs to $F$ ^[7,8].

In theoretical investigations, closed classes of functions serve in the study of logic models ^[9] and proof theory ^[10], facilitating the construction and analyzis of various logical inference systems and their properties ^[11].

In modern applications and engineering, closed classes of functions in multi-valued logic support the development of more efficient algorithms and the optimization of computational processes ^[12], as well as the design of more effective integrated circuits ^[13]. An understanding of closed classes enables the creation of circuits that implement required functions using minimal resources ^[14,15]. Moreover, multi-valued logic has significant potential in data transmission systems, particularly in mobile networks, where efficient handling of traffic aggregation and robustness to noise are critical ^[16,17]. The ability to design compact and resilient circuits using closed classes facilitates optimized bandwidth utilization and improved reliability in dynamic network environments, making this approach especially relevant for next-generation communication technologies. The proposed framework also has significant implications for the analyzis of reliability and performance in systems modelled by Markov processes with a discrete number of states ^[18,19]. Multi-valued logic functions, such as those in class $F$, provide a natural foundation for modeling state transitions in discrete stochastic systems.

For example, ternary communication systems, where signals can assume three distinct levels (e.g., $\{0, 1, 2\}$), allow for a 50% increase in data density compared to binary systems. Excluding majority and choice functions in the logical framework of these systems reduces computational overhead and improves resilience to noise during signal transmission. The exclusion of majority and choice functions also has direct implications for quantum communication channels, where maintaining coherence and minimizing computational complexity are paramount. In quantum channels, logical operations such as superposition and entanglement require precise control to minimize decoherence and ensure reliable data transmission ^[20].

A range of modern applications of multivalued logic, including the design of heterogeneous computing systems, is discussed in ^[21]. The authors demonstrate the advantages of ternary logic over binary logic for designing chipsets and circuits, and they also describe a method for constructing a lattice of closed classes in multivalued logic. Recent advancements in multi-valued logic also have significantly expanded its applications, particularly in the context of cellular automata, neural networks ^[22] and deep learning networks ^[23].

A comprehensive study of closed classes in three-valued logic can be found in ^[24], which provides both a theoretical discussion and an overview of modern applications of nonbinary logic.

In particular, the work ^[25] highlights the importance of multi-valued logic in enhancing memory density and simplifying computational circuits. Building upon these ideas, our results complement prior research by introducing and analyzing the class $F$, which allows for the construction of closed sets of functions while avoiding the complexities associated with majority and choice functions.

In this article, we focus on a class of functions $F$ that satisfy a special condition, denoted $0_x$. This class is of particular interest due to its exclusion of both majority and choice functions, which are known for their computational complexity and sensitivity to noise. By proving that $F$ is finitely generated and exploring its structural properties, we extend the theoretical framework of multi-valued logic and provide new insights into the design of robust computational systems.

Before proceeding with the main arguments, we establish the rigorous definitions necessary for a formal treatment of the problem.

Definition 1 (Majority function). A majority function $\mu(x_1, x_2, \ldots, x_n)$ outputs the value that appears most often among its arguments. Formally, for Boolean variables (0 or 1), it is defined as follows:

A majority function takes the value that appears most frequently among its input arguments ^[5].

The majority function $\mu(x_1, x_2, \dots, x_n)$ determines the most frequently occurring value among its input arguments. In the case of Boolean variables (0 or 1), it outputs $1$ if more than half of the inputs are $1$; $0$ otherwise. The term half of $x$ refers to the midpoint of the total number of inputs. Specifically, if there are $n$ input values, then if more than $n/2$ of them are $1$, the majority function returns $1$ if $n$ is even, the majority function may require tie-breaking (depending on the specific definition used).

Table 1 illustrates the operation of the majority function for selected input cases:

To illustrate the majority function with a larger number of input values, consider the following example: $\mu\; (2, 1, 1, 0, 2, 1, 2, 2, 1, 0) = 1.$

Note that if a closed class $F$ in $k$-valued logic contains majority functions, it remains closed under superposition. Specifically, if $\mu$ and $\nu$ are majority functions in $F$, then the function

also belongs to $F$. Proofs of this fact under various special conditions can be found in ^[26,27,28].

Definition 2 (Choice function). A choice function, typically denoted by $\varphi$, assigns to each non-empty subset $Y \subseteq X$ an element from $Y$. Formally:

It is known that the class of choice functions is also closed under superposition in $k$-valued logic ^[29]. Various aspects of this property have been investigated in ^[3,4,30].

Table 2 provides a comparative analyzis of the majority and choice functions, focusing on their formal definitions, computational complexity, expressiveness, robustness to noise, and applications in multi-valued logic.

1.1.   Rationale for excluding majority and choice functions

In this study, a fundamental aspect is the exclusion of majority and choice functions from the proposed function class $F$. This strategy has significant theoretical and practical justifications, particularly in the contexts of multi-valued logic, circuit design, and computational optimization.

Majority functions are widely employed in redundant digital circuits ^[31,32] to enhance system reliability ^[33]. Choice functions, which select a single element from a given set ^[34], form a well-studied class of functions and are also widely used in electronics.

Majority and choice functions play a fundamental role in multi-valued logic; however, they exhibit certain drawbacks ^[35]:

(1) Computational complexity of majority and choice functions

● Majority functions require computing the most frequently occurring value among the input arguments, which leads to an increase in computational cost as the number of inputs grows. For instance, with $n$ inputs, computing the majority value necessitates at least $O(n)$ comparisons, which becomes particularly problematic in parallel and scalable systems ^[32]. Thus, it can increase computational complexity significantly. Determining a majority among many input variables can require extensive resources, which may be impractical for applications with restricted computational capacity ^[36,37].

● Choice functions select a specific value from a given set of inputs based on a predetermined criterion, necessitating additional parameter control and potentially increasing implementation complexity in digital circuits ^[34].

The exclusion of these functions mitigates the necessity for computationally expensive operations in resource-constrained environments such as circuit design and mobile computing systems ^[17,21].

(2) Majority and choice functions exhibit high sensitivity to noise ^[38]; even small perturbations in input values can lead to different outputs, complicating their use in noise-resilient applications such as data transmission ^[39]. This makes them suboptimal for deployment in high-uncertainty environments. Examples include the following:

● Majority functions are prone to errors in response to minor variations in input values. Specifically, when the number of input arguments is large, even small fluctuations in the input data can significantly alter the computed result ^[38].

● Choice functions may yield unstable outputs in the presence of random perturbations, as the selection process depends on minimal variations in the control argument.

In fields such as quantum computing and telecommunications, the high sensitivity of these functions to noise may result in information loss and increased transmission error rates ^[40,41].

(3) Optimization of Circuit Design and Multi-Valued Logic. The exclusion of majority and choice functions leads to substantial simplifications in circuit architecture and logical models:

● In multi-valued logic, superposition operations are simplified, as they do not require handling the computational overhead associated with majority functions.

● In circuit design, eliminating such functions reduces the number of required logic gates, which is particularly crucial for the development of energy-efficient circuits ^[2].

● In multi-valued logical models, this exclusion facilitates the construction of novel function classes that are resilient to perturbations and noise while preserving expressive power ^[25,42].

Thus, the proposed function class $F$ provides an alternative framework for constructing logical systems, avoiding computationally expensive and noise-sensitive functions while retaining the essential properties of multi-valued logic.

(4) Limited Expressiveness of Choice Functions: A choice function merely selects one of the input values based on a control argument, thus limiting the ability to capture intricate dependencies among variables ^[43]. In complex computational circuits, implementing such functions may demand additional logic to handle control parameters, increasing the implementation overhead.

These limitations motivate the exploration of additional function classes and the construction of finite closed classes that circumvent the complexities introduced by majority and choice functions. Over time, research has addressed various specialized function classes, including partial functions ^[44], functions with constants ^[29], unary functions ^[45], partial Sheffer functions ^[46], and classes encompassing all polynomials ^[47], among others ^[27,48].

Building on these approaches, this research introduces a novel function class that provides an alternative framework for logical system construction, avoiding computationally expensive and noise-sensitive functions while preserving key structural properties of multi-valued logic.

It should be noted that while a trivial generating set such as $\{0, \, x_1x_2\}$ may appear sufficient in simple cases, our construction—incorporating the function $g(x_1, x_2, x_3, x_4)$ and auxiliary functions—provides a more comprehensive framework that not only proves the finite generation of $F$ in $k$-valued logic (for $k > 2$) but also reveals richer structural properties. This approach is in contrast to previous methods that required more intricate arguments and further motivates the study of the lattice of subclasses of $F$ as a promising direction for future research.

2.   Research objectives

This study addresses the following research question: can we construct a finitely generated closed class of multi-valued logic functions that excludes majority and choice functions while remaining computationally expressive?

The primary objective of this research is to develop and analyze such a class while ensuring that it retains essential computational properties relevant to multi-valued logic. In particular, we aim to establish a structured framework that explicitly avoids the computational overhead and noise sensitivity associated with majority and choice functions, without compromising the expressiveness of logical systems.

This study rigorously investigates the structural properties of the function class $F$ under the condition $0_x$, demonstrating its finite generation while ensuring the exclusion of majority and choice functions. Our proofs provide a systematic approach to constructing closed classes in multi-valued logic. To achieve this goal, we:

● Formally define the function class $F$ and establish its fundamental properties.

● Prove its closure under composition, projection, and other key operations.

● Demonstrate that $F$ remains expressive enough to support robust computational models despite the exclusion of majority and choice functions.

● Discuss potential applications of $F$ in circuit design, error-resilient computation, and multi-valued logical modeling.

Thus, this research establishes a novel class of functions that offers an alternative foundation for logical systems, mitigating the computational challenges posed by majority and choice functions while preserving the structural integrity and practical utility of multi-valued logic.

2.1.   Structure of the paper

The paper is organized as follows. In Section 3, we present the main theoretical results of our work, introducing the essential definitions and notations required for our analyzis. In Subsection 3.1, we investigate the fundamental properties of the class $F$ and prove that it excludes majority functions and choice functions. Next, in Subsection 3.2, we supply proofs of our principal result, namely, that the class $F$ is generated by a finite set of functions.

Finally, the conclusion summarizes our findings, discusses possible directions for future research, and considers illustrative examples of applications.

3.   Main results

To facilitate the subsequent exposition, let $P_k$ denote the set of all $k$-valued functions of $n$ variables, where $k$ is a fixed natural number. This set includes all functions that can take one of $k$ values for any combination of $n$ variables.

Definition 3 (Condition $0_x$). We say that a function $f(\tilde{x}) : \{0, 1, 2\}^n \to \{0, 1, 2\}$ of $n$ variables satisfies the condition $0_x$ if there exists an index $i$, $1 \leq i \leq n$, such that

regardless of the values of $x_1, \ldots, x_{i-1}, x_{i+1}, \ldots, x_n$.

The Condition $0x$ (Definition 3) imposes a structural restriction on a function $f: \{0, 1, 2\}^n \to \{0, 1, 2\}$ in multi-valued logic. It states that there must be at least one input variable whose value directly determines the function's output under a specific condition.

More precisely, a function satisfies Condition $0x$ if there exists an index $i$ (where $1 \leq i \leq n$) such that setting $x_i = 0$ forces the function output to be $0$, regardless of the values of all other variables. For example, consider a function $f(x_1, x_2, x_3)$ over ternary logic ($\{0, 1, 2\}$):

If we set $x_1 = 0$, the function still depends on $x_2$ and $x_3$, meaning the output is not necessarily.

Remark. Consider first the Boolean case (i.e., $k = 2$). In this setting, the function

where the product is defined in the usual Boolean sense (e.g., $x \cdot y = \min\{x, y\}$ or equivalently logical $\texttt{AND}$), is a natural and sufficient example of a function satisfying the condition $0x$; indeed, if at least one argument is zero, the product is zero. In Boolean logic, such a trivial construction may indeed appear to generate a substantial portion of the class $F$.

However, when we consider $k$-valued logics with $k > 2$ (for example, ternary logic with $k = 3$), the situation becomes more intricate. In these settings, the function

even if defined appropriately (for instance, by interpreting the product as the minimum operation, $x \cdot y = \min\{x, y\}$), generates only a subset of all functions that satisfy the $0x$ condition. This is because, for $k > 2$, there exist functions whose structural complexity cannot be captured by this simple operation alone. In particular, a richer generating set is required to produce the entire class $F$.

This necessity is illustrated by the introduction of the function

which, through its piecewise definition and the incorporation of additional operations, is capable of generating functions with more complex behavior. Such functions are essential to account for the broader variety of functions that satisfy $0x$ in $k$-valued logics for $k > 2$.

Thus, while the product function serves as an instructive example in the Boolean case, it is insufficient in higher-valued logics, motivating the need for an expanded generating set as demonstrated by the construction of $g(x_1, x_2, x_3, x_4)$.

Consider a different function:

In this case, no matter what values $x_2$ and $x_3$ take, setting $x_1 = 0$ immediately forces $g(x_1, x_2, x_3) = 0$. Thus, $g(x_1, x_2, x_3)$ satisfies Condition $0x$ with respect to $x_1$.

The presence of Condition $0x$ may restrict certain function classes, particularly in relation to closure under superposition. In ternary logic circuits, Condition $0x$ can reduce gate complexity by ensuring that some inputs always enforce a predetermined outcome.

Definition 4 (Closed class $F$ with respect to $0_x$). We define the closed class $F \subseteq P_k$ to be the set of all functions in $P_k$ that satisfy the condition $0_x$.

Remark. Example illustrating the nontriviality of condition $0x$. Consider two cases:

(i) Case without condition $0x$ (standard multi-valued logic function): Let $g(x_1, x_2, x_3) = x_1 + x_2 + x_3$ in a ternary logic system $\{0, 1, 2\}$. If $x_1 = 0$, the function still depends on $x_2$ and $x_3$. Thus, $g(0, 1, 2) = 3$, meaning $x_1 = 0$ does not force the function to 0.

(ii) Case with condition $0x$ (restricted function class $F$). Consider:

Here, setting $x_1 = 0$ immediately forces $h(x_1, x_2, x_3) = 0$, regardless of $x_2, x_3$.

This simplifies logical operations and makes function evaluation more predictable in practical implementations.

3.1.   Properties of the class $F$ satisfying the condition $0_x$

Let us now examine the class $F$ of functions satisfying $0_x$ and its fundamental properties, set out in Theorem 1.

Theorem 1. The class $F$ has the following properties:

(i) Closure under superposition: $F = [F]$.

In other words, if $g$ and $h$ are functions in $F$, then any composition of the form $g\bigl(h_1(x), h_2(x), \ldots, h_m(x)\bigr)$ belongs to $F$.

Proof. If $f \in F$, by definition $f$ satisfies $0_x$. Consider any composition of functions from $F$. Let $g$ and $h$ be in $F$, and form the composition $g\bigl(h_1(x), h_2(x), \ldots, h_m(x)\bigr)$. Since each $h_i$ also satisfies $0_x$, whenever any of its arguments is zero, the entire composition remains zero. Therefore, the resulting composition also lies in $F$. □

If $F$ is not closed under superposition, then there exist functions $g, h \in F$ such that $g(h(x)) \notin F$. As a counterexample, we can consider $h(x_1, x_2) = x_1 + x_2$ (modulo 3) and $g(y) = 1$ if $y = 2$, otherwise $g(y) = 0$. Then, we have the following:

However, in that case $g(h(x))$ does not satisfy $0_x$, violating the structure of $F$.

(ii) Exclusion of the constant-1 function: $1 \notin F$.

Proof. The constant function $1$ (which outputs 1 for all inputs) cannot satisfy $0_x$. Indeed, if $x_i = 0$, the output should be zero to meet the condition $0_x$. This is never the case for the constant function $1$. Hence $1 \notin F$. □

The inclusion of $1$ in $F$ would destroy the structural integrity of $0_x$, as compositions involving $1$ would no longer satisfy the condition. See, if $g(x) = 1$ and $h(x) = x$, then the composition $g(h(x)) = 1$ remains 1 for all $x$, contradicting $0_x$.

(iii) Inclusion in the class $T_0$: $F \subseteq T_0$.

Here, $T_0$ is the class of all functions outputting 0 whenever at least one of their variables is 0.

Proof. Since each function in $F$ satisfies $0_x$, for every $f \in F$ there is an index $i$ such that $f(x_1, \ldots, x_{i-1}, 0, x_{i+1}, \ldots, x_n) = 0$. Therefore, every function in $F$ trivially satisfies the broader property of $T_0$, implying $F \subseteq T_0$. □

If $F$ is not contained in $T_0$, this implies the existence of functions in $F$ that do not always output 0 when a single input is set to 0. As an example consider the function $f(x_1, x_2) = x_1 + x_2$ (modulo 3): if $x_1 = 0$, then $f(0, 2) = 2 \neq 0.$ Hence, $f \notin T_0$, meaning $F \not\subseteq T_{0}$ would fail.

(iv) Non-containment of any precomplete class of unary functions

Recall that a precomplete class of unary functions is one to which no further unary function can be added without losing closure ^[28]. This result shows that $F$ does not contain any such precomplete class.

Proof. All known precomplete classes of unary functions contain the constant function 1 (see, for instance, ^[30]). Since $1 \notin F$ (see part 2 of Theorem 1), $F$ cannot contain any precomplete class of unary functions. □

If $F$ contained a precomplete class, then $F$ would necessarily include all possible unary functions, including the constant-1 function. This contradicts $1 \notin F$, thereby rendering the structure of $F$ inconsistent.

These properties, examined within the framework of multi-valued logic, illuminate how the class $F$ interacts with other classes of functions and their compositions.

Although the trivial generating set $\{0, \, x_1x_2\},$ satisfies the $0x$ condition and suffices in the Boolean case ($k = 2$), it is inadequate for $k > 2$. In higher-valued logics, additional generators (e.g., $g(x_1, x_2, x_3, x_4)$) are required to capture the full structural complexity of $F$.

The relationships between $F$ and majority functions or choice functions are captured by the following two theorems (Theorems 2 and 3).

Theorem 2. Let $\mu$ be a majority function. Then $\mu \notin F$.

Proof. Suppose, for contradiction, that a majority function $\mu(x_1, \ldots, x_n)$ with $n \ge 3$ is in $F$. By the property of $F$, there exists an index $i$ such that

independently of the other variables. Now consider the input vector $\tilde{\alpha}$ such that $\alpha_i = 0$ and $\alpha_j = 1$ for all $j \neq i$. Since more than half of the inputs are 1, the majority function should yield $\mu(\tilde{\alpha}) = 1$. However, from the condition $0_x$ it follows that $\mu(\tilde{\alpha}) = 0$. This contradiction shows that $\mu \notin F$. □

Theorem 3. Let $\varphi$ be a choice function. Then $\varphi \notin F$.

Proof. Assume, contrary to our claim, that the choice function $\varphi(y, x_0, \ldots, x_{k-1})$ belongs to $F$. Consequently, there must be a variable such that if it is zero, then $\varphi$ returns zero.

Case 1: The variable is $y$.

Consider the input vector $\tilde{\alpha} = (\alpha_y, \alpha_0, \ldots, \alpha_{k-1})$ with $\alpha_y = 0$ and $\alpha_0 \neq 0$. By the property of $F$, we must have $\varphi(\tilde{\alpha}) = 0$. However, $\varphi$ is supposed to choose one among the inputs $x_i$ according to the index $y$. Since $y = 0$ is not a valid index for non-zero elements, a contradiction arises.

Case 2: The variable is $x_i$ for some $i \in \{0, 1, \ldots, k-1\}$.

Let $\alpha_y = l \neq i$ and $\alpha_i = 0$ but $\alpha_l \neq 0$. Then, by definition, $\varphi(\tilde{\alpha})$ should output $\alpha_l$, since $y = l$. On the other hand, the condition $0_x$ requires that $\varphi(\tilde{\alpha}) = 0$ because one of its inputs ($x_i$) is zero. This is again a contradiction.

Hence, $\varphi \notin F$. □

Thus, the class $F$ does not include key function types such as majority functions or choice functions, underscoring its distinctive structure in the context of multi-valued logic.

3.2.   Finite generation of the class $F$

Theorem 4. The class $F$ is generated by a finite set of functions.

Proof. Define

where $x \cdot y = \min(x, y)$ and $x \lor y = \max(x, y)$.

Next, consider the function $g$ given by

It is straightforward to verify that $g \in F$.

Example: For $k = 3$, the function $g$ specialises to

Observe that the class $F_1 = [F \cup \{1\}]$ contains the majority function $d_3(x_2, x_3, x_4)$ and therefore is generated by a finite set of functions (see ^[49]).

Consequently, we conclude that $F$ is generated by the function $g(x_1, x_2, x_3, x_4)$ together with functions in $F$ that depend on at most nine variables. Hence, $F$ is finitely generated. □

Example:

Consider a function $f$ in the class $F$ that depends on three variables $x_1, x_2,$ and $x_3$. Define

Recall that $x \cdot y = \min(x, y)$ in this multi-valued logic setting.

The function $f$ can be expressed in terms of the previously defined function $g$ and an auxiliary function $h$:

Then

This construction shows that $f$ is generated by $g$ and functions depending on at most nine variables, thereby confirming that the class $F$ is generated by a finite set of functions.

Theorem 5. The class $[F \cup \{1\}]$ is equivalent to $P_k$.

Proof. Consider an arbitrary function

in the class $F$:

where $h(x_2, \ldots, x_{n+1})$ is an arbitrary $n$-variable function in $P_k$. Clearly,

Hence, for any function

we conclude that $p \in [F \cup \{1\}]$. Therefore,

□

This example illustrates a case in which finite generation cannot be directly established by a single sufficient condition from the initial part of this work. However, the method of constant simulation ^[50,51] demonstrates finite generation by relying on the finite generation of $P_k$.

In a similar manner, one can construct $k$ distinct subclasses of $P_k$ satisfying analogous properties.

Definition 5 (Condition $a_x$). We say that a function $f(\tilde{x})$ satisfies the condition $a_x$ (for any $a = 0, 1, \ldots, k - 1$) if there exists an index $i$, $1 \leq i \leq n$, such that when the variable $x_i = a$, then

regardless of the values of the other variables.

Definition 6 (Class $F_a$). We define the closed class $F_a \subseteq P_k$ to be the set of all functions in $P_k$ that satisfy the condition $a_x$.

For any $a \in \{0, 1, \ldots, k-1\}$, the class $F_a$ has the following properties:

(1) $F_a = [F_a].$ This means that $F_a$ is closed under superposition of its functions.

(2) For any $b \in \{0, 1, \ldots, k-1\}$ with $b \neq a$, we have $b \notin F_a$ and $[F_a \cup \{b\}] = P_k.$ In other words, $F_a$ does not contain the constant function $b$, but including this constant function expands $F_a$ to the entire set $P_k$.

(3) $F_a \subset T_a.$ Recall that

and

We show that

Define $f:\{0, 1, \dots, k-1\}^n\to\{0, 1, \dots, k-1\}$ by

with $b\in\{0, 1, \dots, k-1\}$ and $b\neq a$.

(i) We prove that $f\in T_a$: Let $x = (x_1, \dots, x_n)$ satisfy $\exists i\, (x_i = a)$. Then $\#\{i : x_i = a\}\ge 1$ (and is odd in our construction), so

Thus, $x$ satisfies the condition for membership in $T_a$ and hence $f\in T_a$.

(ii) We prove that $f\notin F_a$: Assume, by way of contradiction, that $f\in F_a$. Then

Fix any $(x_1, \dots, x_{j-1}, x_{j+1}, \dots, x_n)$ such that

Then for $x = (x_1, \dots, x_{j-1}, a, x_{j+1}, \dots, x_n)$, we have

which is even. Therefore, by definition, $f(x) = b\neq a$, contradicting the assumption that $f(x) = a$ for all $x$ with $x_j = a$.

Thus, $f\notin F_a$. Since $f\in T_a$ and $f\notin F_a$, we conclude $F_a \subsetneq T_a.$

(4) Let $\mu$ be a majority function. Then $\mu \notin F_a.$ Majority functions produce output values that do not conform to the condition $a_x$, so they cannot lie in $F_a$.

(5) Let $\varphi$ be a choice function. Then $\varphi \notin F_a.$ A choice function cannot satisfy $a_x$ uniformly for all variables, and thus it cannot be in $F_a$.

These properties highlight the distinct character of the classes $F_a$ within the domain of multi-argument logic functions. They also demonstrate the inherent restrictions on incorporating certain function types, such as majority and choice functions, into these classes.

Remarks

It is worth noting that the method of constant simulation mentioned in the proof is a powerful technique for demonstrating the finite generation of function classes that may not meet simpler sufficient conditions. This technique involves constructing functions within a class that simulate constant functions, thereby broadening the class's expressive capabilities.

Furthermore, the consideration of classes $F_a$ for different values of $a$ provides a comprehensive framework for analyzing functions that impose specific value constraints on certain variables. This approach can be especially useful for studying the structural properties of multi-argument logic functions, with applications in digital circuit design and logical inference systems.

Example:

Let us consider a multi-valued logic with $k = 3$. Denote by $P_3$ the class of all 3-valued logical functions. Define a function $h \in P_3$ by $h(x_2, x_3) = x_2 \lor x_3$, where $\lor$ denotes the logical "or" operation in this setting.

Then we define a function $f$ by

Here, $h(x_2, x_3) = x_2 \lor x_3$, and we observe that $f$ assigns its output based on the value of $x_1$.

This shows that $[F \cup \{1\}]$ coincides with $P_k$, illustrating methods to construct closed subclasses of $P_k$ that meet certain algebraic conditions.

The following theorem establishes that for any value $a$ in a multi-valued logic (where each variable can assume one of $k$ distinct values), the function class $F_a$ can be generated by a finite set of functions.

Theorem 6. For every $a \in \{0, 1, \ldots, k-1\}$, the class $F_a$ is generated by a finite set of functions.

Proof. Define the function $g$ as follows:

where

Clearly, $g \in F_a$ as the following cases demonstrate:

- When $x_1 = 0$, the function output is forced to be 0, satisfying Condition $ax$.

- For $x_1 = 1$, the function behaves as the majority function $d_3$, ensuring expressiveness within $F_a$.

- For $x_1 \geq 2$, the function simply outputs $x_1$, preserving closure within $P_k$.

Observe that the class $F_1 = [F \cup \{1\}]$ includes the majority function $d_3(x_2, x_3, x_4)$ and is therefore finitely generated (see, for instance, ^[52]).

Let

where $A_9$ is the set of all functions in $F_1$ that depend on at most nine variables. By a similar theorem for Boolean functions ^[52], we have $F_1 = [A]$.

Now consider an arbitrary function

Without loss of generality, assume $f(0, x_2, \ldots, x_n) = 0$. Let $\varphi$ be a formula over $A$ that represents $f$. Because $f \in F$, we can take

where $B_9(f)$ is the set of all functions in $F$ (depending on at most nine variables) obtained by identifying variables in $f$.

Define the function $h$ by

Clearly, $h \in F$.

Replace every occurrence of the constant $1$ in $\varphi$ by $h(x_1)$. This yields a new formula $\varphi'$ over

where $B \subseteq F$, and $\varphi'$ represents the same function $f$.

For any input $\tilde{\alpha}$ with $\alpha_1 = 0$, we have $h(\alpha_1) = 0 \neq 1$. Noting that $f(0, x_2, \ldots, x_n) = 0$, $h(0) = 0$, and for all $q \in B_9(f)$, $q(0, x_2, \ldots, x_m) = 0$ (for $m \le 9$), it follows that

Hence, $f$ is generated by $g(x_1, x_2, x_3, x_4)$ and functions in $F$ that depend on at most nine variables. Therefore, $F$ (and consequently $F_a$) is generated by a finite set of functions. □

In this way, the class $F_a$ can be finitely generated for any $a$, thus providing a method to construct closed function classes in multi-valued logic that satisfy specific conditions.

Similarly, one can show the finite generation of the classes $F_a \cap F_b$ for any $a, b \in \{0, 1, \ldots, k-1\}$ with $b \neq a$. We can also establish the following theorem regarding the classes $F_a \cap M$ for any $a \in \{0, 1, \ldots, k-1\}$:

Theorem 7. The intersections of the classes $F_a$ and $F_b$, as well as the intersections of the classes $F_a$ with the class $M$, are finitely generated.

Proof. Let $c \in \{0, 1, \ldots, k-1\}$ with $c \neq a$ and $c \neq b$. Then $c \notin F_a \cap F_b$, and we have

Moreover,

□

Example: Consider functions $f \in F_a$ and $g \in F_b$. Define

Proof that $h\in F_a\cap F_b$. Recall that by definition, a function $f$ belongs to $F_a$ if there exists an index $i$ such that

Similarly, a function $g$ belongs to $F_b$ if there exists an index $j$ such that

In our example, the function

satisfies

and

Thus, $h$ meets the conditions required for membership in both $F_a$ and $F_b$, so that $h\in F_a\cap F_b$. □

In conclusion, we present several propositions concerning the intersection of all classes $F_a$. For instance, Proposition 1 shows that the intersection of all classes $F_a$ for $a = 0, 1, \ldots, k-1$ consists of precisely one function: the function that returns its argument $x$. This proposition essentially states that the intersection of all classes $F_a$ (each satisfying Condition $a_x$) consists of only one function, namely the identity function $f(x) = x$.

Let $p(x_1, \dots, x_n)$ be an arbitrary function in $P_k$. By the method of constant simulation, one can construct a formula $\phi(x_1, \dots, x_n)$ using functions from $F$ and the constant function $1$ such that

Thus, every function in $P_k$ can be represented as a superposition of functions from $F \cup \{1\}$, which implies $P_k \subseteq [F \cup \{1\}].$

Proposition 1. Let $P_k$ be the set of all $k$-valued functions of $n$ variables, where $k \in \mathbb{N}$. For any $c \in \{0, 1, \dots, k-1\}$ such that $c \neq a$ and $c \neq b$, we have:

and

Furthermore,

Proof. Each function in $F_a$ satisfies Condition $a_x$, meaning there exists at least one variable index $i$ such that

Similarly, each function in $F_b$ satisfies Condition $b_x$.

If $f \in F_a \cap F_b$, it must satisfy both conditions simultaneously. Thus, setting $x_i = a$ forces $f(x) = a$, and $x_j = b$ forces $f(x) = b$.

If $f$ is to belong to both classes, it must satisfy these conditions for any choice of $i$ and $j$. The only function that satisfies both conditions is the identity function $f(x) = x$, which directly returns its input.

Thus, the intersection:

If $c \neq a$ and $c \neq b$, then a function $f(x) = c$ is constant and does not satisfy Condition $a_x$ or $b_x$, as it does not depend on its inputs. Hence, $c \notin F_a \cap F_b$.

Since $c \notin F_a \cap F_b$, appending $c$ allows us to construct any function in $P_k$. Specifically, once all constants are included, superposition and projection operations can generate all functions in $P_k$.

Thus,

If we include $a$, then

This follows since adding $a$ allows for the function $f(x) = a$ while maintaining closure properties.

Similarly,

□

Consider $k = 3$ (ternary logic: values $0, 1, 2$) and define $F_0$ as the class of functions where setting any variable to $0$ forces output $0$, and $F_1$ as the class of functions where setting any variable to $1$ forces output $1$. A function $f(x)$ belonging to both $F_0$ and $F_1$ must satisfy

The only possible function satisfying both constraints is the identity function $f(x) = x$. Thus:

Proposition 2. For any $b \in \{0, 1, \ldots, k-1\}$ with $b \neq a$, it follows that

where $M$ is the class of monotonic functions in $P_k$.

Recall, that

That is, $M$ is the class of all monotonic functions in $P_k$, meaning that for any two input vectors $x = (x_1, \dots, x_n)$ and $y = (y_1, \dots, y_n)$ satisfying $x_i \le y_i$ for all $i$, we have $f(x) \le f(y)$. This definition ensures that the function $f$ preserves the natural order on $\{0, 1, \dots, k-1\}$.

Proposition 3.

As an example for Proposition 3, consider the identity function $\operatorname{id}(x) = x$. This function lies in the intersection of all classes $F_0, F_1, \ldots, F_{k-1}$ because, for any value $a$, the identity function satisfies the condition $a_x$.

3.3.   Examples, discussion, and mathematical comparison with previously known classes

To illustrate the significance of the proposed function class $F$, we compare it with previously known classes of multi-valued logic functions. Specifically, we analyze their computational complexity and noise sensitivity, demonstrating the advantages of $F$ under Condition $0x$.

3.4.   Monotonic functions and computational complexity

The study by Alekseev ^[27,47] investigates closed classes containing monotonic functions, which are defined as follows:

These functions are widely used in priority-based systems, digital filtering, and logic design. However, they suffer from high computational complexity, requiring at least $O(n)$ comparisons. Additionally, they exhibit high noise sensitivity, as small variations in input values may significantly affect the output.

3.4.1.   Our result (Function class $F$ with condition $0_x$)

Consider the function:

Unlike monotonic functions:

● Computational complexity is reduced to $O(1)$, as the minimum operation requires constant-time evaluation.

● Noise robustness is improved, as small variations in a single input do not cause abrupt changes in the output.

Remark. In formulas (3.3) and (3.6) below, the symbols $+$ and $-$ denote the usual arithmetic operations of addition and subtraction, respectively, performed on the set of truth values (e.g., $\{0, 1, \dots, k-1\}$ for $k$-valued logic). No modular arithmetic is involved in these operations.

Thus, the function class $F$ offers a computationally efficient and noise-resistant alternative to monotonic closed classes.

The studies by Miller and Thornton ^[1,2] analyze multi-valued logic circuits based on majority and choice functions:

These functions are utilized in quantum circuits, signal processing, and coding theory. However:

● Majority function evaluation requires sorting or counting occurrences of values, leading to $O(n)$ complexity.

● Choice function dependency introduces additional control parameters.

● Both functions are highly sensitive to noise, as small perturbations in inputs may drastically change outputs.

Consider the alternative function:

This function:

● Eliminates the need for sorting or counting while preserving key computational properties.

● Reduces computational complexity to $O(1)$.

● Exhibits greater noise robustness, ensuring stability in uncertain environments.

By excluding majority and choice functions, class $F$ provides an efficient alternative for multi-valued logic implementations.

The work of Zhuk ^[26] explores the structure of complete closed classes in multi-valued logic, demonstrating that the inclusion of majority and choice functions significantly increases the structural complexity of closed function classes. The framework developed in this study provides a constructive refinement of Zhuk's results, showing how expressive multi-valued logic functions can be designed without relying on computationally expensive operations. The proposed function class $F$ offers lower computational complexity: $O(1)$ instead of $O(n)$ and improved noise robustness. Thus, the results presented in this work extend and refine previous studies ^[1,26,27,44].

4.   Conclusions

In this work, we investigated the closed class of functions $F$ that satisfy the condition $0_x$. We proved that this class excludes majority functions and choice functions and that it can be generated by a finite set of functions. Our main results include proofs of the closure of the class $F$ under superposition, the impossibility of incorporating the constant function $1$, and the inclusion $F \subseteq T_0$.

Majority and choice functions are well-known examples of function classes that are finite and closed, yet also possess desirable theoretical properties. By contrast, our theorems establish the existence of a finite closed class $F$ comprising other functions that retain significant theoretical attributes while omitting majority and choice functions. This omission is advantageous in contexts where such functions, known for their computational complexity and sensitivity to noise, may be undesirable.

Our findings align with the structural analyzis of order-preserving classes in three-valued logic ^[42] and extend these ideas by considering classes that exclude majority and choice functions. Future research could explore the integration of lattice-based frameworks, as described in ^[42], to further investigate the structural properties of the class $F$ and related function classes in multi-valued logic.

Consequently, the closed class $F$ subject to $0_x$ exhibits compelling properties that may facilitate further research on closed classes of functions in set theory and logic. From a practical viewpoint, this class also has potential applications in designing computational circuits under multi-valued logic, where avoiding majority and choice functions can yield both simpler and more robust implementations.

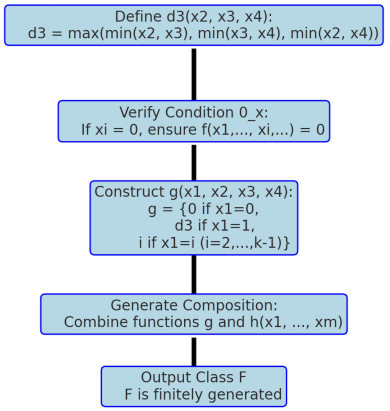
Figure 1 represents the diagram of the algorithmic process for generating functions in the class $F$.

It includes the main steps: 1) Definition of $d_3$: Start with the function $d_3(x_2, x_3, x_4)$ using maximum and minimum operations. 2) Condition $0_x$ verification: Ensure that the functions meet the condition $0_x$ (if any variable is 0, the output is 0). 3) Construction of $g$: Define the function $g(x_1, x_2, x_3, x_4)$ with specific rules depending on $x_1$. 4) Composition construction: Combine functions to form new members of the class $F$. 5) Output Class $F$: Conclude with the finitely generated class $F$.

Algorithm: GENERATE CLOSED CLASS $F$

(I) Initialization:

Define

(b) Initialize the base set $\mathcal{B}$ with projection functions and simple functions that satisfy condition $0_x$.

(c) Define the function $g(x_1, x_2, x_3, x_4)$ as

(d) Add $g$ to $\mathcal{B}$.

(e) Set $\mathcal{F} \gets \mathcal{B}$.

(II) Iterative composition:

(a) Repeat until no new functions are generated:

i. Set $\mathcal{N} \gets \emptyset$.

ii. For every valid composition

with $f, g \in \mathcal{F}$, do:

A. If $h$ satisfies condition $0_x$ and $h \notin \mathcal{F}$, then add $h$ to $\mathcal{N}$.

iii. Update $\mathcal{F} \gets \mathcal{F} \cup \mathcal{N}$.

(III) Termination and output:

(a) Terminate the loop when $\mathcal{N} = \emptyset$ (i.e., no new functions are generated).

(b) Return $\mathcal{F}$ as the closed class $F$.

Notes:

● The function $d_3$ serves as a building block, combining the minimum values of its inputs.

● The function $g$ uses $d_3$ for the case $x_1 = 1$ and ensures that $g(0, x_2, x_3, x_4) = 0$, thereby satisfying condition $0_x$.

● The iterative composition terminates since the number of distinct functions over a finite domain is finite.

Applications in complex systems

The class $F$, characterized by the condition $0_x$, provides intriguing potential applications in the realm of quantum computing. The exclusion of complex functions like majority and choice functions makes $F$ a promising candidate for designing quantum circuits. These circuits often benefit from threshold functions, which can process qubit states with minimal resource overhead while reducing the impact of noise and interactions. Functions from $F$ demonstrate resilience to noise, a critical feature for quantum gates susceptible to decoherence. Threshold-based functions derived from $F$ could contribute to error correction frameworks that utilize multi-valued logic to manage quantum noise more effectively than traditional binary methods.

In the theoretical domain, the class $F$ aligns closely with foundational concepts in quantum mechanics and the mathematics underlying quantum systems:

Multi-valued logic, particularly three-valued logic, provides a natural analogy to quantum states. The values $\{0, 1, 2\}$ can represent projections onto basis vectors in a quantum system. Studying $F$, which respects these projections, could offer new insights into quantum computational models.

The concept of closed classes under superposition mirrors quantum mechanical operators. Investigating how functions in $F$ behave under quantum-like transformations, such as the Hadamard operation, might bridge classical multi-valued logic and quantum computation.

In systems where qubits interact in complex networks, $F$ could serve as a mathematical framework for describing stable states or simplified transitions. This could enhance the design of quantum systems optimized for noise reduction and energy efficiency.

By integrating these ideas, the study of $F$ not only advances multi-valued logic but also paves the way for applications in cutting-edge quantum technologies. Exploring such connections offers a fertile ground for future research, with potential implications for both theoretical advancements and practical implementations in quantum computing.

Future research

The proposed framework for constructing the closed class $F$, characterized by the condition $0_x$, distinguishes itself from alternative methodologies in several key aspects:

● Unlike traditional approaches that rely heavily on the inclusion of majority and choice functions, this work demonstrates that finite closed classes can be constructed effectively while avoiding these computationally intensive functions. This exclusion reduces the complexity associated with these functions, such as sensitivity to noise and implementation overhead.

● The finite generation of $F$ is achieved through the use of a minimal set of functions and elementary operations like superposition. In contrast, many alternative frameworks rely on elaborate structures, such as precomplete classes or extensive sets of initial functions, which may complicate their practical realization.

● The structure of $F$ allows for flexibility in its application, particularly in contexts requiring simplified logical constructs, such as multi-valued circuit design or threshold-based decision systems. By contrast, alternative methods often emphasize theoretical completeness without considering practical constraints.

The proposed approach may potentially give these advantages:

- Computational Efficiency. By excluding functions that are computationally expensive to evaluate, such as majority functions, the proposed framework offers a computationally leaner alternative to traditional closed classes.

- Simplicity of Construction and Scalability. The method leverages straightforward conditions (e.g., $0_x$) and basic logical operations, simplifying the process of constructing the class $F$. This makes the approach accessible and implementable in practical systems. The finite generation property of $F$ ensures that the class remains manageable even as the number of variables increases, a notable improvement over methods requiring exhaustive enumeration of functions.

- Resilience to Noise. The exclusion of majority functions, which are known to be sensitive to input noise, renders the class $F$ suitable for noise-prone environments such as data transmission systems or quantum computing.

This study opens up several promising avenues for future exploration aimed at deepening the theoretical understanding of closed classes in multi-valued logic and broadening their practical applications. Key directions include:

● On the lattice of subclasses of $F$: while the trivial example using the product function illustrates the basic idea of the $0x$ condition, it does not capture the full structural complexity of the class $F$. In fact, constructing the lattice of subclasses of $F$ is an intriguing open problem. A deeper investigation into this lattice is expected to yield novel theoretical insights and practical benefits—for instance, in the optimization of digital circuits. We anticipate that further research in this direction will not only enhance our understanding of multi-valued logic but also contribute to the development of more efficient computational architectures.

● Exploring analogous conditions: A natural extension of this work involves examining closed classes of functions that satisfy conditions similar to $0_x$, but with modifications to accommodate different variable values or configurations. Such investigations could reveal a broader spectrum of functional behaviours and deepen insights into how structural constraints influence the expressiveness and closure properties of function classes. For example, exploring conditions $a_x$ for varying $a$, or even parameterized versions of $0_x$, might illuminate additional theoretical connections and practical applications.

● Applications in complex systems: The class $F$ holds significant potential for application in the design of advanced logical circuits and algorithms. In particular, excluding computationally complex majority and choice functions could lead to more efficient, robust systems capable of operating in environments with noise or limited computational resources. Practical implementations might include fault-tolerant circuit designs, energy-efficient computation, or systems requiring deterministic behavior in uncertain conditions, such as autonomous systems or networked devices.

● Algorithm development: Developing algorithms tailored to generate and optimize closed classes of functions like $F$ represents another fertile area of research. Such algorithms could be geared toward simplifying function representations, improving computational performance, or minimizing resource consumption in hardware implementations. Potential breakthroughs in this area might include heuristic approaches for generating closed classes, as well as optimization techniques to refine existing classes based on application-specific constraints.

● Theoretical applications: Closed classes of functions are indispensable tools in proof theory and logical modeling, where they play a critical role in analyzing inference rules and system properties. Further investigations could assess how the class $F$ contributes to these domains, potentially offering new perspectives on classical logical frameworks. This line of inquiry might also reveal deeper connections between $F$ and well-established constructs in logic, such as modal logics, coalgebraic frameworks, or lattice-based systems.

● Creation of new classes: The construction and study of additional closed classes of functions, particularly those based on constraints analogous to $0_x$, offer a rich area for exploration. These new classes could be designed to address specific challenges in mathematics, theoretical computer science, or applied fields. For instance, studying classes optimized for quantum computing or machine learning algorithms might bridge the gap between abstract logic and cutting-edge technological applications.

By pursuing these directions, researchers have the opportunity to enrich the field of multi-valued logic with novel theoretical constructs while simultaneously driving innovation in practical domains. The intersection of theory and application ensures that this research remains both foundational and impactful, paving the way for a deeper understanding of logic systems and their relevance to modern computational challenges.

Use of AI tools declaration

The author declares Artificial Intelligence (AI) tools were not used in the creation of this article.

Conflict of interest

The author declares that there are no conflicts of interest.