Convergence and quasi-optimality based on an adaptive finite element method for the bilinear optimal control problem

1.   Introduction

Bilinear optimal control problems are types of quintessential optimal control problems governed by a partial differential equation, which investigated in material mechanics, engineering mechanics, and engineering design, etc ^[9,11,22]. Effective numerical methods, such as in ^[1,12,21] for finite element methods, ^[4,5] for spectral Galerkin methods, and ^[6] for fast algorithms, are the key to the successful application of optimal control problems in the practical field. Accordingly, the study of the efficient numerical algorithm for the bilinear optimal control problem has far-reaching theoretical value and application prospects.

The finite element method is frequently applied to solve optimal control problems and uses the thought of mathematical approximation to model the actual physical system. It replaces complex problems with simpler ones by assuming that each element has a suitable, simple approximate solution and then derives a universal satisfaction condition for the solution domain ^[10,23]. Since the actual problem is replaced by a simpler one, this solution is not precise, but approximate. Given that the finite element method has high computational accuracy and can adapt to a variety of complex shapes, it has become an effective engineering analysis method.

Babuška first proposed the adaptive finite element method ^[2]. The adaptive finite element method is an accurate and efficient method of finite element discretization, which saves a lot of calculation time based on ensuring the specified accuracy. Appropriate grids can enormously reduce the errors resulting from the discretization of finite element approximation procedure in copying with an optimal control problem. As the case stands, the solutions for the optimal control problem of the nonlinear system are generally not available. In addition to the complexity and diversity of the nonlinear equations, it is practicable to solve the nonlinear equations with the thought of the adaptive finite element method.

Adaptive finite element methods had popularized for many years, but the theoretical analysis of the entire algorithm has just been actualized. The subject work in the early stage was made by Dörfler ^[13], in which he investigated an adaptive finite element for Poisson's equation by a reduction of energy errors under a mild assumption on the initial grid $\mathcal{T}_{h_0}$. Later, Demlow, Morin, et-al. ^[14,24,25] proved the convergence of adaptive finite element methods without the mild assumption. Then another decisive issue of adaptive finite element methods has been investigated by Binev et al. ^[3]. In the last decades, much work has been done on the concept of total error and the sum of error energy plus oscillations ^[8,12,26]. Recently, Liu and Yan ^[22] found that adaptive finite element methods could be successfully applied in constrained optimal control problems. The later investigations could be found in ^[15,19]. Inspired by these works, Gong and Yan ^[18] investigated the convergence and quasi-optimality of an adaptive finite element for control constrained optimal control problems via applying variation control discretization. Later, Leng and Chen ^[20] studied the convergence of an adaptive finite element method for optimal control problems with integral control constraints.

To proceed, Section 2 next focuses on the bilinear optimal control problem with integral control constraints, which adopt piecewise constant discretization to deal with the control via. For the state and the co-state, by applying continuous piecewise linear discretization, respectively. Section 3 deduce a posteriori error estimate. For the convergence and the quasi-optimality, we prove them relying on quasi-orthogonality and discrete local upper bound. Section 4 based on the mild assumption to the initial grids, obtain the proof of convergence and quasi-optimality employing the solution operator of nonlinear elliptic equations. Section 5 then advances some numerical illustration.

Here are some notations that will be employed in this paper. Let $\Omega$ be a bounded Lipschitz domain on $\mathbb{R}^2$ and $\partial\Omega$ denote the boundary of $\Omega$. We adopt the standard notation $W^{m, q}(\omega)$ for Sobolev space with norm $\|\cdot\|_{m, q, \omega}$ and seminorm $|\cdot|_{m, q, \omega}$. Where $\omega\subset\Omega$, and we will omit the sub description if $\omega = \Omega$. We denote $W^{m, 2}(\Omega)$ by $H^m(\Omega)$ and set $H^1_0(\Omega) = \{v\in H^1(\Omega):v = 0\ \mathrm{on}\ \partial\Omega\}$. For $m = 0 \ \mathrm{and}\ q = 2$, we denote $W^{0, 2}(\omega) = L^2(\omega)$ and set $\|\cdot\|_{0, 2, \omega} = \|\cdot\|_{0, \omega}$. Let $\mathcal{T}_{h_0}$ denote the initial partition of $\bar{\Omega}$ into disjoint triangles. By newest-vertex bisections for $\mathcal{T}_{h_0}$, we obtain a class $\mathbb{T}$ of conforming partitions. For $\mathcal{T}_h, \tilde{\mathcal{T}}_h \in \mathbb{T}$, we use $\mathcal{T}_h\subset\mathcal{\tilde{T}}_h$ to indicate that $\tilde{\mathcal{T}}_h$ is a refinement of $\mathcal{T}_h$, where $h_{T} = |T|^{1/2}$. Denote the $L^2$ inner product by $(\cdot, \cdot)$, and let $C$ be a constant independent of grids size.

2.   A residual-based posteriori error estimates

In this paper, we focus our attention on the following bilinear convex optimal control problem:

where $\Omega$ and $\Omega_U$ are bounded open sets in $\mathbb{R}^2$ with a Lipschitz boundary $\partial\Omega$ and $\partial\Omega_U$. Let $f\in L^2(\Omega)$, and $U_{ad}$ be a closed convex set defined as follows

We take the state space $V = H_0^1(\Omega)$, the control space $U = L^2(\Omega_U)$, and $H = L^2(\Omega)$ to determine the concept of finite element approximation for our discussion with the bilinear optimal control problems (2.1)-(2.2). We first give a weak formula for the state equation

We set a norm $||v||_a = \sqrt{a(v, v)}$, which is equivalent to $||v||_1$. Exist constants $c$ and $C$ that satisfies

Then the bilinear optimal control problem (2.1)-(2.2) can be restated as

It is well known that the optimal control problem (2.4)-(2.5) has a solution $(y, u)$ which was proved in the Theorem 2.2.4 of ^[22], and that if a pair $(y, u)$ is the solution of (2.4)-(2.5), then there exist a costate $p\in V$ such that the triplet $(y, u, p)$ satisfies the following optimality conditions:

For (2.6), since the coercivity of $a(\cdot, \cdot)$, and we set a operator $S:L^2(\Omega)\rightarrow H_{0}^1(\Omega)$ such that $Su = y$. For (2.7), let $S^*$ be the adjoint operator of $S$, we assume that $y-y_d$ is given, such that $S^*(y-y_{d}) = p$. Let $V_h$ be the continuous piecewise linear finite element space for the partition $\mathcal{T}_h\in \mathbb{T}$. We define $U^h$ as the piecewise constant finite element space of $\mathcal{T}_h$. Set $U_{ad}^h = \{v_h\in U^h:\int_{\Omega}v_h\geq 0\}$, then we derive the standard finite element discretization for the bilinear optimal control problem

It is well known that the optimal control problem (2.9)-(2.10) has a solution $(y_h, u_h)$ and that if a pair $(y_h, u_h)\in V_h\times U_{ad}^h$ is the solution of (2.9)-(2.10), then there is a co-state $p_h\in V_h$ such that the triplet $(y_h, u_h, p_h)$ satisfies the following optimality conditions

Similarly, we set a operator $S_{h}$: $U_{ad}^{h} \; \rightarrow \; V_{h}$ such that $Su_{h} = y_{h}$. Let $S_{h}^*$ be the adjoint operator of $S_{h}$ such that $S_{h}^*(y_{h}-y_{d}) = p_{h}$. Let us now introduce some error indicators which we will frequently use in this paper, namely the error $\eta(\cdot)$ and oscillation $osc(\cdot)$. For $\mathcal{T}_h\in \mathbb{T}, \ T\in \mathcal{T}_h$, that are defined by:

where $u_{h}\in U_{ad}^{h}$ and $y_{h}, p_{h}\in V_{h}$, $f_{T}$ is $L^2$-projection of $f$ onto piecewise constant space on $T$ and $f_T = \frac{\int_Tf}{|T|}$. For $\omega\subset \mathcal{T}_h$, such that

Similarly, $\eta_{2, \mathcal{T}_h}^2(u_{h}, y_{h}, \omega), \ \eta_{3, \mathcal{T}_h}^2(u_{h}, y_{h}, \omega)$ and $osc^2_{\mathcal{T}_h}(y_{h}-y_{d}, \omega)$ can be denoted as well.

Before we discuss residual-based posteriori error estimates for the bilinear optimal control problem, we introduce the well-known result for the integral averaging operator ^[12].

Lemma 2.1. Let $\pi_h^a:L^1(\Omega_U)\rightarrow U^h\subset U$ be the integral averaging operator such that

Then for $m = 0, 1$ and $1\leq q\leq\infty$, here

We next discuss the residual-based posteriori error estimates for the bilinear optimal control problem. Moreover, we introduce the following auxiliary problems

Here we state the theorem about a posteriori error estimates.

Theorem 2.1. Let $(y, u, p)\in H_0^1(\Omega) \times U_{ad}\times H_0^1(\Omega)$ be the solution of problems (2.6)-(2.8), and $(y_h, u_h, p_h)\in V_h\times U_{ad}^h\times V_h$ be the solution of problems (2.11)-(2.13). Then exist constants $c$ and $C$ holds

and

Proof. By applying Lemma 2.1, we infer that

where $\pi_h$ is the $L^2-$projection operator onto piecewise constant space on $\mathcal{T}_h$. Therefore, it follows from Theorem 3.1 of ^[16], we derive that

Assume that $e^p = p^h-p_h$, and $e_I^p = \hat{\pi}_he^p$, where $\hat{\pi}_h$ is the average interpolation operator defined in Lemma 3.2 of ^[17], then we obtain

where $||v||_{0, 4}\leq C||v||_1$ is defined in the embedding theorem of ^[7], and the property $||v||_1\leq C$. Then, let $\sigma = \frac{c}{2C}$, we obtain

Similarly, let $e^y = y^h-y_h$, and $e_I^y$ be the average interpolation of $e^y$. It follows from (2.11) and (2.15) that

Thus, it holds that

Note that

Hence, (2.17) follows from (2.19)-(2.21) and (2.22)-(2.24).

To derive the a posteriori lower error bounds for the optimal control problems governed by bilinear elliptic equations we use the standard bubble function technique (see ^[1,17,27]). Let $b_T$ be the standard third order polynomial bubble on $T$ scaled with $b_T = \lambda_1\lambda_2\lambda_3$. We denote by $\{\lambda_1, \lambda_2, \lambda_3\}$ the barycentric coordinates of $T$. Due to $y_h$ is piecewise linear, we set

where $c_1 = \frac{\int_Tb_T^2}{|T|}$ denotes a positive constant, here

Then there holds $\lambda_1\lambda_2\lambda_3 = 0$ on $\partial T$, and satisfies

Moreover, we obtain

thus we can conclude that $w_T\in H^2_0(T)$. Using the results from ^[1,27], we derive that

We set $\hat{T}$ be a reference element, and $\hat{X} = F_T(X) = X+b_T$ be an affine map from $T$ onto $\hat{T}$, we also set $\hat{w} = w\circ F_T^{-1}(\hat{X})$. Thus we conclude that

Where $w_T\in H^2_0(T)$, we obtain that $\hat{w}_T\in H^2_0(\hat{T})$. Using the Poincare's inequality, we deduce the results below

such that

Thus we can obtain that

Then use of bubble function $w_T$ with (2.25) yields

We set $u_hp_h-up = u_h(p_h-p)+(u_h-u)p$, such that

Then by using the Schwarz's inequality, it follows from (2.25) that

assume that $up-u_hp_h = (u-u_h)p+u_h(p-p_h)$. Then there holds

Applying (2.26)-(2.27) and the Poincare's inequality, we obtain

Similarly, we also derive that

Combining Lemma 3.6 of ^[17], we can derive the same result for bilinear elliptic equations

From Lemma 2.1, we infer that

Then using the inverse estimates to infer that

and hence, (2.18) follows from (2.28)-(2.30).

Theorem 2.1 gives reliable and efficient posteriori error estimates. Now we introduce an adaptive finite element algorithm to explain what we mainly investigate in this paper.

Algorithm 2.1. Adaptive finite element algorithm for bilinear optimal control problems:

(0) Given an initial mesh $\mathcal{T}_{h_0}$ and construct finite element space $U_{ad}^{h_0}$ and $V_{h_0}$. Select marking parameter $0 < \theta\leq 1$ and set $k: = 0$.

(1) Solve the discrete bilinear optimal control problem (2.11)-(2.13), then obtain an approximate solution $(y_{h_k}, u_{h_k}, p_{h_k})$ with respect to $\mathcal{T}_{h_k}$.

(2) Compute the local error estimator $\eta_{\mathcal{T}_{h_k}}(T)$ for all $T\in\mathcal{T}_{h_k}$.

(3) Select a minimal subset $\mathcal{M}_{h_k}$ of $\mathcal{T}_{h_k}$ such that

where $\eta_{\mathcal{T}_{h_k}}^2(\omega) = \eta_{1, \mathcal{T}_h}^2(p_h, \omega)+ \eta_{2, \mathcal{T}_h}^2(u_{h}, y_{h}, \omega)+\eta_{3, \mathcal{T}_h}^2(y_{h}, p_{h}, \omega)$ for all $\omega\subset\mathcal{T}_{h_k}$.

(4) Refine $\mathcal{M}_{h_k}$ by bisecting $b\geq 1$ times in passing from $\mathcal{T}_{h_k}$ to $\mathcal{T}_{h_{k+1}}$ and generally additional elements are refined in the process in order to ensure that $\mathcal{T}_{h_{k+1}}$ is conforming.

(5) Solve the discrete bilinear optimal control problem (2.11)-(2.13), then obtain approximate solution $(y_{h_{k+1}}, u_{h_{k+1}}, p_{h_{k+1}})$ with respect to $\mathcal{T}_{h_{k+1}}$.

(6) Set $k = k+1$ and go to step (2).

3.   Convergence analysis

In this section, we first introduce the relevant theorem of reference ^[24], where the authors construct a simple and efficient adaptive finite element methods to ensure a reduction rate of data oscillation, together with an error reduction based on a posteriori error estimators. In addition, we introduce the internal node properties and mark the data oscillations. To derive the residual-type posterior error estimates ^[21], we employ the lemmas as follows.

Lemma 3.1. For all $v\in H^1(\Omega)$, $T_h\in\mathbb{T}, T\in\mathcal{T}_h$, there exists

Here we state the following local perturbation property.

Lemma 3.2. For $\mathcal{T}_h\in \mathbb{T}, \ T\in \mathcal{T}_h$, let $u_{h_1}, u_{h_2}\in U_{ad}^h, \ y_{h_1}, y_{h_2}, p_{h_1}, p_{h_2}\in V_{h}$, we have

Proof. We only give the proof of (3.1) because of the proofs of (3.1), (3.3)-(3.4) are similar. By the definition of $\eta_{2, \mathcal{T}_h}(u_h, y_h, T)$, we deduce that

With the help of inverse estimates and Lemma 3.1, we infer that

Therefore (3.2) follows from (3.5)-(3.6).

By using the similar method with ^[24], we prove the following result.

Lemma 3.3. Let $\mathcal{T}_h\subset\tilde{\mathcal{T}_h}$ for $\mathcal{T}_h, \tilde{\mathcal{T}}_h\in\mathbb{T}. \mathcal{M}_h\subset\mathcal{T}_h$ denotes the set of elements which are marked from $\mathcal{T}_h$ to $\tilde{\mathcal{T}}_h$. Then for $u_h\in U_{ad}^h, \ \tilde{u}_h \in U_{ad}^{\tilde{h}}, \ y_h, p_h\in V_{h}, \ \tilde{y}_h, \tilde{p}_h\in V_{\tilde{h}}$ and any $\delta, \delta_{1}\in(0, 1]$, we have

and

and

and

where $\lambda = 1-2^{-\frac{b}{2}}, \ h_{0} = \max\limits_{{T\in \mathcal{T}_{h_{0}}}}h_{T}$ and $\mathcal{R}_h$ denotes the set of elements which are refined from $\mathcal{T}_h$ to $\tilde{\mathcal{T}}_h$.

Proof. We only give the proof of (3.7)-(3.8) and (3.10) owing to the proof of (3.9) can be prove with (3.8) similarly. From (3.1) of Lemma 3.2, then combining with the Young's inequality yield

Note for $T\in\mathcal{R}_h\subset\mathcal{T}_h$ that $T$ will be bisected at least one time, it holds that

For $T\in\mathcal{T}_h\backslash\mathcal{R}_h$, we obtain

Thus we can conclude that

Hence, (3.7) follows from (3.11)-(3.12).

From Lemma 3.2 and the Young's inequality with parameter $\delta$, we deduce that

Given a marked element $T'\in \mathcal{M}_h$, let $\tilde{\mathcal{T}}_{T'} = \{T\in\tilde{\mathcal{T}}_h:T\subset T'\}$. For $y_h\in V_h\subset V_{\tilde{h}}$, we derive the jump $[\nabla y_h] = 0$ on the interior sides of $\cup\tilde{\mathcal{T}}_{T'}$. Let $b$ be the number of bisections, it implies $h_T = |T|^2\leq(2^{-b}|T'|)^{1/2}\leq2^{-b/2}h_{T'}$, and then it holds that

When $T\in\mathcal{T}_h\backslash\mathcal{M}_h$, we check that

Thus we conclude that

And hence, (3.8) follows from (3.13)-(3.14).

It is obviously that for $T\in\mathcal{T}_h\cap\tilde{\mathcal{T}}_h$, such that

From (3.4) of Lemma 3.2 and the Young's inequality, such that

Brings (3.15) into (3.16), we conclude that (3.10) follows from summing over $T\in\mathcal{T}_h\cap\tilde{\mathcal{T}}_h$ for (3.16).

One difficulty in the proof of the convergence is lack of the orthogonality, thus we have to prove the quasi-orthogonality. We introduce the following fundamental relationships for $\mathcal{T}_{h_i}$, where $\mathcal{T}_{h_{i+1}}\in\mathbb{T}$, $\mathcal{T}_{h_i}\subset\mathcal{T}_{h_{i+1}}$, such that

where $(y, u, p)$ are the solution of (2.6)-(2.8), $(y_{h_i}, u_{h_i}, p_{h_i})$ and $(y_{h_{i+1}}, u_{h_{i+1}}, p_{h_{i+1}})$ are the solution of (2.11)-(2.13) with respect to $\mathcal{T}_{h_i}$ and $\mathcal{T}_{h_{i+1}}$, respectively.

Lemma 3.4. For $\mathcal{T}_{h_i}, \mathcal{T}_{h_{i+1}}\in\mathbb{T}$ and $\mathcal{T}_{h_i}\subset\mathcal{T}_{h_{i+1}}$, such that

and

and

we follow the idea of ^[28] to introduce the quantity $\mathcal{J}^2(h)$ that

Proof. For $\mathcal{T}_{h_{i+1}}$ and from (2.8), we obtain

For $U_{ad}^{h_{i}}\subset U_{ad}^{h_{i+1}}$ and from (3.23), such that

Next, we divide (3.24) into three parts to prove. Firstly, Let $\pi_{h_i}$ be the $L^2-$projection onto $U_{ad}^{h_i}$, then for $T\in\mathcal{T}_{h_i}\cap\mathcal{T}_{h_{i+1}}$, we obtain

Thus we infer that

we denote $\mathcal{R}_h$ be the set of elements that are refined from $\mathcal{T}_{h_i}$ to $\mathcal{T}_{h_{i+1}}$. It follows from the definition of $S_{h}$, there exists

Let $\phi\in H_0^1(\Omega)$ be the solution of the following problem

Thus we obtain that

we denote $\phi_{h_i}$ the standard finite element estimate of $\phi_h$ with respect to $V_{h_i}$. It follows from Proposition 2.1 of ^[18] that for $V_{h_i}\subset V_{h_{i+1}}$

and

and

From Lemma 3.6 of ^[12], we obtain

Then let $\varphi_h\in H_0^1(\Omega)$ be the solution of the following problem

With the help of the standard duality argument, we infer that

where $\varphi_{h_i}$ is the standard finite element estimate of $\varphi_h$ with respect to $V_{\mathcal{T}_{h_i}}$. Then combining with (3.26)-(3.33), there holds that

One easily sees that

Hence, (3.20) follows from (3.17), (3.24), and (3.34)-(3.35).

In order to prove (3.21), we have to provide the following

Thus we conclude that (3.21) follows from (3.18), (3.25), and (3.35)-(3.36).

Now we will give the proof of (3.22).

It is similar to (3.36) yields

Hence, (3.22) follows from (3.19), (3.25), and (3.37)-(3.38).

For $\mathcal{T}_{h_i}\in \mathbb{T}$, we denote $U_{ad}^{h_{i}}, \ V_{h_{i}}$ and the solution $(y_{h_{i}}, u_{h_{i}}, p_{h_{i}})$ of (2.11)-(2.13) with respect to $\mathcal{T}_{h_{i}}$. Then we define the following notations that

We now proceed to prove the contraction of the Algorithm 2.1.

Theorem 3.1. Let $(y, u, p)\in H_0^1(\Omega)\times U_{ad}\times H_0^1(\Omega)$ be the solution of (2.5)-(2.7) and $(y_h, u_h, p_h)\in V_h\times U_{ad}^h\times V_h$ be the solution of (2.10)-(2.12) generated by the adaptive finite element algorithm 1. There exist $\gamma_1 > 0, \ \gamma_2 > 0$ and $\alpha\in(0, 1]$ depending only on the shape of regularity of initial $\mathcal{T}_{h_{0}}$, $b$, $\Omega$ and the marking parameter $\theta\in(0, 1]$ such that

where $h_0$ sufficiently small, and $h_0 \; <$ 1.

Proof. By Theorem 2.1, Lemma 3.3 and Lemma 3.3 yields

where $\mathcal{R}_{h_{i}}$ denote the set of elements which are refined from $\mathcal{T}_{h_{i}}$ to $\mathcal{T}_{h_{i+1}}$. Combining with the upper bound of Theorem 2.1, then choosing parameters $\tilde{\gamma}_1, \tilde{\gamma}_2$, we obtain

We choose

Then we find that

where $c = \min\{\tilde{\gamma}_1(1+\delta_1)(1-2^{-1/2})-C\delta^{-1}, \tilde{\gamma}_2C(2+\delta^{-1})\}$. Then choosing $\beta\in(0, 1)$ and using the marking strategy of Algorithm 2.1 and Theorem 2.1, we derive that

One easily sees that

where

By choosing sufficiently small $\delta < 1$ and $\beta$ such that $\alpha_1\in(0, 1)$. As long as (3.48)-(3.49) are slightly deformed, and combining with (3.44), when $h_0\ll1$ and $\delta_1, \delta$ small enough, we can conclude that

Choosing $\alpha = \max\{\alpha_1, \alpha_2, \alpha_3\},$ and then (3.39) complete the rest of the proof.

4.   Quasi-optimality analysis

In this section, we consider the quasi-optimality for the adaptive finite element method. Firstly we introduce some interpretation of the notations. For $\mathcal{T}_h, \mathcal{T}_{h_1}, \mathcal{T}_{h_2}\in \mathbb{T}$, with the assumption that $\#\mathcal{T}_h$ be the number of elements in $\mathcal{T}_h$, we also set $\mathcal{T}_{h_1}\oplus\mathcal{T}_{h_2}$ be the smallest common conforming refinement of $\mathcal{T}_{h_1}$ and $\mathcal{T}_{h_2}$ ^[12,26], such that

According to ^[20], a function approximation class is defined by

where

and

A localized upper bound will be given in the following lemmas, which play an important role in proving the qusi-optimality for an adaptive finite element method.

Lemma 4.1. For $\mathcal{T}_h, \tilde{\mathcal{T}}_h\in \mathbb{T}$, and $\mathcal{T}_h\subset\tilde{\mathcal{T}}_h$, let $\mathcal{R}_h$ be the set of refined elements from $\mathcal{T}_h$ to $\tilde{\mathcal{T}}_h$. Let $(y_{h}, u_{h}, p_{h})$ and $(\tilde{y}_h, \tilde{u}_h, \tilde{p}_h)$ be the solutions of (2.11)$-$(2.13) with respect to $\mathcal{T}_h$ and $\tilde{\mathcal{T}}_h$, respectively. Then there exists a constant $C$, depending on the shape regularity of initial grids $\mathcal{T}_{h_{0}}$ and $b$ such that

where

Proof. From (3.26)-(3.27) and (3.34)-(3.35), we obtain

By using the results of Lemma 3.6 (see ^[12]), we derive that

Then, it holds that

And thus we conclude that (4.2) follows from (4.3)-(4.5).

In the following lemma, we list the error indicators on the coarse grids that must satisfy a Dörfler property on the refinement one.

Lemma 4.2. Assume that the marking parameter $\theta\in(0, \theta^*)$, where

For $\mathcal{T}_h, \tilde{\mathcal{T}}_h\in\mathbb{T}$ and $\mathcal{T}_h\subset\tilde{\mathcal{T}}_h$, let $(y_{h}, u_{h}, p_{h})$ and $(\tilde{y}_{h}, \tilde{u}_{h}, \tilde{p}_{h})$ be the solutions of (2.11)-(2.13) with respect to $\mathcal{T}_h$ and $\tilde{\mathcal{T}}_h$, respectively. If

is satisfied for $\mu: = \frac{1}{2}\Big(1-\frac{\theta}{\theta^*}\Big)$. Then, the set $\mathcal{R}_h$ of elements which are refined from $\mathcal{T}_h$ to $\tilde{\mathcal{T}}_h$ satisfies the Döfler property

where

for $\omega\subset\mathcal{T}_h$ and $e_{\tilde{\mathcal{T}}_h}^2$, $osc_{\tilde{\mathcal{T}}_h}^2(\tilde{\mathcal{T}}_h)$ similarly to define.

Proof. From (4.6) and Theorem 2.1, we derive

Applications of the triangle inequality yields

Thus, from (4.2), we obtain

From (3.10), for $T\in\mathcal{T}_h\cap\tilde{\mathcal{T}}_h$, it is easy to see that

According to Remark 2.1 of ^[12], there holds for $T\in\mathcal{R}_h$

By adopting (4.7)-(4.9), there holds

where

The following Lemma is essential to prove the quasi-optimality.

Lemma 4.3. Let $(y, u, p)$ and $(\mathcal{T}_{h_i}, U_{ad}^{h_i}, V_{h_i}, y_{h_i}, u_{h_i}, p_{h_i})$ be the solution of (2.6)-(2.8) and the sequence of grids, finite element spaces and discrete solutions produced by Algorithm 2.1, respectively. Assume that the marking parameter $\theta$ satisfies the condition in Lemma 4.2, then the following estimate is valid

if $(u, y, p, y_{d}, f)\in \mathcal{A}^s$.

Proof. Let $\epsilon: = \mu C_1^{-1}(\eta_{\mathcal{T}_{h_i}}^2+osc_{\mathcal{T}_{h_{i}}}^2(\mathcal{T}_{h_{i}}))$, where $C_1$ shall be produced in (4.13). Due to $(u_h, y, p, y_{d}, f)\in\mathcal{A}^s$, then there exists a $\mathcal{T}_{h_\epsilon}\in\mathbb{T}$ and $(y_\epsilon, u_\epsilon, p_\epsilon)\in U_{ad}^{h_\epsilon}\times V_{h\epsilon}\times V_{h_\epsilon}$ such that

Let $(y_*, u_*, p_*)$ be the solution of (2.6)-(2.8) with respect $\mathcal{T}_{h_*} = \mathcal{T}_{h_\epsilon}\oplus\mathcal{T}_{h_i}$ which is the smallest common refinement of $\mathcal{T}_{h_\epsilon}$ and $\mathcal{T}_{h_i}$. Next, we first prove the following estimate

where

Combining with the Young's inequality yield

Note that there holds the similar result to $a(y-y_*, y_*-y_\epsilon)$ and $a(p-p_*, p_*-p_\epsilon)$. Thus combining with (3.17)-(3.19) and (4.14), we find that

From (3.10) with $\mathcal{T}_{h} = \tilde{\mathcal{T}}_{h} = \mathcal{T}_{h_*}$ and $y_h = y_*$, $\tilde{y}_h = y_\epsilon$, such that

For $T'\in\mathcal{T}_{h_\epsilon}$, let $\mathcal{T}_{T'}: = \{T\in\mathcal{T}_{h_*}:T\in T'\}$. There holds

Hence,

And thus we conclude that (4.13) follows from (4.15)-(4.17). Then combining with (4.12), we find that

Note that $\mathcal{R}_{h}$, which is the set of refinement elements from $\mathcal{T}_{h_i}$ to $\mathcal{T}_{h_*}$, it satisfies the marking property of Lemma 4.2 that

Thus we find that (4.10) follows from (4.11) and (4.19).

The following theorem describes the quasi-optimality of an adaptive finite element method.

Theorem 4.1. Let $(y, u, p)$ and $(\mathcal{T}_{h_i}, U_{ad}^{h_i}, V_{h_i}, y_{h_i}, u_{h_i}, p_{h_i})$ be the solution of (2.6)-(2.8). Where the sequence of grids, finite element spaces, and discrete solutions produced by Algorithm 2.1, respectively. Assume that $\mathcal{T}_{h_0}$ satisfies the condition (b) of Section 4 (see ^[3]). Let $(u, y, p, y_{d}, f)\in \mathcal{A}_{s}$, then there holds

provided $h_{0}\ll 1$.

Proof. According to Lemma 2.3 of ^[12], we derive that

Combining (4.21) with Lemma 4.3 leads to

where

An application of Theorem 2.1, such that

Thus we conclude that (4.20) follows from (4.22)-(4.23).

5.   Numerical examples

In this section, we are going to use the following iterations to solve the bilinear optimal control problem numerically.

Algorithm 5.1. It follows from linear optimal control problems, there exist similar algorithms in the reference ^[20], we define the following Algorithm 5.1 based on the bilinear optimal control problem:

Given an initial control $u_h^0\in U_{ad}^{h}$, then substitute it into (5.1) yields $y_{h}^1$. And then substitute $y_{h}^1$ into (5.2) yields $p_{h}^1$. At last, substitute $p_{h}^1$ into (5.3) yields $u_{h}^1$. Repeat the above step, we can solve $(y_h^k, p_h^k, u_h^k)$, for $k = 1, 2, \cdots$, it holds that

where $\mathcal{P}_h$ is the $L^2$-projection from $L^2(\Omega)$ to $U^h$ and $\bar{p}_h^k = \frac{\int_\Omega p_h^k}{|\Omega|}$.

For ease of analysis the solution of bilinear optimal control problem we constructing examples as follows.

Example 1. The first example is a bilinear optimal control problem, we set state equation on $\Omega = (0, 1)^2$, and $\alpha = 0.5$. We take the exact solution as

In Example 1, the state and co-state are approximated by the piecewise linear elements, while piecewise constant elements are used to approximate the control. We compute Example 1 on an adaptive grid and a uniform grid respectively.

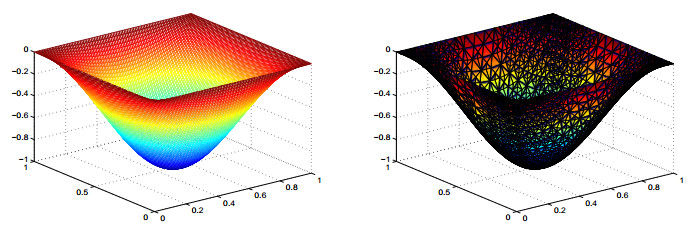
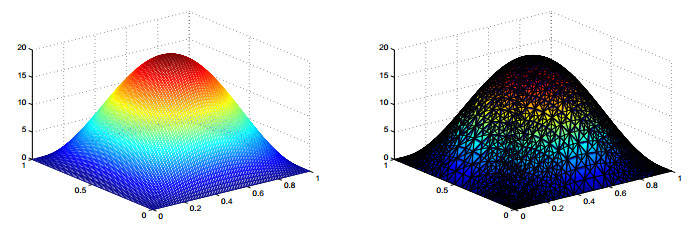
In Figure 1, we plot the profiles of the exact state and the numerical state on adaptive refinement grid with $\theta = 0.3$ and 21 adaptive loops. We plot the profiles of the co-exact state variables and the co-numerical state variables on adaptive refinement grid with $\theta = 0.3$ and 21 adaptive loops in Figure 2 as well. Connecting with Figure 1 and Figure 2, we find that although the solution of Example 1 is smooth, larger gradients can be observed in certain areas. Accordingly, the adaptive finite element method may obtain a much smaller error compared to the uniform refinement.

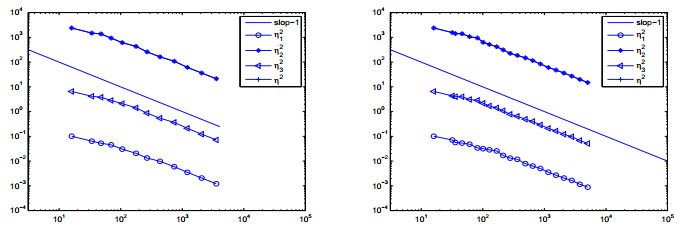
We show the comparisons of convergence history of the errors on adaptively grids with $\theta = 0.3$ and uniformly refined grids with $\theta = 1$ in Figure 3. We can observe $\eta^2$ is approximately parallel to the line slop $-1$ which is the optimal convergence rate we expected by using linear finite elements. This situation confirms the theoretic results in Section 4. But in this example, the solutions of the optimal control are quite smooth. Here is little difference in the convergence history of the errors compared to uniform refinement.

Example 2. In the second example, we choose $\alpha = 0.3$ with the exact solutions on $\Omega = (0, 1)^2$

where $s(x_1, x_2) = (x_1-0.2)^2+(x_2-0.6)^2-0.04$.

Similarly, the state and co-state are approximated by the piecewise linear elements, while piecewise constant elements are used to approximate the control. We compute Example 2 on an adaptive grid and a uniform grid respectively.

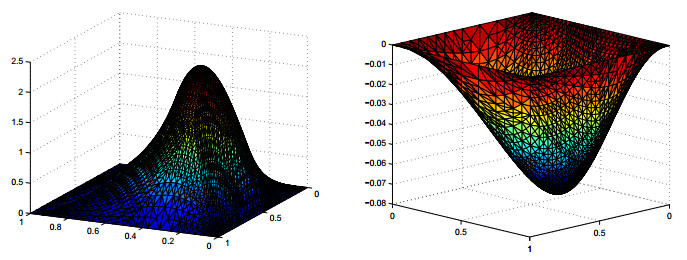
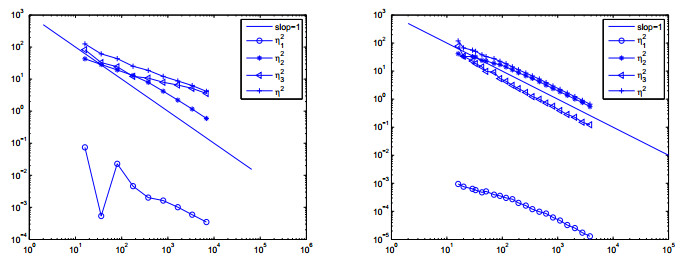
In Figure 4, we plot the profiles of the numerical state and the numerical co-state on 21 adaptive loops with $\theta = 0.3$ for Example 2, both the numerical state and the numerical co-state can be seen in the singularities around the peak. Further, the grids are concentrated at the peak. In Figure 5, we show the convergence history of the estimators. We can see $\eta^2$ is approximately parallel to slop $-1$. From the figure, it is easy to see that the second-order convergence for the reduction of error estimators for the adaptively refined grids. In Example ref{exm2}, the optimal control is not smooth so that there is much difference in using either the uniform or adaptive grids to approximate the control.

Acknowledgments

This work is supported by National Science Foundation of China (11201510), National Social Science Fund of China (19BGL190), China Postdoctoral Science Foundation (2017T100155, 2015M580197), Innovation Team Building at Institutions of Higher Education in Chongqing (CXTDX201601035), Chongqing Research Program of Basic Research and Frontier Technology (cstc2019jcyj-msxmX0280) and Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJZD-K202001201), Youth Innovative Talents Project (Natural Science) of research on humanities and social sciences in Guangdong normal university (2017KQNCX265), Hunan Provincial Education Department of China (18C0196).

Conflict of interest

The authors declare no conflict of interest.