Global dynamics of a cytokine-enhanced viral infection model with distributed delays and optimal control analysis

1.   Introduction

Acquired Immunodeficiency Syndrome (AIDS), a life-threatening condition caused by human immunodeficiency virus (HIV) infection, remains a major global health challenge with significant mortality rates. As a retrovirus, HIV primarily infects cells expressing the ${\rm CD4}$ receptor, notably ${\rm CD4}^+$ T helper lymphocytes—a key component in regulating immune responses. During disease progression, HIV-infected individuals experience a gradual decline in ${\rm CD4}^+$ T cell counts. Clinically, the transition to AIDS is defined when ${\rm CD4}^+$ T cell counts decline below ${\rm 200}$ cells$/$ul, marking severe immunodeficiency and increased susceptibility to opportunistic infections ^[1,2].

In HIV immunopathology, the demise of ${\rm CD4}^+$ T cells can be attributed to three predominant mechanisms: $(1)$ Apoptosis, a non-inflammatory programmed cell death; $(2)$ programmed necrosis, characterized by plasma membrane rupture; and $(3)$ pyroptosis, an intensely inflammatory form of cell death triggered by strong inflammatory signals ^[3]. Nonetheless, studies have indicated that a mere ${\rm 5\%}$ of ${\rm CD4}^+$ T cell demise is attributed to caspase-3-driven apoptosis, with the preponderance of these fatalities being precipitated by caspase-1-induced pyroptosis ^[4,5]. Caspase-1, a pro-inflammatory cysteine protease, mediates both the cleavage of pro-inflammatory cytokines (e.g., IL-1$\beta$, IL-18) and the execution of pyroptotic cell death. Notably, pyroptosis in HIV-infected ${\rm CD4}^+$ T cells generates inflammatory signals that recruit uninfected ${\rm CD4}^+$ T cells, establishing a self-perpetuating cycle of infection and cell death ^[4,6]. This pathological mechanism contributes to viral persistence, as demonstrated by Wang et al. ^[7], who showed that pyroptosis-induced chronic inflammation promotes homeostatic proliferation of memory ${\rm CD4}^+$ T cells—a key reservoir for HIV. These dynamics have been quantitatively characterized through cytokine-enhanced viral infection models ^[8,9,10,11].

Cytotoxic T lymphocytes (CTLs), as the key effector cells of adaptive immunity, play an indispensable role in antiviral immune defense. CTLs can precisely recognize and specifically eliminate HIV-infected host cells, effectively suppressing viral replication and spread within infected cells. Moreover, through the secretion of various cytokines (e.g., IFN-$\gamma$, TNF-$\alpha$), CTLs participate in immunomodulation by enhancing the function of antigen-presenting cells and boosting the activity of other immune cells such as natural killer cells and B cells, thereby establishing a coordinated antiviral immune network. Numerous HIV research models have integrated CTL immune responses into their frameworks, such as ^{[12,13,14,15]}.

Extensive research has established that viral infection of susceptible cells involves a characteristic temporal delay between initial virion contact and productive infection, rather than occurring instantaneously. Recognizing the critical role of time delays in viral dynamics, Jiang and Zhang ^[16] developed a cytokine-enhanced viral infection model featuring a nonlinear incidence rate with discrete time delays. Zhang et al. ^[17] subsequently extended this framework by incorporating CTL immune responses and demonstrating Hopf bifurcation at the immunity-activated equilibrium. However, both studies ^[16,17] overlooked the time delay in inflammatory cytokine production—a critical factor in antiviral immune regulation. Moreover, empirical and theoretical evidence suggest that distributed delays provide more accurate representations of empirical systems compared to discrete delays [18–20]. To address these critical limitations, we develop an advanced modeling framework by introducing two key modifications to the model in ^[17]: (ⅰ) Explicit incorporation of cytokine synthesis delays, and (ⅱ) systematic integration of three distinct distributed-delay mechanisms. These improvements lead to the following enhanced dynamical system:

where $x(t), y(t), c(t), v(t)$, and $z(t)$ represent the concentrations of uninfected ${\rm CD4}^+$ T cells, infected ${\rm CD4}^+$ T cells, inflammatory cytokines, viruses, and CTL immune responsive cells at time $t$, respectively. The term $e^{-m_1 \tau}$ quantifies the survival probability of susceptible cells that were exposed to inflammatory cytokines and viruses at time $t-\tau$ and subsequently became productively infected by time $t$. The terms $e^{-m_2 \tau}$ and $e^{-m_3 \tau}$ represent the probabilities of cytokine production initiation by infected cells at time $t-\tau$ and viral particle maturation and release by time $t$. In model (1.1), we employ the same integration variable $\tau$ across all delay kernels ($e^{-m_1 \tau}$, $e^{-m_2 \tau}$, and $e^{-m_3 \tau}$) since each represents an independent temporal delay in the integration process. This unified notation is adopted without loss of generality for mathematical convenience. Here, $f_i:[0, \infty)\rightarrow [0, \infty)$ represent probability distributions that are supported on a compact support, $f_i(\tau) \geq 0$, and $\int_0^\infty f_i(\tau){\rm d} \tau = 1$ ($i = 1, 2, 3$). All model parameters are strictly positive, with their biological interpretations provided in Table 1.

While a complete cure for HIV remains elusive, current therapeutic strategies utilizing reverse transcriptase inhibitors (RTIs) and protease inhibitors (PIs) have demonstrated efficacy in suppressing viral replication and managing HIV infection. However, the long-term administration of antiretroviral therapies presents significant challenges, including drug toxicity, resistance development, and patient compliance issues. Studies have established that optimized treatment regimens incorporating RTIs and PIs can significantly improve the quality of life for AIDS patients ^[21,22]. Chen et al. ^[9] developed an optimal control framework with four control variables within a cytokine-enhanced viral infection model. Subsequent work has extended this approach to incorporate time-delayed systems [23–25], while computational advances have introduced differential algorithms based on forward-backward difference approximations for numerical implementation ^[22,24,26]. Motivated by the critical role of temporal delays in HIV pathogenesis, we propose an optimal control analysis of a cytokine-enhanced viral infection model incorporating three distinct distributed delays in this paper.

This paper is structured as follows. Section 2 establishes the fundamental properties of model (1.1), proving solution positivity and boundedness while introducing two critical reproduction numbers and characterizing system equilibria. Section 3 demonstrates the global stability of these equilibria through the construction of suitable Lyapunov functionals and application of LaSalle's invariance principle. Section 4 develops the optimal control system using Pontryagin's Maximum Principle. Numerical simulations in Section 5 verify the global stability results and examine delay effects in the optimal control system (4.2). The paper concludes with a discussion of findings in Section 6.

2.   Preliminaries

The initial conditions for system (1.1) are given by:

where $\phi (\theta)e^{\delta \theta }$ is uniformly continuous for $\theta\in(-\infty, 0]$ and $\vert\vert\phi\vert\vert = \sup\limits_{\theta\leq 0} \vert\phi(\theta)\vert e^{\delta \theta } < \infty$ for any $\delta > 0$, $\mathcal{R}_+^5 = \{(x_1, x_2, x_3, x_4, x_5):x_i \geq0, i = 1, 2, 3, 4, 5\}$. Following the fundamental theory of functional differential equations ^[27], system (1.1) admits a unique solution $(x(t), y(t), c(t), v(t), z(t))$ satisfying these initial conditions.

Theorem 2.1. (Positivity and boundedness) For $t > 0$, the solutions of model (1.1) satisfying initial conditions (2.1) are positive and ultimately bounded.

Proof. We first prove the positivity of $x(t)$. Conversely, we assume there exists a $t_1 > 0$ such that $x(t_1) = 0$. From the first equation of (1.1), we can deduce that $\dot{x}(t_1) = \lambda > 0$. Therefore, for $t \in (t_1-\varepsilon, t_1)$ where $\varepsilon > 0$ is sufficiently small, we have $x(t) < 0$. This contradicts the condition that $x(t) > 0$ for $t \in (0, t_1)$. Hence, we have $x(t) > 0$ for all $t > 0$. Next, we will demonstrate that $y(t) > 0, c(t) > 0, v(t) > 0$, and $z(t) > 0$ for all $t > 0$. In fact, suppose that there exists a $t_2 > 0$ for the first time such that $F(t_2) = \min \{y(t_2), c(t_2), v(t_2), z(t_2)\} = 0$. We consider four possible cases:

For case (ⅰ), we have $y(t) > 0$ for $0 < t < t_2$, and $c(t) > 0, v(t) > 0, \; z(t) > 0$ for $0 < t\leq t_2$. From the second equation of (1.1), we can deduce that

Thus, $y(t) < 0$ for all $t\in(0, t_2)$, which causes a contradiction. Similar contradictions arise in cases (ⅱ)–(ⅳ). Therefore, $(x(t), y(t), c(t), v(t), z(t))$ is positive for all $t > 0$.

To demonstrate the boundedness of the system, we begin by analyzing the first equation of model (1.1). We observe that

Solving this differential inequality yields

For non-negative initial conditions in (2.1), this solution implies $\limsup\limits_{t\rightarrow \infty }x(t)\leq \frac{\lambda}{\mu}$, which conclusively establishes the boundedness of $x(t)$. We define $W(t)$ as

which is a continuous function. Differentiating $W(t)$ with respect to $t$, we obtain

where $\bar {\mu} = \min \{\mu, \alpha+d, b\}$. Solving this differential inequality gives

From the non-negativity conditions in (2.1), we conclude $\limsup\limits_{t\rightarrow \infty }W(t)\leq \frac{\lambda \int_0^\infty f_1(\tau)e^{-m_1 \tau}{\rm d} \tau}{\bar {\mu}}$, which implies that $\limsup\limits_{t\rightarrow \infty }y(t)\leq \frac{\lambda \int_0^\infty f_1(\tau)e^{-m_1 \tau}{\rm d} \tau}{\bar {\mu}}$, and $\limsup\limits_{t\rightarrow \infty }z(t)\leq \frac{\eta\lambda \int_0^\infty f_1(\tau)e^{-m_1 \tau}{\rm d} \tau}{p\bar {\mu}}$. Likewise, by leveraging the third and fourth equations of model (1.1), we can derive $\limsup\limits_{t\rightarrow \infty }c(t)\leq \frac{\lambda \sigma \int_0^\infty f_1(\tau)e^{-m_1 \tau}{\rm d} \tau \int_0^\infty f_2(\tau)e^{-m_2 \tau}{\rm d} \tau}{\bar {\mu}q}$ and $\limsup\limits_{t\rightarrow \infty }v(t)\leq \frac{\lambda k \int_0^\infty f_1(\tau)e^{-m_1 \tau}{\rm d} \tau \int_0^\infty f_3(\tau)e^{-m_3 \tau}{\rm d} \tau}{\bar {\mu}\gamma}.$ Consequently, for $t > 0$, the functions $x(t), y(t), c(t), v(t)$, and $z(t)$ are all bounded. □

The model (1.1) admits an infection-free equilibrium given by $E_0 = (x_0, 0, 0, 0, 0)$, where $x_0 = \lambda/\mu$. Following the methodology in ^[28], we derive the basic reproduction number:

where $k_1 = \int_0^\infty f_1(\tau)e^{-m_1 \tau}{\rm d} \tau, k_2 = \int_0^\infty f_2(\tau)e^{-m_2 \tau}{\rm d} \tau, k_3 = \int_0^\infty f_3(\tau)e^{-m_3 \tau}{\rm d} \tau$.

We define $R_0 = R_{01}+R_{02}$, where

Obviously, $R_{01}$ quantifies the expected number of secondary infections caused by inflammatory cytokines, while $R_{02}$ represents the average number of new viruses produced by a single virion. If $R_0 > 1$, an infection equilibrium $E_1 = (x_1, y_1, c_1, v_1, 0)$ is established in model (1.1), where

Similarly, we derive the CTL immune reproductive number $R_1$, defined as the average CTL load produced during the lifespan of a CTL cell:

If $R_1 > 1$, the immunity-activated equilibrium $E^* = (x^*, y^*, c^*, v^*, z^*)$ in model (1.1) can be obtained, where

3.   Global stability of equilibria

Theorem 3.1. If $R_0 \leq 1$, then the infection-free equilibrium $E_0$ of model (1.1) is globally asymptotically stable.

Proof. The Lyapunov functional $V_1(t)$ is characterized as follows:

where

By calculating the time derivative of $V_1(t)$ along the solutions of model (1.1) and applying $\lambda = \mu x_0$, we derive that

Clearly, we have $\dot{V}_1(t)\leq 0$ when $R_0 < 1$, with the equality holding if and only if $x = x_0, c = 0, v = 0$, and $z = 0$. According to [27, Theorem 5.3.1], solutions asymptotically approach $\mathscr{M}_0$, which is the largest invariant subset where $\dot{V}_1(t) = 0$. Substituting $c = 0$ into the third equation of system (1.1) yields

Since $f_2(\tau)e^{-m_2 \tau}$ is non-negative and $\sigma > 0$, this implies $y(t-\tau) = 0$ for all $\tau\geq 0$, and thus $y = 0$. Consequently, the largest invariant set where $\dot{V}_1(t) = 0$ is the singleton $E_0$.

If $R_0 = 1$, we have

where the equality holds if and only if $x = x_0$ and $z = 0$. Substituting $x = x_0$ into the first equation of (1.1) yields $c = 0, v = 0$. Through the third equation (with $c = 0$) or the fourth equation (with $v = 0$) of system (1.1), we further deduce $y = 0$. Thus, the largest invariant set satisfying $\dot{V}_1(t) = 0$ is $\mathscr{M}_0 = E_0$.

Therefore, by applying LaSalle invariance principle, we deduce that the infection-free equilibrium $E_0$ is globally asymptotically stable if $R_0 \leq 1$. □

Theorem 3.2. If $R_0 > 1$ and $R_1\leq1$, then the infection equilibrium $E_1$ of model (1.1) is globally asymptotically stable.

Proof. The Lyapunov functional $V_2(t)$ is defined below:

where

Here, $g(u) = u-1-\ln u, u > 0$. Obviously, $g(1) = 0$, which is the global minimum for $g(u)$. Noting that

the time derivative of $V_2(t)$ along the solutions of model (1.1) is as follows:

Obviously, we can obtain that $\dot{V}_2(t)\leq 0$ if $R_1 < 1$. By [27, Theorem 5.3.1], solutions asymptotically approach $\mathscr{M}_1$, which is the largest invariant subset where $\dot{V}_2(t) = 0$. It can be verified that $\dot{V}_2(t) = 0$ if and only if

and $z = 0$. By substituting $x = x_1$ into the first equation of (1.1) and applying $\lambda = \beta_1 x_1c_1+\beta_2 x_1v_1+\mu x_1$, we derive

Furthermore, inserting $y(t-\tau) = \frac{cy_1}{c_1}$ into the third equation of system (1.1) and employing $k_2 \sigma y_1 = q c_1$, we obtain

This equality implies that $c$ remains constant. Let $c = \tilde{c_1}$. Furthermore, from the identity $\frac{c_1y(t-\tau)}{cy_1} = \frac{v_1y(t-\tau)}{vy_1} = 1$, we obtain $v = \frac{\tilde{c_1} v_1}{c_1}$. Submitting $c = \tilde{c_1}$ and $v = \frac{\tilde{c_1} v_1}{c_1}$ into (3.1), we obtain

which necessarily implies $c_1 = \tilde{c_1}$. Consequently, we establish the identities $y = y_1, c = c_1$, and $v = v_1$. Furthermore, given that $z = 0$, we conclude that the largest invariant set where $\dot{V}_2(t) = 0$ is precisely the singleton $\mathscr{M}_1 = E_1$.

When $R_1 = 1$, employing an analogous approach to the preceding analysis, we conclude that $x = x_1, y = y_1, c = c_1$, and $v = v_1$. Furthermore, substituting the identity $k_1\beta_1 x_1c_1+k_1\beta_2 x_1v_1 = (\alpha+d)y_1$ and by the second equation of (1.1) yields $py_1z = 0$ which implies $z = 0$. Consequently, the largest invariant set satisfying $\dot{V}_2(t) = 0$ reduces to the singleton $\mathscr{M_1} = E_1$.

By applying the LaSalle invariance principle, we obtain the global asymptotic stability of the infection equilibrium $E_1$ for model (1.1). □

Theorem 3.3. If $R_1 > 1$, then the immunity-activated equilibrium $E^*$ of model (1.1) is globally asymptotically stable.

Proof. The Lyapunov functional $V_3(t)$ is defined below:

where

By computing the time derivative of $V_3(t)$ along the trajectories of model (1.1) and applying

we obtain

Thus, we obtain $\dot{V}_3(t)\leq 0$. It can be verified that $\dot{V}_3(t) = 0$ if and only if

According to the LaSalle invariance principle, we obtain the global asymptotic stability of the infection equilibrium $E^*$ for model (1.1). □

4.   Optimal control

To systematically optimize HIV treatment strategies, we propose an optimal control framework incorporating four time-dependent therapeutic interventions:

● $u_1(t)$: Prevents inflammatory cytokines from infecting healthy ${\rm CD4}^+$ T cells.

● $u_2(t)$: Quantifies RTI efficacy in preventing viral reverse transcription.

● $u_3(t)$: Suppresses the production of inflammatory cytokines to mitigate excessive immune activation.

● $u_4(t)$: Represents PI effectiveness in inhibiting viral maturation.

To achieve a balance between simplicity and generality, we employ discrete time delays as an alternative to distributed delays, thereby facilitating our investigation of the following optimal control problem:

During the process of HIV pathogenesis, ${\rm CD4}^+$ T lymphocytes play a dual role as both principal targets for viral infection and central regulators of adaptive immune responses. This dual functionality makes their preservation critical for maintaining host immunity against HIV progression. Meanwhile, CTLs mediate antiviral defense through two distinct mechanisms: (ⅰ) Direct cytolysis of infected cells, and (ⅱ) cytokine-mediated suppression of viral replication. Recognizing these essential roles of ${\rm CD4}^+$ T cells and CTLs in HIV immunopathology, we derive the following objective function for system (4.1):

where $t_f$ denotes treatment duration, and $A_i(i = 1, 2, 3, 4)$ represent the relative costs of the treatments corresponding to the respective controls.

In HIV therapeutic optimization, the central paradigm necessitates establishing an optimal equilibrium between three critical dimensions: (1) Immunological reconstitution via maximal preservation of uninfected ${\rm CD4}^+$ T lymphocyte reservoirs and amplification of CTL effector populations, (2) mitigation of cumulative pharmacological toxicities impacting treatment adherence, and (3) containment of long-term economic burdens associated with combination antiretroviral therapy. These competing constraints mean that a minimization approach would be counterproductive to our fundamental goals of immune system restoration and viral control. Accordingly, we formulate the optimization problem as follows: Find the optimal controls $(u_1^{**}, u_2^{**}, u_3^{**}, u_4^{**})$ that satisfy

where the set of admissible controls $U$ is specified as

Following established techniques ^[9,26], we derive the subsequent theorem concerning the existence of the optimal control.

Theorem 4.1. There exists an optimal control pair $(u_1^{**}, u_2^{**}, u_3^{**}, u_4^{**})\in U$ such that

To derive the optimal control system, we apply Pontryagin's Maximum Principle. The corresponding Hamiltonian function is defined as

where

and

We define the characteristic function $\mathcal{X}_{[m, n]}(t)$ as

Applying Pontryagin's Maximum Principle, we can derive the following theorem.

Theorem 4.2. Let $u_1^{**}, u_2^{**}, u_3^{**}, u_4^{**}$ be optimal controls with corresponding state solutions $x^{**}, y^{**}, c^{**}, v^{**}$, and $z^{**}$ of system (4.1). Then there exist adjoint variables $\lambda_1, \lambda_2, \lambda_3, \lambda_4, \lambda_5$ satisfying the equations

with the transversality conditions

Furthermore, the optimal control is specified as

Proof. Through the application of Pontryagin's Maximum Principle, we derive both the adjoint system and the corresponding transversality conditions, from which

Applying the optimality conditions, we have

Using the constraints on the control set $U$, we derive

Consequently, we obtain the subsequent optimality system:

5.   Numerical simulations

In this section, we present numerical simulations implemented in MATLAB to: (1) Rigorously verify the global asymptotic stability of the equilibrium points through phase portrait analysis; (2) demonstrate the critical role of optimal control in system regulation through comparative studies; and (3) investigate the sensitivity of the controlled system to varying time delays.

Now, we systematically validate the stability properties through three distinct parameter configurations. The parameter values are derived from ^[17] and they are $\lambda = 10, \ \beta_1 = 0.0012, \ \beta_2 = 0.001, \ \mu = 0.1$, $\alpha = 0.1, \ d = 0.75, \ p = 0.001, \ \sigma = 0.25$, $q = 0.1, \ k = 13, \ \gamma = 0.3, \ \eta = 0.33$, $m_1 = m_2 = m_3 = 0.1$, and the initial value is $(50, 3, 60, 2,450)$.

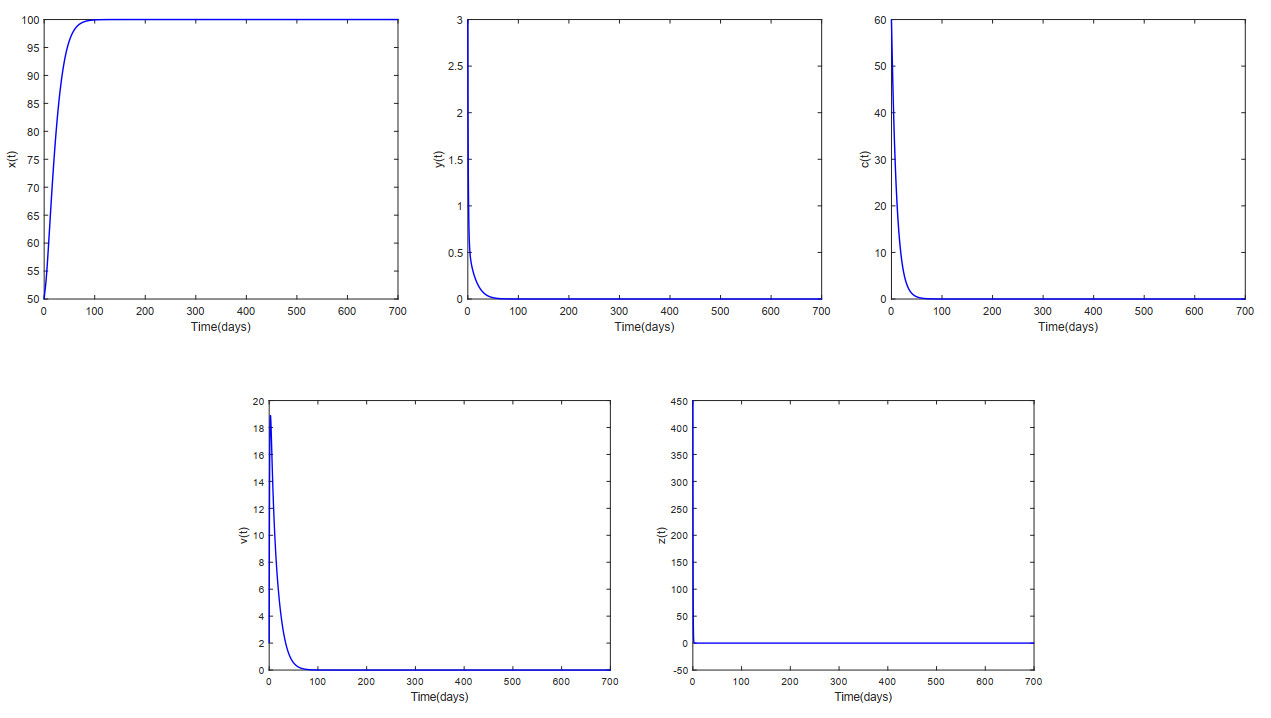
● The infection-free equilibrium $E_0$: Setting $m_1 = 1, \ m_2 = m_3 = 0.1$, and $b = 3$, the calculated basic reproduction number $R_0 = 0.34665 < 1$ demonstrates the global asymptotic stability of $E_0(100, 0, 0, 0, 0)$, as evidenced by phase-space trajectories in Figure 1. This numerical observation aligns precisely with the theoretical predictions of Theorem 3.1.

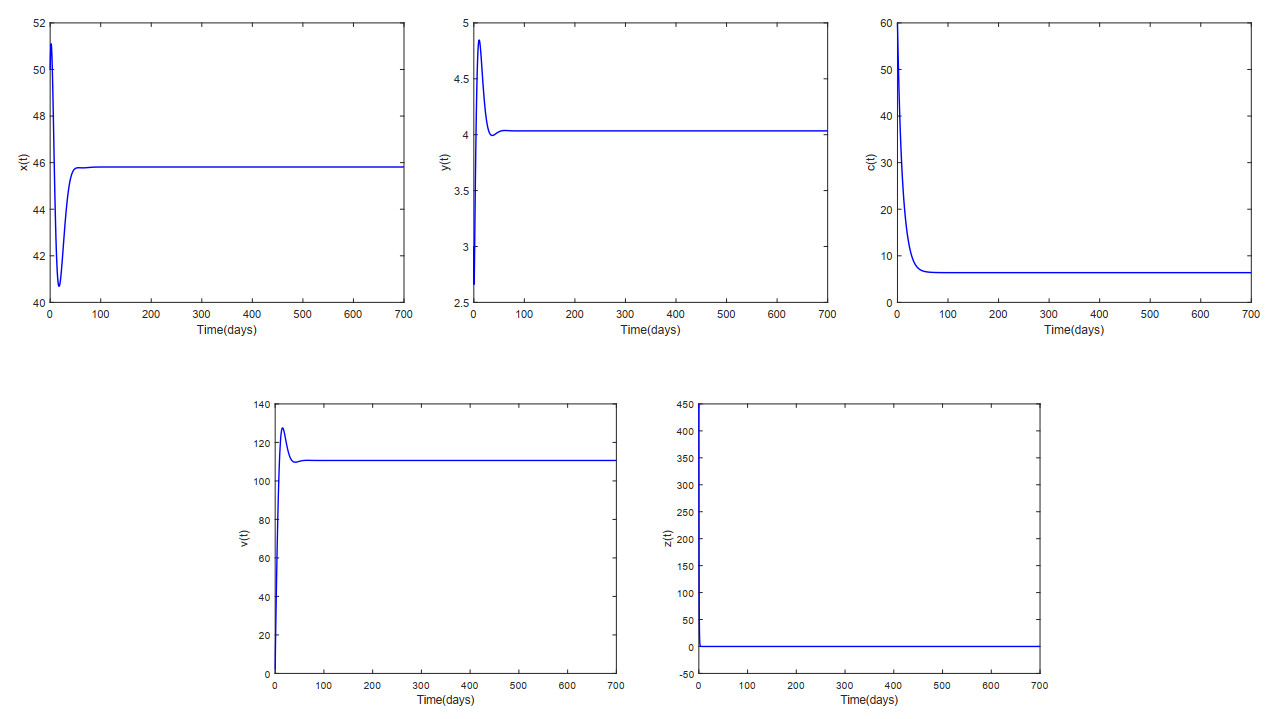
● The immunity-free equilibrium $E_1$: Maintaining equivalent mutation rates $m_1 = m_2 = m_3 = 0.1$, while preserving $b = 3$, we obtain $R_0 = 2.1828 > 1$ and $R_1 = 0.44375 < 1$. Figure 2 reveals the global convergence of solutions toward $E_1(45.8127, 4.0341, 6.382,110.6215, 0)$, thereby confirming Theorem 3.2.

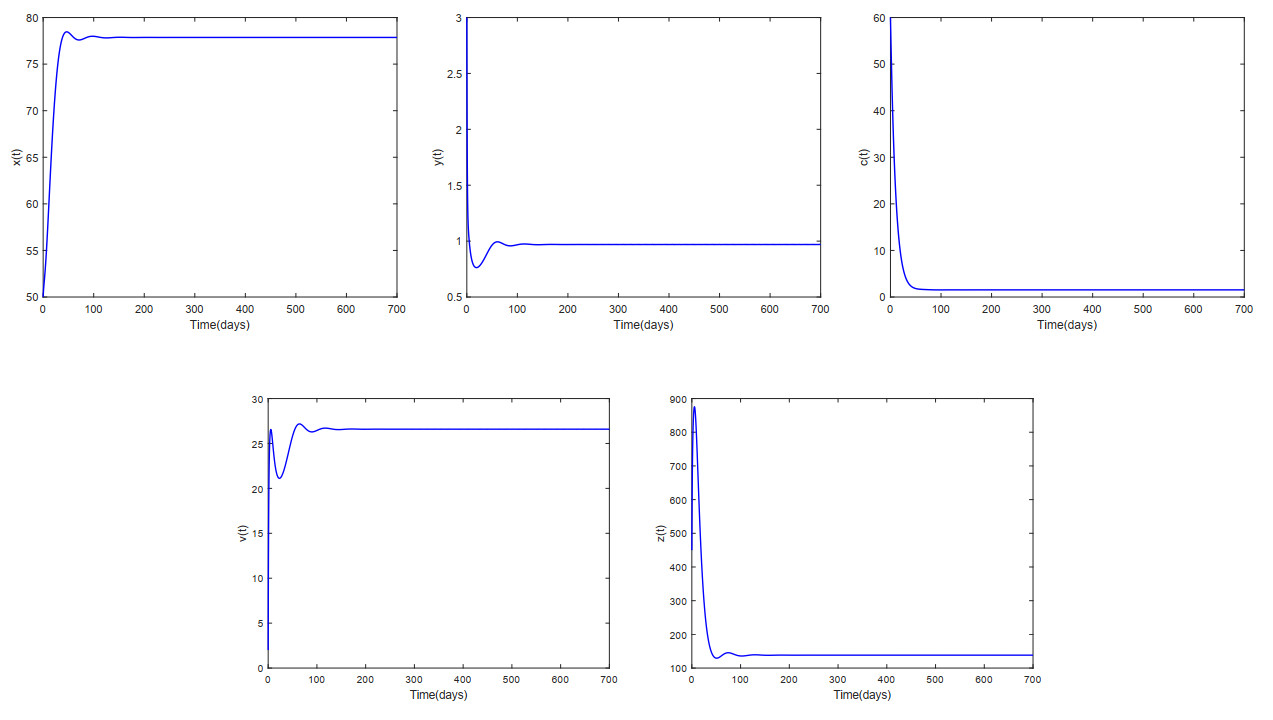
● The immune equilibrium $E^*$: Adjusting parameters to $m_1 = 0.2, \ m_2 = m_3 = 0.1$, and reduced $b = 0.32$, the computed threshold $R_1 = 1.7349 > 1$ triggers the emergence of $E^*(77.8625, 0.9697, 1.5341, 26.5906,138.2788)$. As shown in Figure 3, all trajectories asymptotically approach this endemic equilibrium, conclusively corroborating Theorem 3.3.

Following the numerical approach developed in ^[24], we simulate the optimal control system (4.2) with the following specifications: The terminal time is set to $t_f = 50$ as in ^[24], while other parameters such as $b = 0.32, \ \lambda = 10, \ \beta_1 = 0.0012$, $\beta_2 = 0.001, \ \mu = 0.1, \ \alpha = 0.1, \ d = 0.75$, $p = 0.001, \ \sigma = 0.25, \ q = 0.1, \ k = 13, \ \gamma = 0.3$, $\eta = 0.33, \ m_1 = m_2 = m_3 = 0.1$ are adopted from ^[17]. The control weights are uniformly set to $A_1 = A_2 = A_3 = A_4 = 10$. For computational simplicity without loss of generality, we assume identical time delays $\tau_1 = \tau_2 = \tau_3 = \tau$.

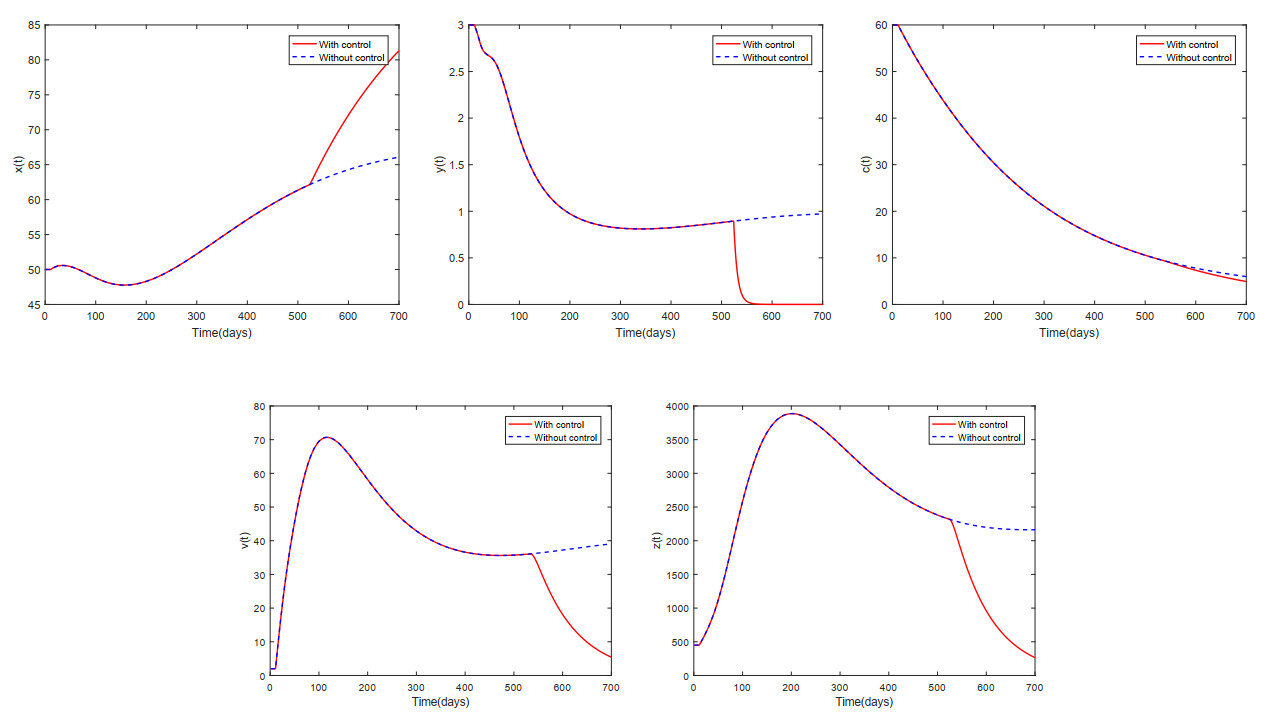
To systematically assess the influence of control strategies on the dynamic system described by the equations, we conduct a comparative analysis of the numerical simulations for the system with and without optimal control at $\tau = 0.4$. As depicted in Figure 4, which shows the trajectories of key variables over time:

● Uninfected ${\rm CD4}^+$ T cells ($x(t)$): Under the impact of control measures, the concentration of uninfected ${\rm CD4}^+$ T cells exhibits a notable upward trend. Specifically, the concentration increased from 66.0828 (without control) to 81.3165 (with control) at $t = 700$, reflecting a 23.1$\%$ increase. This increase indicates that control effectively promotes the maintenance or growth of the population of uninfected immune cells.

● Infected ${\rm CD4}^+$ T cells ($y(t)$), viruses ($v(t)$), and CTL immune responsive cells ($z(t)$): The concentrations of infected cells, viruses, and immune responsive cells all decrease significantly when control is implemented. This suggests that the control strategies are successful in curbing the spread of infection and reducing the overall burden on the immune system.

● Inflammatory cytokines ($c(t)$): At $t = 700$, the concentration of inflammatory cytokines exhibited a marked increase, reaching 5.9767 under controlled conditions compared to 4.9148 in the absence of intervention, representing a 21.61$\%$ elevation. This indicates that the control measures adopted (such as the use of certain drugs, the implementation of specific treatment regimens, etc.) have had an impact on the body's inflammation-related status.

However, implementation of optimal HIV control strategies resulted in a marked increase in uninfected ${\rm CD4}^+$ cell populations, accompanied by rapid declines in infected cell counts, viral load, and immune effector cell numbers. Notably, inflammatory cytokines demonstrated only gradual reduction, exhibiting persistent resistance to therapeutic intervention. These findings align with established clinical evidence ^[29], confirming that while antiretroviral therapy (ART) can partially mitigate ${\rm CD4}^+$ T cell pyroptosis, complete suppression of the inflammatory cascade remains unattainable with current approaches.

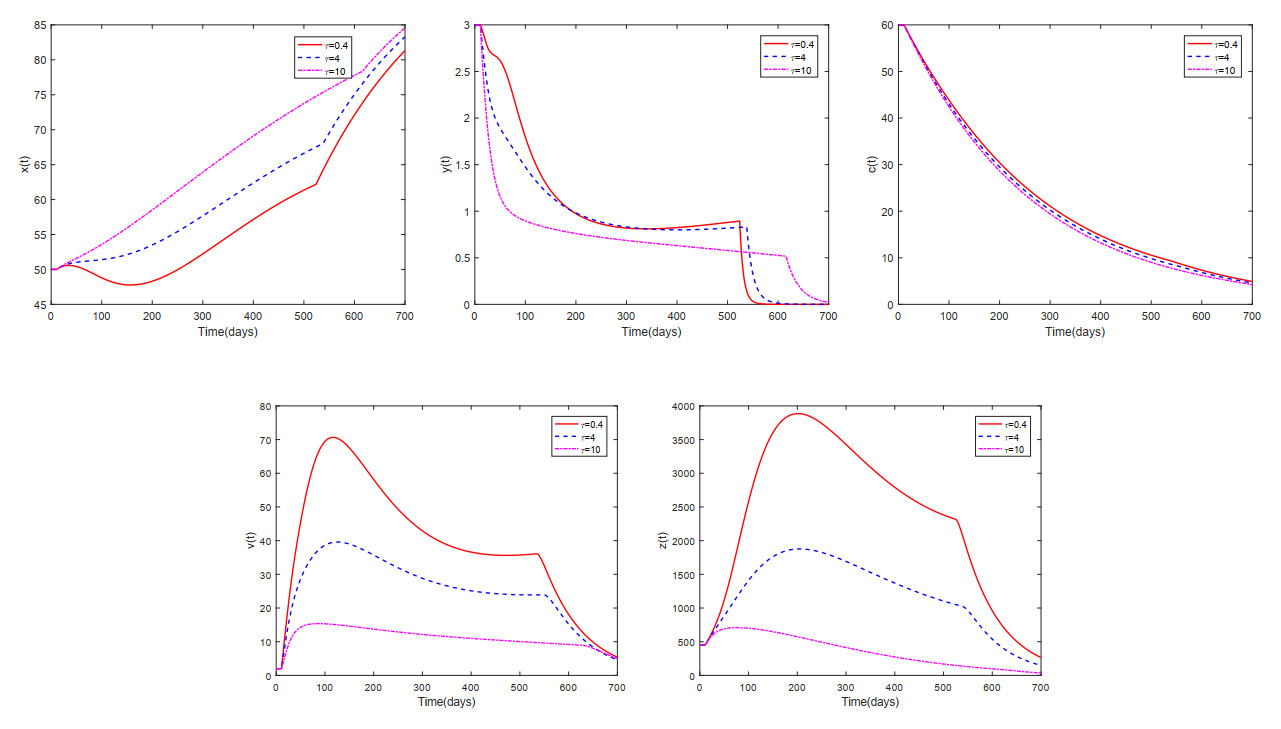
To systematically investigate the temporal effects on optimal control dynamics, we perform a comparative analysis of system variables $x(t), y(t), c(t), v(t)$, and $z(t)$ under distinct time-delay regimes $\tau = 0.4, \ \tau = 4$, and $\tau = 10$ in Figure 5. To demonstrate the time-delay effects more clearly, we analyze the system variables at $t = 300$ under different delay conditions as follows:

● Uninfected ${\rm CD4}^+$ T cells ($x(t)$): The concentration of uninfected ${\rm CD4}^+$ T cells exhibited a progressive increase from 52.2254 at $\tau = 0.4$ to 63.9181 at $\tau = 10$, which implies that prolonged time delays may create a more favorable microenvironment for preserving uninfected cells.

● Infected ${\rm CD4}^+$ T cells ($y(t)$): A contrasting decline was observed in infected ${\rm CD4}^+$ T cells, with concentrations decreasing from 0.8191 ($\tau = 0.4$) to 0.6862 ($\tau = 10$). This trend suggests that extended time delays may disrupt critical phases of the viral infection cycle, consequently reducing the population of infected cells.

● Inflammatory cytokines ($c(t)$): The levels of inflammatory cytokines decreased moderately, from 21.0851 when $\tau = 0.4$ to 19.4179 when $\tau = 10$, suggesting that prolonged time delays may attenuate inflammatory responses, potentially through delayed immune signaling pathways.

● Viruses ($v(t)$): Viral concentration demonstrated a dramatic decline from 42.9187 ($\tau = 0.4$) to 12.1682 ($\tau = 10$), highlighting the inhibitory effect of time delays on viral replication. Extended delays may impair essential lifecycle stages (e.g., reverse transcription, assembly, or release) and disrupt viral fitness.

● CTL immune responsive cells ($z(t)$): CTL cell populations plummeted from 3427 ($\tau = 0.4$) to 413.46 ($\tau = 10$), a 7.3-fold reduction. This sharp decline may stem from diminished antigenic stimulation due to lower viral loads under prolonged delays, leading to reduced clonal expansion of effector CTLs.

Additionally, the fluctuation range of inflammatory cytokines remains minimal across different time delays in Figure 5. This is because ART fails to fully restore cytokine levels to baseline, leading to persistent low-grade secretion of inflammatory factors. Notably, our numerical simulations demonstrate that this constrained variation in inflammatory cytokines reflects effective management of systemic inflammation. Such control is critical for minimizing immune cell damage and fostering the recovery and proliferation of ${\rm CD4}^+$ T lymphocytes and other immune cells, ultimately enhancing the host's antiviral capacity.

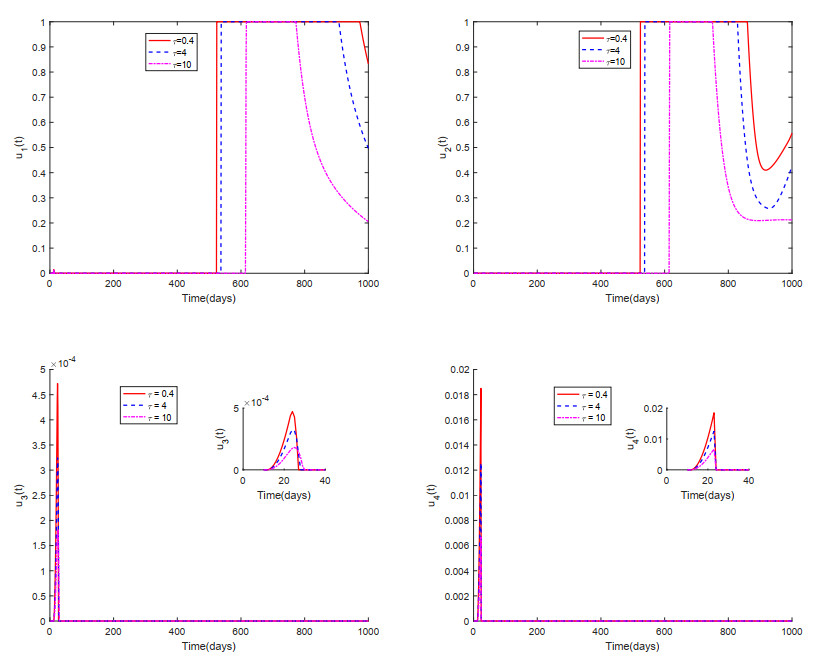
Numerical simulations illustrating the temporal evolution of optimal controls $u_i(t)(i = 1, 2, 3, 4)$ across different time-delay regimes are presented in Figure 6.

● $u_1(t)$ and $u_2(t)$: As the time delay increases, the duration required to reach optimal control intensity decreases significantly: By $74.39\%$ for $u_1(t)$ (from 449 days at $\tau = 0.4$ to 115 days at $\tau = 10$) and $60\%$ for $u_2(t)$ (from 335 days at $\tau = 0.4$ to 134 days at $\tau = 10$). This delay-induced deceleration slows viral infection progression, immune activation, and viral replication, thereby granting the immune system additional time to mount an autonomous response against HIV infection and mitigating disease progression. Consequently, prolonged high-intensity application of $u_1(t)$ and $u_2(t)$ becomes unnecessary under extended delay conditions.

● $u_3(t)$ and $u_4(t)$: While the time required for $u_3(t)$ and $u_4(t)$ to achieve optimal control remains relatively unchanged, their optimal intensity values exhibit significant decreases. Quantitative analysis reveals a $61.58\%$ reduction in peak value for $u_3(t)$ (from $4.7222 \times 10^{-4}$ at $\tau = 0.4$ to $1.8142\times 10^{-4}$ at $\tau = 10$) and a $63.78\%$ decrease in peak value for $u_4(t)$ (from 0.0185 at $\tau = 0.4$ to 0.0067 at $\tau = 10$). This substantial attenuation in control intensity requirements corresponds to the reduction in the virus's transmissibility under extended delay conditions.

These findings suggest distinct clinical implications based on time-delay magnitude. Under minimal time-delay conditions ($\tau \leq0.4$), the observed viral replication activity necessitates immediate intensification of pharmacological intervention to effectively inhibit viral infection and reverse transcription during critical phases. Conversely, extended time-delay scenarios ($\tau \geq 10$) permit gradual dose reduction or frequency modulation of therapeutic agents, mitigating potential adverse effects and drug-resistance development associated with prolonged high-intensity treatment.

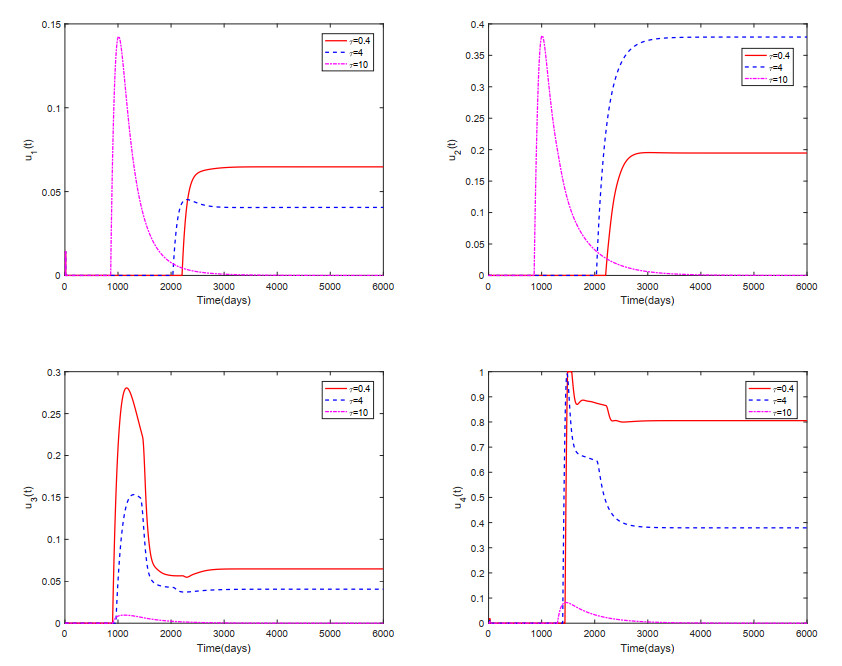
Figure 7 illustrates the temporal evolution of the optimal control $u_i(t)(i = 1, 2, 3, 4)$ over the restricted time domain $t\in[0, 6000]$. Our analysis demonstrates that the values of $u_i(t)(i = 1, 2, 3, 4)$ are gradually approaching $0$ as $\tau$ ranges from $0.4$ to $10$. This phenomenon emerges because sufficiently large time delays, coupled with the host's adaptive responses to therapeutic interventions and inherent feedback regulatory mechanisms, ultimately obviate the necessity for supplementary control measures during prolonged treatment. Notably, as the time delay $\tau$ increases, the peak value of $u_2(t)$ exhibits an initial increase followed by a subsequent decrease. Specifically, when $\tau = 0.4$, the peak magnitude of $u_2(t)$ is 0.1948. As $\tau$ rises to 4, the peak value increases to 0.3791, beyond which it declines and eventually converges to zero. This biphasic response likely reflects a clinically significant transitional phase in HIV treatment: the temporary intensification of control may compensate for emerging stress responses to prior therapy, while subsequent adaptation of both host and pathogen systems, along with disease progression dynamics, collectively permit gradual reduction of intervention intensity.

6.   Conclusions

This study presents a comprehensive analysis of a cytokine-enhanced viral infection model incorporating three distributed delays. We derived two critical epidemiological thresholds—the basic reproduction number ($R_0$) and CTL immune reproduction number ($R_1$)—that fundamentally determine the system's dynamic behavior. Through rigorous mathematical analysis using Lyapunov functionals and LaSalle's Invariance Principle, we established precise conditions guaranteeing global asymptotic stability of all equilibrium points. Furthermore, by applying Pontryagin's Maximum Principle, we developed an optimal control framework that explicitly incorporates time-delay effects.

Through numerical simulations, we verified the global asymptotic stability of three equilibrium points under distinct parameter conditions. Our systematic analysis elucidates the temporal evolution of crucial biological components—uninfected cells, infected cells, inflammatory cytokines, viral load, and immune effector cells—under both controlled and uncontrolled conditions. Furthermore, we performed detailed investigations into the time-dependent behavior of these components under varying time-delay conditions ($\tau = 0.4, \ 4$, and 10). Additionally, we simulated the time-dependent profiles of optimal control strategies $u_i(t)(i = 1, 2, 3, 4)$ across different delay conditions, examining both short-term $[0, 1000]$ and long-term $[0, 6000]$ dynamical behavior.

Our findings conclusively demonstrate that control measures are indispensable in HIV treatment protocols, while also highlighting the critical role of inflammatory cytokine production delays in modeling HIV pathogenesis. Moreover, given the substantial inter-patient variability in time-delay parameters, our results underscore the importance of personalized disease monitoring strategies. Notably, under ideal conditions with sufficiently large time delays, the intensity of optimal control can asymptotically diminish to near-zero levels. This finding underscores two critical implications: (ⅰ) The essential role of incorporating time delays in HIV/AIDS treatment optimization, and (ⅱ) the clinical importance of precisely calibrating therapeutic interventions according to specific delay parameters. These insights not only deepen our theoretical comprehension of HIV pathogenesis but also provide a foundation for more effective, patient-specific treatment approaches.

Author contributions

Cuifang Lv: Writing–original draft, formal analysis, software; Xiaoyan Chen: Methodology, formal analysis, writing–review and editing, funding acquisition; Chaoxiong Du: Writing–review and editing, supervision. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (12301186).

Conflict of interest

The authors assert that no financial interest or personal relationships exist that could have affected the research presented in this paper.