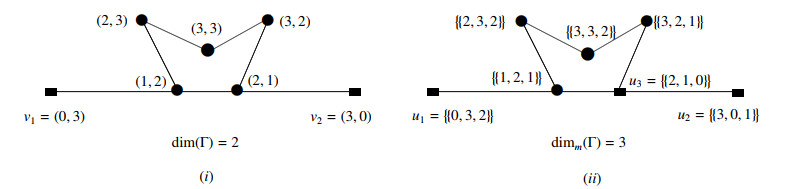Matching some graph dimensions with special generating functions

1.   Introduction

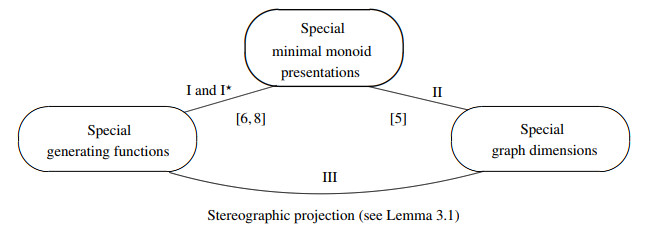
Incorporating separate subjects in mathematics has always been interesting and useful. Succeeding in such an operation will imply new study areas not only in mathematics but also in applied sciences. In this context, a strong connection between special generating functions, namely array polynomials and some Stirling numbers, and minimal monoid presentations obtained by specific semi-direct products of monoids (cf. ^[6,8]), is constructed. This construction is indicated as Ⅰ and I$^\star$ in Figure 1.

On the other hand, in a recent paper ^[5], the first author of this paper has established a one-way connection from the minimal presentations obtained from the semi-direct product of specific monoids and some graph dimensions, namely multiset and outer multiset dimensions (although the definitions of these dimensions will be recalled in Section 2.1, for the fundamental studies about their properties, we refer the reader to, for example, ^[4,10,13,19]). This case is indicated as Ⅱ in Figure 1.

Depending on the structure of minimal presentations either of monoids and on the types of generating functions that have been considered (see Section 2.2), the movement in the matching indicated by Ⅰ is reciprocal (see the last paragraph in the proof of Lemma 3.1 below for more details. This is indicated as I$^\star$ in Figure 1). This is roughly because the minimal presentation for a monoid is unique (see Section 2.4), since it has a minimum number of generators and relators, and, therefore, the types of generating functions chosen yield exactly the same minimal presentations according to their content. However, in Ⅱ, it is not easy (or presumably impossible for the general case) to decide about the corresponding minimal presentation, even if it is always unique since we can obtain different types of monoids for the same graph having specific metric or multiset dimensions. Moreover, this one-way connection in Ⅱ shows the importance of this paper, in other words, the importance of the matching between special graphs having specific dimensions and special generating functions. As the most important consequence of this paper, the cycle indicated in Figure 1 will be completed. Although not explicitly mentioned in this paper, we emphasize that substituting monoids with groups will yield the same expressions presented in this paragraph.

2.   Preliminary material

This section serves as a reminder of known subjects that will be used in our main results in Section 3. Therefore, each topic will be presented as a separate subsection to increase comprehensibility.

2.1.   Fundamentals about graph dimensions

Unless otherwise stated, the graphs considered in this section and in the rest of this paper will be simple and connected. We will denote a graph by $\Gamma$ in this paper. On the other hand, all the detailed knowledge about the graph dimensions of a given $\Gamma$, which will be recalled below as preliminary information, can be found, for example, in research regarding multiset dimension ^[4,19], outer multiset dimension ^[10,13], and metric dimension ^[3,11,18]. We also note that some parts of the paragraphs in this first preliminary section are taken from the first author's recent paper ^[5].

It is well known that the distance between any two vertices is the length of the shortest path within these vertices, and is denoted by $d_\Gamma(u, v)$ for any $u, v \in V(\Gamma)$. A vertex $t \in V(\Gamma)$ resolves a pair of vertices $u, v \in V(\Gamma)$ if $d_\Gamma(u, t) \neq d_\Gamma(v, t)$. For an ordered subset of $k$ vertices $S = \left\{t_1, t_2, \ldots, t_k\right\}$ of $V(\Gamma)$, the representation of distances of a vertex $u \in V(\Gamma)$ with respect to $S$ is the ordered $k$-tuple

$S$ is called a resolving set of $\Gamma$ if all vertices of $\Gamma$ have distinct vectors of distances to the vertices in $S$ (i.e., if every two vertices of $\Gamma$ have distinct representations with respect to $S$). Each vertex of $\Gamma$ is uniquely recognized by the distances from the resolving set for $\Gamma$. The smallest resolving set is called a metric basis, and its cardinality is called the metric dimension of $\Gamma$, which is denoted by $\text{dim}(\Gamma)$. The metric dimension is the minimum cardinality among all resolving sets for $\Gamma$. See the graph in Figure 2(i).

In Figures 2 and 3, all labels are ordered pairs, and multisets indicate representations of distances of the vertices in the corresponding graphs.

In ^[19], looking at the multiset of distances instead of looking at the vector of distances to a given set of vertices came to mind when Charles Delorme suggested in a personal communication to the first author of ^[19] in 2013 that, in his own words, "However, contrary to the case of lists, where a sufficiently large dimension allows the identification of all vertices, it may happen that no dimension provides identification. This is the case if the graph has too many symmetries". This will provide us with a detailed classification of the graphs. Subsequently, the multiset dimension was first introduced in ^[19] as a new variation of the metric dimension. In this case, the multiset representation of a vertex $u \in V(\Gamma)$ with respect to $S = \left\{t_1, t_2, \ldots, t_k\right\} \subseteq V(\Gamma)$ is the multiset

which is a multiset of distances between $u$ and the vertices in $S$ together with their multiplicities (to avoid confusion, the notation $\big\{\{. \}\big\}$ will be used for the multisets in this paper). Then, $S$ is called the multiset resolving set if any two vertices of $\Gamma$ have different multiset representations, that is, $r_m(u | S) \neq r_m(v | S)$ for every pair of distinct vertices $u, v \in V(\Gamma)$. The smallest multiset resolving set with minimum cardinality is called a multiset basis and its cardinality is called the multiset dimension of $\Gamma$ which is denoted by $\text{dim}_m(\Gamma)$. For an example of multiset dimensions, we refer to the graph in Figure 2(ii). Note that the only graphs with multiset dimension $1$ are paths and there is no graph with multiset dimension $2$ (cf. ^[4,19]), and thus the multiset dimension starts from $3$ for any graph other than paths. If there does not exist any multiset basis in the graph $\Gamma$, we directly write $\text{dim}_m(\Gamma) = \infty$, and name it as $\Gamma$ has the infinite multiset dimension. According to this definition, we need to express the following open problem (cf. [5, Open problem 1] and ^[10]), which is still unsolved completely.

Open problem. Is it possible to characterize all graphs that have $\mbox{dim}_m(\Gamma) = \infty$?

Since we aim to find a suitable classification for infinite multiset dimensions via special generating functions, the idea about our aim came to our minds by considering this open problem. We again note that, in ^[5], it has been recently presented a partial solution for this open problem by considering special types of minimal monoid presentations.

The following lemmas will be needed in the proofs of our main theorems. Recall from earlier that the open and closed neighborhood of a vertex $u$ of $\Gamma$ are denoted by $N_G(u)$ and $N_G[u]$, respectively. Also, any two vertices $u$ and $v$ of $\Gamma$ are true twins if $N_G[u] = N_G[v]$ are false twins if $N_G(u) = N_G(v)$. Additionally, vertices $u$ and $v$ are just twins, if they are either true twins or false twins.

Lemma 2.1. ^[10,13] If the graph $\Gamma$ has at least three twins, then two of them have the same multiset representation with respect to any set of vertices of $\Gamma$, and so in this case, it is taken as $\mathit{\text{dim}}_m(\Gamma) = \infty$.

Lemma 2.2. ^[10,13] If there exist only two vertices that have the same multiset resolving sets with respect to any subset of vertices of the graph $\Gamma$, then we have $\mathit{\text{dim}}_m(\Gamma) = \infty$.

As a new variation of these above metric and multiset dimensions, in ^[10], the authors introduced the outer version of the multiset dimension to stay away from the problem of the possible infiniteness of the multiset dimension (see Lemmas 2.1 and 2.2). Later, in ^[13], the topic was further developed, and the existence of new features was demonstrated. Thus, let us reconsider the multiset representation given in Eq (2.1), but this time, let us denote it as

Therefore, the outer multiset resolving set is defined as the set $S$ such that any two vertices outside $S$ have different multiset representations, i.e., such that the multiset representations of vertices $u \notin S$ with respect to $S$ are pairwise different, i.e., such that $r_{ms}(u | S) = r_{ms}(v | S) \Leftrightarrow u = v$ for every $u, v \in V(\Gamma) \setminus S$. After that, an outer multiset resolving set of the smallest possible cardinality is called an outer multiset basis, and the cardinality of an outer multiset basis is the outer multiset dimension of $\Gamma$, denoted by $\text{dim}_{ms}(\Gamma)$. In fact, the structure of outer multiset dimensions avoids the problem of infiniteness of multiset dimensions, since vertices that must be distinguished by a set $S$ are only vertices outside $S$ (see Figure 3 for a graph with an outer multiset dimension $2$ which exposes the difference from multiset dimension as we noted that there are no graphs having multiset dimension $2$). It has been noted in ^[10] and ^[13] that computing $\text{dim}_{ms}(\Gamma)$ is an NP-hard problem and it is also not clear what happens in the case of trees.

Again, according to the same references, a graph $\Gamma$ satisfies $\text{dim}_{ms}(\Gamma) = 1$ if and only if it is a path graph. Also, for complete $K_n$ and cycle $C_n$ graphs, we have $\text{dim}_{ms}(K_n) = n-1$, where $n \geq 6$ and $\text{dim}_{ms}(C_n) = 3$, where $n \in {\mathbb Z}^+$, respectively. At this point, we would like to note that the graph in Figure 2(ii) actually represents not only the multiset dimension but also the outer multiset dimensions with outer multiset resolving set $S = \left\{ u_1, u_2, u_3\right\}$, and so $\text{dim}_{ms}(\Gamma) = 3$.

In ^[2], another new graph dimension is introduced under the name of local multiset dimension, notationally $\text{dim}_{lms}(\Gamma)$. Similarly, as in $\text{dim}_{ms}(\Gamma)$, it was aimed to avoid the problem of the infiniteness of multiset dimensions since a subset $L \subset V(\Gamma)$ is called local resolving set of $\Gamma$ if multiset representations for all adjacent vertices are different from each other. In other words, if $r_{ms}(u | L) \neq r_{ms}(v | L)$ while $uv \in E(\Gamma)$ for every $u, v \in V(\Gamma)$. As usual, the number of elements of a minimum local resolving set is called local multiset dimension. For instance, in Figure 2(ii), we have $\text{dim}_{lms}(\Gamma) = 3$ with the local resolving set $L = \left\lbrace u_1, u_2, u_3 \right\rbrace$.

2.2.   Fundamentals about special generating functions

In this subsection, we will remind basic facts on array polynomials and Stirling numbers. The materials presented here are mostly taken from references ^[6,8].

First, array polynomials, notationally $S_{m}^{n}(x)$, are defined as the generating function $\frac{(e^{t}-1)^{m}e^{tx}}{x!} = \sum_{n = 0}^{\infty }S_{m}^{n}(x)\frac{t^{n}}{n!}$ (see, for instance, ^[9,17]). According to the same references, these polynomials can also be defined as in the generating function form

The coefficients of array polynomials are integers and so they have a huge use in applicable sciences such as system control (cf. ^[16]). These integer coefficients provide an opportunity to use these polynomials in our main theories. The following form of the array polynomials obtained from Eq (2.3) (cf. ^[17]) will also find its way into some proofs.

On the other hand, by ^[15], Stirling numbers of the second kind $S(n, m)$ are defined as the generating function $\frac{(e^{t}-1)^{m}}{m!} = \sum_{n = 0}^{\infty }S(n, m)\frac{t^{n}}{n!}$. However, by [17, Theorem 1 and Remark 2], Stirling numbers can also be defined as in the form of the generating function

In addition to the above formulas, one may also express the Stirling numbers as (cf. ^[15,17])

The main uses of Stirling numbers are combinatorics, number theory, theory of partitions, and discrete probability.

2.3.   The semi-direct product of monoids and its presentation

Let $A$, $K$ be monoids and let $\eta$ be a monoid homomorphism $\eta: A \rightarrow \text{End}(K)$ such that $a \mapsto \eta_a$ $(a \in A)$ and $1 \mapsto id_{\text{End}(K)}$, where $\text{End}(K)$ denotes the collection of endomorphisms of $K$ which is itself a monoid with the identity $id: K \rightarrow K$. Then, we can construct a monoid ${\tilde M} = K \rtimes_\eta A$ with elements $(a, k)$, where $a \in A$ and $k \in K$ under the product $(a, k)(a^\prime, k^\prime) = (aa^\prime, (k\eta_{a^\prime})k^\prime)$. The identity of ${\tilde M}$ is $(1_A, 1_K)$. Then, for any $(a, k) \in {\tilde M}$ where $a \in A$, $k \in K$, we have $(a, k) = (a, 1_K)(1_A, k)$. Moreover, if the generating sets of $A$ and $K$ are defined as ${\mathbf a} = \left\{a_x: x\in {\mathbf x}\right\}$ and ${\mathbf k} = \left\{k_y: y\in {\mathbf y}\right\}$, then the generating set for ${\tilde M}$ is ${{\bf{\tilde m}}} = \left\{(a_x, 1_K), \, (1_A, k_y) : x\in {\mathbf x}, y\in {\mathbf y}\right\}$.

Let ${\cal P}_A = \langle {\mathbf x}\, ; \, {\mathbf r} \rangle$ and ${\cal P}_K = \langle {\mathbf y}\, ; \, {\mathbf s} \rangle$ be presentations of $A$ and $K$, respectively, on the generating sets ${\mathbf a}$ and ${\mathbf k}$. Then, we have isomorphisms $\psi_A^\star: {\tilde M}({\mathcal P}_A)\rightarrow A$, $\left[x\right]_{{\mathcal P}_A} \mapsto a_x$ and $\psi_K^\star: {\tilde M}({\mathcal P}_K)\rightarrow K$, $\left[y\right]_{{\mathcal P}_K} \mapsto k_y$ induced by the functions $\psi_A: {\mathbf x} \rightarrow A$, $x \mapsto a_x$ and $\psi_K: {\mathbf y} \rightarrow K$, $y \mapsto k_y$. For each $y \in {\mathbf y}$ and $x \in {\mathbf x}$, let $y\eta_x$ denote a positive word on ${\mathbf y}$ representing the element $k_y\eta_{a_x}$ of $K$, that is $\psi_K^\star\left[y\eta_x \right]_{{\mathcal P}_K} = k_y\eta_{a_x}$. We note that proving the existence of the equality $\left[y\eta_x \right]_K = \left[y \right]_K \eta_{\left[x \right]_A}$ is the key point to define a semi-direct product (in Section 3, we will present some different situations in separate cases to ensure the existence of this equality). Moreover, let $T_{yx}$ denote the relator $yx = x(y\eta_x)$, and let ${\mathbf t}$ be the set of all relators of the form $T_{yx}$ $(y \in {\mathbf y}$, $x \in {\mathbf x})$. Therefore, a presentation for ${\tilde M}$ on the generating set ${{\bf{\tilde m}}}$ is given by

Now, as a special case of the above material, let us take into account each of $K$ and $A$ as one relator monoids with presentations ${\mathcal P}_K = \langle {\mathbf y} \, ; \, S_+ = S_- \rangle$, where $S:S_+ = S_- \in {\mathbf s}$, and ${\mathcal P}_A = \langle {\mathbf x} \, ; \, R_+ = R_- \rangle$, where $R:R_+ = R_- \in {\mathbf r}$. Assume that the corresponding equality $\left[y\eta_x \right]_K = \left[y \right]_K \eta_{\left[x \right]_A}$ holds in this case. After all, we have the following presentation:

where each $y_j \in {\mathbf y}$ and $x_i \in {\mathbf x}$.

In our main results section (see Section 3), we will mainly consider $A$ as a finite cyclic monoid $C_{\mu, \delta}$ with a presentation $\langle x \, ; \, x^\mu = x^\delta\; (l < k) \rangle$ or as the infinite cyclic monoid ${\mathbb Z}$ with the presentation $\langle x \, ; \, \: \, \rangle$. Therefore, the single relator $R_+ = R_-$ in (2.8) will be the form of $x^\mu = x^\delta$ for the finite case or will be empty for the infinite case while the set of generators ${\mathbf x}$ will be only a single element $x$.

2.4.   Minimality of this presentation

We will recall the terminologies efficiency and minimality for the finitely presented monoid ${\tilde M}$ having a finite presentation ${\mathcal P}_{\tilde M}$ as defined in (2.7). For simplicity, let us denote it by ${\mathcal P}_{\tilde M} = \left[{\mathbf b}\, ; \, {\mathbf d} \right]$. Then, the Euler characteristic of ${\mathcal P}_{\tilde M}$ is defined by $\chi({\mathcal P}_{\tilde M}) = 1 - |{\mathbf b}| + |{\mathbf d}|$, where $|.|$ denotes the number of elements in the set. Also, there exists an upper bound $\delta({\tilde M}) = 1 - \text{rk}_{\mathbb Z}(H_1({\tilde M})) + d(H_2({\tilde M}))$, where $rk_{\mathbb Z}(.)$ denotes the ${\mathbb Z}$-rank of the torsion-free part and $d(.)$ denotes the minimal number of generators. In fact, by ^[1], it is always true that $\chi({\mathcal P}_{\tilde M}) \geq \delta({\tilde M})$. Then, we define $\chi({\tilde M}) = \text{min}\left\{ \chi({\mathcal P}_{\tilde M}) : {\mathcal P}_{\tilde M} \text{ is a finite presentation for } {\tilde M} \right\}$. Thus, for a presentation ${\mathcal P}_{\tilde M}^\prime$ of the monoid ${\tilde M}$, the presentation ${\mathcal P}_{\tilde M}^\prime$ is called minimal if $\chi({\mathcal P}_{\tilde M}^\prime) \leq \chi({\mathcal P}_{\tilde M})$, for all presentations ${\mathcal P}_{\tilde M}$ of ${\tilde M}$, and furthermore ${\mathcal P}_{\tilde M}^\prime$ is called efficient if $\chi({\mathcal P}_{\tilde M}^\prime) = \delta({\tilde M})$. Additionally, ${\tilde M}$ is called efficient if $\chi({\tilde M}) = \delta({\tilde M})$. Thus, efficiency yields minimality.

2.5.   A graph on this presentation

In ^[12], the authors introduced a new graph over the special type of semi-direct product of monoids while considering the presentation of this product, and they exposed the effectiveness of this graph by proving some graph-theoretical properties. We note that an illustration of this mentioned graph can be found in [12, Figure 1]. Without losing the meaning of this graph, a new version of it, which is related to the presentation given in (2.8), can be given as in the following:

Let us call $\Gamma$ to this new version. The vertex set $V(\Gamma)$ contains the following items:

$\texttt{(vtx1)}$ The whole generators ${\mathbf y}$ and single generator $x$ in ${\mathcal P}_{\tilde M}$;

$\texttt{(vtx2)}$ Words of the form $y_j\eta_x$, where $y_j \in {\mathbf y}$ of the related relations in ${\mathcal P}_{\tilde M}$;

$\texttt{(vtx3)}$ Words of the form $y_jy_{j+1}$ if there exists. In other words, the relators obtained by the consecutive generators in the presentation ${\mathcal P}_K$. Here, we do not take $y_jy_{j+2}$, $y_jy_{j+3}$ etc. as vertices to avoid complete graph variants.

$\texttt{(vtx4)}$ (If there exists) words of the form $x^\delta$ of the relation $x^\mu = x^\delta$ whenever $\delta \neq 1$. However, if $\delta = 1$, then it implies $x^\mu = x$ and so, since $x \in V(\Gamma)$, it is not necessary to take $x^\mu \in V(\Gamma)$.

The edge set $E(\Gamma)$ contains the followings items:

$\texttt{(edg1)}$ Match each vertex $y_j$ to unique element $x$ for all $y_j \in {\mathbf y}$;

$\texttt{(edg2)}$ Match each consecutive vertices $y_j$ and $y_{j+1}$ for all $y_j, y_{j+1} \in {\mathbf y}$;

$\texttt{(edg3)}$ Match each consecutive vertices $y_j$ and $y_{j+1}$ to the vertex $y_jy_{j+1}$ from both sides for all $y_j, y_{j+1} \in {\mathbf y}$;

$\texttt{(edg4)}$ Match each vertices $y_j$ to the related vertices $y_j\eta_x$ for all $y_j \in {\mathbf y}$;

$\texttt{(edg5)}$ Match the unique vertex $x$ to each vertices of the form $y_j\eta_x$.

$\texttt{(edg6)}$ (If there exists) match the unique vertex $x$ to the vertex $x^\delta$ if $\delta \neq 1$.

3.   Results

We construct our results in three sections. In each of them, by considering a semi-direct product of special monoids and the corresponding generating function of this product, we will expose their related graph dimensions. To do that, we will adapt the concepts given in Sections 2.1–2.5 to the situations we will examine here. The first step will be the adaptation of the presentation given in (2.8).

Unless stated otherwise, the notation $F_2$ will denote the free abelian monoid rank two, ${\mathbb Z}$ will denote the infinite cyclic monoid, and $C_{\mu, \delta}$ will denote the cyclic monoid of order $\mu$, where $\delta < \mu$. Additionally, in Figures 4–6 drawn below, all labels indicated as generators will show the values of vertices in the corresponding graphs.

Before presenting the main result sections, let us first guarantee the existence of Ⅲ in Figure 1.

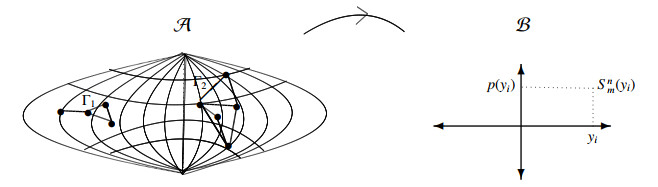
It is known that stereographic projection is a projection of objects from the surface of a sphere onto its equatorial plane, and also a powerful method for solving geometric problems (cf., for example, ^[14,20]). Unlike homotopy equivalence techniques, it preserves only the orientation of lines, nodes, circles, angles, and planes under a restricted ability to preserve position relations (this mentioned preservation is quite enough for our targets here). However, it is extremely useful, as projection problems are very common tools in theoretical mathematics, such as complex analysis, arithmetic geometry, and visualization of lines and planes.

Let ${\mathcal A}$ be a family of representations of graphs having special graph parameters, namely metric, multiset, outer multiset, and local multiset dimensions, on a $3$-dimensional surface of a sphere. On the other hand, let ${\mathcal B}$ be a familial representation of generating functions that can be expressed as array polynomials or Stirling numbers in $xy$-plane.

Lemma 3.1. There exists a stereographic projection from ${\mathcal A}$ to ${\mathcal B}$.

Proof. We will provide a global explanation of the proof rather than presenting it as an algebraic method, as selecting objects within ${\mathcal A}$ and ${\mathcal B}$ for a detailed mathematical proof would make it more difficult to convey our aim (we note that this technique is actively used in structural geology^* under the name of the lower hemisphere). Therefore, ${\mathcal B}$ is the equatorial plane or just a projection of ${\mathcal A}$. Please see the modeling of this approach in Figure 7.

^*One may check the reference https://geo.libretexts.org/@go/page/12507.

We remember that since the image of a circle on the sphere is a circle in the plane and the angle between two lines on the sphere is the same as the angle between their images in the plane^†, these facts are the master logic points for transferring graphs in the family of ${\mathcal A}$ to array polynomials (or Stirling numbers) in the family of ${\mathcal B}$. Nevertheless, the advantages for ${\mathcal A}$ and ${\mathcal B}$ cannot be denied and stated as follows. One may depict each graph in ${\mathcal A}$ in three dimensions, while the array polynomials and Stirling numbers in ${\mathcal B}$ can be expressed as single-variable polynomials, positioning them in the $xy$-plane. On the other hand, this above-indicated transfer can be done with the help of minimal size of words obtained from the minimal monoid presentations as already shown as a reciprocal connection in references ^[6,8]. In some sections below, these connections will be stated as propositions (see Propositions 3.3 and 3.8) when they will be needed.

^†A projection that preserves angles is called a conformal projection.

These are completed with the logical approach for the proof of the lemma.

To strengthen the meaning of the lemma, we should note at this point that the authors of ^[6,8] (in which the first two authors of this paper are also in the list of authors in these references) did catch a reciprocal relationship between array polynomials, kind of Stirling numbers, and minimal monoid presentations without mentioning stereographic projection. To do that, using a method of "pictures over monoid presentations" (see, for instance, ^[1]), which represent minimal monoids in $3$-dimensions on spheres, they have used stereographic projection from the family ${\mathcal C}$, which contains spherical monoid pictures, to the family ${\mathcal A}$. Thus, as a result of this stereographic projection, we obtained I$^\star$ in Figure 1 as a kind of inverse of Ⅰ. □

For the rest of this paper, we will always assume that Lemma 3.1 holds in the proofs of main results.

3.1.   Case of $F_2 \rtimes_\eta {\mathbb Z}$

Recall the development in Section 2.3. Assume that $K = F_2$ presented by $\langle y_1, y_2\, ; \, y_1y_2 = y_2y_1 \rangle$, and $A = {\mathbb Z}$ with the presentation $\langle x\, ; \, \: \rangle$. Additionally, for the matrix ${\mathcal D} = \left[\begin{array}{clcr} \beta_{11} & \beta_{12} \\ \beta_{21} & \beta_{22} \\ \end{array} \right],$ let $\psi$ be an endomorphism $\psi_{\mathcal D}$ of $K$ defined by $\left[y_1\right] \mapsto \left[y_1^{\beta_{11}}y_2^{\beta_{12}}\right]$ and $\left[y_2\right] \mapsto \left[y_1^{\beta_{21}}y_2^{\beta_{22}}\right]$. Therefore, as a special case of the presentation in (2.8), we obtain

for the monoid ${\tilde M} = F_2 \rtimes_{\eta} {\mathbb Z}$, and hence the proof of the following result can be found in ^[1]. Recall that the meanings of the terms efficiency, inefficiency, and minimality mentioned in the following lemma are presented in Section 2.4.

Lemma 3.2. ^[1] The presentation ${\mathcal P}_{\tilde M}$ in (3.1) is efficient if $\det {\mathcal D} \equiv 1 \mod p$, where $p$ is a prime. Additionally, it is minimal but inefficient if $\det {\mathcal D} = 2$.

By the formula of array polynomials in (2.3) and Lemma 3.2, the next result is proven in [6, Theorem 2] for the case ${\det {\mathcal D}} = 2$ and in [6, Theorem 3] for ${\det {\mathcal D}}\neq 2$.

Proposition 3.1. ^[6] Consider the monoid ${\tilde M} = F_2 \rtimes_\eta {\mathbb Z}$ with a presentation

Then, ${\mathcal P}_{\tilde M}$ in (3.2) has a set of generating functions

where $\det {\mathcal D} \neq 2$ and $S_m^n(x)$, $S_m^n(y_1)$, $S_m^n(y_2)$ are defined as in (2.3). According to the minimalism and so uniqueness, the same presentation in (3.2) is determined by the set of generating functions in (3.3).

We should realize that the presentation ${\mathcal P}_{\tilde M}$ in (3.2) is minimal but inefficient if $\det {\mathcal D} = 2$, and it is efficient only if $\det {\mathcal D} \neq 2$ and $\det {\mathcal D} \equiv 1 \mod p$ due to Lemma 3.2. However, since efficiency yields minimality, ${\mathcal P}_{\tilde M}$ is minimal in both cases.

Let us reconsider the formula in (2.5) for Stirling numbers and the presentation in (3.2). By substituting $b$ with $x$, $y_1$, and $y_2$, respectively, we get the following result, which was proven in [6, Corollary 3] as the Stirling numbers version of Proposition 3.1.

Proposition 3.2. ^[6] The presentation ${\mathcal P}_{\tilde M}$ in (3.2) has a set of generating functions

in terms of Stirling numbers, where there is no restriction on $\det {\mathcal D}$, and each term in these equalities is defined as in (2.5). Again, according to the minimalism and uniqueness, the same presentation in (3.2) is determined by the set of generating functions in (3.4).

With the above development, the first main result reads as follows.

Theorem 3.1. If a graph $\Gamma_1$ is obtained from the generating functions as defined in (3.3) and (3.4) with the help of the presentation given in (3.2), then $\Gamma_1$ partially answers the open problem of classifying the infinite multiset dimension by means of metric dimension, outer multiset dimension as well as local multiset dimension.

Before providing the proof, we first note that the word "partially" will be used in the statements of theorems throughout this paper, as our main theory is based on special cases of semi-direct products.

Proof. Suppose that the given presentation ${\mathcal P}_{\tilde M}$ in (3.2) is minimal but inefficient or just efficient. We hence know that the presentation ${\mathcal P}_{\tilde M}$ satisfies $\chi({\mathcal P}_{\tilde M}) \leq \chi({\mathcal P})$, for all presentations ${\mathcal P}$ of ${\tilde M} = K \rtimes_\eta A$. In other words, ${\mathcal P}_{\tilde M}$ certainly satisfies Lemma 3.2 but it may only satisfy minimality while inefficiency or only efficiency because efficiency inherently requires minimality. This tells us that ${\mathcal P}_{\tilde M}$ is in its optimal form. In other words, this ${\mathcal P}_{\tilde M}$ cannot be modified in any way, otherwise its ideal form is distorted. Therefore, being unable to change anything in this set guarantees the preservation of the related graph's value. Essentially, the assumption of minimality prevents any changes to this set. In fact, this is exactly what we need for our proof when obtaining the required graph because knowing that the presentation we are going to work on, which is the starting point of every process, cannot be changed, will increase the correctness of our proof. Thus, the smallest position (or equivalently, optimal form) of the base presentation ${\mathcal P}_{\tilde M}$ gives a big advantage on it since we cannot delete or add a new relator in the set of relations

By Propositions 3.1 and 3.2, we know that there exists a reciprocal matching between special generating functions, namely array polynomials and Stirling numbers, and the minimal presentation given in (3.2). Therefore, every process we will apply to the presentation (3.2) implies that these processes also hold for the mentioned special functions.

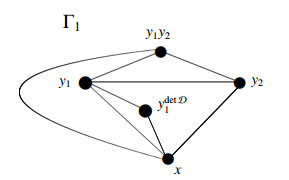
On the other hand, according to the material in Section 2.3, it is easy to understand that the set of relation ${\mathbf k}$ is quite important when one tries to construct the corresponding graph. Since this relation set is obtained by a monoid homomorphism $\eta: A \rightarrow \text{End}(K)$, $[x\eta_{y_j}] = [x]\eta_{[y_j]}$ for all $i \in \left\{1, 2\right\}$, we then get the relators of the form in (3.5). Now, let us prove the existence of the resulting graph $\Gamma_1$ as demonstrated in Figure 4. To do that, we will follow algorithmically the items ${\texttt{(vtx1)}}$–${\texttt{(vtx4)}}$ and ${\texttt{(edg1)}}$–${\texttt{(edg6)}}$ expressed in Section 2.5.

Hence, the vertex set $V(\Gamma_1)$ of the resulting graph $\Gamma_1$ contains the following items:

$\circ$ Total three generators $y_1$, $y_2$ and $x$ which correspond to ${\texttt{(vtx1)}}$.

$\circ$ The words $y_1^{\det {\mathcal D}}$ and $y_1y_2$ which correspond to ${\texttt{(vtx2)}}$.

$\circ$ Since the word $y_1y_2$ already exists by the above item, there is no need for the item given in ${ \texttt{(vtx3)}}$.

$\circ$ Since there is no relation on the generator $x$ in the presentation (3.2), there is no need for the item given in ${\texttt{(vtx4)}}$.

The edge set $E(\Gamma_1)$ contains the following adjacencies:

$\circ$ Match unique $x$ to each vertex $y_1$ and $y_2$ which corresponds to $\texttt{(edg1)}$.

$\circ$ Since the vertices $y_1$ and $y_2$ are consecutive, match these vertices with each other that corresponds to ${\texttt{(edg2)}}$.

$\circ$ Since the vertices $y_1$ and $y_2$ are consecutive, match each of them to the vertex $y_1y_2$ that corresponds to ${\texttt{(edg3)}}$.

$\circ$ Match $y_1$ to the vertex $y_1^{\det {\mathcal D}}$ which gives ${\texttt{edg4)}}$. Notice that we already matched the vertex $y_2$ to $y_1y_2$ in ${\texttt{(edg3)}}$.

$\circ$ Match the unique vertex $x$ to the vertices $y_1^{\det {\mathcal D}}$ and $y_1y_2$. This item corresponds to ${\texttt{(edg5)}}$.

$\circ$ No item ${\texttt{(edg6)}}$ exists for this case.

It is clear from graph $\Gamma_1$ in Figure 4 that the relators in the set (3.5) are the key point since they yield closed symmetric regions by considering the items $\texttt{(edg2)}$–$\texttt{(edg5)}$. The number of closed symmetric regions inside the graph is important in the meaning of determining the multiset dimensions. In other words, according to Lemma 2.1, if the resulting graph $\Gamma$ has at least three symmetric regions, then two of them have the same multiset representation with respect to any set of vertices of $\Gamma$, and in such a case, the multiset dimension of it is infinite. Moreover, the number of closed symmetric regions may also cause the existence of only two vertices that have the same multiset resolving sets with respect to any subset of vertices of the graph (see Lemma 2.2). These two cases can be seen in the graph $\Gamma_1$, which is drawn in Figure 4. Considering these two lemmas and the equation in (2.1), it may be easily seen that $\Gamma_1$ has an infinite multiset dimension.

Another way to see this infinity situation is by determining multiset representations with the help of (2.1). To do that, for simplicity, we replace each vertex as

and then choose a subset $S = \left\{v_2, v_3, v_5\right\} \subset V(\Gamma_1)$ as a resolving set. Then, by the properties on adjacency vertices about calculating multiset dimensions defined in [4, Lemma 2.1] or ^[10,13], we realize that $\dim_m(\Gamma_1) = \infty$. Nevertheless, by taking into account (2.2), we obtain that the outer multiset dimension is $3$. These facts are indicated in Table 1.

Moreover, by considering again the same subset $S = \left\{v_2, v_3, v_5\right\}$, we easily deduce that the local multiset dimension $\text{dim}_{lms}(\Gamma_1) = 3$ since multiset representations of the adjacent vertices are not equal to each other, i.e., $r_{ms}(v_i | S) \neq r_{ms}(v_j | S)$ while $v_iv_j \in E(\Gamma_1)$ for $1 \leq i < j \leq 5$.

The progress in counting dimensions shows us that the assumption of minimality in the base presentation not only gives the number of closed symmetric regions (or invariant symmetry) in the corresponding graph but also determines the minimization of this number.

Since graph $\Gamma_1$ also represents the generating functions defined in Eqs (3.3) and (3.4), the above processes complete the proof of the theorem. Hence, the desired result is proved. □

Example 3.1. Let us consider the matrix ${\mathcal D} = \left[\begin{array}{clcr} 2 & 0 \\ 0 & 1 \\ \end{array} \right].$ Then, by Lemma 3.2, we obtain an inefficient but minimal presentation ${\mathcal P}_{\tilde M}$ which satisfies Proposition 3.2. However, if we consider the matrix ${\mathcal D} = \left[\begin{array}{clcr} 3 & 0 \\ 1 & 1 \\ \end{array} \right],$ then again by the help of Lemma 3.2, we obtain an efficient presentation ${\mathcal P}_{\tilde M}$, which satisfies Propositions 3.1 and 3.2. In both cases, the related graphs (which are completely analogous figures as in Figure 4 except vertex $v_5$ having different labels) partially answer the open problem proved in Theorem 3.1.

3.2.   Case of $F_2 \rtimes_\eta C_{\mu, \delta}$

Similarly as in Section 3.1, let us suppose that $K = F_2$ presented by $\langle y_1, y_2\, ; \, y_1y_2 = y_2y_1 \rangle$. Now, $A$ is a finite cyclic monoid $C_{\mu, \delta}$ with a presentation $\langle x\, ; \, x^\mu = x^\delta \rangle$. For the same endomorphism $\psi$ with the same matrix ${\mathcal D} = \left[\begin{array}{clcr} \beta_{11} & \beta_{12} \\ \beta_{21} & \beta_{22} \\ \end{array} \right],$ as indicated in Section 3.1, the mapping $x \mapsto \psi_x$ induces a well-defined monoid homomorphism $\eta: A \rightarrow \text{End}(F_2)$ if and only if ${\mathcal D}_{\left[x^\mu \right]} = {\mathcal D}_{\left[x^\delta \right]}$, or equivalently, ${\mathcal D}^\mu \equiv {\mathcal D}^\delta \mod d$, where $d \mid (\mu - \delta)$. Then we have a presentation

for the monoid ${\tilde M} = F_2 \rtimes_{\eta} C_{\mu, \delta}$ as a variation of the presentation in (2.8). The necessity and sufficient conditions imply that ${\mathcal P}_{\tilde M}$ is efficient, and other details can be found in [7, Sections 2.1 and 2.2].

When we recall the characteristic and array polynomials regarding ${\mathcal P}_{\tilde M}$ in (3.6) for this section, we will not need the efficiency (or inefficiency while holding minimality) of ${\mathcal P}_{\tilde M}$. In fact, we will state and prove our other main result (see Theorem 3.2 below) under this condition.

By considering the condition ${\mathcal D}^\mu \equiv {\mathcal D}^\delta \mod d$, where $d \mid (\mu - \delta)$, since we certainly have $2 \times 2$-matrices ${\mathcal D}$, ${\mathcal D}^\mu$ and ${\mathcal D}^\delta$, one may take into account the related characteristic polynomials over these three matrices. As a part of generating functions, the authors in ^[8] determined characteristic polynomials over ${\mathcal P}_{\tilde M}$ in (3.6). As a rough reminder, let us assume that $\alpha_1$ and $\alpha_2$ are the only eigenvalues of the matrix ${\mathcal D}$. Since the entries of ${\mathcal D}$ are positive integers, $\alpha_1$ and $\alpha_2$ could be any numbers, including complex ones. However, with a special restriction, let us suppose that these eigenvalues are all real numbers. Considering a fundamental fact, we then have the eigenvalues of ${\mathcal D}^\mu$ as $\alpha_1^\mu$ and $\alpha_2^\mu$ whereas the eigenvalues of ${\mathcal D}^\delta$ as $\alpha_1^\delta$ and $\alpha_2^\delta$. Thus, for a variable $\nu$, the characteristic polynomials over each matrices ${\mathcal D}$, ${\mathcal D}^\mu$ and ${\mathcal D}^\delta$ will be the form of

respectively. Notice that, thinking about (3.7) as a piece of the system of characteristic polynomials that are obtained from any $2 \times 2$-matrix, we realize that there is an infinite number of polynomials as the type in (3.7) since one can find infinite number of matrices having positive integer entries that satisfy the condition ${\mathcal D}^\mu \equiv {\mathcal D}^\delta \mod d$. Nevertheless, by the definition of finite cyclic monoids, for a fixed value of $\mu$, one can choose the value $\delta$ from the set $\left\{ 1, 2, \cdots, \mu-1 \right\}$. Each of these systems in (3.7) will be constructed as the choice of $\delta$ in this set, and so we will have $\mu-1$ times different systems of characteristic polynomials as in (3.7) such that each of them contains an infinite number of polynomials. Building on all this knowledge of characteristic polynomials, the following pre-result was proved in [8, Theorem 1].

Proposition 3.3. ^[8] Up to equivalence, the presentation ${\mathcal P}_{\tilde M}$ in (3.6) is represented by a unique characteristic polynomial defined as in system (3.7).

The above proposition is important for us to show the existence of mutual connection indicated by Ⅰ and I$^\star$ in Figure 1, which is roughly mentioned in the last part in the proof of Lemma 3.1. The detailed and clear explanation of Proposition 3.3 has been given in [8, Theorem 1].

On the other hand, regarding the presentation ${\mathcal P}_{\tilde M}$ in (3.6), the following two results were also proved in [8, Theorems 4 and 5].

Proposition 3.4. ^[8] The presentation ${\mathcal P}_{\tilde M}$ defined in (3.6) has a set of generating functions

where array polynomials $S_m^n(x)$ and $S_m^n(y_i)$ are defined as in (2.4), and $\beta_{ij}$'s are the entries of the matrix ${\mathcal D}$ and $1 \leq i, j \leq 2$.

We have the following result by stating the above proposition more compactly.

Proposition 3.5. ^[8] The presentation ${\mathcal P}_{\tilde M}$ given in (3.6) has a single generating function

where array polynomials $S_m^n(\nu)$ are defined as in (2.4), $\nu$ represents three-ordered variables $(x, y_1, y_2)$ and $\alpha_1, \alpha_2$ are the eigenvalues of the matrix ${\mathcal D}$.

Now, we can prove the other main result in this paper.

Theorem 3.2. If a graph $\Gamma_2$ is obtained from the generating functions as defined in system (3.7) as well as in Propositions 3.4 and 3.5 with the help of ${\mathcal P}_{\tilde M}$ in (3.6), then $\Gamma_2$ does not partially answer the open problem of classifying the infinite multiset dimension using outer multiset dimension, but partially answers this problem by employing a metric dimension.

Proof. We will follow the same line as in the proof of Theorem 3.1.

We first need to realize that there is not any assumption, such as minimality with inefficiency or only efficiency, on the presentation ${\mathcal P}_{\tilde M}$ in (3.6) in the statement of the theorem. Therefore, we do not gain any advantage, such as the optimal form of the base presentation to be used. At the end of the proof, we will see that this disadvantage changes the statement of the theorem and no partial solution with outer multiset dimension can be found (we note that the existence of a partial solution for this case will be investigated in Theorem 3.3 below).

By considering Propositions 3.3–3.5, we know that there is a reciprocal match between special generating functions, namely array polynomials, and the standard presentation in (3.6). Therefore, every process that we will apply to presentation (3.6) yields that these processes are also true for the array polynomials as special generating functions.

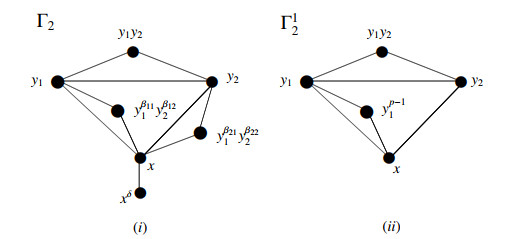
Applying algorithmic steps defined in Section 2.5 as those in the proof of Theorem 3.1, we get graph $\Gamma_2$ in Figure 5(i). In fact, considering graph items in Section 2.5 implies that there are similar situations about closed symmetric regions between the graphs in Figures 4 and 5(i). Thus, by using Lemmas 2.1 and 2.2, we can easily realize that $\Gamma_2$ has the infinite multiset dimension.

We could also have understood that the multiset dimension of graph $\Gamma_2$ is infinite by determining multiset representations defined in (2.1). Thus, for simplicity, let us replace the vertices as

in the graph $\Gamma_2$ drawn in Figure 5(i), and then let us choose a subset $S = \left\{v_1, v_6, v_7\right\} \subset V(\Gamma_2)$ as a resolving set. In fact, $S$ is not only a resolving set for (outer) multiset but also metric representations. Then, by [4, Lemma 2.1] or ^[10,13], we see that $\dim_m(\Gamma_2) = \infty$. Additionally, using (2.2), we unfortunately obtain that the outer multiset dimension is infinite, i.e., $\dim_{ms}(\Gamma_2) = \infty$. In addition, we have $\dim_{lms}(\Gamma_2) = \infty$ for this case as well. See Table $\ref{table:2}$ for the details.

A graph obtained from array polynomials via a standard presentation as in (3.6) cannot solve partially the open problem defined on infinite multiset dimension. However, one may assume that the existence of a partial solution can be considered in terms of metric dimensions. Hence, we derive the desired result.

Example 3.2. Consider the matrix ${\mathcal D} = \left[\begin{array}{clcr} 1 & 4 \\ 0 & 2 \\ \end{array} \right]$ with $\mu = 4$, $\delta = 2$ and $d = 2$. Since ${\mathcal D}^4 \equiv {\mathcal D}^2\mod 2$, we obtain a regular presentation ${\mathcal P}_{\tilde M}$ as given in (3.6) which satisfies Propositions 3.3–3.5 and Eq (3.7). Thus, we have a similar graph as in Figure 5(i). By Theorem 3.2, this graph does not partially answer the open problem of classifying the infinite multiset dimension using outer multiset dimension, but it partially answers this problem employing metric dimension.

Recall that Theorem 3.2 is obtained via a general presentation ${\mathcal P}_{\tilde M}$ in (3.6) without any extra assumptions, such as efficiency or minimality with inefficiency, on it. In the following, with a specific example, we will examine how it would affect the minimality while the inefficiency condition of the presentation on this result. In this context, let us consider the matrix ${\mathcal D} = \left[\begin{array}{clcr} p-1 & 0 \\ 0 & 1 \\ \end{array} \right]$ and an odd prime $p$. Then, we certainly get ${\mathcal D}^{2p+1} \equiv {\mathcal D}^1 \mod p$, and hence, by ^[7], we have the inefficient but minimal presentation

for the monoid ${\tilde M} = F_2 \rtimes_{\eta} C_{2p+1, 1}$ as a special case of the presentation in (3.6). We then have the following generating functions in terms of array polynomials on this minimal presentation (cf. [8, Theorem 7]).

Proposition 3.6. ^[8] The presentation ${\mathcal P}_{\tilde M}$ given in (3.8) has a set of generating functions

where array polynomials $S_m^n(x)$ and $S_m^n(y_i)$ are defined as in (2.4), and also $\alpha_1, \alpha_2$ are the eigenvalues of matrix ${\mathcal D}$.

Moreover, writing Proposition 3.6 in a better way yields the next pre-result (cf. [8, Corollary 2]) similarly to Proposition 3.5.

Proposition 3.7. ^[8] The presentation ${\mathcal P}_{\tilde M}$ given in (3.8) has a single generating function $p(\nu) = S_0^2(\nu) - p S_0^1(\nu) + p-1,$ where array polynomials $S_m^n(\nu)$'s are defined as in (2.4) and $\nu$ represents three-ordered variables $(x, y_1, y_2)$.

Additionally, one may easily state that array polynomials obtained for the presentations in (3.6) and (3.8) are congruent to each other, and so they construct congruence classes. Hence, since these generating functions are based on the characteristic polynomials, the proof of the following proposition [8, Theorem 8] has been done similarly as [8, Proposition 3 and Theorem 1].

Proposition 3.8. ^[8] Each array polynomial obtained from the presentations in (3.6) and (3.8) appears to be a congruence class. In addition, these presentations are represented by a single type of array of polynomials depending on this congruence. This single type may contain a unique congruence class of array polynomials in the case of the efficiency or minimality status of these presentations.

We note that Proposition 3.8 strengthens the importance of Proposition 3.3 (and Lemma 3.1) about the movement in I and I$^\star$ depicted in Figure 1.

The second main result of this section is the following.

Theorem 3.3. If a graph $\Gamma_2^1$ is obtained from the generating functions as defined in Propositions 3.6–3.8 via ${\mathcal P}_{\tilde M}$ in (3.8), then $\Gamma_2^1$ partially answers the open problem of classifying the infinite multiset dimension through outer multiset and metric dimensions.

Proof. We will continue with the same proof techniques we used in Theorems 3.1 and 3.2.

Note that unlike Theorem 3.2, in this result, our presentation ${\mathcal P}_{\tilde M}$ in (3.8) is minimal but inefficient. Therefore, as in the idea of Theorem 3.1, we have a significant advantage where no one can apply an operation on ${\mathcal P}_{\tilde M}$ to obtain a better status of it, which ensures that the resulting graph is certain.

Using the same ideas as in the previous main results and taking into account Propositions 3.6–3.8, there is a mutual correspondence between array polynomials (i.e., special generating functions) and ${\mathcal P}M$ in (3.8). Thus, each process we apply to ${\mathcal P}{\tilde M}$ will also apply to the related array polynomials mentioned in Propositions 3.6 and 3.7. Keeping this in mind, if we apply the items in Section 2.5 similarly as in the proofs of Theorems 3.1 and 3.2, we obtain the graph $\Gamma_2^1$ in Figure 5(ii). Notice that, three edges and one vertex are missing when we compare it with the graph $\Gamma_2$ in Figure 5(i). This is another difference from the result in Theorem 3.2. Nevertheless, we still have closed symmetric regions for the resulting graph, and hence, using Lemmas 2.1 and 2.2, we can figure out that the multiset dimension of $\Gamma_2^1$ is infinite.

The other approach, as we know, is to calculate it using a resolving set and the representations with the formula in (2.1). To do that, for the graph drawn in Figure 5(ii), if we substitute each vertex as

and choose a subset $S = \left\{v_1, v_2\right\} \subset V(\Gamma_2^1)$ as a resolving set both for metric and (outer) multiset representations then, again by ^[4,10,13] and using Equalities (2.1) and (2.2), we obtain $\dim_m(\Gamma_2^1) = \infty$ but $\dim(\Gamma_2^1) = 2 = \dim_{ms}(\Gamma_2^1)$. By the way, again we have $\dim_{lms}(\Gamma_2^1) = \infty$. These calculations are detailed in Table 3.

As the result of what we have done until now, a graph obtained from array polynomials stated in Propositions 3.6 and 3.7 regarding a minimal but inefficient presentation as defined in (3.8) partially solves the open problem on the infinite multiset dimensions in terms of outer multiset and metric dimensions. This completes the proof. □

Example 3.3. If we take $p = 5$ and $\beta_{21} = 4$ in the presentation ${\mathcal P}_{\tilde M}$ defined in (3.8), then it is easily seen that Theorem 3.3 holds.

We remark that $\Gamma_2^1$ is not only an example of $\dim_{ms}(\Gamma_2) = 2$ while $\dim_m(\Gamma_2) = \infty$ but also an example of having the smallest value in the meaning of outer multiset dimensions after path graphs in which the outer multiset dimension of path graphs is $1$. We recall that, by ^[13], $\dim_{ms}(\Gamma_{K_{n}}) = n-1$ for the complete graph $K_n$. Regarding this idea, we obtain the following conclusion, which will be presented without proof.

Corollary 3.1. There certainly exist graphs of array polynomials obtained by means of minimal infinite monoid presentations that have the same second smallest outer multiset dimension $2$ as the complete graph $K_3$.

3.3.   Case of $C_{\gamma, \lambda} \rtimes_\eta C_{\mu, \delta}$

Unlike in the previous sections, here we present a finite case. This subsection will reveal whether infinite monoids based on generating functions are the master factor in the theorems we obtain. However, the construction of this section is quite similar to that in Sections 3.1 and 3.2.

Let $A$ and $K$ be both finite cyclic monoids having presentations ${\mathcal P}_A = \langle x\; ; \; x^\mu = x^\delta \; (\delta < \mu) \rangle$ and ${\mathcal P}_K = \langle y\; ; \; y^{\gamma} = y^{\lambda} \; (\lambda < \gamma) \rangle$, respectively. Suppose $\psi_i$ $(0 < i < \gamma)$ is an endomorphism of $K$. Then we have a mapping $x \rightarrow \text{End}(K)$, $x \mapsto \psi_i$ which induces a homomorphism $\eta : A \rightarrow \text{End}(K)$ such that $x \mapsto \psi_i$ if and only if $\psi_i^\mu = \psi_i^\delta$. For $\psi_i^\mu$ and $\psi_i^\delta$ to be equal, they must agree on the generator $y$ of $K$. Therefore, we certainly need to have $\left[y^{i^\mu} \right] = \left[y^{i^\delta} \right]$, or, by omitting the square brackets, $y^{i^\mu} = y^{i^\delta}$. Then we obtain a presentation

for the monoid ${\tilde M} = C_{\gamma, \lambda} \rtimes_\eta C_{\mu, \delta}$. One may refer to ^[1] for the details of this construction.

By considering the materials in Section 2.4, we can present the next lemma, which has been proved in ^[1]. Let $d = \gamma-\lambda$, $n = i-1$ and $m = i^\mu - i^\delta$ and $p$ be a prime.

Lemma 3.3. ^[1] ${\mathcal P}_{\tilde M}$ in (3.9) is an efficient presentation if and only if $p \mid d$, $p \mid n$, $p \mid \frac{m}{d}$ and $p \mid \frac{m}{n}$. Further, ${\mathcal P}_{\tilde M}$ is minimal but not efficient if $i = 2$, $d \neq 2t$ $(t \in {\mathbb Z}^+)$ and $d \neq 1$.

Example 3.4. As an example of Lemma 3.3, let us take $p = 2$, $\gamma = 10$, $\lambda = 6$, $\mu = 4$, $\delta = 2$ and $i = 3$. So we get $d = 4$, $n = 2$, $m = 3^4 - 3^2$, $\frac{m}{d} = 18$ and $\frac{m}{n} = 36$, which imply an efficient presentation

Nevertheless, if we take $p = 2$, $\gamma = 10$, $\lambda = 3$, $\mu = 4$, $\delta = 2$ and $i = 2$, then we obtain the minimal but inefficient version of the presentation in (3.10) as follows:

Furthermore, in ^[6], it has been proven that there exist some generating functions in terms of array polynomials as in the following proposition.

Proposition 3.9. ^[6] There exists a set of generating functions

for the efficient version of the presentation ${\mathcal P}_M$ in (3.9) while

is a set of generating functions for the minimal but inefficient version of this presentation, where array polynomials $S_m^n(x)$ and $S_m^n(y)$ are defined as in (2.4), $\mu = \delta + r$ for $1 \leq r \leq \mu-1$, and also, for the inefficiency case, $\gamma-\lambda$ is an odd integer.

Theorem 3.4. If a graph $\Gamma_3$ is obtained from the set of generating functions as defined in Proposition 3.9 via presentations as given in (3.9)–(3.11), then $\Gamma_3$ partially answers the open problem of classifying the infinite multiset dimension through outer multiset dimension as well as metric and local multiset dimensions.

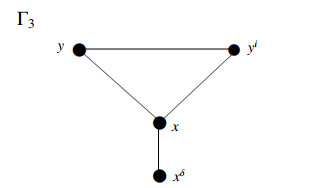
Proof. As in the proofs of the previous main results of this paper, let us first draw the graph related to the presentation ${\mathcal P}_{\tilde M}$ in (3.9). To do that, we will follow the graph definition in Section 2.5 and get the graph $\Gamma_3$ as demonstrated in Figure 6. The vertex set $V(\Gamma_3)$ contains the following items:

$\circ$ Both generators $y$ and $x$ which correspond to ${\texttt{(vtx1)}}$.

$\circ$ The word $y^i$ which corresponds to ${\texttt{(vtx2)}}$.

$\circ$ There is actually no word of the form $y_j y_{j+1}$, and so there is no need for the item given in ${\texttt{(vtx3)}}$.

$\circ$ The word $x^\delta$ of the relator $x^\mu = x^\delta$ whenever $\delta \neq 1$, which corresponds to ${\texttt{(vtx4)}}$.

On the other hand, the edge set $E(\Gamma_3)$ contains the followings:

$\circ$ Match unique $y$ to unique $x$, which corresponds to ${\texttt{(edg1)}}$.

$\circ$ There are no consecutive vertices $y_j$ and $y_{j+1}$, so ${\texttt{(edg2)}}$ and ${\texttt{(edg3)}}$ are not necessary.

$\circ$ Match unique $y$ to the vertex $y^i$, which corresponds to ${ \texttt{(edg4)}}$.

$\circ$ Match unique $x$ to the vertex $y^i$, which corresponds to ${\texttt{(edg5)}}$.

$\circ$ Match the unique vertex $x$ to the vertex $x^\delta$ whenever $\delta \neq 1$. This item corresponds to ${\texttt{(edg6)}}$.

The presentation in (3.9) is a standard form for the semi-direct product of two finite cyclic monoids, and there is no special assumption of minimality on the presentation, whether it is efficient or not. In fact, if we apply the same algorithm as above to each of the presentations in (3.10) and (3.11) by graphing them so that they have minimality, we see that the graphs of these presentations are the same as the graph in Figure 6. The main reason for this is that the relation $yx = xy^i$ exists in the same form in all the presentations (3.9)–(3.11). Another reason is that we absolutely need $\delta \neq 1$ in presentation (3.9) to capture an efficient or minimal but inefficient presentation. Thus, the edge between the vertices $x$ and $x^\delta$ must exist in all cases. As a natural consequence, the graph $\Gamma_3$ in Figure 6 represents all three presentations defined in (3.9)–(3.11).

Since Proposition 3.9 proved the efficient and the minimal but inefficient presentations as given in (3.10) and (3.11), respectively, there is no problem with considering these two presentations after this stage for the sake of proof. Thus, taking into account the sets of generating functions in terms of array polynomials presented in Proposition 3.9, as well as graph $\Gamma_3$ in Figure 6, we can proceed with the analysis.

Now, for simplicity, we replace each vertex as $v_1 = x^\delta$, $v_2 = x$, $v_3 = y$ and $v_4 = y^i$, and then choose a subset $S = \left\{v_1, v_3\right\} \subset V(\Gamma_3)$ as a resolving set. By Eqs (2.1) and (2.2), we get the following multiset and outer multiset representations:

The above list of representations implies that $S$ is a multiset and an outer multiset resolving set. Then, by Lemma 2.2 or because of the equal status of the representations $r_m(v_1|S) = r_m(v_3|S)$, we get directly $\dim_m(\Gamma_3) = \infty$. On the other hand, according to the definition of outer multiset dimensions, since for the vertices $v_1, v_3 \in S$ and $v_2, v_4 \in V(\Gamma_3) \setminus S$, there exists $r_{ms}(v_2|S) \neq r_{ms}(v_4|S)$ but $r_{ms}(v_1|S) = r_{ms}(v_3|S)$, we obtain $\dim_{ms}(\Gamma_3) = 2 = |S|$. Moreover, by taking the same subset $S$ as the metric and local multiset resolving sets, we can see that $\dim(\Gamma_3) = 2 = \dim_{lms}(\Gamma_3)$. Note that in the case of the local multiset dimension, since $r_m(v_1|S) = r_m(v_3|S)$ while $v_1v_3 \notin E(\Gamma_3)$, and the rest of the representations of adjacent vertices are different, we obtain $\dim_{lms}(\Gamma_3) = 2$.

Hence, we arrive at the desired result. □

Example 3.5. Other than Example 3.4, one may give a new application with a presentation ${\mathcal P}_{\tilde M} = \langle y, x\; ; \; y^{4t} = y^{t}, \, x^{3t} = x^t, \, yx = xy^{2} \rangle$, where $t$ is an odd positive integer. Proposition 3.9 clearly holds for ${\mathcal P}_{\tilde M}$, and the graph, which is analogous to the figure in Figure 6, satisfies the statement in Theorem 3.4.

Observation. Due to the structures of graphs in terms of adjacencies of vertices depicted in Figures 4 and 5, the infinite multiset dimensions yield the infinite local multiset dimensions. However, by the reason of the graph obtained from the finite monoid case, although $\dim_{m}(\Gamma_3) = \infty$, we get a finite local multiset dimension $\dim_{lms}(\Gamma_3) = 2$ in the graph given in Figure 6.

The obvious consequence of Theorem 3.4 can be stated as follows.

Corollary 3.2. Graphs of array polynomials obtained using presentations of finite monoids are also given a partial solution to the open problem of infinite multiset dimensions.

Furthermore, although Corollary 3.1 holds for this case, we can also have the following consequence for the metric dimension of $\Gamma_3$. We remind that $\dim(C_n) = 2$ for the cycle graphs and $\dim(K_n) = n-1$ for the complete graphs (cf. ^[10,13]), where $n \in {\mathbb Z}^+$.

Corollary 3.3. There are graphs of array polynomials obtained utilizing minimal presentations of finite monoids that have the same second smallest metric dimension $2$ as the cycle graph $C_n$ or the complete graph $K_3$.

4.   Conclusions

In ^[6,8], the authors made a reciprocal relationship between specific generating functions (namely array polynomials and Stirling numbers) and special minimal (efficient or not) monoid presentations. With the help of this mentioned connection and by considering the recent publication, ^[5], the first author of this paper exposed in this paper a partial solution of the problem (cf. [5, Open problem 3]) matching between specific graph dimensions and special generating functions in terms of metric, multiset, outer multiset, and local multiset dimensions. Therefore, we obtained here some partial answers for the problems indicated in [5, Open problems 1 and 3] in terms of the graphs obtained by special monoid presentations that are related to array polynomials and (in a single case) Stirling numbers.

This paper is one of the examples of matching materials from the branches of algebra (as monoid presentations), analysis (as generating functions), geometry (as stereographic projection), and combinatorics (as simple connected graphs). The story of this paper began with finding a full or at least a partial solution to the problem (originally mentioned in ^[10], and then in [5, Open problems 1]) about the classification of the infinite multiset dimensions of graphs. This indicated a problem that has been investigated in special cases (cf. ^[5]), and the authors of these papers figured out some partial answers.

There is a need to conduct many studies other than obtaining a full classification solution of the infinite multiset dimensions. For instance, one may study whether the full solution of [5, Open problem 3] is the NP-hard problem or not. Another one is to investigate matching special graph dimensions in terms of ideals over non-commutative rings, or more generally on algebras. The type of ideals in these structures would be the master in these studies. Finally, in coding theory, the status of multiset dimensions needs to be investigated.

However, it is worth noting that since graph dimensions are distance-based parameters, they lack substantial real-life applications (for instance, in chemical cell theory, etc.) compared to degree-based graph parameters. Consequently, further research in this area would be highly beneficial.

Author contributions

A. S. Cevik and I. N. Cangul: Conceptualization, Methodology, Visualization; A. S. Cevik, I. N. Cangul and Y. Shang: Investigation, Formal analysis, Resources; A. S. Cevik and Y. Shang: Validation; A. S. Cevik: Writing–original draft; I. N. Cangul and Y. Shang: Writing–review & editing. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

Dr. Yilun Shang and Dr. Ahmet Sinan Cevik are the Guest Editors of special issue "Mathematical properties of complex network and graph theory" for AIMS Mathematics. Dr. Yilun Shang and Dr. Ahmet Sinan Cevik were not involved in the editorial review and the decision to publish this article. The authors declare that they have no conflicts of interest.