The hybrid power mean of the generalized Gauss sums and the generalized two-term exponential sums

1.   Introduction

The study of systems with time delays poses a significant challenge for control researchers and engineers, primarily because stability and performance are often compromised. While most existing research focuses on systems with a single time-varying delay, many practical control applications, particularly in networked systems, necessitate the consideration of multiple time-varying delays ^[1,2,3,4]. This is due to the fact that signals transmitted from one point to another frequently encounter successive delays with varying characteristics. Such systems are commonly found in practical applications, including network control systems, mechanical systems, and biological systems ^[5,6,7]. Consequently, investigating the stability of systems with multiple time delays is essential. Specifically, the practical significance of linear systems with two-time delays has attracted considerable attention in recent years ^[8,9,10,11].

The Lyapunov stability theory is a classical method for analyzing the stability of delay systems ^[12,13,14]. By constructing an appropriate Lyapunov, the changes in the system's energy or state over time can be examined to determine the stability of the system ^{[15,16,17,18]}. Additionally, the linear matrix inequalities (LMIs) method is a commonly used technique in modern control theory ^[19]. This method transforms the stability conditions of delay systems into solvable matrix inequalities, allowing numerical optimization tools to be employed to obtain stability criteria for the system. Numerical simulation is also an effective tool for studying the stability of delay systems. By simulating the dynamic behavior of the system on a computer, the response of the system under different parameters and initial conditions can be observed, thereby analyzing its stability. In practical analyses, multiple methods are often combined, such as integrating the Lyapunov method with matrix inequality approaches, which can yield stronger stability results, especially in complex or high-dimensional delay systems. It is noteworthy that the time delays are assumed to be differentiable, which is a more stringent condition than that in some existing studies ^[20,21]. This limitation may affect the general applicability of our results. Future research could consider relaxing this assumption to include non-differentiable time delays, thereby broadening the scope of the proposed method and enhancing its relevance to practical applications. Addressing this issue could significantly enrich the understanding of the stability of systems with more complex delay structures.

Recently, many studies have constructed enhanced Lyapunov–Krasovskii functions (LKFs) by introducing time-weighted or space-weighted terms and have incorporated various integral inequalities to obtain less conservative stability criteria ^[22,23,24]. For example, the Wirtinger inequality ^[25], the Bessel–Legendre inequality ^[26], and the reciprocally convex inequality (RCI) ^[17] are popular integral inequalities that have been widely applied. Consequently, an increasing number of studies are beginning to improve upon these inequalities to better apply them in different integrals. It is noteworthy that the quadratic function associated with time delay frequently arises in the derivative of the LKFs. Determining the negative definiteness condition (NDC) of this quadratic function has been a crucial topic in developing tractable LMIs over the years. Numerous studies have been conducted on the conditions for ensuring the negative definiteness of quadratic functions; their work has established conditions for constructing the quadratic form reciprocally convex inequality ^[27,28].

The RCI effectively addresses these nonlinear characteristics, enhancing the accuracy of stability analysis. Thus, extending the concept of RCI becomes essential. In light of the recent extensive research on negative determination conditions for quadratic functions, their work has provided the necessary conditions for applying quadratic reciprocally convex inequalities in additive delay systems. The proposed bivariate quadratic reciprocally convex matrix inequality in this paper is inspired by their results. We have derived a bivariate quadratic reciprocally convex matrix inequality (BQRCI) which generalizes the original RCI, facilitating its application to bivariate quadratic functions ^[27]. By utilizing this inequality, we have successfully reduced the conservativeness of the stability criteria, leading to improved stability conditions. In addition, the application of the generalized BQRCI may be diverse, and future research could explore the integration of T-S fuzzy models with the proposed BQRCI framework. This may involve developing stability analysis methods that utilize T-S fuzzy representations to more effectively address complex nonlinear systems ^[29,30]. Furthermore, investigating the robustness of the BQRCI under various uncertainties within T-S fuzzy models could provide new insights and enhance the applicability of our findings in reality scenarios. Such extensions could make significant contributions to the field, offering a more comprehensive understanding of stability for systems characterized by time-varying delays and T-S fuzzy dynamics.

The main contributions of this paper can be summarized as follows:

$1)$ This paper generalized a new bivariate quadratic reciprocally convex inequality and applied this inequality to additive time-varying delay systems to reduce the conservativeness of system stability.

$2)$ Using the Lyapunov–Krasovskii functional method and the new bivariate quadratic reciprocally convex inequality, we obtained a new stability criterion and validated the effectiveness of the proposed method through some numerical examples.

The structure of this paper is as follows: In the second section, we introduce a new inequality related to bivariate quadratic functions, referred to as the improved RCI, called BQRCI. In the next section, we demonstrate the application of this new inequality in LKFs, leading to enhanced stability results and presenting the main theoretical findings. In the final section, we provide four numerical experiments to validate the new stability criterion.

Notations: Let $\mathbb{R}^n$ and $\mathbb{R}^{n \times m}$ denote the sets of $n$-dimensional Euclidean real vectors space and $n \times m$ real matrices. The symbols $\mathbb{S}^n$ and $\mathbb{S}_+^n$ represent the collections of $n \times n$ symmetric matrices and symmetric positive-definite matrices. The notation $diag$ refers to diagonal matrices, while zeros $(m, n)$ indicates the $m \times n$ matrices in $\mathbb{R}$ where all entries are zero. The identity matrix in $\mathbb{R}^{n \times n}$ is denoted by $I_{n}$; let $*$ be the symmetric part of a matrix. Lastly, we define $sym(A) = A + A^T$, where $T$ denotes the transpose of a matrix, and we set $\mu_{21} = \mu_2 - \mu_1$ and $h_{21} = h_2 - h_1$.

2.   Preliminaries

where $y(t) \in \mathbb{R}^n$ represents the state vector, the initial conditions of time delay are $\phi(t) \in \mathbb{R}^n$, and $\mathcal{A }, \mathcal{B} \in \mathbb{R}^{n \times n}$ are the given matrices. The time-varying delays $k_1(t)$ and $k_2(t)$ are differentiable functions that satisfy the following condition:

where $k_i$ and $\mu_i$ ($i = 1, 2$) are given positive constants.

Next, some important lemmas are introduced as follows:

Lemma 2.1. ^[25] For a matrix $R \in \mathbb{S}_+^{n}$, real scalars $a$ and $b$, if there exists a continuous differentiable function $x : [a, b] \rightarrow \mathbb{R}^n$, the following integral inequality holds:

where

Lemma 2.2. ^[27] For a bivariate quadratic function $f(x, y) = p_2x^2+p_1x +q_2y^2+q_1y+r_2xy+r_1$, where $p_2, p_1, q_2, q_1, r_2, r_1\in\mathbb{R}$, and $0\le h_1\le x\le h_2, \mu_1\le y\le\mu_2$, if $f(x, y) < 0$ for $\forall(x, y)\in[h_1, h_2]\times [\mu_1, \mu_2]$, the following inequalities hold:

Lemma 2.3. ^[17] Let $h_1, h_2, \ldots, h_N : \mathbb{R}^n \to \mathbb{R}$ be functions that take positive values in an open subset $H$ of $\mathbb{R}^n$. Then, the reciprocally convex combination of $h_i$ defined over $H$ satisfies the following equations:

subject to $\left\{ b_{i, j} : \mathbb{R}^n \to \mathbb{R}, \ b_{j, i}(t) = b_{i, j}(t), \begin{bmatrix} h_i(t) & b_{i, j}(t) \\ b_{j, i}(t) & h_j(t) \end{bmatrix} \geq 0 \right\}$.

Corollary 2.4. For any real positive scalars $\alpha, \beta, \gamma, \delta$, and holds $\alpha+\beta+\gamma+\delta = 1$, for given $R_{i}\in \mathbb{S}_+^n (i = 1, 2, \ldots, 4)$, and free matrices $H_{12}, H_{13}, H_{14}, H_{23}, H_{24}, H_{34}$, if the size of the matrix is $4\times 4$, the reciprocally convex inequality shows:

where the following restrictive conditions hold:

Remark 2.5. The reciprocally convex inequality can be efficiently applied in the stability of systems with time-varying delays; if the size of the matrix is $n\times n$, the number of restrictive conditions of the matrix inequality is $\frac{n(n-1)}{2}$.

Next, we introduce the bivariate quadratic reciprocally convex inequality based on Lemma 2.3 and Corollary 2.4, and also provide a detailed proof for this novel inequality.

Lemma 2.6. Bivariate quadratic reciprocally convex inequality (BQRCI). For any real positive scalars $\alpha, \beta, \gamma, \delta$, and holds $\alpha+\beta+\gamma+\delta = 1$, for given $R_{i}\in \mathbb{S}_+^n (i = 1, 2, \ldots, 4)$, and free matrices $S_{1j}, S_{2j}, S_{3j}, S_{4j}, S_{5j}, S_{6j}, U_{1j}$, $U_{2j}, U_{3j}, U_{4j}, U_{5j}, U_{6j}, U_{7j}, U_{8j}, U_{9j}$, $U_{10j}, U_{11j}, U_{12j}\in \mathbb{R}^{n\times n} (j = 1, 2)$, such that the following inequality holds:

When the condition below is satisfied:

where

Proof: We first write the difference of inequality in six parts,

For the first part,

where

In other words,

When Eq (2.6) holds,

Similarly, the other five parts can be described by

where

Hence, the lemma is proved whenever (2.7)–(2.11) hold.

Remark 2.7. If the free matrix $U_{1j}, U_{2j}, U_{3j}, U_{4j}, U_{5j}, U_{6j}, U_{7j}, U_{8j}, U_{9j}, U_{10j}, U_{11j}, U_{12j}, \ \text{for}\ j = 1, 2$ is the zero matrix and $S_{i2}$ is also the zero matrix for $i = 1, 2, \cdots 6$, the BQRCI will become the traditional reciprocally convex inequality.

Remark 2.8. As far as we know, a bivariate quadratic reciprocally convex matrix inequality is proposed for the first time, and the new lemma effectively addresses the bivariate quadratic terms generated in the system. Lemma 2.6 has broader applications and achieves less conservativeness.

3.   Stability analysis based on the bivariate quadratic reciprocally convex inequality and the improved Lyapunov–Krasovskii functional

For brevity, the following symbols are defined:

The important notations are denoted as

Then, we propose a new delay-dependent stability criterion for the system based on the bivariate quadratic reciprocally convex matrix inequality and the improved Lyapunov–Krasovskii functional.

Theorem 3.1. For known $k_i > 0$, $\mu_i > 0$ $(i = 1, 2)$, the time delays of the additive system: $k_1(t)$ and $k_2(t)$ follow conditions (2.2); the additive system (2.1) is asymptotically stable if there exists a matrix, $\begin{bmatrix} P_1 & P_2 \\ * & P_3 \end{bmatrix} \in \mathbb{S}^+_{2n}$, $Z_i\in \mathbb{S}^{+}_{n}$ $(i = 1, 2, 3, 4)$, $R_l \in \mathbb{S}^{+}$, for any $l = 1, 2, 3, 4, 5, 6$, $S_{1j}, S_{2j}$, $S_{3j}, S_{4j}, S_{5j}, S_{6j}, U_{1j}, U_{2j}, U_{3j}, U_{4j}, U_{5j}, U_{6j}$, $U_{7j}, U_{8j}, U_{9j}, U_{10j}, U_{11j}, U_{12j}\in \mathbb{R}^{n\times n} (j = 1, 2)$ such that LMIs (3.1)–(3.6) hold.

The important notations are defined:

Let us prove this theorem:

Proof: Choose some LKFs candidate first,

where

Then, we calculate the derivatives of the functionals, which are given by:

Using the Wirtinger-based integral inequality (2.3) to estimate the upper bounds of the derivative of $V_{3}(t)$.

By using Lemma 2.6,

Therefore,

Using Lemma 2.2, from the negative determined condition, $\dot{V} < 0$ holds if the LMIs conditions (3.1)–(3.3) hold.

On the other hand, there are some necessary conditions for the new reciprocally convex matrix inequalities (2.6)–(2.11):

Similarly, using Lemma 2.2 again,

This is ensured by the LMIs (3.4)–(3.6)) based on Lemma 2.2. Consequently, if the LMIs (3.1) to (3.6) are feasible, there exists a sufficiently small $\varepsilon > 0$ such that $\dot{V}(y_t) < -\varepsilon \|y(t)\|^2$. This condition guarantees that system (2.1) with additive time-varying delays and satisfying condition (2.2) is asymptotically stable. The proof is complete.

Remark 3.2. When using Lemma 2.6, we can let $\alpha = \frac{k_1(t)}{k_1+k_2}; \beta = \frac{k_2(t)}{k_1+k_2}; \gamma = \frac{k_2-k_2(t)}{k_1+k_2}; \delta = \frac{k_1 -k_1(t)}{k_1+k_2}$. In this way, the derivative of $V(y_t)$ can become a bivariate quadratic function. In the same way, the necessary condition $\mathbb{A}_{j}\le 0$ for the Lemma (2.6) can also be written as a bivariate quadratic function. The only difference is that the coefficients of $k_1(t)$ and $k_2(t)$ are 0.

Remark 3.3. The LMIs presented in Theorem 3.1 are based on the newly derived bivariate quadratic reciprocally convex inequality. This inequality allows for a more comprehensive application of bivariate quadratic negative definiteness conditions, enabling the formulation of LMIs that effectively utilize the delay information of the systems under discussion. Furthermore, the resulting stability criteria exhibit lower conservativeness without significantly increasing the number of decision variables (NoDVs). Thus, the advantage of the LMIs lies in their foundation on this inequality, which enhances the applicability of negative definiteness conditions while maintaining practical relevance in stability analysis.

4.   Numerical experiments

Example 4.1. Consider the time-varying delay system (2.1) with the given matrices $\mathcal{A}$ and $\mathcal{B}$,

The upper bounds for the delay derivatives, $\mu_1$ and $\mu_2$, are set at 0.1 and 0.8. Our objective is to determine the upper bounds of delays $k_1(t)$ and $k_2(t)$, specifically finding $k_1$ and $k_2$ when one is known. Some previous methods use traditional RCI like ^[31], which do not achieve results as favorable as those obtained by applying BQRCI. Table 1 compares different $k_1$ values with the results from previous studies, including some recent research ^[32,33,34], and Theorem 3.1 under different delay conditions.

As shown in Table 1, the upper bound of $k_2$ obtained using the current method is greater than that of several recent results, such as those in ^[32,33,34], while the NoDVs is smaller than in ^[33]. Therefore, this method effectively controls the increase in computational complexity without significantly raising the number of decision variables, while also achieving less conservativeness for the system.

Example 4.2. Consider the time-varying delay system (2.1) with the given matrices $\mathcal{A}$ and $\mathcal{B}$,

We also assess the decay rates for different values of $k_2$. From Table 2, it can be observed that the upper bound of $k_2$ obtained by the current method is greater than that of several recent results, including ^[31,34,39], and NoDVs is smaller than ^[31,33,39]. Therefore, this method controls the increase of computation without excessively increasing NoDVs. The proposed method can yield an improved stability criterion for additive time-varying delay systems.

Example 4.3. Consider the time-varying delay system (2.1) with the given matrices $\mathcal{A}$ and $\mathcal{B}$,

From Table 3, it can be seen that the upper bound of $k_1$ and $k_2$ obtained by the current method is greater than that of several recent results, including ^[10,32,40]. Therefore, this method achieves less conservativeness for the system.

Example 4.4. By introducing the virtual state and measurement output vectors defined as $y(t) = \left[\begin{array}{llll}\varDelta f & \varDelta P_m & \varDelta P_v & \int \mathcal{A} C E\end{array}\right]^T$ and $z(t) = \left[\mathcal{A} C E \quad \int \mathcal{A} C E\right]^T$, the closed-loop LFC system can be represented as the linear system (2.1), which includes two additive time-varying delays. The system parameters are presented in the following format:

with the parameters given in ^[31]: $\mathcal{M} = 10, \mathcal{D} = 1, \mathcal{T}_{c h} = 0.3, \mathcal{T}_g = 0.1, \mathcal{R} = 0.05$, $\varpi = 21$.

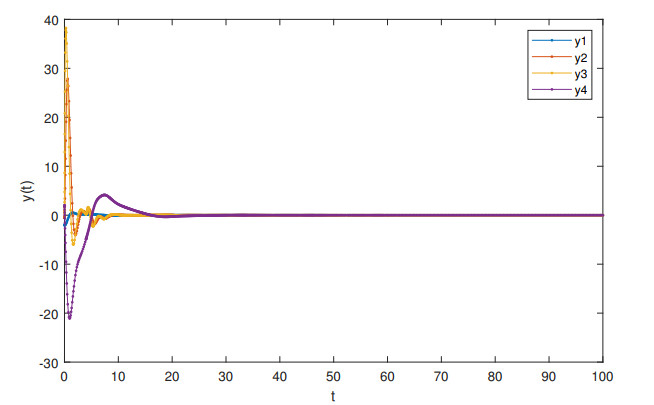
To facilitate comparison with existing results, Figure 1 presents the findings for the case where $\mathcal{K}_I = 0.2$, $\mathcal{K}_P = 0.1$, $\left|\dot{k}_1(t)\right| \leq 0.1$, and $\left|\dot{k}_2(t)\right| \leq 0.8$. A simple simulation is conducted with the assumption of time-varying delays defined as $k_1(t) = \frac{1}{2} \sin(0.2 x(t)) + \frac{1}{2}$ and $k_2(t) = \frac{3.278}{2} \sin\left(\frac{1.6}{3.278} y(t)\right) + \frac{3.278}{2}$. The results of this simulation are illustrated in Figure 1, where the LFC achieves its objectives, and the control system remains stable for MAUB $k = 3.278$. The state responses converge to zero, confirming that system 2.1 is stable as shown in Figure 1 under condition Example 4.4.

5.   Conclusions

In this study, we successfully generalize a bivariate quadratic reciprocally convex inequality that is effectively applied to additive time-varying delay systems, significantly reducing the conservativeness typically associated with stability analyses. By employing the Lyapunov–Krasovskii function method in conjunction with this new inequality, we derive a novel stability criterion. Ensure that the conservativeness of the system decreases while controlling the excessive growth of the NoDVs without significantly increasing the computational burden. The effectiveness of the new approach is demonstrated through four numerical examples, underscoring its practical applicability in enhancing the stability analysis of additive time-varying delay systems.

Use of Generative-AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Author contributions

Xiao Ge: conceptualization, methodology, software MATLAB, writing-review and editing; Xinzuo Ma: software MATLAB, writing-review and editing, validation; Yuanyuan Zhang: methodology, writing-original and draft, software MATLAB, validation; Han Xue: software MATLAB, validation; Seakweng Vong: writing-review and editing, validation, funding acquisition, supervision. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This research is funded by the Science and Technology Development Fund, Macau SAR (File No. 0151/2022/A) and the University of Macau (File No. MYRG-GRG2023-00037-FST-UMDF, MYRG-GRG2024-00100-FST-UMDF). Thanks to Professor SeakWeng Vong for his guidance and help.

Conflict of interest

The authors declare no conflicts of interest.