Stability analysis of Cohen-Grossberg neural networks with time-varying delay by flexible terminal interpolation method

1.   Introduction

In 1983, M. Cohen and S. Grossberg proposed a new type of neural network model (CGNN). In real life, CGNN is broadly used in image processing, speed detection of moving targets, association memory and other fields. Scholars at home and abroad have also studied CGNN from different perspectives. In real-world use, it is paramount to ensure that the designed neural network has strong stability. However, owing to the switching speed of the amplifier and the time delay of the signal during transmission, CGNN may experience a time lag in actual work, which is an important factor causing network instability. In recent years, many studies on stability problems have also been carried out for time-delay neural networks ^{[1,2,3,4,5,6,7,8,9,10,11]}.

The switched system is a model for studying complex systems from the perspective of systems and control^[12,13,14]. Mechanical systems and power systems can be displayed in the form of switched systems, and they can also play a vital function in other fields, including ecological science, energy environment and other fields ^[15]. Simultaneously, the switched system is a complex system composed of a series of succession or dissociation subsystems and switched rules that enable subsystems to switch between them. Switched rules control the operation of the whole switched system, and the switched rules can also be called switched signals, switching laws or switched functions. They are usually based on the segmented constant function of time or status and events. D. Liberzon and A. S. Morse describes in detail the stability, design process and development of the switched system ^[16]. Compared with the previous CGNN research results ^{[17,18,19,20]}, the value of the CGNN ^[21] connection the weight matrix will change over time when combined with a switching system. It can adjust the dynamic behavior of the system through switching rules and strategies, and respond to the dynamic evolution process of the system without cutting. The connection weight matrix of the system is usually fixed and cannot show dynamic changes. A method based on quantitative sliding mode was used to solve the synchronization problem of recursive neural networks with time-varying delays and discrete time ^[22]. In order to reduce the computational complexity, the authors introduced quantitative technology to discretely process the network state and finally used Lyapunov theory and the Barbalat lemma to deduce the convergence of the system. Among them, sliding mode control is a nonlinear control method with strong robustness. It realizes the switching and control of the system state by introducing a sliding surface. It has the characteristics of strong stability, short adjustment time and strong tracking ability, and it can also show the dynamic changes of the system. However, this paper adds the switching system to the traditional CGNN, uses LMIs and quadratic convex inequality to establish the criterion of the gradual stability of SCGNN, and it further studies the stability of SCGNN and the dynamic evolution process of SCGNN.

For CGNN with time-changing delay, it has been proven that the equilibrium point exists and is unique, and the analysis of stability has been widely studied. However, few people optimize the stability of the system. In ^[23] and ^[24], the weighting-delay method and the flexible terminal interpolation method were used to study the recursive neural network, respectively. The generation of time delay is not necessarily uniform, and there may be asymmetry, so it is more conservative to study the impact of time delay on system stability as a fixed interval ^{[25,26,27,28]}, which usually cannot meet the actual needs. However, the above two methods, through one or more parameters, change the length of the interval, divide a fixed interval into multiple variable sub-intervals, and obtain the maximum allowable upper bound of time delay by using LMIs and constructing an appropriate LKF, which reduces the conservatism of the system. Comparing the experimental results of ^[23] and ^[24], the upper bound with the allowable delay obtained by using the flexible terminal interpolation method is larger. In ^[29], through the method of Halanay's inequality and Lyapunov's functional, the authors put forward a new sufficient condition to ensure that the time-changing delay CGNN has a unique equilibrium solution and global stability. In ^[30], based on the non-singular M-matrix theory, the method of transformation matrix is used to carry out an appropriate linear transformation of the M-matrix and turn it into a special form with good properties, so as to achieve the positive judgment of the system and obtain a new criterion to ensure the high-order delay discrete CGNN has global exponential stability. However, all these methods lack consideration for reducing the conservatism of the system.

Therefore, this paper uses the flexible terminal interpolation method to study CGNN with time delays, in order to reduce the conservatism of the system and make its results more general and more practical. Moreover, the flexible terminal interpolation method can be adjusted according to the characteristics of the data to adjust the size of the subinterval through a parameter, which greatly reduces the calculation burden and reduces the calculation time cost while ensuring the accuracy of interpolation.

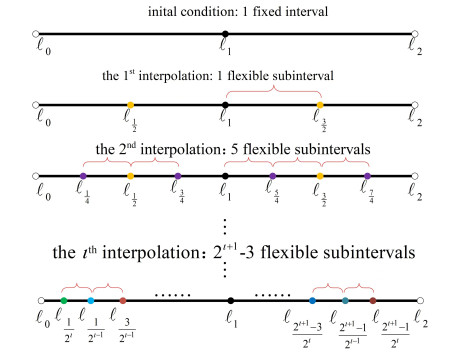
The flexible terminal interpolation method uses $\imath$ interpolation and an adjustable parameter to divide the fixed time-delay interval $[\ell_0, \ell_2]$ to $2^{\imath +1}-3$ flexible time-delay intervals, as shown in Figure 1.

Let the adjustable parameter be $\eth$, and $\ell _1 = \ell (t)$, $\vartheta = 1-\eth$. The terminal point of each subinterval can be expressed as (taking the second interpolation as an example)

$\dot{\ell } _{\frac{1}{2}} = \eth\dot{\ell }(t)$, $\dot{\ell } _{\frac{3}{2}} = \eth\dot{\ell }(t)$, $\dot{\ell } _{\frac{1}{4}} = \eth^{2}\dot{\ell }(t)$, $\dot{\ell } _{\frac{3}{4}} = \eth(2-\eth)\dot{\ell }(t)$.

We can see that the endpoint value of each flexible subinterval is a convex combination of $\ell _0$ and $\ell (t)$, or a convex combination of $\ell _2$ and $\ell (t)$. The terminal of each time interval is adjustable, that is, the delay interval is adjusted as a whole, which will enable us to capture more time delay information, and the stability result will be more accurate and effective.

Notation: $\mathbb{R}^{{\eta} \times {\eta} }$ represents the set of $\eta$-row $\eta$ column matrices in which all elements are real numbers; $Y^{T}$ represents the transpose of the matrix $Y$; $Q > 0$ means that the matrix $Q$ is called a positive fixed matrix; $col[Y_1, Y_2] = [Y^{T}_{1}, Y^{T}_{2}]^{T}$; $He[Y] = Y^{T}+Y$; $diag\{...\}$ is a matrix with all $0$ elements except the diagonal. $\ast$ is the part of the matrix about the symmetry of the main diagonal.

2.   Preparatory knowledge and assumptions

The CGNN with time-varying delays can be described:

where $\hat{\mathfrak{x}}_i(t)\in R^{{\eta} }$ is the state vector of the ith neuron at $t$ moment. $d_i(\hat{\mathfrak{x}}_i(t))$ is the amplification function, $a_i(\hat{\mathfrak{x}}_i(t))$ represents a behaved function, and $\bar{\mathfrak{F}}_i(\cdot)$ denotes the bounded neuronal activations function.

$\mathfrak{B} = (b_{ij})_{{\eta} \times {\eta} }$, $\mathfrak{C} = (c_{ij})_{{\eta} \times {\eta} }$ are the connection weights that reflect how the neuron i connects with the neuron j. $\ell _j(t)$ are the time delay parameters. $\jmath_i = \left [\jmath_1, \jmath_2, ...., \jmath_{\eta} \right]$ denotes the external bias on ith neuron at time t and $\jmath_1, \jmath_2, ...., \jmath_{\eta}$ all are constant.

CGNN (2.1) is transformed into

where

We will need to use the following assumptions and lemma.

Assumption 2.1. Each function $d_i(\hat{\mathfrak{x}}_i(t))$ is bounded and locally continuous, and there exist non-negative constants $\underline{l_i}$ and $\overline{l_i}$ such that $0\le \underline{l_i} \le d_i(\hat{\mathfrak{x}}_i(t))\le\overline{l_i} < +\infty$ for all $\hat{\mathfrak{x}}_i(t)\in R^{{\eta} }$.

Assumption 2.2. Each function $a_i(\hat{\mathfrak{x}}_i(t))$ is bounded and continuous and there exist principal constants $\mu _i > 0$, such that

Assumption 2.3. $\bar{\mathfrak{F}}_i(\cdot)$ is a bounded activation function and there are positive constants $k_i$ $(i = \underline{1, 2, ...{\eta} })$, such that

Definition 2.1. ^[31] For all possible coefficient matrices $\mathfrak{B}$ and $\mathfrak{C}$ in CGNN (2.1) with time-varying delay, when the system remains stable in a certain state, the state is the equilibrium point of the system, and this equilibrium point is asymptotically stable, so it can be said that the model is asymptotically stable.

Definition 2.2. ^[32] System (2.1) remains stable in some states, which are called equilibrium points. The equilibrium point is a constant vector $\hat{\mathfrak{x}}^{*} = (\hat{\mathfrak{x}}^{*}_1, \hat{\mathfrak{x}}^{*}_2, ...., \hat{\mathfrak{x}}^{*}_{\eta})^{T}$, which can make

Lemma 2.1. ^[33] (Quadratic reciprocally convex inequality) For given matrices $J_i\in \mathbb{R}^{{\eta} \times {\eta} }$, real number scalar $q_i, q_j\in [0, 1]$, and $\wp_i\in (0, 1)$ with $\sum_{i = 1}^{{\eta} } \wp_i = 1$, if there exists $T_i\in \mathbb{R}^{{\eta} \times {\eta} }$, $L_{ij}\in \mathbb{R}^{{\eta} \times {\eta} } \; (j > i), \; i = \underline{1, 2, ...{\eta} }$, let the following matrix hold:

Then, for any vector $\zeta _i\in R^{{\eta} }$, the following inequality holds ^[23]:

Theorem 2.1. Under Assumptions 2.1-2.3, if the following inequality condition is satisfied, then the system has only one stable state, and the state (balance point) is unique.

where

for any matrix $\mathfrak{B} = (b_{ij})_{{\eta} \times {\eta} }$,

the $\lambda _{m}(\mathfrak{B}^{T}\mathfrak{B})$ here is the largest of all eigenvalues of the matrix $\mathfrak{B}^{T}\mathfrak{B}$.

Proof. Let $\hat{\mathfrak{x}}^{\ast } = (\hat{\mathfrak{x}}^{\ast }_{1}, \hat{\mathfrak{x}}^{\ast }_{2}, ...., \hat{\mathfrak{x}}^{\ast }_{{\eta} })^{T}$ denote an equilibrium point of neural network model (2.2). Then,

Because $D(\hat{\mathfrak{x}}^{\ast })$ is a positive matrix with zero elements outside the diagonal line, replace (2.7) with

Let

where $\check{\Im}(\hat{\mathfrak{x}}) = (\check{\mathfrak{k}}_1(\hat{\mathfrak{x}}), \check{\mathfrak{k}}_2(\hat{\mathfrak{x}}), ...., \check{\mathfrak{k}}_{\eta} (\hat{\mathfrak{x}}))^{T}$ with

As is well-known, if $\check{\mathfrak{k}}_i(\hat{\mathfrak{x}})$ is a homeomorphism of $R^{{\eta} }$, then (2.8) has a unique solution. From ^[2], it can be seen that $\check{\mathfrak{k}}_i(\hat{\mathfrak{x}})$ in this paper is a homeomorphic map to $R^{{\eta} }$, if $\check{\Im}(\hat{\mathfrak{x}})\ne \check{\Im}(\check{\mathfrak{y}}), \forall \hat{\mathfrak{x}}\ne \check{\mathfrak{y}}$, and also $\hat{\mathfrak{x}}, \check{\mathfrak{y}}\in R^{{\eta} }$, and $\left \| \check{\Im}(\hat{\mathfrak{x}}) \right \| \to \infty$ as $\left \| \hat{\mathfrak{x}} \right \| \to \infty$.

Let $\hat{\mathfrak{x}}\ne \check{\mathfrak{y}}$, which implies two cases:

(I) $\hat{\mathfrak{x}}\ne \check{\mathfrak{y}}$ and $\bar{\mathfrak{F}}(\hat{\mathfrak{x}})-\bar{\mathfrak{F}}(\check{\mathfrak{y}})\ne0$,

($\amalg$) $\hat{\mathfrak{x}}\ne \check{\mathfrak{y}}$ and $\bar{\mathfrak{F}}(\hat{\mathfrak{x}})-\bar{\mathfrak{F}}(\check{\mathfrak{y}}) = 0$.

Now, case (I):

and specify the above equation:

Multiply the left and right of Eq (2.11) by $sgn(\hat{\mathfrak{x}}_i-\check{\mathfrak{y}}_i)$, where

at this time. Then, (2.11) becomes

form which we get

where $\left \| \hat{\mathfrak{x}}-\check{\mathfrak{y}} \right \|_1 = \sum_{i = 1}^{{\eta} }\left | \hat{\mathfrak{x}}_i-\check{\mathfrak{y}}_i \right |$, for $\hat{\mathfrak{x}}-\check{\mathfrak{y}}\ne0, \; \left \| \mathfrak{B} \right \|_1+\left \| \mathfrak{C} \right \|_1 < \frac{\mu _m}{K_m}$, implies that

or

It can be seen that for any $\hat{\mathfrak{x}}\ne \check{\mathfrak{y}}$, the result of $\check{\Im}(\hat{\mathfrak{x}})\ne \check{\Im}(\check{\mathfrak{y}})$.

Now, case ($\amalg$):

from which one can obtain

$\hat{\mathfrak{x}}-\check{\mathfrak{y}}\ne0$ implies that

or

From the above two inequalities, we can understand that when any $\hat{\mathfrak{x}}\ne \check{\mathfrak{y}}$ is arbitrary, it will make $\check{\Im}(\hat{\mathfrak{x}})\ne \check{\Im}(\check{\mathfrak{y}})$.

Substitute $\check{\mathfrak{y}} = 0$ into inequality (2.12) to get

Therefore,

That is, when $\left \|\hat{\mathfrak{x}}\right \|\to \infty$, $\left \| \check{\Im}(\hat{\mathfrak{x}})\right \|\to \infty$.

The above is the whole proof process of Theorem 2.1.

Remark 2.1. In terms of the construction of LKF, different construction methods can solve different types of time delay systems, and the utilization rates of different types of time-delay information are also different. How to construct a LKF with a small amount of computation and less conservativeness is worth further exploration.

3.   Model building and preparation

The system state is translationally transformed so that the equilibrium point is at the origin of the coordinate system. The balance point is set to $\hat{\mathfrak{x}}^{*} = (\hat{\mathfrak{x}}^{*}_1, \hat{\mathfrak{x}}^{*}_2, ...., \hat{\mathfrak{x}}^{*}_{\eta})$, and ${\bar{\kappa}} (t) = \hat{\mathfrak{x}}(t)-\hat{\mathfrak{x}}^{*}$:

or with another way of representation,

where

For the transformed system (3.1), we have

The time-delay neural network model plays a vital role in practical applications: function approximation, parallel calculation, associative memory, etc. Moreover, the main feature of the switching system is that it has a constraint on the state variable. The state variable can be an input variable or output variable. Therefore, further research on SCGNN with time delay is the next step.

Consider the following SCGNN models with time-varying delay:

$\bar{\hbar}({\bar{\kappa}} (t)) = (\bar{\hbar}_1({\bar{\kappa}} _1(t)), \bar{\hbar}_2({\bar{\kappa}} _2(t)), ...., \bar{\hbar}_{\eta} ({\bar{\kappa}} _{\eta} (t)))^{T}$ is an activation function that activates neurons. $\ell$ is bounded, and $\sigma (t):[t_0, +\infty)\longrightarrow N = \left \{\underline{1, 2, ..., N} \right \}$ is a segmented constant function and is related to time $t$. We call it a switch signal to activate a specific subsystem. There are $N$ neural network subsystems. The corresponding switching sequence is represented as $\sigma (t):\left\{ (t_0, \sigma (t_o)), ..., (t_\imath, \sigma (t_\imath)), ..., \mid \sigma (t_\imath)\in N, \imath = 0, 1, ... \right\}$, $t_o$ is the initial time, and $t_\imath$ is the switching moment of the $\imath$th subsystem. At the same time, $\sigma (t_\imath)$ means that the $\imath$th subsystem is activated. For any $\imath$, the matrix $(\mathfrak{B}_{\sigma}, \mathfrak{C}_{\sigma})$ is included in the finite set $\left \{ (\mathfrak{B}_1, \mathfrak{C}_1), (\mathfrak{B}_2, \mathfrak{C}_2), ...(\mathfrak{B}_{\eta}, \mathfrak{C}_{\eta}) \right \}$.

In this article, it is assumed that the switching signal $\sigma (t)$ is not known at the beginning, and $\sigma (t_{\imath}) = \imath$, define the function $\xi (t) = (\xi_1(t), \xi_2(t), ..., \xi_N(t))^{T}$, where $\imath = 1, 2, ..., N$.

$\xi _\imath (t) = \begin{cases}1, & \text{when the switched system is described by the}~ k \text{th mode } \mathfrak{B}_{\sigma (t_\imath)}, \ \mathfrak{C}_{\sigma (t_\imath)}, \\ 0, & \text{otherwise}. \end{cases}$

Now, we can change CGNN (3.2) with switching signal to an expression, that is,

and it follows that $\sum_{\imath = 1}^{N} \xi _\imath (t) = 1$.

Translating the equilibrium point of system (2.1) to the origin: $(\hat{\mathfrak{x}}^{*}_1, \hat{\mathfrak{x}}^{*}_2, ..., \hat{\mathfrak{x}}^{*}_{\eta})$ to $(0, 0, ..., 0)$, at this time, ${\bar{\kappa}} (0) = 0$. Know by Assumption 2.2:

and hence,

Now,

where ${\bar{\kappa}} (t)\in R^{{\eta} }$ is the state vector, $\mu _i\alpha ({\bar{\kappa}} (t))$, $\alpha ({\bar{\kappa}} (t))\mathfrak{B}_{\sigma (t _\imath)}$, $\alpha ({\bar{\kappa}} (t))\mathfrak{C}_{\sigma (t_\imath)}$ are known continuous function matrices.

The time-varying delay $\ell (t)$ satisfies

then, $\ell _0$, $\ell _2$, $\rho _1$, and $\rho _2 > 0$ are constants, which we already knew.

For the activation function $\bar{\hbar}_l(\cdot)$ $(l = \underline{1, 2, ..., {\eta} })$,

where $r_l$ are real numbers, and $R = diag\{r_1, r_2, ..., r_{\eta} \}$.

4.   Main results

Combining the flexible terminal interpolation method with the secondary convex inequality is conducive to capturing more delay information and obtaining sufficient conditions to ensure the stability of CGNN (3.2) with switching signal by selecting the appropriate LKF function.

Theorem 4.1. For given scalars $\ell _0$, $\ell _2$, $\rho _1$, $\rho _2$, $0 < \delta \le \min \{ 1, \frac{1}{\rho _2} \}$ and $\ell (\mathfrak{d}, b) = \ell _{\mathfrak{d}}-\ell _b$, $\varrho = 1-\delta$, the SCGNN (3.2) is asymptotically stable if there exist $Q > 0$, $P_i > 0$, $J > 0$, diagonal matrices $W_1 > 0$, $W_2 > 0$, $\Delta _i > 0 \ (i = 1, 2, ..., 2^{\imath +1})$, matrices $T_i, L_{ij} \ (j > i = 1, 2, ..., 2^{\imath +1}-2)$, $N, M = \begin{bmatrix}M_1 \\M_2 \end{bmatrix}$, making the LMIs (4.1)-(4.4) hold:

where

Proof. Choose the appropriate LKF:

where

with

Find the derivatives of $V_1, \; V_2, \; V_3$ along the trajectory of the system (3.2), respectively.

Now, we use the Wirtinger integral inequality and the quadratic reciprocally convex inequality (Lemma 2.1) to calculate the u-related integral terms in the formula (4.7).

then, $\ell _{\frac{2^{\imath}}{2^{\imath}} } = \ell _1 = \ell (t)$,

For any dimension matrices $M_1$ and $M_2$, use Newton-Leibniz formula to get

and for any matrix $N$, the zero equation below holds:

which is equivalent to

Into there, $\varsigma ^{T}_1(t) = [{\bar{\kappa}} _{t}(\frac{2^{\imath}-1}{2^{\imath}}), {\bar{\kappa}} (t-\ell (t))]$, from (4.6) to (4.7), and it yields

Based on formula (3.6), for any positive diagonal matrix $\Delta _i = diag \{\lambda _1, \lambda _2, ..., \lambda _{\eta} \}$, and there are

Let s be $t$, $t-\ell_\frac{1}{2^{\imath}}$, $t-\ell _\frac{2}{2^{\imath}}$, ..., $t-\ell_\frac{2^{\imath+1}-1}{2^{\imath}}$, and replace $\Delta$ with $\Delta_1$, $\Delta_2$, ..., $\Delta_2^{\imath+1}$, and we can obtain

There, $i = 1, 2, ..., 2^{\imath+1}$,

and for arbitrary straight diagonal matrix $\bar{\Delta } = diag\{\bar{\lambda}_1, \bar{\lambda}_2, ..., \bar{\lambda}_{\eta} \}$, one can gain

Let $s_1$, $s_2$ be $t$, $t-\ell_\frac{1}{2^{\imath}}$, $t-\ell _\frac{2}{2^{\imath}}$, ..., $t-\ell_\frac{2^{\imath+1}-1}{2^{\imath}}$, and replace $\bar{\Delta }$ with $\Delta_{qp}$. This moment, $q = 1, 2, ..., 2^{\imath+1}-1$, $p = 2, 3, ..., 2^{\imath+1}$, $p > q$.

Therefore, the formula (4.11) can be written as

among $\varsigma (t, s) = [\varsigma_{1} (t, s), \dot{{\bar{\kappa}} } (s)]$.

Now, defined $\Psi (t) = {\mathfrak{d}}_2\ell ^{2}(t)+{\mathfrak{d}}_1\ell (t)+{\mathfrak{d}}_0$, ${\mathfrak{d}}_1$ and ${\mathfrak{d}}_0$ are matrices with suitable dimensions (i.e., free matrices). When $\Psi (t)$ meets the condition (4.3) in Theorem 4.1, for $\forall t\in [0, \ell]$, $\Psi (t) < 0$, that is, the system (3.2) is asymptotically stable. The proof is as follows:

Proof. When ${\mathfrak{d}}_2\ge 0$, $\Psi (t)$ is a quadratic function with the opening up, that is, the convex function.

By the property of the convex function, the tangent of its crossing point $(\ell, \Psi (\ell))$ is expressed as

from (4.3): $\Psi (0) < 0, \Psi (\ell) < 0$, $\Psi(t) < 0$.

When ${\mathfrak{d}}_2 < 0$, $\Psi(t)$ is the open and downward quadratic function, that is, the concave function. Choose any $t\in [o, \ell]$,

by (4.3), we can get $\Gamma(0) < 0$.

At the same time, $\Gamma(\ell) = \Psi(\ell) < 0$; therefore, for any $t\in[0, \ell]$, $\Psi(t) < 0$.

We know that $\dot{V}(t)\le \varsigma ^{T}(t)\Psi (t)\varsigma (t)$ and $\varsigma (t) < 0$, and then $\dot{V}(t)\le0$, that is, $\dot{V}(t)$ is negative. From Lyapunov's second theorem, system (3.2) has asymptotic stability.

Remark 4.1. It is proved that the balance point of SCGNN exists and is unique, and only the connection weight matrix with switching rules needs to be processed. That is, $\tilde{\mathfrak{B}} = \mathfrak{B}_{\sigma (t)} = (b_{\imath j})_{{\eta} \times {\eta} }$, $\tilde{\mathfrak{C}} = \mathfrak{C}_{\sigma (t)} = (c_{\imath j})_{{\eta} \times {\eta} }$ where $\sigma (t) = \imath$, $\imath = 1, 2, ..., \eta$, and its value may change over time. However, this paper sets a fixed switching rule, that is, the value of the connection weight matrix can remain unchanged for a period of time, which is equivalent to the connection weight matrix without a switching system, so as to prove that the process is consistent with this paper's Theorem 2.1.

5.   Numerical simulation

Example 1. Take $N = 3$ and consider the SCGNN model with two subsystems:

Among them, the neural network system parameters are

and the connection weight matrix is the following:

Subsystem 1:

Subsystem 2:

Subsystem 3:

In order to satisfy Assumptions 2.1-2.3, take the following parameters: $\underline{l_i} = 1$, $\overline{l_i} = 2$, $\mu _i = 1.2$, $k_i = 1$, $r_1 = 0.4$, $r_2 = 0.8$.

Figures 2-7 depicts the simulation results after customizing the initial value under three subsystems. Based on Theorem 4.1, the system has asymptotic stability.

When $-\rho \le \dot{\ell }(t)\le \rho$, i.e., $-\rho_1 = \rho_2 = \rho$, according to the judgment conditions of Theorem 4.1, we use the LMIs toolbox to calculate and get the maximum upper bounds (MAUBs) allowed to be achieved by time delay, see Table 1.

As can be seen from Table 1, when $\dot{\ell }(t) = \rho = 0.8, \eth = 0.642, \ell_0 = 0, q_1 = q_2 = 0$, the maximum delay obtained by two interpolation is greater than that obtained by one interpolation, which fully reflects that the flexible terminal interpolation method can capture more time-delay information, thus reducing the advantage of conservatism.

6.   Conclusions

This paper analyzes CGNN with time-varying delay and adds a switching system to CGNN to study the asymptotic stability of SCGNN. Starting from the existence and uniqueness of the CGNN equilibrium point, it becomes easier to eliminate the offset. In order to capture more time-delay information, a flexible terminal interpolation method is adopted, and an LKF with more time-delay information is constructed and estimated using a quadratic convex inequality. Additionally, based on the linear matrix inequality, a new criterion for SCGNN asymptotic stability is obtained. Finally, numerical examples and simulation results show that the system can be asymptotically stable under the derivation criterion.

Compared with this paper, recent relevant results ^[34] use the quadratic inequality of real vectors and the LKF method to study the stability of a class of CGNN systems with neutral delay terms and discrete time delay. This CGNN system is more special and complex, fully considering the uncertainties and interference factors in practical applications, which has strong practical significance. In addition to studying the stability of this complex system, further research into the limits and singularities of the system is worth exploring.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Natural Science Foundation of China (62072164 and 11704109).

Conflict of interest

The authors declare no conflicts of interest.