Integrable dynamics and geometric conservation laws of hyperelastic strips

1.   Introduction

The variational problem of finding the stationary points of the functional $\int_{\gamma }f\left(\ \kappa, \lambda \right) ds$, where $\lambda = \tau /\kappa,$ and $\kappa$ and $\tau$ are the curvature and torsion of a space curve $\gamma,$ arises in a number of applications. For example, the case $f\left(\kappa, \lambda \right) = \kappa ^{2}$ is the classical elastic curve problem, in which the physical state of a thin elastic rod in equilibrium is studied when it is subjected to bending. This elasticity problem and its various generalizations, such as hyperelastic curves (see ^[1,2,3]), generalized elastic curves and Lie quadratics (see ^[4,5,6,7]), have a rich history and are actively studied today (see ^[8,9,10,11], etc.). The functional $f\left(\kappa, \lambda \right) = \kappa ^{2}\left(1+\lambda ^{2}\right) ^{2}$ is known as the Sadowsky functional, introduced by M. Sadowsky (1930) to find the formulation of a M öbius strip with minimum energy ^[12] (see ^[13] for a translation). Sadowsky transformed the problem of searching for the equations of equilibrium of a narrow Möbius strip into a one-dimensional variational problem using the geometry of the developable ruled surface. In line with Sadowsky's works on Möbius bands of infinitesimal width, Wunderlich in ^[14] (see ^[15] for a translation) employed an energy minimization principle. This principle asserts that the equilibrium shape of the Möbius band has the lowest bending energy among all possible shapes of the band, reducing the bending energy from a surface integral to a line integral without assuming the band's width is small ^[16]. Using the regression point of the generator (bending line) of a developable surface and the fact that one of the principal normal curvatures is zero on a developable surface, Wunderlich showed that the Willmore functional $\int_{M}H^{2}d\sigma$, whose critical points are known Willmore surfaces (see ^[17]) is proportional to the Sadowsky functional. This implies that a developable surface, whose base curve is a critical curve for this functional under certain boundary conditions, is a Willmore surface. In ^[18], the authors applied a variational geometric approach to elastic strips to define the characteristic shape of a Möbius strip made from an inextensible rectangular sheet. Chubelaschwili and Pinkall obtained integrable solutions of the Sadowsky functional, derived conservation laws of elastic strips by using Euclidean motions, and defined two new integrable systems of elastic strips ^[19]. The theory of elastic strip was developed by Tükel and Yü cesan in Minkowski $3$-space with the Poincaré isometry group (see ^[20,21,22]). Yoon and Yüzba şı studied the properties of elastic strips defined along isotropic curves in a three-dimensional complex space ^[23]. The authors, in ^[24], investigated the force-free consequences for the general functional $f\left(\kappa, \lambda \right)$ for regular space curves and stated that all forceless critical points are spherical curves only for Sadowsky-type functional $\int_{\gamma }C\kappa ^{p}(1+\lambda ^{2})^{p}ds$, where $C\ $is constant, and$\ p\neq 0, 1$. The Sadowsky functional and its various generalizations, which are useful for modeling the behavior of developable surfaces, continue to be developed today by researchers interested in the subject (see ^{[16,25,26,27]}, etc.).

The conformally invariant Willmore energy has attracted considerable interest due to its connection to minimal surfaces in the 3-sphere. Given that many interesting surface measurements depend on shape, it is important to have a more general framework for studying these curvature-dependent functionals ^[28]. Guo ^[29] introduced a class of conformal invariants, defined as generalized Willmore functionals, in the most general sense of these energy functionals and presented generalized Willmore functionals, including structures frequently studied in energy minimization problems such as the Willmore functional and the Chen-Willmore functional (see ^[8,30,31]). Recently, researchers have studied the elasticity of biomembranes using geometric and mathematical models, including some generalizations of the Willmore functional. To explain the mechanical stability and equilibrium shapes of membranes, they have considered the functional whose integrand is defined as a general function of the mean curvature and the Gauss curvature of a surface $M$ embedded in Euclidean $3$-space $\mathbb{R}^{3}$ (see ^[32,33], etc.). One particularly interesting application involves the p-Willmore energy functional discussed in ^[34,35]. In his doctoral thesis ^[34], Gruber introduced the $p$-Willmore functional in $3D$-space forms, which extends the Willmore functional to accommodate different powers of the mean curvature. Accordingly, the critical points of the $p$-Willmore functional defined as $\int_{M}H^{p}d\sigma,$ $p\geq 0\in \mathbb{Z},$ in a $3D$-space form are called $p$-Willmore surfaces (see ^[28,34,36]).

In this paper, we show that the Sadowsky-type functional (for $C = 1$) is proportional to the $p$-Willmore functional using Wunderlich's approach. We define the modified Sadowsky-type functional and derive the Euler-Lagrange (EL) equations characterizing the critical points of this functional. We refer to the rectifying, developable surfaces formed by the extremals of the Sadowsky-type functional as hyperelastic strips (or p-elastic strips). We show that the torsion-free critical curves are nothing but hyperelastic curves. From an integrable geometric opinion, it turns out that it is more convenient to calculate the internal force $W_{0}$ and torque $W_{1}$ in a fixed coordinate system so that $W_{0}$ and $W_{1}$ become conservation fields along hyperelastic strips. We find vector fields $W_{0}$ and $W_{1}$ by creating new variations involving Euclidean translational and rotational motions. Then, we obtain the first and second conservation laws of hyperelastic strips. We hope that these conservation laws will present an open problem that can be explored in the future, as they allow the finding of two new integrable systems that will enable the connection between hyperelastic stirps and spherical hyperelastic curves.

2.   Hyperelastic strips

The terms ribbon or strip are used to describe elastic bodies where the thickness, width, and length vary widely. Since their lengths are much greater than their thickness and width, such objects and their elastic responses are explained according to a 1D theory using the centerline of them. We think an inextensible strip, when developed on a plane, forms a strip bounded by two parallel straight lines. Thanks to the developability feature, no matter how deformed the strip is, it can be reconstructed from an arbitrary reference curve on the surface of the strip. Specifically, the centerline of the strip, which can be defined by its curvature and torsion, is identified as the most natural and suitable choice for this reference curve. This detail emphasizes that the geometry of the strip can be completely determined and interpreted through these intrinsic characteristics (see ^[25,37,38]).

Let $\gamma :[0, \ell]\rightarrow \mathbb{R}^{3}$ be a smooth and regular curve with velocity $\upsilon = \left\Vert \gamma ^{\prime }\right\Vert.$ Since a developable strip is a special case of a ruled surface, we can parametrize the strip with the base curve $\gamma$ as follows:

where $T(t)$ and $B(t)$ are, respectively, the unit tangent and the binormal vector at the point $\gamma(t)$ of $\gamma$. The Frenet formulas for $\gamma$ are shown by

where $N$ is the unit normal vector of $\gamma.$ The generator of the developable surface $F_{\gamma }\left(t, \delta \right)$ makes an angle $\theta = \arctan \left(1/\lambda \right)$ with the positive tangent direction of the curve $\gamma \left(s\right)$ ^[37]. The area element and the mean curvature of the surface are computed as follows:

$F_{\gamma }\left(t, \delta \right)$ parametrized by (2.1) has zero Gaussian curvature, that is, one of the principal curvatures is zero. Since $F_{\gamma }$ is developable and the strip is planar when relaxed, the energy functional can be written as

where $D = \frac{2Yh ^{3}}{3\left(1-\nu ^{2}\right) }$ is the flexural rigidity, $h$ is thickness, $\nu$ is the Poisson's ratio, $Y$ is Young's modulus, and $\kappa _{1} = 2H,$ $p\geq 2.$ Substituting (2.3) into (2.4), we arrive at

where

Note that the equilibrium position for strips with no intrinsic curvature does not depend upon the material properties: Young's modulus is a simple factor, and Poisson's ratio does not enter the energy expression (see, ^[14,39]). Also, in the limit of narrow strips $\omega \lambda ^{\prime }\rightarrow 0,$ we have $V\left(\omega \lambda ^{\prime }\right) \rightarrow 1$ and no derivatives enter the integrand in Eq (2.5). This shows that the $p$-Willmore functional $\int_{M}H^{p}d\sigma$ in these conditions is proportional to the Sadowsky-type functional. Observe that for $\lambda = 0$, this is nothing but a free hyperelastic curve's functional.

According to the Euler formula for parabolic surface points, the common curvature $\kappa = \kappa \left(t\right)$ of the centerline of $F_{\gamma }$ is related to the principal normal curvature $\kappa _{1}$ by $\kappa = \kappa _{1}\left(t\right) \sin ^{2}\theta \left(t\right)$, and drawing attention to the familiar relation $\cot \theta = \lambda$ $\left(\text{ gives }1/\sin ^{2}\theta = 1+\lambda ^{2}\right)$ from the theory of space curves, agreement is reached with Sadowsky for the description of the centerline by

Now, we investigate infinitely narrow rectifying strips formed by using extremals of the Sadowsky-type functional among all space curves with fixed end points and

So, we can give the following definition:

Definition 1. If the centerline $\gamma$ of a rectifying strip $F_{\gamma }$ is a critical curve for the modified Sadowsky-type functional

$\mu$ is a Lagrange multiplier representing the length constraint, then $F_{\gamma }$ is a hyperelastic strip (or p-elastic strip).

Lemma 1. ^[19] Let $\gamma:[0, \ell]\rightarrow \mathbb{R}^{3}$ be a reparametrized curve with its arc length and

a variation of $\gamma$ with a variational vector field

We have

and

Suppose that a reparametrized space curve $\gamma :[0, \ell]\rightarrow \mathbb{R}^{3}$ is the centerline of a hyperelastic strip, and we take a variation of $\gamma$ that has the variational vector field (2.8). Now, we calculate the first variation of the functional (2.7). To minimize the functional

we perform the following computation:

Taking into consideration (2.6), we obtain

Now, from (2.9)–(2.11), we obtain

If these processes continue, the integrand can be written as follows:

where

and

Theorem 1. The critical points of the modified Sadowsky functional (2.7) are characterized by EL equations

We also obtain $b^{\prime } = 0,$ when $\gamma$ is an extremal for $S_{\mu }$ for each variation of $\gamma$, which leaves the integrand of the functional (2.7) invariant.

Proof. Let a reparametrized curve $\gamma$ be a stationary point of $S_{\mu }$. From (2.12), we obtain

Using the fact that $b\left(\ell \right) = b\left(0\right) = 0$ for a proper variation, the boundary conditions are naturally introduced, and we deduce the desired EL equations. These boundary conditions ensure that the variations of $\gamma$ at the endpoints do not contribute to the variation of the functional, highlighting how geometric properties such as the endpoints' positions influence the stability and configuration of the system. On the other hand, it can be observed from (2.12) that $b^{\prime } = 0$ when $\gamma$ is a critical point of the functional (2.7). □

One can see from the EL Eq (2.14) that critical points with torsion-free of the modified Sadowsky-type functional are just hyperelastic curves with torsion-free (see ^[1], for EL equations of hyperelastic curves).

In the following, we can give an obvious application.

Example 1. Let $\gamma (s)$ be a reparametrized planar curve with non-constant curvature $\kappa \left(s\right).$ We know that $\gamma \left(s\right)$ is a borderline elastic curve if $\kappa = \kappa _{0}\sec h\left(\frac{\kappa _{0} }{2}s\right),$ an orbitlike elastic curve if $\kappa = \kappa _{0}dn\left(\frac{\kappa _{0}}{2}s, k\right),$ and a wavelike elastic curve if $\kappa = \kappa _{0}cn\left(\frac{\kappa _{0}}{2k}s, k\right),$ where $dn$ and $cn$ are respectively elliptic delta and cosine functions with parameter $k$, and parameter $\kappa _{0}$ determines the maximum curvature ^[11]. Now suppose that a borderline elastic curve $\gamma$ is the centerline of the rectifying strip $F_{\gamma }.$ Then, we calculate the second derivative of the curvature $\kappa$ of $\gamma$ as follows:

Moreover, we can obtain $\mu = -\frac{\kappa _{0}^{2}}{2}.$ Putting $\kappa, \kappa ^{\prime \prime }$ and $\mu$ in EL Eq (2.14) for $p = 2,$ we obtain that $F_{\gamma }$ is a 2-elastic strip (or elastic strip). Similar processes are also applicable for orbitlike and wavelike elastic curves.

Furthermore, it is demonstrated that circular helices solve EL Eq (2.14). Now, we will illustrate this with an example.

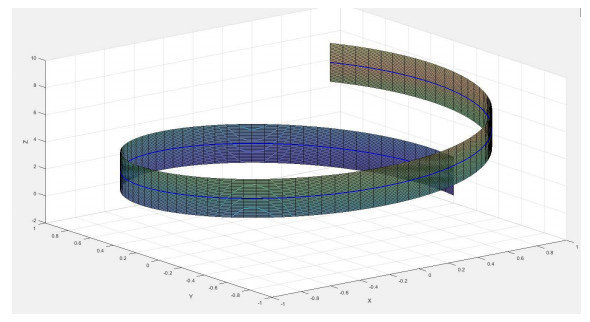
Example 2. Let $\beta \left(s\right) = \left(\cos \frac{ \sqrt{2}s}{2}, \sin \frac{\sqrt{2}s}{2}, \frac{\sqrt{2}s}{2}\right)$ be a unit-speed helix with the curvature and the modified torsion

By using the values (2.15) and EL Eq (2.14), we can see that the rectifying strip

with centerline $\beta$ is a hyperelastic strip chosen $\mu = 1-2p$ (see Figure 1).

3.   Conservation laws of hyperelastic strips

In physics, conserved quantities such as internal forces and torques are interpreted in terms of fundamental conservation laws such as momentum and angular momentum. In the context of elastic strips, conserved quantities are often interpreted as internal forces and torques due to the fundamental conservation laws of linear and angular momentum because they are obtained through Euclidean translations and rotations. These internal forces and torques are necessary to maintain the structural integrity and stability of the ribbon under deformation. While internal forces help maintain the linear stability of the ribbon, torques govern rotational dynamics. In this section, we obtaion the internal force and torgue vector for hyperelastic strips and prove the first and second conservation laws.

Now, we take a variation that consists only of translations, as follows:

with the variation vector field

where $\Gamma$ is an arbitrary vector in $\mathbb{R} ^{3},$ $u_{1} = < \Gamma, T > ,$ $u_{2} = < \Gamma, N >$, and $u_{3} = < \Gamma, B >$. The derivatives, $u_{2}^{\prime },$ $u_{3}^{\prime }$ and $u_{3}^{\prime \prime }$ are calculated as

and

Combine the Eq (2.13) with the derivatives (3.1)–(3.3), and we obtain

where

We know that $b$ is a constant when the Frenet curve $\gamma$ is an extremal of the Sadowsky-type functional. Therefore, $W_{0}$ is a constant for any $\Gamma \in \mathbb{R}^{3}.$

For a variation consisting only of rotations, $\tilde{ \Gamma}\in \mathbb{R}^{3},$ $A_{\delta }\in SO\left(3\right),$ $u_{1} = < \tilde{\Gamma}\times \gamma, T > ,$ $u_{2} = < \tilde{\Gamma}\times \gamma, N >$ and $u_{3} = < \tilde{\Gamma}\times \gamma, B > ,$ we have

By using a similar method, we arrive at

where

is a constant for hyperelastic strips.

We show that hyperelastic strips can be determined by $W_{0}\ $and $W_{1}$ in the following theorems. We call these theorems the first and second conservation laws of hyperelastic strips, respectively.

Theorem 2. A rectifying strip $F_{\gamma }$ is a hyperelastic strip if and only if the force vector $W_{0} = a_{1}T+a_{2}N+a_{3}B$ is constant, where

and

Proof. It suffices to show

because the vector $W_{0}$ is a constant if and only if $f_{1} = f_{2} = 0$ in (3.7)$.$ By using Eq (2.2)$,$ we obtain

On the other hand, from (3.4) and (3.5)$,$ we find

It then follows that the coefficient of $T$ in Eq (3.8) vanishes. Now, by using (3.4)–(3.6), the coefficients of $N$ and $B$ are found as follows:

Equations (3.9) and (3.10) show that $W_{0}$ is a constant if and only if $f_{1} = f_{2} = 0$.□

Theorem 3. For a hyperelastic strip $F_{\gamma }$, the torque vector $W_{1} = s_{1}T+s_{2}N+s_{3}B-\gamma \times W_{0}$ is constant, where

and

Moreover, if $W_{1}$ is a constant but $\gamma$ does not define a hyperelastic strip, then $\left\Vert \gamma \right\Vert$ is conserved.

Proof. Taking into consideration Eq (2.2), we calculate the first derivative of $W_{1}$ as follows:

Substituting (3.11)–(3.13) and the derivatives $s_{1}^{\prime }$, $s_{2}^{\prime }$ and $s_{3}^{\prime }$ in (3.14), we see that the coefficients of$\ T,$ $N$, and $B$ are zero. Thus, Eq (3.14) is reduced to

Equation (3.15) implies that $W_{1}^{\prime } = 0$ when $W_{0}$ is a constant, so we can see from Theorem 2 that $W_{1}$ is constant when $\gamma$ defines a hyperelastic strip.

On the contrary, suppose that $W_{1}$ is a constant vector field but $\gamma$ does not define a hyperelastic strip. From (3.7)$,$ we get

This means that $\gamma \in$ Span $\left\lbrace N, B \right\rbrace$. So we have

□

We give the following example, which provides the condition that a cylindrical helix can define a hyperelastic strip.

Example 3. Let a unit speed curve $\gamma$ be base curve for a hyperelastic strip $F_{\gamma}$ with internal force $W_{0}$. Taking the inner product of both sides of $W_{0} = a_{1}T +a_{2}N+a_{3}B$ with $T$, we obtain

Thus, $\gamma$ is a slope line if $a_{1}$ is a constant. Moreover, $\lambda$ and $\kappa$ must be constants in this case. This means that a hyperelastic strip is defined by a cylindrical helix when $a_{1}$ is a constant.

4.   Conclusions

Sheet, bar, or band-like structures, which are foldable or bendable and deformed solely by bending, have minimum energy when brought into a flat position. Because of these features, the mechanics of curved structures are based on the classical formulation of developable surfaces, and as a matter of fact, the deformation energy calculation resulting from bending combines mechanics with geometry (see ^[18,39,41]). Wunderlich showed that the functional introduced by Sadowsky is proportional to the Willmore functional, which is one of the most important representatives of the minimal surface studies frequently studied in differential geometry, and proved that the structure of a developable band looks like the 1-dimensional structure of thin rods and is determined by the classical equations of thin elastic rods. Elastic strips, which are actively studied today, are developable ruled surfaces formed by stationary points of the Sadowsky functional. The Sadowsky-type functional is a natural generalization of the Sadowsky functional. The Sadowsky-type functional offers a different method and perspective to the problem of finding the extremals of the generalized Willmore functional, which has been frequently studied recently.

In the present work, we show that the Sadowsky functional is proportional to the $p$-Willmore functional. Using a Lagrangian multiplier representing the length constraint, we define the modified Sadowsky-type functional and obtain EL equations characterizing the critical points of this functional. We call a rectifying strip whose base curve is the critical point of a Sadowsky-type functional a hyperelastic strip. We obtain the conservation laws of hyperelastic strips with the help of Euclidean motions. These conservation laws provide a starting point for the open problem of finding new integrable systems of hyperelastic strips corresponding to spherical hyperelastic curves. Different perspectives on the solutions of these derived equation systems can be explored (see ^[42]). On the other hand, hyperelastic curves are a useful tool for generating rotational Chen-Willmore hypersurface samples. It is known that Chen-Willmore hypersurfaces in the Euclidean $n$-space $\mathbb{R}^{n+1}$ and the sphere $\mathbb{S}^{n+1}$ can be obtained with the help of hyperelastic curves in the hyperbolic $2$-plane (see for details ^[8]). For this reason, Chen-Willmore hypersurface samples can be derived with the help of the Hopf transform by establishing connections between new strip types obtained by using conservation laws and spherical hyperelastic curves. There also arises the open problem of studying hyperelastic strips in $n$-dimensional Euclidean space to derive more distinct Chen-Willmore hypersurfaces. This problem can also be considered in non-Euclidean spaces. It may also be useful to work with Minkowski spaces with Poincaré isometry groups.

Author contributions

This paper is entirely designed and executed by Gözde Özkan Tükel, covering all aspects of theoretical development, problem formulation, mathematical analysis, interpretation of results, and paper writing and revision.

Use of AI tools declaration

During the preparation of this work, the author used ChatGPT in order to improve language and readability in the abstract and introduction sections. After using this tool/service, the author reviewed and edited the content as needed and takes full responsibility for the content of the publication.

Conflict of interest

The author declares no conflict of interest.