A reliable analytic technique and physical interpretation for the two-dimensional nonlinear Schrödinger equations

Mahmoud A. E. Abdelrahman; H. S. Alayachi; Mahmoud A. E. Abdelrahman; H. S. Alayachi

doi:10.3934/math.20241185

AIMS Mathematics

2024, Volume 9, Issue 9: 24359-24371. doi: 10.3934/math.20241185

Previous Article Next Article

Research article Special Issues

A reliable analytic technique and physical interpretation for the two-dimensional nonlinear Schrödinger equations

Mahmoud A. E. Abdelrahman ^{1,2
,
,},
H. S. Alayachi ¹

1.
Department of Mathematics, College of Science, Taibah University, Al-Madinah Al-Munawarah, Saudi Arabia
2.
Department of Mathematics, Faculty of Science, Mansoura University, Mansoura, Egypt

Received: 26 April 2024 Revised: 30 June 2024 Accepted: 08 July 2024 Published: 19 August 2024
MSC : 35C08, 35Q40, 35Q55

Nonlinear Schrödinger equations are a key paradigm in nonlinear research, attracting both mathematical and physical attention. This work was primarily concerned with the usage of a reliable analytic technique in order to solve two models of (2+1)-dimensional nonlinear Schrödinger equations. By applying a comprehensible wave transformation, every nonlinear model was simplified to an ordinary differential equation. A number of critical solutions were observed that correlated to various parameters. The provided approach has various advantages, including reducing difficult computations and succinctly presenting key results. Some 2D and 3D graphical representations regarding presented solitons were considered for the appropriate values of the parameters. We also showed the effect of the physical parameters on the dynamical behavior of the presented solutions. Finally, the proposed approach may be expanded to tackle increasingly complicated problems in applied science.
- two-dimensional nonlinear Schrödinger equations,
- closed-form solutions,
- solitons
Citation: Mahmoud A. E. Abdelrahman, H. S. Alayachi. A reliable analytic technique and physical interpretation for the two-dimensional nonlinear Schrödinger equations[J]. AIMS Mathematics, 2024, 9(9): 24359-24371. doi: 10.3934/math.20241185

Related Papers:

Abstract

Nonlinear Schrödinger equations are a key paradigm in nonlinear research, attracting both mathematical and physical attention. This work was primarily concerned with the usage of a reliable analytic technique in order to solve two models of (2+1)-dimensional nonlinear Schrödinger equations. By applying a comprehensible wave transformation, every nonlinear model was simplified to an ordinary differential equation. A number of critical solutions were observed that correlated to various parameters. The provided approach has various advantages, including reducing difficult computations and succinctly presenting key results. Some 2D and 3D graphical representations regarding presented solitons were considered for the appropriate values of the parameters. We also showed the effect of the physical parameters on the dynamical behavior of the presented solutions. Finally, the proposed approach may be expanded to tackle increasingly complicated problems in applied science.

References

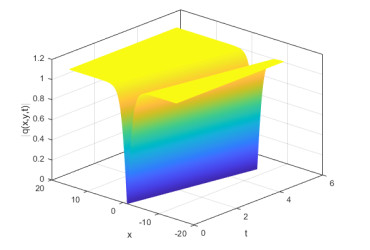
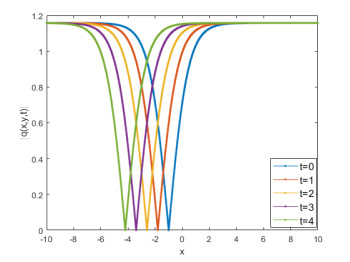
[1]	H. Zhang, X. Yang, Q. Tang, D. Xu, A robust error analysis of the OSC method for a multi-term fourth-order sub-diffusion equation, Comput. Math. Appl., 109 (2022), 180–190. https://doi.org/10.1016/j.camwa.2022.01.007 doi: 10.1016/j.camwa.2022.01.007
[2]	X. Yang, H. Zhang, J. Tang, The OSC solver for the fourth-order sub-diffusion equation with weakly singular solutions, Comput. Math. Appl., 82 (2021), 1–12. https://doi.org/10.1016/j.camwa.2020.11.015 doi: 10.1016/j.camwa.2020.11.015
[3]	H. Zhang, X. Yang, D. Xu, Unconditional convergence of linearized orthogonal spline collocation algorithm for semilinear subdiffusion equation with nonsmooth solution, Numer. Meth. Part. Differ. Equ., 37 (2021), 1361–1373. https://doi.org/10.1002/num.22583 doi: 10.1002/num.22583
[4]	A. F. Daghistani, A. M. T. Abd El-Bar, A. M. Gemeay, M. A. E. Abdelrahman, S. Z. Hassan, A hyperbolic secant-squared distribution via the nonlinear evolution equation and its application, Mathematics, 11 (2023), 4270. https://doi.org/10.3390/math11204270 doi: 10.3390/math11204270
[5]	M. A. E. Abdelrahman, G. Alshreef, Closed-form solutions to the new coupled Konno–Oono equation and the Kaup-Newell model equation in magnetic field with novel statistic application, Eur. Phys. J. Plus, 136 (2021), 455. https://doi.org/10.1140/epjp/s13360-021-01472-2 doi: 10.1140/epjp/s13360-021-01472-2
[6]	Y. Cheng, A. Chertock, M. Herty, A. Kurganov, T. Wu, A new approach for designing moving-water equilibria preserving schemes for the shallow water equations, J. Sci. Comput., 80 (2019), 538–554. https://doi.org/10.1007/s10915-019-00947-w doi: 10.1007/s10915-019-00947-w
[7]	P. Ripa, Conservation laws for primitive equations models with inhomogeneous layers, Geophys. Astrophys. Fluid Dynam., 70 (1993), 85–111. https://doi.org/10.1080/03091929308203588 doi: 10.1080/03091929308203588
[8]	G. Laibe, D. J. Price, Dusty gas with one fluid, Mon. Not. R. Astron. Soc., 440 (2014), 2136–2146. https://doi.org/10.1093/mnras/stu355 doi: 10.1093/mnras/stu355
[9]	Y. Shi, X. Yang, A time two-grid difference method for nonlinear generalized viscous Burgers' equation, J. Math. Chem., 62 (2024), 1323–1356. https://doi.org/10.1007/s10910-024-01592-x doi: 10.1007/s10910-024-01592-x
[10]	C. Li, H. Zhang, X. Yang, A new nonlinear compact difference scheme for a fourth-order nonlinear Burgers type equation with a weakly singular kernel, J. Appl. Math. Comput., 70 (2024), 2045–2077. https://doi.org/10.1007/s12190-024-02039-x doi: 10.1007/s12190-024-02039-x
[11]	H. Zhang, X. Yang, Y. Liu, Y. Liu, An extrapolated CN-WSGD OSC method for a nonlinear time fractional reaction-diffusion equation, Appl. Numer. Math., 157 (2020), 619–633. https://doi.org/10.1016/j.apnum.2020.07.017 doi: 10.1016/j.apnum.2020.07.017
[12]	H. Zhang, X. Yang, D. Xu, An efficient spline collocation method for a nonlinear fourth-order reaction subdiffusion equation, J. Sci. Comput., 85 (2020), 7. https://doi.org/10.1007/s10915-020-01308-8 doi: 10.1007/s10915-020-01308-8
[13]	X. Yang, H. Zhang, Q. Tang, A spline collocation method for a fractional mobile–immobile equation with variable coefficients, Comput. Appl. Math., 39 (2020), 34. https://doi.org/10.1007/s40314-019-1013-3 doi: 10.1007/s40314-019-1013-3
[14]	H.S. Alayachi, The modulations of higher order solitonic pressure and energy of fluid filled elastic tubes, AIP Adv., 13 (2023), 115214. https://doi.org/10.1063/5.0179155 doi: 10.1063/5.0179155
[15]	X. Yang, W. Qiu, H. Zhang, L. Tang, An efficient alternating direction implicit finite difference scheme for the three-dimensional time-fractional telegraph equation, Comput. Math. Appl., 102 (2021), 233–247. https://doi.org/10.1016/j.camwa.2021.10.021 doi: 10.1016/j.camwa.2021.10.021
[16]	H. Zhang, Y. Liu, X. Yang, An efficient ADI difference scheme for the nonlocal evolution problem in three-dimensional space, J. Appl. Math. Comput., 69 (2023), 651–674. https://doi.org/10.1007/s12190-022-01760-9 doi: 10.1007/s12190-022-01760-9
[17]	X. Yang, W. Qiu, H. Chen, H. Zhang, Second-order BDF ADI Galerkin finite element method for the evolutionary equation with a nonlocal term in three-dimensional space, Appl. Numer. Math., 172 (2022), 497–513. https://doi.org/10.1016/j.apnum.2021.11.004 doi: 10.1016/j.apnum.2021.11.004
[18]	H. Zhang, X. Jiang, F. Wang, X. Yang, The time two-grid algorithm combined with difference scheme for 2D nonlocal nonlinear wave equation, J. Appl. Math. Comput., 70 (2024), 1127–1151. https://doi.org/10.1007/s12190-024-02000-y doi: 10.1007/s12190-024-02000-y
[19]	H. G. Abdelwahed, M. A. E. Abdelrahman, M. Inc, R. Sabry, New soliton applications in earth's magnetotail plasma at critical densities, Front. Phys., 8 (2020), 181. https://doi.org/10.3389/fphy.2020.00181 doi: 10.3389/fphy.2020.00181
[20]	S. Zhang, C. Tian, W. Y. Qian, Bilinearization and new multi-soliton solutions for the (4+1)-dimensional Fokas equation, Pramana-J. Phys., 86 (2016), 1259–1267. https://doi.org/10.1007/s12043-015-1173-7 doi: 10.1007/s12043-015-1173-7
[21]	L. Akinyemi, M. Şenol, U. Akpan, K. Oluwasegun, The optical soliton solutions of generalized coupled nonlinear Schrödinger-Korteweg-de Vries equations, Opt. Quant. Electron., 53 (2021), 394. https://doi.org/10.1007/s11082-021-03030-7 doi: 10.1007/s11082-021-03030-7
[22]	F. Mirzaee, S. Rezaei, N. Samadyar, Numerical solution of two-dimensional stochastic time-fractional sine-Gordon equation on non-rectangular domains using finite difference and meshfree methods, Eng. Anal. Bound. Elem., 127 (2021), 53–63. https://doi.org/10.1016/j.enganabound.2021.03.009 doi: 10.1016/j.enganabound.2021.03.009
[23]	M. A. E. Abdelrahman, H. AlKhidhr, A robust and accurate solver for some nonlinear partial differential equations and tow applications, Phys. Scr., 95 (2020), 065212. https://doi.org/10.1088/1402-4896/ab80e7 doi: 10.1088/1402-4896/ab80e7
[24]	Z. Zhou, H. Zhang, X. Yang, CN ADI fast algorithm on non-uniform meshes for the three-dimensional nonlocal evolution equation with multi-memory kernels in viscoelastic dynamics, Appl. Math. Comput., 474 (2024), 128680. https://doi.org/10.1016/j.amc.2024.128680 doi: 10.1016/j.amc.2024.128680
[25]	X. F. Yang, Z. C. Deng, Y. Wei, A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application, Adv. Differ. Equ., 2015 (2015), 117. https://doi.org/10.1186/s13662-015-0452-4 doi: 10.1186/s13662-015-0452-4
[26]	W. Wang, H. Zhang, Z. Zhou, X. Yang, A fast compact finite difference scheme for the fourth-order diffusion-wave equation, Int. J. Comput. Math., 101 (2024), 170–193. https://doi.org/10.1080/00207160.2024.2323985 doi: 10.1080/00207160.2024.2323985
[27]	B. Q. Li, Y. L. Ma, Interaction properties between rogue wave and breathers to the manakov system arising from stationary self-focusing electromagnetic systems, Chaos Soliton. Fract., 156 (2022), 111832. https://doi.org/10.1016/j.chaos.2022.111832 doi: 10.1016/j.chaos.2022.111832
[28]	X. Jin, J. Jiang, J. Chi, X. Wu, Adaptive finite-time pinned and regulation synchronization of disturbed complex networks, Commun. Nonlinear Sci., 124 (2023), 107319. https://doi.org/10.1016/j.cnsns.2023.107319 doi: 10.1016/j.cnsns.2023.107319
[29]	Z. J. Yang, S. M. Zhang, X. L. Li, Z. G. Pang, H. X. Bu, High-order revivable complex-valued hyperbolic-sine-Gaussian solitons and breathers in nonlinear media with a spatial nonlocality, Nonlinear Dyn., 94 (2018), 2563–2573. https://doi.org/10.1007/s11071-018-4510-9 doi: 10.1007/s11071-018-4510-9
[30]	Z. Sun, J. Li, R. Bian, D. Deng, Z. Yang, Transmission mode transformation of rotating controllable beams induced by the cross phase, Opt. Express, 32 (2024), 9201–9212. https://doi.org/10.1364/OE.520342 doi: 10.1364/OE.520342
[31]	M. A. E. Abdelrahman, N. F. Abdo, On the nonlinear new wave solutions in unstable dispersive environments, Phys. Scr., 95 (2020), 045220. https://doi.org/10.1088/1402-4896/ab62d7 doi: 10.1088/1402-4896/ab62d7
[32]	H. G. Abdelwahed, M. A. E. Abdelrahman, S. Alghanim, N. F. Abdo, Higher-order Kerr nonlinear and dispersion effects on fiber optics, Results Phys., 26 (2021), 104268. https://doi.org/10.1016/j.rinp.2021.104268 doi: 10.1016/j.rinp.2021.104268
[33]	J. L. Lebowitz, H. A. Rose, E. R. Speer, Statistical mechanics of the nonlinear Schrödinger equation, J. Stat. Phys., 50 (1988), 657–687. https://doi.org/10.1007/BF01026495 doi: 10.1007/BF01026495
[34]	G. D. McDonald, C. C. N. Kuhn, K. S. Hardman, S. Bennetts, P. J. Everitt, P. A. Altin, et al., Bright solitonic matter-wave interferometer, Phys. Rev. Lett., 113 (2014), 013002. https://doi.org/10.1103/PhysRevLett.113.013002 doi: 10.1103/PhysRevLett.113.013002
[35]	Y. L. Ma, $ N $th-order rogue wave solutions for a variable coefficient Schrödinger equation in inhomogeneous optical fibers, Optik, 251 (2022), 168103. https://doi.org/10.1016/j.ijleo.2021.168103 doi: 10.1016/j.ijleo.2021.168103
[36]	B. Q. Li, Y. L. Ma, Interaction properties between rogue wave and breathers to the manakov system arising from stationary self-focusing electromagnetic systems, Chaos Soliton. Fract., 156 (2022), 111832. https://doi.org/10.1016/j.chaos.2022.111832 doi: 10.1016/j.chaos.2022.111832
[37]	O. V. Marchukov, B. A. Malomed, V. A. Yurovsky, M. Olshanii, V. Dunjko, R. G. Hulet, Splitting of nonlinear-Schrödinger-equation breathers by linear and nonlinear localized potentials, Phys. Rev. A, 99 (2019), 063623. https://doi.org/10.1103/PhysRevA.99.063623 doi: 10.1103/PhysRevA.99.063623
[38]	S. Shen, Z. Yang, X. Li, S. Zhang, Periodic propagation of complex-valued hyperbolic-cosine-Gaussian solitons and breathers with complicated light field structure in strongly nonlocal nonlinear media, Commun. Nonlinear Sci., 103 (2021), 106005. https://doi.org/10.1016/j.cnsns.2021.106005 doi: 10.1016/j.cnsns.2021.106005
[39]	Z. Y. Sun, D. Deng, Z. G. Pang, Z. J. Yang, Nonlinear transmission dynamics of mutual transformation between array modes and hollow modes in elliptical sine-Gaussian cross-phase beams, Chaos Soliton. Fract., 178 (2024), 114398. https://doi.org/10.1016/j.chaos.2023.114398 doi: 10.1016/j.chaos.2023.114398
[40]	S. Shen, Z. J. Yang, Z. G. Pang, Y. R. Ge, The complex-valued astigmatic cosine-Gaussian soliton solution of the nonlocal nonlinear Schrödinger equation and its transmission characteristics, Appl. Math. Lett., 125 (2022), 107755. https://doi.org/10.1016/j.aml.2021.107755 doi: 10.1016/j.aml.2021.107755
[41]	L. M. Song, Z. J. Yang, X. L. Li, S. M. Zhang, Coherent superposition propagation of Laguerre-Gaussian and Hermite-Gaussian solitons, Appl. Math. Lett., 102 (2020), 106114. https://doi.org/10.1016/j.aml.2019.106114 doi: 10.1016/j.aml.2019.106114
[42]	M. Najafi, S. Arbabi, Traveling wave solutions for nonlinear Schrödinger equations, Optik, 126 (2015), 3992–3997. https://doi.org/10.1016/j.ijleo.2015.07.165 doi: 10.1016/j.ijleo.2015.07.165
[43]	M. Dehghan, A. Shokri, A numerical method for two-dimensional Schrödinger equation using collocation and radial basis functions, Comput. Math. Appl., 54 (2007), 136–146. https://doi.org/10.1016/j.camwa.2007.01.038 doi: 10.1016/j.camwa.2007.01.038
[44]	S. V. Mousavi, S. Miret-Artés, On non-linear Schrödinger equations for open quantum systems, Eur. Phys. J. Plus, 134 (2019), 431. https://doi.org/10.1140/epjp/i2019-12965-6 doi: 10.1140/epjp/i2019-12965-6
[45]	W. Huang, C. Xu, S. T. Chu, S. K. Chaudhuri, The finite-difference vector beam propagation method: Analysis and assessment, J. Lightwave Technol., 10 (1992), 295–305. https://doi.org/10.1109/50.124490 doi: 10.1109/50.124490
[46]	A. I. Aliyu, M. Inc, A. Yusuf, D. Baleanu, Optical solitary waves and conservation laws to the (2+1)-dimensional hyperbolic nonlinear Schrödinger equation, Mod. Phys. Lett. B, 32 (2018), 1850373. https://doi.org/10.1142/S0217984918503736 doi: 10.1142/S0217984918503736
[47]	H. Durur, E. Ilhan, H. Bulut, Novel complex wave solutions of the (2+1)-dimensional hyperbolic nonlinear Schrödinger equation, Fractal Fract., 4 (2020), 41. https://doi.org/10.3390/fractalfract4030041 doi: 10.3390/fractalfract4030041
[48]	D. Baleanu, K. Hosseini, S. Salahshour, K. Sadri, M. Mirzazadeh, C. Park, A. Ahmadian, The (2+1)-dimensional hyperbolic nonlinear Schrödinger equation and its optical solitons, AIMS Mathematics, 6 (2021), 9568–9581. https://doi.org/10.3934/math.2021556 doi: 10.3934/math.2021556
[49]	G. Ai-Lin, L. Ji, Exact solutions of (2+1)-dimensional HNLS equation, Commun. Theor. Phys., 54 (2010), 401. https://doi.org/10.1088/0253-6102/54/3/04 doi: 10.1088/0253-6102/54/3/04
[50]	X. Yang, H. Zhang, The uniform $l^{1}$ long-time behavior of time discretization for time-fractional partial differential equations with nonsmooth data, Appl. Math. Lett., 124 (2022), 107644. https://doi.org/10.1016/j.aml.2021.107644 doi: 10.1016/j.aml.2021.107644
[51]	X. Yang, H. Zhang, Q. Zhang, G. Yuan, Simple positivity-preserving nonlinear finite volume scheme for subdiffusion equations on general non-conforming distorted meshes, Nonlinear Dyn., 108 (2022), 3859–3886. https://doi.org/10.1007/s11071-022-07399-2 doi: 10.1007/s11071-022-07399-2
[52]	X. Yang, Z. Zhang, Analysis of a new NFV scheme preserving DMP for two-dimensional sub-diffusion equation on distorted meshes, J. Sci. Comput., 99 (2024), 80. https://doi.org/10.1007/s10915-024-02511-7 doi: 10.1007/s10915-024-02511-7
[53]	X. Yang, Z. Zhang, On conservative, positivity preserving, nonlinear FV scheme on distorted meshes for the multi-term nonlocal Nagumo-type equations, Appl. Math. Lett., 150 (2024), 108972. https://doi.org/10.1016/j.aml.2023.108972 doi: 10.1016/j.aml.2023.108972

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)