Time-delayed feedback control for chaotic systems with coexisting attractors

1.   Introduction

Decision-making is a problem-solving technique for the selection of superlative alternatives. Multi-attribute decision-making (MADM) describes the problems under available alternatives supporting certain criteria. Decision-making is categorized according to the number of decision makers, i.e., individual decision expert and group of decision experts. Multi-attribute group decision-making (MAGDM) is a process in which a panel of decision experts evaluates the most favorable alternative supporting certain characteristics. To solve the MAGDM problems, several techniques have been proposed, including, MOORA method and MULTIMOORA method. Firstly, Brauers and Zavadskas ^[1] established the crisp MOORA method in 2006. The classical MOORA method deals with crisp data to evaluate the favorable alternative under the relative importance of criteria. The MULTIMOORA method was developed by Brauers and Zavadskas ^[2] in crisp set theory. The MULTIMOORA method is described by three approaches, including, the ratio system approach, the reference point approach and the full multiplicative form approach.

Fuzzy sets (FSs), initiated by Zadeh ^[3], has been widely applied in MAGDM problems to deal with uncertain data. The concept of Fermatean fuzzy sets (FFSs), as an extension of FSs, has been proved as one of the most powerful frameworks to handle vague information and imprecise data ^[4]. The cube addition of membership and non-membership degrees must be less or equal to 1 is considered as the vital characteristic of FFSs. Therefore, FFSs are considered as the most powerful framework as compare to FSs, IFSs (intuitionistic fuzzy sets)^[5], and PFSs (Pythagorean fuzzy sets) ^[6]. Based on its flexibility and unique advantage, the proposed work is considered under FF environment.

In group decision-making phenomena, the decision makers often hesitate among several evaluation values. The decision-makers are reluctant to compromise which makes final judgement difficult. The FSs, IFSs, PFSs and FFSs deal with vague information which is in quantitative form. If decision-makers express their opinion in the form of linguistic terms, FSs, IFSs, PFSs and FFSs are not capable of dealing with this information. Realizing this, Zadeh ^[7] introduced the theory of linguistic term sets.

In decision issues, quality of life (QOL) has been a widely used term that scholars from various sectors are interested in quantifying. Particularly in the last decade, the quantity and scope of studies to measure QOL have been expanded. The World Health Organization (WHO) has decided to measure the QOL in different cities to show the condition of developing areas. QOL relates to the individuals' perceptions of their place in life in relation to their objectives, aspirations, standards, and worries, as well as the culture and value systems in which they live. The measurement of QOL helps the economist to identify the needs of people living in a particular city. Therefore, the selection of best urban city is observed as a complicated MAGDM problem.

1.1.   Motivation

The following features of the 2TLFFSs and MULTIMOORA method motivate us to present this paper:

(1) 2TLM is a unique computational technique for representing linguistic data that helps to overcome the shortcomings of classical linguistic models. The disadvantage of traditional models is that some information is lost when the result is not linguistic value. And 2TLM represents linguistic information by using a pair of elements, that is, by $(\mathfrak{\acute{I}}_{p}, \zeta)$, where $\mathfrak{\acute {I}}_{p }$ is a linguistic term, and $\zeta$ is a numerical value known as a symbolic translation, since it is shown to match the LTS (when it fails to exactly match the computed linguistic value). In the decision-making problem, decision experts wish to clarify information about their qualitative information for the evaluation of options, i.e., using linguistic values. 2TLM allows decision experts to express their knowledge of decision and evaluation information in tabular form 2-tuple. The advantages of 2TLM as mentioned above encourage us to present our research work.

(2) The concept of FFS is an extension of the existing FST, as it handles a large amount of linguistic information and provides more space for decision-making experts in membership degrees and non-membership degrees. FFS expands the decision-making space and allows experts to communicate information more accurately.

(3) 2TLFFS accommodates key features of FFS and 2TLTS. 2TLFFS is able to represent membership and non-membership degrees from predefined LTS in the form of 2-tuple linguistic term. Therefore, the unique features of 2TLFFs motivate our research work in the 2TLFF setting.

(4) MULTIMOORA technique has several notable features, including reduced computation time, more comprehensive mathematical calculations, simplicity, and consistency of results. The MULTIMOORA approach enables transparency for decision-making experts because it allows them to express top-level alternatives in linguistic terms rather than numerical values. It consists of three MOORA methods based on ratio analysis, reference point and full multiplicative form methods. The MULIMOORA technique uses the three strategies described above to calculate the subordination level of the alternatives. It uses aggregation methods to combine the subordinate ranks of the alternatives and present the results more accurately.

1.2.   Objectives

Motivated by the distinctive features of 2TLFFSs and MULTIMOORA technique, we have designed a novel 2TLFF-MULTIMOORA method with in 2TLFF context. The objectives of this research are as follows:

(1) The main objective of this study is the development of decision-making technique namely, 2TLFF-MULTIMOORA method to answer the MAGDM issues under the framework of 2TLFFSs.

(2) To aggregate the decision data provided by experts in the form of 2TLFFNs, 2TLFFWA operator and 2TLFFWG operator are designed. These operators are useful to obtain the subordinate ranking of alternatives.

(3) To demonstrate the applicability of our developed technique, we implement the proposed 2TLFF-MULTIMOORA method to a real case study. We have implemented the design approach to a measure the quality of life in urban cities.

(4) To demonstrate the robustness and authenticity of our developed work, we compare our 2TLFF-MULTIMOORA method to check its authenticity with the previous knowledge.

1.3.   Novelty and contribution

To attain the above-mentioned objectives, we have contributed to this research study as follows:

(1) We design a new technique based on the traditional MULTIMOORA method to deal with the emerging MAGDM problem.

(2) The process of the 2TLFF-MULTIMOORA technique is explained with the associated illustrations. We design 2TLFFWA and 2TLFFWG operators to simulate 2TLFFN.

(3) The proposed 2TLFF-MULTIMOORA method consists of three sub-techniques, where the alternatives are ranked by the subordinate rank of all other methods.

(4) The first technique is called the 2TLFF ratio system method, and we apply the 2TLFFWA operator.

(5) The second technique is called the 2TLFF reference point method, where we calculate the reference point and measure the deviation from the reference point.

(6) In the third technique, called 2TLFF full multiplication form, we use the 2TLFFWG operator to measure ranking results.

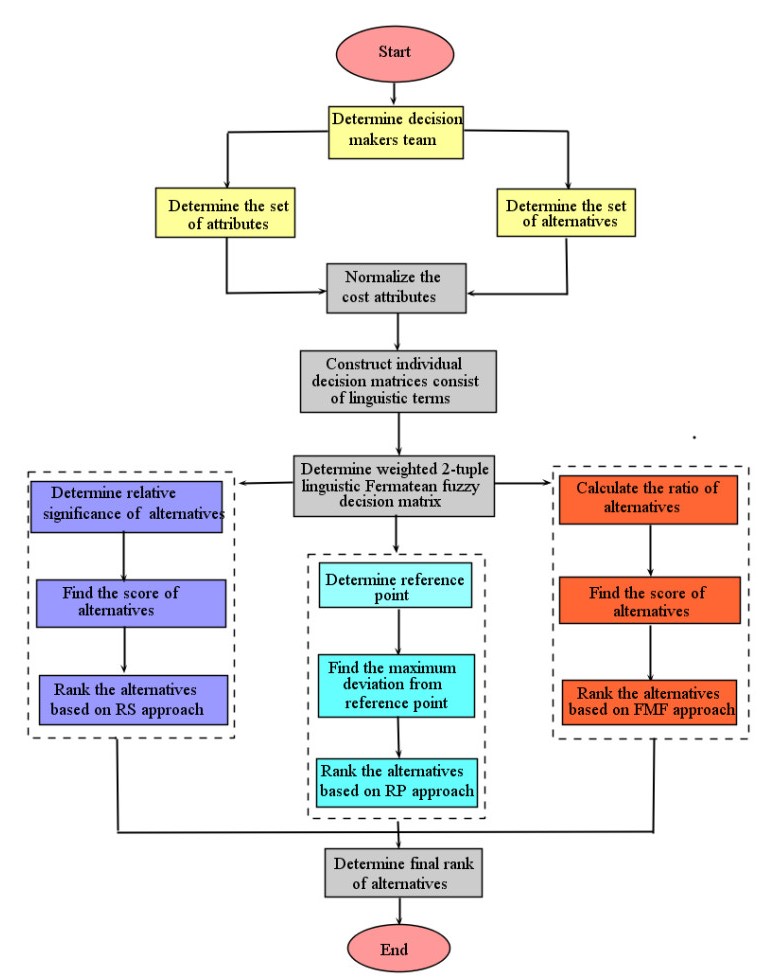
(7) Finally, we rank the options according to dominance theory. We give a graphical description of the proposed method to make the proposed technique more comprehensive and clearer. The presented flowchart explains the proposed method in an efficient manner.

(8) At the end, we apply the 2TLFF-MULTIMOORA method to a real case study consisting of urban quality of life. We have shown that the developed 2TLFF-MULTIMOORA method preserves the correlation between attributes through a precise ranking order.

(9) Furthermore, the proposed 2TLFF-MULTIMOORA method is compared with existing methods to show the versatility of the developed method.

The structure of this research study is narrated as: This research paper comprises seven sections. Section 2 provides the literature review of developed methodology. Section 3 contains preliminary concepts related to 2TLFFSs. Section 4 narrates the proposed algorithm and flow chart of the 2TLFF-MULTIMOORA method. The numerical example to determine the best quality of life in different cities by using the 2TLFF-MULTIMOORA method is discussed in Section 5. Section 6 consists of comparative study of developed methodology. Section 7 describes the advantages of our proposed method. Section 8 presents a conclusion.

2.   Literature review

In the current section, we review the previous studies related to the present study.

Chakraborty ^[8] developed an application of the MOORA method. Karande and Chakraborty ^[9] applied MOORA method in material selection. The MOORA method was characterized by full multiplicative form. Brauers ^[10] discussed the MULTIMOORA method in the construction sector of 20 European countries. Brauers and Zavadskas ^[11] gave the concept of practical application of MULTIMOORA technique. In DM, many real-life problems consist of vague and unclear information because of the vagueness of human judgements. The vague and unclear data cannot be described by crisp set theory. A novel ELECTRE III-based MAGDM approach for bid evaluation was developed in ^[12]. The proposed model is based on generalized comparative linguistic expressions (GCLEs) for the evaluation of bidder performance. Chen et al. ^[13] developed a new collective opinion generation technique and a brief bid evaluation attribute tree was established.

Brauers et al. ^[14] proposed the fuzzy MULTIMOORA method in 2011. Hafezalkotob et al. ^[15] conduct an overview of the MULTIMOORA method in the environment of FSs. Bale$\check{z}$entis and Bale$\check{z}$entis ^[16] extended the MULTIMOORA method. Alkan et al. ^[17] applied the fuzzy MULTIMOORA method for the ranking of renewable energy sources. Liang et al. ^[18] studied the MULTIMOORA method in mining method selection. Fattahi and Khalilzadeh ^[20] extended the MULTIMOORA method for risk evaluation under a fuzzy environment. Dahooie ^[21] improved the fuzzy MULTIMOORA method based on the objective weighting method. A proportional interval type-2 hesitant fuzzy TOPSIS approach was proposed by Chen et al. ^[22] that was based on Hamacher aggregation operators. In IFSs, the membership degree is added with non-membership degree such that their sum is less or equal to 1. Zhang et al. ^[23] combined fuzzy MULTIMOORA method with IFSs and proposed intuitionistic fuzzy MULTIMOORA (IFMULTIMOORA) method for MAGDM problem of the energy storage technologies. Garg and Rani ^[24] proposed an IFMULTIMOORA approach with aggregation operators for the evaluation of solid waste management techniques.

Huang et al. ^[25] extended the fuzzy MULTIMOORA method to PFSs and developed the Pythagorean fuzzy MULTIMOORA (PFMULTIMOORA) method. In PFSs, the sum of squares of membership and non-membership does not exceed from 1. Li et al. ^[26] employed PFMULTIMOORA method for the determination of passenger satisfaction for public transportation. Senapati and Yager ^[27] defined new operations in the environment of Fermatean fuzzy numbers (FFNs). Senapati and Yager ^[28] defined AOs for FFSs and its application in MAGDM. Garg et al. ^[29] defined Fermatean fuzzy Yager AGO. Rani and Mishra ^[30] extended the MULTIMOORA method in the framework of FFSs.

Chen et al. ^[31] developed the MAGDM approach on the basis of MULTIMOORA method with linguistic evaluations. Zhang ^[32] introduced the idea of linguistic intuitionistic FSs (LIFSs). Chen et al. ^[33] proposed a MAGDM approach with linguistic intuitionistic fuzzy numbers (LIFNs). Garg ^[34] developed the notion of linguistic PFSs (LPFSs). Akram et al. ^[35] proposed the concept of linguistic FFSs (LFFSs). For further studies, the reader is suggested to ^{[36,37,38,39,40,41,42,43,44,45,46]}. Ding and Zhong ^[47] proposed the MULTIMOORA method with the two-dimension uncertain linguistic variables (TDULVs). Herrera and Martínez ^[48,49] developed a 2-tuple linguistic model (2TLM). Martínez et al. ^[50] reviewed 2TLM and pointed out some limitations. Bale$\check{z}$entis and Bale$\check{z}$entis ^[51] proposed 2-tuple linguistic fuzzy MULTIMOORA method. Wei ^[52] introduced 2-tuple linguistic intuitionistic FSs (2TLIFSs). Deng et al. ^[53] proposed the concept of 2-tuple linguistic Pythagorean FSs (2TLPFSs) and defined a MAGDM approach on the basis of Hamy mean operators for 2TLPFSs. Deng et al. ^[54] introduced 2-tuple linguistic Pythagorean fuzzy (2TLPF) Heronian mean operators. Recently, Akram et al. ^[55] developed 2TLPF-MULTIMOORA method. Deng and Gao ^[56] introduced 2TLPF-TODIM method. Akram et al. ^[57] introduced 2TLFFSs, their operational laws and 2-tuple linguistic Fermatean fuzzy (2TLFF) aggregation operators. Health and safety risk assessment model that was based on FF linguistic sets and CoCoSo approach and cloud MULTIMOORA method were proposed in ^[58,59].

To cope with MAGDM problems when the evaluation values are expressed in form of linguistic terms (LT), some 2-tuple linguistic fuzzy MAGDM approaches are proposed on the basis of different operators, including, 2TLIFWA, 2TLIFWG, 2TLPF weighted Hamy mean (2TLPFWHM), 2TLPF weighted Dual Hamy mean (2TLPFWDHM), generalized 2TLPF weighted Heronian mean (G2TLPFWHM) and 2TLPF weighted geometric Heronian mean (2TLPFWGHM) operators. These MAGDM approaches do not deal with 2TLFFSs. The 2TLIFWA and 2TLIFWG operators ^[52] do not consider the correlation between input arguments. Although, when sum of MD and NMD exceed from 1, these operators do not give exact results. The 2TLPFWA operator, 2TLPFWG operator, 2TLPFWHM operator, and 2TLPFWDHM operator ^[53] fail to handle MAGDM issues when sum of square of MD and NMD exceed from 1. The ranking values may differ for different parameters. Moreover, they do not handle 2TLFFNs. The G2TLPFWHM and 2TLPFWGHM operators ^[54] take into account a lot of computational effort, and these operators are not suitable for 2TLFFNs. The aggregation operators named as, 2TLFF Hamy mean operator and 2TLFF Dual Hamy mean operator ^[57] are designed to model decision data provided by 2TLFFNs but they lose the relative relevance of the criterion and are insufficiently resilient. These operators have rank reversal problem, in which the ranking order of options is changed when an option is added or removed. Therefore, there is not any precise method to handle MAGDM problems when the decision experts provide evaluation information in the form of 2TLFFNs. The existing approaches only deal with 2TLIFNs and 2TLPFNs. These strategies fail to model the decision data evaluated by 2TLFFNs. Therefore, it is necessary to develop an appropriate method to capture fuzzy evaluation values provided by 2TLFFNs. According to the above study, there is no work on the 2TLFF-MULTIMOORA technique in the existing literature. All MAGDM methods are designed to capture ambiguous data characterized by 2TLIFN or 2TLPFN. These methods cannot solve the decision problem of 2TLFFN evaluation. Existing DM methods named 2TLPF MULTIMOORA method ^[55] and 2TLPF TODIM method ^[56] only consider DM behavior in 2TLPF environment.

The proposed 2TLFF-MULTIMOORA technique on the other hand, copes with the DM problems modeled by 2TLFFNs and generates an integrative result by merging three utility values using a ranking aggregation tool. The three subordinate ranking parts of 2TLFF-MULTIMOORA consist of the fully compensatory model, non-compensatory model and incompletely compensatory model. The designed 2TLFF-MULTIMOORA technique is flexible and robust as it does not bound the decision experts in the environment of 2TLIFNs and 2TLPFNs.

To enhance the readability of our research work, some important abbreviations that are adopted throughout this work are presented in Table 1.

3.   Preliminaries

Definition 3.1. ^[57] Let $Z$ be a universal set and $\mathbb{\dot{L}} = \{\mathfrak{\acute{I}}_{q}|, 0\leq q\leq \tau\}$ be a LTS with odd cardinality $\tau+1$. If $A = \{(\mathfrak{\acute{I}}_{\zeta}, \zeta), (\mathfrak{\acute{I}}_{\varphi}, \varphi)\}$ is defined for $\mathfrak{\acute{I}}_{\zeta}, \mathfrak{\acute{I}}_{\varphi} \in \mathbb{\dot{L}}$ and $\zeta, \varphi \in [-0.5, 0.5)$, where $(\mathfrak{\acute{I}}_{\zeta}, \zeta)$ and $(\mathfrak{\acute{I}}_{\varphi}, \varphi)$ denotes the MD and NMD, respectively, the 2TLFFS is defined as follows:

where $(\mathfrak{\acute{I}}_{\zeta_{q}}, \zeta_{q})$ and $(\mathfrak{\acute{I}}_{\varphi_{q}}, \varphi_{q})$ denote the MD and NMD, and satisfy the conditions that $0\leq \Delta^{-1}(\mathfrak{\acute{I}}_{\zeta_{q}}, \zeta_{q})\leq \tau$, $0\leq \Delta^{-1}(\mathfrak{\acute{I}}_{\varphi_{q}}, \varphi_{q})\leq \tau$ and $0\leq (\Delta^{-1}(\mathfrak{\acute{I}}_{\zeta_{q}}, \zeta_{q}))^{3}+(\Delta^{-1}(\mathfrak{\acute{I}}_{\varphi_{q}}, \varphi_{q})^{3})\leq \tau^{3}$. The pair $\{(\mathfrak{\acute{I}}_{\zeta_{q}}, \zeta_{q}), (\mathfrak{\acute{I}}_{\varphi_{q}}, \varphi_{q})\}$ is defined as 2TLFFN.

Definition 3.2. ^[57] Let $\grave{A} = \{(\mathfrak{\acute{I}}_{\zeta_{1}}, \zeta_{1}), (\mathfrak{\acute{I}}_{\varphi_{1}}, \varphi_{1})\}$ and $\grave{B} = \{(\mathfrak{\acute{I}}_{\zeta_{2}}, \zeta_{2}), (\mathfrak{\acute{I}}_{\varphi_{1}}, \varphi_{2})\}$ be two 2TLFFNs, $\alpha > 0$ then the operational laws on 2TLFFNs are defined in the following:

● $\grave{A}\oplus \grave{B} = \Bigg\{\Delta\left(\tau\sqrt{1-\left(1-\left(\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\zeta_{1}}, \zeta_{1})}{\tau}\right)^{3}\right)\left(1-\left(\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\zeta_{2}}, \zeta_{2})}{\tau}\right)^{3}\right)}\right), \\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \Delta\left(\tau\left(\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\varphi_{1}}, \varphi_{1})}{\tau}\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\varphi_{2}}, \varphi_{2})}{\tau}\right)\right) \Bigg\}.$

● $\grave{A}\otimes \grave{B} = \Bigg\{\Delta\left(\tau\left(\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\zeta_{1}}, \zeta_{1})}{\tau}\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\zeta_{2}}, \zeta_{2})}{\tau}\right)\right), \\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \Delta\left(\tau\sqrt{1-\left(1-\left(\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\varphi_{1}}, \varphi_{1})}{\tau}\right)^{3}\right)\left(1-\left(\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\varphi_{2}}, \varphi_{2})}{\tau}\right)^{3}\right)}\right) \Bigg\}.$

● $\alpha\grave{A} = \Bigg\{\Delta\left(\tau\sqrt{1-\left(1-\left(\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\zeta_{1}}, \zeta_{1})}{\tau}\right)^{3}\right)^{\alpha}}\right), \Delta\left(\tau\left(\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\varphi_{1}}, \varphi_{1})}{\tau}\right)^{\alpha}\right)\Bigg\}.$

● $\grave{A}^{\alpha} = \Bigg\{\Delta\left(\tau\left(\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\zeta_{1}}, \zeta_{1})}{\tau}\right)^{\alpha}\right), \Delta\left(\tau\sqrt{1-\left(1-\left(\dfrac{\Delta^{-1}(\mathfrak{\acute{I}}_{\varphi_{1}}, \varphi_{1})}{\tau}\right)^{3}\right)^{\alpha}}\right)\Bigg\}.$

Definition 3.3. ^[57] Consider $\grave{A} = \{(\mathfrak{\acute{I}}_{\zeta}, \zeta), (\mathfrak{\acute{I}}_{\varphi}, \varphi)\}$ is a 2TLFFN in $\grave{F}$ then $\mathfrak{S}(\grave{A})$ describes the score function and $\mathcal{H}(\grave{A})$ represents the accuracy function of $\grave{A}$ in the following expressions,

We now introduce a new class of aggregation operators and a distance measure for 2TLFFNs.

Definition 3.4. Let $F_{p} = \{(\mathfrak{\acute{I}}_{\zeta_{p}}, \zeta_{p}), (\mathfrak{\acute{I}}_{\varphi_{p}}, \varphi_{p})\}, \; (p = 1, 2, \ldots, y)$ be the set of 2TLFFNs, the 2TLFF arithmetic mean (2TLFFAM) operator is defined as

Definition 3.5. Let $F_{p} = \{(\mathfrak{\acute{I}}_{\zeta_{p}}, \zeta_{p}), (\mathfrak{\acute{I}}_{\varphi_{p}}, \varphi_{p})\}(p = 1, 2, \ldots, y)$ be the set of 2TLFFNs, the 2TLFF geometric mean (2TLFFGM) operator is defined as

Definition 3.6. Let $F_{p} = \{(\mathfrak{\acute{I}}_{\zeta_{p}}, \zeta_{p}), (\mathfrak{\acute{I}}_{\varphi_{p}}, \varphi_{p})\}(p = 1, 2, \ldots, y)$ be the set of 2TLFFNs with the weighting vector defined as $\grave{K} = \{\grave{\gamma_{1}}, \grave{\gamma_{2}}, \ldots, \grave{\gamma_{y}}\}$ such that $\mathop {\mathop \sum \limits^y }\limits_{p = 1} \grave{\gamma_{p}} = 1, \grave{\gamma_{p}}\in [0, 1]$ the 2TLFF weighted average (2TLFFWA) operator is defined as

Definition 3.7. Let $F_{p} = \{(\mathfrak{\acute{I}}_{\zeta_{p}}, \zeta_{p}), (\mathrm{t}_{\varphi_{p}}, \varphi_{p})\}(p = 1, 2, \ldots, y)$ be the set of 2TLFFNs with the weighting vector defined as $\grave{K} = \{\grave{\gamma_{1}}, \grave{\gamma_{2}}, \ldots, \grave{\gamma_{y}}\}$ such that $\mathop {\mathop \sum \limits^y }\limits_{p = 1} \grave{\gamma_{p}} = 1, \grave{\gamma_{p}}\in [0, 1]$ the 2TLFF weighted geometric (2TLFFWG) operator is defined as

Definition 3.8. Let $\mathfrak{T}_{1} = \{(\mathfrak{\acute{I}}_{\zeta_{1}}, \zeta_{1}), (\mathfrak{\acute{I}}_{\varphi_{1}}, \varphi_{1})\}$ and $\mathfrak{T}_{2} = \{(\mathfrak{\acute{I}}_{\zeta_{2}}, \zeta_{2}), (\mathfrak{\acute{I}}_{\varphi_{2}}, \varphi_{2})\}$ be two 2TLFFNs. The mathematical expression to measure the distance between $\mathfrak{T}_{1}$ and $\mathfrak{T}_{2}$ is defined as follows:

4.   Proposed 2-tuple linguistic Fermatean fuzzy MULTIMOORA method

In this section, we will propose an extended version of the MULTIMOORA method to address MAGDM in a 2TLFF environment and evaluate the superlative alternative in decision-making. The 2TLFF-MULTIMOORA method consist of several steps which are defined here. This method consists of three approaches: the 2-tuple linguistic Fermatean fuzzy ratio system (2TLFFRS) approach, the 2-tuple linguistic Fermatean fuzzy reference point (2TLFFRP) approach and the 2-tuple linguistic Fermatean fuzzy full multiplicative form (2TLFFFMF) approach. In all three approaches, the first four steps are the same. In the MAGDM problem, a decision matrix characterizes the values of alternatives supporting certain attributes under a 2-tuple linguistic Fermatean fuzzy environment.

Consider $\grave{Z} = \{\grave{z_{1}}, \grave{z_{2}}, \ldots, \grave{z_{x}}\}$ and $\mathfrak{C} = \{\mathrm{\grave{c_{1}}}, \mathrm{\grave{c_{2}}}, \ldots, \mathrm{\grave{c_{y}}}\}$ be the sets of alternatives and attributes respectively. Let $\grave{K} = \{\grave{\kappa_{1}}, \grave{\kappa_{2}}, \ldots, \grave{\kappa_{y}}\}$ be the set of weights which are assigned to the attributes by decision-makers such that $\mathop {\mathop \sum \limits^y }\limits_{q = 1} \grave{\kappa_{q}} = 1, \grave{\kappa_{q}}\in [0, 1]$. Let $\grave{A} = \{\mathrm{\grave{a_{1}}}, \mathrm{\grave{a_{2}}}, \ldots, \mathrm{\grave{a_{z}}}\}$ be the set of decision makers which are invited to provide the needs of MAGDM problems. Let $K = \{\kappa_{1}, \kappa_{2}, ..., \kappa_{z}\}$ is the set of weights which are assigned to decision-makers such that $\mathop {\mathop \sum \limits^z }\limits_{r = 1} \kappa_{r} = 1, \kappa_{r}\in [0, 1]$. Our aim is to select the superlative alternative from the feasible alternatives supporting certain attributes.

The step-by-step procedure of 2TLFF-MULTIMOORA method is described below:

Step 1. Formation of individual 2TLFF decision matrix (2TLFFIDM)

Each decision-maker investigates the attributes upon which alternatives are selected. The decision makers evaluate the capabilities of alternatives supporting certain criteria and assign the LT to each alternative supporting certain criteria using Table 2. The 2-tuple linguistic Fermatean fuzzy numbers assigned to LT are shown in Table 2. The 2TLFFIDM provided by $\mathrm{\grave{a_{r}}}$ expert is $F^{r} = D(C_{q}(Z_{p}))_{x\times y} = (F^{r}_{pq})_{x\times y}$. Similarly $z$ 2TLFFDMs $F^{1}, F^{2}, \ldots, F^{z}$ are formed by $z$ decision makers as follows:

where $r = 1, 2, ..., z$. Each entry of the individual decision matrix is of the form $(\mu_{pq}, \nu_{pq}) = \Bigg\{\left(\mathfrak{\acute{I}}_{\zeta_{pq}}, \zeta_{pq} \right), \left(\mathfrak{\acute{I}}_{\varphi_{pq}}, \varphi_{pq}\right)\Bigg\}$.

Step 2. Normalization of cost attributes

If cost attributes exist in MAGDM problems, they need to be normalized. The non-economical type of attributes is transformed into beneficial attributes through the following equation:

Step 3. Construction of aggregated 2TLFF decision matrix (A2TLFFDM)

The A2TLFFDM is formed to determine the group decision of experts by combining the individual judgement of decision experts. The A2TLFFDM is constructed with 2TLFFWA operator as follows:

Step 4. Construction of weighted aggregated 2TLFF decision matrix (WA2TLFFDM)

The WA2TLFFDM is constructed with the A2TLFFDM and weight vector $\grave{K}$ of attributes. The entries of WA2TLFFDM are of the form $(\dot{\mu}_{pq}, \dot{\nu}_{pq}) = \Bigg\{\left(\mathfrak{\acute{I}}_{\dot{\zeta}_{pq}}, \dot{\zeta}_{pq} \right), \left(\mathfrak{\acute{I}}_{\dot{\varphi}_{pq}}, \dot{\varphi}_{pq}\right)\Bigg\}$ which are evaluated as follows:

The WA2TLFFDM is constructed as follows:

Step 5. 2TLFF ratio system approach (2TLLFFRS)

(i) Calculate $\grave{Y_{p}}^{+}$ by using the 2TLFFAM operator as follows:

(ii) Defuzzify $\grave{Y_{p}}^{+}$ using the following equation,

(iii) The ranking of alternatives is determined on the basis of $\grave{y_{p}}^{+}$ values from lower to higher level. The alternative which has maximum value of $\grave{y_{p}}^{+}$ will be the favourable alternative.

Step 6. 2TLFF reference point approach (2TLFFRP)

(i) The reference point of alternatives is calculated based on the score value of $\grave{z_{p}}$

or

(ii) Determine the distance of alternatives to each coordinate of reference point by using the following equation,

(iii) Rank the alternatives.

The conclusions are evaluated on the base of the values determined from the reference point. In this approach, we rank the alternatives based on $\max d(\grave{z_{pq}}, \grave{z^{*}_{p}})$ in an decreasing order and the best alternative has lowest value that is $\min_{p}(\max_{p}d(\grave{z_{pq}}, \grave{z^{*}_{p}}))$.

Step 7. 2TLFF full multiplicative approach (2TLFFMF)

(i) Calculate $\grave{A_{p}}^{+}$ by using the 2TLFFGM operator as follows:

(ii) Defuzzify $\grave{A_{p}}^{+}$ using the following equation,

(iii) The alternatives are ranked based on $\grave{a_{p}}^{+}$ value in descending order. The ranking results are compared on the basis of maximum value of $\grave{a_{p}}^{+}$.

Step 8. Final ranking

The final results of alternatives are determined from the ranking of above three approaches. According to the ranking of all three approaches, alternatives are arranged in descending order and the best alternative is determined.

Figure 1 narrates the steps of proposed technique by the following flowchart.

5.   Application

In this section, we describe a case study from the field of urban studies related to quality of life in different cities which illustrates the applicability of our proposed 2TLFF-MULTIMOORA method.

5.1.   Case study: Selection of quality of life in urban cities

5.1.1.   Problem prominence

The studies on QOL (quality of life) have been considered since 1930's and later on it has been become a multidimensional idea that includes other aspects of human life. It is narrated by Li and Weng ^[62] that in developing as well as developed countries, the study on QOL is attaining more and more interest from various fields, including economics, geography, marketing and management. That is, QOL is emerging as an important framework for policy assessment, urban management, planning, and evaluation of cities. According to many researchers, the evaluation of QOL in urban cities is very important on regular basis, as it can be helpful in decision-making regarding urban management and planning ^[63]. Two main approaches to measure the urban QOL are: Objective urban QOL and subjective urban QOL ^[64].

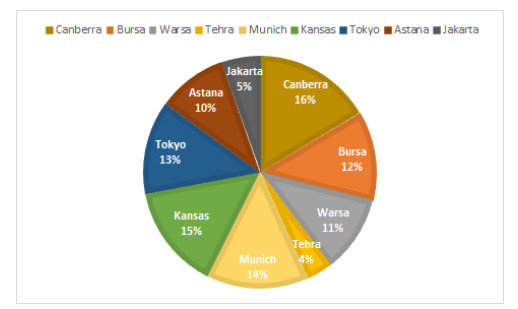
All over the world, urban regions are facing direct competition for different resources due to connectivity in technology and transportation. Economically, this competition is intensifying day by day. One of the essential factors contributing to these inter-city conditions is individuals willing to relocate in pursuit of career opportunities or a better quality of life. This competition is essential for determining a city's future economic and overall developmental success. The ranking of cities motivates the people to visit and relocate to a particular city in which they engage in healthy behavior. Places have been ranked in terms of various aspects of quality of life such as climate change, pollution and health care, etc. The quality of life in different cities in 2022 is shown in Figure 2 (https://www.numbeo.com/quality-of-life/rankings.jsp).

5.1.2.   Problem description

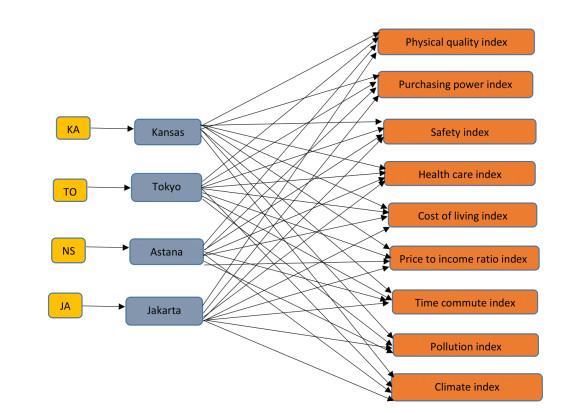
The WHO decides to rank the cities for the strategic policy advice of cities. Since ranking of cities plays a significant role to testify the social and economical structure of cities, four decision-experts $\mathrm{\grave{a_{1}}}, \mathrm{\grave{a_{1}}}, \mathrm{\grave{a_{2}}}, \mathrm{\grave{a_{4}}}$ from the field of urban studies are invited to rank the different places and there are four cities; Kansas (United States), Tokyo (Japan), Astana (Kazakhstan) and Jakarta (Indonesia) which are ranked. The ranking of different cities is evaluated on the basis of a number of aspects. The selection of most suitable city is determined on the basis of the following nine aspects:

● $\mathrm{\grave{c_{1}}}$ stands for the physical quality index (PQI),

● $\mathrm{\grave{c_{2}}}$ stands for the purchasing power index (PPI),

● $\mathrm{\grave{c_{3}}}$ stands for the safety index (SI),

● $\mathrm{\grave{c_{4}}}$ stands for the health care index (HI),

● $\mathrm{\grave{c_{5}}}$ stands for the cost-of-living index (CLI),

● $\mathrm{\grave{c_{6}}}$ stands for the price to income ratio index (PIRI),

● $\mathrm{\grave{c_{7}}}$ stands for the time commute index (TCI),

● $\mathrm{\grave{c_{8}}}$ stands for the pollution index (PI),

● $\mathrm{\grave{c_{9}}}$ stands for the climate index (CI).

The decision makers give their opinion in linguistic terms from the LTS $\mathbb{\dot{L}} = \{\mathfrak{\acute{I}_{0}} = { \text{tremendously bad}}, \mathfrak{\acute{I}_{1}} = { \text{very bad}}, \mathfrak{\acute{I}_{2}} = { \text{bad}}, \mathfrak{\acute{I}_{3}} = { \text{medium bad}}, \mathfrak{\acute{I}_{4}} = { \text{medium}}, \mathfrak{\acute{I}_{5}} = { \text{medium good}}, \mathfrak{\acute{I}_{6}} = { \text{good}}, \mathfrak{\acute{I}_{7}} = { \text{very good}}, \mathfrak{\acute{I}_{8}} = { \text{exceptional}}\}$. The proposed framework for selecting the best city is shown in Figure 3.

The opinion of decision experts in terms of linguistic terms associated with a 2TLFFNs is shown in Table 3.

The set of cities is represented as $\grave{X} = \{KA, TO, NS, JA\}$ and the set of attributes is represented as $\grave{C} = \{PQI, PPI, SI, HI, CLI, PIRI, TCI, PI, CI\}$.

The set of decision experts is shown as $\mathrm{A} = \{\mathrm{\grave{a_{1}}}, \mathrm{\grave{a_{1}}}, \mathrm{\grave{a_{2}}}, \mathrm{\grave{a_{4}}}\}$. The weight vector for the decision experts is $K = \{0.25, 0.25, 0.25, 0.25\}.$ The weights assigned to attributes are given by the set $\grave{K} = \{0.11, 0.11, 0.11, 0.11, 0.11, 0.11, 0.11, 0.11, 0.12\}.$

5.2.   Decision matrix and evaluation process

The stepwise solution of MAGDM problem by 2TLFF-MULTIMOORA method is described below:

$\textbf{Step 1:}$ Table 2 is consist of linguistic terms and their corresponding 2-tuple linguistic Fermatean fuzzy number. The opinion of decision experts towards the alternatives according to attributes is shown in Table 3. The individual 2TLFFDMs of decision experts $\mathrm{\grave{a_{1}}}, \mathrm{\grave{a_{1}}}, \mathrm{\grave{a_{2}}}, \mathrm{\grave{a_{4}}}$ are constructed by using Table 2, and they are shown in Tables 4–7.

$\textbf{Step 2:}$ As $\mathrm{\grave{c_{5}}}$, $\mathrm{\grave{c_{6}}}$, $\mathrm{\grave{c_{7}}}$, $\mathrm{\grave{c_{8}}}$ and $\mathrm{\grave{c_{9}}}$ are cost attributes, these are normalized. The normalized 2TLFFDM (N2TLFFDM) are shown in Tables 8–11.

$\textbf{Step 3:}$ The individual opinion of decision experts having the weight vector $K = \big\{0.25, 0.25, 0.25, 0.25\big\}$ is summarized to form aggregated 2TLFF decision matrix using 2TLFFWA operator which is shown in Table 12.

$\textbf{Step 4:}$ The WA2TLFFDM is constructed with the weight vector of attributes. The weight vector for attributes is $\grave{K} = \{0.11, 0.11, 0.11, 0.11, 0.11, 0.11, 0.11, 0.11, 0.12\}.$ The WA2TLFFDM is shown in Table 13.

$\textbf{Step 5:}$ 2TLFF ratio system approach

(i) In ratio system approach, the $\grave{Y^{+}_{p}}$ are calculated using Eq (4.2) and are shown in Table 14.

(ii) The scores of alternatives are calculated.

(iii) The alternatives are ranked.

Step 6: 2TLFF reference point approach

(i) In this approach, the reference points are calculated from WA2TLFFDM which are shown in Table 15.

(ii) The distance from reference point and each alternative is calculated and the values are shown in Table 16.

(iii) We arranged the alternatives in ascending order to find out their ranking.

Step 7: 2TLFF full multiplicative form approach

(i) The $\grave{A^{+}_{p}}$ are calculated using the Eq (4.4) which are displayed in Table 17.

(ii) The score value of each alternative is calculated.

(iii) The alternatives are ranked which are given in Table 17.

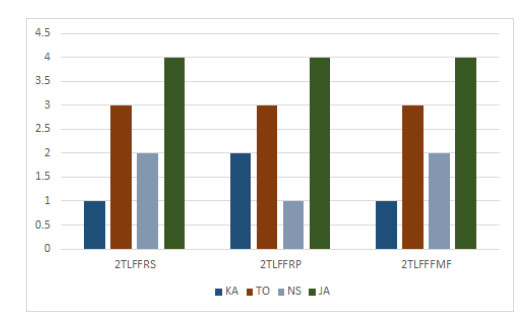
Step 8: In the end, the alternatives are ranked according to the ranking values of all approaches and the results are shown in Table 18.

The ranking results with all three approaches are shown in Figure 4.

6.   Comparative analysis

To verify the validity and significant effect of our developed strategy, we solve the problem by utilizing other approaches, including LPFWA operator ^[34], LPFWG operator ^[34], 2TLPFWHM operator ^[19], 2TLPFWDHM operator ^[19], G2TLPFWHM operator ^[54] and 2TLPFWGHM operator ^[54]. The results are shown in Table 19.

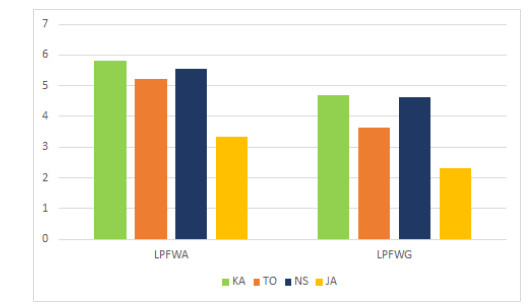
● We utilize LPFWA and LPFWG operators ^[34] to check the efficiency of our proposed method. Although the ranking results are same, but LPFWA and LPFWG fails to consider the correlation between different input arguments. Our proposed 2TLFF-MULTIMOORA method obtains the maximum correlation among input arguments. The score values of alternatives with LPFWA and LPFWG operators are shown in Figure 5.

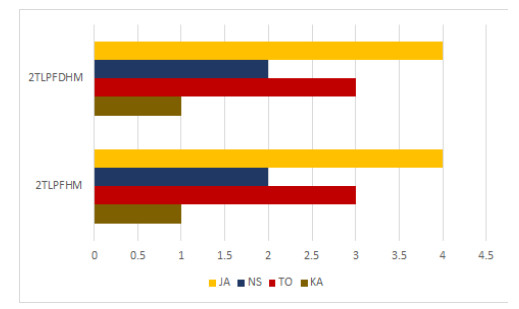
● Compared with 2TLPFWHM and 2TLPFWDHM operators ^[54], the ranking results are same. 2TLPFWHM and 2TLPFWDHM operators involve parameters which may affect the ranking results. In our proposed method, no parameters are involved. This reduces the computational effort. The ranking results with 2TLPFWHM and 2TLPFWDHM operators are described in Figure 6.

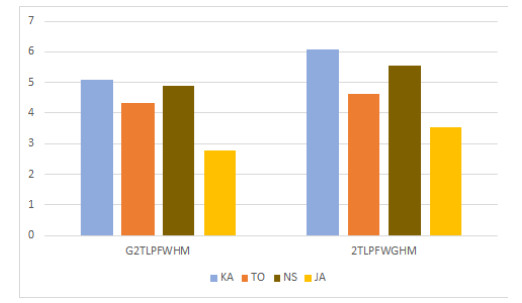
● Compared with G2TLPFWHM and 2TLPFWGHM operators ^[19], the ranking results do not alter. G2TLPFWHM and 2TLPFWGHM operators only capture the correlation between two input arguments. In practical issues, we often need to capture the correlation between all input arguments. Besides this, G2TLPFWHM and 2TLPFWGHM operators involve two parameters which take into account a lot of computational effort. If one of the parameters is zero, no interrelationship among different parameters is considered. The ranking results with G2TLPFWHM and 2TLPFWGHM operators are shown in Figure 7.

The ranking results of our proposed method with all existing approaches are expressed in Table 19 and Figure 8.

Similarities and differences

The main similarities and differences among these counterparts when applied to fuzzy data aggregation are listed as follows:

(1) All the existing techniques (including LPFWA operator, LPFWG operator, 2TLPFWHM operator, 2TLPFWDHM operator, G2TLPFWHM operator and 2TLPFWGHM) are used to solve a decision-making problem under PF environment, whereas the proposed work handles the FF information that is a broader phenomenon.

(2) In existing theories, the various operators are utilized to aggregate the fuzzy data and then the score values are applied to rank the alternatives.

(3) In 2TLFF-MULTIMOORA method, the imprecise data is aggregated through averaging and geometric operators and then MULTIMOORA technique is applied to rank the alternatives.

(4) Although, the ranking results are same through all techniques, but the methodology of 2TLFF-MULTIMOORA technique makes the proposed model more accurate and effective.

(5) Moreover, 2TLPFWHM and 2TLPFWDHM operators involve parameters which may affect the ranking results. In our proposed method, no parameters are involved.

(6) The most prominent feature of our proposed model is that it does not involve any parameters. It makes the computations much easier and also reduces the chance of error.

7.   Discussions and results

The Figures 5–6 reveal that the final ranking results of all alternatives through 2TLFF-MULTIMOORA method are same as through all existing techniques. This verifies the validity and effectiveness of our proposed model. While doing the computations, it can be seen easily that LPFWA and LPFWG does not consider the correlation among distinct input arguments, whereas the proposed method obtains the maximum correlation between these arguments. In case of 2TLPFWHM and 2TLPFWDHM operators, parameters are involved which may change the ranking results, whereas the absence of these parameters, as can be noted in the proposed work, reduces the computational efforts.

Advantages

The above discussion shows that the proposed work owns the following advantages.

● Our proposed 2TLFF-MULTIMOORA method is an effortless tool to solve MAGDM problems as it involves no parameters.

● The decision experts express their opinion by linguistic term.

● The proposed method is divided into three approaches which are used to determine sub-ordinate ranking and final ranking is derived based on these approaches.

● Involvement of three approaches makes the 2TLFF-MULTIMOORA method more flexible and robust.

● The presented method is a more efficient and reasonable approach than other approaches as it allocates the decision-makers to express their judgement in terms of LTS through 2TLFFNs.

● The other MAGDM approaches do not consider the correlation between all input arguments. The proposed methodology obtains maximum correlation for the ranking of alternatives.

8.   Conclusions

In the current paper, the 2TLFF-MULTIMOORA method is being developed to solve the MAGDM problem with vague information. 2TLFFS is a generalized form of FS that considers MD and NMD in terms of LT. The 2TLFF-MULTIMOORA method is a DM approach that consists of three parts: the 2TLFFRS approach, the 2TLFFRP approach, and the 2TLFFFMF approach. The final ranking of the proposed method is fused with the lower rankings of all three approaches. The algorithm designed for the proposed methodology is useful for 2TLFFS, and the 2TLFF-MULTIMOORA method takes three approaches into consideration when considering decision options. The operating rules of the developed technology are shown in the flow chart. The developed method is narrated with numerical examples and the ranking results are testified with other MAGDM approaches. Our future research will focus on certain MCDM, including: (i) Complex intuitionistic fuzzy MULTIMOORA method, (ii) Complex Pythagorean fuzzy MULTIMOORA method, (iii) Complex 2TLIF-MULTIMOORA method, and (iv) Complex 2TLPF-MULTIMOORA method.

Acknowledgments

The research of Santos-García was funded by the Spanish project ProCode-UCM (PID2019-108528RB-C22) from the Ministerio de Ciencia e Innovación.

Conflict of interest

The authors declare no conflict of interest.