Let $ G $ be a finite simple graph and let $ A(G) $ be its adjacency matrix. Then $ G $ is $ singular $ if $ A(G) $ is singular. Suppose $ P_{b_{1}}, P_{b_{2}}, P_{b_{3}} $ are three paths with disjoint vertices, where $ b_i\geq 2 (i = 1, 2, 3) $, and at most one of them is 2. Coalescing together one of the two end vertices of each of the three paths, and coalescing together the other end vertex of each of the three paths, the resulting graph is called the $ \theta $-graph, denoted by $ \theta(b_{1}, b_{2}, b_{3}) $. Let $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ be the graph obtained by merging one end of the path $ P_{s} $ with one vertex of a cycle $ C_{a} $, and merging the other end of the path $ P_{s} $ with one vertex of $ \theta(b_{1}, b_{2}, b_{3}) $ of degree 3. If $ s = 1 $, denote $ \beta(a, b_{1}, b_{2}, b_{3}) = \alpha(a, b_{1}, b_{2}, b_{3}, 1) $. In this paper, we give the necessity and sufficiency condition for the singularity of $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ and $ \beta(a, b_{1}, b_{2}, b_{3}) $, and we also prove that the probability that any given $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ is a singular graph is equal to $ \frac{35}{64} $, the probability that any given $ \beta(a, b_{1}, b_{2}, b_{3}) $ is a singular graph is equal to $ \frac{9}{16} $. From our main results we can conclude that such a $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ graph ($ \beta(a, b_{1}, b_{2}, b_{3}) $ graph) is singular if $ 4|a $ or three $ b_i (i = 1, 2, 3) $ are all odd numbers or exactly two of the three $ b_i (i = 1, 2, 3) $ are odd numbers and the length of the cycle formed by the two odd paths in $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ graph ($ \beta(a, b_{1}, b_{2}, b_{3}) $ graph) is a multiple of 4. The theoretical probability of these graphs being singular is more than half.
Citation: Haicheng Ma, Xiaojie You, Shuli Li. The singularity of two kinds of tricyclic graphs[J]. AIMS Mathematics, 2023, 8(4): 8949-8963. doi: 10.3934/math.2023448
| [1] | Dijian Wang, Dongdong Gao . Laplacian integral signed graphs with few cycles. AIMS Mathematics, 2023, 8(3): 7021-7031. doi: 10.3934/math.2023354 |
| [2] | Kiki A. Sugeng, Fery Firmansah, Wildan, Bevina D. Handari, Nora Hariadi, Muhammad Imran . Several properties of antiadjacency matrices of directed graphs. AIMS Mathematics, 2024, 9(10): 27834-27847. doi: 10.3934/math.20241351 |
| [3] | Zhen Lin . On the sum of the largest $ A_{\alpha} $-eigenvalues of graphs. AIMS Mathematics, 2022, 7(8): 15064-15074. doi: 10.3934/math.2022825 |
| [4] | Bilal A. Rather, Fawad Ali, Nasim Ullah, Al-Sharef Mohammad, Anwarud Din, Sehra . $ A_{\alpha} $ matrix of commuting graphs of non-abelian groups. AIMS Mathematics, 2022, 7(8): 15436-15452. doi: 10.3934/math.2022845 |
| [5] | Imrana Kousar, Saima Nazeer, Abid Mahboob, Sana Shahid, Yu-Pei Lv . Numerous graph energies of regular subdivision graph and complete graph. AIMS Mathematics, 2021, 6(8): 8466-8476. doi: 10.3934/math.2021491 |
| [6] | Syafrizal Sy, Rinovia Simanjuntak, Tamaro Nadeak, Kiki Ariyanti Sugeng, Tulus Tulus . Distance antimagic labeling of circulant graphs. AIMS Mathematics, 2024, 9(8): 21177-21188. doi: 10.3934/math.20241028 |
| [7] | Alaa Altassan, Muhammad Imran, Bilal Ahmad Rather . On $ ABC $ energy and its application to anticancer drugs. AIMS Mathematics, 2023, 8(9): 21668-21682. doi: 10.3934/math.20231105 |
| [8] | Shabbar Naqvi, Muhammad Salman, Muhammad Ehtisham, Muhammad Fazil, Masood Ur Rehman . On the neighbor-distinguishing in generalized Petersen graphs. AIMS Mathematics, 2021, 6(12): 13734-13745. doi: 10.3934/math.2021797 |
| [9] | Jahfar T K, Chithra A V . Central vertex join and central edge join of two graphs. AIMS Mathematics, 2020, 5(6): 7214-7233. doi: 10.3934/math.2020461 |
| [10] | Hengbin Zhang . Automorphism group of the commuting graph of $ 2\times 2 $ matrix ring over $ \mathbb{Z}_{p^{s}} $. AIMS Mathematics, 2021, 6(11): 12650-12659. doi: 10.3934/math.2021729 |
Let $ G $ be a finite simple graph and let $ A(G) $ be its adjacency matrix. Then $ G $ is $ singular $ if $ A(G) $ is singular. Suppose $ P_{b_{1}}, P_{b_{2}}, P_{b_{3}} $ are three paths with disjoint vertices, where $ b_i\geq 2 (i = 1, 2, 3) $, and at most one of them is 2. Coalescing together one of the two end vertices of each of the three paths, and coalescing together the other end vertex of each of the three paths, the resulting graph is called the $ \theta $-graph, denoted by $ \theta(b_{1}, b_{2}, b_{3}) $. Let $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ be the graph obtained by merging one end of the path $ P_{s} $ with one vertex of a cycle $ C_{a} $, and merging the other end of the path $ P_{s} $ with one vertex of $ \theta(b_{1}, b_{2}, b_{3}) $ of degree 3. If $ s = 1 $, denote $ \beta(a, b_{1}, b_{2}, b_{3}) = \alpha(a, b_{1}, b_{2}, b_{3}, 1) $. In this paper, we give the necessity and sufficiency condition for the singularity of $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ and $ \beta(a, b_{1}, b_{2}, b_{3}) $, and we also prove that the probability that any given $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ is a singular graph is equal to $ \frac{35}{64} $, the probability that any given $ \beta(a, b_{1}, b_{2}, b_{3}) $ is a singular graph is equal to $ \frac{9}{16} $. From our main results we can conclude that such a $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ graph ($ \beta(a, b_{1}, b_{2}, b_{3}) $ graph) is singular if $ 4|a $ or three $ b_i (i = 1, 2, 3) $ are all odd numbers or exactly two of the three $ b_i (i = 1, 2, 3) $ are odd numbers and the length of the cycle formed by the two odd paths in $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ graph ($ \beta(a, b_{1}, b_{2}, b_{3}) $ graph) is a multiple of 4. The theoretical probability of these graphs being singular is more than half.
Let $ G $ be a finite undirected simple graph with vertex set $ V(G) = \{v_1, v_2, \ldots, v_n\} $. The adjacency matrix of $ G $ is defined to be the $ n\times n $ matrix $ A(G) = (a_{ij}) $,
| $ \begin{equation*} a_{ij} = \begin{cases} 1 & {{\text{if}}}\; v_i\sim v_j ,\\ 0 & {\text{otherwise,}} \end{cases} \end{equation*} $ |
where $ v_i\sim v_j $ represents the vertices $ v_i $ and $ v_j $ are adjacent. Obviously, $ A(G) $ is a real symmetric matrix with diagonal elements all 0, and its eigenvalues are all real numbers. The eigenvalues of $ A(G) $ are also the eigenvalues of $ G $ and form the spectrum of $ G $. The number of non-zero eigenvalues and zero eigenvalues in the spectrum of $ G $ are called the $ rank $ and the nullity of $ G $, respectively, and denoted by $ r(G) $ and $ \eta(G) $. Obviously $ r(G)+\eta(G) = n $. Then $ G $ is singular if $ A(G) $ is a singular matrix. In other words, $ G $ is singular if and only if 0 is an eigenvalue of $ G $. Singular graphs play a significant role in graph theory, and there are many applications in physics and chemistry, see for instance the survey article [10].
In chemistry, if we represent the atoms by vertices and the bonds by edges in a molecular, we can get a molecular graph [19,20]. The nullity of a molecular graph has many important applications in chemistry [5,6,7,8,11]. For example, the nullity of a graph equal to 0 is a necessary condition for the stability of the chemical properties of the molecule it represents [7]. In 1957, Collatz and Sinogowitz [8] proposed the problem of characterizing all graphs with nullity greater than zero (i.e. the problem of characterizing all singular graphs), which is a very difficult problem. So far, only some special results are known (see [1,3,12,13,17,21,22,23,24,29]). This problem encourages people to study the structural characteristics of singular graphs, and many authors have studied the interaction between the nullity of a graph and its structure (see [4,9,14,15,18]). Recent studies have also shown that singular graphs are related to other fields of mathematics, such as representation theory of finite groups, combinatorial mathematics, algebraic geometry and so on (see [2,16,26,27,28,30]).
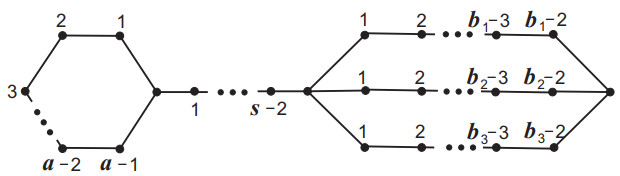
Let $ K_n $, $ P_n $ and $ C_n $ be the complete graph, path and cycle with $ n $ vertices, respectively. Suppose $ P_{b_{1}}, P_{b_{2}}, P_{b_{3}} $ are three paths with disjoint vertices, where $ b_i\geq 2 (i = 1, 2, 3) $, and at most one of them is 2. Coalescing together one of the two end vertices of each of the three paths, and coalescing together the other end vertex of each of the three paths, the resulting graph is called the $ \theta $-graph, denoted by $ \theta(b_{1}, b_{2}, b_{3}) $. Let $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ (or $ \alpha $-graph for short) be the graph obtained by merging one end of the path $ P_{s} $ with one vertex of a circle $ C_{a} $, and merging the other end of the path $ P_{s} $ with one vertex of $ \theta(b_{1}, b_{2}, b_{3}) $ of degree 3, see Figure 1.
If $ s = 1 $, denote $ \beta(a, b_{1}, b_{2}, b_{3}) = \alpha(a, b_{1}, b_{2}, b_{3}, 1) $ (or $ \beta $-graph for short), see Figure 2. Let $ G\cup H $ be the union of two graphs $ G $ and $ H $. The vertex of degree 1 is called the $ pendant\; \; vertex $, and the vertex adjacent to the pendant vertex is called the $ quasi-pendant\; \; vertex $. For the notations and terms which are not defined above, please refer to [5].
We know that whether a graph is singular can be determined from two aspects: one is whether $ 0 $ is its eigenvalue, and the other is whether the determinant of its adjacency matrix is $ 0 $. Many previous research results mainly determine whether a graph is singular from the perspective of the $ 0 $ eigenvalue of graph, only few literatures describe singular graphs from the perspective of determinant, and also very limited literatures study the necessity and sufficiency of singularity of a class of graphs. In this paper, from the perspective of determinant, we give the necessity and sufficiency condition for the singularity of $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ and $ \beta(a, b_{1}, b_{2}, b_{3}) $, and we also prove that the probability that any given $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ is a singular graph is equal to $ \frac{35}{64} $, the probability that any given $ \beta(a, b_{1}, b_{2}, b_{3}) $ is a singular graph is equal to $ \frac{9}{16} $.
We will prove the following results in Section 3.
Theorem 1.1. The graph $ G = \alpha(a, b_{1}, b_{2}, b_{3}, s) $ is singular if and only if one of the following holds.
$ (i) $ $ 4|a $.
$ (ii) $ Three $ b_i (i = 1, 2, 3) $ are all odd numbers.
$ (iii) $ Exactly two of the three $ b_i (i = 1, 2, 3) $ are odd numbers. (1) The length of the cycle formed by the two odd paths in $ G $ is a multiple of 4; (2) $ a $ is even, $ s $ is odd.
$ (iv) $ Exactly one of three $ b_i (i = 1, 2, 3) $ is odd number. $ a $ is even, $ s $ is even, and the length of the cycle formed by the two even paths in $ G $ is a multiple of 4.
$ (v) $ Three $ b_i (i = 1, 2, 3) $ are all even numbers. $ a $ is even, $ s $ is odd.
Corollary 1.2. The graph $ G = \beta(a, b_{1}, b_{2}, b_{3}) $ is singular if and only if one of the following holds.
$ (i) $ $ 4|a $.
$ (ii) $ Three $ b_i (i = 1, 2, 3) $ are all odd numbers.
$ (iii) $ Exactly two of the three $ b_i (i = 1, 2, 3) $ are odd numbers. (1) The length of the cycle formed by the two odd paths in $ G $ is a multiple of 4; (2) $ a $ is even.
$ (iv) $ Three $ b_i (i = 1, 2, 3) $ are all even numbers. $ a $ is even.
Theorem 1.3. The probability that any given $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ is a singular graph is equal to $ \frac{35}{64} $, and the probability that any given $ \beta(a, b_{1}, b_{2}, b_{3}) $ is a singular graph is equal to $ \frac{9}{16}. $
By Theorem 1.1 and Corollary 1.2, we know that the graph $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ ($ \beta(a, b_{1}, b_{2}, b_{3}) $) is singular if $ 4|a $ or three $ b_i (i = 1, 2, 3) $ are all odd numbers or exactly two of the three $ b_i (i = 1, 2, 3) $ are odd numbers and the length of the cycle formed by the two odd paths in $ G $ is a multiple of 4. The smallest singular graph with respect to the number of vertices in $ \alpha $-$ (\beta $-$) $ graphs is $ \alpha(3, 2, 3, 3, 2) $ ($ \beta(3, 2, 3, 3) $), it has 7 (6) vertices. By Theorem 1.3, we find that more than half of the $ \alpha $-$ (\beta $-$) $graphs are singular, that is, the chemical properties of more than half of the chemical molecules with a molecular $ \alpha $-$ (\beta $-$) $ graphs are active and unstable by [7].
Lemma 2.1. [21] Suppose $ G = G_{1}\cup G_{2} \cup\cdots\cup G_{t} $, where $ G_{i} (i = 1, 2, ..., t) $ are connected components of $ G $. Then $ \eta(G) = \sum\limits_{i = 1}^{t}\eta(G_{i}) $. Equivalently, $ G $ is non-singular if and only if each $ G_{i}(i = 1, 2, \ldots, t) $ is non-singular.
Lemma 2.2. [21] Let $ G $ be a graph with a pendant vertex $ v $ and a pendant edge $ vw $, and let $ H = G-v-w $ be the induced subgraph of $ G $ obtained by deleting the vertices $ v $ and $ w $ together with the edges incident to $ w $. Then $ \eta(G) = \eta(H) $. Equivalently, $ G $ non-singular if and only if $ H $ is non-singular.
A subgraph $ H $ of $ G $ is an $ elementary\; \; subgraph $ ($ Sachs\; \; subgraph $) if each component of $ H $ is either a copy of $ K_2 $ or a cycle of $ G $. A $ spanning\; \; elementary\; \; subgraph $ $ (spanning\; \; Sachs\; \; subgraph) $ of $ G $ is an elementary subgraph which contains all vertices of $ G $. A $ matching $ in $ G $ is a set of edges with no shared vertices and a $ perfect\; \; matching $ is a matching that saturates every vertex of $ G $. Obviously, the number of vertices of a graph $ G $ with a perfect matching must be even.
Lemma 2.3. [5] Let $ G $ be a graph of order $ n $, $ A(G) $ be the adjacency matrix of $ G $, then
| $ \det(A(G)) = (-1)^{n}\sum\limits_{H\in\mathcal{H}}(-1)^{p(H)}2^{c(H)}, $ |
where $ \mathcal{H} $ is the set of spanning Sachs subgraphs of $ G $, $ p(H) $ and $ c(H) $ are the number of connected components and cycles in $ H $, respectively.
Note that $ |V(G)| = a+b_{1}+b_{2}+b_{3}+s-6 $. According to the parity of $ b_{1}, b_{2}, b_{3} $ and the symmetry of graph $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $, we divided it into the following four cases to prove.
Case 1. Three $ b_i (i = 1, 2, 3) $ are all odd numbers. In this case, $ G $ has no spanning Sachs subgraph, so $ G $ is singular.
Case 2. Exactly two of the three $ b_i (i = 1, 2, 3) $ are odd numbers. Without losing generality, we assume that $ b_{1} $ is an even number, $ b_{2} $ and $ b_{3} $ are two odd numbers. There are four subcases.
Subcase 2.1. Both $ a $ and $ s $ are odd numbers. In this subcase, $ G $ has no spanning Sachs subgraph containing two cycles, otherwise, the two cycles must be: $ C_{a}\cup C_{b_{i}+b_{j}-2}, \; i, j = 1, 2, 3 $, after deleting the above two cycles, the number of remaining vertices on the path $ P_{s} $ is odd, can not form a perfect matching. The spanning Sachs subgraph of $ G $ containing one cycle is $ C_{b_{2}+b_{3}-2}\cup\frac{a+b_{1}+s-4}{2}P_{2} $ (In fact, there are four kinds of cycles: $ C_{a} $, $ C_{b_{1}+b_{2}-2} $, $ C_{b_{1}+b_{3}-2} $ and $ C_{b_{2}+b_{3}-2} $, but the first three kinds of the above cycles cannot form the spanning Sachs subgraph, because the subgraph obtained by deleting them does not contain perfect matching.), $ G $ has two perfect matchings. By Lemma 2.3,
| $ \det(A(G)) = (-1)^{n}[(-1)^{\frac{a+b_{1}+s-4}{2}+1}\times 2+(-1)^{\frac{a+b_{1}+b_{2}+b_{3}+s-6}{2}}\times 2]. $ |
So, $ G $ is singular if and only if
| $ \begin{align} (-1)^{\frac{a+b_{1}+s-4}{2}+1}\times 2+(-1)^{\frac{a+b_{1}+b_{2}+b_{3}+s-6}{2}}\times 2 = 0. \end{align} $ | (1) |
Simplify Eq (1), we get
| $ \begin{align} (-1)^{\frac{b_{2}+b_{3}-2}{2}}-1 = 0. \end{align} $ | (2) |
Equation (2) holds if and only if $ 4|b_{2}+b_{3}-2 $.
Subcase 2.2. $ a $ is odd, $ s $ is even. In this subcase, the spanning Sachs subgraphs of $ G $ containing two cycles is
| $ C_{a}\cup C_{b_{2}+b_{3}-2}\cup\frac{b_{1}+s-4}{2}P_{2}, $ |
and there are two spanning Sachs subgraphs of $ G $ containing one cycle, they have the form:
| $ C_{a}\cup\frac{b_{1}+b_{2}+b_{3}+s-6}{2}P_{2}, $ |
$ G $ has no perfect matching. By Lemma 2.3, $ G $ is singular if and only if
| $ \begin{align} (-1)^{\frac{b_{1}+s-4}{2}+2}\times 2^{2}+(-1)^{\frac{b_{1}+b_{2}+b_{3}+s-6}{2}+1}\times 2^{2} = 0. \end{align} $ | (3) |
Equation (3) holds if and only if $ 4|b_{2}+b_{3}-2. $
Subcase 2.3. $ a $ is even, $ s $ is odd. In this subcase, $ G $ has no spanning Sachs subgraph, so $ G $ is singular.
Subcase 2.4. Both $ a $ and $ s $ are even. In this subcase, the spanning Sachs subgraph of $ G $ containing two cycles is
| $ C_{a}\cup C_{b_{2}+b_{3}-2}\cup\frac{b_{1}+s-4}{2}P_{2}, $ |
and there are four spanning Sachs subgraphs of $ G $ containing one cycle, they have two of the following two forms:
| $ C_{a}\cup\frac{b_{1}+b_{2}+b_{3}+s-6}{2}P_{2}, \ \ C_{b_{2}+b_{3}-2}\cup\frac{a+b_{1}+s-4}{2}P_{2}, $ |
$ G $ has four perfect matchings. By Lemma 2.3, $ G $ is singular if and only if
| $ \begin{align} (-1)^{\frac{b_{1}+s-4}{2}+2}\times 2^{2}+(-1)^{\frac{b_{1}+b_{2}+b_{3}+s-6}{2}+1}\times 2^{2}+(-1)^{\frac{a+b_{1}+s-4}{2}+1}\times 2^{2}+(-1)^{\frac{a+b_{1}+b_{2}+b_{3}+s-6}{2}}\times 4 = 0. \end{align} $ | (4) |
Simplify Eq (4), we get
| $ \begin{align} (-1)^{\frac{b_{1}}{2}}+(-1)^{\frac{b_{1}+b_{2}+b_{3}}{2}}-(-1)^{\frac{a+b_{1}}{2}}-(-1)^{\frac{a+b_{1}+b_{2}+b_{3}}{2}} = 0. \end{align} $ | (5) |
Equation (5) is equivalent to
| $ \begin{align} [(-1)^{\frac{a}{2}}-1][(-1)^{\frac{b_{1}}{2}}+(-1)^{\frac{b_{1}+b_{2}+b_{3}}{2}}] = 0. \end{align} $ | (6) |
Equation (6) holds if and only if $ 4|a $ or $ 4|b_{2}+b_{3}-2 $.
Case 3. Exactly one of the three $ b_i (i = 1, 2, 3) $ is odd. Without losing generality, we assume that $ b_{3} $ is the odd number, $ b_{1} $ and $ b_{2} $ are two even numbers. There are four subcases.
Subcase 3.1. Both $ a $ and $ s $ are odd numbers. In this subcase, $ G $ has no spanning Sachs subgraph containing two cycles. The spanning Sachs subgraphs of $ G $ containing one cycle are
| $ C_{a}\cup\frac{b_{1}+b_{2}+b_{3}+s-6}{2}P_{2}, \ \ C_{b_{1}+b_{3}-2}\cup\frac{a+b_{2}+s-4}{2}P_{2}, $ |
and
| $ C_{b_{2}+b_{3}-2}\cup\frac{a+b_{1}+s-4}{2}P_{2}, $ |
$ G $ has no perfect matching. By Lemma 2.3, $ G $ is singular if and only if
| $ (-1)^{\frac{b_{1}+b_{2}+b_{3}+s-6}{2}+1}\times 2+(-1)^{\frac{a+b_{2}+s-4}{2}+1}\times 2+(-1)^{\frac{a+b_{1}+s-4}{2}+1}\times 2 = 0. $ |
But this is impossible. So $ G $ is non-singular.
Subcase 3.2. $ a $ is odd, $ s $ is even. In this subcase, the spanning Sachs subgraphs of $ G $ containing two cycles are
| $ C_{a}\cup C_{b_{1}+b_{3}-2}\cup\frac{b_{2}+s-4}{2}P_{2} $ |
and
| $ C_{a}\cup C_{b_{2}+b_{3}-2}\cup\frac{b_{1}+s-4}{2}P_{2}, $ |
$ G $ has no spanning Sachs subgraph containing one cycle. $ G $ has one perfect matching. By Lemma 2.3, $ G $ is singular if and only if
| $ (-1)^{\frac{b_{2}+s-4}{2}+2}\times 2^{2}+(-1)^{\frac{b_{1}+s-4}{2}+2}\times 2^{2}+(-1)^{\frac{a+b_{1}+b_{2}+b_{3}+s-6}{2}} = 0. $ |
But this is impossible. So $ G $ is non-singular.
Subcase 3.3. $ a $ is even, $ s $ is odd. In this subcase, $ G $ has no spanning Sachs subgraph containing two cycles. The spanning Sachs subgraph of $ G $ containing one cycle is
| $ C_{a}\cup\frac{b_{1}+b_{2}+b_{3}+s-6}{2}P_{2}, $ |
$ G $ has two perfect matchings. By Lemma 2.3, $ G $ is singular if and only if
| $ \begin{align} (-1)^{\frac{b_{1}+b_{2}+b_{3}+s-6}{2}+1}\times 2+(-1)^{\frac{a+b_{1}+b_{2}+b_{3}+s-6}{2}}\times 2 = 0. \end{align} $ | (7) |
Simplify Eq (7), we get
| $ \begin{align} (-1)^{\frac{a}{2}}-1 = 0. \end{align} $ | (8) |
Equation (8) holds if and only if $ 4|a $.
Subcase 3.4. Both $ a $ and $ s $ are even numbers. In this subcase, the spanning Sachs subgraphs of $ G $ containing two cycles are
| $ C_{a}\cup C_{b_{1}+b_{3}-2}\cup\frac{b_{2}+s-4}{2}P_{2}, $ |
and
| $ C_{a}\cup C_{b_{2}+b_{3}-2}\frac{b_{1}+s-4}{2}P_{2}. $ |
There are four spanning Sachs subgraphs of $ G $ containing one cycle, they have two of the following two forms:
| $ C_{b_{1}+b_{3}-2}\cup\frac{a+b_{2}+s-4}{2}P_{2}, \ \ C_{b_{2}+b_{3}-2}\cup\frac{a+b_{1}+s-4}{2}P_{2}, $ |
$ G $ has no perfect matching. By Lemma 2.3, $ G $ is singular if and only if
| $ \begin{align} (-1)^{\frac{b_{2}+s-4}{2}+2}\times 2^{2}+(-1)^{\frac{b_{1}+s-4}{2}+2}\times 2^{2}+(-1)^{\frac{a+b_{2}+s-4}{2}+1}\times 2^{2}+(-1)^{\frac{a+b_{1}+s-4}{2}+1}\times 2^{2} = 0. \end{align} $ | (9) |
Simplify Eq (9), we get
| $ \begin{align} [(-1)^{\frac{a}{2}}-1][(-1)^{\frac{b_{1}}{2}}+(-1)^{\frac{b_{2}}{2}}] = 0. \end{align} $ | (10) |
Equation (10) holds if and only if $ 4|a $ or $ 4|b_{1}+b_{2}-2 $.
Case 4. Three $ b_i (i = 1, 2, 3) $ are all even numbers. There are four subcases.
Subcase 4.1. Both $ a $ and $ s $ are odd numbers. In this subcase, $ G $ has no spanning Sachs subgraph containing two cycles. The spanning Sachs subgraphs of $ G $ containing one cycle are
| $ C_{b_{1}+b_{2}-2}\cup\frac{a+b_{3}+s-4}{2}P_{2},\ \ C_{b_{1}+b_{3}-2}\cup\frac{a+b_{2}+s-4}{2}P_{2}, $ |
and
| $ C_{b_{2}+b_{3}-2}\cup\frac{a+b_{1}+s-4}{2}P_{2}, $ |
$ G $ has three perfect matchings. By Lemma 2.3, $ G $ is singular if and only if
| $ (-1)^{\frac{a+b_{3}+s-4}{2}+1}\times 2+(-1)^{\frac{a+b_{2}+s-4}{2}+1}\times 2+(-1)^{\frac{a+b_{1}+s-4}{2}+1}\times 2+(-1)^{\frac{a+b_{1}+b_{2}+b_{3}+s-6}{2}}\times 3 = 0. $ |
But this is impossible. So $ G $ is non-singular.
Subcase 4.2. $ a $ is odd, $ s $ is even. In this subcase, the spanning Sachs subgraphs of $ G $ containing two cycles are
| $ C_{a}\cup C_{b_{1}+b_{2}-2}\cup\frac{b_{3}+s-4}{2}P_{2}, \ \ C_{a}\cup C_{b_{1}+b_{3}-2}\cup\frac{b_{2}+s-4}{2}P_{2}, $ |
and
| $ C_{a}\cup C_{b_{2}+b_{3}-2}\cup\frac{b_{1}+s-4}{2}P_{2}, $ |
There are three spanning Sachs subgraphs of $ G $ containing one cycle, they all has the form:
| $ C_{a}\cup\frac{b_{1}+b_{2}+b_{3}+s-6}{2}P_{2}, $ |
$ G $ has no perfect matching. By Lemma 2.3, $ G $ is singular if and only if
| $ (-1)^{\frac{b_{3}+s-4}{2}+2}\times 2^{2}+(-1)^{\frac{b_{2}+s-4}{2}+2}\times 2^{2}+(-1)^{\frac{b_{1}+s-4}{2}+2}\times 2^{2}+(-1)^{\frac{b_{1}+b_{2}+b_{3}+s-6}{2}+1}\times 2\times 3 = 0. $ |
But this is impossible. So $ G $ is non-singular.
Subcase 4.3. $ a $ is even, $ s $ is odd. In this subcase, $ G $ has no spanning Sachs subgraph, so $ G $ is singular.
Subcase 4.4. Both $ a $ and $ s $ are even numbers. In this subcase, the spanning Sachs subgraphs of $ G $ containing two cycles are
| $ C_{a}\cup C_{b_{1}+b_{2}-2}\cup\frac{b_{3}+s-4}{2}P_{2}, \ \ C_{a}\cup C_{b_{1}+b_{3}-2}\cup\frac{b_{2}+s-4}{2}P_{2}, $ |
and
| $ C_{a}\cup C_{b_{2}+b_{3}-2}\cup\frac{b_{1}+s-4}{2}P_{2}. $ |
The spanning Sachs subgraphs containing one cycle includes: three $ C_{a}\cup\frac{b_{1}+b_{2}+b_{3}+s-6}{2}P_{2} $, two $ C_{b_{1}+b_{2}-2}\cup\frac{a+b_{3}+s-4}{2}P_{2} $, two $ C_{b_{1}+b_{3}-2}\cup\frac{a+b_{2}+s-4}{2}P_{2} $ and two $ C_{b_{2}+b_{3}-2}\cup\frac{a+b_{1}+s-4}{2}P_{2} $. $ G $ has six perfect matchings. By Lemma 2.3, $ G $ is singular if and only if
| $ (-1)^{\frac{b_{3}+s-4}{2}+2}\times2^{2}+(-1)^{\frac{b_{2}+s-4}{2}+2}\times2^{2} +(-1)^{\frac{b_{1}+s-4}{2}+2}\times 2^{2}+(-1)^{\frac{b_{1}+b_{2}+b_{3}+s-6}{2}+1}\times 2\times 3 $ |
| $ \begin{align} +(-1)^{\frac{a+b_{3}+s-4}{2}+1}\times 2\times 2+(-1)^{\frac{a+b_{2}+s-4}{2}+1}\times 2\times 2+(-1)^{\frac{a+b_{1}+s-4}{2}+1}\times 2\times 2+(-1)^{\frac{a+b_{1}+b_{2}+b_{3}+s-6}{2}}\times 6 = 0. \end{align} $ | (11) |
Multiply both sides of Eq (11) by
| $ (-1)^{\frac{a+b_{1}+b_{2}+b_{3}+s-6}{2}}\times\frac{1}{2}, $ |
we get
| $ [(-1)^{\frac{a+b_{1}+b_{2}-2}{2}}+(-1)^{\frac{a+b_{1}+b_{3}-2}{2}}+(-1)^{\frac{a+b_{2}+b_{3}-2}{2}}]\times 2+[(-1)^{3}\times(-1)^{\frac{b_{1}+b_{2}-2}{2}} $ |
| $ \begin{align} +(-1)^{3}\times(-1)^{\frac{b_{1}+b_{3}-2}{2}}+(-1)^{3}\times(-1)^{\frac{b_{2}+b_{3}-2}{2}}]\times 2+[(-1)^{\frac{a}{2}+1}\times 3+3] = 0. \end{align} $ | (12) |
Simplify Eq (12), we get
| $ \begin{align} [(-1)^{\frac{a}{2}}-1][(-1)^{\frac{b_{1}+b_{2}-2}{2}}+(-1)^{\frac{b_{1}+b_{3}-2}{2}}+(-1)^{\frac{b_{2}+b_{3}-2}{2}}]\times 2+[1-(-1)^{\frac{a}{2}}]\times 3 = 0. \end{align} $ | (13) |
That is
| $ \begin{align} [(-1)^{\frac{a}{2}}-1][((-1)^{\frac{b_{1}+b_{2}-2}{2}}+(-1)^{\frac{b_{1}+b_{3}-2}{2}}+(-1)^{\frac{b_{2}+b_{3}-2}{2}})\times 2-3] = 0. \end{align} $ | (14) |
Equation (14) holds if and only if
| $ (-1)^{\frac{a}{2}}-1 = 0. $ |
So $ G $ is singular if and only if $ 4|a. $
To sum up, we have completed the proof of Theorem 1.1.
Take $ s = 1 $ in Theorem 1.1 and Corollary 1.2 is obviously.
Now, we prove Theorem 1.3.
Let $ X $ be a random event, $ p(X) $ represents the probability that event $ X $ will occur, $ p(XY) $ represents the probability that events $ X $ and $ Y $ occur simultaneously, and $ p(Y|X) $ represents the probability that event $ Y $ will occur under the condition that event $ X $ occurs.
Let $ U $ be the random event: the graph $ \alpha(a, b_{1}, b_{2}, b_{3}, s) $ is a singular graph.
$ A $ indicates the random event: $ 4|a $.
$ B_{1} $ indicates the random event: three $ b_i(i = 1, 2, 3) $ are all odd numbers.
$ C_{1} $ indicates the random event: exactly two of the three $ b_i (i = 1, 2, 3) $ are odd numbers, and the length of the cycle formed by the two odd paths in $ G $ is a multiple of 4.
$ C_{2} $ indicates the random event: exactly two of the three $ b_i (i = 1, 2, 3) $ are odd numbers, $ a $ is even, and $ s $ is odd.
Suppose $ B_{2} = C_{1}\cup C_{2} $.
$ B_{3} $ indicates the random event: exactly one of three $ b_i (i = 1, 2, 3) $ is odd number. $ a $ is even, $ s $ is even, and the length of the cycle formed by the two even paths in $ G $ is a multiple of 4.
$ B_{4} $ indicates the random event: three $ b_i (i = 1, 2, 3) $ are all even numbers. $ a $ is even, $ s $ is odd.
Then
| $ \begin{align*} p(A) = \frac{1}{4},\ \ p(B_{1}) = \binom{3}{3}(\frac{1}{2})^{3} = \frac{1}{8}, \end{align*} $ |
| $ \begin{align*} p(B_{2}) = p(C_{1}\cup C_{2}) = p(C_{1})+p(C_{2})-p(C_{1}C_{2}) = \binom{3}{2}(\frac{1}{2})^{3}(\frac{1}{2}+\frac{1}{4}-\frac{1}{8}) = \frac{15}{64}, \end{align*} $ |
| $ \begin{align*} p(B_{3})& = \binom{3}{1}(\frac{1}{2})^{3}\times(\frac{1}{2})^{3} = \frac{3}{64},\ \ p(B_{4}) = \binom{3}{0}(\frac{1}{2})^{3}\times(\frac{1}{2})^{2} = \frac{1}{32},\\ p(AB_{1})& = p(A)p(B_{1}) = \frac{1}{4}\times\frac{1}{8} = \frac{1}{32}, \end{align*} $ |
| $ \begin{align*} p(AB_{2}) = p(A)p(B_{2}|A) = p(A)[p(C_{1}|A)+p(C_{2}|A)-p(C_{1}C_{2}|A)] = \frac{1}{4}\binom{3}{2}(\frac{1}{2})^{3}(\frac{1}{2}+\frac{1}{2}-\frac{1}{4}) = \frac{9}{128}, \end{align*} $ |
| $ \begin{align*} &p(AB_{3}) = p(A)p(B_{3}|A) = \frac{1}{4}\binom{3}{1}(\frac{1}{2})^{3}\times(\frac{1}{2})^{2} = \frac{3}{128},\\ &p(AB_{4}) = p(A)p(B_{4}|A) = \frac{1}{4}\binom{3}{0}(\frac{1}{2})^{3}\times\frac{1}{2} = \frac{1}{64}. \end{align*} $ |
So
| $ \begin{align*} p(U) & = p(A\cup B_{1}\cup B_{2}\cup B_{3}\cup B_{4})\\ & = p(A)+p(B_{1})+p(B_{2})+p(B_{3})+p(B_{4})-p(AB_{1})-p(AB_{2})-p(AB_{3})-p(AB_{4})\\ & = \frac{1}{4}+\frac{1}{8}+\frac{15}{64}+\frac{3}{64}+\frac{1}{32}-\frac{1}{32}-\frac{9}{128}-\frac{3}{128}-\frac{1}{64} = \frac{35}{64}. \end{align*} $ |
Let $ V $ be the random event: the graph $ \beta(a, b_{1}, b_{2}, b_{3}) $ is a singular graph.
$ A $ indicates the random event: $ 4|a $.
$ B_{1} $ indicates the random event: three $ b_i(i = 1, 2, 3) $ are all odd numbers.
$ C_{1} $ indicates the random event: exactly two of the three $ b_i (i = 1, 2, 3) $ are odd numbers, and the length of the cycle formed by the two odd paths in $ G $ is a multiple of 4.
$ C'_{2} $ indicates the random event: exactly two of the three $ b_i (i = 1, 2, 3) $ are odd numbers, $ a $ is even.
Suppose $ B'_{2} = C_{1}\cup C'_{2} $.
$ B'_{4} $ represents a random event: three $ b_i (i = 1, 2, 3) $ are all even numbers, $ a $ is even.
Then
| $ \begin{align*} p(A) = \frac{1}{4},\ \ p(B_{1}) = \frac{1}{8}, \ \ p(AB_{1}) = \frac{1}{32}, \end{align*} $ |
| $ \begin{align*} p(B'_{2}) = p(C_{1}\cup C'_{2}) = p(C_{1})+p(C'_{2})-p(C_{1}C'_{2}) = \binom{3}{2}(\frac{1}{2})^{3}(\frac{1}{2}+\frac{1}{2}-\frac{1}{4}) = \frac{9}{32}, \end{align*} $ |
| $ \begin{align*} p(B'_{4}) = \binom{3}{0}(\frac{1}{2})^{3}\times(\frac{1}{2}) = \frac{1}{16}, \end{align*} $ |
| $ \begin{align*} p(AB'_{2}) = p(A)p(B'_{2}|A) = p(A)[p(C_{1}|A)+p(C'_{2}|A)-p(C_{1}C'_{2}|A)] = \frac{1}{4}\binom{3}{2}(\frac{1}{2})^{3}(\frac{1}{2}+1-\frac{1}{2}) = \frac{3}{32}, \end{align*} $ |
| $ \begin{align*} p(AB'_{4}) = p(A)p(B'_{4}|A) = \frac{1}{4}\binom{3}{0}(\frac{1}{2})^{3} = \frac{1}{32}. \end{align*} $ |
So
| $ \begin{align*} p(V) & = p(A\cup B_{1}\cup B'_{2}\cup B'_{4})\\ & = p(A)+p(B_{1})+p(B'_{2})+p(B'_{4})-p(AB_{1})-p(AB'_{2})-p(AB'_{4})\\ & = \frac{1}{4}+\frac{1}{8}+\frac{9}{32}+\frac{1}{16}-\frac{1}{32}-\frac{3}{32}-\frac{1}{32} = \frac{9}{16}. \end{align*} $ |
Hence we have finished the proof of Theorem 1.3.
We know that a connected graph $ G $ is a tree, a unicycle graph, a bicyclic graph and a tricyclic graph if and only if
| $ |E(G)| = |V(G)|-1,\ |V(G)|,\ |V(G)|+1\; {\text{and}}\; |V(G)|+2, $ |
respectively. Merging one end of the path $ P_{s} $ with one vertex of $ C_{a} $, and merging the other end of the path $ P_{s} $ with one vertex of $ C_{b} $, the resulting graph is called the $ \infty $-graph, denoted by $ \infty(a, s, b) $, see Figure 3.
Every unicyclic graph contains a cycle $ C_{n} $ as its induced subgraph. While the cycle $ C_{n} $ is singular if and only if $ 4|n $. Bicyclic graphs can be divided into two kinds, one is $ \infty $-graph as its induced subgraph, the other is $ \theta $-graph as its induced subgraph.
Theorem 4.1. The graph $ G = \theta(b_{1}, b_{2}, b_{3}) $ is singular if and only if one of the following holds.
$ (i) $ Three $ b_i(i = 1, 2, 3) $ are all odd numbers.
$ (ii) $ The parity of the three $ b_i(i = 1, 2, 3) $ is not the same, and the length of the cycle formed by the two paths with the same parity in $ G $ is a multiple of 4.
Proof. Note that $ |V(G)| = b_{1}+b_{2}+b_{3}-4 $. According to the parity of $ b_{1}, b_{2}, b_{3} $ and the symmetry of graph $ \theta(b_{1}, b_{2}, b_{3}) $, we divided it into the following four cases to prove.
Case 1. Three $ b_i (i = 1, 2, 3) $ are all odd numbers. In this case, $ G $ has no spanning Sachs subgraph, so $ G $ is singular.
Case 2. Exactly two of the three $ b_i (i = 1, 2, 3) $ are odd numbers. Without losing generality, we assume that $ b_{1} $ is an even number, $ b_{2} $ and $ b_{3} $ are two odd numbers. The spanning Sachs subgraph of $ G $ containing one cycle is
| $ C_{b_{2}+b_{3}-2}\cup\frac{b_{1}-2}{2}P_{2}, $ |
$ G $ has two perfect matchings. By Lemma 2.3, $ G $ is singular if and only if
| $ \begin{align} (-1)^{\frac{b_{1}-2}{2}+1}\times 2+(-1)^{\frac{b_{1}+b_{2}+b_{3}-4}{2}}\times 2 = 0. \end{align} $ | (15) |
Simplify Eq (15), we get
| $ \begin{align} (-1)^{\frac{b_{2}+b_{3}-2}{2}}-1 = 0. \end{align} $ | (16) |
Equation (16) holds if and only if $ 4|b_{2}+b_{3}-2 $.
Case 3. Exactly one of the three $ b_i (i = 1, 2, 3) $ is odd. Without losing generality, we assume that $ b_{3} $ is the odd number, $ b_{1} $ and $ b_{2} $ are two even numbers. The spanning Sachs subgraph of $ G $ containing one cycle are
| $ C_{b_{1}+b_{3}-2}\cup\frac{b_{2}-2}{2}P_{2}, $ |
and
| $ C_{b_{2}+b_{3}-2}\cup\frac{b_{1}-2}{2}P_{2}, $ |
$ G $ has no perfect matching. By Lemma 2.3, $ G $ is singular if and only if
| $ \begin{align} (-1)^{\frac{b_{2}-2}{2}+1}\times 2+(-1)^{\frac{b_{1}-2}{2}+1}\times 2 = 0. \end{align} $ | (17) |
Equation (17) holds if and only if $ 4|b_{1}+b_{2}-2 $.
Case 4. Three $ b_i (i = 1, 2, 3) $ are all even numbers. The spanning Sachs subgraph of $ G $ containing one cycle are
| $ C_{b_{1}+b_{2}-2}\cup\frac{b_{3}-2}{2}P_{2}, \ \ C_{b_{1}+b_{3}-2}\cup\frac{b_{2}-2}{2}P_{2}, $ |
and
| $ C_{b_{2}+b_{3}-2}\cup\frac{b_{1}-2}{2}P_{2}, $ |
$ G $ has three perfect matchings. By Lemma 2.3, $ G $ is singular if and only if
| $ (-1)^{\frac{b_{3}-2}{2}+1}\times 2+(-1)^{\frac{b_{2}-2}{2}+1}\times 2+(-1)^{\frac{b_{1}-2}{2}+1}\times 2+(-1)^{\frac{b_{1}+b_{2}+b_{3}-4}{2}}\times 3 = 0. $ |
But this is impossible. So $ G $ is non-singular.
Hence we have finished the proof of Theorem 4.1.
Theorem 4.2. The graph $ G = \infty(a, s, b) $ is singular if and only if one of the following holds.
$ (i) $ The length of at least one of the two cycles is a multiple of 4, i.e. $ 4|a $ or $ 4|b $.
$ (ii) $ $ s $ is odd. (1) The length of two cycles is even; (2) The length of two cycles is odd, but module $ 4 $ is not congruence.
Proof. Note that $ |V(G)| = a+b+s-2 $. According to the parity of $ a, b, s $ and the symmetry of graph $ \infty(a, s, b) $, we divided it into the following two cases to prove.
Case 1. $ s $ is an even number.
Subcase 1.1. Both $ a $ and $ b $ are even numbers. Where the spanning Sachs subgraph of $ G $ with two cycles is $ C_{a}\cup C_{b}\cup\frac{s-2}{2}P_{2} $. The spanning Sachs subgraphs containing one cycle includes two $ C_{a}\cup \frac{b+s-2}{2}P_{2} $, two $ C_{b}\cup \frac{a+s-2}{2}P_{2} $; $ G $ has 4 perfect matchings.
By Lemma 2.3, $ G $ is singular if and only if
| $ (-1)^{\frac{s-2}{2}+2}\times 2^{2}+(-1)^{\frac{b+s-2}{2}+1}\times 2\times 2+(-1)^{\frac{a+s-2}{2}+1}\times 2\times 2+(-1)^{\frac{a+b+s-2}{2}}\times 4 = 0, $ |
multiply both sides of above equation by $ (-1)^{\frac{a+b+s-2}{2}}\times\frac{1}{4} $, we get
| $ (-1)^{\frac{a+b}{2}+2}+(-1)^{\frac{a}{2}+1}+(-1)^{\frac{b}{2}+1}+1 = 0, $ |
that is
| $ (-1)^{\frac{a+b}{2}}-(-1)^{\frac{a}{2}}-(-1)^{\frac{b}{2}}+1 = 0, $ |
the above equation holds if and only if
| $ [(-1)^{\frac{a}{2}}-1][(-1)^{\frac{b}{2}}-1] = 0, $ |
if and only if $ 4|a $ or $ 4|b $.
Subcase 1.2. Only one of $ a $ and $ b $ is even. Without losing generality, we assume that $ a $ is an even number, $ b $ is an odd number. Where the spanning Sachs subgraph of $ G $ with two cycles is: $ C_{a}\cup C_{b}\cup\frac{s-2}{2}P_{2} $. The spanning Sachs subgraph of $ G $ with one cycle includes two $ C_{b}\cup \frac{a+s-2}{2}P_{2} $. $ G $ has no perfect matching.
By Lemma 2.3, $ G $ is singular if and only if
| $ (-1)^{\frac{s-2}{2}+2}\times 2^{2}+(-1)^{\frac{a+s-2}{2}+1}\times 2\times 2 = 0, $ |
multiply both sides of above equation by $ (-1)^{\frac{a+s-2}{2}}\times\frac{1}{4} $, we get
| $ (-1)^{\frac{a}{2}}-1 = 0, $ |
if and only if $ 4|a $.
Subcase 1.3. Both $ a $ and $ b $ are odd numbers. Where the spanning Sachs subgraph of $ G $ containing two cycles is $ C_{a}\cup C_{b}\cup\frac{s-2}{2}P_{2} $. $ G $ has no spanning Sachs subgraph containing one cycle, and $ G $ has one perfect matching.
By Lemma 2.3, $ G $ is singular if and only if
| $ (-1)^{\frac{s-2}{2}+2}\times 2^{2}+(-1)^{\frac{a+b+s-2}{2}} = 0. $ |
But this is impossible. So $ G $ is non-singular.
Case 2. $ s $ is an odd number.
Subcase 2.1. Both $ a $ and $ b $ are even numbers. In this subcase, $ G $ has no spanning Sachs subgraph, so $ G $ is singular.
Subcase 2.2. Only one of $ a $ and $ b $ is even. Without losing generality, we assume that $ a $ is an even number, $ b $ is an odd number. There is no the spanning Sachs subgraph of $ G $ with two cycles. The spanning Sachs subgraph of $ G $ with one cycle is $ C_{a}\cup \frac{b+s-2}{2}P_{2} $. $ G $ has 2 perfect matchings.
By Lemma 2.3, $ G $ is singular if and only if
| $ (-1)^{\frac{b+s-2}{2}+1}\times 2+(-1)^{\frac{a+b+s-2}{2}}\times 2 = 0, $ |
multiply both sides of above equation by $ (-1)^{\frac{a+b+s-2}{2}}\times\frac{1}{2} $, we get
| $ (-1)^{\frac{a}{2}}-1 = 0, $ |
if and only if $ 4|a $.
Subcase 2.3. Both $ a $ and $ b $ are odd numbers. Where there is no spanning Sachs subgraph of $ G $ with two cycles. The spanning Sachs subgraph of $ G $ with one cycle are: $ C_{a}\cup \frac{b+s-2}{2}P_{2} $, $ C_{b}\cup \frac{a+s-2}{2}P_{2} $. $ G $ has no perfect matching.
By Lemma 2.3, $ G $ is singular if and only if
| $ (-1)^{\frac{b+s-2}{2}+1}\times 2+(-1)^{\frac{a+s-2}{2}+1}\times 2 = 0, $ |
multiply both sides of above equation by $ (-1)^{\frac{a+s-2}{2}}\times\frac{1}{2} $, we get
| $ (-1)^{\frac{a+b}{2}}-1 = 0, $ |
if and only if $ a $ and $ b $ module $ 4 $ is not congruence.
Hence we have finished the proof of Theorem 4.2.
By Theorems 4.1 and 4.2, it is easy to calculate that the probability that $ \theta(b_{1}, b_{2}, b_{3}) $ is a singular graph is equal to $ \frac{1}{2} $, the probability that $ \infty(a, s, b) $ is a singular graph is equal to $ \frac{17}{32} $.
Similarly to the bicyclic graphs, the tricyclic graphs can be divided into 15 kinds according to the induced subgraphs it contains. Denote the set of tricyclic graphs which contains the $ \alpha $-graph and the $ \beta $-graph as its induced subgraphs by $ \mathcal{T}(\alpha) $ and $ \mathcal{T}(\beta) $, respectively. Then using Lemmas 2.1 and 2.2, Theorems 1.1, 4.1 and 4.2, and Corollary 1.2, we can determine the singular graphs in the $ \mathcal{T}(\alpha) $ and $ \mathcal{T}(\beta) $.
For random graphs, some scholars have studied the variables on random graphs, for instance, Shang [25] obtained the lower and upper bounds of distance Estrada index of random bipartite graph. However, although the probability of singular graphs is mentioned, we do not consider the singularity of random graphs in this paper, so readers can study the singularity of random graphs.
In this paper, we first define two kinds of tricyclic graphs, the $ \alpha $-graph and $ \beta $-graph, then give the necessity and sufficiency condition for the singularity of $ \alpha $-graph and $ \beta $-graph, and obtain the probability that any given two kinds of graphs are singular graphs. Our results enriches the study of singularity of graphs.
We are grateful to the anonymous referees for many friendly and helpful revising suggestions that greatly improved the presentation of the paper. This work was supported by NSFC Grant (11561056; 11701324) and the Natural Science Foundation of Qinghai Province, China (2022-ZJ-924).
There are no conflicts interest for this paper.
| [1] | F. Ashraf, H. Bamdad, A note on graphs with zero nullity, MATCH Commun. Math. Comput. Chem., 60 (2008), 15–19. |
| [2] | A. S. AL-Tarimshawy, Singular graphs, arXiv, 2018. https://doi.org/10.48550/arXiv.1806.07786 |
| [3] | M. Brown, J. W. Kennedy, B. Servatius, Graph singularity, Graph Theory Notes, 25 (1993), 23–32. |
| [4] |
B. Cheng, B. Liu, On the nullity of graphs, Electron. J. Linear Algebra, 16 (2007), 60–67. https://doi.org/10.13001/1081-3810.1182 doi: 10.13001/1081-3810.1182

|
| [5] | D. Cvetković, M. Doob, H. Sachs, Spectra of graphs-theory and application, Academic Press, 1980. |
| [6] | D. Cvetković, I. Gutman, The algebraic multiplicity of the number zero in the spectrum of a bipartite graph, Mat. Ves., 9 (1972), 141–150. |
| [7] |
D. Cvetković, I. Gutman, N. Trinajstic, Graphical studies on the relations between the structure and reactivity of conjugated system: the role of non-bonding molecular orbitals, J. Mol. Struct., 28 (1975), 289–303. https://doi.org/10.1016/0022-2860(75)80099-8 doi: 10.1016/0022-2860(75)80099-8

|
| [8] |
L. Collatz, U. Sinogowitz, Spektren endlicher grafen, Abh. Math. Semin. Univer. Hamburg, 21 (1957), 63–77. https://doi.org/10.1007/BF02941924 doi: 10.1007/BF02941924

|
| [9] |
Y. Z. Fan, K. S. Qian, On the nullity of bipartite graphs, Linear Algebra Appl., 430 (2009), 2943–2949. https://doi.org/10.1016/j.laa.2009.01.007 doi: 10.1016/j.laa.2009.01.007

|
| [10] | I. Gutman, B. Borovićanin, Nullity of graphs: an updated survey, Zb. Rad., 14 (2011), 137–154. |
| [11] | A. Graovac, I. Gutman, N. Trinajstić, Topological approach to the chemistry of conjugated molecules, Springer, 1977. |
| [12] |
I. Gutman, I. Sciriha, On the nullity of line graphs of trees, Discrete Math., 232 (2001), 35–45. https://doi.org/10.1016/S0012-365X(00)00187-4 doi: 10.1016/S0012-365X(00)00187-4

|
| [13] |
J. M. Guo, W. G. Yan, Y. N. Yeh, On the nullity and the matching number of unicyclic graphs, Linear Algebra Appl., 431 (2009), 1293–1301. https://doi.org/10.1016/j.laa.2009.04.026 doi: 10.1016/j.laa.2009.04.026

|
| [14] |
S. Hu, X. Tan, B. Liu, On the nullity of bicyclic graphs, Linear Algebra Appl., 429 (2008), 1387–1391. https://doi.org/10.1016/j.laa.2007.12.007 doi: 10.1016/j.laa.2007.12.007

|
| [15] | W. Li, A. Chang, On the trees with maximum nullity, MATCH Commun. Math. Comput. Chem., 56 (2006), 501–508. |
| [16] |
J. M$\ddot{u}$ller, M. Neunh$\ddot{o}$fer, Some computations regarding Foulkes' conjecture, Exp. Math., 14 (2005), 277–283. https://doi.org/10.1080/10586458.2005.10128928 doi: 10.1080/10586458.2005.10128928

|
| [17] |
M. Nath, B. K. Sarma, On the null spaces of acyclic and unicyclic singular graphs, Linear Algebra Appl., 427 (2007), 42–54. https://doi.org/10.1016/j.laa.2007.06.017 doi: 10.1016/j.laa.2007.06.017

|
| [18] |
G. R. Omidi, On the nullity of bipartite graphs, Graphs Combin., 25 (2009), 111–114. https://doi.org/10.1007/s00373-008-0825-5 doi: 10.1007/s00373-008-0825-5

|
| [19] |
L. Pogliani, From molecular connectivity indices to semiempirical connectivity terms: recent trends in graph theoretical descriptors, Chem. Rev., 100 (2000), 3827–3858. https://doi.org/10.1021/cr0004456 doi: 10.1021/cr0004456

|
| [20] |
M. Randić, Aromaticity of polycyclic conjugated hydrocarbons, Chem. Rev., 103 (2003), 3449–3605. https://doi.org/10.1021/cr9903656 doi: 10.1021/cr9903656

|
| [21] | I. Sciriha, On singular line graphs of trees, Congr. Numer., 135 (1998), 73–91. |
| [22] |
I. Sciriha, On the construction of graphs of nullity one, Discrete Math., 181 (1998), 193–211. https://doi.org/10.1016/S0012-365X(97)00036-8 doi: 10.1016/S0012-365X(97)00036-8

|
| [23] |
I. Sciriha, A characterization of singular graphs, Electron. J. Linear Algebra, 16 (2007), 451–462. https://doi.org/10.13001/1081-3810.1215 doi: 10.13001/1081-3810.1215

|
| [24] |
I. Sciriha, P. W. Fowler, On nut and core singular fullerenes, Discrete Math., 308 (2008), 267–276. https://doi.org/10.1016/j.disc.2006.11.040 doi: 10.1016/j.disc.2006.11.040

|
| [25] |
Y. Shang, Further results on distance Estrada index of random graphs, Bull. Malays. Math. Sci. Soc., 41 (2018), 531–544. https://doi.org/10.1007/s40840-016-0306-6 doi: 10.1007/s40840-016-0306-6

|
| [26] |
M. Sharma, R. K. Nath, Y. Shang, On $g$-noncommuting graph of a finite group relative to its subgroups, Mathematics, 9 (2021), 3147. https://doi.org/10.3390/math9233147 doi: 10.3390/math9233147

|
| [27] |
J. Siemons, A. Zalesski, Remarks on singular Cayley graphs and vanishing elements of simple groups, J. Algebraic Combin., 50 (2019), 379–401. https://doi.org/10.1007/s10801-018-0860-0 doi: 10.1007/s10801-018-0860-0

|
| [28] |
A. Sltan, A. AL-Tarimshawy, J. Siemons, Singular graphs with dihedral group action, Discrete Math., 344 (2021), 112119. https://doi.org/10.1016/j.disc.2020.112119 doi: 10.1016/j.disc.2020.112119

|
| [29] |
X. Tang, B. Liu, On the nullity of unicyclic graphs, Linear Algebra Appl., 408 (2005), 212–220. https://doi.org/10.1016/j.laa.2005.06.012 doi: 10.1016/j.laa.2005.06.012

|
| [30] |
Z. Wang, Y. Mao, K. C. Das, Y. Shang, Nordhaus-Gaddum-type results for the Steiner Gutman index of graphs, Symmetry, 12 (2020), 1711. https://doi.org/10.3390/sym12101711 doi: 10.3390/sym12101711

|
| 1. | Haicheng Ma, Yanbo Gao, Xiaojie You, The Singularity of Three Kinds of New Tricyclic Graphs, 2024, 16, 2073-8994, 1416, 10.3390/sym16111416 | |
| 2. | Haicheng Ma, The Singularity of the K4 Homeomorphic Graph, 2024, 14, 2075-1680, 17, 10.3390/axioms14010017 |