1.
Introduction and preliminaries
The study of the sum of independent and identically distributed random variables ∑ni=1Xi is hardly avoidable in probability theory and related fields. This sequence of sums {∑ni=1Xi,n∈N} is called the random walk. Let us define the stochastic process
where u∈N0:=N∪{0}, κ∈N and random variables Xi,i∈N are independent, identically distributed, non-negative and integer-valued. If κ=1, the defined process (1.1) is known as a discrete-time risk model; see [1]. Allowing κ∈N, we call the process (1.1) a generalized premium discrete-time risk model; see [2]. Such types of processes appear in insurance mathematics (ruin theory), arguing that they describe an insurer's wealth in time moments n∈N, where u means the initial surplus (also called capital or reserve), κ denotes the premium rate (earnings per unit of time), i.e., (n+1)κ−nκ=κ, and the random walk {∑ni=1Xi,n∈N} represents the expenses (payoffs) caused by random size claims. Then, one can become curious to know whether the initial surplus u plus the gained premiums κn are sufficient to cover the incurred random expenses ∑ni=1Xi. More precisely, one aims to know whether W(n)>0 for all n∈{1,2,…,T} when T is some fixed natural number or T→∞. The positivity of W(n) is of course associated with the probability. For the model given in (1.1), we define the finite time survival probability:
and the ultimate time survival probability:
Both φ(u,T) and φ(u) are nothing but distribution functions of the provided integer-valued sequence of sums of random variables; these functions are left-continuous, non-decreasing and step functions if we allow u∈R. Also, φ(∞)=1 if EX<κ; see Section 2. In particular, φ(0) is interpreted as the ultimate time survival probability when an insurer starts the activity with no initial surplus, i.e., when u=0. Then, the insurer maintains chances to "persist alive" if the payoff's size in the first moment of time n=1 is less than κ, i.e., if X1<κ.
Calculation of φ(u,T) is simple; see, for instance, [2,Theorem 1]. Let us turn to the ultimate time survival probability φ(u). The law of total probability and rearrangements in (1.2) imply
see [2,page 3].
By setting u=0 in (1.3), we get
to calculate the probability φ(κ) when x0>0, we must know the initial ones φ(0),φ(1),…,φ(κ−1). The calculation of φ(u), when u=κ,κ+1,…, using the recurrence equation (1.3), requires φ(0),φ(1),…,φ(κ−1) too. The needed quantity of these initial values is X distribution-dependent, as some of the probabilities x0,x1,…,xκ−1 may equal to zero, cf. (1.4) when P(X>j)=1 for some j⩾0. The paper [2] deals with finding the mentioned initial values φ(0),φ(1),…,φ(κ−1), and it is shown there that they can be found by calculating the limits of certain recurrent sequences. For instance, if κ=2 and x0>0, then it follows by (1.4) that
where (see [3,pages 2 and 3])
and φ(∞)=1 if EX<2.
Calculating the limits in (1.5) and aiming to prove that the provided determinant 2×2 never vanishes; in paper [3], it was proved the connection to the solutions of s2=GX(s), where s∈C,|s|⩽1 and GX(s) is the probability-generating function of the random variable X. On top of that, it was realized in [3] that the values of φ(0) and φ(1) in (1.5) can be derived by using the classical stationarity property for the distribution of the maximum of a reflected random walk; see [4,Chapter Ⅵ,Section 9]. Using the mentioned stationarity property, the generating function of φ(u+1),u∈N0 for κ=2 was found in [3,Theorem 5]; however, this required the finiteness of the second moment of the random variable X, i.e., EX2<∞. In this article, we extend the work in [3] and find the generating function of φ(u+1),u∈N0 for an arbitrary κ∈N. Moreover, we show that the requirement of EX2<∞ is redundant and provide exact expressions of φ(u),u∈N0 via solutions of systems of linear equations which are based on the roots of sκ=GX(s) and Vandermonde-like matrices.
For the short overview of the literature, we mention that the references [1,5,6,7,8,9,10,11,12,13] are known as the classical ones on the wide subject of renewal risk models, while [14,15,16] might be mentioned as the recent ones. The main reason for so much literature is that the ruin theory, being random walk-based, is heavily dependent on the random walk's structural assumptions, such as the independence of random variables, their distributions, etc. This work is also closely related to branching and Galton-Watson processes and queueing theory; see [17] and related papers. See also [18] or [19, Figure 1] on random walk occurrence in number theory. Last but not least, it is worth mentioning that Vandermonde matrices have a broad range of occurrences, from pure mathematics to many other applied sciences; see [20] and related works.
2.
Several auxiliary notations and the net profit condition
Let
where x+=max{0,x}, x∈R is the positive part function and the random variables Xi and κ∈N are the same as in the model (1.1). Let us denote the probability mass function of the random variable M by
Then, the ultimate time survival probability definition (1.2) implies that
In general, the random variable M can be extended, i.e., P(M=∞)>0; however, the condition EX<κ ensures
see [2,Lemma 1]. This condition EX<κ is called the net profit condition, and it is crucial because survival is impossible, i.e., φ(u)=0 for all u∈N0, if EX⩾κ, except for a few trivial cases when P(X=κ)=1; see [2,Theorem 9]. Intuitively, it is clear that long-term survival by the model (1.1) is impossible if the threatening claim amount X on average is equal or greater to the collected premium κ per unit of time.
For s∈C, let us denote the generating function of φ(1),φ(2),… as follows:
and the probability-generating functions of the random variables X and M:
Then, Ξ(s) and GM(s), for |s|<1, satisfy the relation
In many examples, the radius of convergence of GX(s) or GM(s) is larger than one. See [3,Lemma 8] for more properties of the probability-generating function in |s|⩽1.
3.
Main results
In this section, based on the previously introduced notations and relation (1−s)Ξ(s)=GM(s) in (2.2), we formulate the main results of the work.
Theorem 3.1. Let us consider the model defined in (1.1) and suppose that the net profit condition EX<κ holds. Then, the probability mass functions of the random variables M and X satisfy the following two equalities:
We prove Theorem 3.1 in Section 5.
Equality (3.1) implies the following relation among the probabilities π0, π1, ….
Corollary 3.1. Let πi=P(M=i),i∈N0 and FX(u)=∑ui=0xi,u∈N0 be the distribution function of the random variable X. Then, for κ∈N, the following equalities hold:
Proof of Corollary 3.1. The n-th derivative of both sides of the equality (3.1) and s→0 gives
or
Let us turn to the survival probabilities φ(1),φ(2),… generating function Ξ(s). It is easy to see that the equalities (2.2) and (3.1) imply
Therefore, in a similar way that the recurrence equation (1.3) requires the initial values of φ(0), φ(1), …, φ(κ−1), the generating function Ξ(s) in (3.4) (the equality (3.3) as well) requires π0,π1,…,πκ−1, κ∈N. These probabilities can be solved by using the relations (3.1) and (3.2) and this is achievable as provided in Items (i)–(iv) below:
(i) We can choose |s|⩽1 such that the left-hand side of (3.1) vanishes, i.e., the roots of sκ=GX(s).
If the net profit condition G′X(1)=EX<κ holds and the greatest common divisor of powers of s in sκ=GX(s) is one, there are exactly κ−1 roots of sκ=GX(s) in |s|<1 when counted with their multiplicities. This fact is implied by Rouché's theorem and estimate |GX(s)|⩽1<|λsκ| when λ>1 and |s|=1, which means that, because of the fundamental theorem of algebra, both functions λsκ and λsκ−GX(s) have κ zeros in |s|<1. When λ→1+, there is always one root out of those κ in |s|<1 migrating to s=1 (s=1 is always the root of sκ=GX(s)), and some to other boundary points |s|=1 (roots of unity) if the greatest common divisor of powers of s in sκ=GX(s) is greater than one; see [21,Chapter 10], [22,Remark 10] and [3,Section 4,Lemmas 9 and 10 therein].
(ii) Let α≠1 be a root of sκ=GX(s) in |s|⩽1 and denote π:=(π0,π1,…,πκ−1)T as the column vector. Then, by (3.1) and
it holds that
where FX(u) is the distribution function of X.
(iii) Let α1,…,ακ−1≠1 be the roots of sκ=GX(s) in |s|⩽1. Then, by (i), (ii) and (3.2),
If Aπ=B denotes the system (3.5), x0>0 and α1,α2,…,ακ−1≠1 are the roots of multiplicity one, then, according to Lemma 4.2 proved in Section 4, the determinant |A|≠0 and, therefore, π=A−1B.
(iv) Suppose the root α≠1 of sκ=GX(s) in |s|⩽1 is of multiplicity l∈{2,3,…,κ−1},κ⩾3. Then, according to the equality (3.1) in Theorem 3.1 and (ii), the derivatives
and, to avoid identical lines in matrix A, we can set up the modified system (3.5) by replacing its lines (except the last one) with the corresponding derivatives (3.6). If x0>0, such a modified main matrix A remains non-singular, as proved in Lemma 4.3 of Section 4.
Note 1: The condition x0>0 does not lose generality. If P(X>j)=1 for some j∈{0,1,…,κ−2},κ⩾2 and the net profit condition remains valid (note that P(X>κ−1) implies EX⩾κ), then there is a reduction the order of recurrence in (1.3) and, consequently, some terms in the sums of (3.1) and (3.2) equal zero, causing corresponding adjustments in the system (3.5) or its modified version described in (iv). We then end up dividing by some xj+1 instead of x0 where needed. For instance, if x0=0 and x1>0, we then can express φ(κ−1) from (1.4) dividing by x1. See also [2,Theorem 7] and Corollary 3.2 when x0=0. Also, the both sides of sκ=GX(s) can be canceled by some power of s≠0 if P(X>j)=1 for some j∈{0,1,…,κ−2},κ⩾2.
We further denote by |A| the determinant of the matrix A where Mi,j, i,j∈{1,2,…,κ}, κ∈N are its minors and the matrix A is the main matrix in (3.5) or its modification replacing the coefficients by derivatives, as described in (iv).
The equality (3.4) and thoughts listed in (i)–(iv) allow us to formulate the following statement.
Theorem 3.2. Let |s|<1 and sκ−GX(s)≠0. If the net profit condition EX<κ holds, then the survival probability-generating function is given by
where ˜πi=πi/(κ−EX),
and the matrix A is created as provided in (i)–(iv).
Moreover, the initial values for the recurrence equation (1.3), including φ(κ), are
We prove Theorem 3.2 in Section 5.
Note 2: We agree that, for κ=1, the matrix A=(x0), its determinant |A|=x0 and the minor M1,1=1. Recall that x0 gets replaced by some xj+1 if P(X>j)=1 for some j∈{0,1,…,κ−2},κ⩾2 and the net profit condition holds; see Note 1.
The next statement provides possible expressions of ˜π0,˜π1,…,˜πκ−1 and φ(0),φ(1),…,φ(κ), κ∈N.
Theorem 3.3. Suppose that x0>0 and α1,α2,…,ακ−1≠1 are the roots of multiplicity one of sκ=GX(s) in |s|⩽1. Then, the values ~πi=πi/(κ−EX) for i=0,1,…,κ−1 admit the following representation:
and the initial values for the recurrence equation (1.3), including φ(κ), are
κ⩾2, where
Note that ∏0j=1(⋅)=∑1⩽j1<j0⩽…(⋅)=1 in Theorem 3.3, and we prove this theorem in Section 5.
In view of Theorems 3.2 and 3.3, we give several separate expressions on Ξ(s).
Corollary 3.2. If κ=1, then
If κ=2 and x0>0, then
where α∈[−1,0) is the unique root of GX(s)=s2.
If κ=2, x0=0 and x1>0, then
where ˜GX(s)=∑∞i=0xi+1si,|s|⩽1.
Proof of Corollary 3.2. The provided Ξ(s) expressions are implied by Theorem 3.2. Recall that s2=GX(s),x0>0 has the unique real root α∈[−1,0). In addition, when x0>0, then α=−1 is the root of s2=GX(s) iff P(X∈2N0)=1; see [3,Section 4 and Corollary 15 therein] and the description (i) in Section 3.
4.
Lemmas
In this section, we formulate and prove several auxiliary statements needed to derive the main results stated in Section 3.
Lemma 4.1. The random variable
where x+=max{0,x} is the positive part of x∈R, admits the following distribution property:
Proof. The proof is straightforward according to the definition of M and basic properties of the maximum. Indeed,
See also, [22,Lemma 5.2], [3,Lemma 25] and [4,page 198].
Lemma 4.2. Let α1,…,ακ−1≠1 be the roots of multiplicity one of sκ=GX(s) in the region |s|⩽1, and suppose that the probability x0 is positive. Then, the determinant |A| of the main matrix in (3.5) is
Proof. Let us calculate the determinant
We first put forward x0 from the last column. Then, multiplying the last column by FX(κ−1),FX(κ−2),…,FX(1), respectively, and subtracting it from the first, the second, etc., columns, we obtain
Proceeding the similar with the penultimate column of the last determinant (to put forward x0 and rearrange) and so on and applying the basic determinant properties, we obtain that
The last determinant is nothing but the well-known Vandermonde determinant; see for example [23,Section 6.1]. Thus,
because the roots α1,α2,…,ακ−1 are distinct and lie in the region |s|⩽1, s≠1.
Lemma 4.3. Let |s|⩽1. Suppose some roots α1,…,ακ−1≠1 of GX(s)=sκ are multiple, and assume that the probability x0 is positive. Then, the modified main matrix in (3.5), after replacing its lines (except the last one) by the derivatives (3.6), remains non-singular.
Proof. In short, the statement follows because the derivative is a linear mapping. More precisely, let us assume that α1 is of multiplicity two. Then, there exists such sufficiently close to zero δ∈R∖{0} that the matrix with the replaced second line
is non-singular, see the expression of the determinant in Lemma 4.2. Then, subtracting the second line from the first in (4.1), dividing the first line by δ afterward and letting δ→0, we get the desired line replacement using the derivative.
The proof is analogous for higher derivatives and/or more multiple roots.
5.
Proofs of the main results
In this section, we prove the statements formulated in Section 3. Let us start with the proof of Theorem 3.1.
Proof of Theorem 3.1. By Lemma 4.1 and the rule of total expectation,
which implies the equality (3.1):
To prove the second equality (3.2) in Theorem 3.1, we take the derivative of both sides of (3.1) with respect to s:
We now let s→1− in the last equality. It is easy to see that
and
because the net profit condition EX<κ holds. Before calculating lims→1−S1, we observe that EX2=∞⇔EM=∞ and EX2<∞⇔EM<∞; see [24,Theorems 5 and 6]. Therefore, the requirement EX2<∞ implies lims→1−S1=0 immediately. However, lims→1−S1=0 despite EM=∞. Indeed, if G′M(s)→∞ as s→1−, then
where
for any N∈{2,3,…}; see [22,Lemma 5.5]. Thus, the equality (3.2) follows and the theorem is proved.
Proof of Theorem 3.2. For sκ−GX(s)≠0, the equality (3.4) and division by 1−s (see (ii) in Section 3) imply
By the system (3.5), including its modified version described in (iv) in Section 3, and the recalled notations π=(π0,π1,…,πκ−1)T and ˜πi=πi/(κ−EX), we obtain
Thus, the expression of Ξ(s) in (3.7) follows.
The claimed equalities on φ(u) for u=1,…,κ are evident due to the obtained expression of π and φ(u+1)=∑ui=0πi,u∈N0 provided in (2.1). It can be seen that the recurrence equation (1.3) yields
Proof of Theorem 3.3. We calculate the minors Mκ,1,Mκ,2,…,Mκ,κ of the following matrix:
Following the calculation of determinant |A| in the proof of Lemma 4.2, we get
Note that Mκ,1 is defined for κ⩾1 and M1,1=1 by agreement. The next one
Similarly as before, Mκ,2 is defined for κ⩾2 only, and M2,2=x0+FX(1)α, where α∈[−1,0) is the unique root of s2=GX(s); see (i) in Section 3 and [3,Section 4 and Corollary 15 therein].
Proceeding,
and so on until the last minor:
The statement on expressions of ˜π0,˜π1,…,˜πκ−1 follows dividing the obtained minors (multiplied by −1 where needed) by the determinant |A|.
We now prove the claimed formulas of φ(0),φ(1),…,φ(κ), κ∈N. By the recurrence equation (1.3) with u=0, φ(u+1)=∑ui=0πi, u∈N0 and the already proved expression of πκ−1,κ∈N in Theorem 3.3,
The formula for φ(1) is evident because φ(1)=π0, where the expression of π0 is already proved in Theorem 3.3, too. The rest is clear by calculating the sum φ(u+1)=∑ui=0πi, u∈N0, where πi are given in the first part of Theorem 3.3.
6.
Particular examples
In this section, we give several examples illustrating the applicability of theoretical statements formulated in Section 3. The required numerical computations were performed by using Wolfram Mathematica [25]. As mentioned in Section 1, in [2], it has been proved that the required initial values for the recurrence equation (1.3) can be approximately found by calculating certain recurrent limits, while results of this work in Section 3, in many instances, provide exact closed-form expressions of the survival probabilities. Therefore, in some considered examples here, we check if the calculated exact value of φ matches the previously known approximate one.
Example 6.1. Suppose the random claim amount X is Bernoulli-distributed, i.e., 1−P(X=0)=p=P(X=1),0<p<1 and the premium κ∈N. We find the ultimate time survival probability-generating function Ξ(s) and calculate φ(u),u∈N0.
If κ=1, in view of the first part of Corollary 3.2 and the recurrence equation (1.3), it is trivial that Ξ(s)=1/(1−s),|s|<1 and φ(0)=x0φ(1)=1−p, φ(u)=1, u∈N. In other words, the ultimate time survival is guaranteed if the initial surplus u∈N and the maximal claim size is one in the model u+n−∑ni=1Xi.
If κ⩾2, it is easy to understand that u+κn−∑ni=1Xi>0 for all n∈N, u∈N0, regardless of the size of Xi; consequently, φ≡1, Ξ(s)=1/(1−s),|s|<1.
Example 6.2. Suppose that the random claim amount X is distributed geometrically with the parameter p∈(0,1), i.e., P(X=i)=p(1−p)i, i=0,1,…, and the premium rate equals two, i.e., κ=2. We find the ultimate time survival probability-generating function Ξ(s) and calculate φ(0) and φ(1) when the net profit condition is satisfied, i.e., EX<2.
We start with an observation on the net profit condition:
Then, according to Theorem 3.1 and the description (i) in Section 3,
when 1/3<p<1, and by Corollary 3.2 with κ=2 and x0=p>0,
For κ=2, u=0 and 1/3<p<1, the recurrence equation (1.3) or Theorem 3.3 yields
One may check that, for p=101/300,
and that coincides with the approximate values of φ(0) and φ(1) in [2,page 12] obtained via recurrent sequences.
Example 6.3. Suppose that X attains the natural values only, i.e., x0=0, x1>0, κ=2 and the net profit condition is satisfied EX<2. We provide the ultimate time survival probability φ(u) formulas for all u∈N0.
Let us recall that
The recurrence equation (1.3) and Corollary 3.2 for x0=0 and x1>0 imply
which echoes and widens the statement of Theorem 3 in [2], providing another method of φ(u),u⩾2 calculation.
Example 6.4. Suppose that the random claim amount X is distributed geometrically with the parameter p=101/300, i.e., P(X=i)=p(1−p)i, i=0,1,…, and the premium rate equals three, i.e., κ=3. We set up the ultimate time survival probability-generating function Ξ(s) and calculate or provide formulas for φ(u),u∈N0.
First, we observe that the net profit condition is satisfied, i.e., EX=199/101<3. We now follow the statement of Theorem 3.1 and the surrounding comments beneath it. Then, for p=101/300, the equation
has two complex conjugate solutions α1:=−0.368094+0.522097i and α2:=−0.368094−0.522097i inside the unit circle |s|<1. Then, by Theorem 3.2,
where (π0,π1,π2)=(0.582072,0.0818989,0.0658497) is the unique solution of
with appropriate numerical characteristics of the provided distribution. Theorem 3.3 and the recurrence equation (1.3) imply
The provided values of φ(0),φ(1),φ(2) and φ(3) coincide with the ones given in [2,page 14], where they are obtained approximately from certain recurrent sequences.
Example 6.5. Suppose x0=0.128, x1=0.576, x2=0.264, x3=0.032, ∑3i=0xi=1 and κ=3. We set up the ultimate time survival probability-generating function Ξ(s) and calculate φ(u),u∈N0.
For the provided distribution EX=1.2<3, the equation
has one root s=−4/11=:α of multiplicity two. Then, according to Theorem 3.1 and the comments (i)–(iv) beneath it, we create the modified system, replacing the second line with the corresponding derivatives:
which implies (π0,π1,π2)=(1,0,0); consequently
One may observe that the obtained result is expected, because u+3n−∑ni=1Xi>0 for all n∈N, except when u=0 and Xi attains the value of 3.
7.
Conclusions
This work shows that, if certain conditions are met, there exist exact closed-form expressions of the ultimate time survival probability
where the roots of sκ=GX(s), the distance κ−EX>0 and the distribution function FX(s) are involved; see Theorem 3.3. Moreover, having the values of the probability mass function
we can get the exact expression of the survival probability-generating function
see Theorem 3.2. As mentioned in Section 1, the expression of survival φ(u) or ruin 1−φ(u) probability is heavily dependent on what type of random variables generate the random walk
The random variables Xi in the sequence (7.1) can be discrete/continuous or dependent/independent, and their quantity for each n∈N can be deterministic/random, etc. Equally, the premium, or just an intercept technically, κ∈N in (7.1) influences the sequence's distribution, too. As demonstrated, the ultimate time survival probabilities φ(u) are solutions of systems of linear equations, which are based on the roots of sκ=GX(s). The recent work in [22] shows that similar systems can be used to find φ(u) when Xi are distributed differently. Thus, it is of interest to study the sequence (7.1), assuming various other mentioned options for Xi and κ; see, for instance, [26,27,28,29]. Also, the broadness of a random walk's occurrence in mathematics and other applied sciences indicates that this work and referenced research should not be applicable to ruin theory only.
Acknowledgments
The author appreciates any kind of constructive criticism of the paper and thanks professor Jonas Šiaulys for the detailed reading of the first draft of the manuscript. Sincere thanks to the anonymous reviewers for their work.
Conflict of interest
The author declares no conflict of interest.









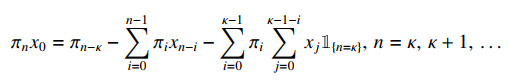




 DownLoad:
DownLoad: