1.
Introduction
Solitary solutions (or solitons) have been a mainstay in the field of nonlinear dynamics since their rediscovery in the Fermi-Pasta-Ulam-Tsingou experiment after almost a century of obscurity [1]. While the roots of solitary solutions are in physics, the analysis of such phenomena has branched out into numerous other disciplines including (but not limited to) engineering [2], biology [3,4] and neuroscience [5].
Some examples of recent publications on solitary solutions in various research fields are given below. Symbolic computation is used in conjunction with the modified rational expansion method to construct several types of solitary solutions to the Jimo-Miwa equation [6]. A soliton potential of Bose-Einstein condensates loaded into a one-dimensional four color lattice is constructed using analytical techniques in [7]. Four types of solitary to the Camassa–Holm equation, which are used to model shallow water dynamics, are constructed in [8]. The existence of polariton-type solitons in microcavity wires is investigated in [9].
Bifurcation and traveling wave solutions to the Manakov model (an extension of Schrödinger's equation) are derived in [10]. A fractional time-coupled Schrödinger's model and its exact traveling wave solutions are considered in [11]. Stationary optical solitons and exact solutions to a generalized Shcrödinger system important in the optical fiber theory are derived in [12], while such solutions to another optical system are considered in [13]. Exact solutions to a stochastic fractional long-short wave interaction system are first obtained in [14].
A deep-learning based method for the construction of solitary solutions to higher-order Korteweg-de-Vries (KdV) and Boussinesq equations is presented in [15]. The wave breaking of solitary wave solutions to the Novikov equation, a higher dimension generalization of the KdV model, is considered in [16]. Soliton solutions for the nonlinear sine-Gordon equation with Neumann boundary conditions are constructed using a meshless collocation method in [17]. Bright and dark solitary solutions to a heat transport with relaxational effects at a nanoscale are shown to exist in [18].
A class of ansatz methods have been successfully applied to various types of Schrödinger's equations [19,20] and other models of quantum physics [21]. More recently, ansatz techniques have been used to construct Gaussian solutions for a class of Schrödinger equations with logarithmic nonlinearity [22] and analytical traveling-wave solutions to a generalized Gross-Pitaevskii equation [23].
The main objective of this paper is to construct kink solitary solutions to the following system of Riccati equations with diffusive coupling via the generalized differential operator technique:
where x=x(t;c,u,v), y=y(t;c,u,v), c,u,v,ak,bk,γ1,γ2∈R and k=0,1,2.
The construction of solitary solutions to Riccati-type systems similar to (1.1) have been the subject of intensive research during the last decades. A variety of approaches based on the generalized differential operator have been developed [24]. Such techniques are superior to direct balancing (or ansatz) methods, as they can be used not only to construct solitary solutions, but also the necessary and sufficient existence conditions for the existence of such solutions. Bright and dark solitary solutions and their necessary and sufficient existence conditions in a Riccati-type with multiplicative coupling are constructed in [25].
Note that (1.1) has only diffusive coupling terms. Due to this absence of interaction between diffusive and multiplicative coupling, (1.1) possesses unique dynamics and properties with respect to its solitary solutions. Multiplicative coupling of the same system (terms γxy in both equations) has already been considered in [25]. An important property of multiplicative coupling is that the coupling term can only become equal to zero if one of the solutions becomes zero. This is not the case for diffusive coupling – the coupling term becomes zero if the functions x and y coincide. Due to this effect, it can be expected that diffusive coupling would yield a larger nomenclature of solitary solutions compared to the multiplicative case.
Furthermore, the generalized differential operator scheme presented in this paper discusses a novel way of applying such operators in conjunction with computer algebra for the stepwise construction of kink solitary solutions. Moreover, the techniques outlined in detail in this paper can be applied to any system of differential equations and further extended to construct higher-order (such as bright/dark) solitary solutions.
2.
Preliminaries
2.1. Solitary solutions
Solitary solutions considered in this paper have the following form [24,26]:
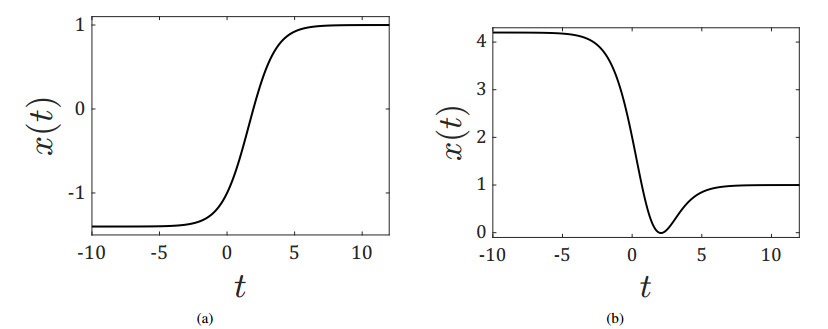
where σ1,σ2,η∈R, xk,yk,tk∈C, k=1,…,n and n defines the order of the solitary solution. Note that n=1 and n=2 correspond to kink and dark/bright solitary solutions [26]. Typical waveforms of kink and dark/bright solitary solutions are depicted in Figure 1. Note that kink solutions are monotonous, while higher-order solitary solutions can have local extrema: In general, an n-th order solitary solution (2.1) can have at most n−1 minima or maxima [27].
Expressions (2.1) and (2.2) can be simplified by introducing the following substitutions:
which transform (2.1) and (2.2) into the simplified form:
where ˆxk=ˆcxk; ˆyk=ˆcyk and ˆtk=ˆctk. Note that expressions (2.4) and (2.5) can be rearranged in the following way:
where λj=λj(ˆc,u,v), ρj=ρj(ˆc,u,v), μj=μj(ˆc,u,v) and νj=νj(ˆc,u,v) (j=1,…n).
2.2. The inverse balancing technique
The inverse balancing technique is applied before the construction of solitary solutions in order to determine the necessary existence conditions of such solutions in (1.1). Note that inverse balancing is distinct from direct balancing (also referred to as ansatz methods) in the sense that the goal of the procedure is not to construct solutions to differential equations, but to determine the necessary existence conditions for solutions of some fixed analytical form.
The first step of this procedure is to insert a solitary solution as an ansatz into the given system of differential equations, thus, obtaining a system of linear equations with respect to the parameters of the differential equations. If the resulting system is solvable with some conditions imposed on the parameters of the solitary solutions, then those conditions correspond to the existence criteria for the respective solitary solution. However, if the obtained linear system is degenerate, then the solitary solution of respective order cannot exist in the analyzed model. A broader discussion and examples of this technique are given in [25].
2.3. The generalized differential operator technique
Let us consider the following system of ordinary differential equations:
where P and Q are analytic functions.
Let Dα denote the partial differentiation operator with respect to the variable α. The generalized differential operator Dˆcuv corresponding to system (2.8) is defined as follows [24]:
The solution to system (2.8) can be expressed using (2.9) in the following form [24]:
2.4. The construction of closed-form solitary solutions
2.4.1. Linear recurring sequences for the construction of solitary solutions
Properties of linear recurring sequences exploited for the determination of the existence of closed-form solitary solutions are discussed in this section.
Let:
and
where H(m)p denotes the m-th order Hankel determinant with respect to the sequence (pj;j=0,1,…).
The sequence (pj;j=0,1,…) is called an m-th order linear recurring sequence if there exists such m∈N that satisfies the following condition:
The elements of the sequence (pj;j=0,1,…) can then be expressed as follows [28]:
where λ1,…,λm are constant coefficients and ρ1,…,ρm are roots of the following characteristic polynomial:
Note that (2.14) holds true only if equation (2.15) has distinct roots ρ1,…,ρm.
Analogously, if
then (qj;j=0,1,…) is a linear recurring sequence of order m and can be expressed as:
where μ,…,μm are constant coefficients and ν1,…,νm are roots of the characteristic polynomial analogous to (2.15).
2.4.2. Application of linear recurring sequences in (2.10)
It has been shown in [24] that if the following conditions hold true for all ˆc,u,v:
then series solutions (2.10) can be expressed in the closed-form:
Note that if both sets of characteristic roots ρk, νk (k=1,…,m) each have at least one zero, then expressions (2.20) correspond to the solitary solutions (2.6)-(2.7). In relation to this, the following property of linear recurrence sequences is presented. Let (wj;j=0,1,…) be an m-th order linear recurring sequence with one zero characteristic root. Then, the truncated sequence (wj;j=1,2,…) is (m−1)-th order linear recurring sequence [25]. In other words, when constructing solitary solutions (2.6)-(2.7), one may consider the sequences starting with the elements p1 and q1, respectively.
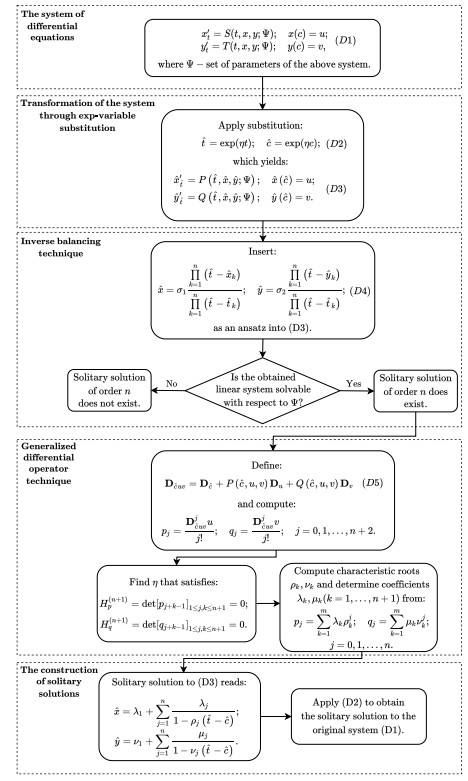
The procedure used for the construction of solitary solutions is summarized in Figure 2.
3.
The determination of the maximum possible order of solitary solutions to (1.1)
In this section, the maximum order of the solitary solutions (2.4)–(2.5) to (1.1) is determined by applying the inverse balancing technique outlined in the Section 2.2.
First, the system of differential equations (1.1) is transformed via the substitutions (2.3) as follows:
Note that substitution (2.3) is necessary - since the sequence of coefficients (2.15) does not form a linear recurring sequence for the untransformed system (1.1).
Let the order of the solitary solutions be n=2 (dark/bright solitons):
Inserting (3.2)–(3.3) into (3.1) and taking ˆt=ˆt1,ˆt2,ˆx1,ˆx2,ˆy1,ˆy2,0 yields the following system of linear equations with respect to the parameters γ1, γ2, ak, bk(k=0,1,2):
The solutions to the obtained linear system (3.4) exist only if one or both of the following conditions hold true:
1. ˆtk=ˆxl for some k,l=1,2. In this case, solutions (3.2)–(3.3) are kink solitary solutions;
2. b2=a2=0.
The first case - corresponding to n=1 - will be considered in the further sections, while the second condition is trivial since it leads to a linear system of differential equations (1.1). Therefore, the maximal order of solitary solutions to (1.1) is n=1, and bright/dark or higher order solitary solutions do not exist in the analyzed system.
4.
The construction of solitary solutions to (1.1)
4.1. The derivation of necessary existence conditions of kink solitary solutions to (1.1)
Inverse balancing technique (see Section 2.2) is applied in this section in order to derive the necessary existence conditions of kink solitary solutions to (1.1).
Let the order of the solitary solutions be n=1:
Inserting (4.1)–(4.2) as an ansatz into (3.1) and taking ˆt=ˆt1,ˆx1,ˆy1,0 yields the following system of linear equations with respect to the parameters γ1, γ2, ak, bk(k=0,1,2):
The solution to the obtained linear system (4.3) reads:
where γ1,γ2∈R are chosen arbitrarily. Note that the linear system (4.3) can be solved without any necessary existence conditions imposed on the parameters of the solitary solutions (4.1)–(4.2).
4.2. The determination of the parameter η of kink solitary solutions (4.1)–(4.2) to (1.1)
In this section, parameter η of kink solitary solutions (4.1)–(4.2) is determined by applying the results presented in Sections 2.3 and 2.4.
First, a generalized differential operator Dˆcuv corresponding to system (3.1) is defined in the following way:
Next, coefficients pj and qj(j=0,1,2,3) are computed using (2.11). The expressions of coefficients pj,qj,j=1,2,3 read:
As demonstrated in the Section 2.4, parameter η must satisfy the conditions below:
where H(2)p and H(2)q are the following Hankel determinants:
Then, the value of the parameter η for which the conditions (4.12)–(4.13) hold true is determined using the procedure outlined below:
1. Since kink solitary solutions (4.1), (4.2) form straight lines in the phase, the initial condition parameters u,v corresponding to a particular solution do satisfy a linear relationship. Thus, the following substitution is introduced
which transforms (4.12) into a fifth order polynomial with respect to u:
Naturally, condition (4.12) is satisfied if H(2,k)p=0 for all (k=0,…,5).
2. Parameter α is computed from the equation H(2,5)p=0, yielding:
and the obtained expression is inserted into equations H(2,k)p=0 (k=0,…,4).
3. Parameter η is computed from the equation H(2,4)p=0, yielding:
and the obtained expression is inserted into equations H(2,k)p=0 (k=0,…,3). Note that this value of η depends only on the parameters of the considered system of differential equations. Therefore, for a given system, η remains constant.
4. Parameter β is computed from the equation H(2,3)p=0, yielding:
and the obtained expression is inserted into equations H(2,k)p=0 (k=0,1,2).
5. Equation H(2,2)p=0 is rearranged, resulting in the following equality:
Note that condition (4.20) ensures that the two remaining equations H(2,k)p=0 (k=0,1) hold true. Applying (4.20) to (4.17)–(4.19) yields:
Moreover, note that applying relations (4.15) and (4.20)–(4.23) to H(2)q yields H(2)q=0.
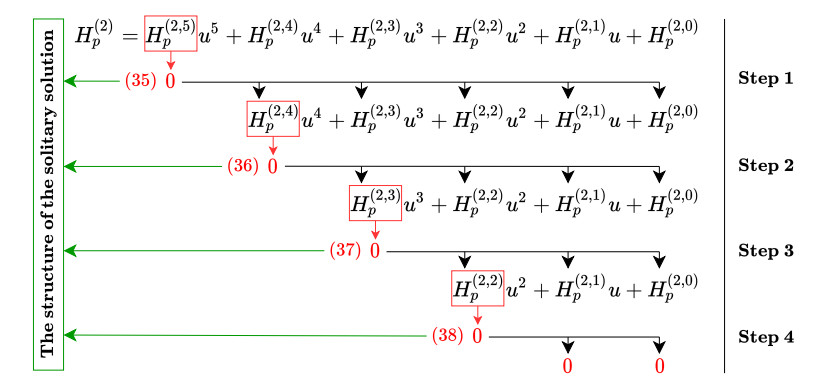
The procedure outlined above is depicted in the schematic diagram in Figure 3. Note that the algorithm displayed in Figure 3 has to be initiated from the coefficient that corresponds to the highest power of u, thus solving the equation H(2,5)p=0. Initiating the computations via H(2,k)p=0,k≠5 would not yield the described result.
The Riccati system (1.1) and the generalized differential operator (4.5) are symmetrical with respect to the coefficients ak,bk(k=0,1,2) and γ1,γ2. Thus, the computations presented above can be repeated for H(2)q with results that are obtained by replacing ak with bk, γ1 with γ2 and vice versa in (4.20) and (4.22).
All explicit analytical expressions obtained during the application of the procedure presented above are given in the supplementary file one (accessed via the GitHub repository https://bit.ly/3BuIIo3).
The results listed above are summarized in the following lemma.
Lemma 4.1. The system of differential equations (1.1) admits kink solitary solutions (4.1)–(4.2) if, and only if, (4.15) and (4.20)–(4.23) do hold true.
4.3. The construction of kink solitary solutions (4.1)–(4.2) to (1.1)
Let the conditions (4.15) and (4.20)–(4.23) hold true, then the sequences (pj;j=0,1,…) and (qj;j=0,1,…) have a single zero characteristic root each (see the last paragraph of the Section 2.4):
The remaining characteristic roots ρ2 and ν2 are computed from the following characteristic equations:
Solving (4.25) yields:
Relations (2.14) and (2.17) yield the following systems of linear equations with respect to λ1,λ2 and μ1,μ2:
Note that 00 is taken to be equal to one [29]. Solutions to (4.27)–(4.28) read:
Thus, kink solitary solutions to (3.1) read:
Rearranging (4.30), (4.31) yields:
where the parameters read:
Since \(\widehat{x}_1 = \widehat{c} x_1, \widehat{y}_1 = \widehat{c} y_1, \widehat{t}_1 = \widehat{c} t_1\), the parameters \(x_1, y_1, t_1\) of kink solutions \(x, y\) read:
where
Then, kink solitary solutions to the original system of differential equations (1.1) can be written as:
4.4. Isomorphism between the parameters of kink solitary solutions (4.37)–(4.38) and the parameters of the system (1.1)
Note that (4.20) and (4.22) lead to the following functional relations:
where k=1,2.
Analogously, equalities in (4.4) are written in the form representing functional relations between parameters of the system and parameters of the solitary solutions:
Note that parameters x1,y1,t1 are related to ˆx1,ˆy1,ˆt1 through relationships ˆx1=ˆcx1,ˆy1=ˆcy1,ˆt1=ˆct1.
Furthermore, solving (4.4) with respect to σ1,σ2,x1,y1 yields:
The parameters of (1.1) and the solitary solution can be grouped into two categories:
● Parameters of the system of differential equations (1.1): γ1, γ2, al, bl(l=0,1,2).
● Parameters of the kink solitary solutions (4.37)–(4.38): η, c, σ1, σ2, x1, y1, t1.
Then, the following mappings between parameters in the two categories can be constructed:
The mapping τt1,γ1,γ2,η is defined by (4.41) and the mapping τ−1t1,γ1,γ2,η is given by (4.40).
Mappings τt1,γ1,γ2,η and τ−1t1,γ1,γ2,η define an isomorphism between the parameters of kink solitary solutions σ1, x1, σ2, y1 and the parameters of the Riccati system a1, a2, b1, b2, where t1, γ1, γ2, η are chosen arbitrarily and a0, b0 are computed from (4.39).
5.
Numerical experiments
Consider the following system of Riccati equations with diffusive coupling:
where x=x(t;c,u,v), y=y(t;c,u,v), c,u,v∈R and the coefficients ak,bk(k=0,1,2), γ1,γ2 in (1.1) are as follows:
Note that condition (4.20) does hold true.
According to Lemma 4.1, system (5.1) admits kink solitary solutions if, and only if, the following constraint holds true:
where α and β are computed using the stepwise computational scheme outlined in section three. All explicit analytical expressions obtained during the application of this procedure are given in the supplementary file two (accessed via the GitHub repository https://bit.ly/3BuIIo3).
The analytical expressions of kink solitary solutions to (5.1) are then obtained using the results presented in Section 4.3 as follows:
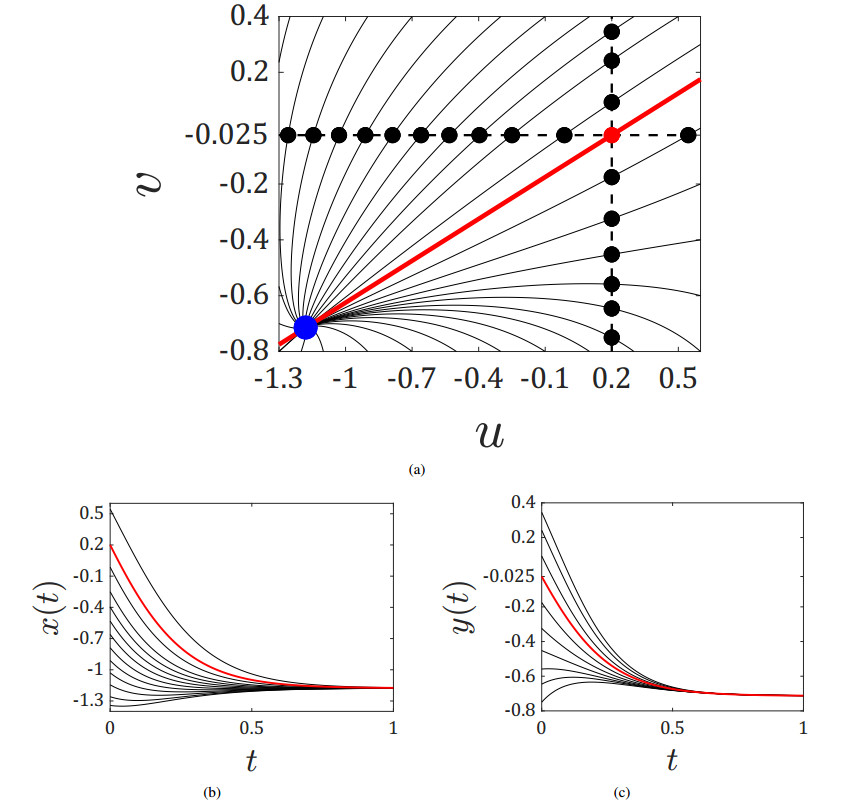
The system (5.1) is integrated using numerical techniques; results are displayed in Figure 4. Part (a) of Figure 4 illustrates the phase portrait of the system, where solitary and non-solitary solutions to (5.1) correspond to solid red and black lines respectively. Note, that the red line depicts the constraint (5.3). Part (b) of Figure 4 displays solitary (red line) and non-solitary (black lines) solutions to (5.1) obtained by fixing v=−0.025. Analogously, part (c) of Figure 4 displays solitary (red line) and non-solitary (black lines) solutions to (5.1) obtained by fixing u=0.2.
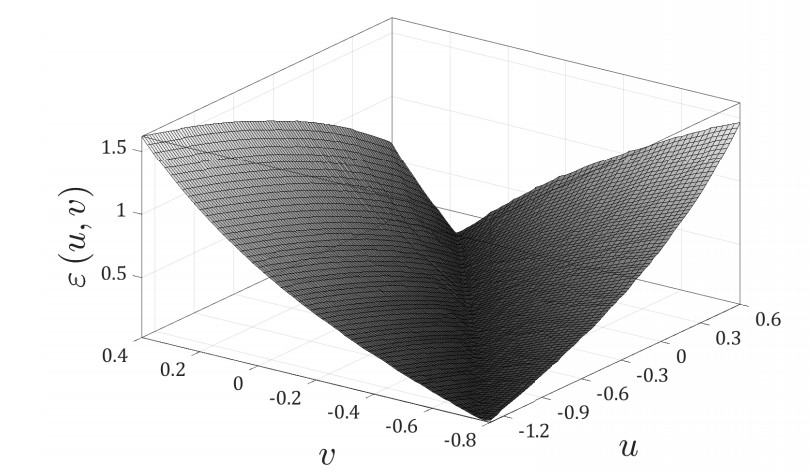
The validity of constraint (5.3) can be verified by the following computational experiment. Let ˜x(jh,u,v) and ˜y(jh,u,v) denote the approximate numerical solutions to (5.1) at c=0, obtained using the constant step numerical integrator with the step-size h=0.1 (j=0,…,100). The difference between the approximate numerical solution and the kink solitary solution (5.4)-(5.5) is then defined as follows:
The distribution of ε(u,v) is displayed in Figure 5. Is is clear that the values of ε(u,v) are closest to zero on the line v=12u−18.
6.
Conclusions
Kink solitary solutions to a system of Riccati differential equations with diffusive coupling were constructed via the generalized differential operator technique aided by computer algebra computations. The presented scheme was also used to derive necessary and sufficient existence conditions for kink solitary solutions with respect to the Riccati system parameters. This approach allowed us to determine analytical conditions that generate the constraints that the solitary solutions must satisfy in both the space of system parameters and the space of solution parameters. Furthermore, it was proven via the inverse balancing technique that (1.1) cannot admit bright/dark and higher-order solitary solutions under any conditions.
The presented stepwise approach (Section 4.2) is a powerful tool for the construction of analytical solutions to nonlinear differential equations. Note that this technique is not limited to system (1.1), but can potentially be applied to a variety of both Riccati-type equations and more general ordinary differential equations (ODEs) with polynomial nonlinearity.
The obtained results are counterintuitive. Even though diffusive coupling can be perceived as less limiting than multiplicative coupling, the multiplicative case yields both kink and bright-dark solitary solutions, while diffusive coupling results only in kink solitary solutions.
Solitary solutions have special properties that make them especially important in the analysis of propagating waves. Problems concerning propagating waves arise from partial differential equations (PDEs), which are transformed to ODEs via a linear wave-variable substitution. Analysis of these ODEs allows the consideration of wave propagation in various nonlinear equations.
While the analysis of solitary solutions in PDEs is enabled by the wave-variable substitution, many approaches (such as the exp-function method) for the construction of solutions to the obtained ODE have gotten a significant amount of criticism [30,31]. Conversely, the techniques presented in this paper do not have the drawbacks of the exp-function method: While computer algebra is applied, the presented approach also allows the derivation of necessary and sufficient conditions for the existence of solitary solutions.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
Minvydas Ragulskis is an editorial board member for AIMS Mathematics and was not involved in the editorial review or the decision to publish this article. All authors declare that there are no competing interests.









 DownLoad:
DownLoad: