1.
Introduction
A function plays very vital role in studying real analysis, numerical analysis, functional analysis and statistical analysis etc. Properties of a function like continuity, differentiability increase its importance in the subjects of mathematical analysis, economics, differential equations etc. A convex function defined about a century ago has fascinating geometric and analytical properties, due to which it is studied frequently in the subjects of mathematical analysis and optimization theory. Its extended form is the well-known Jensen inequality which in particular generates several classical inequalities. In the development of the theory of mathematical inequalities its role is significant. Description of a convex function in different convenient forms motivates the researchers to extend its concept in the form of new definitions and notions. Especially, to generalize and refine the classical inequalities for convex functions, it can be found in the literature that researchers have defined many new classes of functions.
In the theory of inequalities the class of convex functions has been considered at very large scale in past few decades, see [1,2,3,4,5] and references therein.
A function f defined on an interval I is called convex if the following inequality is satisfied [6]:
A function f is said to be convex with respect to a strictly monotone function g if f∘g−1 is a convex function, see [7,Definition 1.19,p.7]. An analytic representation (1.1) of convex function provides the motivation to define new classes of functions. By including some convenient parameters and functions, various numerous generalizations, extensions and refinements have been introduced. For example in [8,9,10,11,12], authors have defined m-convex, h-convex, s-convex, Godunova-Levin convex, Godunova-Levin s-convex, (α,m)-convex, (h−m)-convex, (s,m)-convex and P-convex functions. All such functions can be reproduced from the following class of functions called (α,h−m)-convex functions.
Let J⊆R be an interval containing (0,1) and let h:J→R be a non-negative function, h≢0. A function f:[0,b]→R is said to be (α,h−m)-convex, if f is non-negative and for all x,y∈[0,b], (α,m)∈[0,1]2, t∈(0,1), we have
see [4] for more details.
In [13], authors defined a new notion of functions as follows:
Let h:J⊂R→R be a function with h≢0. A function f:I→R is said to be (α,h−m)-convex with respect to a strictly monotone function g:K⊂I→R, if f,h≥0 and for each x,y∈I, we have
where (α,m)∈[0,1]2 and t∈(0,1). This idea is extended and in [14] refined (α,h−m)-convex function has been introduced which provide refinements of various kinds of convex functions which have been studied in [15,16,17] can be reproduced.
Let h:J⊆R→R be a function with J containing (0,1). A function f:I→R is called refined (α,h−m)-convex function, if f,h≥0 and for each x,y∈I, we have
where (α,m)∈(0,1]2 and t∈(0,1), see [14] for more details.
The aim of this work is to introduce refined (α,h−m)-convex function with respect to strictly monotone function. By applying this new definition we will establish generalized Riemann-Liouville fractional integral inequalities. These inequalities will also provide refinements of Riemann-Liouville fractional integral inequalities for specific functions involved in Definition 2.1.
Fractional calculus operators of differentiation and integration are key factors in generalizing classical concepts of calculus. The role of derivatives and their applications in diverse fields of science and engineering is remarkable. Fractional calculus operators generalize all the classical phenomena related to usual derivative and integration, see [18] for more details.
The Riemann-Liouville fractional and derivative integral operators are the most classical well-known integrals and derivatives of fractional order defined as follows:
Definition 1.1. [18] Let f∈L1[u,v]. Then Riemann-Liouville fractional integrals of order β of a function f are given as follows:
where
and ℜ(β)>0.
Definition 1.2. [19] Let f∈L1[u,v]. Then k-fractional Riemann-Liouville integrals of order β of a function f are given as follows:
where
and ℜ(β),k>0. Using Γk(β)=kβk−1Γ(βk) in (1.5) and (1.6), one can get
and
The Hadamard inequality is of immense importance in the theory of inequalities and a lot of work has been published about this inequality in the past few decades, see [20,21,22,23]. The Hadamard inequality is stated as follows:
Let f be a convex function on [u,v] with u<v. Then, the following inequality holds:
A number of numerous generalizations and refinements of the inequality (1.9) have been published in recent years, see [11,14,24]. Keeping in view these results we aim to find some new refinements of existing inequalities by using refined (α,h−m)-convex functions with respect to a strictly monotone function. These results are also applicable for k-fractional version of Riemann-Liouville integrals which are also given in this paper.
The rest of the paper is organized as follows: In Section 2, we define a new class of convex functions, namely refined (α,h−m)-convex function with respect to a strictly monotone function and establish Hadamard type inequalities by using this class of functions. The k-analogue versions of these results are given in Section 3. Moreover, the results of this paper are connected with already published inequalities. In Section 4, we give concluding remarks.
2.
Main results
Definition 2.1. Let h:J⊆R→R be a function with (0,1)⊆J. Also, let K,I are intervals in R such that K⊂I. A function f:I→R is called refined (α,h−m)-convex function with respect to strictly monotone function g:K→R, range(g)⊂I if f,h≥0 and for each x,y∈I, we have
where (α,m)∈(0,1]2 and t∈(0,1).
By comparing inequalities (1.3) and (2.1), it can be realized that if 0<h(t)<1, then (2.1) reduces to the following refinement of (α,h−m)-convex function with respect to strictly monotone function g:
Next, we give some examples as follows:
Example 2.1. The function x2+1 is (1,Id−1)-convex as well as refined (1,Id−1)-convex with respect to x on (0,1). But on (1,∞), it is (1,Id−1)-convex but not refined (1,Id−1)-convex with respect to x.
Example 2.2. Let g(x)=xp for x∈(0,∞) and p∈R∖{0}. Then g is strictly monotone function (strictly increasing for p>0 and strictly decreasing for p<0) and g−1(x)=x1p. By using Definition 2.1, we have
By replacing x with xp and y with yp, we get
Inequality (2.4) gives the definition of refined (α,h−m)−p-convex function given in [25]. Whereas for p=−1, the inequality (2.3) reduces to the following inequality:
By replacing x with 1x and y with 1y, we get
that is f∘g−1 is refined harmonically (α,h−m)-convex function defined in [25].
For h(t)=t in (2.1), we get definition for refined (α,m)-convex function with respect to a strictly monotone function g stated as follows:
Definition 2.2. A function f:I→R is called refined (α,m)-convex function with respect to a strictly monotone function g:K⊂I→R, if for each x,y∈I, we have
where (α,m)∈(0,1]2 and t∈(0,1).
By taking h(t)=t and m=1, (2.1) gives the definition for refined α-convex function with respect to a strictly monotone function g stated as follows:
Definition 2.3. A function f:I→R is called refined α-convex function with respect to a strictly monotone function g:K⊂I→R, if for each x,y∈I, we have
where m∈(0,1] and t∈(0,1).
By taking α=1, (2.1) gives the definition of refined (h−m)-convex function with respect to a strictly monotone function g stated as follows:
Definition 2.4. Let h:J⊆R→R be a function with J containing (0,1). A function f:I→R is called refined (h−m)-convex function with respect to a strictly monotone function g:K⊂I→R, if f,h≥0 and for each x,y∈I, one have the inequality
where m∈[0,1] and t∈(0,1).
By taking α=1=m, (2.1) gives the definition of refined h-convex function with respect to a strictly monotone function g stated as follows:
Definition 2.5. Let h:J⊆R→R be a function with J containing (0,1). A function f:I→R is called refined h-convex function with respect to a strictly monotone function g:K⊂I→R, if f,h≥0 and for each x,y∈I, one have the inequality
where t∈(0,1).
By taking α=1 and h(t)=ts, (2.1) gives the definition of refined (s,m)-convex function with respect to a strictly monotone function g stated as follows:
Definition 2.6. A function f:I→R is called refined (s,m)-convex function with respect to a strictly monotone function g:K⊂I→R, if for each x,y∈I, we have
where (s,m)∈(0,1]2 and t∈(0,1).
By taking α=1 and h(t)=t, (2.1) gives the definition of refined m-convex function with respect to a strictly monotone function g stated as follows:
Definition 2.7. A function f:I→R is called refined m-convex function with respect to a strictly monotone function g:K⊂I→R, if for each x,y∈I, we have
where m∈(0,1] and t∈(0,1).
Now, we give the following Hadamard type inequalities for Riemann-Liouville fractional integral operators via refined (α,h−m)-convex function with respect to a strictly monotone function g.
Theorem 2.1. Let f:[u,mv]→R with 0≤u<mv and f∈L1[u,v]. Also, suppose that f≥0 is refined (α,h−m)-convex function with respect to a strictly monotone function g. Then for (α,m)∈(0,1]2, the following fractional integral inequality holds:
with β>0.
Proof. Since f is refined (α,h−m)-convex function with respect to a strictly monotone function g, by using (2.1), one can have the following inequality:
By setting x=tu+m(1−t)v and y=um(1−t)+vt in (2.14), the following inequality can be yielded:
Now, by integrating the above inequality over the interval [0,1] after multiplying with tβ−1, one can have the following inequality:
On the right hand side by applying definition of refined (α,h−m)-convexity with respect to a strictly monotone function g, one can obtain the following inequality:
Making change of variables, then by applying Definition 1.1 and multiplying by β, one can easily obtain the inequality required in (2.13). The proof is completed.
Remark 2.1. (i) For g(x)=x, (2.13) reduces to [14,Theorem 1].
(ii) For m=α=1 and h(t)=t, (2.13) reduces to [24,Theorem 3.1].
(iii) For β=1 along with the conditions of (ii), (2.13) reduces to [24,Theorem 2.1].
(vi) For h(t)=t along with the condition of (i), (2.13) reduces to [14,Corollary 1].
(vii) For α=1 along with the condition of (i), (2.13) reduces to [14,Corollary 2].
(viii) For α=1 and h(t)=ts along with the condition of (i), (2.13) reduces to [14,Corollary 4].
(ix) For α=1 and h(t)=t along with the condition of (i), (2.13) reduces to [14,Corollary 5].
(x) For m=1 in the result of (x), (2.13) reduces to [14,Corollary 6].
By imposing an additional condition, we get the following result which shows the extension of Theorem 2.1.
Theorem 2.2. Along with} the assumptions of Theorem 2.1, if h is bounded above by 1√2, then the following inequality holds:
Proof. By using the condition h(t)≤1√2, one can have h(tα)h(1−tα)≤12. Integrating over [0,1] after multiplying with tβ−1, we get the following inequality:
Since f is refined (α,h−m)-convex function with respect to a strictly monotone function g, by using (2.1), one can have the following inequality:
From inequalities (2.13), (2.18) and (2.19), one can get (2.17).
Remark 2.2. (i) For g(x)=x, (2.17) reduces to [14,Theorem 2].
(ii) For g(x)=xp, (2.17) reduces to [25,Theorem 2].
(iii) For α=1 along with the condition of (i), (2.17) reduces to [14,Corollary 3].
(v) For α=1 along with the condition of (ii), (2.17) reduces to [25,Corollary 3].
Corollary 2.1. Using h(t)=t, (2.13) gives the fractional integral inequality for refined (α,m)-convex function with respect to a strictly monotone function g in the following form:
Corollary 2.2. Applying α=1, (2.13) gives the fractional integral inequality for refined (h−m)-convex function with respect to strictly monotone function g in the following form:
Corollary 2.3. Applying α=1 and h(t)=ts, (2.13) gives the fractional integral inequality for refined (s,m)-convex function with respect to a strictly monotone function g in the following form:
where B(1+s,s+β) is the beta function.
Corollary 2.4. Applying α=1 and h(t)=t, (2.13) gives the inequality for refined m-convex function with respect to a strictly monotone g in the following form:
Corollary 2.5. Applying α=1, (2.17) gives the fractional integral inequality for refined (h−m)-convex function with respect to a strictly monotone function g in the following form:
Theorem 2.3. Under the assumption of Theorem 2.1, the following fractional integral inequality holds:
with β>0.
Proof. We use the inequality (2.14) to prove this theorem. By setting x=tu2+m(2−t2)v and y=um(2−t2)+tv2 in (2.14), one can get the following inequality:
By integrating the above inequality over the interval [0,1] after multiplying with tβ−1, one can have the following inequality:
On the right hand side by applying definition of refined (α,h−m)-convexity with respect to a strictly monotone function g, one can obtain the following inequality:
Making change of variables, then by applying Definition 1.1 and multiplying by β, one can easily obtain the inequality required in (2.25).
Remark 2.3. (i) For g(x)=x, (2.25) reduces to [14,Theorem 3].
(ii) For β=m=α=1 and h(t)=t, (2.25) reduces to [24,Theorem 2.1].
(iii) For h(t)=t along with the condition of (i), (2.25) reduces to [14,Corollary 7].
(iv) For α=1 along with the condition of (i), (2.25) reduces to [14,Corollary 8].
(v) For α=1 and h(t)=ts along with the condition of (i), (2.25) reduces to [14,Corollary 10].
(vi) For α=1 and h(t)=t along with the condition of (i), (2.25) reduces to [14,Corollary 11].
(vii) For m=1 in the result of (i), (2.25) reduces to [14,Corollary 12].
By imposing an additional condition, we get the following result which shows the extension of Theorem 2.3. We will leave the proof for reader.
Theorem 2.4. Along with the assumptions of Theorem 2.3, if h is bounded above by 1√2, then the following inequality holds:
Remark 2.4. (i) For g(x)=x, (2.28) reduces to [14,Theorem 4].
(ii) For g(x)=xp, (2.28) reduces to [25,Theorem 4].
(iii) For α=1 along with the condition of (i), (2.28) reduces to [14,Corollary 9].
(iv) For α=1 along with the condition of (ii), (2.28) reduces to [25,Corollary 7].
Corollary 2.6. Applying h(t)=t in (2.25), the following fractional integral inequality for refined (α,m)-convex function with respect to a strictly monotone function g is obtained.
Corollary 2.7. Applying α=1 in (2.25), the following fractional integral inequality for refined (h−m)-convex function with respect to a strictly monotone function g is obtained.
Corollary 2.8. Applying α=1 and h(t)=ts, (2.25) gives the fractional integral inequality for refined (s,m)-convex function with respect to a strictly monotone function g in the following form:
Remark 2.5. If m=1 in (2.31), then the result for s-tgs convex function is obtained.
Corollary 2.9. Applying α=1 and h(t)=t, (2.25) gives the inequality for refined m-convex function with respect to a strictly monotone function g in the following form:
Corollary 2.10. Applying α=1, (2.28) gives the following inequality:
3.
Some extensions and examples
This section presents extensions of some results of Section 2 into k-fractional versions.
Theorem 3.1. Under the assumption of Theorem 2.1, the following inequality for k-fractional integral holds:
with β,k>0.
Proof. Using (1.7) and (1.8) after replacing β by βk in the proof of Theorem 2.1, we get the above inequality (3.1).
Theorem 3.2. Under the assumption of Theorem 2.3, for k>0, the following inequality holds for k-fractional integrals:
with β>0.
Proof. Using (1.7) and (1.8) after replacing β by βk in the proof of Theorem 2.3, we get the above inequality (3.2).
Remark 3.1. (i) For g(x)=x all the results of this section coincide with the results of [14,Section 3].
(ii) For g(x)=xp all the results of this section coincide with the results of [25,Section 3].
Next, we consider some examples of strictly monotone functions and provide the corresponding inequalities.
Example 3.1. For g(x)=xp, (2.13) gives the following results for refined (α,h−m)−p-convex function.
Case 3.1. For p>0, we have
Case 3.2. For p<0, we have
Example 3.2. For g(x)=ln(x) with g−1(x)=ex, (2.13) gives the following result:
Remark 3.2. (i) For h(t)=t, (3.3) reduces to [25,Corollary 2.1].
(ii) For α=1, (3.3) reduces to [25,Corollary 2.2].
(iii) For α=1 and h(t)=ts, (3.3) reduces to [25,Corollary 4].
Example 3.3. For g(x)=xp, (2.25) gives the following results for refined (α,h−m)−p-convex function.
Case 3.3. For p>0, we have
Case 3.4. For p<0, we have
Example 3.4. For g(x)=ln(x) with g−1(x)=ex, (2.25) gives the following result:
Remark 3.3. (i) For h(t)=t, (3.6) reduces to [25,Corollary 5].
(ii) For α=1, (3.6) reduces to [25,Corollary 6].
(iii) For α=1 and h(t)=ts, (3.6) reduces to [25,Corollary 8].
4.
Conclusions
We have introduced a new class of convex functions that provides refinements of many known classes of functions related with convexity. Inequalities for Riemann-Liouville fractional integral operators have been established for this class of functions. Moreover, connection with already published results is given in the form of remarks and some examples are considered. Furthermore, for 0<h(t)<1, the refinements of the results of [13] can be obtained.
Acknowledgements
This research received funding support from the National Science, Research and Innovation Fund (NSRF), Thailand.
Conflict of interest
The authors declare that they have no competing interests.









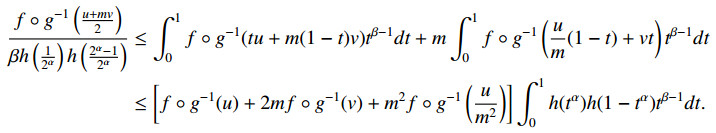
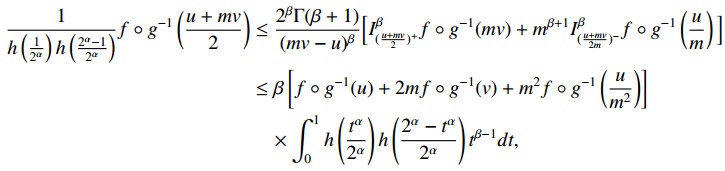
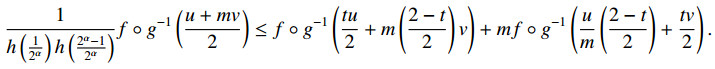
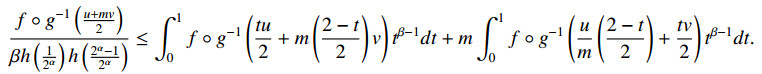
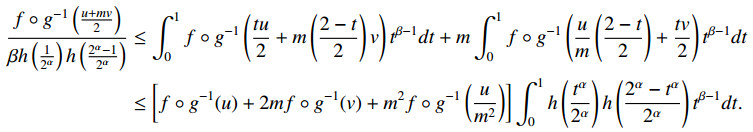
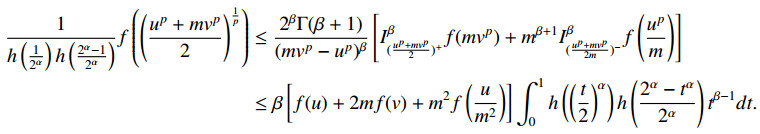
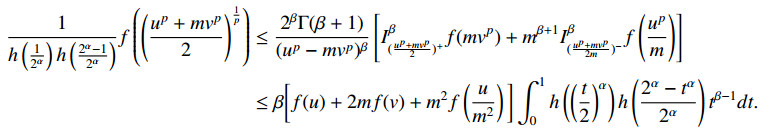
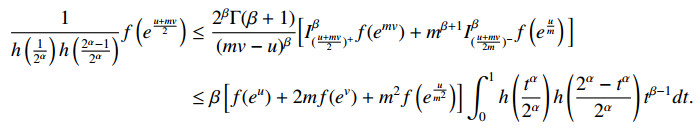




 DownLoad:
DownLoad: