1.
Introduction
Due to their broad use in research and engineering, fractional differential equations have been studied for many decades. The numerical solutions to fractional differential equations are of tremendous interest. No approach provides an accurate solution for fractional differential equations. Approximate solutions can only be generated using series solution methods or linearization. Nonlinear phenomena can be observed in numerous engineering and scientific disciplines, such as chemical kinetics, nonlinear spectroscopy, solid state physics, fluid physics, computational biology, quantum mechanics, and thermodynamics, among others. Nonlinearity is defined by various nonlinear partial differential equations of greater order. For all physical systems, nonlinear models describe fundamental events [1,2]. Most of the properties of science and nature described by employing non-linear partial differential equations are strongly connected with the basic properties of scientific fields. Recently, partial differential equations have been utilised to examine properties of several real-world problems likely to arise in plasma physics, population ecology, fluid mechanics, solid state physics, shallow-water wave propagation, quantum mechanics, heat, biology and optical fibers. Furthermore, their mathematical frameworks have also been described to literary works [3,4,5]. Theoretical partial differential equations analysis offers a wide range of applications. It's worth noting that there are certain really difficult equations that even supercomputers can't solve. All one can do in these situations is an attempt to get qualitative data about the answer. Moreover, the formulation of the equation, as well as its associated side conditions, is significant. A physical or technical issue model is frequently used to generate the equation. It is not immediately clear that the model is continuous in that it results in a solved partial differential equation [6,7,8]. Furthermore, in most circumstances, the answer should be one of a kind and stable under minor data disruptions. Theoretical comprehension of the equation aids in determining whether or not these requirements are satisfied. Several methods for solving classical partial differential equations have already been suggested, and several solutions have been discovered [9,10,11,12,13].
Because of its extensive applicability range, the nonlinear Schrodinger equation (NLSE) is one kind of PDE whose study has had a lot of success for decades. Different types of NLSE are used to represent specific phenomena in diverse areas, including nonlinear optics [16,17], fluid dynamics [18], and Bose-Einstein Delicacy [19,20] among others. The nonlinearity to create additional light on the disruption, that happens when electromagnetic pulses travel in the optical extreme [21,22] is a distinguishing feature among the forms of the discovered NLSE. Furthermore, studies on the soliton and numerical solutions for NLSEs have been described in the literature [23] utilising various techniques. The current research varies from previous works on the Schrödinger-KdV problem in that it has identified an accurate numerical solution using a series scheme developed using a non singular kernel operator.
Transformations are intrinsically intriguing, because they facilitate the solution of mathematical problems such as ordinary, partial, and fractional-order differential equations by researchers. Laplace and Fourier transformations are two well-known transformations that were initially utilized to solve ordinary and partial differential equations. Later, in the field of fractional calculus, these transformations were applied to differential equations of fractional order. In recent years, scholars have proposed numerous more transformations to address a vast array of mathematical difficulties. In this study, inspired by the aforementioned research, we present the Shehu transform, a Laplace-type integral transform for solving both ordinary and partial differential equations. The integral transform described is applied successfully to both ordinary and partial differential equations. Using the Laplace or Fourier integral transforms, it is simple to validate the results obtained in the applications section. The Shehu transform is represented throughout this work by the operator S.
In this paper, we enhance the Shehu transform decomposition method (STDM) and the homotopy perturbation Shehu transform technique (HPSTM) in order to discover an approximation to the aforementioned problem. Adomian decomposition methodology (ADM) is a well-known systematic method for solving deterministic or stochastic operator equations, including ordinary differential equations (ODEs), partial differential equations, integral equations, and integro-differential equations, among others. The ADM is an advanced method that provides quick algorithms for approximate analytic answers and numerical simulations in applied sciences and engineering. In 1998, however, he developed the homotopy perturbation technique [26,27]. The applications of the homotopy perturbation method, which are thoroughly discussed in [28,29,30,31,32], have recently received considerable interest. This method views the solution as the sum of an infinite series, which typically converges to precise solutions rapidly. This method has been applied to a variety of mathematical problems.
2.
Basic definitions
In order to perform our research, we require various terminologies and postulate outcomes from a literature.
Definition 2.1. Shehu transform (ST) for a mapping U(μ) containing exponential order defined on the set of mappings is described as follows [33,34,35]:
where U(μ) is denoted by S[U(μ)]=S(ε,υ), is stated as
The following is an example of a supportive ST:
Definition 2.2. The inverse ST of a function U(μ) is described as [33,34,35]
Lemma 2.3. Consider ST of U1(μ) and U2(μ) as P(ε,υ) and Q(ε,υ), respectively [33,34,35],
where γ1 and γ2 are unspecified terms.
Lemma 2.4. The ST of the Caputo fractional derivative (CFD) is defined as [33,34,35]
3.
Homotopy perturbation Shehu transform method [36]
In order to understand the basic idea, we give the general implementation of the given technique.
with initial conditions
Here D℘η represents the fractional differential operator, P1 and Q1 represent the linear and nonlinear terms respectively.
Apply Shehu transform to (3.1),
From (3.3) we have
Using the inverse Shehu transform to Eq. (3.4), we get
The term H(μ) comes in result of source term and the given initial sources. Now, by homotopy perturbation method
The nonlinear terms are derived as
for He's polynomials Hk as
Putting (3.7) and (3.8) in equation (3.5)
By rearranging based on powers of p-terms, we obtain
Thus we easily calculate φk(μ,η), with the help of which we get convergent series. At p→1, we have
The series form solution converges quickly towards the exact solution.
4.
Shehu transform decomposition method [37]
In order to understand the basic idea, we give the general implementation of the given technique.
having initial sources
Where D℘η=∂℘∂η℘ represents the fractional differential operator, P1 and Q1 represent the linear and nonlinear terms and R1 is the source term.
Apply Shehu transform to (4.1),
Applying the differentiation property of Shehu transform, we get
From (4.3) we have
Using the inverse Shehu transform
STDM series form solution of φ(μ,η) is defined as
The nonlinear terms Q1 is defined as
The nonlinear terms by means of Adomian polynomials is determined as
By putting Eq (4.6) and Eq (4.8) into (4.5), we obtain
we define the following terms,
the general for m≥1, is defined as
5.
Applications
In this section, the solution to time-fractional Schrödinger-KdV equation is derived by implementing STDM and HPSTM.
Example
Consider the time-fractional Schrödinger-KdV equation of the following form
having initial conditions
At ℘=1, the exact solution of Eq (5.1) is
Apply Shehu transform to (5.1),
Applying the Shehu transform differentiation property, we have
Using the Shehu inverse transform
Now, by homotopy perturbation method
where Hk(μ) He's polynomials representing the nonlinear terms. The He's polynomials first few terms are given by
By rearranging based on powers of p-terms, we obtain
At p→1 we have
STDM Solution
Apply Shehu transform to (5.1),
Applying the Shehu transform differentiation property, we have
Using the Shehu inverse transform
STDM series form solution of φ(μ,η), ζ(μ,η) and ϕ(μ,η) are defined as:
Where the Adomian polynomials ζϕ=∑∞m=0Am, φϕ=∑∞m=0Bm and −6ϕϕμ+2φϕμ+2ζζμ=∑∞m=0Cm and the nonlinear terms have been characterised. Thus, Eq. (5.11) can be rewritten as
The nonlinear terms by means of Adomian polynomials is determined as,
On comparing both sides of Eq (5.12), we get
For m=0
For m=1
For m=2
The STDM remaining solution elements like ξm ζm and ϕm for (m≥3) are simply to calculate. Hence, we define the series form solution as follows:
6.
Result and discussion
This section explains the numerical solution to the time-fractional Schrödinger-KdV equation. Example 5.1 is graphical simulation is shown in Figure 1. Figure 1 is a graphical depiction of the solution acquired by the offered methods and the exact outcome of Example 5.1. Figure 2 depicts the results of proposed techniques with α=0.90 and α=0.80, respectively. Example 5.1 depicts the analysis to several fractional decimal places. Figure 3 depicts the reaction to the solution for various α values. The solution of Example 5.1 is depicted graphically in Figures 4 and 5. Figure 4 depicts the graphical simulations of the suggested methods' results for α=1 and the precise answer, while Figure 5 depicts the graphs for the solution of Example 5.1 for α=0.9 and α=0.8. Figure 6 depicts the graphical comparison for distinct α values, respectively.
7.
Conclusions
Using two novel methodologies, the solutions to several non-linear fractional Schrödinger-KdV equations are shown in this study. HPSTM and STDM are the most basic and uncomplicated approaches that can be utilized to solve FPDEs and associated systems successfully. The obtained results show that the suggested methods are reliable and that it may be applied to nonlinear coupled fractional evolution problems. They also show that the proposed methods are very efficient and powerful methodologies for obtaining nonlinear coupled time fractional differential equations solutions. The proposed methods key advantage is that it have less computing than other numerical and analytical approximate methods, resulting in a significant improvement in solving coupled fractional nonlinear equations over existing methods in the open literature. The suggested method's applications for solving the time fractional coupled Schrödinger-KdV equation demonstrate its simplicity, validity, and efficiency. As future work, we plan to extend the apply of HPSTM and STDM system to investigate higher dimensional physical applications. So, this indicates that the aforesaid approach is a remarkably and proper potent approach in achieving the analytical and approximate results of many linear and nonlinear fractional problems arising in engineering and applied physics.
Conflicts of interest
The authors declare that there are no conflicts of interest regarding the publication of this article.
Acknowledgment
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Research Groups Program under grant RGP.2/15/43. This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation, (grant number B05F650018).










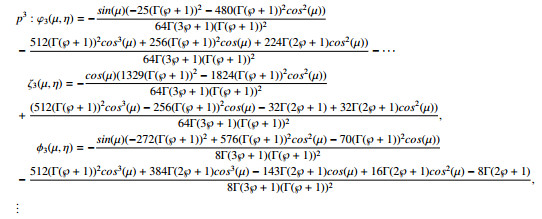
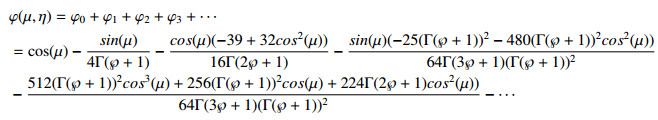
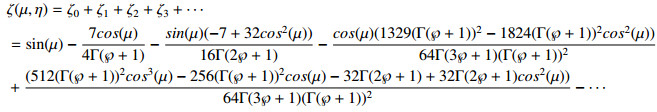
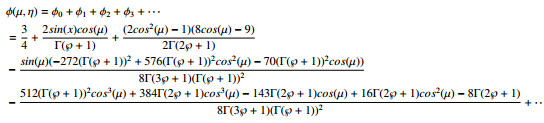
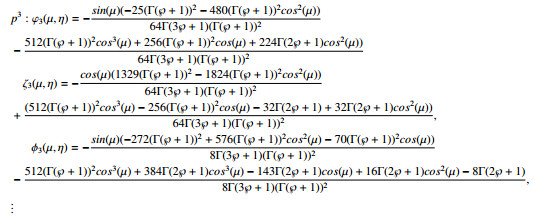

 DownLoad:
DownLoad:








