Extinction behavior for a parabolic $ p $-Laplacian equation with gradient source and singular potential

Dengming Liu; Luo Yang; Dengming Liu; Luo Yang

doi:10.3934/math.2022054

AIMS Mathematics

2022, Volume 7, Issue 1: 915-924. doi: 10.3934/math.2022054

Previous Article Next Article

Research article

Extinction behavior for a parabolic $p$ -Laplacian equation with gradient source and singular potential

Dengming Liu ^,,
Luo Yang

School of Mathematics and Computational Science, Hunan University of Science and Technology, Xiangtan, Hunan 411201, China

Received: 17 June 2021 Accepted: 11 October 2021 Published: 18 October 2021
MSC : 35K20, 35K55

We concern with the extinction behavior of the solution for a parabolic $p$ -Laplacian equation with gradient source and singular potential. By energy estimate approach, Hardy-Littlewood-Sobolev inequality, a series of ordinary differential inequalities, and super-solution and sub-solution methods, we obtain the conditions on the occurrence of the extinction phenomenon of the weak solution.

Keywords:

Citation: Dengming Liu, Luo Yang. Extinction behavior for a parabolic $p$ -Laplacian equation with gradient source and singular potential[J]. AIMS Mathematics, 2022, 7(1): 915-924. doi: 10.3934/math.2022054

Related Papers:

[1]	Aslı Alkan, Halil Anaç . The novel numerical solutions for time-fractional Fornberg-Whitham equation by using fractional natural transform decomposition method. AIMS Mathematics, 2024, 9(9): 25333-25359. doi: 10.3934/math.20241237
[2]	Hussain Gissy, Abdullah Ali H. Ahmadini, Ali H. Hakami . The travelling wave phenomena of the space-time fractional Whitham-Broer-Kaup equation. AIMS Mathematics, 2025, 10(2): 2492-2508. doi: 10.3934/math.2025116
[3]	Aslı Alkan, Halil Anaç . A new study on the Newell-Whitehead-Segel equation with Caputo-Fabrizio fractional derivative. AIMS Mathematics, 2024, 9(10): 27979-27997. doi: 10.3934/math.20241358
[4]	Qasem M. Tawhari . Advanced analytical techniques for fractional Schrödinger and Korteweg-de Vries equations. AIMS Mathematics, 2025, 10(5): 11708-11731. doi: 10.3934/math.2025530
[5]	M. Mossa Al-Sawalha, Osama Y. Ababneh, Rasool Shah, Amjad khan, Kamsing Nonlaopon . Numerical analysis of fractional-order Whitham-Broer-Kaup equations with non-singular kernel operators. AIMS Mathematics, 2023, 8(1): 2308-2336. doi: 10.3934/math.2023120
[6]	Faeza Lafta Hasan, Mohamed A. Abdoon, Rania Saadeh, Ahmad Qazza, Dalal Khalid Almutairi . Exploring analytical results for (2+1) dimensional breaking soliton equation and stochastic fractional Broer-Kaup system. AIMS Mathematics, 2024, 9(5): 11622-11643. doi: 10.3934/math.2024570
[7]	Musawa Yahya Almusawa, Hassan Almusawa . Numerical analysis of the fractional nonlinear waves of fifth-order KdV and Kawahara equations under Caputo operator. AIMS Mathematics, 2024, 9(11): 31898-31925. doi: 10.3934/math.20241533
[8]	Thongchai Botmart, Ravi P. Agarwal, Muhammed Naeem, Adnan Khan, Rasool Shah . On the solution of fractional modified Boussinesq and approximate long wave equations with non-singular kernel operators. AIMS Mathematics, 2022, 7(7): 12483-12513. doi: 10.3934/math.2022693
[9]	Mohammad Alqudah, Safyan Mukhtar, Albandari W. Alrowaily, Sherif. M. E. Ismaeel, S. A. El-Tantawy, Fazal Ghani . Breather patterns and other soliton dynamics in (2+1)-dimensional conformable Broer-Kaup-Kupershmit system. AIMS Mathematics, 2024, 9(6): 13712-13749. doi: 10.3934/math.2024669
[10]	Muhammad Farman, Ali Akgül, Kottakkaran Sooppy Nisar, Dilshad Ahmad, Aqeel Ahmad, Sarfaraz Kamangar, C Ahamed Saleel . Epidemiological analysis of fractional order COVID-19 model with Mittag-Leffler kernel. AIMS Mathematics, 2022, 7(1): 756-783. doi: 10.3934/math.2022046

Abstract

1. Introduction

The enrichment of day-to-day existence is the cornerstone of the environment and sentient creatures. Time is constantly a global autonomous factor in the cosmos, and eternity is often referred to as such. Furthermore, scholars are continuously in need of a technology that can assist them in describing the current phase and forecasting the development of many real-world occurrences ^{[1,2,3,4,5,6,7,8]}. In this way, renowned scholars and physicists like Newton and Leibniz separately suggested the method of calculus from their respective individual perspectives. Subsequently, several scholars and practitioners believed that a basic formula might be used to examine practically all theories on the planet rather than any other forms of resources or machines. However, numerous academics from different fields have previously confirmed that the idea of conventional calculus with differential and integral operators underestimates certain crucial and fascinating phenomena ^{[9,10,11,12,13,14,15]}. Others with inherent features, non-Markovian dynamics, and some others in general ^{[16,17,18,19,20]}. Besides that, analysts are indeed completely eager to describe and invent a conceptual technique to address many of the reported flaws.

Fractional calculus (FC) was developed shortly after conventional calculus, but numerous scientists and researchers are now considering the conception and ideas of FC to explain essence in a comprehensive way, especially following the revelation of conventional calculus' restrictions. Various researchers established and cultivated the key foundation ^{[21,22,23,24]} with the help of innovative characteristics and associated ramifications for FC. A special function theory is used to construct novel fractional formulations. Many academics have employed these operators to analyze and illustrate multiple systems and difficulties connected to intriguing behaviours ^{[25,26,27,28]}. In 2016, Atangana and Baleanu suggested a revolutionary operator that overcomes all of the restrictions of the prespecified interpreters using the Mittag-Leffler function ^[29].

Partial differential equations (PDEs) with non-linearities are used to represent a number of scenarios in physical science and engineering, extending from magnetism to complexities. Spatial PDEs are frequently employed in domains including nano-science, bio-engineering, epidemiology, and hydrodynamics to simulate dynamic behaviour events. Fractional-order PDEs have subsequently sparked considerable interest due to their broad implications in a variety of scientific disciplines, including optimization, image reformation, decision theory, signal transmission, remote sensing and network recognition, and hydrodynamics ^{[30,31,32,33]}. Because most design procedures are recognized to be complex, finding a numerical or approximate result is extremely challenging. The most complex strategies can be represented using an adequate collection of PDEs. A considerable effort has gone into inventing a convergent approach that is both convenient and simple. The new iterative method (NIM) ^[34], homotopy analysis method (HAM) ^[35], Lie symmetry analysis (LSA) ^[36], and Laguerre wavelets collocation method (LWCM) ^[37], residue power series method (RPSM) ^[33] are just a few of the latest estimated strategies for getting realistic findings for complex PDEs.

Whitham-Broer-Kaup equations (WBKEs) ^[38] were discovered to characterize the dynamic characteristics of waves that propagate in hydrodynamics. Whitham, Broer, and Kaup ^[39,40,41] established the coupled strategy for the aforementioned model. This formula describes the dispersion of superficial ripples of liquid with a specified permeation family. The classical form of WBKE is presented as follows:

$\begin{eqnarray} &&\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \bar{\mathbf{t}}}+\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\bar{g}\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} = 0, \\&& \frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \bar{\mathbf{t}}}+\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\bar{p}\frac{\partial^{3}\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\bar{g}\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}} = 0, \end{eqnarray}$

(1.1)

where $\bar{p}$ and $\bar{g}$ are constants stated in distinct dispersion energies, correspondingly, and $\Phi(\varkappa, \bar{\mathbf{t}})$ is the linear speed, and $\Psi(\varkappa, \bar{\mathbf{t}})$ is the altitude that detracts from the fluid equilibrium condition, respectively. Exploration of complex PDE systems has been a significant subject of concern ^[42,43,44] in past times. Intellectuals have devised a slew of ways to investigate the analytical solutions to nonlinear PDEs. Authors ^[45] have employed the homotopy perturbation method to solve WBKE. Ray ^[46] obtained the travelling wave solution of WBKE. Tian ^[47] provides exact and explicit WBKE solutions in shallow water. Veeresha et al. ^[48] stimulated efficient technique for coupled fractional WBKE describes the propagation of shallow water waves.

Furthermore, $\bar{\mathbf{q}}$ -HATM is taken into account, as was proposed by Singh et al. ^[49]. This method, which is the combination of a conventional method termed HAM (developed by Liao with the help of the basic notion of topology ^[50,51]) and the Aboodh transform ^[52] is employed in this model. The enhanced methodology is presented to solve the shortcomings of the traditional approach, such as large calculation, effectiveness, primary storage, and others. Furthermore, HAM does not necessitate additional convolutions, instabilities, hypotheses, or physical component assessment. As a result, the predicted approach does not demand the aforementioned prerequisites, and it provides various features that may be used to change and regulate the convergence region, as well as increase the reliability of the generated result. Numerous authors state that the proposed framework approach has been implemented in several real-world simulations and situations that encompass various processes ^[53,54,55]. The investigation employed recently developed fractional operators and methods to evaluate a system of nonlinear complex systems that describes significant behaviors.

In the upcoming sections, we shall go over several of the fundamentals briefly. Sections 3 and 4 describe the basic response process and its relevance to the analyzed system, respectively. The key findings for the investigated interacting mechanism are obtained in Section 5, the consistently highlighted are numerically illustrated in Section 6, and we end with several comments on the acquired outcomes in the last portion of Section 7.

2. Preliminaries

In this part, we revisit certain key concepts, ideas, and terminologies connected to fractional derivative formulations involving power law and ML as a kernel, as well as the Aboodh transform's specific ramifications.

Definition 2.1. (^[23]) The fractional derivative of Caputo (CFD) is specifically defined as:

$\begin{eqnarray} \, _{0}^{c}\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\mathbf{f}(\bar{\mathbf{t}}) = \begin{cases} \frac{1}{\Gamma(r-\delta)}\int\limits_{0}^{\bar{\mathbf{t}}}\frac{\mathbf{f}^{(r)}(\varkappa_{1})}{(\bar{\mathbf{t}}-\varkappa_{1})^{\delta+1-r}}d\varkappa_{1}, \; \; r-1 < \delta < r, \\ \frac{d^{r}}{d\bar{\mathbf{t}}^{r}}\mathbf{f}(\bar{\mathbf{t}}), \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \delta = r. \end{cases} \end{eqnarray}$

(2.1)

Definition 2.2. (^[29]) The $ABC$ derivative operator is specifically defined as:

$\begin{eqnarray} \, _{a_{1}}^{ABC}\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\big(\mathbf{f}(\bar{\mathbf{t}})\big) = \frac{\mathbb{N}(\delta)}{1-\delta}\int\limits_{a_{1}}^{\bar{\mathbf{t}}}\mathbf{f}^{\prime}(\bar{\mathbf{t}})E_{\delta}\Big[-\frac{\delta(\bar{\mathbf{t}}-\varkappa_{1})^{\delta}}{1-\delta}\Big]d\varkappa_{1}, \end{eqnarray}$

(2.2)

where $\mathbf{f}\in H^{1}(a_{1}, a_{2}) (Sobolev \; space), \; a_{1} < a_{2}, \delta\in[0, 1]$ and $\mathbb{N}(\delta)$ indicates normalization function as $\mathbb{N}(\delta) = \mathbb{N}(0) = \mathbb{N}(1) = 1.$

Definition 2.3. (^[29]) The $ABC$ fractional integral operator is expressed in the form:

$\begin{eqnarray} \, _{a_{1}}^{ABC}\bar{I}_{\bar{\mathbf{t}}}^{\delta}\big(\mathbf{f}(\bar{\mathbf{t}})\big) = \frac{1-\delta}{\mathbb{N}(\delta)}\mathbf{f}(\bar{\mathbf{t}})+\frac{\delta}{\Gamma(\delta)\mathbb{N}(\delta)}\int\limits_{a_{1}}^{\bar{\mathbf{t}}}\mathbf{f}(\varkappa_{1})(\bar{\mathbf{t}}-\varkappa_{1})^{\delta-1}d\varkappa_{1}. \end{eqnarray}$

(2.3)

Definition 2.4. (^[52]) Aboodh transform for mapping $\mathbf{f}(\bar{\mathbf{t}})$ of exponential order over the set of functions is defined as

$\begin{eqnarray} \mathcal{P} = \Big\{\mathbf{f}:\big\vert\mathbf{f}(\bar{\mathbf{t}})\big\vert < B\exp(p_{\jmath}\vert \bar{\mathbf{t}}\vert), \; if\; \bar{\mathbf{t}}\in(-1)^{\jmath}\times[0, \infty), \; \jmath = 1, 2;\; (B, p_{1}, p_{2} > 0)\Big\} \end{eqnarray}$

(2.4)

is expressed as

$\begin{eqnarray} \mathcal{A}[\mathbf{f}(\bar{\mathbf{t}})] = \mathbf{F}(\omega) \end{eqnarray}$

(2.5)

is described as

$\begin{eqnarray} \mathcal{A}[\mathbf{f}(\bar{\mathbf{t}})] = \frac{1}{\omega}\int\limits_{0}^{\infty}\mathbf{f}(\bar{\mathbf{t}})\exp(-\omega \bar{\mathbf{t}})d\bar{\mathbf{t}}, \; \; p_{1}\leq \omega\leq p_{2}. \end{eqnarray}$

(2.6)

Definition 2.5. ^[56] The following is the Aboodh transform of CFD operator:

$\begin{eqnarray} \mathcal{A}\Big\{\, _{0}^{c}\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\big(\mathbf{f}(\bar{\mathbf{t}})\big), \bar{\mathbf{t}}\Big\} = \omega^{\delta}\mathbf{F}(\omega)-\sum\limits_{\kappa = 0}^{\mathbf{n}-1}\frac{\mathbf{f}^{(\kappa)}(0)}{\omega^{2-\delta+\kappa}}, \; \; \mathbf{n}-1 < \delta < \mathbf{n}, \; \mathbf{n}\in\mathbb{N}. \end{eqnarray}$

(2.7)

Definition 2.6. (^[57]) The $ABC$ fractional derivative operator has the following Aboodh transform:

$\begin{eqnarray} \mathcal{A}\Big\{\, _{0}^{ABC}\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\big(\mathbf{f}(\bar{\mathbf{t}})\big), \bar{\mathbf{t}}\Big\}(\delta) = \frac{\mathbb{N}(\delta)(\mathbf{F}(\omega)-\omega^{-2}\mathbf{f}(0))}{1-\delta+\delta \omega^{-\delta}}. \end{eqnarray}$

(2.8)

Definition 2.7. (^[58])The ML function for single parameter is defined as

$\begin{eqnarray} E_{\delta}(z) = \sum\limits_{\kappa = 0}^{\infty}\frac{z_{1}^{\kappa}}{\Gamma(\kappa\delta+1)}, \; \; \delta, z_{1}\in\mathbb{C}, \; \Re(\delta)\geq0. \end{eqnarray}$

(2.9)

3. Road map of $\bar{\mathbf{q}}$ -homotopy analysis transform method

The methodology of the proposed approach is presented using Caputo and Atangana-Baleanu fractional derivatives for the model (1.1) of arbitrary order. Here, we surmise a fractional order nonlinear system of the type:

Case I. (Caputo fractional derivative operator)

$\begin{eqnarray} \, _{a_{1}}^{c}\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\Phi(\varkappa, \bar{\mathbf{t}})+\mathfrak{R}\Phi(\varkappa, \bar{\mathbf{t}})+\mathfrak{N}\Phi(\varkappa, \bar{\mathbf{t}}) = \mathcal{F}(\varkappa, \bar{\mathbf{t}}), \; \; \mathbf{n}-1 < \delta\leq \mathbf{n}, \end{eqnarray}$

(3.1)

supplemented with the initial conditions (ICs)

$\begin{eqnarray} \Phi(\varkappa, 0) = \Phi_{0}(\varkappa), \end{eqnarray}$

(3.2)

where $\, _{a_{1}}^{c}\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}$ indicates the Caputo derivative of $\Phi(\varkappa, \bar{\mathbf{t}}).$

In view of the differentiation rule of Aboodh transform on (3.1), we obtain

$\begin{eqnarray} \omega^{\delta}\mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})]-\sum\limits_{\kappa = 0}^{\mathbf{n}-1}\frac{\Phi^{(\kappa)}(\varkappa, 0)}{\omega^{2-\delta+\kappa}}+\mathcal{A}\big[\mathfrak{R}\Phi(\varkappa, \bar{\mathbf{t}})+\mathfrak{N}\Phi(\varkappa, \bar{\mathbf{t}})\big] = \mathcal{A}\big[\mathcal{F}(\varkappa, \bar{\mathbf{t}})\big]. \end{eqnarray}$

(3.3)

After simplification, we have

$\begin{eqnarray} \mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})]-\frac{1}{\omega^{\delta}}\sum\limits_{\kappa = 0}^{\mathbf{n}-1}\frac{\Phi^{(\kappa)}(\varkappa, 0)}{\omega^{2-\delta+\kappa}}+\mathcal{A}\big[\mathfrak{R}\Phi(\varkappa, \bar{\mathbf{t}})+\mathfrak{N}\Phi(\varkappa, \bar{\mathbf{t}})\big] = \frac{1}{\omega^{\delta}}\mathcal{A}\big[\mathcal{F}(\varkappa, \bar{\mathbf{t}})\big]. \end{eqnarray}$

(3.4)

The non-linearity factor can be described as

$\begin{eqnarray} \mathfrak{N}\big[\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]&& = \mathcal{A}\big[\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]-\frac{1}{\omega^{\delta}}\sum\limits_{\kappa = 0}^{\mathbf{n}-1}\frac{\Phi^{(\kappa)}(\varkappa, 0)}{\omega^{2-\delta+\kappa}}+\frac{1}{\omega^{\delta}}\mathcal{A}\big[\mathfrak{R}\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]+\frac{1}{\omega^{\delta}}\mathcal{A}\big[\mathfrak{N}\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]\\&&\quad-\frac{1}{\omega^{\delta}}\mathcal{A}\big[\mathcal{F}(\varkappa, \bar{\mathbf{t}})\big], \end{eqnarray}$

(3.5)

where $\bar{\mathbf{q}}\in[0, 1/\mathbf{n}].$ Then, we demonstrate the non-zero auxiliary and embedding factor $\hbar,$ and $\bar{\mathbf{q}},$ respectively, by the classical approach as below

$\begin{eqnarray} (1-\mathbf{n}\bar{\mathbf{q}})\mathcal{A}\big[\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})-\Phi_{0}(\varkappa, \bar{\mathbf{t}})\big] = \hbar \bar{\mathbf{q}}\mathcal{H}(\varkappa, \bar{\mathbf{t}})\mathfrak{N}\big[\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big], \end{eqnarray}$

(3.6)

where $\mathcal{A}$ symbolize Aboodh transform, $\mathcal{H}(\varkappa, \bar{\mathbf{t}})$ represents the nonzero auxiliary mapping and $\varphi(\varkappa, \bar{\mathbf{t}}; \bar{\mathbf{q}})$ is an unknown mapping. Also, $\Phi_{0}(\varkappa, \bar{\mathbf{t}})$ is the IC of $\Phi(\varkappa, \bar{\mathbf{t}}).$

Furthermore, for $\bar{\mathbf{q}} = 0$ and $\bar{\mathbf{q}} = 1/\mathbf{n}$ , then the subsequent assumptions hold true

$\begin{eqnarray} \varphi(\varkappa, \bar{\mathbf{t}};0) = \Phi_{0}(\varkappa, \bar{\mathbf{t}}), \; \; \; \; \; \; \; \; \; \varphi\Big(\varkappa, \bar{\mathbf{t}};\frac{1}{\mathbf{n}}\Big) = \Phi(\varkappa, \bar{\mathbf{t}}). \end{eqnarray}$

(3.7)

Consequently, by amplifying $\bar{\mathbf{q}}$ from $0$ to $1/\mathbf{n},$ the solution $\varphi(\varkappa, \bar{\mathbf{t}}; \bar{\mathbf{q}})$ tends from $\Phi_{0}(\varkappa, \bar{\mathbf{t}})$ to the result $\Phi(\varkappa, \bar{\mathbf{t}}).$ Develop the mapping $\varphi(\varkappa, \bar{\mathbf{t}}; \bar{\mathbf{q}})$ in sequence form with the aid of Taylor theorem, one can achieve close to $\bar{\mathbf{q}}$ as

$\begin{eqnarray} \varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}}) = \Phi_{0}(\varkappa, \bar{\mathbf{t}})+\sum\limits_{\mathbf{r} = 1}^{\infty}\Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})\bar{\mathbf{q}}^{\mathbf{r}}, \end{eqnarray}$

(3.8)

where

$\begin{eqnarray} \Phi_{0}(\varkappa, \bar{\mathbf{t}}) = \frac{1}{\mathbf{r}!}\frac{\partial^{\mathbf{r}}\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})}{\partial \bar{\mathbf{q}}^{\mathbf{r}}}\Big\vert_{\bar{\mathbf{q}} = 0}. \end{eqnarray}$

(3.9)

With the aid of supplementary linear operator, $\Phi_{0}(\varkappa, \bar{\mathbf{t}}), \; \mathbf{n}, \; \hbar,$ then the (3.9) approaches at $\bar{\mathbf{q}} = 1/\mathbf{n}$ and it yields a solution of (3.3), so we have

$\begin{eqnarray} \Phi(\varkappa, \bar{\mathbf{t}}) = \Phi_{0}(\varkappa, \bar{\mathbf{t}})+\sum\limits_{\mathbf{r} = 0}^{\infty}\Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})\Big(\frac{1}{\mathbf{n}}\Big)^{\mathbf{r}}. \end{eqnarray}$

(3.10)

The $\mathbf{r}$ -times differentiation of (3.7) considering $\bar{\mathbf{q}}$ and dividing by $\mathbf{r}!,$ later on substituting $\bar{\mathbf{q}} = 0,$ we have

$\begin{eqnarray} \mathcal{A}\big[\Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})-\mathcal{K}_{\mathbf{r}}\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})\big] = \hbar\mathcal{R}_{\mathbf{r}}(\overrightarrow{\Phi}_{\mathbf{r}-1}), \end{eqnarray}$

(3.11)

where the vectors are presented as follows:

$\begin{eqnarray} \overrightarrow{\Phi}_{\mathbf{r}} = \big[\Phi_{0}(\varkappa, \bar{\mathbf{t}})+\Phi_{1}(\varkappa, \bar{\mathbf{t}})+....+\Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})\big]. \end{eqnarray}$

(3.12)

Employing the inverse Aboodh transform on (3.12), yields

$\begin{eqnarray} \Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}}) = \mathcal{K}_{\mathbf{r}}\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\big[\mathcal{R}_{\mathbf{r}}(\overrightarrow{\Phi}_{\mathbf{r}-1})\big], \end{eqnarray}$

(3.13)

where

$\mathcal{R}_{\mathbf{r}}(\overrightarrow{\Phi}_{\mathbf{r}-1}) = \mathcal{A}\big[\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})\big]-\Big(1-\frac{\mathcal{K}_{\mathbf{r}}}{\mathbf{n}}\Big)\bigg(\sum\limits_{\kappa = 0}^{\mathbf{n}-1}\frac{\Phi^{(\kappa)}(\varkappa, 0)}{\omega^{2-\delta+\kappa}}+\frac{1}{\omega^{\delta}}\mathcal{A}\big[\mathcal{F}(\varkappa, \bar{\mathbf{t}})\big]\bigg)\\ +\frac{1}{\omega^{\delta}}\mathcal{A}\big[\mathcal{R}({\Phi}_{\mathbf{r}-1}+\mathcal{H}_{\mathbf{r}-1})\big],$

(3.14)

and

$\begin{eqnarray} \kappa_{\mathbf{r}} = \begin{cases} 0, \; \; \; \; \mathbf{r}\leq1\\ 1, \; \; \; \; \mathbf{r} > 1. \end{cases} \end{eqnarray}$

(3.15)

In (3.33), $\mathcal{H}_{\mathbf{r}}$ indicates the homotopy polynomial and is described as

$\begin{eqnarray} \mathcal{H}_{\mathbf{r}} = \Phi_{0}(\varkappa, \bar{\mathbf{t}}) = \frac{1}{\mathbf{r}!}\frac{\partial^{\mathbf{r}}\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})}{\partial \bar{\mathbf{q}}^{\mathbf{r}}}\Big\vert_{\bar{\mathbf{q}} = 0} \end{eqnarray}$

(3.16)

and

$\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}}) = \varphi_{0}+\bar{\mathbf{q}}\varphi_{1}+q^{2}\varphi_{2}+...\; .$

Combining (3.14) and (3.16), we have

$\begin{eqnarray} \Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})&& = (\kappa_{\mathbf{r}}+\hbar)\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})-\Big(1-\frac{\kappa_{\mathbf{r}}}{\mathbf{n}}\Big)\mathcal{A}^{-1}\bigg(\sum\limits_{\kappa = 0}^{\mathbf{n}-1}\frac{\Phi^{(\kappa)}(\varkappa, 0)}{\omega^{2-\delta+\kappa}}+\frac{1}{\omega^{\delta}}\mathcal{A}\big[\mathcal{F}(\varkappa, \bar{\mathbf{t}})\big]\bigg)\\&&\quad+\hbar\mathcal{A}^{-1}\bigg(\frac{1}{\omega^{\delta}}\mathcal{A}\big[\mathcal{R}({\Phi}_{\mathbf{r}-1}+\mathcal{H}_{\mathbf{r}-1})\big]\bigg). \end{eqnarray}$

(3.17)

The series solution by $\bar{\mathbf{q}}$ -HATM is expressed as

$\begin{eqnarray} \Phi(\varkappa, \bar{\mathbf{t}}) = \sum\limits_{\mathbf{r} = 0}^{\infty}\Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}}). \end{eqnarray}$

(3.18)

Case II. (ABC fractional derivative operator)

$\begin{eqnarray} \, _{a_{1}}^{ABC}\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\Phi(\varkappa, \bar{\mathbf{t}})+\mathfrak{R}\Phi(\varkappa, \bar{\mathbf{t}})+\mathfrak{N}\Phi(\varkappa, \bar{\mathbf{t}}) = \mathcal{F}(\varkappa, \bar{\mathbf{t}}), \; \; \mathbf{n}-1 < \delta\leq \mathbf{n}, \end{eqnarray}$

(3.19)

supplemented with the initial conditions (ICs)

$\begin{eqnarray} \Phi(\varkappa, 0) = \Phi_{0}(\varkappa), \end{eqnarray}$

(3.20)

where $\, _{a_{1}}^{ABC}\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}$ indicates the AB fractional derivative in the Caputo sense of $\Phi(\varkappa, \bar{\mathbf{t}}).$

In view of the differentiation rule of Aboodh transform on (3.19), we obtain

$\frac{\omega^{\delta}\mathbb{N}(\delta)}{\delta+(1-\delta) \omega^{\delta}}\mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})]-\frac{\delta+(1-\delta) \omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\frac{\Phi(\varkappa, 0)}{\omega^{2}}+\mathcal{A}\big[\mathfrak{R}\Phi(\varkappa, \bar{\mathbf{t}})+\mathfrak{N}\Phi(\varkappa, \bar{\mathbf{t}})\big] \\ = \mathcal{A}\big[\mathcal{F}(\varkappa, \bar{\mathbf{t}})\big].$

(3.21)

After simplification, we have

$\mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})]-\frac{1}{\omega^{2}}\Phi(\varkappa, 0)+\frac{\delta+(1-\delta) \omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\big[\mathfrak{R}\Phi(\varkappa, \bar{\mathbf{t}})+\mathfrak{N}\Phi(\varkappa, \bar{\mathbf{t}})\big] \\ = \frac{\delta+(1-\delta) \omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\big[\mathcal{F}(\varkappa, \bar{\mathbf{t}})\big].$

(3.22)

The non-linearity factor can be described as

$\mathfrak{N}\big[\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big] = \mathcal{A}\big[\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]-\frac{\Phi(\varkappa, 0)}{\omega^{2}}+\frac{\delta+(1-\delta) \omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\big[\mathfrak{R}\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]+\\ \frac{\delta+(1-\delta) \omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\big[\mathfrak{N}\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]\\ -\frac{\delta+(1-\delta) \omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\big[\mathcal{F}(\varkappa, \bar{\mathbf{t}})\big],$

(3.23)

where $\bar{\mathbf{q}}\in[0, 1/\mathbf{n}].$ Then, we demonstrate the non-zero auxiliary and embedding factor $\hbar,$ and $\bar{\mathbf{q}},$ respectively, by the classical approach as below

(3.24)

Furthermore, for $\bar{\mathbf{q}} = 0$ and $\bar{\mathbf{q}} = 1/\mathbf{n}$ , then the subsequent assumptions hold true

(3.25)

(3.26)

where

(3.27)

With the aid of supplementary linear operator, $\Phi_{0}(\varkappa, \bar{\mathbf{t}}), \; \mathbf{n}, \; \hbar,$ then the (3.27) approaches at $\bar{\mathbf{q}} = 1/\mathbf{n}$ and it yields a solution of (3.23), so we have

(3.28)

The $\mathbf{r}$ -times differentiation of (3.25) considering $\bar{\mathbf{q}}$ and dividing by $\mathbf{r}!,$ later on substituting $\bar{\mathbf{q}} = 0,$ we have

(3.29)

where the vectors are presented as follows:

(3.30)

Employing the inverse Aboodh transform on (3.30), yields

(3.31)

where

$\begin{eqnarray} \mathcal{R}_{\mathbf{r}}(\overrightarrow{\Phi}_{\mathbf{r}-1})&& = \mathcal{A}\big[\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})\big]-\Big(1-\frac{\mathcal{K}_{\mathbf{r}}}{\mathbf{n}}\Big)\bigg(\frac{\Phi(\varkappa, 0)}{\omega^{2}}+\frac{\delta+(1-\delta) \omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\big[\mathcal{F}(\varkappa, \bar{\mathbf{t}})\big]\bigg)\\&&\quad+\frac{\delta+(1-\delta) \omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\big[\mathcal{R}({\Phi}_{\mathbf{r}-1}+\mathcal{H}_{\mathbf{r}-1})\big], \end{eqnarray}$

(3.32)

and

$\begin{eqnarray} \kappa_{\mathbf{r}} = \begin{cases} 0, \; \; \; \; \mathbf{r}\leq1\\ 1, \; \; \; \; \mathbf{r} > 1. \end{cases} \end{eqnarray}$

(3.33)

In (3.33), $\mathcal{H}_{\mathbf{r}}$ indicates the homotopy polynomial and is described as

(3.34)

and

$\varphi(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}}) = \varphi_{0}+\bar{\mathbf{q}}\varphi_{1}+q^{2}\varphi_{2}+...\; .$

Combining (3.32) and (3.34), we have

$\begin{eqnarray} \Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})&& = (\kappa_{\mathbf{r}}+\hbar)\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})-\Big(1-\frac{\kappa_{\mathbf{r}}}{\mathbf{n}}\Big)\mathcal{A}^{-1}\bigg(\frac{\Phi(\varkappa, 0)}{\omega^{2}}+\frac{\delta+(1-\delta) \omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\big[\mathcal{F}(\varkappa, \bar{\mathbf{t}})\big]\bigg)\\&&\quad+\hbar\mathcal{A}^{-1}\bigg(\frac{\delta+(1-\delta) \omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\big[\mathcal{R}({\Phi}_{\mathbf{r}-1}+\mathcal{H}_{\mathbf{r}-1})\big]\bigg). \end{eqnarray}$

(3.35)

The series solution by $\bar{\mathbf{q}}$ -HATM is expressed as

(3.36)

Theorem 3.1. (Convergence of the series solutions) Suppose $\Phi_{\mathbf{n}}(\varkappa, \bar{\mathbf{t}})$ and $\Phi(\varkappa, \bar{\mathbf{t}})$ are defined in the Banach space $(\mathfrak{B}[0, \mathbf{T}], \|.\|).$ The series solution defined in $(3.18)$ converges to the solution of the $(3.1)$ , if $\lambda\in(0, 1).$

Proof. Consider the sequence $\{S_{\mathbf{n}}\}$ , which is the partial sum of the (3.18), and we have to prove $\{S_{\mathbf{n}}\}$ is the Cauchy sequence in $(\mathfrak{B}[0, \mathbf{T}], \|.\|).$ Now consider

$\begin{eqnarray*} \big\|S_{\mathbf{n}+1}(\varkappa, \bar{\mathbf{t}})-S_{\mathbf{n}}(\varkappa, \bar{\mathbf{t}})\big\|&& = \big\|\Phi_{\mathbf{n}+1}(\varkappa, \bar{\mathbf{t}})\big\|\nonumber\\&&\leq\lambda\big\|\Phi_{\mathbf{n}}(\varkappa, \bar{\mathbf{t}})\big\| \nonumber\\&&\leq\lambda^{2}\big\|\Phi_{\mathbf{n}-1}(\varkappa, \bar{\mathbf{t}})\big\|\leq...\leq\lambda^{\mathbf{n}}\big\|\Phi_{0}(\varkappa, \bar{\mathbf{t}})\big\|. \end{eqnarray*}$

Now, for every $\mathbf{n}, \mathbf{m}\in\mathbb{N}\; (\mathbf{m}\leq\mathbf{n})$

$\begin{eqnarray*} \big\|S_{\mathbf{n}}-S_{\mathbf{m}}\big\|&& = \big\|(S_{\mathbf{n}}-S_{\mathbf{n}-1})+(S_{\mathbf{n}-1}-S_{\mathbf{n}-2})+...+(S_{\mathbf{m}+1}-S_{\mathbf{m}})\big\|\nonumber\\&&\leq\big\|S_{\mathbf{n}}-S_{\mathbf{n}-1}\big\|+\big\|S_{\mathbf{n}-1}-S_{\mathbf{n}-2}\big\|+...+\big\|S_{\mathbf{m}+1}-S_{\mathbf{m}}\big\|\nonumber\\&&\leq(\lambda^{\mathbf{n}}+\lambda^{\mathbf{n}-1}+...\lambda^{\mathbf{m}+1})\big\|\Phi_{0}\big\|\nonumber\\&&\leq\lambda^{\mathbf{m}+1}(\lambda^{\mathbf{n}-\mathbf{m}-1}+\lambda^{\mathbf{n}-\mathbf{m}-2}+...+\lambda+1)\big\|\Phi_{0}\big\|\nonumber\\&&\leq\lambda^{\mathbf{m}+1}\Big(\frac{1-\lambda^{\mathbf{n}-\mathbf{m}}}{1-\lambda}\Big)\big\|\Phi_{0}\big\|. \end{eqnarray*}$

Since $0 < \lambda < 1,$ therefore $\big\|S_{\mathbf{n}}-S_{\mathbf{m}}\big\| = 0.$ Thus $\{S\}_{\mathbf{n}}$ is the Cauchy sequence. This completes the proof.

4. Test examples

Example 4.1. Surmise that the fractional-order WBKEs is presented as follows:

$\begin{eqnarray} &&\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\Phi(\varkappa, \bar{\mathbf{t}})+\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} = 0, \; \; 0 < \delta\leq1, \\&& \mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\Psi(\varkappa, \bar{\mathbf{t}})+\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+3\frac{\partial^{3}\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}} = 0, \end{eqnarray}$

(4.1)

supplemented with ICs

$\begin{eqnarray} &&\Phi(\varkappa, 0) = \frac{1}{2}-8\tanh(-2\varkappa), \\&&\Psi(\varkappa, 0) = 16-16\tanh^{2}(-2\varkappa). \end{eqnarray}$

(4.2)

Proof. Primarily, we demonstrate how to solve (4.1) in two different scenarios.

Case I: Initially, we employ the Caputo fractional derivative operator considered with the Aboodh transform and $\bar{q}$ -HATM.

Employing the Aboodh transform on (4.1), we have

$\begin{eqnarray} &&\mathcal{A}\big[\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\Phi(\varkappa, \bar{\mathbf{t}})\big] = -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg], \\&& \mathcal{A}\big[\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\Psi(\varkappa, \bar{\mathbf{t}})\big] = -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+3\frac{\partial^{3}\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg]. \end{eqnarray}$

(4.3)

It follows that

$\omega^{\delta}\mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})]-\sum\limits_{\kappa = 0}^{\mathbf{n}-1}\frac{\Phi^{(\kappa)}(\varkappa, 0)}{\omega^{2-\delta+\kappa}} = -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg], \\ \omega^{\delta}\mathcal{A}[\Psi(\varkappa, \bar{\mathbf{t}})]-\sum\limits_{\kappa = 0}^{\mathbf{n}-1}\frac{\Psi^{(\kappa)}(\varkappa, 0)}{\omega^{2-\delta+\kappa}} = -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+3\frac{\partial^{3}\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}\\ -\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg].$

(4.4)

Therefore, we have

$\mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})] = \frac{1}{\omega^{2}}\Phi(\varkappa, 0)-\frac{1}{\omega^{\delta}}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg], \\ \mathcal{A}[\Psi(\varkappa, \bar{\mathbf{t}})] = \frac{1}{\omega^{2}}\Psi(\varkappa, 0)-\frac{1}{\omega^{\delta}}\mathcal{A}\\ \bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+3\frac{\partial^{3}\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg].$

(4.5)

With the aid of (4.5), the non-linearity can be expressed as

$\begin{eqnarray} &&\mathcal{N}_{1}\big[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}}), \varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]\\&& = \mathcal{A}\Bigg[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})-\frac{1}{\omega^{2}}\varphi_{1}(\varkappa, 0)+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg]\Bigg], \\&& \mathcal{N}_{2}\big[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}}), \varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]\\&& = \mathcal{A}\Bigg[\varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})-\frac{1}{\omega^{2}}\varphi_{2}(\varkappa, 0)+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\\&&\quad+3\frac{\partial^{3}\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg]\Bigg].\\ \end{eqnarray}$

(4.6)

Utilizing the methodology described in Section 3, the $\mathbf{r}$ th order deformation equation is described as

$\begin{eqnarray} \mathcal{A}\big[\Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})-\mathcal{K}_{\mathbf{r}}\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})\big] = \hbar\mathcal{R}_{1, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big], \end{eqnarray}$

(4.7)

where

$\begin{eqnarray} \mathcal{R}_{1, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big]&& = \mathcal{A}\Bigg[\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})-\Big(1-\frac{\kappa_{\mathbf{r}}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(\frac{1}{2}-8\tanh(-2\varkappa)\big)\Big)\\&&\quad+\frac{1}{\omega^{\delta}}\bigg\{\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Phi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}+\frac{\partial\Phi_{\mathbf{r}-1}}{\partial \varkappa}+\frac{\partial\Psi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}\bigg\}\Bigg], \\\mathcal{R}_{2, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big]&& = \mathcal{A}\Bigg[\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})-\Big(1-\frac{\kappa_{\mathbf{r}}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(16-16\tanh^{2}(-2\varkappa)\big)\Big)\\&&\quad+\frac{1}{\omega^{\delta}}\bigg\{\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Phi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}+\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Psi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{\mathbf{r}-\jmath-1}}{\partial \varkappa}\\&&\quad+3\frac{\partial^{3}\Phi_{\mathbf{r}-1-\jmath}}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi_{\mathbf{r}-1-\jmath}}{\partial \varkappa^{2}}\bigg\}\Bigg].\\ \end{eqnarray}$

(4.8)

Thanks to the inverse Aboodh transform, we attain

$\begin{eqnarray} &&\Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}}) = \mathcal{K}_{\mathbf{r}}\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\mathcal{R}_{1, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big], \\&&\Psi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}}) = \mathcal{K}_{\mathbf{r}}\Psi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\mathcal{R}_{2, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big]. \end{eqnarray}$

(4.9)

In view of ICs, we have

$\begin{eqnarray} &&\Phi_{0}(\varkappa, \bar{\mathbf{t}}) = \frac{1}{2}-8\tanh(-2\varkappa), \\&&\Psi_{0}(\varkappa, \bar{\mathbf{t}}) = 16-16\tanh^{2}(-2\varkappa). \end{eqnarray}$

(4.10)

In order to obtain $\Phi_{0}(\varkappa, \bar{\mathbf{t}})$ and $\Psi_{0}(\varkappa, \bar{\mathbf{t}}),$ choosing $\mathbf{r} = 1$ in (4.8), then we acquire

$\begin{eqnarray} &&\Phi_{1}(\varkappa, \bar{\mathbf{t}}) = \mathcal{K}_{1}\Phi_{0}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\mathcal{R}_{1, 1}\big[\overrightarrow{\Phi}_{0}, \overrightarrow{\Psi}_{0}\big], \\&&\Psi_{1}(\varkappa, \bar{\mathbf{t}}) = \mathcal{K}_{1}\Psi_{0}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\mathcal{R}_{2, 1}\big[\overrightarrow{\Phi}_{0}, \overrightarrow{\Psi}_{0}\big]. \end{eqnarray}$

(4.11)

For $\mathbf{r} = 1,$ then (4.8) diminish to

$\mathcal{R}_{1, 1}\big[\overrightarrow{\Phi}_{0}, \overrightarrow{\Psi}_{0}\big] = \mathcal{A}\big[\Phi_{0}(\varkappa, \bar{\mathbf{t}})\big]-\Big(1-\frac{\kappa_{1}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\frac{1}{2}-8\tanh(-2\varkappa)\Big)\\\quad+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}, \\ \mathcal{R}_{2, 1}\big[\overrightarrow{\Phi}_{0}, \overrightarrow{\Psi}_{0}\big] = \mathcal{A}\big[\Psi_{0}(\varkappa, \bar{\mathbf{t}})\big]-\Big(1-\frac{\kappa_{1}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(16-16\tanh^{2}(-2\varkappa)\big)\\\quad+\frac{1}{\omega^{\delta}}\mathcal{A}\\ \bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+3\frac{\partial^{3}\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}.\\$

(4.12)

Plugging (3.33) and (4.12) in (4.11), then we have

$\Phi_{1}(\varkappa, \bar{\mathbf{t}}) = \hbar\mathcal{A}^{-1}\bigg[\frac{1}{\omega^{2}}\Big(\frac{1}{2}-8\tanh(-2\varkappa)\Big)-\Big(1-\frac{0}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\frac{1}{2}-8\tanh(-2\varkappa)\Big)\\ \quad+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}\bigg], \\ \Psi_{1}(\varkappa, \bar{\mathbf{t}}) = \hbar\mathcal{A}^{-1}\bigg[\frac{1}{\omega^{2}}\big(16-16\tanh^{2}(-2\varkappa)\big)-\Big(1-\frac{0}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(16-16\tanh^{2}(-2\varkappa)\big)\\ \quad+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+3\frac{\partial^{3}\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}\bigg].\\$

(4.13)

Thus, we have

$\begin{eqnarray} \Phi_{1}(\varkappa, \bar{\mathbf{t}}) = -8\hbar\sec h^{2}(-2\varkappa)\frac{\bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}, \; \; \; \; \Psi_{1}(\varkappa, \bar{\mathbf{t}}) = -32\hbar\sec h^{2}(-2\varkappa)\tanh(-2\varkappa)\frac{\bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}. \end{eqnarray}$

(4.14)

Analogously, for $\mathbf{r} = 2,$ then (4.11) and (4.12) yields

$\begin{eqnarray} \Phi_{2}(\varkappa, \bar{\mathbf{t}})&& = \mathbf{n}\Phi_{1}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\bigg[\mathcal{A}[\Phi_{1}(\varkappa, \bar{\mathbf{t}})]\big]-\Big(1-\frac{\mathbf{n}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\frac{1}{2}-8\tanh(-2\varkappa)\Big)\\&&\quad+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Phi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}\bigg], \\ \Psi_{2}(\varkappa, \bar{\mathbf{t}})&& = \mathbf{n}\Psi_{1}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\bigg[\mathcal{A}[\Psi_{1}(\varkappa, \bar{\mathbf{t}})]\big]-\Big(1-\frac{\mathbf{n}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(16-16\tanh(-2\varkappa)\big)\\&&\quad+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Phi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} +\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\\&&\quad+ \Psi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} +3\frac{\partial^{3}\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}\bigg]. \end{eqnarray}$

(4.15)

After simplification, the foregoing procedure reduces as mentioned

$\begin{eqnarray} \Phi_{2}(\varkappa, \bar{\mathbf{t}})&& = -8(\mathbf{n}+\hbar)\hbar sech^{2}(-2\varkappa)\frac{\bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}-16\hbar^{2}\sec h^{2}(-2\varkappa)\\&&\quad\times\Big(4sech^{2}(-2\varkappa)-8\tanh^{2}(-2\varkappa)+3\tanh(-2\varkappa)\Big)\frac{\bar{\mathbf{t}}^{2\delta}}{\Gamma(2\delta+1)}, \\ \Psi_{2}(\varkappa, \bar{\mathbf{t}})&& = -32(\mathbf{n}+\hbar)\hbar sech^{2}(-2\varkappa)\tanh(-2\varkappa)\frac{\bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}-32\hbar^{2}\sec h^{2}(-2\varkappa)\\&&\quad\times\Big(40\sec h^{2}(-2\varkappa)\tanh(-2\varkappa)+96\tanh^{2}(-2\varkappa)-2\tanh^{2}(-2\varkappa)\\&&\quad-32\tanh^{3}(-2\varkappa)-25\sec h^{2}(-2\varkappa)\Big)\frac{\bar{\mathbf{t}}^{2\delta}}{\Gamma(2\delta+1)}. \end{eqnarray}$

(4.16)

Similarly, we evaluate the remaining term. Then, we have

$\begin{eqnarray} \Phi(\varkappa, \bar{\mathbf{t}})&& = \Phi_{0}(\varkappa, \bar{\mathbf{t}})+\sum\limits_{\mathbf{r} = 1}^{\infty}\Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})\Big(\frac{1}{\mathbf{n}}\Big)^{\mathbf{r}}, \\\Psi(\varkappa, \bar{\mathbf{t}})&& = \Psi_{0}(\varkappa, \bar{\mathbf{t}})+\sum\limits_{\mathbf{r} = 1}^{\infty}\Psi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})\Big(\frac{1}{\mathbf{n}}\Big)^{\mathbf{r}}. \end{eqnarray}$

(4.17)

Case II: Secondly, we employ the ABC fractional derivative operator considered with the Aboodh transform and $\bar{q}$ -HATM.

Employing the Aboodh transform on (4.1), we have

$\begin{eqnarray} &&\frac{\omega^{\delta}\mathbb{N}(\delta)}{\delta+(1-\delta)\omega^{\delta}}\mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})]-\frac{\Phi(\varkappa, 0)}{\omega^{2}} = -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg], \\&& \frac{\omega^{\delta}\mathbb{N}(\delta)}{\delta+(1-\delta)\omega^{\delta}}\mathcal{A}[\Psi(\varkappa, \bar{\mathbf{t}})]-\frac{\Psi(\varkappa, 0)}{\omega^{2}} = -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\\&&\quad+3\frac{\partial^{3}\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg].\\ \end{eqnarray}$

(4.18)

Therefore, we have

$\begin{eqnarray} \mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})]&& = \frac{1}{\omega^{2}}\Phi(\varkappa, 0)-\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg], \\ \mathcal{A}[\Psi(\varkappa, \bar{\mathbf{t}})]&& = \frac{1}{\omega^{2}}\Psi(\varkappa, 0)-\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\\&&\quad+3\frac{\partial^{3}\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg].\\ \end{eqnarray}$

(4.19)

With the aid of (4.19), the non-linearity can be expressed as

$\mathcal{N}_{1}\big[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}}), \varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]\\ = \mathcal{A}\Bigg[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})-\frac{1}{\omega^{2}}\varphi_{1}(\varkappa, 0)+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} \\ +\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg]\Bigg], \\ \mathcal{N}_{2}\big[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}}), \varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]\\ = \mathcal{A}\Bigg[\varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})-\frac{1}{\omega^{2}}\varphi_{2}(\varkappa, 0)+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\\ \quad+3\frac{\partial^{3}\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg]\Bigg].\\$

(4.20)

Utilizing the methodology described in Section 3, the $\mathbf{r}$ th order deformation equation is described as

$\begin{eqnarray} \mathcal{A}\big[\Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})-\mathcal{K}_{\mathbf{r}}\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})\big] = \hbar\mathcal{R}_{1, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big], \end{eqnarray}$

(4.21)

where

$\begin{eqnarray} \mathcal{R}_{1, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big]&& = \mathcal{A}\Bigg[\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})-\Big(1-\frac{\kappa_{\mathbf{r}}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(\frac{1}{2}-8\tanh(-2\varkappa)\big)\Big)\\&&\quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\bigg\{\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Phi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}+\frac{\partial\Phi_{\mathbf{r}-1}}{\partial \varkappa}+\frac{\partial\Psi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}\bigg\}\Bigg], \\\mathcal{R}_{2, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big]&& = \mathcal{A}\Bigg[\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})-\Big(1-\frac{\kappa_{\mathbf{r}}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(16-16\tanh^{2}(-2\varkappa)\big)\Big)\\&&\quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\bigg\{\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Phi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}+\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Psi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{\mathbf{r}-\jmath-1}}{\partial \varkappa}\\&&\quad+3\frac{\partial^{3}\Phi_{\mathbf{r}-1-\jmath}}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi_{\mathbf{r}-1-\jmath}}{\partial \varkappa^{2}}\bigg\}\Bigg].\\ \end{eqnarray}$

(4.22)

Thanks to the inverse Aboodh transform, we attain

(4.23)

In view of ICs, we have

$\begin{eqnarray} &&\Phi_{0}(\varkappa, \bar{\mathbf{t}}) = \frac{1}{2}-8\tanh(-2\varkappa), \\&&\Psi_{0}(\varkappa, \bar{\mathbf{t}}) = 16-16\tanh^{2}(-2\varkappa). \end{eqnarray}$

(4.24)

In order to obtain $\Phi_{0}(\varkappa, \bar{\mathbf{t}})$ and $\Psi_{0}(\varkappa, \bar{\mathbf{t}}),$ choosing $\mathbf{r} = 1$ in (4.23), then we acquire

(4.25)

For $\mathbf{r} = 1,$ then (4.22) diminish to

$\begin{eqnarray} \mathcal{R}_{1, 1}\big[\overrightarrow{\Phi}_{0}, \overrightarrow{\Psi}_{0}\big]&& = \mathcal{A}\big[\Phi_{0}(\varkappa, \bar{\mathbf{t}})\big]-\Big(1-\frac{\kappa_{1}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\frac{1}{2}-8\tanh(-2\varkappa)\Big)\\&&\quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}, \\ \mathcal{R}_{2, 1}\big[\overrightarrow{\Phi}_{0}, \overrightarrow{\Psi}_{0}\big]&& = \mathcal{A}\big[\Psi_{0}(\varkappa, \bar{\mathbf{t}})\big]-\Big(1-\frac{\kappa_{1}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(16-16\tanh^{2}(-2\varkappa)\big)\\&&\quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\\&&\quad+3\frac{\partial^{3}\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}. \end{eqnarray}$

(4.26)

Plugging (3.33) and (4.26) in (4.25), then we have

$\begin{eqnarray} \Phi_{1}(\varkappa, \bar{\mathbf{t}})&& = \hbar\mathcal{A}^{-1}\bigg[\frac{1}{\omega^{2}}\Big(\frac{1}{2}-8\tanh(-2\varkappa)\Big)-\Big(1-\frac{0}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\frac{1}{2}-8\tanh(-2\varkappa)\Big)\\&&\quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}\bigg], \\ \Psi_{1}(\varkappa, \bar{\mathbf{t}})&& = \hbar\mathcal{A}^{-1}\bigg[\frac{1}{\omega^{2}}\big(16-16\tanh^{2}(-2\varkappa)\big)-\Big(1-\frac{0}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(16-16\tanh^{2}(-2\varkappa)\big)\\&&\quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\\&&\quad+3\frac{\partial^{3}\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}\bigg]. \end{eqnarray}$

(4.27)

Thus, we have

$\begin{eqnarray} \Phi_{1}(\varkappa, \bar{\mathbf{t}})&& = \frac{-8\hbar\sec h^{2}(-2\varkappa)}{\mathbb{N}(\delta)}\bigg\{\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)\bigg\}, \\\Psi_{1}(\varkappa, \bar{\mathbf{t}})&& = -\frac{32\hbar\sec h^{2}(-2\varkappa)\tanh(-2\varkappa)}{\mathbb{N}(\delta)}\bigg\{\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)\bigg\}, \end{eqnarray}$

(4.28)

Analogously, for $\mathbf{r} = 2,$ then (4.25) and (4.26) yields

$\Phi_{2}(\varkappa, \bar{\mathbf{t}}) = \mathbf{n}\Phi_{1}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\bigg[\mathcal{A}[\Phi_{1}(\varkappa, \bar{\mathbf{t}})]\big]-\Big(1-\frac{\mathbf{n}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\frac{1}{2}-8\tanh(-2\varkappa)\Big)\\ \quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Phi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}\bigg], \\ \Psi_{2}(\varkappa, \bar{\mathbf{t}}) = \mathbf{n}\Psi_{1}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\bigg[\mathcal{A}[\Psi_{1}(\varkappa, \bar{\mathbf{t}})]\big]-\Big(1-\frac{\mathbf{n}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(16-16\tanh(-2\varkappa)\big)\\ \quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Phi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} +\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\\ \quad+ \Psi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} +3\frac{\partial^{3}\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{3}}-\frac{\partial^{2}\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}\bigg].$

(4.29)

After simplification, the foregoing procedure reduces as mentioned

$\Phi_{2}(\varkappa, \bar{\mathbf{t}}) = -\frac{8(\mathbf{n}+\hbar)\hbar sech^{2}(-2\varkappa)}{\mathbb{N}(\delta)}\bigg\{\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)\bigg\}\\ \quad-\frac{16\hbar^{2}}{\mathbb{N}^{2}(\delta)}\sec h^{2}(-2\varkappa)\Big(4sech^{2}(-2\varkappa)-8\tanh^{2}(-2\varkappa)+3\tanh(-2\varkappa)\Big)\\ \quad\times\bigg\{\frac{\delta^{2}\bar{\mathbf{t}}^{2\delta}}{\Gamma(2\delta+1)}+2\delta(1-\delta)\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)^{2}\bigg\}, \\ \Psi_{2}(\varkappa, \bar{\mathbf{t}}) = -\frac{32(\mathbf{n}+\hbar)\hbar}{\mathbb{N}(\delta)} sech^{2}(-2\varkappa)\tanh(-2\varkappa)\bigg\{\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)\bigg\}-\frac{32\hbar^{2}}{\mathbb{N}^{2}(\delta)}\sec h^{2}(-2\varkappa)\\ \quad\times\Big(40\sec h^{2}(-2\varkappa)\tanh(-2\varkappa)+96\tanh^{2}(-2\varkappa)-2\tanh^{2}(-2\varkappa)\\ \quad-32\tanh^{3}(-2\varkappa)-25\sec h^{2}(-2\varkappa)\Big)\bigg\{\frac{\delta^{2}\bar{\mathbf{t}}^{2\delta}}{\Gamma(2\delta+1)}+2\delta(1-\delta)\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)^{2}\bigg\}.$

(4.30)

Similarly, we evaluate the remaining term. Then, we have

(4.31)

For $\delta = 1,$ then the integer-order solution of (4.1) is

$\begin{eqnarray} \Phi(\varkappa, \bar{\mathbf{t}})&& = \frac{1}{2}-8\tanh \Big(-2\big(\varkappa-\frac{\bar{\mathbf{t}}}{2}\big)\Big), \\ \Psi(\varkappa, \bar{\mathbf{t}})&& = 16-16\tanh^{2} \Big(-2\big(\varkappa-\frac{\bar{\mathbf{t}}}{2}\big)\Big), \\ \end{eqnarray}$

(4.32)

Example 4.2. Surmise that the fractional-order WBKEs is presented as follows:

$\begin{eqnarray} &&\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\Phi(\varkappa, \bar{\mathbf{t}})+\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} = 0, \; \; 0 < \delta\leq1\\&& \mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\Psi(\varkappa, \bar{\mathbf{t}})+\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}} = 0, \end{eqnarray}$

(4.33)

supplemented with ICs

$\begin{eqnarray} &&\Phi(\varkappa, 0) = \zeta-\kappa\coth\big(\kappa(\varkappa+\theta)\big), \\&&\Psi(\varkappa, 0) = -\kappa^{2}cosec h^{2}\big(\kappa(\varkappa+\theta)\big). \end{eqnarray}$

(4.34)

Proof. Primarily, we demonstrate how to solve (4.33) in two different scenarios.

Case I: Initially, we employ the Caputo fractional derivative operator considered with the Aboodh transform and $\bar{q}$ -HATM.

Employing the Aboodh transform on (4.33), we have

$\begin{eqnarray} &&\mathcal{A}\big[\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\Phi(\varkappa, \bar{\mathbf{t}})\big] = -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg], \\&& \mathcal{A}\big[\mathbf{D}_{\bar{\mathbf{t}}}^{\delta}\Psi(\varkappa, \bar{\mathbf{t}})\big] = -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg]. \end{eqnarray}$

(4.35)

It follows that

$\begin{eqnarray} &&\omega^{\delta}\mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})]-\sum\limits_{\kappa = 0}^{\mathbf{n}-1}\frac{\Phi^{(\kappa)}(\varkappa, 0)}{\omega^{2-\delta+\kappa}} = -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg], \\&& \omega^{\delta}\mathcal{A}[\Psi(\varkappa, \bar{\mathbf{t}})]-\sum\limits_{\kappa = 0}^{\mathbf{n}-1}\frac{\Psi^{(\kappa)}(\varkappa, 0)}{\omega^{2-\delta+\kappa}} = -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg].\\ \end{eqnarray}$

(4.36)

Therefore, we have

$\begin{eqnarray} &&\mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})] = \frac{1}{\omega^{2}}\Phi(\varkappa, 0)-\frac{1}{\omega^{\delta}}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg], \\&& \mathcal{A}[\Psi(\varkappa, \bar{\mathbf{t}})] = \frac{1}{\omega^{2}}\Psi(\varkappa, 0)-\frac{1}{\omega^{\delta}}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg].\\ \end{eqnarray}$

(4.37)

With the aid of (4.37), the non-linearity can be expressed as

$\mathcal{N}_{1}\big[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}}), \varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]\\ = \mathcal{A}\Bigg[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})-\frac{1}{\omega^{2}}\varphi_{1}(\varkappa, 0)+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg]\Bigg], \\ \mathcal{N}_{2}\big[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}}), \varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]\\ = \mathcal{A}\Bigg[\varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})-\frac{1}{\omega^{2}}\varphi_{2}(\varkappa, 0)+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg]\Bigg].$

(4.38)

Utilizing the methodology described in Section 3, the $\mathbf{r}$ th order deformation equation is described as

$\begin{eqnarray} \mathcal{A}\big[\Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})-\mathcal{K}_{\mathbf{r}}\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})\big] = \hbar\mathcal{R}_{1, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big], \end{eqnarray}$

(4.39)

where

$\begin{eqnarray} \mathcal{R}_{1, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big]&& = \mathcal{A}\Bigg[\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})-\Big(1-\frac{\kappa_{\mathbf{r}}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(\frac{1}{2}-8\tanh(-2\varkappa)\big)\Big)\\&&\quad+\frac{1}{\omega^{\delta}}\bigg\{\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Phi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi_{\mathbf{r}-1}}{\partial \varkappa}+\frac{\partial\Psi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}\bigg\}\Bigg], \\\mathcal{R}_{2, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big]&& = \mathcal{A}\Bigg[\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})-\Big(1-\frac{\kappa_{\mathbf{r}}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(16-16\tanh^{2}(-2\varkappa)\big)\Big)\\&&\quad+\frac{1}{\omega^{\delta}}\bigg\{\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Phi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}+\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Psi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{\mathbf{r}-\jmath-1}}{\partial \varkappa}\\&&\quad-\frac{1}{2}\frac{\partial^{2}\Psi_{\mathbf{r}-1}}{\partial \varkappa^{2}}\bigg\}\Bigg].\\ \end{eqnarray}$

(4.40)

Thanks to the inverse Aboodh transform, we attain

(4.41)

In view of ICs, we have

$\begin{eqnarray} &&\Phi_{0}(\varkappa, \bar{\mathbf{t}}) = \zeta-\kappa\coth\big(\kappa(\varkappa+\theta)\big), \\&&\Psi_{0}(\varkappa, \bar{\mathbf{t}}) = -\kappa^{2}cosec h^{2}\big(\kappa(\varkappa+\theta)\big). \end{eqnarray}$

(4.42)

In order to obtain $\Phi_{0}(\varkappa, \bar{\mathbf{t}})$ and $\Psi_{0}(\varkappa, \bar{\mathbf{t}}),$ choosing $\mathbf{r} = 1$ in (4.40), then we acquire

(4.43)

For $\mathbf{r} = 1,$ then (4.40) diminish to

$\begin{eqnarray} \mathcal{R}_{1, 1}\big[\overrightarrow{\Phi}_{0}, \overrightarrow{\Psi}_{0}\big]&& = \mathcal{A}\big[\Phi_{0}(\varkappa, \bar{\mathbf{t}})\big]-\Big(1-\frac{\kappa_{1}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\zeta-\kappa\coth\big(\kappa(\varkappa+\theta)\big)\Big)\\&&\quad+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}, \\ \mathcal{R}_{2, 1}\big[\overrightarrow{\Phi}_{0}, \overrightarrow{\Psi}_{0}\big]&& = \mathcal{A}\big[\Psi_{0}(\varkappa, \bar{\mathbf{t}})\big]-\Big(1-\frac{\kappa_{1}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(-\kappa^{2}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\big)\\&&\quad+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}.\\ \end{eqnarray}$

(4.44)

Plugging (3.33) and (4.44) in (4.43), then we have

$\begin{eqnarray} \Phi_{1}(\varkappa, \bar{\mathbf{t}})&& = \hbar\mathcal{A}^{-1}\bigg[\frac{1}{\omega^{2}}\Big(\zeta-\kappa\coth\big(\kappa(\varkappa+\theta)\big)\Big)-\Big(1-\frac{0}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\zeta-\kappa\coth\big(\kappa(\varkappa+\theta)\big)\Big)\\&&\quad+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}\bigg], \\ \Psi_{1}(\varkappa, \bar{\mathbf{t}})&& = \hbar\mathcal{A}^{-1}\bigg[\frac{1}{\omega^{2}}\big(-\kappa^{2}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\big)-\Big(1-\frac{0}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(-\kappa^{2}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\big)\\&&\quad+\frac{1}{\omega^{\delta}}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}\bigg].\\ \end{eqnarray}$

(4.45)

Thus, we have

$\begin{eqnarray} &&\Phi_{1}(\varkappa, \bar{\mathbf{t}}) = -\zeta\hbar\kappa^{2}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\frac{\bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}, \\&&\Psi_{1}(\varkappa, \bar{\mathbf{t}}) = -\zeta\hbar\kappa^{2}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\coth\big(\kappa(\varkappa+\theta)\big)\frac{\bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}, \end{eqnarray}$

(4.46)

Analogously, for $\mathbf{r} = 2,$ then (4.43) and (4.44) yields

$\Phi_{2}(\varkappa, \bar{\mathbf{t}}) = \mathbf{n}\Phi_{1}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\bigg[\mathcal{A}[\Phi_{1}(\varkappa, \bar{\mathbf{t}})]\big]-\Big(1-\frac{\mathbf{n}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\zeta-\kappa\coth\big(\kappa(\varkappa+\theta)\big)\Big)\\ +\frac{1}{\omega^{\delta}}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\Phi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}\bigg], \\ \Psi_{2}(\varkappa, \bar{\mathbf{t}}) = \mathbf{n}\Psi_{1}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\bigg[\mathcal{A}[\Psi_{1}(\varkappa, \bar{\mathbf{t}})]\big]-\Big(1-\frac{\mathbf{n}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(16-16\tanh(-2\varkappa)\big)\\ +\frac{1}{\omega^{\delta}}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Phi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} +\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\\ + \Psi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} -\frac{1}{2}\frac{\partial^{2}\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}\bigg].$

(4.47)

After simplification, the foregoing procedure reduces as mentioned

$\Phi_{2}(\varkappa, \bar{\mathbf{t}}) = -\zeta(\mathbf{n}+\hbar)\hbar \kappa^{2}cosech^{2}\big(\kappa(\varkappa+\theta)\big)\frac{\bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+\zeta\hbar^{2}\kappa^{4}cosech^{2}\big(\kappa(\varkappa+\theta)\big)\\ \times\bigg\{\frac{2\zeta\kappa \Gamma(2\delta+1)\bar{\mathbf{t}}^{3\delta}}{\Gamma(3\delta+1)\Gamma^{2}(\delta+1)}-\frac{\bar{\mathbf{t}}^{2\delta}\big(3\coth^{2}\big(\big(\kappa(\varkappa+\theta)\big)-1\big)\big)}{\Gamma(2\delta+1)}\bigg\}, \\ \Psi_{2}(\varkappa, \bar{\mathbf{t}}) = -\zeta(\mathbf{n}+\hbar)\hbar \kappa^{2}cosech^{2}\big(\kappa(\varkappa+\theta)\big)\coth\big(\kappa(\varkappa+\theta)\big)\frac{\bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+\frac{2\zeta\kappa^{5}\hbar^{2}cosech^{2}\big(\kappa(\varkappa+\theta)\big)}{\Gamma(\delta+1)}\\ \times\bigg\{\frac{\bar{\mathbf{t}}^{3\delta}\big(\zeta\kappa cosech^{2}\big(3coth^{2}(\big(\kappa(\varkappa+\theta)\big)-1)\big)+2\zeta\kappa cosech^{2}\coth^{2}\big(\kappa(\varkappa+\theta)\big)\big)}{\Gamma(\delta+1)\Gamma(3\delta+1)}\\ -\frac{2\bar{\mathbf{t}}^{\delta}\zeta\coth(3cosech^{2}(\big(\kappa(\varkappa+\theta)\big)-1))}{\Gamma(2\delta+1)}\bigg\}.$

(4.48)

Similarly, we evaluate the remaining term. Then, we have

(4.49)

Case II: Secondly, we employ the ABC fractional derivative operator considered with the Aboodh transform and $\bar{q}$ -HATM.

Employing the Aboodh transform on (4.33), we have

$\frac{\omega^{\delta}\mathbb{N}(\delta)}{\delta+(1-\delta)\omega^{\delta}}\mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})]-\frac{\Phi(\varkappa, 0)}{\omega^{2}} = -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg], \\ \frac{\omega^{\delta}\mathbb{N}(\delta)}{\delta+(1-\delta)\omega^{\delta}}\mathcal{A}[\Psi(\varkappa, \bar{\mathbf{t}})]-\frac{\Psi(\varkappa, 0)}{\omega^{2}} =\\ -\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg].$

(4.50)

Therefore, we have

$\mathcal{A}[\Phi(\varkappa, \bar{\mathbf{t}})] = \frac{1}{\omega^{2}}\Phi(\varkappa, 0)-\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg], \\ \mathcal{A}[\Psi(\varkappa, \bar{\mathbf{t}})] = \frac{1}{\omega^{2}}\Psi(\varkappa, 0)-\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\\ \mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg].$

(4.51)

With the aid of (4.51), the non-linearity can be expressed as

$\mathcal{N}_{1}\big[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}}), \varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]\\ = \mathcal{A}\Bigg[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})-\frac{1}{\omega^{2}}\varphi_{1}(\varkappa, 0)+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg]\Bigg], \\ \mathcal{N}_{2}\big[\varphi_{1}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}}), \varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})\big]\\ = \mathcal{A}\Bigg[\varphi_{2}(\varkappa, \bar{\mathbf{t}};\bar{\mathbf{q}})-\frac{1}{\omega^{2}}\varphi_{2}(\varkappa, 0)+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\\ \mathcal{A}\bigg[\Phi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg]\Bigg].\\$

(4.52)

Utilizing the methodology described in Section 3, the $\mathbf{r}$ th order deformation equation is described as

$\begin{eqnarray} \mathcal{A}\big[\Phi_{\mathbf{r}}(\varkappa, \bar{\mathbf{t}})-\mathcal{K}_{\mathbf{r}}\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})\big] = \hbar\mathcal{R}_{1, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big], \end{eqnarray}$

(4.53)

where

$\mathcal{R}_{1, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big] = \mathcal{A}\Bigg[\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})-\Big(1-\frac{\kappa_{\mathbf{r}}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(\zeta-\kappa\coth\big(\kappa(\varkappa+\theta)\big)\big)\Big)\\ \quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\bigg\{\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Phi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi_{\mathbf{r}-1}}{\partial \varkappa}+\frac{\partial\Psi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}\bigg\}\Bigg], \\\mathcal{R}_{2, \mathbf{r}}\big[\overrightarrow{\Phi}_{\mathbf{r}-1}, \overrightarrow{\Psi}_{\mathbf{r}-1}\big] = \mathcal{A}\Bigg[\Phi_{\mathbf{r}-1}(\varkappa, \bar{\mathbf{t}})-\Big(1-\frac{\kappa_{\mathbf{r}}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(-\kappa^{2}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\big)\Big)\\ \quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\bigg\{\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Phi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{\mathbf{r}-1-\jmath}}{\partial \varkappa}+\sum\limits_{\jmath = 0}^{\mathbf{r}-1}\Psi_{\jmath}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{\mathbf{r}-\jmath-1}}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi_{\mathbf{r}-1}}{\partial \varkappa^{2}}\bigg\}\Bigg].$

(4.54)

Thanks to the inverse Aboodh transform, we attain

(4.55)

In view of ICs, we have

(4.56)

In order to obtain $\Phi_{0}(\varkappa, \bar{\mathbf{t}})$ and $\Psi_{0}(\varkappa, \bar{\mathbf{t}}),$ choosing $\mathbf{r} = 1$ in (4.55), then we acquire

(4.57)

For $\mathbf{r} = 1,$ then (4.54) diminish to

$\mathcal{R}_{1, 1}\big[\overrightarrow{\Phi}_{0}, \overrightarrow{\Psi}_{0}\big] = \mathcal{A}\big[\Phi_{0}(\varkappa, \bar{\mathbf{t}})\big]-\Big(1-\frac{\kappa_{1}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\zeta-\kappa\coth\big(\kappa(\varkappa+\theta)\big)\Big)\\ +\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}, \\ \mathcal{R}_{2, 1}\big[\overrightarrow{\Phi}_{0}, \overrightarrow{\Psi}_{0}\big] = \mathcal{A}\big[\Psi_{0}(\varkappa, \bar{\mathbf{t}})\big]-\Big(1-\frac{\kappa_{1}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(-\kappa^{2}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\big)\\ +\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}.$

(4.58)

Plugging (3.33) and (4.58) in (4.57), then we have

$\begin{eqnarray} \Phi_{1}(\varkappa, \bar{\mathbf{t}})&& = \hbar\mathcal{A}^{-1}\bigg[\frac{1}{\omega^{2}}\Big(\zeta-\kappa\coth\big(\kappa(\varkappa+\theta)\big)\Big)-\Big(1-\frac{0}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\zeta-\kappa\coth\big(\kappa(\varkappa+\theta)\big)\Big)\\&&\quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}\bigg], \\ \Psi_{1}(\varkappa, \bar{\mathbf{t}})&& = \hbar\mathcal{A}^{-1}\bigg[\frac{1}{\omega^{2}}\big(-\kappa^{2}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\big)-\Big(1-\frac{0}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(-\kappa^{2}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\big)\\&&\quad+\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}-\frac{1}{2}\frac{\partial^{2}\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}\bigg]. \end{eqnarray}$

(4.59)

Thus, we have

$\begin{eqnarray} \Phi_{1}(\varkappa, \bar{\mathbf{t}})&& = -\frac{\zeta\hbar\kappa^{2}}{\mathbb{N}(\delta)}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\bigg\{\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)\bigg\}, \\\Psi_{1}(\varkappa, \bar{\mathbf{t}})&& = -\frac{\zeta\hbar\kappa^{2}}{\mathbb{N}(\delta)}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\coth\big(\kappa(\varkappa+\theta)\big)\bigg\{\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)\bigg\}, \end{eqnarray}$

(4.60)

Analogously, for $\mathbf{r} = 2,$ then (4.57) and (4.58) yields

$\Phi_{2}(\varkappa, \bar{\mathbf{t}}) = \mathbf{n}\Phi_{1}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\bigg[\mathcal{A}[\Phi_{1}(\varkappa, \bar{\mathbf{t}})]\big]-\Big(1-\frac{\mathbf{n}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\Big(\zeta-\kappa\coth\big(\kappa(\varkappa+\theta)\big)\Big)\\ +\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Phi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{1}{2}\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\frac{\partial\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\bigg\}\bigg], \\ \Psi_{2}(\varkappa, \bar{\mathbf{t}}) = \mathbf{n}\Psi_{1}(\varkappa, \bar{\mathbf{t}})+\hbar\mathcal{A}^{-1}\bigg[\mathcal{A}[\Psi_{1}(\varkappa, \bar{\mathbf{t}})]\big]-\Big(1-\frac{\mathbf{n}}{\mathbf{n}}\Big)\frac{1}{\omega^{2}}\big(16-16\tanh(-2\varkappa)\big)\\ +\frac{\delta+(1-\delta)\omega^{\delta}}{\omega^{\delta}\mathbb{N}(\delta)}\mathcal{A}\bigg\{\Phi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}+\Phi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Psi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} +\Psi_{0}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa}\\ + \Psi_{1}(\varkappa, \bar{\mathbf{t}})\frac{\partial\Phi_{0}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa} -\frac{1}{2}\frac{\partial^{2}\Psi_{1}(\varkappa, \bar{\mathbf{t}})}{\partial \varkappa^{2}}\bigg\}\bigg],$

(4.61)

After simplification, the foregoing procedure reduces as mentioned

$\Phi_{2}(\varkappa, \bar{\mathbf{t}}) = -(\mathbf{n}+\hbar)\frac{\zeta\kappa^{2}}{\mathbb{N}(\delta)}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\bigg\{\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)\bigg\}\\ -\frac{\zeta\kappa^{4}\hbar^{2}}{\mathbb{N}^{2}(\delta)}cosech^{2}\big(\kappa(\varkappa+\theta)\big)\big(3coth^{2}(\big(\kappa(\varkappa+\theta)\big)-1)\big)\\ \times\bigg\{\frac{\delta^{2}\bar{\mathbf{t}}^{2\delta}}{\Gamma(2\delta+1)}+2\delta(1-\delta)\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)^{2}\bigg\}+\frac{2\hbar^{2}\zeta^{2}\kappa^{5}}{\mathbb{N}^{3}(\delta)}cosech^{2}\big(\kappa(\varkappa+\theta)\big)\\ \times\bigg\{\frac{\delta^{3}\bar{\mathbf{t}}^{3\delta}}{\Gamma(3\delta+1)}+3\delta^{2}(1-\delta)\frac{ \bar{\mathbf{t}}^{2\delta}}{\Gamma(2\delta+1)}+3\delta(1-\delta)^{2}\frac{ \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)^{3}\bigg\}, \\ \Psi_{2}(\varkappa, \bar{\mathbf{t}}) = -(\mathbf{n}+\hbar)\frac{\zeta\hbar\kappa^{2}}{\mathbb{N}(\delta)}cosec h^{2}\big(\kappa(\varkappa+\theta)\big)\coth\big(\kappa(\varkappa+\theta)\big)\bigg\{\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)\bigg\}\\ -\frac{2\zeta\hbar^{2}}{\mathbb{N}^{2}(\delta)}coth^{2}\big(3cosech^{2}\big(\kappa(\varkappa+\theta)-1\big)\bigg\{\frac{\delta^{2}\bar{\mathbf{t}}^{2\delta}}{\Gamma(2\delta+1)}+2\delta(1-\delta)\frac{\delta \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)^{2}\bigg\}\\ +\frac{2\hbar^{2}\zeta\kappa^{5}}{\mathbb{N}^{3}(\delta)}\Big(\zeta\kappa cosech^{2}\big(\kappa(\varkappa+\theta)\big)\big(3coth^{2}\big(\kappa(\varkappa+\theta)-1\big)+2\zeta\kappa cosech^{2}\big(\kappa(\varkappa+\theta)\big)\big(coth^{2}\big(\kappa(\varkappa+\theta)\big)\big)\Big)\\ \times\bigg\{\frac{\delta^{3}\bar{\mathbf{t}}^{3\delta}}{\Gamma(3\delta+1)}+3\delta^{2}(1-\delta)\frac{ \bar{\mathbf{t}}^{2\delta}}{\Gamma(2\delta+1)}+3\delta(1-\delta)^{2}\frac{ \bar{\mathbf{t}}^{\delta}}{\Gamma(\delta+1)}+(1-\delta)^{3}\bigg\}.$

(4.62)

Similarly, we evaluate the remaining term. Then, we have

(4.63)

For $\delta = 1,$ then the integer-order solution of (4.33) is

$\begin{eqnarray} \Phi(\varkappa, \bar{\mathbf{t}})&& = \zeta-\kappa\coth\big(\kappa(\varkappa+\theta-\zeta \bar{\mathbf{t}})\big), \\ \Psi(\varkappa, \bar{\mathbf{t}})&& = -\kappa^{2}cosech^{2}\big(\kappa(\varkappa+\theta-\zeta \bar{\mathbf{t}})\big). \end{eqnarray}$

(4.64)

5. Numerical results and their physical interpretation

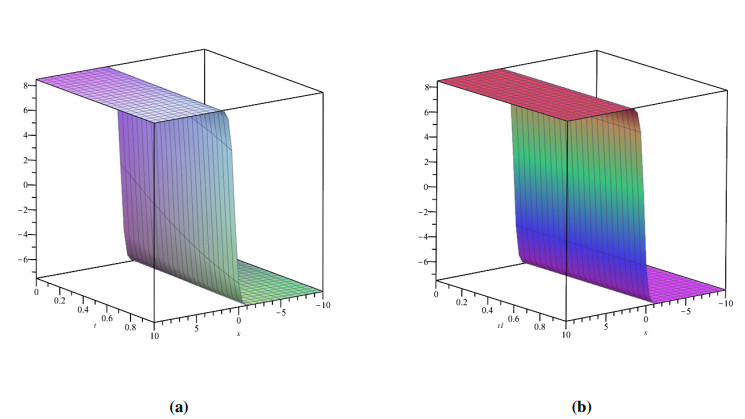
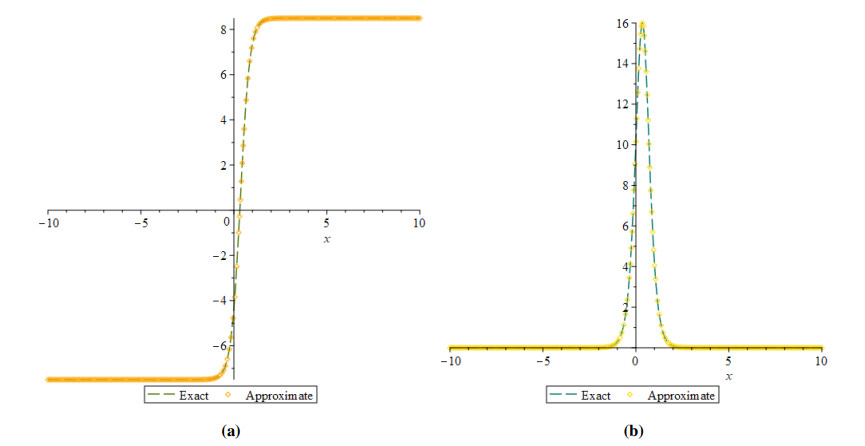
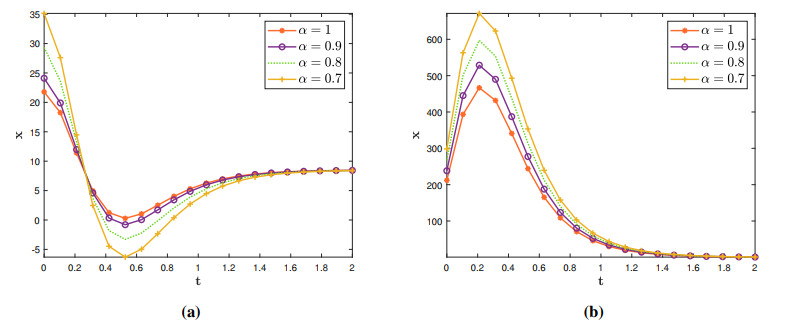
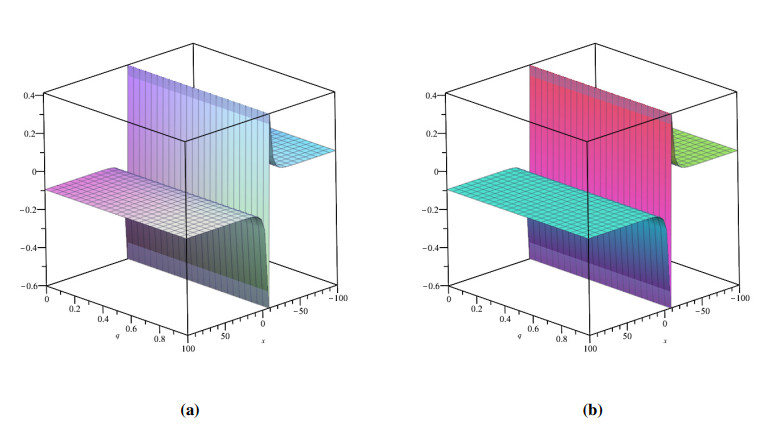
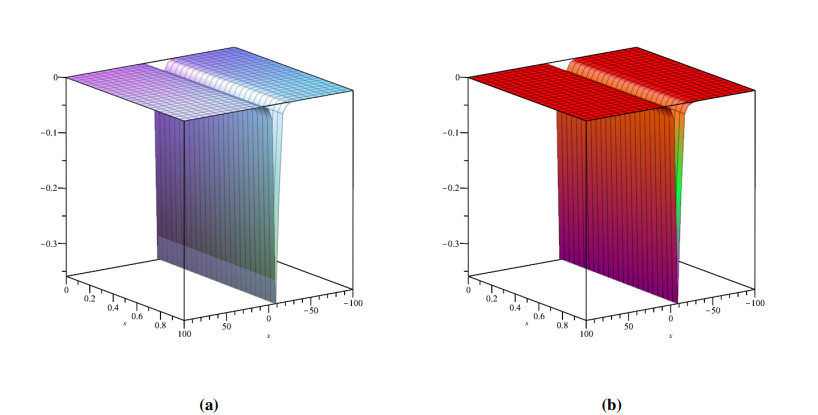
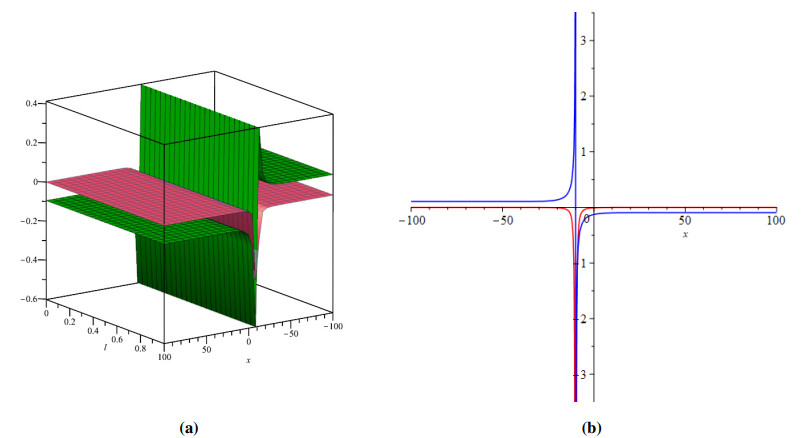
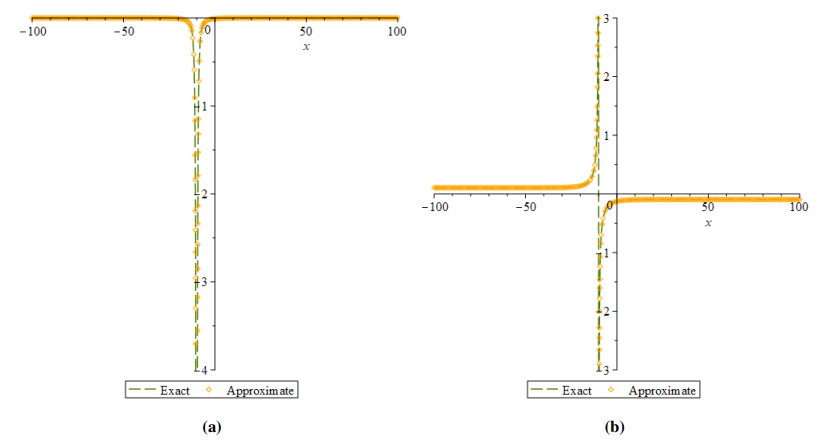
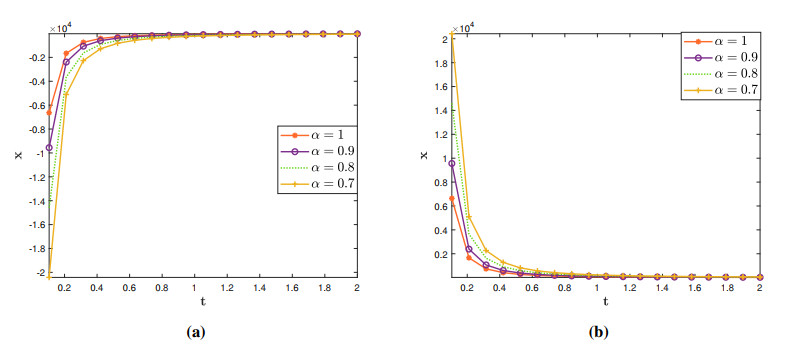
The fractional WBKE is solved using the $\bar{q}$ -HATM merged with the Aboodh transform. For the most part, MATLAB 21 has been implemented. The mathematical models eqrefkb1 and (4.33) were carried out in an attempt to determine that the prospective approach would result in increased reliability via the Caputo and ABC fractional derivative operators. The projected method, as shown by the effort it will lead, provides amazing precision in respect to the approach described in these articles ^[59,60], which is referenced for both of the instances in Tables 1 and 2. For Example 4.1, and examine the correlation of generated results to precise responses and approximate solutions for both $\Phi(\varkappa, \bar{\mathbf{t}})$ and $\Psi(\varkappa, \bar{\mathbf{t}}),$ respectively. The behaviour of coupled system of (4.1) is presented in as a three-dimensional and two-dimensional plots. illustrates the exact and approximate two-dimensional behaviour of $\Phi(\varkappa, \bar{\mathbf{t}})$ and $\Psi(\varkappa, \bar{\mathbf{t}}),$ respectively. This behaviour shows how the exact and approximate solutions are in close agreement with each other. The behavior of derived findings for the Example 4.1 involving various fractional and integer order is shown in . Also, the $\bar{q}$ -HATM results for different $\hbar$ are shown in Figure 5, which help us customize and manage the convergence area. – show the significance of the asymptotic component in the $q$ -HATM formulation.

Table 1. Comparison analysis in respects of absolute error between ADM ^[59], VIM ^[60] and

$\bar{q}$ -HATM for the approximate findings of

$\Phi(\varkappa, \bar{\mathbf{t}})$ at

$\mathbf{n} = 1, \; \hbar = -1$ and

$\delta = 1$ for Example 4.2.

$(\varkappa, \bar{\mathbf{t}})$	$\big\vert\Phi_{E}-\Phi_{ADM}\big\vert$	$\big\vert\Phi_{E}-\Phi_{VIM}\big\vert$	$\big\vert\Phi_{E}-\Phi_{\bar{q}-HATM(CFD)}\big\vert$	$\big\vert\Phi_{E}-\Phi_{\bar{q}-HATM(ABC)}\big\vert$
(0.1, 0.1)	8.16297 $\times10^{-7}$	6.35269 $\times10^{-5}$	5.89129 $\times10^{-17}$	5.55112 $\times10^{-17}$
(0.1, 0.3)	7.64247 $\times10^{-7}$	1.90854 $\times10^{-4}$	5.89129 $\times10^{-17}$	5.55112 $\times10^{-17}$
(0.1, 0.5)	7.16083 $\times10^{-7}$	3.18549 $\times10^{-4}$	5.89129 $\times10^{-17}$	5.55112 $\times10^{-17}$
(0.2, 0.1)	3.26243 $\times10^{-6}$	6.18430 $\times10^{-5}$	5.89129 $\times10^{-17}$	5.55112 $\times10^{-17}$
(0.2, 0.3)	3.05458 $\times10^{-6}$	1.85945 $\times10^{-4}$	5.89129 $\times10^{-17}$	5.55112 $\times10^{-17}$
(0.2, 0.5)	2.86226 $\times10^{-6}$	3.10352 $\times10^{-4}$	7.798625 $\times10^{-16}$	7.77156 $\times10^{-16}$
(0.3, 0.1)	3.26243 $\times10^{-6}$	6.18430 $\times10^{-5}$	5.89129 $\times10^{-17}$	5.55112 $\times10^{-17}$
(0.3, 0.3)	3.05458 $\times10^{-6}$	1.85945 $\times10^{-4}$	5.89129 $\times10^{-17}$	5.55112 $\times10^{-17}$
(0.3, 0.5)	2.86226 $\times10^{-6}$	3.10352 $\times10^{-4}$	7.798625 $\times10^{-16}$	7.77156 $\times10^{-16}$
(0.4, 0.1)	1.30286 $\times10^{-5}$	5.87746 $\times10^{-5}$	5.89129 $\times10^{-17}$	5.55112 $\times10^{-17}$
(0.4, 0.3)	1.22000 $\times10^{-5}$	1.76574 $\times10^{-4}$	5.89129 $\times10^{-17}$	5.55112 $\times10^{-17}$
(0.4, 0.5)	1.14333 $\times10^{-5}$	2.44707 $\times10^{-4}$	5.89129 $\times10^{-17}$	5.55112 $\times10^{-17}$
(0.5, 0.1)	2.03415 $\times10^{-5}$	5.72867 $\times10^{-5}$	0	0
(0.5, 0.3)	1.90489 $\times10^{-5}$	1.72102 $\times10^{-4}$	1.73301 $\times10^{-16}$	1.11022 $\times10^{-16}$
(0.5, 0.5)	1.78528 $\times10^{-5}$	2.87241 $\times10^{-4}$	6.74434 $\times10^{-17}$	6.10623 $\times10^{-16}$

| Show Table

DownLoad: CSV

Table 2. Comparison analysis in respects of absolute error between ADM ^[59], VIM ^[60] and

$\bar{q}$ -HATM for the approximate findings of

$\Psi(\varkappa, \bar{\mathbf{t}})$ at

$\mathbf{n} = 1, \; \hbar = -1$ and

$\delta = 1$ for Example 4.2.

$(\varkappa, \bar{\mathbf{t}})$	$\big\vert\Phi_{E}-\Phi_{ADM}\big\vert$	$\big\vert\Phi_{E}-\Phi_{VIM}\big\vert$	$\big\vert\Phi_{E}-\Phi_{\bar{q}-HATM(CFD)}\big\vert$	$\big\vert\Phi_{E}-\Phi_{\bar{q}-HATM(ABC)}\big\vert$
(0.1, 0.1)	4.81902 $\times10^{-4}$	1.23033 $\times10^{-4}$	1.453423 $\times10^{-18}$	1.73472 $\times10^{-18}$
(0.1, 0.3)	4.50818 $\times10^{-4}$	1.76000 $\times10^{-4}$	2.90009 $\times10^{-17}$	2.60209 $\times10^{-17}$
(0.1, 0.5)	4.22221 $\times10^{-4}$	2.69597 $\times10^{-4}$	1.98220 $\times10^{-16}$	1.80411 $\times10^{-16}$
(0.2, 0.1)	9.76644 $\times10^{-4}$	2.69597 $\times10^{-4}$	3.94560 $\times10^{-9}$	3.82100 $\times10^{-9}$
(0.2, 0.3)	9.13502 $\times10^{-4}$	2.69597 $\times10^{-4}$	2.34188 $\times10^{-7}$	2.34188 $\times10^{-7}$
(0.2, 0.5)	8.55426 $\times10^{-4}$	2.69597 $\times10^{-4}$	1.78935 $\times10^{-16}$	1.73472 $\times10^{-16}$
(0.3, 0.1)	1.48482 $\times10^{-3}$	2.69597 $\times10^{-4}$	3.89567 $\times10^{-18}$	3.46945 $\times10^{-18}$
(0.3, 0.3)	1.38858 $\times10^{-3}$	2.69597 $\times10^{-4}$	5.89129 $\times10^{-17}$	5.55112 $\times10^{-17}$
(0.3, 0.5)	1.30009 $\times10^{-3}$	2.69597 $\times10^{-4}$	1.69879 $\times10^{-16}$	1.61329 $\times10^{-16}$
(0.4, 0.1)	2.00705 $\times10^{-3}$	2.69597 $\times10^{-4}$	2.91458 $\times10^{-18}$	2.60209 $\times10^{-18}$
(0.4, 0.3)	1.87661 $\times10^{-3}$	2.69597 $\times10^{-4}$	1.98455 $\times10^{-17}$	1.73472 $\times10^{-17}$
(0.4, 0.5)	1.75670 $\times10^{-3}$	2.69597 $\times10^{-4}$	1.59884 $\times10^{-16}$	1.52656 $\times10^{-16}$
(0.5, 0.1)	2.54396 $\times10^{-3}$	2.69597 $\times10^{-4}$	8.98734 $\times10^{-19}$	8.67362 $\times10^{-19}$
(0.5, 0.3)	2.37815 $\times10^{-3}$	2.69597 $\times10^{-4}$	2.98823 $\times10^{-17}$	2.08167 $\times10^{-17}$
(0.5, 0.5)	2.22578 $\times10^{-3}$	2.69597 $\times10^{-4}$	1.48878 $\times10^{-16}$	1.43982 $\times10^{-16}$

| Show Table

DownLoad: CSV

Figure 1. Illustration in three dimensions of the exact and approximate solutions for

$\Phi(\varkappa, \bar{\mathbf{t}})$ of Example 4.1 when

$\delta = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 2. Illustration in three dimensions of the exact and approximate solutions for

$\Psi(\varkappa, \bar{\mathbf{t}})$ of Example 4.1 when

$\delta = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 3. (a) Three-dimensional illustration (b) Two-dimensional illustrations of the approximate solutions for

$\Phi(\varkappa, \bar{\mathbf{t}})$ and

$\Psi(\varkappa, \bar{\mathbf{t}})$ , respectively, of Example 4.1 when

$\delta = 0.8$ .

DownLoad: Full-Size Img PowerPoint

Figure 4. (a) Two-dimensional illustration of the exact and approximate solutions of

$\Phi(\varkappa, \bar{\mathbf{t}})$ of Example 4.1 when

$\delta = 1, \; \; \hbar = -1, \; \mathbf{n} = 1$ and

$\bar{\mathbf{t}} = 0.7.$ (b) (a) Two-dimensional illustration of the exact and approximate solutions of

$\Psi(\varkappa, \bar{\mathbf{t}})$ of Example 4.1 when

$\delta = 1, \; \; \hbar = -1, \; \mathbf{n} = 1$ and

$\bar{\mathbf{t}} = 0.7$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. (a) Two-dimensional illustration of the approximate solutions of

$\Phi(\varkappa, \bar{\mathbf{t}})$ of Example 4.1 having multiple fractional order when

$\hbar = -1, \; \mathbf{n} = 1$ and

$\bar{\mathbf{t}} = 0.7.$ (b) Two-dimensional illustration of the approximate solutions of

$\Psi(\varkappa, \bar{\mathbf{t}})$ of Example 4.1 having multiple fractional order when

$\hbar = -1, \; \mathbf{n} = 1$ and

$\bar{\mathbf{t}} = 0.7$ .

DownLoad: Full-Size Img PowerPoint

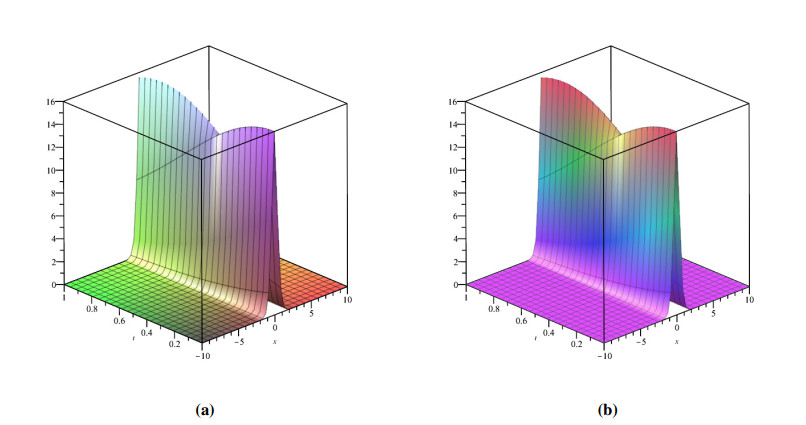
Furthermore, Figure 6 depicts the characteristics of produced results in relation to precise values for Example 4.2, with Figure 7 demonstrating the preciseness of the achieved result and approximate solution. Figure 8 shows the performance of the resulting approach for a couple of WBKE model 4.33, in two and three dimensional views. The characteristics of acquired treatment for specific may be seen in Figure 9, which help us govern the converged zone. Subsequently, the multiple fractional orders are depicted in Figure 10, and the integer-order depicts the converging domain for the WBKE. Example 4.1 and Example 4.2 address the correlated texture of the WBKEs, which are presented in Figures 6–10, respectively, to assist in considering the characteristics of coupled equations.

Figure 6. Illustration in three dimensions of the exact and approximate solutions for

$\Phi(\varkappa, \bar{\mathbf{t}})$ of Example 4.2 when

$\delta = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. Illustration in three dimensions of the exact and approximate solutions for

$\Psi(\varkappa, \bar{\mathbf{t}})$ of Example 4.2 when

$\delta = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 8. Illustration in three dimensions of the exact and approximate solutions for

$\Phi(\varkappa, \bar{\mathbf{t}})$ of Example 4.2 when

$\delta = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 9. (a) Two-dimensional illustration of the approximate solutions of

$\Phi(\varkappa, \bar{\mathbf{t}})$ of Example 4.2 having multiple fractional order when

$\hbar = -1, \; \mathbf{n} = 1$ and

$\bar{\mathbf{t}} = 0.7.$ (b) Two-dimensional illustration of the approximate solutions of

$\Psi(\varkappa, \bar{\mathbf{t}})$ of Example 4.2 having multiple fractional order when

$\hbar = -1, \; \mathbf{n} = 1$ and

$\bar{\mathbf{t}} = 0.7$ .

DownLoad: Full-Size Img PowerPoint

Figure 10. (a) Two-dimensional illustration of the approximate solutions of

$\Phi(\varkappa, \bar{\mathbf{t}})$ of Example 4.2 having multiple fractional order when

$\hbar = -1, \; \mathbf{n} = 1$ and

$\bar{\mathbf{t}} = 0.7.$ (b) Two-dimensional illustration of the approximate solutions of

$\Psi(\varkappa, \bar{\mathbf{t}})$ of Example 4.2 having multiple fractional order when

$\hbar = -1, \; \mathbf{n} = 1$ and

$\bar{\mathbf{t}} = 0.7$ .

DownLoad: Full-Size Img PowerPoint

6. Conclusions

In this investigation, we employed $\bar{\mathbf{q}}$ -HATM outcomes to construct the solution for a prospective dynamical model, WBKE. More interestingly, we investigated the Mittag-Leffler function, a revolutionary fractional operator that is generated with the help of a singular/non-singular fractional operator. These formulations aid experts in emulating the performance of a variety of real-world systems. The present investigation illuminates the employed nonlinear behaviors in a way that is clearly appropriate for the time instant and the time history, which can be effectively demonstrated using the fractional calculus idea. The graphs depicting the simulated interactions in this work can help practitioners determine several intriguing and important consequences of examining the paired process. They demonstrate the influence of the fractional operator by using an inexpensive approach to solve real-world situations. The current study can aid in the exploration of increasingly complicated and dynamic systems, as well as the acquisition of additional repercussions of particular instances of WBKE. The graphic representations provided are quite helpful in comprehending the networks' intricacy. The computational domain is used to verify the effectiveness and to demonstrate how the result moves from a mathematical formulation to an approximate finding as the series of solution components accumulates. Also, the proposed technique generates a new solution by avoiding any convolutions, transformations, or perturbations. Furthermore, we can state that the present investigation will assist scholars in demonstrating the characteristics of various frameworks.

Acknowledgements

This research was supported by Taif University Research Supporting Project Number (TURSP2020/96), Taif University, Taif, Saudi Arabia.

Conflict of interest

The authors declare that they have no competing interests.

References

[1]	M. Badiale, G. Tarantello, A Sobolev-hardy inequality with applications to a nonlinear elliptic equation arising in astrophysics, Arch. Rational Mech. Anal., 163 (2002), 259–293. doi: 10.1007/s002050200201. doi: 10.1007/s002050200201
[2]	Z. Chaouai, A. E. Hachimi, Qualitative properties of weak solutions for $p$ -Laplacian equations with nonlocal source and gradient absorption, B. Korean Math. Soc., 57 (2020), 1003–1031. doi: 10.4134/BKMS.b190720. doi: 10.4134/BKMS.b190720
[3]	X. M. Deng, J. Zhou, Global existence, extinction, and non-extinction of solutions to a fast diffusion $p$ -Laplcae evolution equation with singular potential, J. Dyn. Control Syst., 26 (2020), 509–523. doi: 10.1007/s10883-019-09462-5. doi: 10.1007/s10883-019-09462-5
[4]	J. S. Guo, B. Hu, Blowup rate estimates for the heat equation with a nonlinear gradient source term, Discrete Cont. Dyn. Syst., 20 (2008), 927–937. doi: 10.3934/dcds.2008.20.927. doi: 10.3934/dcds.2008.20.927
[5]	R. G. Iagar, Ph. Laurençot, Positivity, decay, and extinction for a singular diffusion equation with gradient absorption, J. Funct. Anal., 262 (2012), 3186–3239. doi: 10.1016/j.jfa.2012.01.013. doi: 10.1016/j.jfa.2012.01.013
[6]	D. M. Liu, C. L. Mu, Cauchy problem for a doubly degenerate parabolic equation with inhomogeneous source and measure data, Differ. Integral Equ., 27 (2014), 1001–1012.
[7]	D. M. Liu, C. L. Mu, Extinction for a quasilinear parabolic equation with a nonlinear gradient source, Taiwan. J. Math., 18 (2014), 1329–1343. doi: 10.11650/tjm.18.2014.3863. doi: 10.11650/tjm.18.2014.3863
[8]	D. M. Liu, C. L. Mu, Extinction for a quasilinear parabolic equation with a nonlinear gradient source and absorption, J. Appl. Anal. Comput., 5 (2015), 114–137. doi: 10.11948/2015010. doi: 10.11948/2015010
[9]	D. M. Liu, C. L. Mu, Critical extinction exponent for a doubly degenerate non-divergent parabolic equation with a gradient source, Appl. Anal., 97 (2018), 2132–2141. doi: 10.1080/00036811.2017.1359557. doi: 10.1080/00036811.2017.1359557
[10]	D. M. Liu, C. Y. Liu, Global existence and extinction singularity for a fast diffusive polytropic filtration equation with variable coefficient, Math. Probl. Eng., 2021 (2021), 5577777. doi: 10.1155/2021/5577777. doi: 10.1155/2021/5577777
[11]	D. M. Liu, L. Yang, Extinction phenomenon and decay estimate for a quasilinear parabolic equation with a nonlinear source, Adv. Math. Phys., 2021 (2021), 5569043. doi: 10.1155/2021/5569043. doi: 10.1155/2021/5569043
[12]	W. J. Liu, B. Wu, A note on extinction for fast diffusive $p$ -Laplacian with sources, Math. Method. Appl. Sci., 31 (2008), 1383–1386. doi: 10.1002/mma.976. doi: 10.1002/mma.976
[13]	P. Quittner, P. Souplet, Superlinear parabolic problems: Blow-up, global existence and steady states, Springer Science & Business Media, 2007. doi: 10.1007/978-3-7643-8442-5.
[14]	P. Souplet, J. L. Vázquez, Stabilization towards a singular steady state with gradient blow-up for a diffusion-convection problem, Discrete Cont. Dyn. Syst., 14 (2006), 221–234. doi: 10.3934/dcds.2006.14.221. doi: 10.3934/dcds.2006.14.221
[15]	Z. Tan, Non-Newton filtration equation with special medium void, Acta Math. Sci., 24 (2004), 118–128. doi: 10.1016/S0252-9602(17)30367-3. doi: 10.1016/S0252-9602(17)30367-3
[16]	Y. Tian, C. L. Mu, Extinction and non-extinction for a $p$ -Laplacian equation with nonlinear source, Nonlinear Anal., 69 (2008), 2422–2431. doi: 10.1016/j.na.2007.08.021. doi: 10.1016/j.na.2007.08.021
[17]	J. L. Vázquez, The porous medium equation: Mathematical theory, New York: Oxford University Press, 2007. doi: 10.1093/acprof:oso/9780198569039.001.0001.
[18]	M. X. Wang, Nonlinear elliptic equations, Beijing: Science Press, 2010.
[19]	Z. Q. Wu, J. N. Zhao, J. X. Yin, H. L. Li, Nonlinear diffusion equations, New Jersey: World Scientific Publishing, 2001. doi: 10.1142/9789812799791.
[20]	Z. C. Zhang, Gradient blowup rate for a viscous Hamilton-Jacobi equation with degenerate diffusion, Arch. Math., 100 (2013), 361–367. doi: 10.1007/s00013-013-0505-4. doi: 10.1007/s00013-013-0505-4
[21]	Z. C. Zhang, Y. Li, Blowup and existence of global solutions to nonlinear parabolic equations with degenerate diffusion, Electron. J. Differ. Eq., 2013 (2013), 264.
[22]	J. Zhou, A multi-dimension blow-up problem to a porous medium diffusion equation with special medium void, Appl. Math. Lett., 30 (2014), 6–11. doi: 10.1016/j.aml.2013.12.003. doi: 10.1016/j.aml.2013.12.003
[23]	J. Zhou, Global existence and blow-up of solutions for a non-Newton polytropic filtration system with special volumetric moisture content, Comput. Math. Appl., 71 (2016), 1163–1172. doi: 10.1016/j.camwa.2016.01.029. doi: 10.1016/j.camwa.2016.01.029

This article has been cited by:

1.	Timilehin Kingsley Akinfe, Adedapo Chris Loyinmi, An improved differential transform scheme implementation on the generalized Allen–Cahn equation governing oil pollution dynamics in oceanography, 2022, 6, 26668181, 100416, 10.1016/j.padiff.2022.100416
2.	Saima Rashid, Fahd Jarad, Hajid Alsubaie, Ayman A. Aly, Ahmed Alotaibi, A novel numerical dynamics of fractional derivatives involving singular and nonsingular kernels: designing a stochastic cholera epidemic model, 2023, 8, 2473-6988, 3484, 10.3934/math.2023178
3.	Maysaa Al-Qurashi, Sobia Sultana, Shazia Karim, Saima Rashid, Fahd Jarad, Mohammed Shaaf Alharthi, Identification of numerical solutions of a fractal-fractional divorce epidemic model of nonlinear systems via anti-divorce counseling, 2022, 8, 2473-6988, 5233, 10.3934/math.2023263
4.	Saima Rashid, Bushra Kanwal, Muhammad Attique, Ebenezer Bonyah, Ibrahim Mahariq, An Efficient Technique for Time-Fractional Water Dynamics Arising in Physical Systems Pertaining to Generalized Fractional Derivative Operators, 2022, 2022, 1563-5147, 1, 10.1155/2022/7852507
5.	M. S. Alqurashi, Saima Rashid, Bushra Kanwal, Fahd Jarad, S. K. Elagan, A novel formulation of the fuzzy hybrid transform for dealing nonlinear partial differential equations via fuzzy fractional derivative involving general order, 2022, 7, 2473-6988, 14946, 10.3934/math.2022819
6.	Zharasbek Baishemirov, Abdumauvlen Berdyshev, Dossan Baigereyev, Kulzhamila Boranbek, Efficient Numerical Implementation of the Time-Fractional Stochastic Stokes–Darcy Model, 2024, 8, 2504-3110, 476, 10.3390/fractalfract8080476
7.	Kingsley Timilehin Akinfe, A reliable analytic technique for the modified prototypical Kelvin–Voigt viscoelastic fluid model by means of the hyperbolic tangent function, 2023, 7, 26668181, 100523, 10.1016/j.padiff.2023.100523
8.	P Karunakar, S Chakraverty, TD Rao, K Ramesh, AK Hussein, Fuzzy fractional shallow water wave equations: analysis, convergence of solutions, and comparative study with depth as triangular fuzzy number, 2024, 99, 0031-8949, 125216, 10.1088/1402-4896/ad8afd

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(2498) PDF downloads(79) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Mathematics

Extinction behavior for a parabolic $p$ -Laplacian equation with gradient source and singular potential

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. Road map of $\bar{\mathbf{q}}$ -homotopy analysis transform method

4. Test examples

5. Numerical results and their physical interpretation

6. Conclusions

Acknowledgements

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Catalog

AIMS Mathematics

Extinction behavior for a parabolic p p -Laplacian equation with gradient source and singular potential

Related Papers:

Abstract

1. Introduction

2. Preliminaries

3. Road map of ˉq \bar{\mathbf{q}} -homotopy analysis transform method

4. Test examples

5. Numerical results and their physical interpretation

6. Conclusions

Acknowledgements

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Extinction behavior for a parabolic $p$ -Laplacian equation with gradient source and singular potential

3. Road map of $\bar{\mathbf{q}}$ -homotopy analysis transform method