A free boundary problem with a Stefan condition for a ratio-dependent predator-prey model

1.   Introduction

Let $G$ be a nontrivial connected graph with vertex set $V = V(G)$. The distance between two vertices $u$ and $v$ in graph $G$ is the length of the shortest path between $u$ and $v$, denoted as $d_{G}(u, v)$ and abbreviated as $d(u, v)$. The maximum distance between any two vertices in graph $G$ is called the diameter of the graph, denoted as $d$. Let $S$ be a subset of $t$ vertices in graph $G$, where $t\ge 2$ and $t$ is a positive integer. If $S$ is an independent set and every two vertices in $S$ have the same neighborhood, or if $S$ is a clique and every two vertices in $S$ have the same closed neighborhood, then the $t$ vertices in $S$ are called $t$-tuplets. In particular, if $t = 2$, then these two vertices are called twins, and if $t = 3$, then these three vertices are called triplets. Let the diameter be $d\ge 2$ of the graph $G$. The red-white coloring $c$ of the graph $G$ is defined as assigning each vertex in the graph $G$ to be either red or white with at least one vertex assigned to be red, and the color of the vertex $v$ is denoted as $c(v)$. Each vertex $v$ is associated with a $d$-vector $\overrightarrow{d} (v) = (a_{1}, a_{2}, \dots, a_{d})$, called the code of $v$, where the $i$th coordinate of the $d$-vector is the number of red vertices at distance $i$ from vertex $v$, where $1\le i\le d$. If $a_{j} = a_{j+1} = \cdots = a_{j+s}$, the subsequence $\left (a_{j}, a_{j+1}, \dots a_{j+s} \right)$ is denoted as $\left (a_{j}^{s+1} \right)$. Specifically, if $a_{1} = a_{2} = \cdots = a_{n} = 1$, the sequence $(1, 1, \dots, 1)$ is abbreviated as $\left (1^{n}\right).$ If a red-white coloring of a graph $G$ such that every vertex in the graph $G$ has a different code, the coloring is said to be an identification coloring or an $ID$-coloring of the graph $G$. A graph possessing an $ID$-coloring is said to be an $ID$-graph. The number of red vertices in the $ID$-coloring is called the identification coloring number, and the smallest identification coloring number of a graph $G$ is called the $ID$-number of the graph, or simply $ID(G)$. A lollipop graph $T_{m, n+1}$ is a graph obtained by coinciding a vertex on the cycle $C_{m}\;$$(m\ge 3)$ with a vertex of degree 1 on the path $P_{n+1}$ $(n\ge 1)$. Then, the order of graph $T_{m, n+1}$ is $m+n$, and $m$ and $n$ are positive integers.

Over the last decades, there has been an increasing interest in studying methods for uniquely identifying vertices in graphs, and one of the best known methods is combining distance and coloring. For example, for metric dimension for a nontrivial connected graph of order $n$, find an ordered set $W = \left \{ w_{1}, w_{2}, \dots, w_{k} \right \}$ of $k$ vertices in the graph $G$, $1\le k\le n$, with each vertex $v$ in the graph $G$ associated with a $k$-vector$\left (a_{1}, a_{2}, \dots a_{k} \right)$, where the $i$th coordinate $a_{i}$ represents the distance $d\left (v, w_{i} \right)$ between the vertex $v$ and $w_{i}$, such that different vertices in the graph $G$ have different $k$-vectors, which can be usually chosen to be $W = V(G)$, and the smallest dimension of such a set $W$ is called the metric dimension of the graph $G$. Equivalently, the metric dimension of a connected graph $G$ can be defined as the minimum number of vertices of the same color, for example, red, in the graph $G$ such that for any two vertices $u$ and $v$ in the graph $G$, there exists a red vertex that satisfies $d\left (u, w \right) \ne d\left (v, w \right)$. These concepts were independently introduced by Slater ^[1] and Harary and Melter ^[2], and have been studied by many people, such as ^[3,4]. In 1988, Slater ^[1,5] described the usefulness of these concepts when dealing with the US Coast Guard's Loran stations (remote navigation aids.) and Johnson of Upjohn Pharmaceuticals used this concept in an attempt to develop the capability of large chemical map datasets ^[6,7]. These concepts have been investigated by people in many different applications, for example, ^{[8,9,10,11,12,13]}.

In recent years, scholars have increasingly studied vertex identification and achieved results. Compared to general graphs, special classes of graphs are more favored by scholars. In ^[14], Gary Chartrand et al. introduced $ID$-coloring and studied the identification coloring numbers of cycles and paths. Yuya Kono and Ping Zhang studied the identification coloring numbers of special trees ^[15], caterpillars ^[16], as well as prism graphs and grid graphs ^[17]. Inspired by these, this paper uses $d$-vectors to study the identification coloring numbers of lollipop graphs.

2.   Preliminaries

Lemma 2.1. ^[14] Let $c$ be a red-white coloring of a connected graph $G$ where there is at least one vertex of each color. If $x$ is a red vertex and $y$ is a white vertex, then $\overrightarrow{d} \left (x \right) \ne \overrightarrow{d} \left (y \right)$.

Lemma 2.2. ^[14] There is no $ID$-coloring of a connected graph with exactly two red vertices.

Lemma 2.3. ^[14] A nontrivial connected graph $G$ has $ID\left (G \right) = 1$ if, and only if, $G$ is a path.

Lemma 2.4. ^[14] For each integer $n \ge 4$, there is an $ID$-coloring of $P_{n+1}$ with exactly $r$ red vertices if, and only if, $r = 1$ or $3\le r\le n$.

Lemma 2.5. ^[14] For each integer $n \ge 6$, there is an $ID$-coloring of $C_{m}$ with exactly $r$ red vertices if, and only if, $3\le r\le m-3$. Consequently, $ID\left (C_{m} \right) = 3$ for $n \ge 6$.

From the proof procedure of Theorems 3.1 and 4.4 in the literature ^[14], Lemmas 2.6 and 2.7 are obtained, respectively.

Lemma 2.6. ^[14] Assuming the path $P_{n+1} = w_{0}w_{1}w_{2}\dots w_{n}\; \left (n\ge 3 \right)$, a red-white coloring $c$ is defined on $P_{n+1}$, where the $r$ vertices $w_{i}$, where $n-r\le i\le n-2$ and $i = n$, are assigned as red, and the remaining vertices are assigned as white. It is then proven that this coloring is an $ID$-coloring of the path $P_{n+1}$.

Lemma 2.7. ^[14] Assuming the cycle $C_{m} = v_{0}v_{1}v_{2}\dots v_{i-1}v_{i}\dots v_{m-2}v_{m-1}v_{0}\; \left (m\ge 6 \right)$, a red-white coloring $c$ is defined on $C_{m}$, where the $r$ vertices $v_{i}$, where $m-r-1\le i\le m-3$ and $i = m-1$, are assigned as red, and the remaining vertices are assigned as white. It is then proven that this coloring is an $ID$-coloring of the cycle $C_{m}$.

Lemma 2.8. ^[14] A connected graph $G$ of diameter 2 is an $ID$-graph if, and only if, $G = P_{3}$.

Lemma 2.9. ^[14] Let $c$ be an $ID$-coloring of a connected graph $G$. If $u$ and $v$ are twins of $G$, then $c\left (u \right) \ne c\left (v \right)$. Consequently, if $G$ is an $ID$-graph, then $G$ is triplet free.

Lemma 2.10. ^[15] Let $G$ be a connected graph with an $ID$-coloring $c$. If $H$ is a connected subgraph of $G$ such that (i) $H$ contains all red vertices in $G$ and (ii) $d_{H}\left (x, y \right) = d_{G} \left (x, y \right)$ for every two vertices $x$ and $y$ of $H$, then the restriction of $c$ to $H$ is an $ID$-coloring of $H$.

3.   The main results

In a lollipop graph $T_{m, n+1}$, if all of its vertices are assigned as red, then due to the symmetry of the cycle $C_{m}$, it is known that there must be at least two vertices on the cycle $C_{m}$ with the same $d$-vector. Therefore, there is no $ID$-coloring of $T_{m, n+1}$ with an identification coloring number of $m+n$.

Since the diameter of the graph $T_{3, 2}$ is $d = 2$, it is known from Lemma 2.8 that $T_{3, 2}$ is not an $ID$-graph.

Theorem 3.1. The lollipop graph $T_{3, n+1} \left (n\ge 2 \right)$ has an identification coloring number of $r$ for an $ID$-coloring if, and only if, $3\le r\le n+1$.

Proof. In $T_{3, n+1},$ let $C_{3} = v_{0}v_{1}v_{2}v_{0}$ and $P_{n+1} = v_{0}w_{1}w_{2}\dots w_{n-1}w_{n}$. First, we prove the necessity, by Lemmas 2.2 and 2.3, $3\le r\le n+1$. Suppose $r = n+2$. At this point, there is only one white vertex in the graph if there exists an $ID$-coloring in $T_{3, n+1}$, because $v_{1}$ and $v_{2}$ are twins. By Lemma 2.9, $v_{1}$ and $v_{2}$ have different color assignments and one can assign $v_{2}$ as white, then the rest of the vertices are assigned as red, and, at this point, $\overrightarrow{d} \left (v_{1} \right) = \overrightarrow{d}\left (w_{n} \right) = \left (1^{n+1} \right)$, that is, there exists no $ID$-coloring of $T_{3, n+1}$ with exactly $n+2$ red vertices.

The following is a proof of sufficiency. Assume that $3\le r\le n+1$, and define a red-white coloring $c$ of the graph $T_{3, n+1}$ by assigning $v_{1}$ and $w_{i}$ to red, where $1\le i\le r-1$, and the rest of the vertices to white, and the following proof that this coloring is an $ID$-coloring. By Lemma 2.1, the $d$-vectors of the red vertices are different from those of the white vertices, so we only consider the $d$-vectors of the two vertices with the same color. From Lemmas 2.6 and 2.10, all red vertices on $T_{3, n+1}$ have different $d$-vectors and all white vertices on $P_{n+1}$ have different $d$-vectors. Moreover, $v_{0}$ is the only white vertex whose first coordinate of the $d$-vector is 2, so we only need to consider whether the $d$-vector of $v_{2}$ is the same as that of the white vertices on $P_{n+1}$. $\overrightarrow{d} \left (v_{2} \right) = \left (1^{r}, 0^{n-r+1} \right)$, the only white vertex in $w_{i} \left (1\le i\le n \right)$ that satisfies the first coordinate of the $d$-vector is $w_{r}$, and with $\overrightarrow{d} \left (w_{r} \right) = \left (1^{r-1}, 0, 1, 0^{n-r} \right)$, it is clear that $\overrightarrow{d} \left (v_{2} \right) \ne \overrightarrow{d}\left (w_{i} \right).$ Thus, $c$ is an $ID$-coloring.

Theorem 3.2. The lollipop graph $T_{4, n+1} \left (n\ge 1 \right)$ has an identification coloring number of $r$ for an $ID$-coloring when $n = 1$ or $n = 2$ if, and only if, $r = 3$; when $n\ge 3$ if, and only if, $3\le r\le n+2$.

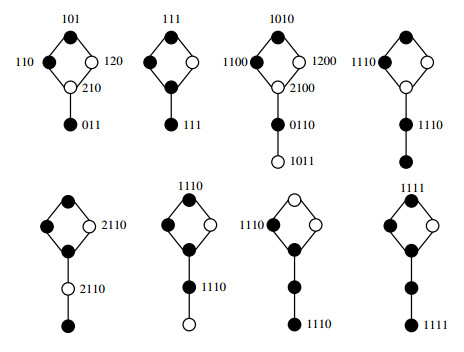
Proof. In $T_{4, n+1},$ let $C_{4} = v_{0}v_{1}v_{2}v_{3}v_{0}$ and $P_{n+1} = v_{0}w_{1}w_{2}\dots w_{n-1}w_{n}$. Since $v_{1}$ and $v_{3}$ are twins, if there exists an $ID$-coloring, according to Lemma 2.9, $v_{1}$ and $v_{3}$ must be assigned different colors. From Figure 1, when $n = 1$ or $n = 2$, if, and only if, $r = 3$. Now, consider $n\ge 3$.

First, we prove the necessity. It is known from Lemmas 2.2 and 2.3 that $3\le r\le n+3$. Assuming $r = n+3$, then there is only one white vertex in the graph, denoted as $v_{3}$. In this case, we have $\overrightarrow{d} \left (v_{2} \right) = \overrightarrow{d}\left (w_{n} \right) = \left (1^{n+2} \right)$. Therefore, there does not exist an $ID$-coloring in $T_{4, n+1}$ with exactly $r = n+3$ red vertices.

The sufficiency is proved below. Assuming $3\le r\le n+1$, define a red-white coloring $c$ of the graph $T_{4, n+1}$, where $v_{1}$ and $w_{i}$ are assigned red, with $1\le i\le r-1$, and the remaining vertices are assigned white. It is to be proven that this coloring is an $ID$-coloring. By Lemma 2.1, it is known that the $d$-vectors of red vertices and white vertices are different, so we only need to consider the vectors of vertices of the same color. By Lemmas 2.6 and 2.10, it is known that the vectors of all red vertices in $T_{4, n+1}$ are different, and the $d$-vectors of all white vertices on $P_{n+1}$ are different. Additionally, $v_{0}$ is the unique white vertex with a $d$-vector whose first coordinate is 2, so we only need to consider whether $v_{2}$ and $v_{3}$ have the same $d$-vector as the white vertices on $P_{n+1}$. The subsequence formed by the first two coordinates of $\overrightarrow{d} \left (v_{2} \right)$ is $(1, 0)$, and the subsequence formed by the first two coordinates of $\overrightarrow{d} \left (v_{3} \right)$ is $(0, 2)$. If the first coordinate of $\overrightarrow{d} \left (w_{i} \right)$ is 1, then its subsequence formed by the first two coordinates is $(1, 1)$; if the first coordinate of $\overrightarrow{d} \left (w_{i} \right)$ is 0, then its subsequence formed by the first two coordinates is $(0, 1)$ or $(0, 0)$. Therefore, the $d$-vector of $v_{2}$, $v_{3}$, and all white vertices on $P_{n+1}$ are also different. In conclusion, it is known that the $d$-vectors of all vertices in $T_{4, n+1}$ are different, and, therefore, $c$ is an $ID$-coloring.

Theorem 3.3. The lollipop graph $T_{5, n+1} \left (n\ge 1 \right)$ has an identification coloring number of $r$ for an $ID$-coloring. When $n = 1$ if, and only if, $r = 3$ or $r = 4$. When $n\ge 2$ if, and only if, $3\le r\le n+4$.

Proof. In $T_{5, n+1}$, let $C_{5} = v_{0}v_{1}v_{2}v_{3}v_{4}v_{0}$ and $P_{n+1} = v_{0}w_{1}w_{2}\dots w_{n-1}w_{n}$. From Figure 2, it is known that when $n = 1$, the condition holds if, and only if, $r = 3$ or $r = 4$. Now, we consider the case when $n\ge 2$.

First, it is necessary to prove that $3\le r\le n+4$ based on Lemmas 2.2 and 2.3. Then, we proceed to prove sufficiency. By Lemma 2.1, it is known that the $d$-vectors of red vertices and white vertices are different, so we only need to consider the $d$-vectors of vertices of the same color.

Case 1. $3\le r\le n+2.$

Define the red-white coloring $c$ of graph $T_{5, n+1}$. Assign $v_{i}$ and $w_{j}$ to white, where $i\in \left \{ 1, 3, 4 \right \}$, $r-1\le j\le n$, and the remaining vertices are assigned to red. We will now prove that this coloring is an $ID$-coloring. By Lemmas 2.6 and 2.10, all red vertices have different $d$-vectors and all white vertices on $P_{n+1}$ have different $d$-vectors. Moreover, $v_{1}$ is the only white vertex whose first coordinate of the $d$-vector is 2, so we only need to consider whether the $d$-vectors of $v_{3}$ and $v_{4}$ are the same as those of the white vertices on $P_{n+1}$. Since $\overrightarrow{d}\left (v_{3} \right) = \left (1^{r}, 0^{n+2-r} \right)$ and $\overrightarrow{d}\left (v_{4} \right) = \left (1, 2, 1^{r-3}, 0^{n-r+3} \right)$, if the first coordinate of $\overrightarrow{d}\left (w_{j} \right)$ is 1, then we have $j = r-1$, at which point $\overrightarrow{d}\left (w_{r-1} \right) = \left (1^{r-1}, 0, 1, 0^{n-r+1} \right)$, so $\overrightarrow{d}\left (v_{3} \right) \ne \overrightarrow{d}\left (v_{4} \right)$ and $\overrightarrow{d}\left (v_{3} \right) \ne \overrightarrow{d}\left (w_{j} \right)$, $\overrightarrow{d}\left (v_{4} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Thus, $c$ is an $ID$-coloring.

Case 2. $r = n+3.$

We define a red-white coloring $c$ of the graph $T_{5, n+1}$, where $v_{0}$ and $v_{4}$ are assigned white, and the remaining vertices are assigned red. It is to be proven that this coloring is an $ID$-coloring.

To start, the first coordinate of $\overrightarrow{d}\left (v_{0} \right)$ is 2, while the first coordinate of $\overrightarrow{d}\left (v_{4} \right)$ is 1, so $\overrightarrow{d}\left (v_{0} \right) \ne \overrightarrow{d}\left (v_{4} \right)$. Now, we consider the $d$-vectors of the red vertices.

$\overrightarrow{d}\left (v_{1} \right) = \left (1, 2, 1^{n-1}, 0 \right)$, $\overrightarrow{d}\left (v_{2} \right) = \left (2, 0, 1^{n} \right)$, $\overrightarrow{d}\left (v_{3} \right) = \left (1^{n+2} \right)$. It is obvious that the $d$-vectors of all red vertices on $C_{5}$ are different.

Next, we prove that the $d$-vectors of red vertices on cycles and paths are different. If the first coordinate of the $d$-vector of vertex $w_{j}$ on the path is 1, then $j = 1$ or $j = n$. When $j = 1$, the subsequence formed by the first three coordinates of $\overrightarrow{d}\left (w_{1} \right)$ is $(1, 1, 2)$ or $(1, 2, 2)$ or $(1, 2, 3)$, and it is obvious that $\overrightarrow{d}\left (w_{1} \right) \ne \overrightarrow{d}\left (v_{i} \right)$. When $j = n$, then $\overrightarrow{d}\left (w_{n} \right) = \left (1^{n-1}, 0, 1, 2 \right)$, and it is obvious that $\overrightarrow{d}\left (w_{n} \right) \ne \overrightarrow{d}\left (v_{i} \right)$. If the subsequence formed by the first two coordinates of the $d$-vector of vertex $w_{j}$ is $(2, 0)$, then $j = 2$ and $n = 3$. In this case, $\overrightarrow{d}\left (w_{2} \right) = \left (2, 0, 1, 2 \right)$, and it is obvious that $\overrightarrow{d}\left (w_{2} \right) \ne \overrightarrow{d}\left (v_{i} \right)$.

We prove that the $d$-vectors of red vertices on paths are different, with $\overrightarrow{d}\left (w_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{n+2} \right)$, $\overrightarrow{d}\left (w_{j} \right) = (b_{1},$ $b_{2},$ $\dots,$ $b_{n+2})$. When $1\le i < j\le \frac{n+1}{2}$, $a_{i} = 1$, and $b_{i} = 2$, then $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$; when $\frac{n+1}{2} \le i < j\le n$, $a_{n+1-j} = 2$, and $b_{n+1-j} = 1$, then $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$; when $1\le i < \frac{n+1}{2}$ and $\frac{n+1}{2} < j\le n$, $\overrightarrow{d}\left (w_{i} \right) = \left (2^{i-1}, 1, \dots \right)$ and $\overrightarrow{d}\left (w_{j} \right) = \left (2^{n-j}, 1, \dots \right)$, if $i-1\ne n-j$, obviously, there is $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$, if $i-1 = n-j$; when $w_{i}$ and $w_{j}$ are adjacent, $a_{i+1} = 1$ and $b_{i+1} = 0$; when $w_{i}$ and $w_{j}$ are not adjacent, $a_{i+1} = 2$ and $b_{i+1} = 1$, that is, $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Therefore, $c$ is an $ID$-colored.

Case 3. $r = n+4.$

Define the red-white coloring $c$ of the graph $T_{5, n+1}$, with $v_{4}$ assigned as white and the remaining vertices assigned as red. We will now prove that this coloring is an $ID$-coloring. We consider the $d$-vector of the red vertices.

$\overrightarrow{d}\left (v_{0} \right) = \left (2, 3, 1^{n-2}, 0, 0 \right)$, $\overrightarrow{d}\left (v_{1} \right) = \left (2, 2, 1^{n-1}, 0 \right)$, $\overrightarrow{d}\left (v_{2} \right) = \left (2, 1^{n+1} \right)$, $\overrightarrow{d}\left (v_{3} \right) = \left (1, 2, 1^{n} \right)$. Therefore, the $d$-vectors of all red vertices on $C_{5}$ are distinct.

Next, we prove that the $d$-vectors of red vertices on cycles and paths are distinct. By contradiction, assume $\overrightarrow{d}\left (v_{i} \right) = \overrightarrow{d}\left (w_{j} \right)$. Let the last nonzero coordinate of $\overrightarrow{d}\left (v_{i} \right)$ be $a_{t}$ and the last nonzero coordinate of $\overrightarrow{d}\left (w_{j} \right)$ be $b_{s}$. Then, $s = t$, and it is obvious that $t = d\left (v_{i}, w_{n} \right) = d\left (v_{i}, v_{0} \right)+n$, so $s = d\left (w_{j}, v_{2} \right)$. In this case, $a_{t} = 1$ and $b_{t} = 2$, so $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$, which is a contradiction.

We also prove that the $d$-vectors of red vertices on paths are distinct. Let $\overrightarrow{d}\left (w_{i} \right) = (a_{1}, a_{2},$ $\dots,$ $a_{n+2})$, $\overrightarrow{d}\left (w_{j} \right) = (b_{1}, b_{2},$ $\dots,$ $b_{n+2})$. When $1\le i < j\le \frac{n-1}{2}$, $a_{i+2} = 3$ and $b_{i+2} = 2$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $\frac{n-1}{2} \le i < j\le n$, $a_{n+1-j} = 2$ and $b_{n+1-j} = 1$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $1\le i < \frac{n-1}{2}$ and $\frac{n-1}{2} < j\le n$, $\overrightarrow{d}\left (w_{i} \right) = \left (2^{i+1}, 3, \dots \right)$ and $\overrightarrow{d}\left (w_{j} \right) = \left (2^{n-j}, 1, \dots \right)$, and it is clear that $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right).$ Therefore, $c$ is an $ID$-coloring.

Theorem 3.4. The lollipop graph $T_{6, n+1}\; \left (n\ge 1 \right)$ has an $ID$-coloring with identification coloring number $r$. When $n = 1$ if, and only if, $3\le r\le 5$. When $n = 2$ or $n = 3$ if, and only if, $3\le r\le 7$. When $n\ge 4$ if, and only if, $3\le r\le n+5$.

Proof. In $T_{6, n+1},$ let $C_{6} = v_{0}v_{1}v_{2}v_{3}v_{4}v_{5}v_{0}$, $P_{n+1} = v_{0}w_{1}w_{2}\dots w_{n-1}w_{n}$. To begin, prove the necessity. By Lemmas 2.2 and 2.3, we know that $3\le r\le n+5$, assuming that $r = n+5$. At this point in time, the graph $T_{6, n+1}$ has only one white vertex, and if any vertex $w_{i}$ on $P_{n+1}$ is assigned to be white.By the symmetry of the cycle, at this point, there must be $\overrightarrow{d}\left (v_{1} \right) = \overrightarrow{d}\left (v_{5} \right)$. If $v_{0}$ or $v_{3}$ is assigned to be white, there is also $\overrightarrow{d}\left (v_{1} \right) = \overrightarrow{d}\left (v_{5} \right)$. Therefore, if there exists a $ID$-coloring of $T_{6, n+1}$, only $v_{i}$ can be assigned as white, where $i\in \left \{ 1, 2, 4, 5 \right \}$. From Figure 3, when $n = 1$, if, and only if, $3\le r\le 5$; when $n = 2$ or $n = 3$, if, and only if, $3\le r\le 7$.

The following proof of sufficiency only requires consideration of $n \ge 4$. From Lemma 2.1, we know that red vertices have different $d$-vectors to white vertices, so we only need to consider two vertices of the same color.

Case 1. $3\le r\le n+3.$

Define the red-white coloring $c$ of the graph $T_{6, n+1}$, where $v_{i}$ and $w_{j}$ are assigned as white, where $i\in \left \{ 2, 4, 5 \right \}$, $r-2\le j\le n$, and the remaining vertices are assigned as red. It is to be proved that this coloring is an $ID$-coloring.

From Lemmas 2.6 and 2.10, it is known that all $d$-vectors of the red vertices are different, and all $d$-vectors of the white vertices on $P_{n+1}$ are different. Additionally, $v_{2}$ is the only white vertex with the first coordinate of its $d$-vector being 2. Therefore, we only need to consider whether the $d$-vectors of $v_{4}$, $v_{5}$, and the white vertices on $P_{n+1}$ are the same. First, any white vertex $w_{j}$ on $P_{n+1}$ definitely has the subsequence $(0, 1)$, while $v_{4}$ and $v_{5}$ do not have the subsequence $(0, 1)$. Hence, it is clear that $\overrightarrow{d}\left (v_{4} \right) \ne \overrightarrow{d}\left (w_{j} \right)$ and $\overrightarrow{d}\left (v_{5} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Second, the second coordinate of $\overrightarrow{d}\left (v_{4} \right)$ is 1, while the second coordinate of $\overrightarrow{d}\left (v_{5} \right)$ is 3, so $\overrightarrow{d}\left (v_{4} \right) \ne \overrightarrow{d}\left (v_{5} \right)$. Therefore, $c$ is an $ID$-coloring.

Case 2. $r = n+4.$

In this case, there are only two white vertices in the graph. Define the red-white coloring $c$ of the graph $T_{6, n+1}$, where $w_{n-1}$ and $v_{5}$ are assigned as white, and the remaining vertices are assigned as red. It is to be proved that this coloring is an $ID$-coloring.

Since the second coordinate of $\overrightarrow{d}\left (v_{5} \right)$ is 3 and the second coordinate of $\overrightarrow{d}\left (w_{n-1} \right)$ is 1, it follows that $\overrightarrow{d}\left (v_{5} \right) \ne \overrightarrow{d}\left (w_{n-1} \right)$. Next, consider the $d$-vectors of the red vertices.

Only $\overrightarrow{d}\left (w_{n} \right)$ has the first coordinate as 0, while the first coordinate of the $d$-vectors of the other red vertices is 1 or 2. Therefore, the $d$-vector of $w_{n}$ is different from the $d$-vectors of the other red vertices.

$\overrightarrow{d}\left (v_{0} \right) = \left (2, 3, \dots \right)$, $\overrightarrow{d}\left (v_{1} \right) = \left (2, 2, 2, \dots \right)$, $\overrightarrow{d}\left (v_{2} \right) = \left (2, 2, 1, \dots \right)$, $\overrightarrow{d}\left (v_{3} \right) = \left (2, 1, 1, \dots \right)$, $\overrightarrow{d}\left (v_{4} \right) = \left (1, 2, 2, \dots \right)$. It is evident that the $d$-vectors of all red vertices on $C_{6}$ are different.

It is to be proved that the $d$-vectors of the red vertices on the cycle and path are different. By contradiction, assume $\overrightarrow{d}\left (v_{i} \right) = \overrightarrow{d}\left (w_{j} \right)$. Let $a_{t}$ be the last non-zero coordinate of $\overrightarrow{d}\left (v_{i} \right)$ and $b_{s}$ be the last non-zero coordinate of $\overrightarrow{d}\left (w_{j} \right)$. Then $s = t$, and it is clear that $t = d\left (v_{i}, w_{n} \right) = d\left (v_{i}, v_{0} \right)+n$, so $s = d\left (w_{j}, v_{3} \right)$. In this case, $a_{t-1}\in \left \{ 0, 1 \right \}$ while $b_{t-1}\in \left \{ 2, 3 \right \}$, so $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$, which is a contradiction.

It is also to be proved that the $d$-vectors of the red vertices on the path are different. Let $\overrightarrow{d}\left (w_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{n+3} \right)$ and $\overrightarrow{d}\left (w_{j} \right) = (b_{1}, b_{2},$ $\dots,$ $b_{n+3})$. When $1\le i < j\le \frac{n-3}{2}$, $a_{i+2} = 3$ while $b_{i+2} = 2$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $\frac{n-3}{2} \le i < j\le n-2$, $a_{n-1-j} = 2$ and $b_{n-1-j} = 1$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $1\le i < \frac{n-3}{2}$ and $\frac{n-3}{2} < j\le n-2$, $\overrightarrow{d}\left (w_{i} \right) = \left (2^{i+1}, 3, \dots \right)$ and $\overrightarrow{d}\left (w_{j} \right) = \left (2^{n-j-1}, 1, \dots \right)$, and it is clear that $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Therefore, $c$ is an $ID$-coloring.

Case 3. $r = n+5.$

Define the red-white coloring $c$ of the graph $T_{6, n+1}$, where $v_{5}$ is assigned as white and the remaining vertices are assigned as red. It is to be proved that this coloring is an $ID$-coloring. Consider the $d$-vectors of the red vertices.

The $d$-vectors of $v_{0}$, $v_{1}$, $v_{2}$, $v_{3}$, and $v_{4}$ have subsequences consisting of the first three coordinates, which are $(2, 3, 2)$, $(2, 2, 2)$, $(2, 2, 1)$, $(2, 1, 1)$, and $(1, 2, 2)$, respectively. Therefore, it is evident that the $d$-vectors of all red vertices on $C_{6 }$ are different.

It is to be proved that the $d$-vectors of the red vertices on the cycle and path are different. By contradiction, assume $\overrightarrow{d}\left (v_{i} \right) = \overrightarrow{d}\left (w_{j} \right)$. Let $a_{t}$ be the last nonzero coordinate of $\overrightarrow{d}\left (v_{i} \right)$ and $b_{s}$ be the last nonzero coordinate of $\overrightarrow{d}\left (w_{j} \right)$. Then, $s = t$, and it is clear that $t = d\left (v_{i}, w_{n} \right) = d\left (v_{i}, v_{0} \right)+n$, so $s = d\left (w_{j}, v_{3} \right)$. In this case, $a_{t-1} = 1$ while $b_{t-1}\in \left \{ 2, 3 \right \}$, so $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$, which is a contradiction.

It is also to be proved that the $d$-vectors of the red vertices on the path are different. Let $\overrightarrow{d}\left (w_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{n+3} \right)$ and $\overrightarrow{d}\left (w_{j} \right) = (b_{1}, b_{2},$ $\dots,$ $b_{n+3})$. When $1\le i < j\le \frac{n-1}{2}$, $a_{i+2} = 3$ while $b_{i+2} = 2$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $\frac{n-1}{2} \le i < j\le n$, $a_{n+1-j} = 2$ and $b_{n+1-j} = 1$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $1\le i < \frac{n-1}{2}$ and $\frac{n-1}{2} < j\le n$, $\overrightarrow{d}\left (w_{i} \right) = \left (2^{i+1}, 3, \dots \right)$ and $\overrightarrow{d}\left (w_{j} \right) = \left (2^{n-j}, 1, \dots \right)$, and it is clear that $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Therefore, $c$ is an $ID$-coloring.

Theorem 3.5. The lollipop graph $T_{m, n+1} \; \left (m\ge 7, n\ge 1 \right)$ has an identification coloring number of $r$ as an $ID$-coloring when $n \ne \frac{m}{2}$ if, and only if, $3\le r\le m+n-1$. When $n = \frac{m}{2}$, it has an identification coloring number of $r$ as an $ID$-coloring if, and only if, $3\le r\le m+n-2$.

Proof. Let the vertex where $C_{m}$ and $P_{n+1}$ overlap be denoted as $v_{0}$ in $T_{m, n+1}$. Suppose $C_{m} = v_{0}v_{1}v_{2}\dots$ $v_{i-1}$ $v_{i}\dots v_{m-2}v_{m-1}v_{0}$, $P_{n+1} = v_{0}w_{1}w_{2}\dots w_{n-1}w_{n}$, and the diameter of the cycle $C_{m}$ be denoted as $d_{1}$. First, we prove the necessity. From Lemmas 2.2 and 2.3, it is known that $3\le r\le m+n-1$. When $n = \frac{m}{2}$, the graph $T_{m, n+1}$ has only one white vertex. If we assign any vertex $w_{i}$ on $P_{n+1}$ as white, by the symmetry of the cycle, it is certain that $\overrightarrow{d}\left (v_{1} \right) = \overrightarrow{d}\left (v_{m-1} \right)$. If we assign $v_{0}$ or $v_{\frac{m}{2}}$ as white, we also have $\overrightarrow{d}\left (v_{1} \right) = \overrightarrow{d}\left (v_{m-1} \right)$. Therefore, if $T_{m, n+1}$ has an $ID$-coloring, only $v_{i}$, where $1\le i\le d_{1}-1$ or $d_{1}+1\le i\le m-1$, can be assigned as white. In this case, $\overrightarrow{d} \left (v_{1} \right) = \overrightarrow{d}\left (w_{1} \right) = \left (0, 1^{i-1}, 0, 1^{d_{1}-i-1 }, 0^{d_{1} } \right) +\left (2^{d_{1}-1 }, 1, 1, 0^{d_{1}-1 } \right)$, which means when $m\ge 7$ and $n \ne \frac{m}{2}$, there does not exist an $ID$-coloring of $T_{m, n+1}$ with exactly $m+n-1$ red vertices.

Next, we prove the sufficiency. From Lemma 2.1, it is known that the $d$-vectors of the red vertices are different from those of the white vertices, so we only need to consider vertices of the same color. We consider the following four cases: (1) $3\le r\le m-3$; (2) $r = m-2$; (3) $m-1\le r\le m+n-2$; (4) $r = m+n-1$.

Case 1. $3\le r\le m-3.$

Define the red-white coloring $c$ of the graph $T_{m, n+1}$, assigning $r$ vertices as red. When $d_{1}+r\le m$, assign $v_{i}$ as red, where $d_{1}+2\le i\le d_{1}+r$ and $i = d_{1}$, and the remaining vertices as white. When $d_{1}+r > m$, assign $v_{i}$ as red, where $0\le i\le d_{1}+r-m$, $i = d_{1}$, and $d_{1}+2\le i\le m-1$, and assign the remaining vertices as white. It is then proven that this coloring is an $ID$-coloring. From Lemmas 2.7 and 2.10, it is known that the $d$-vectors of all red vertices in $T_{m, n+1}$ are different, and the $d$-vectors of all white vertices on $C_{m}$ are different. Next, it is proven that the $d$-vectors of the white vertices on $C_{m}$ and $P_{n+1}$ are different. Let $t$ be the position of the last nonzero coordinate in the $d$-vector of $v_{i}$, and let $s$ be the position of the last nonzero coordinate in the $d$-vector of $w_{j}$. In this case, $t \le d_{1}$ and $s > d_{1}$, which implies $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Therefore, $c$ is an $ID$-coloring.

Case 2. $r = m-2.$

Define the red-white coloring $c$ of the graph $T_{m, n+1}$, assigning $v_{i}$ and $w_{j}$ as white, where $2 \le j\le n$, $i\in \left \{ 0, m-3, m-2 \right \}$, and the remaining vertices as red. It is then proven that this coloring is an $ID$-coloring. First, consider the $d$-vectors of the white vertices. Only $\overrightarrow{d}\left (v_{0} \right)$ has the first coordinate as 3, while the first coordinates of the $d$-vectors of the other white vertices are 0 or 1, so the $d$-vector of $v_{0}$ is different from the $d$-vectors of the other white vertices.

$\overrightarrow{d}\left (v_{m-3} \right) = \left (1, 2, \dots \right)$, $\overrightarrow{d}\left (v_{m-2} \right) = \left (1, 1, \dots \right)$, therefore, $\overrightarrow{d}\left (v_{m-3} \right) \ne \overrightarrow{d}\left (v_{m-2} \right)$. The only white vertex $w_{i}\; (2\le i\le n)$ with a $d$-vector whose first coordinate is 1 is $w_{2}$, and $\overrightarrow{d}\left (w_{2} \right) = \left (1, 0, \dots \right)$, so it is obvious that $\overrightarrow{d}\left (v_{m-2} \right) \ne \overrightarrow{d}\left (w_{i} \right)$ and $\overrightarrow{d}\left (v_{m-3} \right) \ne \overrightarrow{d}\left (w_{i} \right)$, where $2 \le j\le n$.

Next, it is proven that the $d$-vectors of the white vertices on the path are different. Let $\overrightarrow{d}\left (w_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{d_{1}+n} \right)$, $\overrightarrow{d}\left (w_{j} \right) = (b_{1},$ $b_{2},$ $\dots, b_{d_{1}+n})$, where $a_{i-1}$ is the first nonzero coordinate of $\overrightarrow{d}\left (w_{i} \right)$ and $b_{j-1}$ is the first nonzero coordinate of $\overrightarrow{d}\left (w_{j} \right)$. Since $i < j$, it follows that $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$.

Furthermore, consider the $d$-vectors of the red vertices. The $d$-vectors of $w_{1}$ and $v_{m-1}$ have the first coordinate as 0, while the first coordinates of the $d$-vectors of the other red vertices are 1 or 2, so the $d$-vectors of $w_{1}$ and $v_{m-1}$ are different from the $d$-vectors of the other red vertices. Additionally, the last nonzero coordinate of $\overrightarrow{d}\left (w_{1} \right)$ is at position $d_{1}+1$, while the last nonzero coordinate of $\overrightarrow{d}\left (v_{m-1} \right)$ is at position $d_{1}$, so $\overrightarrow{d}\left (w_{1} \right) \ne \overrightarrow{d}\left (v_{m-1} \right)$.

It is also proven that the $d$-vectors of the red vertices on the cycle are all different. Let $\overrightarrow{d}\left (v_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{d_{1}+n} \right)$, $\overrightarrow{d}\left (v_{j} \right) = (b_{1}, b_{2}, \dots, b_{d_{1}+n})$, when $1\le i < j\le \frac{m-3}{2}$, $a_{i} = 1$, and $b_{i} = 2$. In this case, $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$; when $\frac{m-3}{2} \le i < j\le m-4$, $a_{m-3-j} = 2$ and $b_{m-3-j} = 1$, so $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$; when $1\le i < \frac{m-3}{2}$ and $\frac{m-3}{2} < j\le m-4$, $\overrightarrow{d}\left (v_{i} \right) = \left (2^{i-1}, 1, \dots \right)$ and $\overrightarrow{d}\left (v_{j} \right) = \left (2^{m-j-4}, 1, \dots \right)$; if $i-1 \ne m-4-j$, then $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$; if $i-1 = m-4-j$, when $x$ and $y$ are adjacent, $a_{i+1} = 2$ and $b_{i+1} = 0$; when $x$ and $y$ are not adjacent, $a_{i+1} = 3$, $b_{i+1} = 1$; in this case, $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$. Therefore, $c$ is an $ID$-coloring.

Case 3. $m-1\le r\le m+n-2.$

Subcase 3.1. $r-m+2 \ne \frac{m}{2}.$

Define the red-white coloring $c$ of the graph $T_{m, n+1}$, assigning $v_{i}$ and $w_{j}$ as white, where $i\in \left \{ 0, m-1 \right \}$, and $r-m+3\le j\le n$, and the remaining vertices as red. Let $k = r-m+2$. It is then proven that this coloring is an $ID$-coloring.

Considering the $d$-vectors of the white vertices, $\overrightarrow{d}\left (v_{0} \right)$ has the first coordinate as 2, while the first coordinates of the $d$-vectors of the other white vertices are 1 or 0. It is then proven that $v_{m-1}$ and the $d$-vectors of $w_{i} (k+1\le i\le n)$ on the path are different. As $\overrightarrow{d}\left (v_{m-1} \right) = \left (1, 3, \dots \right)$, if $i = k+1$, then $\overrightarrow{d}\left (w_{i} \right) = \left (1, 1, \dots \right)$ or $\overrightarrow{d}\left (w_{i} \right) = \left (1, 0, \dots \right)$, and it is clear that $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (v_{m-1} \right)$. If $i > k+1$, then the first coordinate of $\overrightarrow{d}\left (w_{i} \right)$ is 0, and again, $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (v_{m-1} \right)$. When $x = w_{i}$ and $y = w_{j}$, the first nonzero coordinate of $\overrightarrow{d}\left (w_{i} \right)$ is $a_{i-k}$, and the first nonzero coordinate of $\overrightarrow{d}\left (v_{m-1} \right)$ is $b_{j-k}$, because $i \ne j$, $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Thus, all the $d$-vectors of the white vertices are different. Next, it is considered the $d$-vectors of the red vertices.

It is also proven that the $d$-vectors of the red vertices on the cycle are all different. Let $\overrightarrow{d}\left (v_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{d_{1}+n} \right)$, $\overrightarrow{d}\left (v_{j} \right) = (b_{1}, b_{2}, \dots, b_{d_{1}+n})$; when $1\le i < j\le \frac{m-1}{2}$, $a_{i} = 1$ and $b_{i} = 2$; in this case, $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$; when $\frac{m-1}{2} \le i < j\le m-2$, $a_{m-1-j} = 2$ and $b_{m-1-j} = 1$, so $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$; when $1\le i < \frac{m-1}{2}$ and $\frac{m-3}{2} < j\le m-2$, $\overrightarrow{d}\left (v_{i} \right) = \left (2^{i-1}, 1, \dots \right)$ and $\overrightarrow{d}\left (v_{j} \right) = \left (2^{m-j-2}, 1, \dots \right)$; if $i-1 \ne m-2-j$, then $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$; if $i-1 = m-2-j$, when $x$ and $y$ are adjacent, $a_{i+1} = 1$ and $b_{i+1} = 0$; when $x$ and $y$ are not adjacent, $a_{i+1} = 2$ and $b_{i+1} = 1$; in this case, $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$.

It is to be proved that the $d$-vectors of the red vertices on the cycle and path are different. By contradiction, assume $\overrightarrow{d}\left (v_{i} \right) = \overrightarrow{d}\left (w_{j} \right)$. Let $a_{t}$ be the last nonzero coordinate of $\overrightarrow{d}\left (v_{i} \right)$ and $b_{s}$ be the last nonzero coordinate of $\overrightarrow{d}\left (w_{j} \right)$. Then, $s = t$, and it is clear that $t = d\left (v_{i}, w_{n} \right) = d\left (v_{i}, v_{0} \right)+n$, so $s = d\left (w_{j}, v_{d_{1}} \right)$. If $m$ is odd, then $a_{t} = 1$ and $b_{t} = 2$, which gives $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. If $m$ is even, then $d(v_{i}, v_{d_{1}}) = d(w_{j}, w_{k})$. In this case, $a_{t-1}\in \left \{ 1, 2 \right \}$ and $b_{t-1}\in \left \{ 2, 3 \right \}$. If $a_{t-1} = 1$ or $b_{t-1} = 3$, it is clear that $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Next, consider the case $a_{t-1} = b_{t-1} = 2$. When $a_{t-1} = 2$, then $t-1 = d_{1}$, which means $j = 1$. If $k = 1$, then $i = d_{1}$, and in this case, the first coordinate of $\overrightarrow{d}\left (w_{1} \right)$ is 0, while the first coordinate of $\overrightarrow{d}\left (v_{d_{1}} \right)$ is 2, which leads to a contradiction. If $k \ge 2$, then the first coordinate of $\overrightarrow{d}\left (w_{1} \right)$ is 1. If the first coordinate of $\overrightarrow{d}\left (v_{i} \right)$ is 1, then $i = 1$ or $i = m-2$. When $i = 1$, then $k = d_{1} = \frac{m}{2}$, leading to a contradiction. When $i = m-2$, the subsequence formed by the first three coordinates of $\overrightarrow{d}\left (v_{m-2} \right)$ is $(1, 1, 3)$, while the subsequence formed by the first three coordinates of $\overrightarrow{d}\left (w_{1} \right)$ is $(1, 1, 2)$ or $(1, 2, 2)$ or $(1, 2, 3)$. It is evident that $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$.

It is also to be proved that the $d$-vectors of the red vertices on the path are different. Let $\overrightarrow{d}\left (w_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{d_{1}+n} \right)$, $\overrightarrow{d}\left (w_{j} \right) = (b_{1}, b_{2}, \dots, b_{d_{1}+n})$. When $1\le i < j\le \frac{k+1}{2}$, $a_{i} = 1$ while $b_{i} = 2$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $\frac{k+1}{2} \le i < j\le k$, $a_{k+1-j} = 2$ and $b_{k+1-j} = 1$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $1\le i < \frac{k+1}{2}$ and $\frac{k+1}{2} < j\le k$, $\overrightarrow{d}\left (w_{i} \right) = \left (2^{i-1}, 1, \dots \right)$ and $\overrightarrow{d}\left (w_{j} \right) = \left (2^{k+1-j}, 1, \dots \right)$, if $i-1 \ne k+1-j$, then $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$; if $i-1 = k+1-j$, when $x$ and $y$ are adjacent, $a_{i+1} = 1$ and $b_{i+1} = 0$, when $x$ and $y$ are not adjacent, $a_{i+1} = 2$ and $b_{i+1} = 1$, in this case $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Therefore, $c$ is an $ID$-coloring.

Subcase 3.2. $r-m+2 = \frac{m}{2}.$

Define the red-white coloring $c$ of the graph $T_{m, n+1}$, assigning $v_{m-2}$ and $w_{j}$ as white, where $d_{1}+1\le j\le n$ and $j = d_{1}-1$, and the remaining vertices as red. Let $k = r-m+2$. In this case, $m \ge 8$, which means $k \ge 4$. It is then proven that this coloring is an $ID$-coloring.

Considering the $d$-vectors of the white vertices. First, the first coordinate of $\overrightarrow{d}\left (v_{m-2} \right)$ and $\overrightarrow{d}\left (w_{d_{1}-1} \right)$ is 2, while the first coordinate of the $d$-vectors of the other white vertices is 1 or 0. Hence, $v_{m-2}$ and $w_{d_{1}-1}$ are different from the $d$-vectors of the other white vertices. Second, $\overrightarrow{d}\left (v_{m-2} \right) = \left (2, 2, \dots \right)$, and $\overrightarrow{d}\left (w_{d_{1}-1} \right) = \left (2, 1, \dots \right)$, and it is evident that $\overrightarrow{d}\left (v_{m-2} \right) \ne \overrightarrow{d}\left (w_{d_{1}-1} \right)$. Lastly, it is proven that the $d$-vectors of the white vertices on the path are all different. Let $\overrightarrow{d}\left (w_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{d_{1}+n} \right)$, and $\overrightarrow{d}\left (w_{j} \right) = (b_{1}, b_{2}, \dots, b_{d_{1}+n})$. In this case, the first nonzero coordinate of $\overrightarrow{d}\left (w_{i} \right)$ is $a_{i-k}$, and the first nonzero coordinate of $\overrightarrow{d}\left (w_{j} \right)$ is $b_{j-k}$. Since $i \ne j$, $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Therefore, all the $d$-vectors of the white vertices are different. Next, it is considered the $d$-vectors of the red vertices.

Only $\overrightarrow{d}\left (w_{d_{1}} \right)$ has the first coordinate as 0, and only $\overrightarrow{d}\left (v_{0} \right)$ has the first coordinate as 3, while the first coordinates of the $d$-vectors of the other red vertices are 1 or 2. Additionally, $v_{m-1}$ is the only red vertex with a subsequence of the first two coordinates as $(1, 3)$, so $v_{0}$, $v_{m-1}$, and $w_{d_{1}}$ have $d$-vectors that are all different from those of the other red vertices.

It is also proven that the $d$-vectors of the red vertices on the cycle are all different. Let $\overrightarrow{d}\left (v_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{d_{1}+n} \right)$, $\overrightarrow{d}\left (v_{j} \right) = (b_{1}, b_{2}, \dots, b_{d_{1}+n})$; when $1\le i < j\le \frac{m-3}{2}$, $a_{i+1} = 3$ and $b_{i+1} = 2$; in this case, $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$; when $\frac{m-3}{2} \le i < j\le m-3$, $a_{m-2-j} = 2$ and $b_{m-2-j} = 1$, so $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$; when $1\le i < \frac{m-3}{2}$ and $\frac{m-3}{2} < j\le m-3$, $\overrightarrow{d}\left (v_{i} \right) = \left (2^{i}, 3, \dots \right)$ and $\overrightarrow{d}\left (v_{j} \right) = \left (2^{m-j-3}, 1, \dots \right)$, then $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$.

It is to be proved that the $d$-vectors of the red vertices on the cycle and path are different. By contradiction, assume $\overrightarrow{d}\left (v_{i} \right) = \overrightarrow{d}\left (w_{j} \right)$. Let $a_{t}$ be the last nonzero coordinate of $\overrightarrow{d}\left (v_{i} \right)$ and $b_{s}$ be the last nonzero coordinate of $\overrightarrow{d}\left (w_{j} \right)$. Then, $s = t$, and it is clear that $t = d\left (v_{i}, w_{n} \right) = d\left (v_{i}, v_{0} \right)+n$, so $s = d\left (w_{j}, v_{d_{1}} \right)$. In this case, $a_{t-1}\in \left \{ 0, 1\right \}$ while $b_{t-1}\in \left \{ 2, 3 \right \}$, so $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$, which is a contradiction.

It is also to be proved that the $d$-vectors of the red vertices on the path are different. Let $\overrightarrow{d}\left (w_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{d_{1}+n} \right)$ and $\overrightarrow{d}\left (w_{j} \right) = (b_{1}, b_{2}, \dots, b_{d_{1}+n})$. When $1\le i < j\le \frac{k-2}{2}$, $a_{i+1} = 3$ while $b_{i+1} = 2$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $\frac{k-2}{2} \le i < j\le k-2$, $a_{k-1-j} = 2$ and $b_{k-1-j} = 1$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $1\le i < \frac{k-2}{2}$ and $\frac{k-2}{2} < j\le k-2$, $\overrightarrow{d}\left (w_{i} \right) = \left (2^{i}, 3, \dots \right)$ and $\overrightarrow{d}\left (w_{j} \right) = \left (2^{k-1-j}, 1, \dots \right)$, and it is clear that $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Therefore, $c$ is an $ID$-coloring.

Case 4. $r = m+n-1.$

The $ID$-coloring of $T_{8, 3}$ and $T_{12, 3}$ with $m+n-1$ red vertices is shown in Figure 4. Now, consider the red-white coloring of $T_{m, n+1}$, if $n = 2$, $m \ne 8$ and $m \ne 12$.

When $n \ne \frac{m}{2}$, define the red-white coloring $c$ of the graph $T_{m, n+1}$, assigning $v_{m-2}$ as white and the remaining vertices as red. It is then proven that this coloring is an $ID$-coloring. Consider the $d$-vectors of the red vertices.

Only the first coordinate of $\overrightarrow{d}\left (v_{0} \right)$ is 3, while the first coordinates of the $d$-vectors of the other red vertices are 1 or 2. Additionally, $v_{m-1}$ is the only red vertex with a subsequence of the first two coordinates as $(1, 3)$, so $v_{0}$, $v_{m-1}$, and the $d$-vectors of the other red vertices are all different.

It is also proven that the $d$-vectors of the red vertices on the cycle are all different. Let $\overrightarrow{d}\left (v_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{d_{1}+n} \right)$, $\overrightarrow{d}\left (v_{j} \right) = (b_{1}, b_{2}, \dots, b_{d_{1}+n})$; when $1\le i < j\le \frac{m-3}{2}$, $a_{i+1} = 3$ and $b_{i+1} = 2$; in this case, $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$; when $\frac{m-3}{2} \le i < j\le m-3$, $a_{m-2-j} = 2$ and $b_{m-2-j} = 1$, so $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$; when $1\le i < \frac{m-3}{2}$ and $\frac{m-3}{2} < j\le m-3$, $\overrightarrow{d}\left (v_{i} \right) = \left (2^{i}, 3, \dots \right)$ and $\overrightarrow{d}\left (v_{j} \right) = \left (2^{m-j-3}, 1, \dots \right)$, then $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (v_{j} \right)$.

It is to be proved that the $d$-vectors of the red vertices on the cycle and path are different. By contradiction, assume $\overrightarrow{d}\left (v_{i} \right) = \overrightarrow{d}\left (w_{j} \right)$. Let $a_{t}$ be the last nonzero coordinate of $\overrightarrow{d}\left (v_{i} \right)$ and $b_{s}$ be the last nonzero coordinate of $\overrightarrow{d}\left (w_{j} \right)$. Then, $s = t$, and it is clear that $t = d\left (v_{i}, w_{n} \right) = d\left (v_{i}, v_{0} \right)+n$, so $s = d\left (w_{j}, v_{d_{1}} \right)$. If $m$ is odd, then $a_{t} = 1$ and $b_{t} = 2$, which gives $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. If $m$ is even, then $d(v_{i}, v_{d_{1}}) = d(w_{j}, w_{n})$. In this case, $a_{t-1}\in \left \{ 1, 2 \right \}$ and $b_{t-1}\in \left \{ 2, 3 \right \}$. If $a_{t-1} = 1$ or $b_{t-1} = 3$, it is clear that $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Next, consider the case $a_{t-1} = b_{t-1} = 2$. When $a_{t-1} = 2$, then $t-1 = d_{1}$, which means $j = 1$. If $n = 1$, then $i = d_{1}$, and in this case, the first coordinate of $\overrightarrow{d}\left (w_{1} \right)$ is 1, while the first coordinate of $\overrightarrow{d}\left (v_{d_{1}} \right)$ is 2, which leads to a contradiction. If $n = 2$, then $\overrightarrow{d}\left (w_{1} \right) = \left (2, 2, 1, \dots \right)$, and in this case, either $i = d_{1}-1$ or $i = d_{1}+1$. When $i = d_{1}-1$, if $a_{3} = 1$, then $d\left (v_{d_{1}-1}, v_{m-2} \right) = 3$, which leads to $m = 8$, a contradiction. When $i = d_{1}+1$, if $a_{3} = 1$, then $d\left (v_{d_{1}+1}, v_{m-2} \right) = 3$, which leads to $m = 12$, a contradiction. If $n \ge 3$, then the first two coordinates of $\overrightarrow{d}\left (w_{1} \right)$ form the subsequence $(2, 3)$. If the second coordinate of $\overrightarrow{d}\left (v_{i} \right)$ is 3, then $i = 1$, and in this case, $n = \frac{m}{2}$, a contradiction. Therefore, $\overrightarrow{d}\left (v_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$.

It is also to be proved that the $d$-vectors of the red vertices on the path are different. Let $\overrightarrow{d}\left (w_{i} \right) = \left (a_{1}, a_{2}, \dots, a_{d_{1}+n} \right)$ and $\overrightarrow{d}\left (w_{j} \right) = (b_{1}, b_{2}, \dots, b_{d_{1}+n})$. When $1\le i < j\le \frac{n}{2}$, $a_{i+1} = 3$ while $b_{i+1} = 2$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $\frac{n}{2} \le i < j\le n$, $a_{n+1-j} = 2$ and $b_{n+1-j} = 1$, so $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. When $1\le i < \frac{n}{2}$ and $\frac{n}{2} < j\le n$, $\overrightarrow{d}\left (w_{i} \right) = \left (2^{i}, 3, \dots \right)$ and $\overrightarrow{d}\left (w_{j} \right) = \left (2^{n-j}, 1, \dots \right)$, and it is clear that $\overrightarrow{d}\left (w_{i} \right) \ne \overrightarrow{d}\left (w_{j} \right)$. Therefore, $c$ is an $ID$-coloring.

4.   Conclusions

This study established the identification coloring number for lollipop graphs by constructing explicit vertex colorings, determining the minimum number of red vertices required for unique vertex identification. The results contribute to the growing body of research on $ID$-graphs, providing insights into the structural properties that enable efficient distinguishing colorings. Future work could extend these methods to other graph classes or explore algorithmic approaches to optimal $ID$-colorings.

Author contributions

Gaixiang Cai: Conceptualization, Methodology, Formal analysis, Writing–review and editing; Fengru Xiao: Investigation, Visualization, Writing–original draft; Guidong Yu: Funding acquisition, Supervision. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was jointly supported by the key project of natural science research in universities of Anhui Province (2024AH051088), Anqing Normal University Graduate Education Quality Engineering Project (2022xxsfkc038), the Natural Science Foundation of China (No.11871077), the NSF of Anhui Province (No.1808085MA04), the NSF of Anhui Provincial Department of Education (KJ2020A0894; KJ2021A0650).

Conflict of interest

The authors declare no conflicts of interest.