Convergence and quasi-optimality based on an adaptive finite element method for the bilinear optimal control problem

1.   Introduction

Hyers–Ulam stability is concerned with ascertaining whether, given a solution of a perturbed equation, a solution to the unperturbed equation exists that remains close to the given solution of the perturbed equation. The recent monographs from Brzdęk et al. ^[1] and Tripathy ^[2] provide excellent overviews of the area. Initially, much of the Hyers–Ulam stability analysis for differential and difference equations was concerned with linear equations. For example, Baias et al. ^[3] investigated the Hyers–Ulam stability of first-order linear difference equations. Similarly, Bora and Shankar ^[4], Chen and Si ^[5], and Kerekes et al. ^[6] explored the Hyers–Ulam stability of second-order linear difference equations. Additionally, Novac et al. ^[7] and Shen and Li ^[8] examined the Hyers–Ulam stability of higher order linear difference equations. Furthermore, Buşe et al. ^[9] analyzed the stability of first-order matrix two-dimensional differential and difference systems. However, there is a growing interest in the analysis of Hyers–Ulam stability for nonlinear equations, which may be conditional stability. It is often the case in nonlinear analysis that the perturbation must be bounded above and the initial condition must be bounded above or below for Hyers–Ulam stability to be possible. Popa et al. ^[10] explore approximate solutions of the logistic equation and Hyers–Ulam stability, followed by Onitsuka ^[11,12] investigating conditional Hyers–Ulam stability and its application to the logistic model and approximate solutions of the generalized logistic equation, respectively. Also in the continuous case, Backes et al. establish conditional Lipschitz shadowing for ordinary differential equations in ^[13]. In the discrete case, Jung and Nam ^[14] analyze the Hyers–Ulam stability of the Pielou logistic difference equation, while Nam ^[15,16,17] studies the Hyers–Ulam stability of elliptic, hyperbolic, and loxodromic Möbius difference equations, respectively. Models in population ecology can be continuous or discrete. One of the advantages of the discrete case is modeling seasonal reproduction rather than continuous reproduction. See, for example, ^[18]. Models in economics can also be continuous or discrete. One can model logistically the relationship between advertising and sales of a product as a series of discrete expenditures, of step-size $h$, with diminishing impact on sales over time, see for example ^[19].

Motivated by these works and the relative sparsity of results related to conditional Hyers–Ulam stability and its application to nonlinear difference equations, in this study, we address the logistic growth $h$-difference equation for step-size $h$. As $h$ converges to zero, it will be demonstrated that our conditional stability results are consistent with those derived for the continuous case. In contrast, setting $h = 1$ leads to significant advancements over previous research. We successfully identify the optimal lower bound of the initial value and the upper bound of the perturbation amplitude, which are essential for ensuring stability in nonlinear systems. Most importantly, we demonstrate a substantial improvement in the Hyers–Ulam stability constant, a measure of stability, compared to prior work.

This study will proceed as follows. In Section 2, we introduce the discrete logistic equation model, define conditional Hyers–Ulam stability, and derive important inequalities related to solutions of the logistic model and solutions of perturbations on the model. We explain that the perturbations must be bounded above in size, while the initial population size must be bounded away from zero for stability to occur. In Section 3 there are three technical lemmas based on the relative smallness of the perturbation and the relative largeness of the initial condition. In Section 4 we present the main result, proving the conditions under which the discrete logistic model is Hyers–Ulam stable and giving a Hyers–Ulam stability constant. In Section 5 we provide detailed examples with both analytical and numerical evidence that illustrate our results and the conditional nature of the Hyers–Ulam stability. In Section 6, we conduct a sensitivity analysis on each parameter of the logistic model, emphasizing its relevance to ecological applications. In the final section, we present the conclusions drawn from this research.

2.   Discrete logistic equation model

The form of the discrete logistic equation model that we study in this work is based on the discussion found in [20, Section 2.4]. Given $h > 0$, set

and define

We consider the logistic growth $h$-difference equation

where $P$ is the population size at time $t$ of some species, $r > 0$ is a growth-rate coefficient, $h > 0$ is the step size, and $K > 0$ is the carrying capacity. When $h = 1$, this equation is called the Beverton–Holt equation (see ^[21,22]). Let $\varepsilon > 0$ be arbitrarily given. Then the following equations

and

for $t \ge 0$, where $q$: ${\mathbb{T}}\rightarrow {\mathbb{R}}$, are perturbations of (2.1) that will play a key role in the analysis that follows below. Throughout this paper, we assume the initial conditions

We can see that the right-hand side of (2.1)–(2.4), respectively, is well defined with respect to $P > 0$, $\beta > 0$, $\ell > 0$, and $u > 0$. That is, the right-hand sides of these equations are continuously differentiable with respect to the positive dependent variable. Consequently, if a positive initial condition (2.5) is given, then the local existence and uniqueness of the solutions are guaranteed in the positive domain (for more details, see [23, Section 8.2]). However, we must pay attention to the global existence of the solutions. By limiting the initial values and the relative size of the allowed perturbations, the existence of global solutions is guaranteed (see Proposition 2).

Definition 1. Let

be the maximal interval of existence for a function $P$. Let $D$ be a nonempty subset of the real numbers. Define the class of functions $\mathcal{C}_D$ as

Let

The nonlinear $h$-difference equation

is conditionally Hyers–Ulam stable in class $\mathcal{C}_D$ on $\left[0, \; \min\left\{T_P, T_{\phi}\right\}\right)_h$, with $\mathcal{S}$ if there exists a constant $\mathcal{H} > 0$ such that for every $\varepsilon\in \mathcal{S}$ and every approximate solution $\phi\in\mathcal{C}_D$ that satisfies

there exists a solution $P\in\mathcal{C}_D$ of (2.6) such that

Such a constant $\mathcal{H}$ is known as a Hyers–Ulam stability constant for (2.6) on $\left[0, \; \min\left\{T_P, T_{\phi}\right\}\right)_h$.

Note that if

then this definition is precisely the canonical definition of Hyers–Ulam stability. In addition, note that Definition 1 does not require the uniqueness of a solution to (2.6) or (2.7).

Proposition 2. Let

and

be the solutions of (2.1)–(2.4) with initial condition (2.5), respectively. If

then

and

hold for all $t \in (0, \infty)_h.$

Proof. Assume that

This proof is divided into four steps.

Step 1. Define

for $P\ge 0$ and $h, r, K > 0$. Note that $F$ is the function that appears on the right-hand side of (2.1). Clearly, the two equilibrium points of (2.1) are $P \equiv 0$ and $K$ determined by

where $P\equiv K$ is attracting and $P\equiv 0$ is repelling. Now, we examine the shape of the function $F$. Define

Since

we see that $F'(P) > 0$ for $0 < P < P^*$, $F'(P^*) = 0$, and $F'(P) < 0$ for $P > P^*$. This implies that the function $F(P)$ takes the maximum value

when

Moreover, we see that $F(P) > 0$ on $(0, K)$ and $F(P) < 0$ on $(K, \infty)$.

Step 2. At the outset, we prove

for all $t\in[0, T_\ell)_h$ with $T_\ell = \infty$, where $\ell$ is determined by (2.3). Now, we consider the function $F(\ell)-\varepsilon$, which is the function that appears on the right-hand side of (2.3).

Case (a). First, we consider the case

where $F_{\max}$ is defined by (2.9). Then,

so that $P = P^*$ is the unique equilibrium point of (2.3). Thus,

is the unique global solution of (2.3) with

By the uniqueness of the solutions, $\ell(0) > P^*$ implies $\ell(t) > P^*$ for all $t\in[0, T_\ell)_h$. In addition, since

holds for $\ell > P^*$, we have $\Delta_h\ell < 0$ for $\ell > P^*$. This implies that

and $\ell(t) > P^*$ for all $t\in[0, \infty)_h$.

Case (b). Next, we will consider the case

where $F_{\max}$ is given by (2.9). In this case, we have

where $P^*$ is given by (2.8). This indicates that (2.3) has two positive equilibria $Q_1$ and $Q_2$ that satisfy

and

Now

is a globally unique solution of (2.3).

As

for

we have $\Delta_h\ell > 0$ for

Consequently, summing this inequality yields

Because of this and the uniqueness of the solutions, we have

means

Therefore, if

then

On the other hand, because

holds for $\ell > Q_2$, we have $\Delta_h\ell < 0$ for $\ell > Q_2$. Consequently, if $\ell(0) > Q_2$, then

and so if $\ell(0) > Q_2$, then

Considering Cases (a) and (b) together, we can conclude that

implies the global existence of the solution $\ell(t)$ of (2.3) and $\ell(t)\ge P^*$ for all $t\in[0, \infty)_h$.

Step 3. We prove

for $t\in[0, \infty)_h$. Let

for

Our goal here is to show that $\delta(t)\le 0$ for all

By way of contradiction, let

be the first input value such that $\delta(t_1) > 0$. Since

by initial condition (2.5), $\delta(t)\le 0$ for all $t\in[0, t_1-h]_h$. Then, we have

for $t\in[0, t_1-h]_h$. Let

Then

from the inequality above, and checking the regressivity condition for $\alpha$, we have

so $\alpha$ is a positively regressive function. Considering this coefficient function $\alpha$, let

It follows from the quotient rule on time scales that

Since $\alpha$ is a positively regressive function, we have

This yields

since

Summing this inequality and using $\delta(0) = 0$, we have

a contradiction of the assumption $\delta(t_1) > 0$. Thus, we have

for all

In a similar manner, we have that

for all

Hence

Next we show that

We consider the function $F(u)+\varepsilon$, which is the function that appears on the right-hand side of (2.4).

In this case, there is $Q_3 > K$ such that

that is, $u \equiv Q_3$ is the unique positive equilibrium point of (2.4). Since

for $u > Q_3$, we have $\Delta_h u < 0$ for $u > Q_3$. Hence, if $u(0) > Q_3$ implies that

for all $t \in [0, T_u)_h$, and thus $T_u = \infty$ when $u(0) > Q_3$. On the other hand, if

then we can obtain $T_u = \infty$. Actually, from (2.10) and the uniqueness of the solution, we have

This means that $T_u = \infty$ when

Therefore, we have

for any case. Furthermore, since (2.4) holds, $\beta(t)$ is always sandwiched between $\ell(t)$ and $u(t)$, so

also holds.

Step 4. We show that

for $t\in(0, \infty)_h$. Note that we have already shown in Step 3 that

Clearly, $T_P = \infty$ is true. Let

for $t\in[0, \infty)_h$. From the above inequality with $q(t) \equiv 0$, in other words, $P$ replaces $\beta$ above if $q(t) \equiv 0$, we see that

for $t\in[0, \infty)_h$. By $\mathscr{D}(0) = 0$, that is

we have

This implies that

By way of contradiction, we suppose that there exists $t_2 > 0$ such that $\mathscr{D}(t_2) \le 0$ and $\mathscr{D}(t) > 0$ for $t\in[h, t_2-h]_h$. Then, we have

Let

Then

from the inequality above and checking the regressivity condition for $\varphi$, we have

so $\varphi$ is a positively regressive function. Considering this coefficient function $\varphi$, let

It follows that

Since $\varphi$ is a positively regressive function, we have

This yields

since

Summing this inequality and using $\mathscr{D}(0) = 0$, we have

a contradiction of the assumption $\mathscr{D}(t_2)\le 0$. Thus, we have $P(t) < u(t)$ for all $t\in(0, \infty)_h$. In a similar manner, we have that $\ell(t) < P(t)$ for all $t\in(0, \infty)_h$. □

To illustrate the proposition, the following example is provided.

Example 3. Consider (2.1)–(2.4) with

According to Proposition 2, if

hold, then the solutions

and

of (2.1)–(2.4), respectively, with initial condition (2.5) satisfy

and

for all $t\in[0, \infty)_1$.

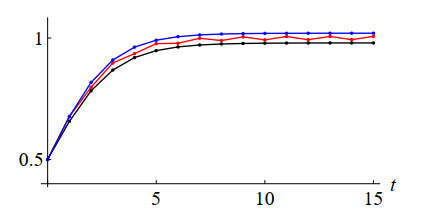
Figure 1 illustrates the solution orbits of (2.2) (red) with $h = r = K = 1$ and $q(t) = 0.01(-1)^t$, (2.3) (black), and (2.4) (blue), given the initial condition

and $\varepsilon = 0.01$. Notice that the solution orbit of (2.2) (red) is bounded between the others.

Remark 4. Let

Define

for

and $h, r, K > 0$. By the proof of Proposition 2, we see that

for $t \ge 0$ and $\ell(t) \in \left(-\frac{K}{hr}, \infty\right)$. Summing this inequality, we have

for $t \ge 0$ and $\ell(t) \in \left(-\frac{K}{hr}, \infty\right)$. This inequality implies that for any $h > 0$ there exists $t_h\ge 0$ such that

for $t \ge t_h$ and $\ell(t) \in \left(-\frac{K}{hr}, \infty\right)$. This shows that any solution $\ell(t)$ of (2.3) with $\ell(0) \in {\mathbb{R}}$ diverges to $-\infty$ as $h \rightarrow 0^+$.

On the other hand, any solution $P(t)$ of Eq (2.1) satisfying

exists globally in time and is greater than or equal to

In fact, (2.1) has two equilibria $P = 0$, $K$; $F(P) > 0$ for $0 < P < K$; and

holds. As $F(P) > 0$ for

we have $\Delta_h P > 0$ for

Consequently, summing this inequality yields

Because of this and the uniqueness of the solutions, we have

means

for all $t\ge 0$. This implies that $|P(t)-\ell(t)|$ diverges to $\infty$ as $h \rightarrow 0^+$; that is, Eq (2.1) is not conditionally Hyers–Ulam stable in class $\mathcal{C}_D$ on $[0, \infty)_h$ when $h \rightarrow 0^+$, where

Therefore, we can see that

is the threshold value.

Remark 5. Let

and

Define

for

and $h, r, K > 0$. By the proof of Proposition 2, we see that

for

and

is the unique equilibrium point of (2.3); and

for

Let $\ell(0) = P_0$. Then, we have

for $t\ge 0$ and

Summing this inequality, we have

for $t\ge 0$ and

This inequality implies that for any $h > 0$, there exists $t_h\ge 0$ such that

for $t \ge t_h$ and

In a similar manner as Remark 4, we see that Eq (2.1) is not conditionally Hyers–Ulam stable on $[0, \infty)_h$ when $h \rightarrow 0^+$. Therefore, we can conclude that

is the threshold value.

3.   Technical lemmas

Before presenting the main theorem and its proof in the next section, we give some important lemmas.

Lemma 6. Suppose that

Let

and

be the solutions of (2.1), (2.3), and (2.4) with initial condition (2.5), respectively. Then,

and

and

hold for all $t\in(0, \infty)_h$.

Proof. By Proposition 2, we have

and

for all $t\in(0, \infty)_h$. As the proofs of the two inequalities in the statement above are the same, the second one is omitted. For convenience, we write

for $t\in(0, \infty)_h$. Since (2.1) can be solved directly for $P$, we have

Notice that $P(t, P_0)$ is increasing in $P_0$. For fixed $t\ge 0$, it thus follows that

for $t\in(0, \infty)_h$. Also notice that for fixed $t$ the function $F$ is decreasing in $P > 0$ and $\ell > 0$, since

This yields

for $t \in (0, \infty)_h$. Thus, we obtain the first inequality in the statement of this lemma. □

Lemma 7. Let $\varepsilon > 0$, and let

Then the function

solves the linear $h$-difference equation

with the initial condition $\Omega(0) = 0$.

Proof. For simplicity, let $\alpha = 1+hr$,

First, we show that the function $\Omega_p(t)$ is a particular solution of Eq (3.3). This fact can be confirmed by direct calculation, but to aid in the calculation, we calculate some difference operators in advance. In fact, by

we have

It follows from the quotient rule on time scales that

Thus, $\Omega_p(t)$ is a particular solution of Eq (3.3).

Next we consider the function $e_{\mathscr{F}}(t, 0)$. Since

holds, $\mathscr{F}$ is a positively regressive function. Hence $e_{\mathscr{F}}(t, 0)$ solves the linear $h$-difference equation

and is positive for $t \in [0, \infty)_h$. From the superposition principle, we see that

is a solution to Eq (3.3). Moreover, we have

Therefore, the statement in the lemma is true. □

Lemma 8. Let $\varepsilon > 0$, and let $\omega(t)$ satisfy $\omega(0) = 0$ and the linear $h$-difference inequality

for $t \in [0, \infty)_h$, where $\mathscr{F}(t)$ is given by (3.1). Let $\Omega(t)$ be given by (3.2). Then

for all $t \in [0, \infty)_h$.

Proof. Define

Note that by Lemma 7, $\Omega(t)$ is the solution of Eq (3.3) with $\Omega(0) = 0$. Then $\delta(0) = 0$. By way of contradiction, we suppose that there exists $t_1 > 0$ such that $\delta(t_1) < 0$ and $\delta(t)\ge 0$ for $t\in[0, t_1-h]_h$. Then, we have

for $t\in[0, t_1-h]_h$. As shown in the proof of the previous lemma, $\mathscr{F}$ is a positively regressive function, and

holds. Consequently,

Since $\mathscr{F}$ is a positively regressive function, we have

This yields

since

Summing this inequality and using $\delta(0) = 0$, we have

a contradiction of the assumption $\delta(t_1) < 0$. Thus, we have

for all $t \in [0, \infty)_h$. □

4.   Conditional Hyers–Ulam stability

The following theorem is the main result obtained in this study.

Theorem 9. Suppose that

Let

and

be the solutions of (2.1) and (2.2) with initial condition (2.5), respectively. Then,

and

holds for all $t\in[0, \infty)_h$. That is, Eq (2.1) is conditionally Hyers–Ulam stable with Hyers–Ulam stability constant

Proof. Assume that

Let

and

be the solutions of (2.1)–(2.4) with (2.5), respectively. It follows from Proposition 2 that

and

hold for all $t \in (0, \infty)_h$. As a result,

Let

for $t \in (0, \infty)_h$. Then, we have

for $t \in (0, \infty)_h$. Using Lemma 6,

holds for all $t\in(0, \infty)_h$, where $\mathscr{F}(t)$ is given by (3.1). Note that by (2.5), we have

and

and so that

for all $t\in[0, \infty)_h$. Now we consider the function $\Omega(t)$ defined by (3.2). Then, by Lemma 8,

for all $t \in [0, \infty)_h$. In a similar manner, we have that

for all $t \in [0, \infty)_h$. Hence we obtain

for all $t\in[0, \infty)_h$. As shown in the proof of Lemma 7, $\mathscr{F}$ is a positively regressive function, and $e_{\mathscr{F}}(t, 0) > 0$ for $t\in[0, \infty)_h$. In addition, by (3.1), $\mathscr{F}$ is non-positive for $t\in[0, \infty)_h$. That is, $\Delta_he_{\mathscr{F}}(t, 0) \le 0$ for $t\in[0, \infty)_h$. Hence, we see that

for $t\in[0, \infty)_h$. Using this, we obtain

for all $t\in[0, \infty)_h$. □

Remark 10. Theorem 9 implies the following fact: the Eq (2.1) is conditionally Hyers–Ulam stable in class $\mathcal{C}_D$ on $[0, \infty)_h$, with

and with a Hyers–Ulam stability constant

where

For the three key constants given here, we note that as the step-size $h > 0$ tends to zero, we have

These limiting values match the values found for the continuous logistic model [11, Example 3.2].

Remark 11. If $h = 1$, then (2.1) can be rewritten as the iteration equation

Letting

we see that

This is an example of a loxodromic Möbius difference equation. For more on Hyers–Ulam stability of loxodromic Möbius difference equations, see Nam ^[17].

In 2017, Jung and Nam [14, Example 4.1] gave an example of the conditional Hyers–Ulam stability of the iteration equation

which is equivalent to (4.1), where

Their result, expressed in the terms of our paper, is as follows: The Eq (4.1) (resp., (2.1)) is conditionally Hyers–Ulam stable in class $\mathcal{C}_{D^*}$ on

with

and with a Hyers–Ulam stability constant

where

We note here that the term "conditional Hyers–Ulam stability'' is not used in ^[14], and their original result shows that if $\beta(0)$ is in $D^*$, then there exists $P(t)$ which satisfies (4.1) and

for all $t\in {\mathbb{N}}_0$, where $\beta(t)$ is a solution of (2.2). In our paper settings, $\beta(0) = P(0)$ (see (2.5)), so the first term on the right-hand side is $0$. The second term can be evaluated as follows:

Thus, we have the Hyers–Ulam stability constant $\mathcal{H}^*$.

We now compare the three important constants obtained in Theorem 9 with those appearing in the above mentioned $\mathcal{S}^*$, $D^*$, and $\mathcal{H}^*$, but note that the negative region of $D^*$ is omitted since it is not of interest in our paper. First, we compare our result with theirs for the upper bound of $\varepsilon$. Using

we have

From this inequality, we can claim that our result (Theorem 9) is sharper than theirs because a smaller $\varepsilon$ is more stable. Next, we compare the infimum values of the initial value. Since

holds, we can claim that our result (Theorem 9) is sharper than theirs for this point. Simply from the qualitative aspect of ensuring Hyers–Ulam stability, we can conclude that our result that guarantees Hyers–Ulam stability for larger $\varepsilon$ and smaller initial value is sharp.

Finally, we compare the Hyers–Ulam stability constants. Define

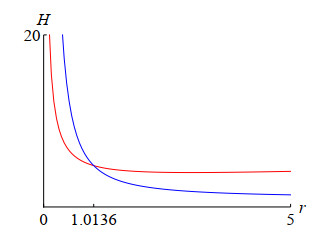
for $r > 0$. The graphs of functions $H$ and $H^*$ are shown in Figure 2. The red curve shows the graph for $H$, and the blue curve shows the graph for $H^*$.

Note that $r \approx 1.013624$ solves

Thus, if $0 < r < 1.013624$, then our Hyers–Ulam stability constant

is better than theirs. However, this statement may be reversed if $r > 1.013624$. But, the next section gives an example where this conjecture is not necessarily true (see Example 13).

There is a reason why the Hyers–Ulam stability constants diverge as $r$ approaches $0$. If $h = 1$ and $r = 0$, then (4.1) (resp., (2.1)) and (2.2) become

and

with

for all $t\in {\mathbb{N}}_0$. We put

Then we have a solution

Since

is any solution of the equation $\Delta P(t) = 0$, where $C$ is an arbitrary constant, we see that

This means that (4.1) is not Hyers–Ulam stable on ${\mathbb{N}}_0$. Therefore, it is a natural consequence that

In addition, we have

That is, $H^*(r)$ is much larger near $r = 0$ than $H(r)$.

5.   Examples

In this section we present detailed examples with specific parameter values that illustrate our main conditional stability results.

Example 12. In (2.1), (2.3), and (2.4) take $h = 1$, $r = \frac{1}{3}$, $K = 9$, $\varepsilon = \frac{3}{5}$, and

According to Theorem 9, since

and

then solutions

and

of (2.1), (2.3), and (2.4), respectively, with initial condition (2.5) satisfy

and

for all $t\in[0, \infty)_h$. Note that in this specific instance we have

and

where

so that we have the numerical comparison for $t = 0, \ldots, 10$ given in Table 1.

In the two right-most columns of Table 1, we see that inequality (5.1) holds and the conditional Hyers–Ulam stability is guaranteed.

If we keep all the parameter values the same but take $\varepsilon = \frac{4}{5}$ instead of $\varepsilon = \frac{3}{5}$, then

and the right-hand side of (5.1) becomes

so one of the hypotheses of Theorem 9 is not met. Indeed, below we compare the values for solutions

and

of (2.1) and (2.3), respectively, with initial condition (2.5). We have the numerical comparison for $t = 0, \ldots, 20$ given in Table 2.

We see that inequality (5.1) does not hold eventually in the right-most column of Table 2 since

using (5.2), making the equation unstable. This shows the impact of the value of the perturbation $\varepsilon$ being too large, as noted in Remark 4, and highlights the conditional nature of the Hyers–Ulam stability result in Theorem 9.

Example 13. In (2.1), (2.3), and (2.4), take $h = K = 1$, $r = 3$, and $\varepsilon = P_0 = \frac{1}{3}$. According to Theorem 9, since

then solutions

and

of (2.1), (2.3), and (2.4), respectively, with initial condition (2.5), satisfy

and

for all $t\in[0, \infty)_h$. Note that in this specific instance we have

and

so that we have the numerical comparison for $t = 0$, $\ldots$, $10$ given in Table 3.

In the two right-most columns of Table 3, we see that inequality (5.3) holds and the conditional Hyers–Ulam stability is guaranteed.

Note that we cannot use the results of Jung and Nam ^[14] for this example because $\varepsilon$ and $P_0$ are the critical values given in Theorem 9 (see also Remark 11). Let $H^*(r)$ be given in (4.2). That is, $H^*(r)$ is a Hyers–Ulam stability constant derived in ^[14]. In this example, $r = 3$, so we can see from Figure 2 that $H^*(3)$ is smaller than our constant $H(3)$. Actually, we have

But, in the two right-most columns of Table 3, we see that the inequality

does not hold for all $t$. From this fact, it becomes clear that their result shows that the Hyers–Ulam stability constant can be smaller when $r > 1.013624$ because $\varepsilon$ and $P_0$ are more limited than ours.

If we keep all the parameter values the same but take $\varepsilon = \frac{2}{5}$ instead of $\varepsilon = \frac{1}{3}$, then

and the right-hand side of (5.3) becomes

so one of the hypotheses of Theorem 9 is not met. Indeed, if we compare the values for solutions

and

of (2.1) and (2.3), respectively, with initial condition (2.5), we have the numerical comparison for $t = 0, \ldots, 20$ given in Table 4.

We see that inequality (5.3) does not hold for all $t$ in the right-most column of Table 4 since

using (5.4), for some $t\in[0, \infty)_h$, making the equation unstable. This shows the impact of the value of the perturbation $\varepsilon$ being too large, as noted in Remark 4, and highlights the conditional nature of the Hyers–Ulam stability result in Theorem 9.

Finally, again take $h = K = 1$, $r = 3$, and $\varepsilon = \frac{1}{3}$, but let

In this case, note that

so again one of the hypotheses of Theorem 9 is not met. Note that in this specific instance we have

Indeed, if we compare the values for solutions

and

of (2.1) and (2.3), respectively, with initial condition (2.5), we have the numerical comparison for $t = 0, \ldots, 8$ given in Table 5.

Since

and

the equation is unstable. This shows the impact of the value of $P_0$ being too small, as noted in Remark 5, and highlights the conditional nature of the Hyers–Ulam stability result in Theorem 9.

6.   Sensitivity analysis

We now proceed to investigate the local sensitivity analysis related to the parameters of Eq (2.1). It is important to note that the population dynamics represented by the logistic model are biologically meaningful within the range $0 < P < K$. Therefore, we perform the local sensitivity analysis under the assumption that $0 < P < K$.

Since Eq (2.1) can be rewritten as

if we further define

and

we obtain the following difference equation:

First, we perform a sensitivity analysis of the parameter $K$, which represents the carrying capacity. Differentiating (6.1) with respect to $K$, we obtain

Therefore, the sensitivity coefficient for the parameter $K$ is dependent on the population size, $x(n)$. Given that

we observe that the sensitivity is low when the population is small (when $x(n)$ approaches 0), and the sensitivity is high when the population is large (when $x(n)$ approaches $K$).

Next, we perform a sensitivity analysis of the parameter $r$, which represents the growth rate. Differentiating (6.1) with respect to $r$, we obtain

Define the function

for $0 < x < K$. Then

This demonstrates that the sensitivity is low when the population is small or large (when $x(n)$ approaches 0 or $K$), and the sensitivity is high when the population is at an intermediate level (when $x(n)$ approaches $\frac{K}{2}$).

From the form of (6.1), we arrive at the same conclusion regarding the sensitivity with respect to $h$, as $h$ plays a role analogous to $r$.

Let us recall that the Hyers–Ulam stability constant in Theorem 9 is

The parameters $K$, $r$, and $h$ all influence the initial value and $\varepsilon$, which represents the margin of error in (6.1) and its perturbed equation. However, the Hyers–Ulam stability constant can be chosen independently of $K$. In other words, the carrying capacity is unrelated to the error between the approximate solution and the true solution of (6.1). Therefore, we can conclude that the carrying capacity $K$ is sensitive when the population is large, but even if some perturbation is added to the equation, it does not affect the error between the approximate solution and the true solution, so it is a parameter that does not need to be treated very delicately. On the other hand, $r$ and $h$ exhibit sensitivity when the population is at an intermediate level, and they also influence the error between the approximate solution and the true solution. In many cases, $h$ is fixed in advance, and from a biological perspective, it is important to investigate how the population changes from the intermediate stage. Therefore, the parameter to which we should truly pay attention is $r$, which represents the growth rate.

Example 14. In (2.1) and (2.2) take

According to Theorem 9, if

hold, then solutions

and

of (2.1) and (2.2), respectively, with initial condition (2.5) satisfy

and

for all $t\in[0, \infty)_1$. Table 6 shows the upper bounds of $\varepsilon$, the lower bounds of $P_0$, and the Hyers–Ulam stability constants, all of which depend on $r$.

Now, we consider (2.2) with

and

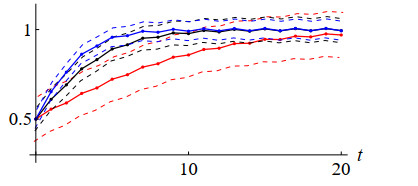
Figure 3 shows the solution orbits for the equation with initial condition

when $r = 0.2$ (red), 0.5 (black), and 0.8 (blue). In addition, the dashed curves show the $\frac{1+r}{\sqrt{1+r}-1}\varepsilon$-neighborhoods around the solution orbits, where $\varepsilon = 0.01$. As mentioned above, the sensitivity for $r$ is high near the solution of the equation to $\frac{1}{2}$, and as a result, the three solution orbits are significantly different.

7.   Conclusions

We establish robust conditional Hyers–Ulam stability results for the logistic $h$-difference equation, also known as the Beverton–Holt equation if $h = 1$, for any constant step-size $h > 0$. As $h$ tends to zero, our results recover known results for the conditional stability of the continuous logistic-growth model. Additionally, departing from the methodology employed by Jung and Nam ^[14] in case $h = 1$, we introduce a novel approach to derive sharper results. Specifically, we explicitly determine the optimal lower bound for the initial value region and the upper bound for the perturbation amplitude, demonstrating an improvement over their findings. Furthermore, our analysis yields a sharper Hyers–Ulam constant, which quantifies the error between the true and approximate solutions. Given that a smaller Hyers–Ulam constant indicates greater stability and is desirable for practical applications, our results offer a substantial advancement in precision. The sharpness of our derived bounds and constants is substantiated through illustrative examples.

Author contributions

Douglas R. Anderson: conceptualization, methodology, writing—original draft; writing—review and editing, visualization; Masakazu Onitsuka: conceptualization, methodology, writing—original draft, writing—review and editing, conducted the numerical simulations. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The second author is supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI (Grant number: JP20K03668).

Conflict of interest

The authors declare no conflicts of interest.