The present research paper is related to the analytical solution of fractional-order nonlinear Swift-Hohenberg equations using an efficient technique. The presented model is related to the temperature and thermal convection of fluid dynamics which can also be used to explain the formation process in liquid surfaces bounded along a horizontally well-conducting boundary. In this work Laplace Adomian decomposition method is implemented because it require small volume of calculations. Unlike the variational iteration method and Homotopy pertubation method, the suggested technique required no variational parameter and having simple calculation of fractional derivative respectively. Numerical examples verify the validity of the suggested method. It is confirmed that the present method's solutions are in close contact with the solutions of other existing methods. It is also investigated through graphs and tables that the suggested method's solutions are almost identical with different analytical methods.
Citation: Jiabin Xu, Hassan Khan, Rasool Shah, A.A. Alderremy, Shaban Aly, Dumitru Baleanu. The analytical analysis of nonlinear fractional-order dynamical models[J]. AIMS Mathematics, 2021, 6(6): 6201-6219. doi: 10.3934/math.2021364
| [1] | Saima Rashid, Sobia Sultana, Bushra Kanwal, Fahd Jarad, Aasma Khalid . Fuzzy fractional estimates of Swift-Hohenberg model obtained using the Atangana-Baleanu fractional derivative operator. AIMS Mathematics, 2022, 7(9): 16067-16101. doi: 10.3934/math.2022880 |
| [2] | Sajjad Ali Khan, Kamal Shah, Poom Kumam, Aly Seadawy, Gul Zaman, Zahir Shah . Study of mathematical model of Hepatitis B under Caputo-Fabrizo derivative. AIMS Mathematics, 2021, 6(1): 195-209. doi: 10.3934/math.2021013 |
| [3] | Maysaa Al-Qurashi, Saima Rashid, Fahd Jarad, Madeeha Tahir, Abdullah M. Alsharif . New computations for the two-mode version of the fractional Zakharov-Kuznetsov model in plasma fluid by means of the Shehu decomposition method. AIMS Mathematics, 2022, 7(2): 2044-2060. doi: 10.3934/math.2022117 |
| [4] | Muammer Ayata, Ozan Özkan . A new application of conformable Laplace decomposition method for fractional Newell-Whitehead-Segel equation. AIMS Mathematics, 2020, 5(6): 7402-7412. doi: 10.3934/math.2020474 |
| [5] | Azzh Saad Alshehry, Naila Amir, Naveed Iqbal, Rasool Shah, Kamsing Nonlaopon . On the solution of nonlinear fractional-order shock wave equation via analytical method. AIMS Mathematics, 2022, 7(10): 19325-19343. doi: 10.3934/math.20221061 |
| [6] | Ihtisham Ul Haq, Nigar Ali, Hijaz Ahmad, Taher A. Nofal . On the fractional-order mathematical model of COVID-19 with the effects of multiple non-pharmaceutical interventions. AIMS Mathematics, 2022, 7(9): 16017-16036. doi: 10.3934/math.2022877 |
| [7] | Amjad Ali, Iyad Suwan, Thabet Abdeljawad, Abdullah . Numerical simulation of time partial fractional diffusion model by Laplace transform. AIMS Mathematics, 2022, 7(2): 2878-2890. doi: 10.3934/math.2022159 |
| [8] | Gulalai, Shabir Ahmad, Fathalla Ali Rihan, Aman Ullah, Qasem M. Al-Mdallal, Ali Akgül . Nonlinear analysis of a nonlinear modified KdV equation under Atangana Baleanu Caputo derivative. AIMS Mathematics, 2022, 7(5): 7847-7865. doi: 10.3934/math.2022439 |
| [9] | Ihsan Ullah, Aman Ullah, Shabir Ahmad, Hijaz Ahmad, Taher A. Nofal . A survey of KdV-CDG equations via nonsingular fractional operators. AIMS Mathematics, 2023, 8(8): 18964-18981. doi: 10.3934/math.2023966 |
| [10] | Yousef Jawarneh, Humaira Yasmin, Abdul Hamid Ganie, M. Mossa Al-Sawalha, Amjid Ali . Unification of Adomian decomposition method and ZZ transformation for exploring the dynamics of fractional Kersten-Krasil'shchik coupled KdV-mKdV systems. AIMS Mathematics, 2024, 9(1): 371-390. doi: 10.3934/math.2024021 |
The present research paper is related to the analytical solution of fractional-order nonlinear Swift-Hohenberg equations using an efficient technique. The presented model is related to the temperature and thermal convection of fluid dynamics which can also be used to explain the formation process in liquid surfaces bounded along a horizontally well-conducting boundary. In this work Laplace Adomian decomposition method is implemented because it require small volume of calculations. Unlike the variational iteration method and Homotopy pertubation method, the suggested technique required no variational parameter and having simple calculation of fractional derivative respectively. Numerical examples verify the validity of the suggested method. It is confirmed that the present method's solutions are in close contact with the solutions of other existing methods. It is also investigated through graphs and tables that the suggested method's solutions are almost identical with different analytical methods.
In the last few decades, the researchers have shown significant interest in fractional calculus in different areas, such as edge detection, electromagnetic, engineering, viscoelasticity, electrochemistry, cosmology, turbulence, diffusion, signal processing material science, physics and acoustics. It has been proved by many researchers that the integer-order models are generalized by fractional-order portray the complex phenomena in a very effective approach [1,2,3]. Various dynamical systems in physics and engineering are also modeled by using fractional-order differential equations. Many researchers have contributed a lot to provide an outstanding history of the derivative of fractional-order, such as Caputo [4], Yin et al.[5], Rashid et al., Arife et al. [6] and Oldham and Spanier [7,8].
The majority of science problems are nonlinear and it isn't easy to find its analytical solutions. The physical problems are mostly designed by using higher nonlinear partial differential equations (PDEs). It is challenging to find the exact or analytical solutions for such problems. However, in the last several centuries, many scientists have made significant progress and adopted various techniques to solve nonlinear PDEs. Recently in [9,10,11,12], Arqub et al. have implemented the Hilbert space reproduction kernel technique along with the iterative computational method to extended the semi-analytical approaches to other time fractional-order PDEs. In [13], the author examined approximate methods for certain groups of Robin time-fractional PDEs by fitting the kernel reproduction algorithm [14]. Sadly, many nonlinear problems can not be solved by analytical techniques. Moreover, the traditional numerical methods have to provide linearization, transformation, discretization and perturbation to solve the nonlinear models [15,16,17,18,19,20].
In 1980, Adomian developed an effective technique is known as Adomian Decomposition Method (ADM) to solve differential equations describing physical phenomena [21]. Further, ADM is modified by using Laplace transformation. As a result, a new method is developed, known as Laplace-ADM (LADM). LADM possesses the basic properties of both Laplace transformation and ADM. S.A Khuri [22] introduced LADM. This technique works effectively for PDEs of both initial and boundary value problems. LADM is also used in several research article to achieve an analytical solution, such as Whitham-Broer-Kaup equations [23], third-order dispersive fractional PDEs [24], fractional-order telegraph equations [25], fisher's equation [26], time-fractional model of Navier-Stokes equation [27] and Keller-Segel equation [28].
In the current article, the analytical solution of the following Swift-Hohenberg (SH) equation.
| ∂βu∂tβ=γu−(1+∂2∂x2)u−u3, γ∈R, 0<β≤1, | (1.1) |
where a and b are parameters. This is among the most fundamental equations suggested by Jack Swift and Pierre Hohenberg in 1977, which is related to the temperature and thermal convection of fluid dynamics [29]. A nonlinear parabolic equation is the SH equation, which also explains the formation process in liquid surfaces bounded along a horizontally well-conducting boundary. The broad field of SH equation is used in engineering and science problems from hydrodynamics of fluids to complex patterns [30,31]. Density gradient-driven liquid convection occurs in streams of geophysical fluid in the atmosphere, oceans and mantle of the earth. The mathematical model for the convection of Rayleigh-Benard includes the equations of Navier-Stokes combined with the temperature formula for transport. The S-H equation plays a vital role in the various branches of science, including fluid mechanics, such as laser studies [32] and Taylor-Couette flow [30] nonlinear optics.
The SH equation's solution was analyzed by some researchers using various methods, such as Vishal et al., that used the Homotopy Perturbation Transform Method (HPTM) [33]. The Homotopy Analysis Method (HAM) [34], Merdan, who used the method of variational iteration utilizing the Riemann-Liouville derivative [35], Khan et al., who used the differential transform method [36], Prakasha et al., applied is residual power series method and others [37,38,39,40].
In this research work, the analytical solution of SH equation is investigated by using Laplace Adomian decomposition method. In the prior literature, the solution of SH equation was handled by using Variational iteration method and Homotopy analysis method. It is observed that the proposed method is simple and straightforward as compared to other existing techniques. Moreover, the suggested method has greater accuracy and requires fewer calculations than other methods. The method is applied easily to achieve the solutions of fractional problems. The representation has confirmed the closed relation between the exact and obtained results. The fractional-order solutions are convergent to the solution of the integer-order problem.
The Caputo definition of the fractional derivative of order β is described as [1,2,3,7]
| ∂βg(t)∂tβ=1Γ(m−β)∫x0(x−t)m−β−1g(m)(t)dt, for m−1<β≤m, m∈N. |
Hence, we have the following properties [1,2,3,7]
| JβJαg(t)=Jβ+α, α,γ≥0.Jβtγ=Γ(γ+1)Γ(β+γ+1)tβ+γ, γ>−1, t>0.JβDβg(t)=g(t)−m−1∑k=0gk(0+)tkk!, t>0, m−1<β≤m. |
The Laplace transform of G(s) of g(t) is defined by [22]
| G(s)=L[g(t)]=∫∞0e−stg(t)dt. |
The Laplace transform of fractional derivative is [22]
| L(Dβtg(t))=sβG(s)−m−1∑k=0sβ−1−kg(k)(0),m−1<β<m. |
In this section, LADM is implemented to solve FPDEs [22].
For this first consider the following FPDE, that is
| ∂βu∂tβ+Lu(x,t)+Nu(x,t)=q(x,t),x,t≥0,0<β≤1, | (3.1) |
with initial condition
| u(x,0)=k(x). | (3.2) |
The fractional derivative in equation (3.1) is expressed in Caputo sense. The linear and nonlinear terms are denoted by L and N respectively. The q is the sources term.
Taking both sides Laplace transformation of Eq (3.1),
| sβL[u(x,t)]−sβ−1u(x,0)=L[q(x,t)]−L[Lu(x,t)+Nu(x,t)], |
| L[u(x,t)]=k(x)s+1sβL[q(x,t)]−1sβL[Lu(x,t)+Nu(x,t)]. | (3.3) |
The LADM solution is [22]
| u(x,t)=∞∑j=0uj(x,t), | (3.4) |
The nonlinear term in the problem is expressed as
| Nu(x,t)=∞∑j=0Aj, | (3.5) |
where
| Aj=1j![djdλj[N∞∑j=0(λjuj)]]λ=0,j=0,1,2,⋯, | (3.6) |
is called Adomian polynomials.
substitution (3.4) and (3.5) in Eq (3.3), we get
| L[∞∑j=0u(x,t)]=k(x)s+1sβL[q(x,t)]−1sβL[L∞∑j=0uj(x,t)+∞∑j=0Aj]. | (3.7) |
Applying the decomposition method, we get
| L[u(x,t))]=k(x)s+1sβL[q(x,t)], |
| L[u1(x,t)]=−1sβL[Lu0(x,t)+A0]. |
In general, it can be written as
| L[uj+1(x,t)]=−1sβL[Luj(x,t)+Aj],j≥1. | (3.8) |
Using inverse Laplace transform to Eq (3.8)
| u0(x,t)=k(x,t) |
| uj+1(x,t)=−L−1[1sβL[Luj(x,t)+Aj]]. | (3.9) |
Consider the fractional equation SH with the form dispersion [33,34,39]
| ∂βu(x,t)∂tβ+∂4u(x,t)∂x4+2∂2u(x,t)∂x2+(1−a)u(x,t)+u3(x,t)=0,0<β≤1, | (4.1) |
with initial condition
| u(x,0)=110sin(πxl) | (4.2) |
Taking Laplace transform of Eq (4.1),
| L[∂βu(x,t)∂tβ]=−L[∂4u(x,t)∂x4+2∂2u(x,t)∂x2+(1−a)u(x,t)+u3(x,t)], |
| sβL[u(x,t)]−sβ−1[u(x,0)]=−L[∂4u(x,t)∂x4+2∂2u(x,t)∂x2+(1−a)u(x,t)+u3(x,t)]. |
Using inverse transformation
| u(x,t)=L−1[u(x,0)s−1sβL{∂4u(x,t)∂x4+2∂2u(x,t)∂x2+(1−a)u(x,t)+u3(x,t)}], |
| u(x,t)=110sin(πxl)−L−1[1sβL{∂4u(x,t)∂x4+2∂2u(x,t)∂x2+(1−a)u(x,t)+u3(x,t)}], |
Using ADM procedure, we get
| ∞∑j=0uj(x,t)=110sin(πxl)−L−1[1sβL{∞∑j=0∂4uj(x,t)∂x4+2∞∑j=0∂2uj(x,t)∂x2+(1−a)∞∑j=0uj(x,t)+∞∑j=0Aj}], |
| u0(x,t)=110sin(πxl), | (4.3) |
| ∞∑j=1uj(x,t)=−L−1[1sβL{∞∑j=1∂4uj−1(x,t)∂x4+2∞∑j=1∂2uj−1(x,t)∂x2+(1−a)∞∑j=1uj−1(x,t)+∞∑j=1Aj−1}], | (4.4) |
where the nonlinear terms in the above equations are represented by Adomian polynomials Aj [41]. Whose components are defined as
| Aj=1j![djdλj{N(∞∑j=0(λjuj))}]λ=0,j=0,1,2,⋯, |
Here the nonlinear term is
| N(u)=u3 | (4.5) |
For j=0
| A0=N(λ0u0),A0=N(u0). |
Using Eq (4.15)
| A0=u30, |
j=1
| A1=11![ddλ{N(λ0u0+λ1u1)}]λ=0, |
| A1=[ddλ{N(u0+λu1)}]λ=0, |
| A1=[ddλ{(u0+λu1)3}]λ=0, |
| A1=[3(u0+λu1)2u1]λ=0, |
| A1=3u20u1, |
Similarly
| A2=3u20u2+3u0u21. |
For j=1
| u1(x,t)=−L−1[1sβL{∂4u0(x,t)∂x4+2∂2u0(x,t)∂x2+(1−a)u0(x,t)+u30(x,t)}], |
| u1(x,t)=[sin(πxl)1000l4{100π4−200π2l2+101l4−100l4a−l4cos2(πxl)}]tβΓ(β+1). |
For j=2
| u2(x,t)=−L−1[1sβL{∂4u1(x,t)∂x4+2∂2u1(x,t)∂x2+(1−a)u1(x,t)+3u20(x,t)u1(x,t)}], |
| u2(x,t)=1100000l8[sin(πxl){−8400cos2(πxl)π4l4+2400cos2(πxl)π2l6−20400l8a+10403l8−406l8cos2(πxl)+10000l8a2+3l8cos4(πxl)+10000π8−40000π6l2+62400π4l4−41200π2l6−20000π4l4a+40000π2l6a+400l8acos2(πxl)}]t2βΓ(2β+1), |
The LADM solution for example 1 is
| u(x,t)=u0(x,t)+u1(x,t)+u2(x,t)+..., |
| u(x,t)=110sin(πxl)+[sin(πxl)1000l4{100π4−200π2l2+101l4−100l4a−l4cos2(πxl)}]×tβΓ(β+1)+1100000l8[sin(πxl){−8400cos2(πxl)π4l4+2400cos2(πxl)π2l6−20400l8a+10403l8−406l8cos2(πxl)+10000l8a2+3l8cos4(πxl)+10000π8−40000π6l2+62400π4l4−41200π2l6−20000π4l4a+40000π2l6a+400l8acos2(πxl)}]t2βΓ(2β+1)+..., |
In Table 1, the VIM and LADM solutions of example 9.1 are compared at different fractional orders β=0.5 and 1. The corresponding results are seems to be very similar and confirmed the validity of the present technique.
| x | VIM(β=0.5) | LADM(β=0.5) | VIM(β=1) | LADM(β=1) |
| 0.00 | 0.00000000 | 0.00000000 | 0.0000000 | 0.0000000 |
| 0.25 | 0.03085341 | 0.03085341 | 0.0347097 | 0.0347097 |
| 0.50 | 0.06652018 | 0.06652018 | 0.0704722 | 0.0704722 |
| 0.75 | 0.10743665 | 0.10743665 | 0.1062671 | 0.1062671 |
| 1.00 | 0.14795188 | 0.14795188 | 0.1382405 | 0.1382405 |
| 1.25 | 0.17838674 | 0.17838674 | 0.1607941 | 0.1607941 |
| 1.50 | 0.18974562 | 0.18974562 | 0.1689702 | 0.1689702 |
| 1.75 | 0.17838674 | 0.17838674 | 0.1607941 | 0.1607941 |
| 2.00 | 0.14795188 | 0.14795188 | 0.1382405 | 0.1382405 |
DownLoad:
CSV
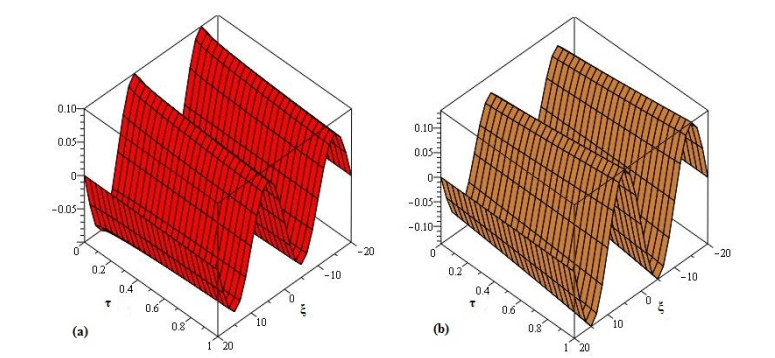
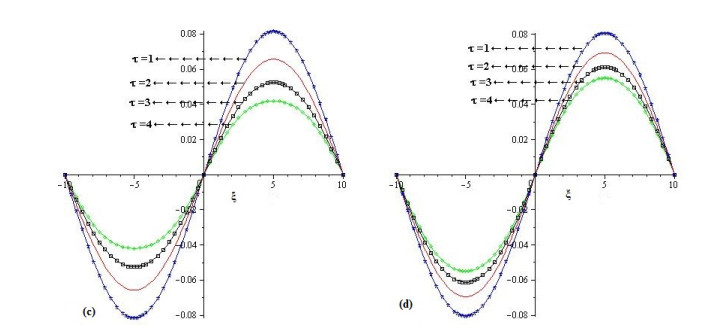
In Figure 1, the LADM solutions at fractional orders β=0.75 and 1 are plotted. The graph (a) represent the solution of example 1 at β=1 while graph (b) is the plot of LADM solution at β=0.75. In Figure 2, the LADM solutions at fractional orders β=0.75 and 1 are plotted at t=1,2,3 and 4 in the domain −10<x<10. The graphs (c) and (d) of Figure 2 represent the LADM solutions at fractional orders β=1 and 0.75 respectively.
Consider the fractional SH equation with dispersion of the form [33,34,39]
| ∂βu(x,t)∂tβ+∂4u(x,t)∂x4+2∂2u(x,t)∂x2−a∂3u(x,t)∂x3−bu(x,t)−2u2(x,t)+u3(x,t)=0,0<β≤1, | (4.6) |
with initial condition
| u(x,0)=110sin(πxl). | (4.7) |
Taking Laplace transform of Eq (4.6),
| L[∂βu(x,t)∂tβ]=−L[∂4u(x,t)∂x4+2∂2u(x,t)∂x2−a∂3u(x,t)∂x3−bu(x,t)−2u2(x,t)+u3(x,t)], |
| sβL[u(x,t)]−sβ−1[u(x,0)]=−L[∂4u(x,t)∂x4+2∂2u(x,t)∂x2−a∂3u(x,t)∂x3−bu(x,t)−2u2(x,t)+u3(x,t)]. |
Using inverse transformation
| u(x,t)=L−1[u(x,0)s−1sβL{∂4u(x,t)∂x4+2∂2u(x,t)∂x2−a∂3u(x,t)∂x3−bu(x,t)−2u2(x,t)+u3(x,t)}], |
| u(x,t)=110sin(πxl)−L−1[1sβL{∂4u(x,t)∂x4+2∂2u(x,t)∂x2−a∂3u(x,t)∂x3−bu(x,t)−2u2(x,t)+u3(x,t)}], |
Using ADM procedure, we get
| ∞∑j=0uj(x,t)=110sin(πxl)−L−1[1sβL{∞∑j=0∂4uj(x,t)∂x4+2∞∑j=0∂2uj(x,t)∂x2−a∞∑j=0∂3uj(x,t)∂x3−b∞∑j=0uj(x,t)−2∞∑j=0Aj+∞∑j=0Bj}], |
| u0(x,t)=110sin(πxl), | (4.8) |
| ∞∑j=1uj(x,t)=−L−1[1sβL{∞∑j=1∂4uj−1(x,t)∂x4+2∞∑j=1∂2uj−1(x,t)∂x2−a∞∑j=1∂3uj−1(x,t)∂x3−b∞∑j=1uj−1(x,t)−2∞∑j=1Aj−1+∞∑j=1Bj−1}], | (4.9) |
where the nonlinear terms in the above equations are represented by Adomian polynomials Aj and Bj [41]. Whose components are defined as
| Aj=1j![djdλj{N(∞∑j=0(λjuj))}]λ=0, Bj=1j![djdλj{N(∞∑j=0(λjuj))}]λ=0,j=0,1,2,⋯, |
Here the nonlinear term is
| N1(u)=u2, N2(u)=u3. | (4.10) |
For j=0
| A0=N(λ0u0), B0=N(λ0u0),A0=N(u0), B0=N(u0), |
| A0=u20, B0=u30, |
j=1
| A1=11![ddλ{N(λ0u0+λ1u1)}]λ=0, B1=11![ddλ{N1(λ0u0+λ1u1)}]λ=0, |
| A1=[ddλ{N(u0+λu1)}]λ=0, B1=[ddλ{N1(u0+λu1)}]λ=0, |
| A1=[ddλ{(u0+λu1)2}]λ=0, B1=[ddλ{(u0+λu1)3}]λ=0, |
| A1=[2(u0+λu1)2u1]λ=0, B1=[3(u0+λu1)2u1]λ=0, |
| A1=2u0u1, B1=3u20u1. |
Similarly
| A2=2u0u2+2u0u1, B2=3u20u2+3u0u21. |
For j=1
| u1(x,t)=−L−1[1sβL{∂4u0(x,t)∂x4+2∂2u0(x,t)∂x2−a∂3u0(x,t)∂x3−bu0(x,t)−2u20(x,t)+u30(x,t)}], |
| u1(x,t)=[−sin(πxl)π410l4+sin(πxl)π210l2−acos(πxl)π310l3+bsin(πxl)10l+sin2(πxl)50l−sin3(πxl)10000]tβΓ(β+1). |
For j=2
| u2(x,t)=−L−1[1sβL{∂4u1(x,t)∂x4+2∂2u1(x,t)∂x2−a∂3u1(x,t)∂x3−bu1(x,t)−4u0(x,t)u1(x,t)+3u20(x,t)u1(x,t)}], |
| u2(x,t)=1100000l8[−600π2l6sin(πxl)−10000a2π6l2sin(πxl)−3000aπ3l5cos3(πxl)−8400π4l4cos2(πxl)sin(πxl)−20000bπ4l4sin(πxl)+20000bπ2l6sin(πxl)+20000aπ7lcos(πxl)−20000π5l3cos(πxl)+1200π2l6sin(πxl)cos2(πxl)−20000aπ3l5bcos(πxl)−20000aπ3l5cos(πxl)sin(πxl)+10000π8sin(πxl)−100l8−20000π6l2sin(πxl)+36000π4l4cos2(πxl)+12400π4l4sin(πxl)−12000π2l6cos2(πxl)+10000b2l8sin(πxl)+2400aπ3l5cos(πxl)+803l8sin(πxl)−20000π4l4+6000bl8−400bl8sin(πxl)+8000π2l6+200l8cos2(πxl)−100l8cos4(πxl)−6000bl8cos2(πxl)−806l8sin(πxl)cos2(πxl)+3l8sin(πxl)cos4(πxl)+400bl8sin(πxl)cos2(πxl)]t2βΓ(2β+1). |
The LADM solution for example 2 is
| u(x,t)=u0(x,t)+u1(x,t)+u2(x,t)+..., |
| u(x,t)=110sin(πxl)+[−sin(πxl)π410l4+sin(πxl)π210l2−acos(πxl)π310l3+bsin(πxl)10l+sin2(πxl)50l−sin3(πxl)10000]tβΓ(β+1)+1100000l8[−600π2l6sin(πxl)−10000a2π6l2sin(πxl)−3000aπ3l5cos3(πxl)−8400π4l4cos2(πxl)sin(πxl)−20000bπ4l4sin(πxl)+20000bπ2l6sin(πxl)+20000aπ7lcos(πxl)−20000π5l3cos(πxl)+1200π2l6sin(πxl)cos2(πxl)−20000aπ3l5bcos(πxl)−20000aπ3l5cos(πxl)sin(πxl)+10000π8sin(πxl)−100l8−20000π6l2sin(πxl)+36000π4l4cos2(πxl)+12400π4l4sin(πxl)−12000π2l6cos2(πxl)+10000b2l8sin(πxl)+2400aπ3l5cos(πxl)+803l8sin(πxl)−20000π4l4+6000bl8−400bl8sin(πxl)+8000π2l6+200l8cos2(πxl)−100l8cos4(πxl)−6000bl8cos2(πxl)−806l8sin(πxl)cos2(πxl)+3l8sin(πxl)cos4(πxl)+400bl8sin(πxl)cos2(πxl)]t2βΓ(2β+1)..., |
In Table 2, the solutions comparison of LADM and HPM is given at fractional orders β=0.5 and 1. It has been observed that LADM has the higher degree of accuracy as compare to HPM.
| x | HPM(β=0.5) | LADM(β=0.5) | HPM(β=1) | LADM(β=1) |
| 0.25 | 0.00327554 | 0.00327554 | 0.0023907 | 0.0023907 |
| 0.50 | 0.01120703 | 0.01120703 | 0.0063240 | 0.0063240 |
| 0.75 | 0.01963618 | 0.01963618 | 0.0104008 | 0.0104008 |
| 1.00 | 0.02849853 | 0.02849853 | 0.0145955 | 0.0145955 |
| 1.25 | 0.03771459 | 0.03771459 | 0.0188774 | 0.0188774 |
| 1.50 | 0.04719094 | 0.04719094 | 0.0232104 | 0.0232104 |
| 1.75 | 0.05682173 | 0.05682173 | 0.0275542 | 0.0275542 |
| 2.00 | 0.06649076 | 0.06649076 | 0.0318643 | 0.0318643 |
DownLoad:
CSV
In Figure 3, the LADM solutions at fractional orders β=0.75 and 1 are plotted. The graph (a) represent the solution of example 2 at β=1 while graph (b) is the plot of LADM solution at β=0.75. In Figure 4, the LADM solutions at fractional orders β=0.75 and 1 are plotted at t=1,2,3 and 4 in the domain −10<x<10. The graphs (c) and (d) of Figure 4 represent the LADM solutions at fractional orders β=1 and 0.75 respectively.
Consider the following non-linear S-H equation with dispersion
| ∂βu(x,t)∂tβ+(1−r)u(x,t)+2∂2u(x,t)∂x2+∂4u(x,t)∂x4−u2(x,t)+(∂u(x,t)∂x)2=0, 0<β≤1 | (4.11) |
with initial condition
| u(x,0)=ex. | (4.12) |
Taking Laplace transform of Eq (4.11),
| L[∂βu(x,t)∂tβ]=−L[(1−r)u(x,t)+2∂2u(x,t)∂x2+∂4u(x,t)∂x4−u2(x,t)+(∂u(x,t)∂x)2], |
| sβL[u(x,t)]−sβ−1[u(x,0)]=−L[(1−r)u(x,t)+2∂2u(x,t)∂x2+∂4u(x,t)∂x4−u2(x,t)+(∂u(x,t)∂x)2]. |
Using inverse transformation
| u(x,t)=L−1[u(x,0)s−1sβL{(1−r)u(x,t)+2∂2u(x,t)∂x2+∂4u(x,t)∂x4−u2(x,t)+(∂u(x,t)∂x)2}], |
| u(x,t)=ex−L−1[1sβL{(1−r)u(x,t)+2∂2u(x,t)∂x2+∂4u(x,t)∂x4−u2(x,t)+(∂u(x,t)∂x)2}], |
Using ADM procedure, we get
| ∞∑j=0uj(x,t)=ex−L−1[1sβL{(1−r)∞∑j=0uj(x,t)+2∞∑j=0∂2uj(x,t)∂x2+∞∑j=0∂4uj(x,t)∂x4−∞∑j=0Aj+∞∑j=0Bj}], |
| u0(x,t)=ex, | (4.13) |
| ∞∑j=1uj(x,t)=−L−1[1sβL{(1−r)∞∑j=0uj(x,t)+2∞∑j=0∂2uj(x,t)∂x2+∞∑j=0∂4uj(x,t)∂x4−∞∑j=0Aj+∞∑j=0Bj}], | (4.14) |
where the nonlinear terms in the above equations are represented by Adomian polynomials Aj and Bj [41]. Whose components are defined as
| Aj=1j![djdλj{N(∞∑j=0(λjuj))}]λ=0, Bj=1j![djdλj{N1(∞∑j=0(λjuj))}]λ=0, j=0,1,2,⋯, |
Here the nonlinear term is
| N(u)=u2, N1(u)=(ux)2. | (4.15) |
For j=0
| A0=N(λ0u0), B0=N1(λ0u0),A0=N(u0), B0=N1(u0). |
Using Eq (4.5)
| A0=u20, B0=(u0x)2, |
j=1
| A1=11![ddλ{N(λ0u0+λ1u1)}]λ=0, B1=11![ddλ{N1(λ0u0+λ1u1)}]λ=0, |
| A1=[ddλ{N(u0+λu1)}]λ=0, B1=[ddλ{N1(u0+λu1)}]λ=0, |
| A1=[ddλ{(u0+λu1)2}]λ=0, B1=[ddλ{(u0x+λu1x)2}]λ=0, |
| A1=2[(u0+λu1)u1]λ=0, B1=2[(u0x+λu1x)u1x]λ=0, |
| A1=2u0u1, B1=2(u0xu1x). |
Similarly
| A2=u0u1+u0u1, B2=(u0u2)x+(u0u1)x. |
For j=1
| u1(x,t)=−L−1[1sβL{(1−r)u0(x,t)+2∂2u0(x,t)∂x2+∂4u0(x,t)∂x4−A0+B0}], |
| u1(x,t)=(r−4)extβΓ(β+1). |
For j=2
| u2(x,t)=−L−1[1sβL{(1−r)u1(x,t)+2∂2u1(x,t)∂x2+∂4u1(x,t)∂x4−A1+B1}], |
| u2(x,t)=(r−4)ext2βΓ(2β+1).⋮ |
The LADM solution for example 3 is
| u(x,t)=u0(x,t)+u1(x,t)+u2(x,t)+⋯+un(x,t). |
| u(x,t)=ex+(r−4)extβΓ(β+1)+(r−4)ext2βΓ(2β+1)+⋯+(r−4)ex∞∑n=3tnβΓ(nβ+1). | (4.16) |
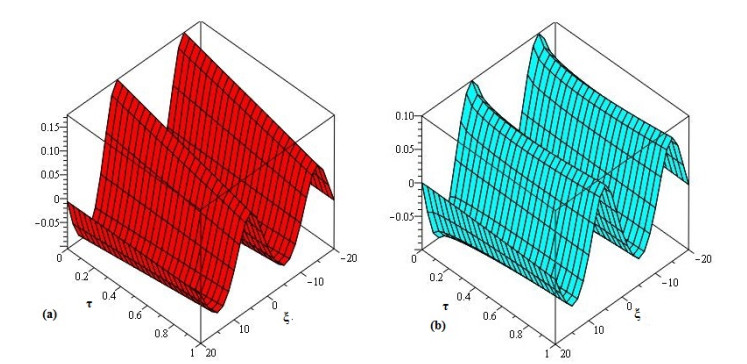
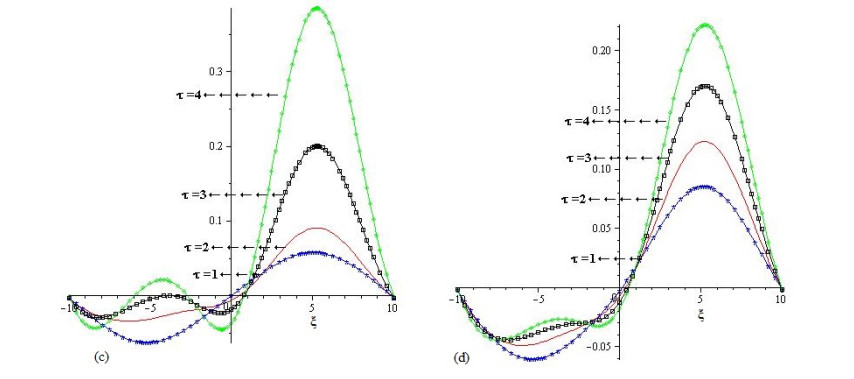
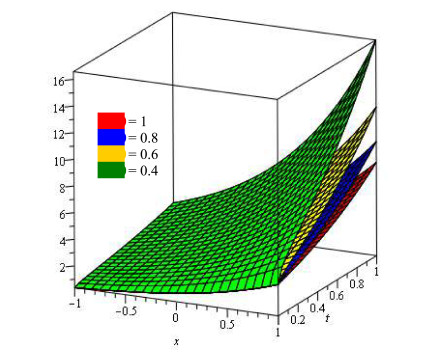
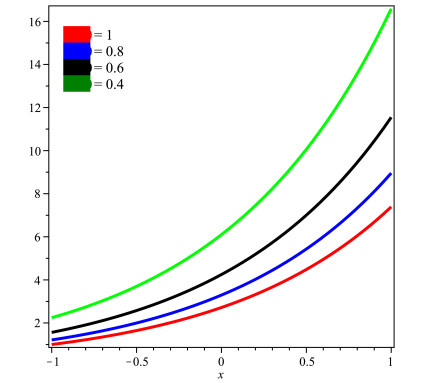
In Figure 5, the LADM solutions of 3D graph at different fractional-orders β=1,0.8,0.6 and 0.4 are plotted. In Figure 6, the LADM solutions graph of 2D at different fractional-orders β=1,0.8,0.6 and 0.4 are plotted at t=1 in the domain −1<x<1.
In this research paper, the Laplace-Adomian decomposition method is found to be a simple and effective technique to solve the Swift-Hohenberg equations of fractional-order. The implementation of the proposed method has been done for some numerical examples of Swift-Hohenberg equations. The solution of these examples are in good contact with other analytical techniques such as the variational iteration method and the homotopy perturbation method. The present method has simple, accurate and straightforward implementation to solve fractional-order Swift-Hohenberg equations. It is also investigated that the proposed method has simple procedure and required a small volume of calculations as compared to other analytical methods. In conclusion, the suggested approach is considered to be a sophisticated tool for the solution of other fractional-order differential equations.
The authors declare no conflict of interest.
Conceptualization, H.K. and R.S.; Methodology, H.K.; Software, R.S.; Validation, J.X. and D.B.; Formal Analysis, A.A.; Investigation, H.K. J.X. and D.B.; Resources, H.K. and S.A.; Writing-Original Draft Preparation, R.S.; Writing-Review and Editing, H.K. and D.B; Visualization, J.X.; Supervision, D.B.; Project Administration, A.A, Funding, J.X.
Natural Science Foundation of Neijiang Normal University (No.14ZB06).
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia for founding this work through Research Groups program under grant number (R.G.P2./99/41).
| [1] | K. B. Oldham, J. Spanier, The Fractional Calculus, vol. 111 of Mathematics in science and engineering, 1974. |
| [2] | A. A. A. Kilbas, H. M. Srivastava, J. J. Trujillo, Theory and applications of fractional differential equations, Elsevier Science Limited, 204 (2006). |
| [3] | K. S. Miller, B. Ross, An introduction to the fractional calculus and fractional differential equations, Wiley, 1993. |
| [4] |
M. Caputo, Linear models of dissipation whose Q is almost frequency independent-II, Geophys. J. Int., 13 (1967), 529-539. doi: 10.1111/j.1365-246X.1967.tb02303.x
|
| [5] | F. Yin, J. Song, X. Cao, A general iteration formula of VIM for fractional heat-and wave-like equations, J. Appl. Math., 2013. |
| [6] |
A. S. Arife, S. K. Vanani, F. Soleymani, The Laplace homotopy analysis method for solving a general fractional diffusion equation arising in nano-hydrodynamics, J. Comput. Theor. Nanosci., 10 (2013), 33-36. doi: 10.1166/jctn.2013.2653
|
| [7] | K. Oldham, J. Spanier, The fractional calculus theory and applications of differentiation and integration to arbitrary order, Elsevier, 1974. |
| [8] |
R. Shah, H. Khan, S. Mustafa, P. Kumam, M. Arif, Analytical solutions of fractional-order diffusion equations by natural transform decomposition method, Entropy, 21 (2019), 557. doi: 10.3390/e21060557
|
| [9] |
N. H. Sweilam, A. A. Elaziz El-Sayed, S. Boulaaras, Fractional-order advection-dispersion problem solution via the spectral collocation method and the non-standard finite difference technique, Chaos, Solitons Fractals, 144 (2021), 110736. doi: 10.1016/j.chaos.2021.110736
|
| [10] |
A. J. Munoz-Vzquez, J. D. Snchez-Torres, M. Defoort, S. Boulaaras, Predefined-time convergence in fractional-order systems, Chaos, Solitons Fractals, 143 (2021), 110571. doi: 10.1016/j.chaos.2020.110571
|
| [11] | R. Guefaifia, S. M. Boulaaras, B. Cherif, T. Radwan, Infinite Existence Solutions of Fractional Systems with Lipschitz Nonlinearity, J. Function Spaces, 2020 (2020). |
| [12] |
O. A. Arqub, Fitted reproducing kernel Hilbert space method for the solutions of some certain classes of time-fractional partial differential equations subject to initial and Neumann boundary conditions, Comput. Math. Appl., 73 (2017), 1243-1261. doi: 10.1016/j.camwa.2016.11.032
|
| [13] | O. A. Arqub, Numerical solutions for the Robin time-fractional partial differential equations of heat and fluid flows based on the reproducing kernel algorithm, Int. J. Numer. Methods Heat Fluid Flow, 2018. |
| [14] |
O. A. Arqub, Z. Odibat, M. Al-Smadi, Numerical solutions of time-fractional partial integrodifferential equations of Robin functions types in Hilbert space with error bounds and error estimates, Nonlinear Dynam., 94 (2018), 1819-1834. doi: 10.1007/s11071-018-4459-8
|
| [15] | N. Mehmood, N. Ahmad, Existence results for fractional order boundary value problem with nonlocal non-separated type multi-point integral boundary conditions, AIMS Math., 5 (2019), 385-398. |
| [16] |
H. K. Nashine, R. W. Ibrahim, Solvability of a fractional Cauchy problem based on modified fixed point results of non-compactness measures, AIMS Math., 4 (2019), 847-859. doi: 10.3934/math.2019.3.847
|
| [17] |
S. Bushnaq, S. Ali, K. Shah, M. Arif, Approximate solutions to nonlinear fractional order partial differential equations arising in ion-acoustic waves, AIMS Math., 4 (2019), 721-739. doi: 10.3934/math.2019.3.721
|
| [18] |
Y. Chu, M. MA. Khater, Y. S. Hamed, Diverse novel analytical and semi-analytical wave solutions of the generalized (2+1)-dimensional shallow water waves model, AIP Advances, 11 (2021), 015223. doi: 10.1063/5.0036261
|
| [19] | M. Khater, U. Ali, M. A. Khan, A. A. Mousa, R. A. M. Attia, A new numerical approach for solving 1D Fractional diffusion-wave equation, J. Function Spaces, 2021 (2021). |
| [20] |
M. M. A. Khater, R. A. M. Attia, C. Park, D. Lu, On the numerical investigation of the interaction in plasma between (high & low) frequency of (Langmuir & ion-acoustic) waves, Results Physics, 18 (2020), 103317. doi: 10.1016/j.rinp.2020.103317
|
| [21] | G. Adomian, Solving frontier problems of physics: The decomposition method, With a preface by Yves Cherruault, Fundamental Theories of Physics, Kluwer Academic Publishers Group, Dordrecht, 1 (1994). |
| [22] |
S. A. Khuri, A Laplace decomposition algorithm applied to a class of nonlinear differential equations, J. Appl. Math., 1 (2001), 141-155. doi: 10.1155/S1110757X01000183
|
| [23] |
A. Ali, K. Shah, R. A. Khan, Numerical treatment for traveling wave solutions of fractional Whitham-Broer-Kaup equations, Alex. Eng. J., 57 (2018), 1991-1998. doi: 10.1016/j.aej.2017.04.012
|
| [24] |
R. Shah, H. Khan, M. Arif, P. Kumam, Application of LaplaceAdomian decomposition method for the analytical solution of third-order dispersive fractional partial differential equations, Entropy, 21 (2019), 335. doi: 10.3390/e21040335
|
| [25] |
H. Khan, R. Shah, P. Kumam, D. Baleanu, M. Arif, An efficient analytical technique, for the solution of fractional-order telegraph equations, Mathematics, 7 (2019), 426. doi: 10.3390/math7050426
|
| [26] | A. Ali, L. Humaira, K. Shah, Analytical solution of general fishers equation by using Laplace Adomian decomposition method, J. Pure Appl. Math., 2 (2018), 1-4. |
| [27] |
S. Mahmood, R. Shah, M. Arif, Laplace adomian decomposition method for multi dimensional time fractional model of Navier-Stokes equation, Symmetry, 11 (2019), 149. doi: 10.3390/sym11020149
|
| [28] |
F. Haq, K. Shah, Q. M. Al-Mdallal, F. Jarad, Application of a hybrid method for systems of fractional order partial differential equations arising in the model of the one-dimensional Keller-Segel equation, Eur. Phys. J. Plus, 134 (2019), 1-11. doi: 10.1140/epjp/i2019-12286-x
|
| [29] |
F. T. Akyildiz, D. A. Siginer, K. Vajravelu, R. A. V. Gorder, Analytical and numerical results for the Swift Hohenberg equation, Appl. Math. Comput., 216 (2010), 221-226. doi: 10.1016/j.amc.2010.01.041
|
| [30] |
J. Lega, J. V. Moloney, A. C. Newell, Swift-Hohenberg equation for lasers, Phys. Rev. Lett., 73 (1994), 2978. doi: 10.1103/PhysRevLett.73.2978
|
| [31] |
H. Sakaguchi, H. R. Brand, Localized patterns for the quintic complex Swift-Hohenberg equation, Physica D: Nonlinear Phenomena, 117 (1998), 95-105. doi: 10.1016/S0167-2789(97)00310-2
|
| [32] |
P. C. Hohenberg, J. B. Swift, Effects of additive noise at the onset of Rayleigh-Bnard convection, Phys. Rev. A, 46 (1992), 4773. doi: 10.1103/PhysRevA.46.4773
|
| [33] |
K. Vishal, S. Das, S. H. Ong, P. Ghosh, On the solutions of fractional Swift Hohenberg equation with dispersion, Appl. Math. Comput., 219 (2013), 5792-5801. doi: 10.1016/j.amc.2012.12.032
|
| [34] |
K. Vishal, S. Kumar, S. Das, Application of homotopy analysis method for fractional Swift Hohenberg equation revisited, Appl. Math. Model., 36 (2012), 3630-3637. doi: 10.1016/j.apm.2011.10.001
|
| [35] |
M. Merdan, A numeric analytic method for time-fractional Swift Hohenberg (SH) equation with modified Riemann Liouville derivative, Appl. Math. Model., 37 (2013), 4224-4231. doi: 10.1016/j.apm.2012.09.003
|
| [36] | N. A. Khan, N. U. Khan, M. Ayaz, A. Mahmood, Analytical methods for solving the time-fractional Swift Hohenberg (SH) equation, Comput. Math. Appl. 61 (2011), 2182-2185. |
| [37] |
S. McCalla, B. Sandstede, Snaking of radial solutions of the multi-dimensional Swift Hohenberg equation: A numerical study, Physica D: Nonlinear Phenomena, 239 (2010), 1581-1592. doi: 10.1016/j.physd.2010.04.004
|
| [38] |
N. A. Kudryashov, D. I. Sinelshchikov, Exact solutions of the Swift Hohenberg equation with dispersion, Commun. Nonlinear Sci., 17 (2012), 26-34. doi: 10.1016/j.cnsns.2011.04.008
|
| [39] | W. Li, Y. Pang, An iterative method for time-fractional Swift-Hohenberg equation, Adv. Math. Phys., 2018 (2018). |
| [40] |
P. Bakhtiari, S. Abbasbandy, R. A. V. Gorder, Reproducing kernel method for the numerical solution of the 1D Swift Hohenberg equation, Appl. Math. Comput., 339 (2018), 132-143. doi: 10.1016/j.amc.2018.07.006
|
| [41] |
A. M. Wazwaz, A reliable modification of Adomian decomposition method, Appl. Math. Comput., 102 (1999), 77-86. doi: 10.1016/S0096-3003(98)10024-3
|
| 1. | Naveed Iqbal, Ali Akgül, Rasool Shah, Abdul Bariq, M. Mossa Al-Sawalha, Akbar Ali, Hemen Dutta, On Solutions of Fractional-Order Gas Dynamics Equation by Effective Techniques, 2022, 2022, 2314-8888, 1, 10.1155/2022/3341754 | |
| 2. | Ismail Gad Ameen, Rasha Osman Ahmed Taie, Hegagi Mohamed Ali, Two effective methods for solving nonlinear coupled time-fractional Schrödinger equations, 2023, 70, 11100168, 331, 10.1016/j.aej.2023.02.046 | |
| 3. | Hegagi Mohamed Ali, Hijaz Ahmad, Sameh Askar, Ismail Gad Ameen, Efficient Approaches for Solving Systems of Nonlinear Time-Fractional Partial Differential Equations, 2022, 6, 2504-3110, 32, 10.3390/fractalfract6010032 | |
| 4. | Hassan Khan, Poom Kumam, Qasim Khan, Fairouz Tchier, Kanokwan Sitthithakerngkiet, Ioannis Dassios, A New Modified Analytical Approach for the Solution of Time-Fractional Convection–Diffusion Equations With Variable Coefficients, 2022, 10, 2296-424X, 10.3389/fphy.2022.900502 | |
| 5. | Meshari Alesemi, Naveed Iqbal, Ahmed A. Hamoud, C. Rajivganthi, The Analysis of Fractional-Order Proportional Delay Physical Models via a Novel Transform, 2022, 2022, 1099-0526, 1, 10.1155/2022/2431533 | |
| 6. | Humaira Yasmin, Numerical Analysis of Time-Fractional Whitham-Broer-Kaup Equations with Exponential-Decay Kernel, 2022, 6, 2504-3110, 142, 10.3390/fractalfract6030142 | |
| 7. | Khursheed Jamal Ansari, Fatima Ilyas, Kamal Shah, Aziz Khan, Thabet Abdeljawad, On new updated concept for delay differential equations with piecewise Caputo fractional-order derivative, 2023, 1745-5030, 1, 10.1080/17455030.2023.2187241 | |
| 8. | NEHAD ALI SHAH, PRAVEEN AGARWAL, JAE DONG CHUNG, SAAD ALTHOBAITI, SAMY SAYED, A. F. ALJOHANI, MOHAMED ALKAFAFY, ANALYSIS OF TIME-FRACTIONAL BURGERS AND DIFFUSION EQUATIONS BY USING MODIFIEDq-HATM, 2022, 30, 0218-348X, 10.1142/S0218348X22400126 | |
| 9. | Noufe H. Aljahdaly, Ravi P. Agarwal, Thongchai Botmart, The analysis of the fractional-order system of third-order KdV equation within different operators, 2022, 61, 11100168, 11825, 10.1016/j.aej.2022.05.032 | |
| 10. | Divya Raghavan, J. F. Gómez-Aguilar, N. Sukavanam, Analytical approach of Hilfer fractional order differential equations using iterative Laplace transform method, 2023, 61, 0259-9791, 219, 10.1007/s10910-022-01419-7 | |
| 11. | Mohammed Kbiri Alaoui, Rabia Fayyaz, Adnan Khan, Rasool Shah, Mohammed S. Abdo, Fathalla A. Rihan, Analytical Investigation of Noyes–Field Model for Time-Fractional Belousov–Zhabotinsky Reaction, 2021, 2021, 1099-0526, 1, 10.1155/2021/3248376 | |
| 12. | Hassan Khan, Adnan Khan, Rasool Shah, Dumitru Baleanu, A novel fractional case study of nonlinear dynamics via analytical approach, 2024, 39, 1005-1031, 276, 10.1007/s11766-024-4148-y | |
| 13. | Muhammad Arshad, hassan Khan, Qadim Khan, Samia Bushnaq, A new and efficient numerical algorithm to solve fractional boundary value problems, 2025, 0037-8712, 10.5269/bspm.75377 |
Figures(6) / Tables(2)
Jiabin Xu, Hassan Khan, Rasool Shah, A.A. Alderremy, Shaban Aly, Dumitru Baleanu. The analytical analysis of nonlinear fractional-order dynamical models[J]. AIMS Mathematics, 2021, 6(6): 6201-6219. doi: 10.3934/math.2021364
| x | VIM(β=0.5) | LADM(β=0.5) | VIM(β=1) | LADM(β=1) |
| 0.00 | 0.00000000 | 0.00000000 | 0.0000000 | 0.0000000 |
| 0.25 | 0.03085341 | 0.03085341 | 0.0347097 | 0.0347097 |
| 0.50 | 0.06652018 | 0.06652018 | 0.0704722 | 0.0704722 |
| 0.75 | 0.10743665 | 0.10743665 | 0.1062671 | 0.1062671 |
| 1.00 | 0.14795188 | 0.14795188 | 0.1382405 | 0.1382405 |
| 1.25 | 0.17838674 | 0.17838674 | 0.1607941 | 0.1607941 |
| 1.50 | 0.18974562 | 0.18974562 | 0.1689702 | 0.1689702 |
| 1.75 | 0.17838674 | 0.17838674 | 0.1607941 | 0.1607941 |
| 2.00 | 0.14795188 | 0.14795188 | 0.1382405 | 0.1382405 |
DownLoad:
CSV
| x | HPM(β=0.5) | LADM(β=0.5) | HPM(β=1) | LADM(β=1) |
| 0.25 | 0.00327554 | 0.00327554 | 0.0023907 | 0.0023907 |
| 0.50 | 0.01120703 | 0.01120703 | 0.0063240 | 0.0063240 |
| 0.75 | 0.01963618 | 0.01963618 | 0.0104008 | 0.0104008 |
| 1.00 | 0.02849853 | 0.02849853 | 0.0145955 | 0.0145955 |
| 1.25 | 0.03771459 | 0.03771459 | 0.0188774 | 0.0188774 |
| 1.50 | 0.04719094 | 0.04719094 | 0.0232104 | 0.0232104 |
| 1.75 | 0.05682173 | 0.05682173 | 0.0275542 | 0.0275542 |
| 2.00 | 0.06649076 | 0.06649076 | 0.0318643 | 0.0318643 |
DownLoad:
CSV
| x | VIM(β=0.5) | LADM(β=0.5) | VIM(β=1) | LADM(β=1) |
| 0.00 | 0.00000000 | 0.00000000 | 0.0000000 | 0.0000000 |
| 0.25 | 0.03085341 | 0.03085341 | 0.0347097 | 0.0347097 |
| 0.50 | 0.06652018 | 0.06652018 | 0.0704722 | 0.0704722 |
| 0.75 | 0.10743665 | 0.10743665 | 0.1062671 | 0.1062671 |
| 1.00 | 0.14795188 | 0.14795188 | 0.1382405 | 0.1382405 |
| 1.25 | 0.17838674 | 0.17838674 | 0.1607941 | 0.1607941 |
| 1.50 | 0.18974562 | 0.18974562 | 0.1689702 | 0.1689702 |
| 1.75 | 0.17838674 | 0.17838674 | 0.1607941 | 0.1607941 |
| 2.00 | 0.14795188 | 0.14795188 | 0.1382405 | 0.1382405 |
| x | HPM(β=0.5) | LADM(β=0.5) | HPM(β=1) | LADM(β=1) |
| 0.25 | 0.00327554 | 0.00327554 | 0.0023907 | 0.0023907 |
| 0.50 | 0.01120703 | 0.01120703 | 0.0063240 | 0.0063240 |
| 0.75 | 0.01963618 | 0.01963618 | 0.0104008 | 0.0104008 |
| 1.00 | 0.02849853 | 0.02849853 | 0.0145955 | 0.0145955 |
| 1.25 | 0.03771459 | 0.03771459 | 0.0188774 | 0.0188774 |
| 1.50 | 0.04719094 | 0.04719094 | 0.0232104 | 0.0232104 |
| 1.75 | 0.05682173 | 0.05682173 | 0.0275542 | 0.0275542 |
| 2.00 | 0.06649076 | 0.06649076 | 0.0318643 | 0.0318643 |
