1.
Introduction
The fractional diffusion equation (FDE), which is obtained by replacing the first-order time derivative and/or second-order space derivative in the standard diffusion equation by a generalized derivative of fractional order respectively, were successfully used for modelling relevant physical processes, see [1,5,14,15,21]. Recently the research on inverse problems connected with fractional derivatives becomes more and more popular. Since Cheng in [2] studied an inverse problem on fractional diffusion equation, many topics are well discussed [11,12,23,26,27]. For the problem of fractional numerical differentiation, in [17,18], the authors give different regularization methods. In [13,26,30], some inverse source problems for fractional diffusion equations are considered. In [25,28], Liu et al consider the backward time-fractional diffusion problem. In [4,8,10,16], many results on inverse coefficient problems are established. For more reference on inverse problems for fractional diffusion equations, please consult the survey paper [9]. However, in some situation of anomalous diffusion, the diffusion indexes and the diffusion coefficient are unknown. This leads to determination of coefficients which is a classical inverse problem. It should be mentioned that most of the existing literature investigate the determination of only one unknown parameter or functions. However, in many practical situations, one wishes to simultaneously reconstruct more than one physical parameters. To the authors' knowledge, there are few works on this aspect. For examples, in [4], the fractional order α in tDα∗u(x,t)=△u(x,t) is determined by an analytic method. In [24], the fractional orders α,β in tDα∗u(x,t)=−(−△)β2u(x,t) are reconstructed by the classical Levenberg-Marquardt method based on disrete least squares functional. The simultaneous inversion for the fractional order α and the space-dependent diffusion coefficient has been considered in [2,10]. In this paper, we reconstruct three important parameters in the time-space fractional diffusion equation from only one boundary measurement.
Let us consider the time and space-symmetric fractional diffusion equation in one-dimensional space
subject to homogeneous Neumann boundary conditions
and the initial condition
where u is a solute concentration, κ>0 represents the diffusion coefficient. tDα∗ is the Caputo time fractional derivative of order α (0<α<1) with the starting point at t=0 defined as follows [19]:
The symmetric-space fractional derivative (−△)β2 of order β (1<β≤2) is defined by [3,6,7]. For readability, we reproduce the following definition for (−△)β2, 1<β≤2:
Definition 1. [29] Suppose the Laplace operator −△ has a complete set of orthonormal eigenfunctions φn corresponding to eigenvalues λ2n on a bounded domain D, i.e., (−△)φn=λ2nφn on a bounded domain D, B(φ)=0 on ∂D is one of the standard three homogeneous boundary conditions. Let
then for any f∈Gγ: (−△)β2 is defined by
In the case of α=1,β=2, Eq (1.1) reduces to the classical diffusion equation. For 0<α<1,β=2, Eq (1.1) models subdiffusion due to particles having long-tailed resting times. For α=1,1<β<2, Eq (1.1) corresponds to the Lévy process. Hence the solution of (1.1) is important for describing the competition between these two anomalous diffusion processes.
If α,β,κ,f(x) are given, the solution for the direct problem of Eqs (1.1)–(1.3) can be obtained analytically by the method of separation of variables: Setting u(x,t)=X(x)T(t) and substituting into (1.1) yields
Letting ω is the separation constant, we obtain two fractional ordinary linear differential equations for X(x) and T(t) as
respectively. Following the definition of fractional Laplacian (−△)β2 defined on a bounded domain, Eq (1.5) can be expressed as
Hence under homogeneous Neumann conditions, the eigenvalues are ωn=λβn=(nπL)β(1<β≤2) for n=0,1,2,⋯ and the corresponding eigenfunctions are xn=cos(nπxL). Finally, the analytical solution of Eqs (1.1)–(1.3) is
where
Here we have used the result Eα,1(0)=1, where Eα,β(z) is the Mittag-Leffler function defined by
By a similar method to [22], we can prove that (1.8) certainly gives the weak solution to Eqs (1.1)–(1.3).
Consider the following inverse problem:
Given g(t):=u(0,t) (or ˜g(t):=u(L,t)) with unknown α,β,κ, we want to recover the orders α,β and the coefficient κ from the data g(t) (or ˜g(t)).
Usually g(t) is measured and only available data on g(t) is its perturbation gδ(t), we assume that there exists a known noise level δ such that
where the norm ‖⋅‖ denotes L2-norm.
In this paper, our main work is to give the uniqueness result on determination of α,β,κ from the data g(t) and two numerical methods for solving the inverse problems. Although in the paper [24], the authors give a uniqueness result on a similar problem, the result holds only for 0<α<1/2 and sufficiently large T. Our result do not require this restriction and holds for 0<α<1 and a finite T. This is done by adding some more smoothness assumption on the initial data f(x).
Throughout this paper, sometimes we denote the solution of the problem as u(x,t)=u(α,β,κ,x,t) to show its dependence on α,β,κ.
2.
Inverse problem and its uniqueness
Now from (1.8), we have the relationship:
The uniqueness of the inverse problem is stated as follows:
Theorem 1. Suppose that u1(α1,β1,κ1;x,t) and u2(α2,β2,κ2;x,t) represent the solutions of the inverse problem with α=α1,β=β1,κ=κ1 and α=α2,β=β2,κ=κ2 respectively. We assume that the initial data satisfies
If u1(α1,β1,κ1;0,t)=u2(α2,β2,κ2;0,t) (0<t<T), then
Proof. From Eq (2.1), we have
By assumption u1(α1,β1,κ1;0,t)=u2(α2,β2,κ2;0,t), it yields that
for 0<t<T.
As an initial step, we will prove that α1=α2.
By the definition of Mittag-Leffler function, we have
And by the same argument, we obtain
From Eq (2.4), the following result
holds true. Now, we need to estimate the terms:
and
According to the inequality
where δ0,C0 are some positive constants, we get
Furthermore, we recall that f(x)∈H4(0,L), then
where C1 is a constant independent on n.
For the term on the right-side hand of Eq (2.9),
holds, when 0<ϵ0<3/2 and 0<ε<α1. Since
then
On the other hand, by Cauchy-Schwarz inequality
Noting that ϵ0<3/2 and 1<β1<2, then 2(1+ϵ0−4)<2(β1+ϵ0−4)<−1. Combining (2.10), we can conclude that
Therefore,
with small ε>0. Similarly, we can verify that
with small ε>0.
Inserting the above two equalities into (2.7), we have
If α2<α1, then
holds for t→0. That means
for t→0. However, this is impossible. Because if ∑∞n=1κ2(nπL)β2fn=0, then due to fn>0,1<β2≤2,
This is a contradiction. Hence α2<α1 does not hold. Similarly, α2>α1 does not hold, too. As a result, we get α1=α2.
Next, we will prove that β1=β2,κ1=κ2.
Now we have the following equation from (2.4)
for α1=α2=α. By the analytic proposition of Eα,1(t), the above equation holds for t>0. First for 0<α<1, we have the Laplace transform of Mittag-Leffler function:
Taking Laplace transform on both sides of Eq (2.20), we have
i.e.,
That is
We can analytically continue both sides of (2.24) in η. So (2.24) holds for
Now we deduce that κ1(nπL)β1=κ2(nπL)β2. From (2.24), W. L. O. G., we assume that κ1(nπL)β1<κ2(nπL)β2. Then we can take a suitable disc R1 which includes −κ1(nπL)β1|n=1 but does not include {−κ1(nπL)β1}n≥2∪{−κ2(nπL)β2}n≥1. According to (2.24) and the analyticity of both sides of (2.24), we have
and hence, the Cauchy integral formula and Cauchy integral theorem yield
However, f1≠0, i.e., 2πif1≠0. Therefore κ1(nπL)β1<κ2(nπL)β2 does not hold.
By the same argument, κ1(nπL)β1>κ2(nπL)β2 does not hold, either. Therefore, there holds κ1(nπL)β1=κ2(nπL)β2. Now, we are in the position to prove κ1=κ2, β1=β2 from κ1(nπL)β1=κ2(nπL)β2. It is easy to see that if κ1≠κ2 or β1≠β2 then there must exist at least a constant n such that κ1(nπL)β1≠κ2(nπL)β2. By analysis of its contrapositivity, we easily have κ1=κ2, β1=β2.
In general, the conditions (2.2) is not easy for one to verify. Therefore we give the weak conditions for the uniqueness:
Theorem 2. Suppose that u1(α1,β1,κ1;x,t) and u2(α2,β2,κ2;x,t) represent the solutions of the inverse problem with α=α1,β=β1,κ=κ1 and α=α2,β=β2,κ=κ2 respectively. We assume that the initial data satisfies
If u1(α1,β1,κ1;0,t)=u2(α2,β2,κ2;0,t) for 0<t<T, then
α1=α2,β1=β2,κ1=κ2.
Proof. W. L. O. G, let L=1,φn(x)=√2cosnπx for n∈N and φ0(x)=1. Then we consider
Then
Setting fn=(f,φn)√2 for n∈N and f0=(f,1), we have
Assume
Then due to Podlubny [19] (p.34),
Since f∈D((−△)βk/2) and (−△)βk/2 is self-adjoint for k=1,2, we have
Hence we have
Now we can prove that α1=α2.
Indeed we assume that α1<α2. Dividing (2.29) by tα1, we obtain
By α1<α2, letting t→0, we obtain k1Γ(α1+1)(−△)β1/2f(0)=0, which contradicts (2.29).
The uniqueness proof on β and κ is the same as that in Theorem 1.
Remark on (2.29). We can satisfy (2.29) by a generous condition by the comparison principle of (−△)β/2.
3.
Two numerical methods
In this section, we propose two numerical methods for solving this problem based least squares functional. The first is based on Tikhonov method in the function space. The second method is based on the classical Levenberg-Marquardt optimization method in the discrete Euclid space.
3.1. Tikhonov method combined with the gradient flow
Denote a=(αβκ)∈R3, let u(x,t;a):=u(α,β,κ)(x,t) be the unique solution of forward problem. A feasible way to numerical computation for the unknown a is to solve the following minimization problem.
The gradient ∇J(a) of the functional J(a) is given by
If let ∇J(a) = 0, then we can get the Euler equation for the minimizer. However, it is a nonlinear equation and is not easily be solved directly. Here we turn to the approximate solution by the iterative method. Using the gradient flow method with an initial value a0, we get
where t is the artificial time. Using a simple method, i.e. the explicit Euler method, we arrives the following iteration schemes with a time step size τ:
i.e.,
3.2. Levenberg-Marquardt method
Because in most of the practical applications, the data are measured at discrete times. Assume the measured data is given by gδ(ti),i=0,1,⋯,q. Let us consider the minimization problem in discrete case:
where u(a;0,ti) is the computed data from the forward problem with a given a, which is used to fit the measured data. A standard method for solving this least squares problem is the Levenberg-Marquardt method with a damped parameter ˜λ which plays the same role as the regularization parameter λ in Tikhonov method. For readability, we give the details of this algorithm:
A updated sequences is given by
where Δaj is the updated stepsize of aj in each iteration step j. We consider the the minimization problem about Δaj at each iteration step j:
Make the Taylor expansion for u(aj+Δaj;0,ti) at aj and take a linear approximation, we have
Plus this into (3.6), we get
However, this least square problem is ill-posed due to the original problem, therefore we consider the Tikhonov method:
where ∇trau(a;0,ti)⋅aj is computed by finite difference method and is given by ∇trau(a;0,ti)⋅aj≈∑3k=1u(ajk+h;0,ti)−u(ajk;0,ti)hΔajk. Now the minimization problem (3.8) is a linear problem and can be easily solved for the updated stepsize Δaj with a regularization ˜λ.
3.3. Numerical test
In this section, we consider a simple example to show the effectiveness of the aforementioned two algorithms, i.e., Tikhonov method and Levenberg-Marquardt method. We want to determine the parameters (α,β,κ) in the following problem
The exact solution is given by
Now the input data g(t):=u(0,t) is obtained and the noisy data gδ(t) is generated in the following way:
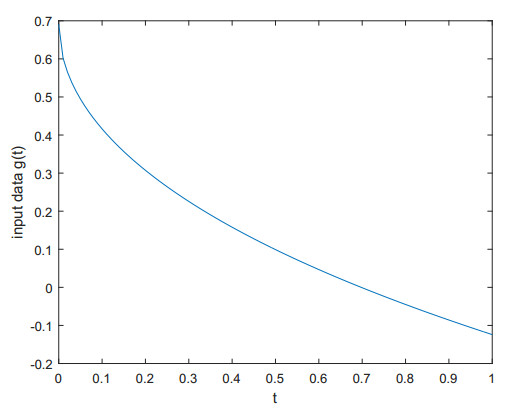
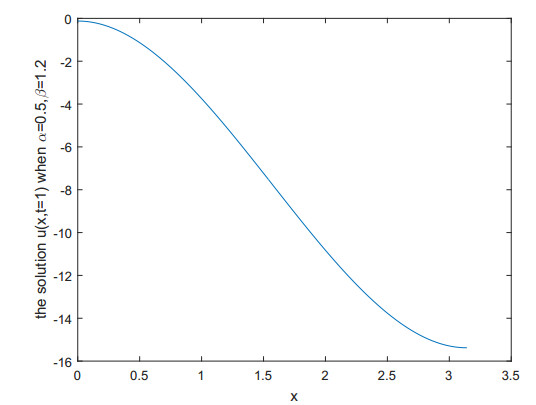
where σ(t)=θr(t) and r(t) is a random number between [0,1] and θ=max{g(t)}∗η% is the noise level. In the numerical experiment, we fix the parameters T=1,η=1. The algorithm of calculating Mittag effler function is given in [20]. First we plot the solution u(x,t=1) of direct problem when α=0.5,β=1.2,κ=0.10, which is shown in Figure 1. The input exact data g(t) is displayed in Figure 2.
The exact fractional orders and diffusion coefficient are α=0.5,β=1.2,κ=0.10.
In the numerical test for the Tikhonov method, the parameters and their values in the computation are listed below:
1. Summing idex of u(x,t) in (3.12): n=20 is taken.
2. The number of ti=i/q∈[0,1],(i=0,⋯,q) and q=20 in two methods (q is the total points for trapezoidal rule of the numerical integral in (3.4)).
3. Stepsizes τs(s=α,β,κ) in (3.4) for coputing the derivatives ∂u∂α, ∂u∂β and ∂u∂κ by finite difference method: τα=τβ=τκ=0.01.
4. The initial guess for (α,β,κ)=(0.4,1.0,0.05).
5. The regularization parameter λ=0.001.
6. The iterative step size is τ=(0.07,0.01,0.02).
6. Stop criterion: when ‖aj+1−aj‖≤0.01.
Finally we obtain the approximate value (α,β,κ)=(0.5289,1.1836,0.0943). Keep the same parameters with the damped parameter ˜λ=0.001, we use the Levenberg-Marquardt method to get the approximate value where we don't use the Matlab optimization toolbox on Levenberg-Marquardt method.
This result shows the numerical methods are effective. Here we list more results using the above parameters for the Levenberg-Marquardt method. First we fix the initial guess for α=0.1,κ=0.05 and let β range from 1 to 1.4. The numerical results are displayed in Table 1.
The numerical results show that the methods are stable.
4.
Conclusions
In this paper, we give the proof of uniqueness for determining three parameters in a time-space fractional diffusion equation by means of observation data from accessible boundary. By our uniqueness result a Tikhonov method and the Levenberg-Marquardt method are tested preliminarily. Some further research on the stability of the proposed methods will be investigated in the future.
Acknowledgments
The authors are grateful to the anonymous referees for their insightful comments and suggestions which contributed to greatly improve the original version of the manuscript. The authors would like to thank for the Prof. Masahiro Yamamoto's important comments on Theorem 2.
This work is partially supported by the Natural Science Foundation of China (No. 11661072), the Natural Science Foundation of Northwest Normal University, China (No. NWNU-LKQN-17-5).
Conflict of interest
There is no conflict of interest.









 DownLoad:
DownLoad: