In this paper, we investigate the existence of stable standing waves for the nonlinear Schrödinger equation with inverse-power potential and combined power-type and Choquard-type nonlinearities
$ i \partial_t\psi+\triangle \psi+\frac{\gamma}{|x|^\alpha}\psi+\lambda_1|\psi|^p\psi +\lambda_2(I_\beta\ast|\psi|^q)|\psi|^{q-2}\psi = 0,\; \; (t,x)\in [0,T^\star)\times \mathbb{R}^N. $
By using concentration compactness principle, when one nonlinearity is focusing and $ L^2 $-critical, the other is defocusing and $ L^2 $-supercritical, we prove the existence and orbital stability of standing waves. We extend the results of Li-Zhao in paper [
Citation: Yile Wang. Existence of stable standing waves for the nonlinear Schrödinger equation with inverse-power potential and combined power-type and Choquard-type nonlinearities[J]. AIMS Mathematics, 2021, 6(6): 5837-5850. doi: 10.3934/math.2021345
In this paper, we investigate the existence of stable standing waves for the nonlinear Schrödinger equation with inverse-power potential and combined power-type and Choquard-type nonlinearities
$ i \partial_t\psi+\triangle \psi+\frac{\gamma}{|x|^\alpha}\psi+\lambda_1|\psi|^p\psi +\lambda_2(I_\beta\ast|\psi|^q)|\psi|^{q-2}\psi = 0,\; \; (t,x)\in [0,T^\star)\times \mathbb{R}^N. $
By using concentration compactness principle, when one nonlinearity is focusing and $ L^2 $-critical, the other is defocusing and $ L^2 $-supercritical, we prove the existence and orbital stability of standing waves. We extend the results of Li-Zhao in paper [
In this paper, we consider the following nonlinear Schrödinger equation (NLS) with inverse-power potential, and combined general power-type nonlinearity and Choquard-type nonlinearity
| $ \begin{equation} \left\{ \begin{array}{l} i \partial_t\psi+\triangle \psi+\frac{\gamma}{|x|^\alpha}\psi+\lambda_1|\psi|^p\psi +\lambda_2(I_\beta\ast|\psi|^q)|\psi|^{q-2}\psi = 0,\; \; (t,x)\in [0,T^\star)\times \mathbb{R}^N,\\ \psi(0,x) = \psi_0(x),\; \; \; x\in \mathbb{R}^N, \end{array} \right. \end{equation} $ | (1.1) |
where $ N\geq3 $, $ \psi:[0, T^\star)\times \mathbb{R}^{N}\rightarrow \mathbb{C} $ is the complex valued function with $ 0 < T^\star\leq \infty $, $ \psi_0\in H^1 $, $ \gamma\in(0, +\infty) $, $ \alpha\in(0, 2) $, $ \lambda_1\in\mathbb{R}\setminus\{0\} $ and $ \lambda_2\in\mathbb{R}\setminus\{0\} $, $ \frac{4}{N}\leq p < \frac{4}{N-2} $, $ 1+\frac{2+\beta}{N}\leq q < \frac{N+\beta}{N-2} $, $ \ast $ denotes the convolution, $ I_\beta:\mathbb{R}^N\rightarrow \mathbb{R} $ is the Riesz potential that defined for every $ x\in \mathbb{R}^N\setminus\{0\} $ by
| $ \begin{equation} I_\beta(x) = \frac{\Gamma(\frac{N-\beta}{2})}{\Gamma(\frac{\beta}{2})\pi^{N/2}2^\beta|x|^{N-\beta}}, \end{equation} $ | (1.2) |
$ \beta\in(0, N) $ and $ \Gamma $ is the Gamma function.
Because of important applications of (1.1) in physics, it has received much attention both from physics (see [1,2,3,4,5]) and mathematics (see [6,7,8,9,10,11,12,13]), and has been widely studied for a long time. The operator $ -\triangle-\frac{\gamma}{|x|} $ with Coulomb potential provides a quantum mechanical description of the Coulomb force between two charged particles and corresponds to having an external attractive long-range potential due to the presence of a positively charged atomic nucleus, see, e.g., [2,3,14].
We are interested in the standing wave solutions of (1.1), namely solutions of the form $ \psi(t, x) = e^{i\omega t}u(x) $, where $ \omega\in\mathbb{R} $ is a frequency and $ u\in H^1 $ is a nontrivial solution to the elliptic equation
| $ \begin{equation} -\triangle u+\omega u-\frac{\gamma}{|x|^\alpha}u-\lambda_1|u|^pu-\lambda_2(I_\beta\ast|u|^q)|u|^{q-2}u = 0. \end{equation} $ | (1.3) |
The Eq (1.3) is variational, whose action functional is defined by
| $ \begin{equation*} S_\omega(u): = E_\gamma(u)+\frac{\omega}{2}\| u\|_{L^2}^2, \end{equation*} $ |
where the corresponding energy $ E_\gamma(u) $ is defined by
| $ \begin{align} E_\gamma(u)&: = \frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u|^2dx-\frac{\gamma}{2}\int_{\mathbb{R}^{N}}\frac{|u|^2}{|x|^\alpha}dx-\frac{\lambda_1}{p+2}\int_{\mathbb{R}^{N}}|u|^{p+2}dx -\frac{\lambda_2}{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|u|^q)|u|^qdx. \end{align} $ | (1.4) |
For the evolutional type Eq (1.1), one of the important problems is to consider the stability of standing waves. Then, we recall the definition of orbital stability of set $ \mathcal{M} $.
Definition 1.1. The set $ \mathcal{M} $ is said to be orbitally stable if, for any $ \epsilon > 0 $, there exists $ \delta > 0 $ such that for any initial data $ \psi_0 $ satisfying
| $ \inf\limits_{u\in \mathcal{M}}\|\psi_0-u\|_{H^1} < \delta, $ |
the corresponding solution $ \psi(t) $ of (1.1) with initial data $ \psi_0 $ satisfies
| $ \inf\limits_{u\in \mathcal{M}}\|\psi(t)-u\|_{H^1} < \epsilon, $ |
for all $ t > 0 $.
In view of this definition, in order to study the stability, we require that (1.1) has a unique global solution, at least for initial data $ \psi_0 $ sufficiently close to $ \mathcal{M} $. In the $ L^2 $-subcritical case, all solutions for NLS exist globally. Hence, the stability of standing waves has been studied extensively in this case, see, e.g., [11,14,15,16].
For (1.1), when two nonlinearities are both focusing $ L^2 $-subcritical, i.e., $ \lambda_1\in(0, +\infty) $, $ \lambda_2\in(0, +\infty) $, $ 0 < p < 4/N $, $ 1+\beta/N < q < 1+(2+\beta)/N $, or when one nonlinearity is focusing $ L^2 $-subcritical and the other is focusing $ L^2 $-critical, i.e., $ \lambda_1\in(0, +\infty) $, $ \lambda_2\in(0, +\infty) $, $ 0 < p < 4/N $, $ q = 1+(2+\beta)/N $ and $ 0 < \|\psi_0\|_{L^2} < \|Q_q\|_{L^2} $, $ Q_q $ be a ground state of elliptic equation
| $ \begin{equation} -\Delta Q+Q = \lambda_2(I_\beta\ast|Q|^q)|Q|^{q-2}Q\; \; \; in\; \mathbb{R}^{N}, \end{equation} $ | (1.5) |
the solution $ \psi(t) $ of (1.1) with the initial data $ \psi_0 $ exists globally. In these cases, Li and Zhao in [14] used the concentration compactness principle to study the existence and orbital stability of standing waves. When one nonlinearity is focusing and $ L^2 $-critical, the other is defocusing and $ L^2 $-supercritical, all solutions of (1.1) exist globally (see Lemma 2.7). Therefore, in this case, whether there exist stable standing waves is an interesting problem. To the best of our knowledge, there are no stability results for (1.1) with a defocusing $ L^2 $-supercritical nonlinearity.
To this purpose, applying the idea by Cazenave and Lions in [17], we consider the following constrained minimization problem:
| $ \begin{equation} G_\eta: = \inf\{E_\gamma(u):u\in A(\eta)\}, \end{equation} $ | (1.6) |
where $ E_\gamma(u) $ is defined by (1.4) and
| $ A(\eta): = \{u\in H^1,\; \|u\|_{L^2}^2 = \eta,\; \eta > 0\}. $ |
We will see later (Lemma 2.8) that the above minimizing problem is well-defined. Let us denote
| $ \begin{equation} K(\eta): = \{u\in A(\eta),\; \; E_\gamma(u) = G_\eta\}. \end{equation} $ | (1.7) |
Our main results are as follows:
Theorem 1.2. Let $ N \geq 3 $, $ \gamma\in(0, +\infty) $, $ \alpha\in(0, 2) $, $ \beta\in(0, N) $, $ \lambda_1\in(-\infty, 0) $, $ \lambda_2\in(0, +\infty) $, $ \frac{4}{N} < p < \frac{4}{N-2} $, $ q = 1+\frac{2+\beta}{N} $. Then, there exists $ \gamma_0 > 0 $ sufficiently small such that $ 0 < \gamma < \gamma_0 $, for any $ \eta\in(\|Q_q\|_{L^2}^2, \infty) $, $ Q_q $ be a ground state of elliptic Eq (1.5), the set $ K(\eta) $ is not empty and orbitally stable.
Theorem 1.3. Let $ N \geq 3 $, $ \gamma\in(0, +\infty) $, $ \alpha\in(0, 2) $, $ \beta\in(0, N) $, $ \lambda_1\in(0, +\infty) $, $ \lambda_2\in(-\infty, 0) $, $ p = \frac{4}{N} $, $ 1+\frac{2+\beta}{N} < q < \frac{N+\beta}{N-2} $. Then, there exists $ \gamma_0 > 0 $ sufficiently small such that $ 0 < \gamma < \gamma_0 $, for any $ \eta\in(\|W_p\|_{L^2}^2, \infty) $, where $ W_p $ is the ground state of the following equation:
| $ \begin{equation*} -\Delta W+W = \lambda_1|W|^pW\; \; \; in\; \mathbb{R}^{N}. \end{equation*} $ |
Then, the set $ K(\eta) $ is not empty and orbitally stable.
Since the proof of Theorem 1.2 and Theorem 1.3 is similar, we only prove Theorem 1.2.
In this section, we recall some preliminary results that will be used later.
Lemma 2.1. ([17], Lemma 7.6.1) Let $ 1\leq p < \infty $. If $ \alpha < N $ is such that $ 0\leq \alpha\leq p $, then $ \frac{|u(\cdot)|^p}{|\cdot|^\alpha}\in L^1 $ for every $ u\in W^{1, p}(\mathbb{R}^N) $. Furthermore,
| $ \begin{equation} \int_{\mathbb{R}^{N}}\frac{|u|^p}{|x|^\alpha}dx\leq (\frac{p}{N-\alpha})^\alpha\|u\|_{L^p}^{p-\alpha}\|\nabla u\|_{L^p}^\alpha \end{equation} $ | (2.1) |
for every $ u\in W^{1, p}(\mathbb{R}^N) $.
Lemma 2.2. ([14], Lemma 2.2) Let $ N\geq 3 $, $ \alpha\in(0, 2) $, $ \gamma\in\mathbb{R} $. Then for any $ \epsilon > 0 $, there exists a constant $ \delta = \delta(\epsilon, \|u\|_{L^2}^2) > 0 $ such that
| $ \begin{equation} \epsilon\int_{\mathbb{R}^{N}}|\nabla u|^2dx-\gamma\int_{\mathbb{R}^{N}}\frac{|u|^2}{|x|^\alpha}dx\geq-\delta(\epsilon,\|u\|_{L^2}^2) \end{equation} $ | (2.2) |
for any $ u\in H^1 $.
Proof. It obviously holds for $ \gamma\leq0 $. Now, we use (2.1) to prove the Lemma for $ \gamma > 0 $. According to (2.1) and the Young inequality, we have
| $ \begin{align*} \int_{\mathbb{R}^{N}}\frac{|u|^2}{|x|^\alpha}dx&\leq(\frac{2}{N-\alpha})^\alpha(\frac{2-\alpha}{2}\|u\|_{L^2}^2+\frac{\alpha}{2}\|\nabla u\|_{L^2}^2)\\ & = \epsilon\|\nabla u\|_{L^2}^2+\delta(\epsilon,\|u\|_{L^2}^2), \end{align*} $ |
we arrive at the conclusion.
Lemma 2.3. ([18]) Let $ N \geq 3 $, $ \beta\in(0, N) $, and $ q $, $ q' > 1 $ be constants such that
| $ \frac{1}{q}+\frac{N-\beta}{N}+\frac{1}{q'} = 2. $ |
Assume that $ u\in L^q $ and $ v\in L^{q'} $, then there exists a sharp constant $ C(N, \beta, q) $ independent of $ u $ and $ v $, such that
| $ \left|\int_{\mathbb{R}^{N}}\int_{\mathbb{R}^{N}}\frac{u(x)v(y)}{|x-y|^{N-\beta}}dxdy\right|\leq C(N,\beta,q)\|u\|_{L^q}\|v\|_{L^{q'}}. $ |
By the Hardy-Littlewood-Sobolev inequality above and the Sobolev embedding theorem, we obtain
| $ \begin{equation} \int_{\mathbb{R}^{N}}(I_\beta\ast|u|^q)|u|^qdx\leq C\left(\int_{\mathbb{R}^{N}}|u|^{\frac{2Nq}{N+\beta}}dx\right)^{1+\frac{\beta}{N}}\leq C\|u\|_{H^1}^{2q} \end{equation} $ | (2.3) |
for any $ q\in [1+\frac{\beta}{N}, \frac{N+\beta}{N-2}] $, $ C > 0 $ is a constant depending only on $ N $, $ \beta $ and $ q $.
Lemma 2.4. ([12,19,20]) Let $ N\geq 3 $, $ \beta\in(0, N) $, $ 1+\frac{\beta}{N} < q < \frac{N+\beta}{N-2} $, then for all $ u\in H^1 $,
| $ \begin{equation} \int_{\mathbb{R}^{N}}(I_\beta\ast|u|^q)|u|^qdx\leq C(\beta,q)\|\nabla u\|_{L^2}^{Nq-N-\beta}\|u\|_{L^2}^{N+\beta-Nq+2q}, \end{equation} $ | (2.4) |
the best constant $ C(\beta, q) $ is defined by
| $ C(\beta,q) = \frac{2q}{2q-Nq+N+\beta}\left(\frac{2q-Nq+N+\beta}{Nq-N-\beta}\right)^{\frac{Nq-N-\beta}{2}}\|Q_q\|_{L^2}^{2-2q}, $ |
where $ Q_q $ is the ground state of elliptic Eq (1.5). In particular, in the $ L^2 $-critical case, i.e., $ q = 1+\frac{2+\beta}{N} $, $ C(\beta, q) = q\|Q_q\|_{L^2}^{2-2q} $. Moreover, the following Poho$ \check{z} $aev's identities hold true:
| $ \begin{equation} \|\nabla Q_q\|_{L^2}^2 = \frac{Nq-N-\beta}{2q}\lambda_2\int_{\mathbb{R}^{N}}(I_\beta\ast|Q_q|^q)|Q_q|^qdx = \frac{Nq-N-\beta}{2q-Nq+N+\beta}\|Q_q\|_{L^2}^{2}. \end{equation} $ | (2.5) |
Lemma 2.5. ([17]) Let $ N\geq3 $ and $ \{u_n\} $ be a bounded sequence in $ H^1 $ satisfying:
| $ \int_{\mathbb{R}^N}|u_n|^2dx = \mu, $ |
where $ \mu > 0 $ is fixed. Then there exists a subsequence $ \{u_{n_k}\} $ satisfying one of the three possibilities:
(1) $ (compactness) $ there exists $ \{y_{n_k}\}\subset\mathbb{R}^N $ such that $ |u_{n_k}(\cdot+y_{n_k})|^2 $ is tight, i.e., for all $ \epsilon > 0 $, there exists $ R < \infty $, such that
| $ \int_{B_R(y_{n_k})}|u_{n_k}(x)|^2dx\geq\mu-\epsilon; $ |
(2) $ (vanishing) $ $ \lim\limits_{k\rightarrow\infty}\sup\limits_{y\in\mathbb{R}^N}\int_{B_R(y)}|u_{n_k}(x)|^2dx = 0 $ for all $ R < \infty $;
(3) $ (dichotomy) $ there exists $ \sigma\in(0, \mu) $ such that for any $ \epsilon > 0 $, there exist $ k_0\geq1, \; \{y_{n_k}\}\subset\mathbb{R}^N $ and $ u_{n_k}^{(1)}, \; u_{n_k}^{(2)} $ bounded in $ H^1 $ satisfying for $ k\geq k_0 $:
| $ |u_{n_k}^{(1)}|+|u_{n_k}^{(2)}|\leq|u_{n_k}|; $ |
| $ \left|\int_{\mathbb{R}^N}|u_{n_k}|^{p'}dx-\int_{\mathbb{R}^N}|u_{n_k}^{(1)}|^{p'}dx-\int_{\mathbb{R}^N}|u_{n_k}^{(2)}|^{p'}dx \right|\rightarrow0\; as\; k\rightarrow\infty \; for\; all\; 2\leq p' < 2N/(N-2); $ |
| $ \lim\limits_{k\rightarrow \infty}\|u_{n_k}^{(1)}\|_{L^2}^2 = \sigma,\; \lim\limits_{k\rightarrow \infty}\|u_{n_k}^{(2)}\|_{L^2}^2 = \mu-\sigma; $ |
| $ d_{n_k}: = dist(Supp\; u_{n_k}^{(1)},\; Supp\; u_{n_k}^{(2)})\rightarrow\infty\; as\; k\rightarrow\infty; $ |
| $ \liminf\limits_{k\rightarrow\infty}\int_{\mathbb{R}^N}(|\nabla u_{n_k}|^2-|\nabla u_{n_k}^{(1)}|^2-|\nabla u_{n_k}^{(2)}|^2)dx\geq0. $ |
Lemma 2.6. Let $ N \geq 3 $, $ \lambda_1\in(-\infty, 0) $, $ \lambda_2\in(0, +\infty) $, $ \frac{4}{N} < p < \frac{4}{N-2} $, $ q = 1+\frac{2+\beta}{N} $, or $ N \geq 3 $, $ \lambda_1\in(0, +\infty) $, $ \lambda_2\in(-\infty, 0) $, $ p = \frac{4}{N} $, $ 1+\frac{2+\beta}{N} < q < \frac{N+\beta}{N-2} $. The initial data $ \psi_0\in H^1 $, there exists $ T = T(\|\psi_0\|_{H^{1}}) $ such that (1.1) admits a unique solution $ \psi\in C([0, T], H^{1}) $. Let $ [0, T^\star) $ be the maximal time interval on which the solution $ \psi $ is well-defined, if $ T^\star < \infty $, then $ \|\psi(t)\|_{H^{1}}\rightarrow\infty $ as $ t\uparrow T^\star $. Moreover, for all $ 0\leq t < T^\star $, the solution $ \psi(t) $ satisfies the following conservation of mass and energy:
| $ (1)\; conservation\; of\; mass:\; \; \; \|\psi(t)\|_{L^2} = \|\psi_0\|_{L^2}, $ |
| $ (2)\; conservation\; of\; energy:\; \; \; E_\gamma(\psi(t)) = E_\gamma(\psi_0). $ |
Lemma 2.7. Let $ N \geq 3 $, $ \gamma\in(0, +\infty) $, $ \alpha\in(0, 2) $, $ \beta\in(0, N) $, $ \lambda_1\in(-\infty, 0) $, $ \lambda_2\in(0, +\infty) $, $ \frac{4}{N} < p < \frac{4}{N-2} $, $ q = 1+\frac{2+\beta}{N} $, or $ N \geq 3 $, $ \gamma\in(0, +\infty) $, $ \alpha\in(0, 2) $, $ \lambda_1\in(0, +\infty) $, $ \lambda_2\in(-\infty, 0) $, $ p = \frac{4}{N} $, $ 1+\frac{2+\beta}{N} < q < \frac{N+\beta}{N-2} $, then the solution $ \psi(t) $ of (1.1) with $ \psi_0 $ exists globally.
Proof. We prove the first case firstly. By the Hardy-Littlewood-Sobolev and the Young inequalities, we have
| $ \begin{align} \int_{\mathbb{R}^{N}}(I_\beta\ast|\psi(t)|^q)|\psi(t)|^qdx\leq C\|\psi(t)\|^{2q}_{L^{\frac{2Nq}{N+\beta}}}&\leq C\|\psi(t)\|_{L^2}^{2q(1-\theta)}\|\psi(t)\|_{L^{p+2}}^{2q\theta}\\ &\leq\epsilon_1\|\psi(t)\|_{L^{p+2}}^{p+2}+C(\epsilon_1,\|\psi(t)\|_{L^2}), \end{align} $ | (2.6) |
where $ \theta = \frac{(p+2)(Nq-N-\beta)}{Nqp} $. Under the conservation laws, we deduce that
| $ \begin{equation} (1-\epsilon)\|\nabla \psi(t)\|_{L^2}^2\leq2E_\gamma(\psi(0))+\delta(\epsilon,\|\psi(t)\|_{L^2}^2)+(\frac{2\lambda_1}{p+2}+\epsilon_1)\|\psi(t)\|_{L^{p+2}}^{p+2}+C(\epsilon_1,\|\psi(t)\|_{L^2}), \end{equation} $ | (2.7) |
where $ \frac{2\lambda_1}{p+2}+\epsilon_1 < 0 $ for $ \lambda_1 < 0 $ and $ \epsilon_1 > 0 $ small sufficiently. By choosing $ \epsilon = \frac{1}{2} $, we deduce from (2.7) that
| $ \begin{equation} \|\nabla \psi(t)\|_{L^2}^2\leq4E_\gamma(\psi(0))+\delta(\frac{1}{2},\|\psi(t)\|_{L^2}^2)+C(\epsilon_1,\|\psi(t)\|_{L^2}), \end{equation} $ | (2.8) |
which implies the boundedness of $ \|\nabla \psi(t)\|_{L^2} $.
In the following, we prove the second case. By the Gagliardo-Nirenberg and the Young inequalities, we have
| $ \begin{align} \|\psi(t)\|^{p+2}_{L^{p+2}}&\leq C\|\psi(t)\|^{p+2-\frac{pN}{2}}_{L^2}\|\nabla\psi(t)\|^{\frac{pN}{2}}_{L^2}\\ &\leq \epsilon_2\|\nabla\psi(t)\|^{2}_{L^2}+C(\epsilon_2,\|\psi(t)\|_{L^2}). \end{align} $ | (2.9) |
Under the conservation laws, we get
| $ \begin{align} (1-\epsilon-\epsilon_2)\|\nabla \psi(t)\|_{L^2}^2\leq2E_\gamma(\psi(0))+\delta(\epsilon,\|\psi(t)\|_{L^2}^2)+C(\epsilon_2,\|\psi(t)\|_{L^2}). \end{align} $ | (2.10) |
By choosing $ \epsilon = \frac{1}{2} $, $ \epsilon_2 = \frac{1}{4} $, we deduce from (2.10) that
| $ \begin{equation} \|\nabla \psi(t)\|_{L^2}^2\leq8E_\gamma(\psi(0))+\delta(\frac{1}{2},\|\psi(t)\|_{L^2}^2)+C(\frac{1}{4},\|\psi(t)\|_{L^2}), \end{equation} $ | (2.11) |
which implies the boundedness of $ \|\nabla \psi(t)\|_{L^2} $.
And we arrive at the conclusion.
Lemma 2.8. Let $ N \geq 3 $, $ \gamma\in(0, +\infty) $, $ \alpha\in(0, 2) $, $ \beta\in(0, N) $, $ \lambda_1\in(-\infty, 0) $, $ \lambda_2\in(0, +\infty) $, $ \frac{4}{N} < p < \frac{4}{N-2} $, $ q = 1+\frac{2+\beta}{N} $, and $ \eta\in(\|Q_q\|_{L^2}^2, \infty) $, $ Q_q $ be the ground state of elliptic Eq (1.5), there exists $ \gamma_0 > 0 $ sufficiently small such that $ 0 < \gamma < \gamma_0 $. Then, there exist $ \bar{u}\in H^1 $ such that $ G_\eta = E_\gamma(\bar{u}) $.
Proof. We proceed in four steps.
Step 1. For any $ \eta\in(\|Q_q\|_{L^2}^2, \infty) $, $ G_\eta = \inf\limits_{u\in A(\eta)}E_\gamma(u) $ is well-defined and $ G_\eta < 0 $.
We deduce from (2.2) and (2.6) that
| $ \begin{align} E_\gamma(u)&\geq(\frac{1}{2}-\frac{\epsilon}{2})\|\nabla u\|_{L^2}^2-\delta(\epsilon,\|u\|_{L^2}^2)+\frac{|\lambda_1|}{p+2}\|u\|_{L^{p+2}}^{p+2}-\epsilon_1\|u\|_{L^{p+2}}^{p+2}-C(\epsilon_1,\|u\|_{L^2})\\ & = (\frac{1}{2}-\frac{\epsilon}{2})\|\nabla u\|_{L^2}^2+\left(\frac{|\lambda_1|}{p+2}-\epsilon_1\right)\|u\|_{L^{p+2}}^{p+2}-\delta(\epsilon,\|u\|_{L^2}^2)-C(\epsilon_1,\|u\|_{L^2})\\ &\geq -\delta(\epsilon,\|u\|_{L^2}^2)-C(\epsilon_1,\|u\|_{L^2}) > -\infty \end{align} $ | (2.12) |
by choosing $ \epsilon $ and $ \epsilon_1 $ sufficiently small. Therefore, $ E_\gamma(u) $ is bounded from below on $ A(\eta) $, that is, $ G_\eta $ is well defined.
In the following, we show that $ G_\eta < 0 $ for all $ \eta\in(\|Q_q\|_{L^2}^2, \infty) $. For $ q = 1+\frac{2+\beta}{N} $, we have
| $ N+\beta-Nq+2q = \frac{2\beta+4}{N},\; \; Nq-N-\beta = 2,\; \; C(\beta,q) = q\|Q_q\|_{L^2}^{\frac{-(2\beta+4)}{N}}. $ |
We can obtain from (2.2) and (2.4) that
| $ \begin{align} E_\gamma(u)&\geq(\frac{1}{2}-\frac{\epsilon}{2})\|\nabla u\|_{L^2}^2-\delta(\epsilon,\|u\|_{L^2}^2)-\frac{\lambda_2}{2q}C(\beta,q)\|u\|_{L^2}^{N+\beta-Nq+2q}\|\nabla u\|_{L^2}^{Nq-N-\beta}\\ & = \frac{1}{2}\left[1-\epsilon-\lambda_2\left(\frac{\|u\|_{L^2}^2}{\|Q_q\|_{L^2}^2}\right)^{\frac{\beta+2}{N}}\right]\|\nabla u\|_{L^2}^2-\delta(\epsilon,\|u\|_{L^2}^2), \end{align} $ | (2.13) |
by choosing $ \epsilon $ and $ \lambda_2 $ both sufficiently small, for any $ u\in H^1 $ and $ \|u\|_{L^2}^2 = \eta\leq\|Q_q\|_{L^2}^2 $, we can not judge that whether $ E_\gamma(u) < 0 $ or $ E_\gamma(u) > 0 $.
In fact, for $ \eta > \|Q_q\|_{L^2}^2 $, we set $ v = \mu Q_q $, $ \mu = \frac{\sqrt{\eta}}{\|Q_q\|_{L^2}} > 1 $, $ \|v\|_{L^2}^2 = \eta $. Let $ v_\lambda = \lambda^{\frac{N}{2}}v(\lambda x) $ for $ \lambda > 0 $, $ \|v_\lambda\|_{L^2}^2 = \|v\|_{L^2}^2 = \eta $. It follows from (2.5) that
| $ \begin{align} \frac{1}{2}\|\nabla v\|_{L^2}^2-\frac{\lambda_2}{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|v|^q)|v|^qdx& = \frac{\mu^2}{2}\|\nabla Q_q\|_{L^2}^2-\frac{\lambda_2}{2q}\mu^{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|Q_q|^q)|Q_q|^qdx\\ & = \frac{N}{2(N+\beta+2)}(\lambda_2\mu^2-\lambda_2\mu^{2q})\int_{\mathbb{R}^{N}}(I_\beta\ast|Q_q|^q)|Q_q|^qdx < 0, \end{align} $ | (2.14) |
where $ 2 < 2q $. Hence, we can deduce from (2.14) that
| $ \begin{align} E_\gamma(v_\lambda)& = \frac{\lambda^2}{2}\|\nabla v\|_{L^2}^2-\frac{\gamma}{2}\lambda^\alpha\int_{\mathbb{R}^{N}}\frac{|v|^2}{|x|^\alpha}dx -\frac{\lambda_1\lambda^{\frac{Np}{2}}}{p+2}\|v\|_{L^{p+2}}^{p+2} -\frac{\lambda_2\lambda^2}{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|v|^q)|v|^qdx\\ & = \lambda^2\left(\frac{1}{2}\|\nabla v\|_{L^2}^2-\frac{\lambda_2}{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|v|^q)|v|^qdx -\frac{\gamma}{2}\lambda^{\alpha-2}\int_{\mathbb{R}^{N}}\frac{|v|^2}{|x|^\alpha}dx\right) +\frac{|\lambda_1|\lambda^{\frac{Np}{2}}}{p+2}\|v\|_{L^{p+2}}^{p+2} < 0 \end{align} $ | (2.15) |
for $ \lambda > 0 $ sufficiently small and $ 2 < \frac{Np}{2} $. Therefore, we can obtain from (2.15) that $ G_\eta < 0 $ for all $ \eta\in(\|Q_q\|_{L^2}^2, \infty) $.
Step 2. $ \eta\in(\|Q_q\|_{L^2}^2, \infty)\mapsto G_\eta $ is a continuous mapping.
For any $ \eta\in(\|Q_q\|_{L^2}^2, \infty) $, let $ \eta_n\in(\|Q_q\|_{L^2}^2, \infty) $ such that $ \eta_n\rightarrow \eta $ as $ n $ large enough. From the definition of $ G_{\eta_n} $, for any $ \varepsilon > 0 $ sufficiently small, let $ u_n\in A(\eta_n) $ such that
| $ E_\gamma(u_n)\leq G_{\eta_n}+\varepsilon, $ |
(2.12) implies that $ \{u_n\} $ is bounded in $ H^1 $. We set $ \rho_n: = \sqrt{\frac{\eta}{\eta_n}}u_n $, $ \rho_n\in A(\eta) $, we have
| $ \begin{align} G_\eta\leq E_\gamma(\rho_n)& = \frac{1}{2}\frac{\eta}{\eta_n}\|\nabla u_n\|_{L^2}^2-\frac{\gamma}{2}\frac{\eta}{\eta_n}\int_{\mathbb{R}^{N}}\frac{|u_n|^2}{|x|^\alpha}dx -\frac{\lambda_1}{p+2}\left(\sqrt{\frac{\eta}{\eta_n}}\right)^{p+2}\|u_n\|_{L^{p+2}}^{p+2}\\ &\; \; \; -\frac{\lambda_2}{2q}\left(\sqrt{\frac{\eta}{\eta_n}}\right)^{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|u_n|^q)|u_n|^qdx\\ & = E_\gamma(u_n)+o_n(1)\\ &\leq G_{\eta_n}+\varepsilon+o_n(1). \end{align} $ | (2.16) |
On the other hand, given a minimizing sequence $ \{v_n\}\subset A(\eta) $ for $ E_\gamma $, we have
| $ \begin{equation} E_\gamma(v_n)\leq G_\eta+\varepsilon. \end{equation} $ | (2.17) |
Set $ y_n: = \sqrt{\frac{\eta_n}{\eta}}v_n $, $ y_n\in A(\eta_n) $, we have
| $ \begin{equation} G_{\eta_n}\leq E_\gamma(y_n)\leq G_\eta+\varepsilon+o_n(1), \end{equation} $ | (2.18) |
which, together with (2.16), gives that
| $ \begin{equation} \lim\limits_{n\rightarrow \infty}G_{\eta_n} = G_\eta\; \; for\; any\; \eta\in(\|Q_q\|_{L^2}^2,\infty). \end{equation} $ | (2.19) |
Step 3. For $ \eta \in(\|Q_q\|_{L^2}^2, \infty) $, we have $ G_\eta < G_{\eta_1}+G_{\eta-\eta_1} $ for all $ \eta_1\in(\|Q_q\|_{L^2}^2, \eta) $.
Let $ \{u_n\} $ be a minimizing sequence for (1.6) such that $ E_\gamma(u_n)\rightarrow G_\eta $. Every minimizing sequence for (1.6) is bounded in $ H^1 $ and bounded from below in $ L^{\frac{4}{N+\beta}+2} $. Since $ G_\eta < 0 $, we have $ E_\gamma(u_n)\leq\frac{G_\eta}{2} $ for $ n $ large enough. It follows from the definition of $ E_\gamma(u_n) $ and (2.6) that
| $ \begin{equation} \|u\|_{L^{\frac{4}{N+\beta}+2}}^{2q}\geq\frac{1}{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|u_n|^q)|u_n|^qdx\geq-E_\gamma(u_n)\geq-\frac{G_\eta}{2} > 0, \end{equation} $ | (2.20) |
we set $ -\frac{G_\eta}{2} = C^1 $. There exists a constant $ \tau $ such that $ \lim\limits_{n\rightarrow \infty}\|\nabla u_n\|_{L^2}\geq\tau > 0 $. Otherwise, if $ \lim\limits_{n\rightarrow \infty}\|\nabla u_n\|_{L^2} = 0 $, by the Gagliardo-Nirenberg inequality, we have $ \lim\limits_{n\rightarrow \infty}\|u_n\|_{L^{p+2}}^{p+2} = 0 $, which, together with (2.1) and (2.4), yields that $ 0 > G_\eta = \lim\limits_{n\rightarrow \infty}E_\gamma(u_n) = 0 $, which is impossible. Hence, the minimizing problem (1.6) can be rewritten as
| $ \begin{equation*} G_\eta: = \inf\{E_\gamma(u):u\in A(\eta),\; \|\nabla u\|_{L^2}\geq\tau\}. \end{equation*} $ |
Set $ C^0 = (\frac{2}{N-\alpha})^{\alpha} > 0 $, we can obtain from (2.1) that
| $ \begin{equation*} \gamma\int_{\mathbb{R}^{N}}\frac{|u|^2}{|x|^\alpha}dx\leq \gamma C^0\eta^{\frac{2-\alpha}{2}}\|\nabla u\|_{L^2}^{\alpha} < \gamma_0 C^0\eta^{\frac{2-\alpha}{2}}\|\nabla u\|_{L^2}^{\alpha}, \end{equation*} $ |
and it follows easily that
| $ \begin{align*} &\|\nabla u\|_{L^2}^2-\gamma\int_{\mathbb{R}^{N}}\frac{|u|^2}{|x|^\alpha}dx\notag\geq\tau^{\alpha}\left(\tau^{2-\alpha}-\gamma C^0\eta^{\frac{2-\alpha}{2}}\right) > \tau^{\alpha}\left(\tau^{2-\alpha}-\gamma_0 C^0\eta^{\frac{2-\alpha}{2}}\right) > 0 \end{align*} $ |
for $ 0 < \gamma < \gamma_0 $ and $ \gamma_0 > 0 $ small sufficiently, we set $ \tau^{\alpha}\left(\tau^{2-\alpha}-\gamma_0 C^0\eta^{\frac{2-\alpha}{2}}\right) = C^2 $. For $ t\in(1, \infty) $, set $ \tilde{u}(x): = u(t^{-\frac{1}{N}}x) $, $ \|\tilde{u}\|_{L^2}^2 = t\|u\|_{L^2}^2 $. We have
| $ \begin{align} G_{t\eta}&\leq \liminf\limits_{n\rightarrow\infty}E_\gamma(\tilde{u})\\ & = \liminf\limits_{n\rightarrow\infty}\left(tE_\gamma(u)+\|\nabla u\|_{L^2}^2(\frac{t^{1-\frac{\alpha}{N}}}{2}-\frac{t}{2}) -\gamma\int_{\mathbb{R}^{N}}\frac{|u|^2}{|x|^\alpha}dx(\frac{t^{1-\frac{\alpha}{N}}}{2}-\frac{t}{2}) +\frac{\lambda_2t-\lambda_2t^{1+\frac{\beta}{N}}}{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|u|^q)|u|^qdx\right)\\ & = tG_\eta+(\frac{t^{1-\frac{\alpha}{N}}}{2}-\frac{t}{2})\liminf\limits_{n\rightarrow\infty}\left(\|\nabla u\|_{L^2}^2-\gamma\int_{\mathbb{R}^{N}}\frac{|u|^2}{|x|^\alpha}dx\right)+\frac{\lambda_2t-\lambda_2t^{1+\frac{\beta}{N}}}{2q}\liminf\limits_{n\rightarrow\infty}\int_{\mathbb{R}^{N}}(I_\beta\ast|u_n|^q)|u_n|^qdx\\ &\leq tG_\eta+(\frac{t^{1-\frac{\alpha}{N}}}{2}-\frac{t}{2})C^2+(\lambda_2t-\lambda_2t^{1+\frac{\beta}{N}})C^1 < tG_\eta. \end{align} $ | (2.21) |
Consequently,
| $ \begin{equation} G_\eta < \frac{\eta_1}{\eta}\frac{\eta}{\eta_1}G_{\eta_1}+\frac{\eta-\eta_1}{\eta}\frac{\eta}{\eta-\eta_1}G_{\eta-\eta_1} = G_{\eta_1}+G_{\eta-\eta_1} \end{equation} $ | (2.22) |
for all $ \eta_1 \in(\|Q_q\|_{L^2}^2, \eta) $.
Step 4. Now, let us apply the concentration compactness principle in $ H^1 $ to the minimizing sequence $ \{u_n\} $. There exists a subsequence $ \{u_{n_k}\} $ such that one of the three possibilities in Lemma 2.5 holds.
First, we prove that the vanishing cannot occur.
Suppose by contradiction that
| $ \lim\limits_{k\rightarrow \infty} \sup\limits_{y\in\mathbb{R}^N}\int_{B_1(y)}|u_{n_k}|^2dx = 0, $ |
by Lion's Lemma, we have $ u_{n_k}\rightarrow0 $ in $ L^m $ as $ k\rightarrow\infty $ for all $ m\in(2, \frac{2N}{N-2}) $. Hence,
| $ \int_{\mathbb{R}^{N}}|u_{n_k}|^{p+2}dx\rightarrow0\; \; as\; \; k\rightarrow\infty\; \; for\; \; 2 < p+2 < 2N/(N-2). $ |
By the domain decomposition, the Hölder inequality and $ \alpha\in(0, 2) $, we have
| $ \begin{align} \int_{\mathbb{R}^N}\frac{|u|^2}{|x|^\alpha}dx& = \int_{B_1(0)}\frac{|u|^2}{|x|^\alpha}dx+\int_{B_1^c(0)}\frac{|u|^2}{|x|^\alpha}dx\\ &\leq\||x|^{-\alpha}\mathcal{X}_{B_1(0)}\|_a\||u|^2\|_{a'}+\||x|^{-\alpha}\mathcal{X}_{B_1^c(0)}\|_b\||u|^2\|_{b'}\\ & = C_1\|u\|_{2a'}^2+C_2\|u\|_{2b'}^2 \end{align} $ | (2.23) |
where $ \frac{1}{a}+\frac{1}{a'} = 1 $, $ \frac{1}{b}+\frac{1}{b'} = 1 $. $ a < N/\alpha $, $ b > N/\alpha $, $ N/\alpha-a $ and $ b-N/\alpha $ are both sufficiently small. By (2.23) and the Sobolev inequality, we have
| $ \int_{\mathbb{R}^{N}}\frac{|u_{n_k}|^2}{|x|^\alpha}dx\rightarrow0\; \; as\; \; k\rightarrow\infty. $ |
It follows from (2.3) that
| $ \begin{equation*} \int_{\mathbb{R}^{N}}(I_\beta\ast|u_{n_k}|^q)|u_{n_k}|^qdx\rightarrow0\; \; as\; \; k\rightarrow\infty. \end{equation*} $ |
Thus,
| $ \begin{equation*} G_\eta = \lim\limits_{k\rightarrow \infty}E_\gamma(u_{n_k}) = \lim\limits_{k\rightarrow \infty}\frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u_{n_k}|^2dx\geq0, \end{equation*} $ |
which contradicts $ G_\eta < 0 $ in step 1. Therefore, the vanishing cannot occur.
Subsequently, we prove that the dichotomy does not occur.
Suppose by contradiction that the dichotomy can occur. Then there exist a constant $ \xi\in(0, \eta) $ and two bounded sequences $ \{u_{n_k}^{(1)}\}, \{u_{n_k}^{(2)}\}\subset H^1 $ such that
| $ \begin{equation} \|u_{n_k}^{(1)}\|_{L^2}^2\rightarrow\xi,\; \; \|u_{n_k}^{(2)}\|_{L^2}^2\rightarrow(\eta-\xi)\; \; as\; k\rightarrow\infty, \end{equation} $ | (2.24) |
| $ \begin{equation} \|u_{n_k}-u_{n_k}^{(1)}-u_{n_k}^{(2)}\|_{L^{p+2}}\rightarrow0\; \; as\; \; k\rightarrow\infty\; \; for\; \; 2 < p+2 < 2N/(N-2), \end{equation} $ | (2.25) |
| $ \begin{equation} \liminf\limits_{k\rightarrow\infty}\int_{\mathbb{R}^N}(|\nabla u_{n_k}|^2-|\nabla u_{n_k}^{(1)}|^2-|\nabla u_{n_k}^{(2)}|^2)dx\geq0. \end{equation} $ | (2.26) |
Similarly, we have
| $ \begin{equation} \int_{\mathbb{R}^{N}}(I_\beta\ast|u_{n_k}|^q)|u_{n_k}|^qdx -\int_{\mathbb{R}^{N}}(I_\beta\ast|u_{n_k}^{(1)}|^q)|u_{n_k}^{(1)}|^qdx-\int_{\mathbb{R}^{N}}(I_\beta\ast|u_{n_k}^{(2)}|^q)|u_{n_k}^{(2)}|^qdx\rightarrow0\; \; as\; k\rightarrow\infty, \end{equation} $ | (2.27) |
and
| $ \begin{equation} \int_{\mathbb{R}^{N}}\frac{|u_{n_k}|^2}{|x|^\alpha}dx -\int_{\mathbb{R}^{N}}\frac{|u_{n_k}^{(1)}|^2}{|x|^\alpha}dx-\int_{\mathbb{R}^{N}}\frac{|u_{n_k}^{(2)}|^2}{|x|^\alpha}dx\rightarrow0\; \; as\; k\rightarrow\infty. \end{equation} $ | (2.28) |
Indeed, let $ u_{n_k} = u_{n_k}^{(1)}+u_{n_k}^{(2)}+v_{n_k} $, in view of $ u_{n_k}^{(1)}u_{n_k}^{(2)} = 0 $, by the direct calculation, we obtain that
| $ \begin{align*} \int_{\mathbb{R}^N}\frac{|u_{n_k}|^2}{|x|^\alpha}dx& = \int_{\mathbb{R}^N}\frac{|u_{n_k}^{(1)}+u_{n_k}^{(2)}+v_{n_k}|^2}{|x|^\alpha}dx\\ & = \int_{\mathbb{R}^N}\frac{|u_{n_k}^{(1)}|^2+|u_{n_k}^{(2)}|^2+|v_{n_k}|^2+2Re(u_{n_k}^{(1)}\bar{v}_{n_k})+2Re(u_{n_k}^{(2)}\bar{v}_{n_k})}{|x|^\alpha}dx\\ & = \int_{\mathbb{R}^N}\frac{|u_{n_k}^{(1)}|^2+|u_{n_k}^{(2)}|^2}{|x|^\alpha}dx+\delta(\epsilon), \end{align*} $ |
where $ \delta(\epsilon)\rightarrow 0 $ as $ \epsilon\rightarrow 0 $. By (2.25)–(2.28), we obtain that
| $ \begin{align*} G_\eta&\geq\liminf\limits_{k\rightarrow\infty}E_\gamma(u_{n_k}^{(1)})+\liminf\limits_{k\rightarrow\infty}E_\gamma(u_{n_k}^{(2)})\\ &\geq \liminf\limits_{k\rightarrow\infty}G_{\|u_{n_k}^{(1)}\|_{L^2}^2}+\liminf\limits_{k\rightarrow\infty}G_{\|u_{n_k}^{(2)}\|_{L^2}^2}, \end{align*} $ |
which combine with (2.19) and (2.24), we get
| $ G_\eta\geq G_\xi+G_{\eta-\xi}, $ |
which is a contradiction with (2.22). Hence, the dichotomy cannot occur.
Finally, we have ruled out both vanishing and dichotomy, then we deduce that there exists a sequence $ \{y_{n_k}\}\subset \mathbb{R}^N $ such that for all $ \epsilon > 0 $, there exists $ R(\epsilon) > 0 $ such that for all $ k\geq1 $
| $ \begin{equation} \int_{B_{R(\epsilon)}(y_{n_k})}|u_{n_k}(x)|^2dx\geq\mu-\epsilon. \end{equation} $ | (2.29) |
Denote $ \hat{u}_{n_k}(x) = u_{n_k}(x+y_{n_k}) $, we assume that $ \{y_{n_k}\} $ is bounded, then there exists a $ \hat{u} $ such that, up to a subsequence,
| $ \begin{equation} \left\{ \begin{array}{l} \hat{u}_{n_k}\rightharpoonup \hat{u}\; \; weakly\; \; in\; \; H^1;\\ \hat{u}_{n_k}\rightarrow \hat{u}\; \; strongly\; \; in\; \; L^m_{loc}(\mathbb{R}^N),\; \; \forall\; \; m\in [2,\frac{2N}{N-2}). \end{array} \right. \end{equation} $ | (2.30) |
(2.29), together with (2.30), implies that
| $ \int_{B_{R(\epsilon)}(0)}|\hat{u}(x)|^2dx\geq\mu-\epsilon. $ |
Thus $ \int_{\mathbb{R}^{N}} |\hat{u}(x)|^2dx = \mu $, i.e., $ \hat{u}_{n_k}\rightarrow\hat{u} $ strongly in $ L^2 $. By the Gagliardo-Nirenberg inequality, $ \hat{u}_{n_k}\rightarrow\hat{u} $ strongly in $ L^m $ for $ m \in [2, \frac{2N}{N-2}) $. Then (2.30) can be rewritten as
| $ \begin{equation} \left\{ \begin{array}{l} \hat{u}_{n_k}\rightharpoonup \hat{u}\; \; weakly\; \; in\; \; H^1;\\ \hat{u}_{n_k}\rightarrow \hat{u}\; \; strongly\; \; in\; \; L^m,\; \; \forall\; \; m\in [2,\frac{2N}{N-2}). \end{array} \right. \end{equation} $ | (2.31) |
In the following, we claim that $ \{y_{n_k}\} $ is bounded. Suppose by contradiction that $ \{y_{n_k}\} $ is unbounded. For
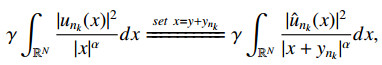
|
by the domain decomposition and $ \alpha\in(0, 2) $, $ R > 0 $ is fixed, we know
| $ \begin{equation*} \int_{\mathbb{R}^{N}}\frac{|\hat{u}_{n_k}(x)|^2}{|x+y_{n_k}|^\alpha}dx = \int_{B_R(0)}\frac{|\hat{u}_{n_k}(x)|^2}{|x+y_{n_k}|^\alpha}dx +\int_{B_R^c(0)}\frac{|\hat{u}_{n_k}(x)|^2}{|x+y_{n_k}|^\alpha}dx: = I_1+I_2. \end{equation*} $ |
On $ B_R(0) $, we have
| $ |x+y_{n_k}|\geq |y_{n_k}|-|x|\geq |y_{n_k}|-R\rightarrow\infty\; \; as\; \; k\rightarrow\infty, $ |
which, together with (2.31), shows that $ I_1\rightarrow0 $ as $ k\rightarrow\infty $. On the other hand, on $ B_R^c(0) $, by the Cauchy convergence of improper integrals and $ \hat{u}\in L^2 $, for any $ \epsilon > 0 $, we have
| $ \begin{equation} \int_{B_R^c(0)}|\hat{u}(x)|^2dx < \epsilon, \end{equation} $ | (2.32) |
which, together with (2.31), yields that
| $ \int_{B_R^c(0)}|\hat{u}_{n_k}(x)-\hat{u}(x)|^2dx\leq\int_{\mathbb{R}^{N}}|\hat{u}_{n_k}(x)-\hat{u}(x)|^2dx\rightarrow0\; \; as\; \; k\rightarrow\infty, $ |
then we have
| $ \int_{B_R^c(0)}|\hat{u}_{n_k}(x)|^2dx-\int_{B_R^c(0)}|\hat{u}(x)|^2dx\rightarrow0\; \; as\; \; k\rightarrow\infty. $ |
Consequently, $ I_2\rightarrow0 $ as $ k\rightarrow\infty $. Therefore, we have
| $ \begin{equation} \gamma\int_{\mathbb{R}^{N}}\frac{|\hat{u}_{n_k}(x)|^2}{|x+y_{n_k}|^\alpha}dx\rightarrow0\; \; as\; k\rightarrow\infty. \end{equation} $ | (2.33) |
Denote
| $ E_0(u): = \frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u|^2dx-\frac{\lambda_1}{p+2}\int_{\mathbb{R}^{N}}|u|^{p+2}dx-\frac{\lambda_2}{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|u|^q)|u|^qdx $ |
and
| $ G_\eta^0: = \inf\{E_0(u):u\in A(\eta)\}. $ |
We know that $ G_\eta^0 $ is attained by a nontrivial function $ w $, that is, $ G_\eta^0 = \inf\limits_{w\in A(\eta)}E_0(w) $. Moreover, the above steps hold for $ \gamma = 0 $. Thus,
| $ \begin{align*} G_\eta &\geq \liminf\limits_{k\rightarrow\infty}(\frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla \hat{u}_{n_k}|^2dx-\frac{\lambda_1}{p+2}\int_{\mathbb{R}^{N}}|\hat{u}_{n_k}|^{p+2}dx -\frac{\lambda_2}{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|\hat{u}_{n_k}|^q)|\hat{u}_{n_k}|^qdx)\\ & = \liminf\limits_{k\rightarrow\infty}E_0(\hat{u}_{n_k})\geq G_\eta^0. \end{align*} $ |
Hence, $ G_\eta\geq G_\eta^0 $. By the definition of $ G_\eta $, we have
| $ \begin{equation*} G_\eta^0 > G_\eta^0-\frac{\gamma}{2}\int_{\mathbb{R}^{N}}\frac{|w|^2}{|x|^\alpha}dx = E_\gamma(w)\geq G_\eta, \end{equation*} $ |
which contradicts $ G_\eta\geq G_\eta^0 $. Hence, $ \{y_{n_k}\} $ is bounded. We may assume, going if necessary to a subsequence, $ \lim\limits_{k\rightarrow\infty}y_{n_k} = \hat{y} $ for some $ \hat{y}\in \mathbb{R}^N $. Consequently, we have
| $ \begin{align*} \|u_{n_k}(x)-\hat{u}(x-\hat{y})\|_{L^m}&\leq \|u_{n_k}(x)-\hat{u}(x-y_{n_k})\|_{L^m}+\|\hat{u}(x-y_{n_k})-\hat{u}(x-\hat{y})\|_{L^m}\\ & = \|u_{n_k}(x+y_{n_k})-\hat{u}(x)\|_{L^m}+\|\hat{u}(x-y_{n_k})-\hat{u}(x-\hat{y})\|_{L^m}, \end{align*} $ |
from (2.31) and $ \lim\limits_{k\rightarrow\infty}y_{n_k} = \hat{y} $ for some $ \hat{y}\in \mathbb{R}^N $, we have
| $ \begin{equation*} \|u_{n_k}(x)-\hat{u}(x-\hat{y})\|_{L^m}\rightarrow0\; \; as\; \; k\rightarrow\infty\; for\; any\; m\in[2,2N/(N-2)). \end{equation*} $ |
We define $ \bar{u}(x) = \hat{u}(x-\hat{y}) $. Consequently,
| $ \begin{align*} G_\eta& = \lim\limits_{k\rightarrow\infty}(\frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla u_{n_k}|^2dx-\frac{\gamma}{2}\int_{\mathbb{R}^{N}}\frac{|u_{n_k}|^2}{|x|^\alpha}dx-\frac{\lambda_1}{p+2}\int_{\mathbb{R}^{N}}|u_{n_k}|^{p+2}dx -\frac{\lambda_2}{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|u_{n_k}|^q)|u_{n_k}|^qdx)\\ &\geq \frac{1}{2}\int_{\mathbb{R}^{N}}|\nabla \bar{u}|^2dx-\frac{\gamma}{2}\int_{\mathbb{R}^{N}}\frac{|\bar{u}|^2}{|x|^\alpha}dx-\frac{\lambda_1}{p+2}\int_{\mathbb{R}^{N}}|\bar{u}|^{p+2}dx -\frac{\lambda_2}{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|\bar{u}|^q)|\bar{u}|^qdx\\ & = E_\gamma(\bar{u})\geq G_\eta. \end{align*} $ |
By the definition of $ G_\eta $, we see that $ \bar{u} $ is a minimizer of $ G_\eta $, $ \lim\limits_{k\rightarrow\infty}\|\nabla u_{n_k}\|_{L^2}^2 = \|\nabla \bar{u}\|_{L^2}^2 $, and hence $ u_{n_k}\rightarrow \bar{u} $ in $ H^1 $.
Proof. By Lemma 2.7, we see that the solution $ \psi $ of (2.1) exists globally. Suppose by contradiction that there exist sequences $ \{u_{0, n}\}\subset H^1 $ and $ \{t_n\}\subset\mathbb{R}^+ $ and a constant $ \epsilon > 0 $ such that for all $ n\geq1 $,
| $ \begin{equation} \inf\limits_{z\in K(\eta)}\|u_{0,n}-z\|_{H^1} < \frac{1}{n}, \end{equation} $ | (3.1) |
| $ \begin{equation} \inf\limits_{z\in K(\eta)}\|u_{n}(t_n)-z\|_{H^1}\geq\epsilon, \end{equation} $ | (3.2) |
where $ u_{n}(t) $ is the solution to (1.1) with initial data $ u_{0, n} $. From (3.1), there exists $ \{z_n\}\subset K(\eta) $ such that
| $ \inf\limits_{z_n\in K(\eta)}\|u_{0,n}-z_n\|_{H^1} < \frac{2}{n}, $ |
and there exists $ z\in K(\eta) $ such that
| $ \lim\limits_{n\rightarrow \infty}\|z_{n}-z\|_{H^1} = 0. $ |
Hence, we get
| $ \lim\limits_{n\rightarrow \infty}\|u_{0,n}\|_{L^2}^2 = \|z\|_{L^2}^2 = \eta,\; \; \lim\limits_{n\rightarrow \infty}E_\gamma(u_{0,n}) = E_\gamma(z) = G_\eta. $ |
By the conservation of mass and energy, we have
| $ \lim\limits_{n\rightarrow \infty}\|u_{n}(t_n)\|_{L^2}^2 = \eta,\; \; \lim\limits_{n\rightarrow \infty}E_\gamma(u_{n}(t_n)) = E_\gamma(z) = G_\eta, $ |
then $ \{u_{n}(t_n)\} $ is bounded in $ H^1 $.
Set $ \breve{u}_n = \frac{\sqrt{\eta}u_{n}(t_n)}{\|u_{n}(t_n)\|_{L^2}} $, $ \|\breve{u}\|_{L^2}^2 = \eta $, we deduce that
| $ \begin{align*} E_\gamma(\breve{u}_n)& = \frac{\eta}{\|u_{n}(t_n)\|_{L^2}^2}E_\gamma(u_{n}(t_n)) +\left(\left(\frac{\sqrt{\eta}}{\|u_{n}(t_n)\|_{L^2}}\right)^2-\left(\frac{\sqrt{\eta}}{\|u_{n}(t_n)\|_{L^2}}\right)^{p+2}\right)\frac{\lambda_1}{p+2}\int_{\mathbb{R}^{N}}|u_{n}(t_n)|^{p+2}dx\\ &+\left(\left(\frac{\sqrt{\eta}}{\|u_{n}(t_n)\|_{L^2}}\right)^2 -\left(\frac{\sqrt{\eta}}{\|u_{n}(t_n)\|_{L^2}}\right)^{2q}\right)\frac{\lambda_2}{2q}\int_{\mathbb{R}^{N}}(I_\beta\ast|u_{n}(t_n)|^q)|u_{n}(t_n)|^qdx\\ & = E_\gamma(u_{n}(t_n))+o_n(1), \end{align*} $ |
which implies that
| $ \lim\limits_{n\rightarrow \infty}E_\gamma(\breve{u}_n) = \lim\limits_{n\rightarrow \infty}E_\gamma(u_{n}(t_n)) = G_\eta. $ |
Hence, $ \{\breve{u}_n\}\subset A(\eta) $ is a minimizing sequence of $ E_\gamma $. There exists $ \breve{z}\in K(\eta) $ such that
| $ \lim\limits_{n\rightarrow \infty}\|\breve{u}_n-\breve{z}\|_{H^1} = 0, $ |
by the definition of $ \breve{u}_n $, we know
| $ \lim\limits_{n\rightarrow \infty}\|\breve{u}_n-u_{n}(t_n)\|_{H^1} = \lim\limits_{n\rightarrow \infty}\left(\frac{\sqrt{\eta}}{\|u_{n}(t_n)\|_2}-1\right)\|u_{n}(t_n)\|_{H^1} = 0. $ |
We can get that
| $ \lim\limits_{n\rightarrow \infty}\|u_{n}(t_n)-\breve{z}\|_{H^1} = 0, $ |
which contradicts (3.2). Hence, $ K(\eta) $ is orbitally stable. This completes the proof.
The authors declare that they have no competing interests.
| [1] |
R. Y. Chiao, E. Garmire, C. H. Townes, Self-trapping of optical beams, Phys. Rev. Lett., 13 (1964), 479–482. doi: 10.1103/PhysRevLett.13.479

|
| [2] |
J. P. Dong, Y. Lu, Infinite wall in the fractional quantum mechanics, J. Math. Phys., 62 (2021), 032104. doi: 10.1063/5.0026816

|
| [3] | L. R., Spectrum of atomic hydrogen: G. W. Series, Nuclear Physics, 6 (1958), 135–136. |
| [4] | C. Sulem, P. L. Sulem, The nonlinear Schrödinger equation: Self-focusing and wave collapse, New York: Springer, 1999. |
| [5] | V. E. Zakharov, Collapse of Langmuir waves, Sov. Phys. Jetp, 35 (1972), 908–914. |
| [6] |
A. Bensouilah, V. D. Dinh, S. H. Zhu, On stability and instability of standing waves for the nonlinear Schrödinger equation with an inverse-square potential, J. Math. Phys., 59 (2018), 101505. doi: 10.1063/1.5038041

|
| [7] |
B. H. Feng, H. H. Zhang, Stability of standing waves for the fractional Schrödinger-Choquard equation, Comput. Math. Appl., 75 (2018), 2499–2507. doi: 10.1016/j.camwa.2017.12.025

|
| [8] |
B. H. Feng, R. P. Chen, Q. X. Wang, Instability of standing waves for the nonlinear Schrödinger-Poisson equation in the $L^2$-critical case, J. Dyn. Diff. Equat., 32 (2020), 1357–1370. doi: 10.1007/s10884-019-09779-6

|
| [9] |
B. H. Feng, L. J. Cao, J. Y. Liu, Existence of stable standing waves for the Lee-Huang-Yang corrected dipolar Gross-Pitaevskii equation, Appl. Math. Lett., 115 (2021), 106952. doi: 10.1016/j.aml.2020.106952

|
| [10] | B. H. Feng, R. P. Chen, J. Y. Liu, Blow-up criteria and instability of normalized standing waves for the fractional Schrödinger-Choquard equation, Adv. Nonlinear Anal., 10 (2021), 311–330. |
| [11] |
T. Cazenave, P. L. Lions, Orbital stability of standing waves for some nonlinear Schrödinger equations, Commun. Math. Phys., 85 (1982), 549–561. doi: 10.1007/BF01403504

|
| [12] |
B. H. Feng, X. X. Yuan, On the Cauchy problem for the Schrödinger-Hartree equation, Evol. Equ. Control The., 4 (2015), 431–445. doi: 10.3934/eect.2015.4.431

|
| [13] | B. H. Feng, Q. X. Wang, Strong instability of standing waves for the nonlinear schrödinger equation in trapped dipolar quantum gases, J. Dyn. Diff. Equat., (2020). |
| [14] |
X. F. Li, J. Y. Zhao, Orbital stability of standing waves for Schrödinger type equations with slowly decaying linear potential, Comput. Math. Appl., 79 (2020), 303–316. doi: 10.1016/j.camwa.2019.06.030

|
| [15] |
Z. P. Cheng, M. B. Yang, Stability of standing waves for a generalized Choquard equation with potential, Acta Appl. Math., 157 (2018), 25–44. doi: 10.1007/s10440-018-0162-5

|
| [16] |
X. Luo, H. Y. Ye, Multiplicity and stability of standing waves for the nonlinear Schrödinger-Poisson equation with a harmonic potential, Math. Methods Appl. Sci., 42(2019), 1844–1858. doi: 10.1002/mma.5478

|
| [17] | T. Cazenave, Semilinear Schrödinger Equations, New York: American Mathematical Society, 2003. |
| [18] | E. H. Lieb, Analysis, 2 Eds., Graduate Studies in Mathematics, 14 (1997). |
| [19] |
B. H. Feng, R. P. Chen, J. J. Ren, Existence of stable standing waves for the fractional Schrödinger equations with combined power-type and Choquard-type nonlinearities, J. Math. Phys., 60 (2019), 051512. doi: 10.1063/1.5082684

|
| [20] |
V. Moroz, J. V. Schaftingen, Groundstates of nonlinear Choquard equations: existence, qualitative properties and decay asymptotics, J. Funct. Anal., 265 (2013), 153–184. doi: 10.1016/j.jfa.2013.04.007

|
| 1. | Chao Shi, Existence of stable standing waves for the nonlinear Schrödinger equation with mixed power-type and Choquard-type nonlinearities, 2022, 7, 2473-6988, 3802, 10.3934/math.2022211 | |
| 2. | Qiuying Li, Xiaoxiao Zheng, Zhenguo Wang, Orbital stability of periodic standing waves of the coupled Klein-Gordon-Zakharov equations, 2023, 8, 2473-6988, 8560, 10.3934/math.2023430 | |
| 3. | Jianlun Liu, Ziheng Zhang, Rui Guo, Ground state normalized solutions to Schrödinger equation with inverse-power potential and HLS lower critical Hartree-type nonlinearity, 2025, 44, 2238-3603, 10.1007/s40314-025-03131-z |