Modification of Takari natural sand based silica with BSA (SiO₂@BSA) for biogenic amines compound adsorbent

1.   Introduction

The human immunodeficiency virus (HIV) is a kind of retrovirus and it is the cause of acquired immunodeficiency syndrome (AIDS) ^[1]. CD$4^+$ T-cells are targeted of HIV, which are the most abundant white blood cells of the immune system and play a major role in protecting the body from infection. When HIV infection occurs, the virus attacks the CD$4^+$ T-cells and tries to replicate itself. The process of infection completes is called the HIV life cycle ^[2], which carried out in five stages: Stage Ⅰ: (binding and fusion) when HIV is entering into the CD$4^+$ T-cell, it is detected and bound by receptors at the cell membrane and then it has been fused, which allows HIV to enter inside the CD$4^+$ T-cell. Stage Ⅱ: (reverse transcription) within the CD$4^+$ T-cell, HIV releases and uses reverse transcriptase enzyme to convert its genetic material RNA to DNA, which allows HIV to enter the CD$4^+$ T-cell nucleus. Stage Ⅲ: (integration and transcription) within the nucleus of CD$4^+$ T-cell, HIV releases and uses integrase enzyme to integrate its viral DNA into DNA of the CD$4^+$ T-cell, this is called proviral DNA. Afterward, the cell is motivated, it will turn on the transcription of the proviral DNA to produce the viral RNA and move out of the nucleus to the cytoplasm. Stage Ⅳ: (replication and assembly) within the cytoplasm, the viral RNA begins to use the machinery of the CD$4^+$ T-cell to make long chains of HIV proteins, which are the building blocks for HIV replication. After that HIV protein and RNA move to the surface of the cell membrane and assemble into immature HIV. Stage Ⅴ: (budding) the immature HIV pushes itself out of the host cell and releases protease enzyme to split the long protein chains in the immature virus. Lastly, it becomes a mature virus which makes effects on other CD$4^+$ T-cells. Antiretroviral therapy is the use of HIV medicines to treat HIV infection and to protect the immune system by blocking the virus from reproducing at different stages of the HIV life cycle for instances fusion inhibitors, reverse transcription inhibitors, integrase inhibitors, and protease inhibitors ^[3,4,5].

Mathematical modeling and simulations were used as an essential instrument to forecast the possibility and severity of diseases and allow information to know its dynamic behavior of the infection. These models are useful tools and play a significant role to explain the dynamics of the immunological response to HIV infection, we refer readers to some books, see. ^[6,7,8]. Presenting some important previous works about the HIV model, researchers commonly used mathematical expressions in the form of differential equations to establish the relation between HIV viruses and uninfected CD$4^+$ cells, and the effect of drug therapy on infected cells is described by mathematical models. In $1989$, Perelson ^[9] initiated a simple model for the HIV infection and analyzed some dynamics behavior of the HIV infection of CD$4^+$ T-cells in $1993$ with his team ^[10]. In $2004$, Tuckwell et al. ^[11] studied the dynamics behavior of solutions in the two-component model of the HIV infection model as follows:

where $S$ is denoted the uninfected CD$4^+$ T-cells, $I$ is denoted the density of infected such cells, $\lambda$ is constant rate, $\mu_{1}$ is their per capita death rate, $\mu_{2}$ is the rate of disappearance of infected cells, and $k$ is infection rate. After three years, Rong et al. ^[12] developed a mathematical model of HIV model to predicate the initial constraints that shape the evolution of viral resistance to antiretroviral drugs in $2007$ as:

where they considered three compartments of CD$4^+$ T-cells including concentration of uninfected (susceptible) cells $S$, infected cells $I$ in eclipse phase, and free HIV virus particles in the blood cells $V$. Here denotes $\delta$ death rate of infected $S$ cells and includes the possibility of death by bursting of infected $S$ cells, hence $\delta \geq \mu_{1}$. Further, the parameter $b$ is the rate at which infected cells return to the uninfected class, while $c$ is the death rate of the virus and $N$ is the average number of viral particles produced by an infected cell, where $k$ is the rate of infection.

In $2009$, Srivastava et al. ^[13] presented a primary infection model with reverse transcriptase (RT) inhibitor which takes place before the infected cell starts producing the virus. They studied the dynamics of the uninfected CD$4^+$ T-cells, the virus population, and the infected CD$4^+$ T-cells. They also distinguished the infected class of CD$4^+$ T-cells into two subclasses: Pre-RT class which is the phase of the infected cells in which the reverse transcription is not completed and post-RT class which is the phase of those infected cells in which the reverse transcription is completed. The model of integer order is shown of the form:

with the initial conditions $(S(0), I(0), V(0), L(0))^{\mathbb{T}} = (S_{0}, 0, 0, L_{0})^{\mathbb{T}}$, where $(\cdot)^{\mathbb{T}}$ represents the transpose operation, $S$, $I$, $V$ and $L$ are denoted the density of susceptible CD$4^+$ T-cells, the density of infected CD$4^+$ T-cells in pre-RT class, the density of infected CD$4^+$ T-cells in post-RT class and the density of virus, respectively. The stability and numerical results are obtained in their work. The unknown parameters will be provide in the details in Section $3$.

The researchers used differential equations to applied in various areas to real-world problems. Since the theory of differential equations is well-known for applied researchers. It has popular in many fields and is working on different aspects of the mentioned area. In the last three centuries, various researchers developed fractional-order differential equations. It was extensively applied in various areas to real-world problems; see ^[14,15,16]. The well-known aspects that has been established recently are existence theory, stability analysis, numerical and optimization methods. The mathematician researchers introduced the different fractional derivatives that have been provided in fractional calculus. There are many types of research studies that have been created by using fractional derivatives and apply them to the HIV model. For examples; In $2009$, Ding and Ye ^[17] studied the stability of equilibrium for a fractional HIV infection of CD$4^+$ T-cells model and numerical simulations presented. In $2011$, Ertürk et al. ^[18] discussed an approximated solution of a fractional HTLV-I infection of CD$4^+$ T-cells model using a multi-step generalized differential transform method. In $2012$, Arafa et al. ^[19] constructed and analyzed fractional modeling dynamics of HIV and CD$4^+$ T-cells during primary infection. The generalized Euler method (GEM) used to find a numerical solution of this model. A few years later, Arafa et al. ^[20] studied and analyzed the behavior of solutions for a fractional-order model of HIV infection with CD$4^+$ T-cells in Caputo sense by using the GEM. In $2017$, Arshad et al. ^[21] analyzed the effects of the HIV infection model on CD$4^{+}$ T-cell population based on a Caputo fractional derivative. By applying a finite difference approximation, the numerical scheme has been proposed. Khan et al. ^[22] established the stability results and numerical solutions of the fractional HIV/AIDS model in sense of an Atangana-Baleanu derivative operator. In $2019$, Lichae et al. ^[23] studied an HIV-1 infection model of CD$4^{+}$ T-cells with a description of the effect of antiviral drug treatment under a Caputo fractional derivative. The approximate solution has been gained by applying the Laplace transform and the Adomian decomposition method. Ferrari et al. ^[24] presented an HIV model under Caputo fractional derivative, which the presences of a reverse transcriptase inhibitor based on ^[13] is indicated. They proved the existence and uniqueness of the model and shown that the model is positive invariance. The equilibrium points and their stability of the model are also investigated. Recently, the qualitative theory has been interested and applied to mathematical models. For example, in $2020$, Khan et al. ^[25] studied and analyzed the existence and stability results for the fractional order HIV-TB model with the Mittag-Leffler kernel. Further, numerical solutions are obtained. The HIV model under the Caputo-Fabrizio fractional derivative is studied by Nazir et al. ^[26]. They obtained the existence criterias of the solutions by using fixed point theory. The stability of the concerned solution is also showed in the Hyers-Ulam sense. The approximate solution of the model is verified by using the technique of Laplace transform with the Adomian decomposition method. Abdeljawad et al. ^[27] studied the existence of solutions of the q-fractional difference equations with help of Krasnoselskii's fixed point theorem and show the results by the Lotka-Volterra model. Abdeljawad and co-workers ^[28] applied the Banach fixed point theorem to prove existence results for the discrete fractional differences in sense of the discrete Mittage-Leffler kernel and numerical results were provided for the presence of the results. Khan et al. ^[29] discussed the existence of solutions and stability for the fractional-order advection-diffusion model in sense of the Mittag-Leffler kernel and shown the results numerically. Khan et al. ^[30] studied the time-fractional COVID-19 model with the help of the corrector-predictor method in the sense of a generalized Caputo fractional derivative ^[31]. The existence results are investigated by using Schauder's and Weissinger's fixed point theorems. Many papers have been developed under various types of fractional derivatives, see ^{[32,33,34,35,36,37,38,39,40,41,42,43,44,45]} and references cited therein.

Inspired by the mentioned discussion previously works in the HIV infection model with CD$4^+$ T-cells, we consider the model ^[13] under the generalized Caputo fractional derivative ^[31]. The main aim of this research is to examine the existence and uniqueness of the solutions for the fractional HIV model via the famous fixed point theorems such as Banach's and Larey-Schauder's nonlinear alternative. Moreover, stability analysis in the context of various Ulam's stability is discussed. Finally, we use the predictor-corrector algorithm proposed by Erturk et al. ^[30] to find the approximate solutions of the fractional HIV model for various fractional derivative orders.

This paper is organized as follows: Some preliminary facts, viral definitions, theoretical results, and descriptions of the fractional HIV model are presented in Section $2$. In Section $3$, we derive the relation between the Volterra integral equation and the proposed model. Also, with the help of these models, the existence and uniqueness of solutions are discussed by using the concepts of Banach's fixed point theorem and Larey-Schuader's nonlinear alternative. In Section $4$, Ulam's stability of the proposed model in the frame of Ulam-Hyers, generalized Ulam-Hyers, Ulam-Hyers-Rassias, and generalized Ulam-Hyers-Rassias is provided. As an application, the general numerical scheme and numerical simulations illustrate the theoretical results in Section $5$. Finally, the details of the conclusion have been completed in Section $6$.

2.   Preliminaries

2.1.   Background materials

This section gives some notations, basic definitions, and fundamental results of generalized fractional derivative and integral operators which are useful throughout this paper, see more details in ^[31,46,47].

Definition 2.1. (^[46]). The generalized fractional integral of the function $f$, ${_{}^{\rho}}\mathcal{I}_{a^+}^{\alpha}$, of order $\alpha > 0$ where $\rho > 0$, is expressed (provided it exists) as:

and $\Gamma(\cdot)$ represents the Gamma function.

Definition 2.2. (^[47]). The generalized Riemann-type fractional derivative of the function $f$, ${_{}^{\rho}}\mathfrak{D}_{a^+}^{\alpha}$, of order $\alpha > 0$ where $\rho > 0$, is defined by

where $\delta = t^{1-\rho} \frac{d}{dt}$ and $n-1 < \alpha \leq n$.

Definition 2.3. (^[47]). The generalized Caputo-type fractional derivative of a function $f$, $_{C}^{\rho}\mathfrak{D}_{a^+}^{\alpha}$, of order $\alpha > 0$ where $\rho > 0$, is defined by

where $n = [\alpha] + 1$. In case of $0 < \alpha < 1$, we have

Definition 2.4. (^[31]). The new generalized Caputo-type fractional derivative of a function $f$, ${}^{C\rho}\mathfrak{D}_{a^+}^{\alpha}$, of order $\alpha > 0$ where $\rho > 0$, is defined by

where $n-1 < \alpha \leq n$.

Lemma 2.5. (^[31]). Let $f \in \mathcal{C}^{n}([a, b])$, $n-1 < \alpha \leq n$ and $\rho > 0$. Then, for $0 \leq a < t \leq b < \infty$, the following relation holds:

In particular, if $0 < \alpha \leq 1$, we have

Lemma 2.6. (Banach fixed point theorem ^[48]). Let $X$ be a Banach space, and $D$ be a non-empty and closed subset of $X$. If the operator $\mathcal{Q}: D\to D$ is a contraction, then, $\mathcal{Q}$ has a fixed point in $D$.

Lemma 2.7. (Leray-Schauder nonlinear alternative ^[49]). Let $X$ be a Banach space, $C$ a closed, convex subset of $X$, $U$ an open subset of $C$ and $0\in U.$ Suppose that $\mathcal{D}:\overline{U}\to C$ is a continuous, compact (that is, $\mathcal{D}(\overline{U})$ is a relatively compact subset of $C$) map. Then either (i) $\mathcal{D}$ has a fixed point in $\overline{U}$; or (ii) there is a $x\in\partial U$ (the boundary of $U$ in $C$) and $\nu \in (0, 1)$ with $x = \nu\mathcal{D}(x)$.

2.2.   Model description

This work is based on the HIV models proposed by ^[13,24], which are considered the antiretroviral therapy of reverse transcriptase (RT) inhibitor. The unknown variables could be considered in the model represent the following: $S(t)$ is the density of susceptible CD$4^+$ T-cells; $I(t)$ is the density of infected CD$4^+$ T-cells before reverse transcription (pre-RT class); $V(t)$ is the density of infected CD$4^+$ T-cells in which reverse transcription is completed (post-RT class) and so are capable of producing virus; $L(t)$ is the virus density. Besides, the following positive parameters have been considered: $\lambda$ is inflows rate of CD$4^+$ T-cells; $k$ is an interaction infection rate of CD$4^+$ T-cells; $\mu_1$ is the natural death rate of CD$4^+$ T-cells; $\eta$ is the efficacy of RT inhibitor $(\eta \in (0, 1))$; $\sigma$ is transition rate of pre-RT class infected CD$4^+$ T-cells to pose-RT class; $b$ is reverting rate of infected cells to uninfected class due to non-completion of reverse transcription; $\mu_2$ is the death rate of infected CD$4^+$ T-cells; $\omega$ is the death rate of actively infected CD$4^+$ T-cells; $N$ is the total number of viral particles produced by an infected CD$4^+$ T-cells; $c$ is the clearance rate of the virus.

We study the HIV model infection with CD$4^+$ T-cells (1.3) under the generalized Caputo fractional derivative ^[31] and the meaning of all parameters is shown in the previous section:

where ${}^{C\rho}\mathfrak{D}_{0^+}^{\alpha}(\cdot)$ is the generalized Caputo-type fractional derivative of order $\alpha$ with $0 < \alpha \leq 1$ and $\rho > 0$. We simplify the model (2.7) for easy description in the following setting:

where the nonlinear functions $g_{1}$–$g_{4}$ are given by

with the initial conditions $(S(0), I(0), V(0), L(0))^{\mathbb{T}} = (S_{0}, I_{0}, V_{0}, L_{0})^{\mathbb{T}}$.

3.   Existence results

This section discusses the existence and uniqueness of solutions of the proposed model by helping fixed point theorems.

Let $\mathbb{E} = \mathcal{C}([0, T], \mathbb{R})$ denotes the Banach space of all continuous functions from $[0, T]$ to $\mathbb{R}$ equipped with the norm defined by

and $S$, $I$, $V$, $L \in \mathbb{E}$. In view of Lemma $2.5$, the model (2.7) can be written of the initial value problem

which is equivalent to the Volterra integral equation

where $\xi(t) = (S(t), I(t), V(t), L(t))^{\mathbb{T}}$ with the initial conditions $\xi(0) = (S_{0}, I_{0}, V_{0}, L_{0})^{\mathbb{T}}$, and $\mathcal{G}(t, \xi(t)) = (g_{i}(t, S, I, V, L))^{\mathbb{T}}$ for $i = 1, 2, 3, 4$.

In view of the integral equation (3.2), an operator $\mathcal{Q} : \mathbb{E} \to \mathbb{E}$ defined by

It should be noticed that the problem (3.1) which is equivalent to the model (2.7) has solutions if and only if the operator $\mathcal{Q}$ has fixed points.

3.1.   Uniqueness result via Banach's fixed point theorem

Theorem 3.1. Assume that a function $\mathcal{G} : [0, T] \to \mathbb{R}$ is continuous such that:

$(H_1)$ there exists a constant $\mathcal{L}_{\mathcal{G}} > 0$ such that

for any $\xi_{1}$, $\xi_{2} \in \mathbb{E}$ and for all $t\in [0, T]$.

If

then the problem (3.1) has a unique solution on $[0, T]$. Consequently, the model (2.7) has a unique solution on $[0, T]$.

Proof. Early the proving, we convert the problem (3.1) into a fixed point problem, $\xi = \mathcal{Q}\xi$, where $\mathcal{Q}$ is given as in (3.3). Applying the Banach contraction principle, we show that $\mathcal{Q}$ has a unique fixed point, which is the unique solution of the problem (3.1).

Let $\sup_{t\in [0, T]}\vert \mathcal{G}(t, 0)\vert = M_1 < \infty$. Setting $B_{r_1} = \{\xi \in \mathbb{E} : \Vert \xi \Vert \leq r_{1}\}$ with

Note that $B_{r_1}$ is a bounded, closed, and convex subset of $\mathbb{E}$.

Step Ⅰ. We show that $\mathcal{Q}B_{r_1} \subset B_{r_1}$.

For any $\xi \in B_{r_1}$, we have

which implies that $\mathcal{Q}B_{r_1} \subset B_{r_1}$.

Step Ⅱ. We show that $\mathcal{Q} : B_{r_1} \to B_{r_1}$ is a contraction.

For any $\xi_{1}$, $\xi_{2} \in \mathbb{E}$ and each $t\in [0, T]$, we have

which implies that $\Vert \mathcal{Q}\xi_{1} - \mathcal{Q}\xi_{2}\Vert \leq [(\mathcal{L}_{\mathcal{G}}T^{\rho\alpha})/(\rho^{\alpha}\Gamma(\alpha+1))] \Vert \xi_{1} - \xi_{2}\Vert$. As $(\mathcal{L}_{\mathcal{G}}T^{\rho\alpha})/(\rho^{\alpha}\Gamma(\alpha+1)) < 1$, then the operator $\mathcal{Q}$ is a contraction. Hence, as a result of the Banach contraction principle (Lemma $2.6$), the operator $\mathcal{Q}$ has a fixed point. Therefore, the problem (3.1) has a unique solution on $[0, T]$. Consequently, the model (2.7) has a unique solution on $[0, T]$. The proof is completed.

3.2.   Existence result via Leray-Schauder's nonlinear alternative

The Leray-Schauder's nonlinear alternative (Lemma $2.7$) is presented for our first existence result.

Theorem 3.2. Assume that:

$(H_{2})$ there exists a function $q \in \mathcal{C}([0, T], \mathbb{R}^+)$ and a continuous nondecreasing function $\mathcal{H} : [0, \infty) \to [0, \infty)$ which is subhomogeneous (that is, $\mathcal{H}(\mu \xi) \leq \mu \mathcal{H}(\xi)$, for all $\mu \geq 1$ and $\xi \in \mathbb{E}$), such that

where $q_{0} = \sup_{t\in [0, T]}\{q(t)\}$.

$(H_{3})$ there exists a constant $M_{2} > 0$ such that

Then, the problem (3.1) which is equivalent with the model (2.7) has at least one solution on $[0, T]$.

Proof. Let the operator $\mathcal{Q}$ be defined by (3.3). Firstly, we show that the operator $\mathcal{Q}$ maps bounded sets (balls) into bounded set in $\mathbb{E}$. For a positive constant $r_2 > 0$, let $B_{r_2} = \{\xi \in \mathbb{E} : \Vert \xi \Vert \leq r_{2} \}$ be a bounded ball in $\mathbb{E}$. From assumption $(H_2)$, for $t \in [0, T]$, we have

which leads to

Secondly, we show that the operator $\mathcal{Q}$ maps bounded sets into equicontinuous sets of $\mathbb{E}$. Let $\tau_1, \tau_2 \in [0, T]$ with $\tau_1 < \tau_2$ and $\xi \in B_{r_2}$. Then, we obtain

Clearly, which independent of $\xi \in B_{r_2}$, the right hand side of the inequality (3.7) tends to zero as $\tau_2 \to \tau_1$. Therefore, by the Arzelá-Ascoli theorem, $\mathcal{Q} : \mathbb{E} \to \mathbb{E}$ is completely continuous.

Finally, we show that the boundedness of the set of all solutions to $\xi = \kappa \mathcal{Q} \xi$ for $\kappa \in (0, 1)$. Let $\xi \in \mathbb{E}$ be a solution. Then, for $t \in [0, T]$, and following computation similar process to the first step, we get

Taking the norm into the both sides of the above inequality, for $t\in [0, T]$, which implies that

In view of $(H_3)$, there exists a constant $M_{2} > 0$ such that $\Vert \xi \Vert \neq M_{2}$. Let us set $\mathbb{K} : = \{\xi \in \mathbb{E} : \Vert \xi \Vert < M_{2}\}$.

Note that the operator $\mathcal{Q} : \overline{\mathbb{K}} \to \mathcal{C}$ is continuous and completely continuous. From the choice of $\overline{\mathbb{K}}$, there is no $\xi \in \partial \mathbb{K}$ such that $\xi = \kappa\mathcal{Q}\xi$ for some $\kappa \in (0, 1)$. Hence, by the nonlinear alternative of Leray-Schauder type (Lemma $2.7$), we deduce that the operator $\mathcal{Q}$ has a fixed point $\xi \in \overline{\mathbb{K}}$ which implies that the model (2.7) has at least one solution on $[0, T]$. The result is desired.

4.   Ulam-Hyers stability

In this section, we are developing some sufficient conditions under which the model (2.7) will satisfy the assumptions of the different types of Ulam's stability such as Ulam-Hyers stable, generalized Ulam-Hyers stable, Ulam-Hyers-Rassias stable, and generalized Ulam-Hyers-Rassias stable.

Before we state the Ulam's stability theorem, the following definitions are needed. Let $\epsilon > 0$ be a positive real number and $\Phi_{\mathcal{G}} : [0, T] \to \mathbb{R}^+$ be a continuous function. We consider the following inequalities:

where $\epsilon = \max (\epsilon_{j})^{\mathbb{T}}$ for $j = 1, 2, 3, 4$.

Definition 4.1. ^[50] The problem (3.1) is said to be Ulam-Hyers stable if there exists a constant $C_{\mathcal{G}} > 0$ such that for every $\epsilon > 0$ and for each solution $z \in \mathbb{E}$ of the inequality (4.1) there exists a solution $\xi \in \mathbb{E}$ of the problem (3.1) with

where $C_{\mathcal{G}} = \max(C_{\mathcal{G}_j})^{\mathbb{T}}$ for $j = 1, 2, 3, 4$.

Definition 4.2. ^[50] The problem (3.1) is said to be generalized Ulam-Hyers stable if there exists a function $\Phi_{\mathcal{G}} \in \mathcal{C}(\mathbb{R}^{+}, \mathbb{R}^{+})$, with $\Phi_{\mathcal{G}}(0) = 0$ such that, for each solution $z\in \mathbb{E}$ of inequality (4.2), there exists a solution $\xi\in \mathbb{E}$ of the problem (3.1) such that

where $\Phi_{\mathcal{G}} = \max(\Phi_{\mathcal{G}_j})^{T}$ for $j = 1, 2, 3, 4$.

Definition 4.3. ^[50] The problem (3.1) is said to be Ulam-Hyers-Rassias stable with respect to $\Phi_{\mathcal{G}} \in \mathcal{C}([0, T], \mathbb{R}^{+})$ if there exists a real number $M_{\Phi_{\mathcal{G}}} > 0$ such that for each $\epsilon > 0$ and for each solution $z\in \mathbb{E}$ of the inequality (4.2) there exists a solution $\xi\in \mathbb{E}$ of the problem (3.1) with

Definition 4.4. ^[50] The problem (3.1) is said to be generalized Ulam-Hyers-Rassias stable with respect to $\Phi_{\mathcal{G}}\in \mathcal{C}([0, T], \mathbb{R}^{+})$ if there exists a real number $M_{\Phi_{\mathcal{G}}} > 0$ such that for each solution $z\in \mathbb{E}$ of the inequality (4.3), there exists a solution $\xi\in \mathbb{E}$ of the problem (3.1) with

Remark 4.5. It is clear that (i) Definition $4.1$ $\Rightarrow$ Definition $4.2$; (ii) Definition $4.3$ $\Rightarrow$ Definition $4.4$; (iii) Definition $4.3$ for $\Phi_{\mathcal{G}}(\cdot) = 1$ $\Rightarrow$ Definition $4.1$.

Remark 4.6. A function $z \in \mathbb{E}$ is a solution of the inequality (4.1) if and only if there exists a function $w \in \mathbb{E}$ (which depends on $z$) such that the following properties:

(i) $|w(t)|\leq \epsilon$, $w = \max(w_j)^{\mathbb{T}}$, $\forall t \in [0, T]$.

(ii) $^{C\rho}\mathfrak{D}_{0^+}^{\alpha}z(t) = \mathcal{G}(t, z(t)) + w(t)$, $\forall t\in [0, T]$.

Remark 4.7. A function $z \in \mathbb{E}$ is a solution of the inequality (4.2) if and only if there exists a function $v \in \mathbb{E}$ (which depends on $z$) such that the following properties:

(i) $|v(t)|\leq \epsilon \Phi_{\mathcal{G}}(t)$, $v = \max(v_j)^{\mathbb{T}}$, $\forall t \in [0, T]$.

(ii) $^{C\rho}\mathfrak{D}_{0^+}^{\alpha}z(t) = \mathcal{G}(t, z(t)) + v(t)$, $\forall t\in [0, T]$.

4.1.   The Ulam-Hyers stability and generalized Ulam-Hyers stability

We demonstrate an important role that will be used in the proofs of Ulam-Hyers stability and generalized Ulam-Hyers stability.

Lemma 4.8. Let $\alpha \in (0, 1]$ and $\rho > 0$. If $z \in \mathbb{E}$ is a solution of the inequality (4.1), then $z$ is a solution of the following inequality

Proof. Let $z$ be a solution of the inequality (4.1). In view of Remark $4.6$ $(ii)$, we obtain

Thus, the solution of the problem (4.9) can be written

By applying Remark $4.6$ $(i)$,

Therefore, the inequality (4.8) is achieved.

Next, we investigate the Ulam-Hyers stability and generalized Ulam-Hyers stability results.

Theorem 4.9. Assume that $\mathcal{G} : [0, T]\times\mathbb{R} \to \mathbb{R}$ is continuous for every $\xi \in \mathbb{E}$. If $(H_{1})$ and (3.4) are satisfied, then the problem (3.1) which is equivalent to the model (2.7) is Ulam-Hyers and, consequently, generalized Ulam-Hyers stable on $[0, T]$.

Proof. Suppose that $\epsilon > 0$ and let $z\in \mathbb{E}$ be any solution of the inequality (4.1). Let $\xi \in \mathbb{E}$ be the unique solution of the problem (3.1),

By using (3.2) and Lemma $4.8$ with the property of triangle inequality, we get

This implies that $|z(t) - \xi(t)| \leq C_{\mathcal{G}} \epsilon$, where

Hence, the model (2.7) is Ulam-Hyers stable. Now, by setting $\Phi_{\mathcal{G}}(\epsilon) = C_{\mathcal{G}}\epsilon$ such that $\Phi_{\mathcal{G}}(0) = 0$ yields that the model (2.7) is generalized Ulam-Hyers stable. The proof is completed.

4.2.   The Ulam-Hyers-Rassias stability and generalized Ulam-Hyers-Rassias stability

We assume that the following assumption:

$(H_{4})$ There exists an increasing function $\Phi_{\mathcal{G}} \in \mathbb{E}$ and there exists $\lambda_{\Phi_{\mathcal{G}}} > 0$, such that for any $t \in [0, T]$, the following integral inequality

Let us present an important lemma that will be used in the proofs of the Ulam-Hyers-Rassias stability and generalized Ulam-Hyers-Rassias stability results.

Lemma 4.10. Let $\alpha \in (0, 1]$ and $\rho > 0$. If $z \in \mathbb{E}$ is a solution of the inequality (4.2), then $z$ is a solution of the following inequality

Proof. Let $z$ be a solution of the inequality (4.2). In view of Remark $4.7$ $(ii)$, we obtain

Thus, the solution of the problem (4.12) can be written

By applying Remark $4.7$ $(i)$,

Hence, the inequality (4.8) is achieved.

In the last result, we are ready to prove the Ulam-Hyers-Rassias stability and generalized Ulam-Hyers-Rassias stability results.

Theorem 4.11. Assume that $\mathcal{G} : [0, T]\times\mathbb{R} \to \mathbb{R}$ is continuous for every $\xi \in \mathbb{E}$. If $(H_{1})$, $(H_3)$ and (3.4) are satisfied, then the problem (3.1) which is equivalent to the model (2.7) is Ulam-Hyers-Rassias and, consequently, generalized Ulam-Hyers-Rassias stable on $[0, T]$.

Proof. Let $\epsilon > 0$ and $z\in \mathbb{E}$ be the solution of the inequality (4.3). Let $\xi \in \mathbb{E}$ be the unique solution of the problem (3.1). By applying (3.2) and Lemma $4.10$, we have

which implies that $|z(t)-\xi(t)| \leq \frac{\lambda_{\Phi_{\mathcal{G}}}}{1 - \frac{\mathcal{L}_{\mathcal{G}} T^{\rho\alpha}}{\rho^{\alpha}\Gamma(\alpha+1)}} \epsilon \Phi_{\mathcal{G}}(t)$. By setting

we get the following inequality

Therefore, the model (2.7) is Ulam-Hyers-Rassias stable. Moreover, if we set $\epsilon = 1$, in (4.13), with $\Phi_{\mathcal{G}}(0) = 0$, then the model (2.7) is generalized Ulam-Hyers-Rassias stable. The proof is completed.

5.   Simulation results and discussion

In this section, the fractional variant of the HIV model under consideration via the generalized Caputo fractional derivative is numerically simulated by using the predictor-corrector algorithm as proposed in ^[30].

The first step of the algorithm, the interval $[0, T]$ is divided into $n$ unequal subintervals $\{[t_k, t_{k+1}], k = 0, 1, \ldots, n-1\}$ using the mesh points

where $h = \frac{T^\rho}{n}$. The approximate solutions of the HIV model (2.7) can be written as

where

and

According to the biological works of literature ^[13,24], we will consider the model's constant parameters and initial states as shown in Table 1.

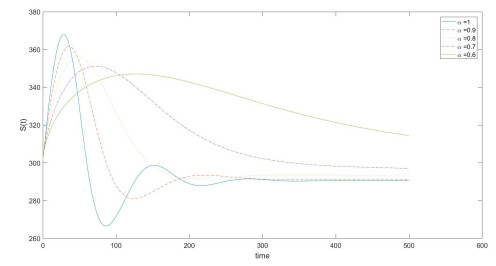
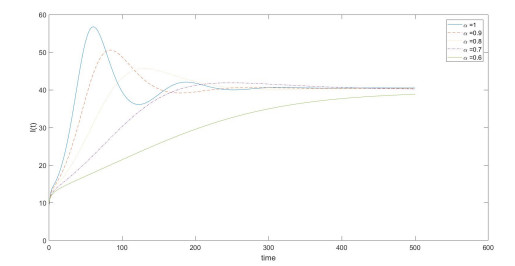
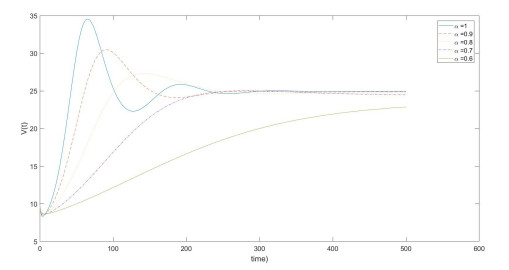
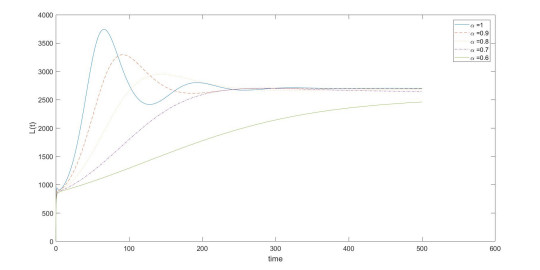
For the prediction of the epidemiology of the HIV model, we calculate the numerical solutions of the model (2.7) for various fractional orders, see illustrative Figures 1-4. All figures represent the comparison of the amount of susceptible CD$4^+$ T-cells populations, the concentration of the infected CD$4^+$ T-cells in pre-RT class, the concentration of the infected CD$4^+$ T-cells in post-RT class, and the population of HIV virus, respectively, for the fractional orders $\alpha = 1$, $0.9$, $0.8$, $0.7$, $0.6$ with $\rho = 0.97$ and $n = 3000$.

It can be easily seen that when the values of fractional orders $\alpha$ approach to $1$, the solutions $S_{\alpha}(t)$ decrease to the integer order soluion $S_{1}(t) = S(t)$ of the classical model ^[13], see in Figure 1, but the solutions $I_\alpha(t), V_\alpha(t)$ and $L_\alpha(t)$ also increase to the interger order solution $I_{1}(t) = I(t)$, $V_{1}(t) = V(t)$ and $L_{1}(t) = L(t)$, respectively, of the classical model ^[13] as see in Figures 2-4.

6.   Conclusions

The analysis of the mathematical model of HIV infections with antiretroviral therapy involving the generalized Caputo fractional derivative established in this paper. We showed that the solution of the considered model (2.7) exists and has at least one solution with the help of the Larey-Schauder nonlinear alternative and the unique solution proved by using Banach's fixed point theorem. The stability of the solution was examined by employing the various Ulam's stability such as Ulam-Hyers stable, generalized Ulam-Hyers stable, Ulam-Hyers-Rassias stable, and generalized Ulam-Hyers-Rassias stable. Further on using the predictor-corrector algorithm, we illustrated the approximate solutions for the different fractional-order $\alpha$ via the Matlab program and we concluded that the solutions of the considered model (2.7) tend to the standard solution when the fractional order $\alpha \rightarrow 1$. For further work, one can be developed and applied to the different types of fractional derivatives with the similar techniques in many real-world problems. We hope that this work would be a good alternative way for various researches.

Acknowledgement

J. Kongson and C. Thaiprayoon would like to thank for funding this work through the Center of Excellence in Mathematics (CEM) and Burapha University. W. Sudsutad would like to thanks King Mongkut's University of Technology North Bangkok for the support of this work.

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.