Study of implicit-impulsive differential equations involving Caputo-Fabrizio fractional derivative

1.   Introduction

In recent decades, fractional differential equations have received great attention from the researchers in many applied fields such as physics, biology, chemistry and other fields of sciences and engineering ^{[1,2,3,4,5,6,7,32]}. Due to many applications, this area has been studied with different fractional derivatives such as Riemman-Liouvile, Caputo, Hilfer and Hadamard type fractional derivatives ^{[8,9,10,11,12,30,31]}. Further, the fractional time derivatives are importance reactive-transport, since solutes may interact immobile porous medium in highly non-linear ways, some of the investigator using fractional time derivatives for the solution of space-time fractional diffusion equations ^[41,42]. But now a days the researchers are studying a new type of fractional derivative which is called Caputo-Fabrizio fractional derivative. This fractional derivative is also known as a non-singular kernel or exponential kernel type derivative. In 2015, Caputo and Fabrizio together introduced this derivative ^[13]. Latter on, Caputo-Fabrizio derivatives was used by many researchers for modeling various problems in engineering sciences (look for example some articles ^[35,36]. Further, this type of derivative have many applications. Such as it is use an exponential decay kernel to a novel HIV/AIDS epidemic model that includes an anti-retrovirus treatment compartment ^[37], and also some researcher apply this new type of the fractional derivative for the dynamical system with both chaotic and non-chaotic behaviors ^[38], hyper-chaotic behaviors, optimal control and synchronization ^[39], nonstandard finite difference scheme and non-identical synchronization of a novel fractional chaotic system ^[40]. Furthermore, the researchers studied the aforementioned area looking for results of existence, uniqueness and stability. Some of the articles we refer to see the reader to earlier works ^{[14,15,16,17,18]}.

On the other hand, impulsive differential equations (IDEs) have played an important role in the modeling of phenomena, chiefly in the description of dynamics to sudden changes as well as other phenomena such as crops, diseases, etc. The said differential systems have been used to designate the model since the previous century. For the fundamentals theory on IDEs the reader can consult the monographs of Burton and Simeonov ^[19], Lakshmikantham et al. ^[20], Benchohra et al. ^[21]. Recently, impulsive FDEs are increasingly used to constitute an impulsive control theory. This theory is used to model some physical phenomena. The said area has become a very important direction in IDEs theory. Further numerous applications of IDEs to problems arising in satellite orbital transfer ^[24], ecosystem management ^[25], electrical engineering ^[26], etc. Here refer for further applications on IDEs ^[28,29,33]. When reviewing the existence literature, we see that very rarely it has been investigated IFDEs with the participation of the CFFD. For instance recently author ^[22] investigated the following problem of IDE with CFFD as

where $_{0}^{\mathcal{CF}}{\mathcal{D}}^{\omega}_{{r}}$ represent CFFD of order $\omega$, $\mathcal{J} = [0, \mathcal{T}]$, $\mathfrak{u}_{0}\in\mathcal{R}$, the given function $\mathfrak{f}:\mathcal{J}\times\mathcal{R}\rightarrow \mathcal{R},$ $\mathcal{I}_{k}:\mathcal{R}\rightarrow \mathcal{R}$ are continuous. Where $\Delta\mathfrak{u}({r}_{k})$ represent change of right and left hand limit of the discontinuity points ${r}_{k}$, it is define as $\Delta\mathfrak{u}({r}_{k}) = \mathfrak{u}({r}_{k}^{+})-\mathfrak{u}({r}_{k}^{-})$.

Inspired by the research work as mentioned above, we intend to work on implicit-IFDEs involving CFFD of the form:

where $_{0}^{\mathcal{CF}}{\mathcal{D}}^{\omega}_{{r}}$ represents the CFFD of order $0 < \omega < 1,$ $\mathfrak{g}: \mathcal{J} \times \mathcal{R} \times \mathcal{R} \longrightarrow \mathcal{R}, \; \; \mathcal{I}_{k}:\mathcal{R}\longrightarrow \mathcal{R}$ and $\mathfrak{f}:\mathcal{R}\longrightarrow \mathcal{R}$ are continuous function. Where $\Delta\mathfrak{u}({r}_{k})$ represent change of right and left hand limit of the discontinuity points ${r}_{k}$, it is define as $\Delta\mathfrak{u}({r}_{k}) = \mathfrak{u}({r}_{k}^{+})-\mathfrak{u}({r}_{k}^{-})$. By using Krasnoselskii's and Banach fixed point theorems, we establish the existence theory for the considered problem. Also we develop some results for Hyers-Ulam (H-U) and generalized (G-H-U) stability. Pertinent example is given to verify our results. Further keeping in mind that right hand side of problem (1.2) vanish at $r = 0$ as suggested in ^[43].

In this article, we use a new type of fractional derivative with non-singular kernel involving non-local initial condition and implicit functions is proposed. The introduced fractional derivative includes as a special case Caputo-Fabrizio fractional derivative, and also study the implicit-FDEs with using impulsive condition for the solution of existence, uniqueness and stability results. Next take two counter examples to verify the necessary results.

In section 2, some basics preliminaries on fractional calculus are presented. In section 3, We develop a results and discussion of implicit-IFDEs using an arbitrary non-singular kernel, such as Caputo-Fabrizio fractional derivative. In section 4, we will investigate the stability results of Hyers-Ulam and generalize Hyers-Ulam stability for the proposed problem of implicit-IFDEs. In section 5, take some counter examples and its graphs to verify the necessary results. In the last section 6, take concluding remarks of our article.

2.   Basic results

In this part of our article, we need to provide some basic results and definitions of fractional calculus. We derived our main results through using these basic results.

Definition 1. ^[27] For $0 < \omega < 1, \; \; \mathfrak{u}\in \mathcal{H}^{1}(0, a).$ The CFFD for a function $\mathfrak{u}$ of order $\omega$ is defined as

where $\mathcal{M}({\omega})$ is a normalization constant depending on $\omega$.

Definition 2. ^[27] For $0 < \omega < 1,$ the fractional integral for a function $\mathfrak{u}$ is given by

When $\omega = 1,$ then we get first order classical integral using Remark 1. This convergent has been proved in ^[34].

Remark 1. ^[22] Note that according to the previous definition, the fractional integral of a function $\mathfrak{u}$ with order $0 < \omega < 1$ is an average between function $\mathfrak{u}$ and its integral of one. Imposing

it can be concluded that

Lemma 1. ^[22] The unique solution of the given initial value problem

is given by

where

Let $\mathcal{C}(\mathcal{J}, \mathcal{R})$ be the space of all continuous functions defined on the interval $\mathcal{J}$ endowed with the usual supremum norm, that as:

Let the set of functions

and there exist $\mathfrak{u}({r}_{k}^{+})$ and $\mathfrak{u}({r}_{k}^{-}), \; \; k = 1, 2, 3, 4, ..., m.$ The given set is Banach space with the norm is defined as:

Theorem 1. ^[23] Let $\mathcal{Y}$ be non empty, convex and closed subset of $\mathcal{X}.$ Consider two operators $\mathcal{T}$, $\mathcal{S}$ such that

1) $\mathcal{T}({y}_{1})+ \mathcal{S}({y}_{2}) \in \mathcal{Y},$ for all ${y}_{1}, {y}_{2}\in \mathcal{Y}.$

2) $\mathcal{T}$ is contraction operator.

3) $\mathcal{S}$ is continuous and compact.

then there exists at least one solution ${y}\in \mathcal{X}$ such that $\mathcal{T}({y})+\mathcal{S}({y}) = {y}$.

3.   Results and discussion

The present section of our paper is reserved to investigate the existence and uniqueness for the solution of the implicit-IFDEs by Krasnoselskii's and Banach fixed point theorems.

Lemma 2. Suppose $0 < \omega < 1$ and $\tau:\mathcal{J}\rightarrow \mathcal{R}$ be continuous. A function $\mathfrak{u}\in \mathcal{X}$ is the solution of the given impulsive problem:

If and only if it satisfies

Proof. Suppose $\mathfrak{u}(r)$ satisfies (3.1). If $r\in[0, r_{1}],$ then

Using Lemma 1, we get

Now applying impulsive condition $\mathfrak{u}(r_{1}^{-})$, one has

Again if $r\in[r_{1}, r_{2}],$ then

Again using Lemma 1, we can obtain

Further using (3.4), we get

Upon further simplification, we have

Again using impulsive condition $\mathfrak{u}(r_{2}^{-})$ in (3.5), we obtain

If $r\in [r_{2}, r_{3}]$, then

Again using Lemma 1, we can obtain

By using (3.6), we get

Further simplify, we get

Furthermore, continue this process we obtain for $r\in [r_{k}, r_{k+1}]$ as

Similarly, if $\mathfrak{u}(r)$ satisfies (3.2), then we can prove that $\mathfrak{u}(r)$ is the solution of (3.1). This complete the proof.

Corollary 1. In view of Lemma 2, the solution of the said problem (1.2) is given by

For the sake of simplicity, we use ${\mathfrak{g}}(r, \mathfrak{u}(r), \ _{0}^{\mathcal{CF}}\mathcal{D}^{\omega}_{r}\mathfrak{u} (r)) = \delta_{\mathfrak{u}}(r)$ and ${\mathfrak{g}}(r, \bar{\mathfrak{u}}(r), \ _{0}^{\mathcal{CF}}\mathcal{D}^{\omega}_{r}\bar{\mathfrak{u}} (r)) = \bar{\delta}_{\mathfrak{u}}(r)$ also at $r = 0$, we use $\delta_\mathfrak{u}(0) = \delta_{0}.$ Further, for qualitative results, we need to transform the proposed problem (1.2) to fixed point problem, we need to define an operator $\mathcal{T}:\mathcal{X}\rightarrow \mathcal{X}$ defined as:

First of all we introduce some hypothesis which are needed:

$(H_{1})$ The function $\mathfrak{g}:\mathcal{J}\times\mathcal{R}\times\mathcal{R}\rightarrow \mathcal{R}$ is continuous.

$(H_{2})$ There exist positive constants $C_{\mathfrak{g}} > 0$ and $0 < C^{*}_{\mathfrak{g}} < 1,$ such that

$(H_{3})$ The function $\mathcal{I}_{k}:\mathcal{R}\rightarrow \mathcal{R}$ are continuous and there exists positive constant $0 < L_{k} < 1$ with $\sum_{k = 1}^{n}L_{k} < 1,$ such that

for all $\mathfrak{u}, \bar{\mathfrak{u}}\in \mathcal{R}$, $k = 1, 2, 3, ..., n.$ Further we use $\sum_{k = 1}^{n}L_{k} = L_{I}$ throughout the paper.

$(H_{4})$ The function $\mathfrak{f}:\mathcal{R}\rightarrow \mathcal{R}$ is continuous and there exists constant $0 < K_{f} < 1,$ such that

Theorem 2. Under the hypothesis $H_{1}$–$H_{4}$, the impulsive problem (1.2) has a unique solution if

Proof. Suppose for each $r\in \mathcal{J}$ and any $\mathfrak{u}(r), \bar{\mathfrak{u}}(r)\in \mathcal{X}$, we have in view of (3.7)

where $\delta_{\mathfrak{u}}(r) = \mathfrak{g}(r, \mathfrak{u}(r), \delta_{\mathfrak{u}}(r)),$ so

Continuing the above process, so we obtain

Using the hypothesis $(H_{3})$, $(H_{4})$ and (3.9) in Eq (3.8), we get

Taking maximum on both side, we get

Hence the constant given as

Therefore, the operator $\mathcal{T}$ is contraction, so the operator has a unique fixed point, therefore the said problem (1.2) has a unique solution.

Next second main result is based on the Krasnoselskii's fixed-point theorem. For this results we need some hypothesis which is given below.

$(H_{5})$ There exist some positive constants $P_{\mathfrak{g}}, Q_{\mathfrak{g}}, R_{\mathfrak{g}} > 0$ and $0 < Q_{\mathfrak{g}} < 1,$ such that

for each $r\in \mathcal{J}$ and $\mathfrak{u}(r), \delta_{\mathfrak{u}}(r)\in \mathcal{R}.$

$(H_{6})$ There exists positive constant $K_{f}^{*} > 0,$ such that

for $\mathfrak{u}(r)\in \mathcal{R}.$

Theorem 3. Under the hypothesis $(H_{2})$–$(H_{6})$ are satisfied, then the implicit-impulsive problem (1.2) has at least one solution if

Proof. For the proof of this theorem, we need to define two operators from (3.7), we have

and

Let us define a set for a real number $q > 0$ as $H = \{\mathfrak{u}(r)\in \mathcal{X}: \|\mathfrak{u}\|_{PC}\leq q\}$, we need to show the operator $\mathcal{T}_{1},$ is contraction. For this suppose $\mathfrak{u}(r), \bar{\mathfrak{u}}(r) \in \mathcal{X},$ we have

Using hypothesis $(H_{3})$, $(H_{4})$ and (3.9), then taking maximum on both side, we get

Here the given constant is

Hence the operator $\mathcal{T}_{1}$ is contraction. Next we need to prove that the operator $\mathcal{T}_{2}$ is compact and continuous, for this $\mathfrak{u}(r)\in \mathcal{X},$ we have

where

Upon further simplification, we have

Using (3.11) in (3.10) and then taking maximum, we get

where

Hence the operator $\mathcal{T}_{2}$ is bounded. Further suppose $r_{1} < r_{2}$ in $\mathcal{J},$ we have

Using (3.11) in (3.12), we get

Taking maximum on right hand side, we have

Further

Obviously, from (3.13), we look that if $r_{1}\rightarrow r_{2},$ then the right hand side of the Eq (3.13) goes to zero, so $|\mathcal{T}_{2}\mathfrak{u}(r_{2})-\mathcal{T}_{2}\mathfrak{u}(r_{1})|\rightarrow 0$ as if $r_{1}\rightarrow r_{2}.$ Hence we observe that the right-hand side of (3.13) goes to zero uniformly. Therefore, the operator $\mathcal{T}_{2}$ is equicontinuou. Therefore the operator $\mathcal{T}_{2}$ is compact by Arzelá-Ascoli theorem. Hence in view of Krasnoselskii theorem, we conclude that (1.2) has at least one solution.

4.   Stability results

In this part of our article, we will investigate the stability of H-U and g-U-H stability for the problem of implicit-IFDEs.

Definition 3. $\langle$ H-U stable $\rangle$

The said implicit-impulsive problem (1.2), is H-U stable if any $\epsilon > 0$ for the given inequality

Then, there exists unique solution $\bar{\mathfrak{u}}(r)$ with a constant $\mathcal{Z}$ such that

Definition 4. $\langle$ Generalized H-U stable $\rangle$ Our implicit-impulsive problem is g-H-U stable if there exists non-decreasing function $\mathfrak{\phi}:(0, T)\rightarrow (0, \infty)$, such that

With $\phi(0) = 0, \; \phi(T) = 0.$

Also we discuss important remark here which is used in this section as:

Remark 2. Suppose there exists a function $\Psi(r)$, which is depend on $\mathfrak{u}\in \mathcal{X}$ with $\Psi(0) = 0, \; \; \Psi(T) = 0$ such that

(1) $|\Psi(r)| \leq \epsilon, \; \forall\; r\in\mathcal{J},$

(2) $_{0}^{\mathcal{CF}}{\mathcal{D}}^{\omega}_{r}\mathfrak{u}(r) = \mathfrak{g}(r, \mathfrak{u}(r), _{0}^{\mathcal{CF}}{\mathcal{D}}^{\omega}_{r}\mathfrak{u}(r)) + \Psi(r), \; \forall\; \; r\in\mathcal{J}.$

Lemma 3. The solution of given proposed problem

is

where $\delta_{\mathfrak{u}}(r) = \mathfrak{g}(r, \mathfrak{u}(r), _{0}^{\mathcal{CF}}{\mathcal{D}}^{\omega}_{r}\mathfrak{u}(r))$ and $\Psi(0) = 0.$ Further, from the solution (4.1), we get

Proof. The solution of (4.1) can be easily obtained through using Lemma 2. Although from the solution it is clear to become result (4.2), by using Remark 2.

Theorem 4. Under the Lemma 3, solution of the said implicit-impulsive problem (1.2), is H-U and g-H-U stable if

Proof. Suppose $\mathfrak{u}(r)\in\mathcal{X}$ be any solution of the mentioned problem (1.2) and $\bar{\mathfrak{u}}(r)\in\mathcal{X}$ be unique solution of the said problem, then we need to consider

Using (4.2), (3.9) and hypothesis $H_{3}, H_{4}$ and then taking maximum on both side, we get

Upon further simplification

Hence from the above inequality, we get

which gives

Therefore, solution is H-U stable. And there exists non-decreasing function $\phi\in\mathcal{X}$. Then from Eq (4.3), we can be write as

with $\phi(0) = \phi(T) = 0.$ Therefore, solution of the implicit-impulsive problem (1.2) is g-H-U stable.

5.   Illustrative example

In this section, we study counter example to verify our results.

Example 1. Considered the implicit-IFDEs problem

Here $\omega = \frac{1}{5}$ and ${_{0}^{{\mathcal{CF}}}\mathcal{D}^{\frac{1}{5}}_{r}\mathfrak{u}(r)} = \delta_{\mathfrak{u}}(r),$ we can set

and

Clearly $\mathfrak{f}$ and $\mathfrak{g}$ are continuous functions. Now for $\mathfrak{u}(r), \; \bar{\mathfrak{u}}(r)\in\mathcal{X}, \; \delta_{\mathfrak{u}}(r), \; \bar{\delta}_{\mathfrak{u}}(r)\in\mathcal{R}$ and $r\in[0, 1].$ Now, we consider

Applying maximum on both side, so we get

Which satisfy hypothesis $H_{2}$, we have

Now next we set for $\mathfrak{u}(r), \; \bar{\mathfrak{u}}(r)\in\mathcal{X},$ we have

Hence, hypothesis $H_{3}$, is satisfied, so $L = \frac{1}{55}.$ Next we consider a function $\mathfrak{f}(\mathfrak{u}) = \frac{\cos|\mathfrak{u}|}{15},$ for $\mathfrak{u}, \; \bar{\mathfrak{u}}\in\mathcal{R},$ we have

Therefore, $H_{4}$, is satisfied, so $K_{f} = \frac{1}{15}.$ Further, we need to verify the condition of the theorems, for this we know that $\omega = \frac{1}{5}$ and $G_{\omega} = \frac{4}{5}, Q_{\omega} = \frac{1}{5}$, we have the condition of theorem 2 is

Therefore, the condition of Theorem 2, is satisfied, hence the mentioned implicit-impulsive problem (5.1) has a unique solution. Further, we need to verify the condition of the theorem 3, we have

Also the condition of Theorem 3, holds, so the solution of the said problem (5.1), is at least one solution. In the last, we need to verify the stability results, for this, we verify the condition of the Theorem 4, we have

Therefore, condition of the Theorem 4, is satisfied, hence the solution of the problem (5.1), has H-U and g- H-U stable.

Remark 3. Here we consider the given Example 1 and provide the graphical presentation in Figure 1. We present graphical presentation of solution at different values of fractional order $\omega = 0.45, 0.65. 0.85$ and at the given values of impulsive points $r_1 = \frac{1}{4}, \ r_2 = \frac{1}{2}, \ r_3 = \frac{3}{4}.$

From Figure 1, we see the stability behavior for different fractional order.

Example 2. Take another implicit-IFDEs problem

Here $\omega = \frac{1}{7}$ and ${_{0}^{{\mathcal{CF}}}\mathcal{D}^{\frac{1}{7}}_{r}\mathfrak{u}(r)} = \delta_{\mathfrak{u}}(r),$ we can set

and

Clearly $\mathfrak{f}$ and $\mathfrak{g}$ are continuous functions. For $\mathfrak{u}(r), \; \bar{\mathfrak{u}}(r)\in\mathcal{X}, \; \delta_{\mathfrak{u}}(r), \; \bar{\delta}_{\mathfrak{u}}(r)\in\mathcal{R}$ and $r\in[0, 1].$ Consider,

Taking maximum on both side, we get

One can see that the hypothesis $H_{2}$ is satisfy, we have

Next consider for $\mathfrak{u}(r), \; \bar{\mathfrak{u}}(r)\in\mathcal{X},$ we have

Hence, the hypothesis $H_{3}$, is satisfied, where $L_{I} = \frac{1}{35}.$

Next we consider a function $\mathfrak{f}(\mathfrak{u}) = \frac{\sin(|\mathfrak{u}|)}{25},$ for $\mathfrak{u}, \; \bar{\mathfrak{u}}\in\mathcal{R},$ we have

Here $K_{f} = \frac{1}{25},$ so the hypothesis $H_{3}$, is satisfied.

Moreover, we need to verify the sufficient conditions of the theorems. For this we have $\omega = \frac{1}{7}$ and $G_{\omega} = \frac{6}{7}, Q_{\omega} = \frac{1}{7}$. First we have to verify the condition of the Theorem 2, is

One can see that condition of the Theorem 2, is satisfied. Therefore, the implicit-impulsive problem (5.2) has a unique solution.

Further, verify condition of the Theorem 3, we have

Also holds condition of the Theorem 3, hence solution of the said problem (5.2), is at least one solution. In the last, we need to verify the stability results, for this, we have to verify condition of the Theorem 4, we get

Therefore, condition of the Theorem 4, is satisfied, hence the solution of the problem (5.2), has H-U and g-H-U stable.

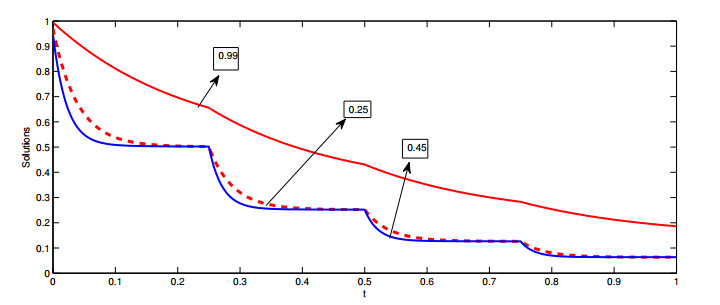
Remark 4. Here we consider the given Example 2 and provide the graphical presentation in Figure 2. We present graphical presentation of solution at different values of fractional order $\omega = 0.25, 0.45. 0.99$ and at the given values of impulsive points $r_1 = \frac{1}{4}, \ r_2 = \frac{1}{2}, \ r_3 = \frac{3}{4}.$ From Figure 2, we see the stability behavior for different fractional order.

6.   Conclusions

We have in fact obtained some conditions necessary for the solution of existence, uniqueness and stability of the said implicit-impulsive FDEs with involving CFFD. we obtain this conditions using the fixed point theorem as Krasnoselskii's and Banach contraction principle. In this article, we have used Banach's contraction theorem for the uniqueness of solution and Krasnoselskii's fixed point theorem for the existence of the solution for the said problem (1.2). Also we have studied this problem for the stability of H-U and g-H-U stable. All the results have been demonstrated by a proper example. We have also presented the solution through graph by taking different fractional order and impulsive points using RKM methods.

Acknowledgment

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through research groups program under Grant number R.G.P.1/195/42. This research was funded by King Mongkut's University of Technology North Bangkok. Contract no.KMUTNB-62-KNOW-022.

Conflict of interest

No conflict of interest exist.