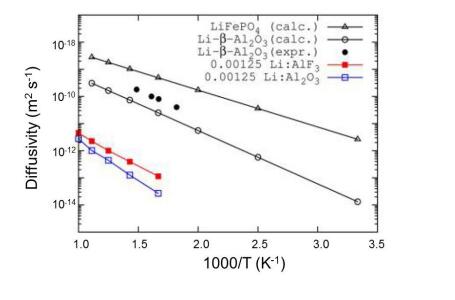
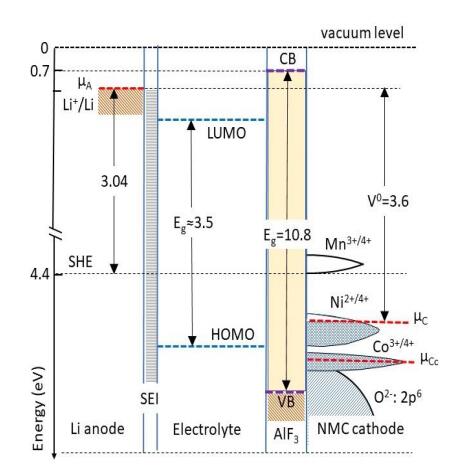
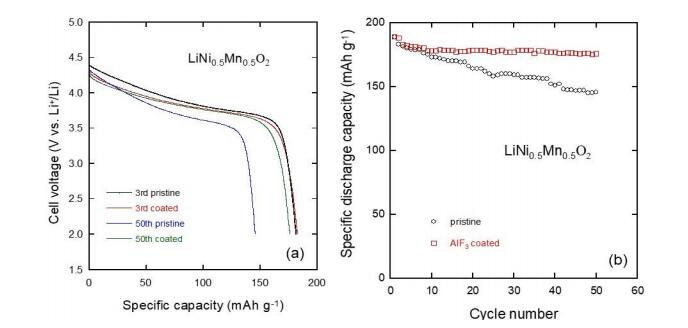
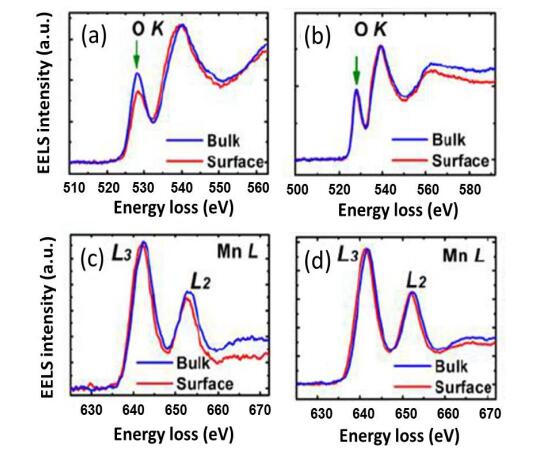
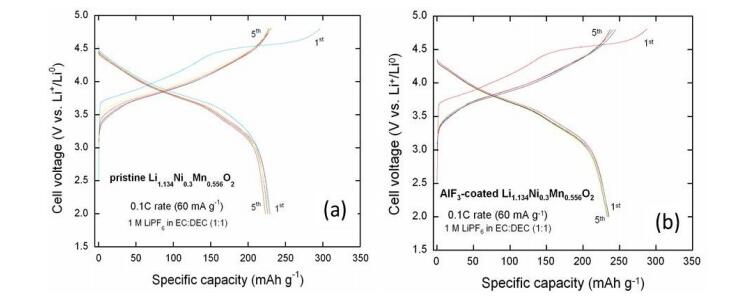
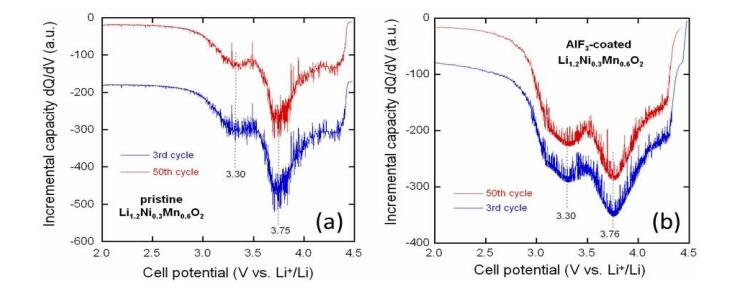
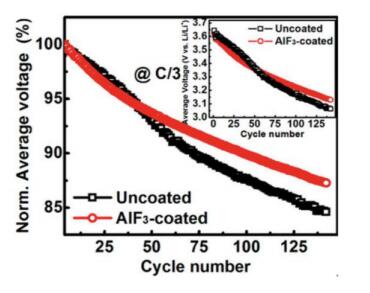
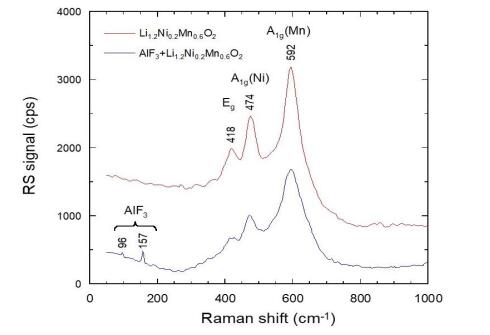
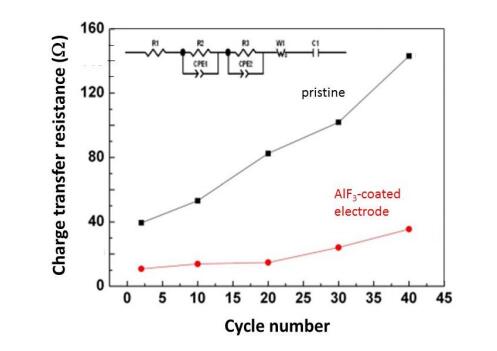
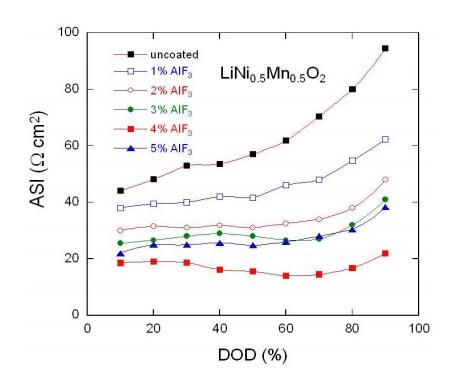
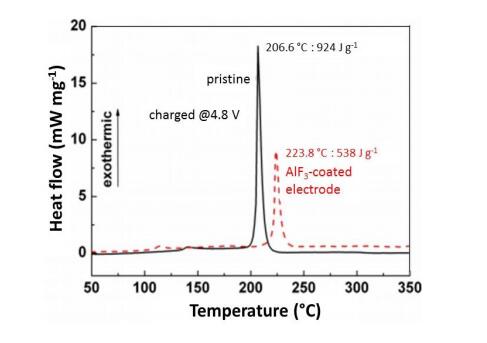
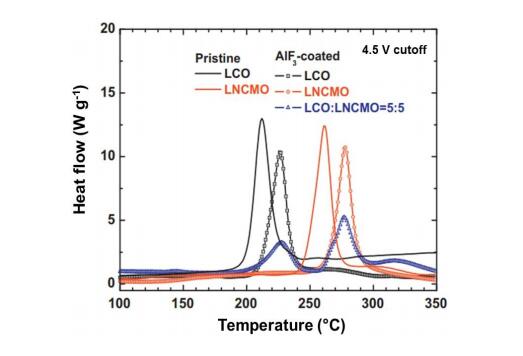
In response to the ever worsening of the environment by consumption of fossil fuels, energy storage systems like lithium-ion batteries that offer high energy efficiency have evoked a great interest as power sources from portable electronics to electric vehicles. However, the improvement of calendar and cycling life together with safety issues require sophisticated technology to prevent degradation mechanisms. The surface modification of the electrode materials is part of the solution. In this paper, the surface coverage of cathode materials by aluminum fluoride is reviewed. The effect of AlF3 coating on electrochemical performance is examined at various deposit amounts with a comparison of the capacity retention and cycling stability of the different systems proposed in the literature.
1.
Introduction
In any country, there are people who are going through a difficult life situation. This difficulty can have been caused by an epidemic [1], a natural disaster [2], a war [3]; however, one of the primary reasons for a hard life is poverty [4,5]. The scarcity of financial resources to get safe shelter, clean water, nutritious food, adequate sanitation, and medical relief can result in a life-threatening condition. In 2020, about 800 million people in the world faced hunger [6]. The recent COVID-19 pandemic pushed tens of millions of people into extreme poverty, by disrupting their livelihoods [7].
Fortunately, part of the poor population is supported by charitable foundations (such as non-governmental organizations and religious institutions) and philanthropists [8,9]. In fact, people help each other to overcome a critical moment by donating money, clothes, food, expertise, time. As a consequence, the resource differences among wealthy and underprivileged persons are decreased, at least slightly. In evolutionary terms, the practice of charity reduces the fitness differences of unrelated individuals [10,11].
Game theory has been a framework commonly used to study the emergence and persistence of collective cooperative behavior [12,13,14,15,16,17] (for reviews, see [18,19,20]). This theory assumes that the players are rational; that is, they play to maximize their own payoffs [21]. Therefore, they must be selfish and self-interested. A paradigmatic game usually employed in these studies is the prisoner's dilemma [22,23,24,25]. In its original single-trial version, mutual cooperation yields the highest collective payoff, but the highest individual payoff can only be obtained by defecting, which is considered the rational choice for both players [18,19,20,21,22,23,24,25]. Mutual defection, however, yields the second worst payoff for both players. Since real people tend to be more cooperative than theoretically predicted [12,26,27,28,29,30], modifications have been proposed in order to promote cooperation in the prisoner's dilemma. In the iterated version of this game, cooperation can be established via reciprocity [10,18,19,20,31]. In the spatial version, cooperation can be sustained by the topological structure of the social contact network [10,19,20,32]. Other variations take into account punishment for defection [33], memory of previous encounters [34], learning mechanisms [35], scale-free complex networks [36].
Donating is a particular type of cooperative behavior found in humans and other animals, such as bats and chimpanzees [10]. Studies on this behavior have also interested the business world. For instance, there are analyzes addressing the link between corporate financial performance and corporate philanthropy [37,38,39]. From the company perspective, the aims of the strategic philanthropy are concomitantly to generate social benefits and to promote the brand reputation, which can be converted into financial returns. Thus, altruism and capitalism can find win-win solutions.
There are several experimental [40,41,42] and theoretical [43,44,45] studies on charitable activities. For instance, there are studies about the social network supporting charity in New York City [46], about the optimal location of charity boxes for maximizing public donations [47], and about gamification of donation-based crowdfunding campaigns to improve the engagement of users [48]. Recently, investigations on charity were motivated by the COVID-19 pandemic [49,50,51]. A usual theoretical approach is to analyze a donor's utility function looking for an optimal solution [43,44,45]. In this article, the donation behavior is modeled by using game theory.
The prisoner's dilemma is not convenient for modeling altruistic interactions, even when such interactions are mainly motivated by self-interest. Hence, the spread of charitable practice is here investigated by using a new game-theoretical model. In the proposed model, the players are potential donors with two possible donation behaviors and the payoffs express the (tangible) psychological benefits of making (or not) a donation. This approach was not found in the literature. Our main goal is to determine how the percentage of donors is affected by the values of the model parameters.
The remainder of this article is organized as follows. In Section 2, the proposed model is described. In addition, the differences between this model and the prisoner's dilemma are stressed. In Section 3, the results obtained from computer simulations are presented. In Section 4, the practical implications of these results are discussed. These implications are especially important in times of crisis.
2.
The model
Consider a square lattice composed of n×n cells, in which each cell represents an individual. To prevent edge effects, the left and right edges are connected and the top and bottom edges are connected too; thus, a three-dimensional torus is formed from a two-dimensional lattice. Consider also that each individual contacts the eight surrounding neighbors (which is known as Moore neighborhood of unitary radius [52]). Since all N=n2 individuals in this social network are equivalent from a geographical point of view, their spatial locations are irrelevant. Despite its simplicity, this kind of connectivity pattern has been used in several theoretical works on epidemiology [53], game theory [54], and opinion dynamics [55], for instance.
Assume that each individual is a potential donor. In this society, there are two types of donors, denoted by I (from intrinsic) and E (from extrinsic). The percentage of I-individuals is p; hence, the percentage of E-individuals is 1−p. At each time step t, each potential benefactor can give (donate) or keep (not donate). These actions are denoted by G and K, respectively. In this study, the charitable cause (for instance, children's support, food distribution, homeless services) is not specified. The donated amount is also not stipulated; what matters here is only the practice of charity. The payoffs received by the individuals reflect their personal satisfaction as a consequence of their acts. In addition, the received payoffs are neither accumulated nor shared from one time step to the next.
In this model, I-individuals represent those who help others for pure altruism. They are intrinsically engaged in charitable activities in the sense that they are not influenced by the neighbors' actions. Their motivations come from internalized beliefs and values. Here, at each time step, each I-individual makes a donation with probability q. In other words, an I-individual plays G with probability q and K with probability 1−q, regardless the payoffs received by this individual or by the neighbors in previous time steps. If the donation is made, the I-individual receives the payoff Y; if not, the received payoff is X. It is assumed that Y>X, since an I-individual is happier when a donation is completed.
In this model, E-individuals make charitable donations to acquire social acceptance and prestige. They are extrinsically motivated in the sense that their actions are driven by peer pressure. Here, at each time step, each E-individual plays either G or K and becomes aware of the action chosen by each one of the eight neighbors. There are four possible combinations: (G,G), (G,K), (K,K), and (K,G). In each combination, the first letter denotes the action of this E-individual and the second letter denotes the action of a neighbor (which can be an E or an I-individual). Table 1 shows the payoffs of this charity game. As shown in this table, an E-individual receives R for (G,G), S for (G,K), P for (K,K), and T for (K,G). Since there are eight neighbors, each E-individual receives eight payoffs per time step. These eight payoffs are summed up. Then, at the time step t+1, each E-individual will play the same action of the neighbor who received the highest payoff in the time step t. This strategy is called copycat or "best takes all" rule. It was already used in other studies [32,56] and it is suitable in this model for E-individuals. In fact, as they are motivated by social pressure, it is natural to consider that they will imitate the better performing neighbor in the hope of increasing their prestige or avoiding social sanctions. The purpose of imitating successful behaviors is also supported by the economics literature [57,58].
For E-individuals, a positive reputation is built by doing charitable acts; hence, it is reasonable to assume that S>R>P>T. Thus, the highest payoff S is obtained when this E-individual donates and the neighbor does not; therefore, the worst payoff T refers to the opposite situation. The second highest payoff R is received when the E-individual and the neighbor simultaneously donate. The second lowest payoff P is received when both simultaneously do not donate. For simplicity, assume that Y=R and X=T; thus, the satisfaction scores of both types of donors are related.
The average number of donors at t=1 (the initial time step) is Npq, because only I-individuals play at t=1 (since E-individuals copy the most successful neighbor, they start to play at t=2, after I-individuals playing once). Therefore, p=0 or q=0 implies no donors for t≥2. In fact, if there is no I-individual (p=0) or all I-individuals never donate (q=0), then E-individuals will not donate too as time passes (recall that E-individuals are driven by peer pressure).
In this manuscript, numerical simulations are performed by varying N (the population size), p (the proportion of the two types of benefactors), q (the probability of I-individuals playing G), and Y (the highest payoff of an I-individual, which is equal to the payoff of an E-individual when such an E-individual and the neighbor donate). Throughout each numerical simulation, the actions of all individuals are simultaneously updated. The results obtained in these simulations are presented in the next section.
Before continuing, it is relevant to point out the differences between the charity game and the prisoner's dilemma. Observe that the inequality concerning the payoffs for E-individuals in the charity game shown in Table 1 is different from that found in the prisoner's dilemma [10,18,19,20,21,22,23,24,25,26,31,32,33,34,35,36,56]. In this dilemma, two individuals are arrested and accused of jointly committing a crime. The individuals are separately interrogated and each one can either remain silent or admit to committing the crime. The first action is usually denoted by C (from cooperation) and the second action by D (from defection). When the individual chooses C, the received payoff is either R or S, if the partner plays either C or D, respectively. When the individual chooses D, the received payoff is either T or P, if the partner plays either C or D, respectively. In this classic game, T>R>P>S (and 2R>T+S) [10,18,19,20,21,22,23,24,25,26,31,32,33,34,35,36,56]. Assume that the two suspects involved in the prisoner's dilemma can be replaced by two E-individuals in the charity game. In addition, assume that the actions C and D in the prisoner's dilemma respectively correspond to actions G and K in the charity game. Notice that, by comparing these two games side by side, they are not equivalent, because the highest and the lowest payoffs are switched; that is, for the proposed model S>R>P>T.
3.
Numerical results
Computer simulations were performed by taking X=T=−1, P=0, and S=6. They were run for 200 time steps. The goal is to investigate how the number of donors (individuals that play G) is affected by the values of N, p, q, and Y=R. In these simulations, N=1024 or 4096, p∈[0,1], q∈[0,1], and Y∈[0.5,5.0].
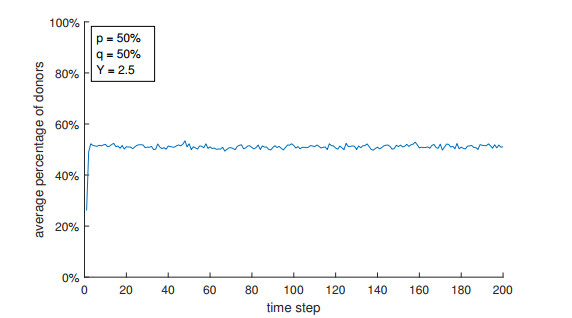
Figure 1 exhibits the time evolution of the percentage of donors δ for N=4096 (n=64), p=0.5, q=0.5, and Y=2.5. After a few time steps, this percentage fluctuates around 0.51±0.02. The average value of the percentage of donors, denoted by ˉδ, and the corresponding standard deviation, denoted by Δ, were computed by taking into account the last 150 time steps. Observe that, in the first time step, ˉδ=pq=0.25 (as mentioned in the previous section).
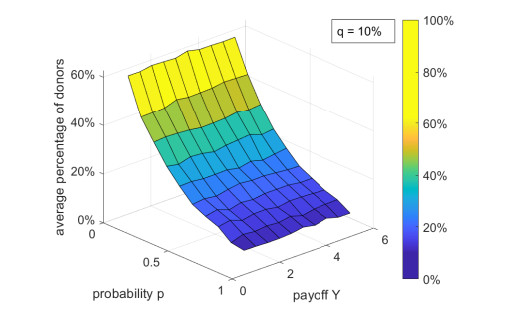
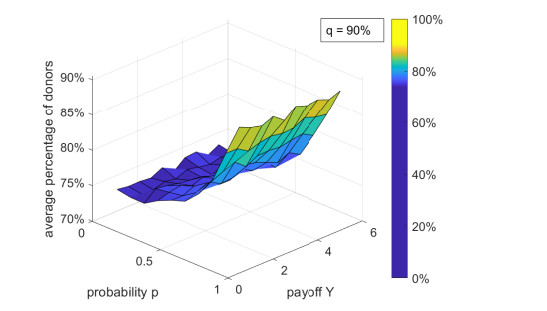
Figures 2 and 3 present the average percentage of donors ˉδ in function of p and Y for q=0.1 and q=0.9, respectively. In both figures, ˉδ is not significantly affected by Y; however, in Figure 2, ˉδ tends to decrease with p and, in Figureg 3, ˉδ tends to increase with p. In these plots, the standard deviation Δ (not shown in the Figures) decreases with p; for instance, in both plots, Δ=7% for p=0.1 and Δ=1% for p=0.9,
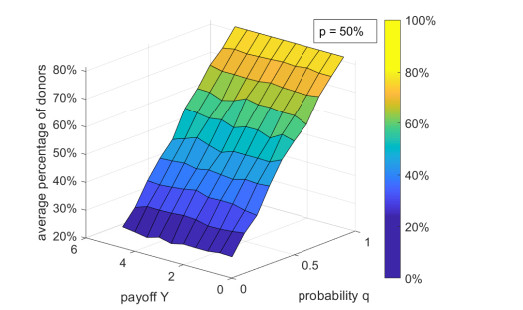
Figure 4 presents ˉδ in function of q for Y for p=0.5. This plot confirms that ˉδ does not significantly vary with Y and it increases with q. Also, Δ is not affected by Y and q. In this Figure, Δ=2% for all values of ˉδ.
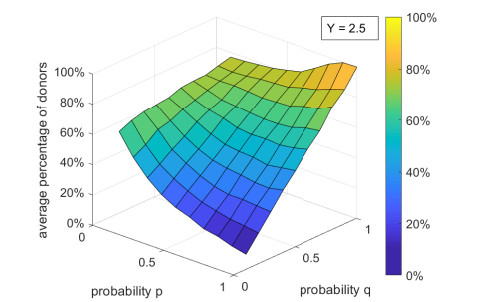
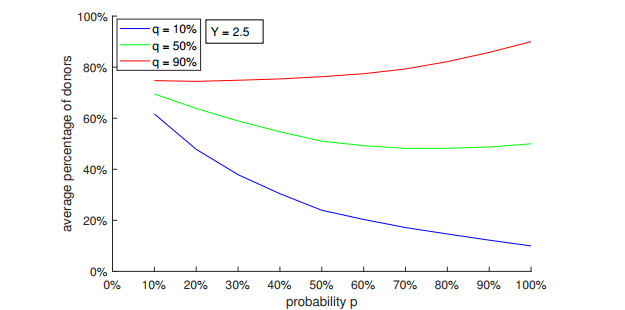
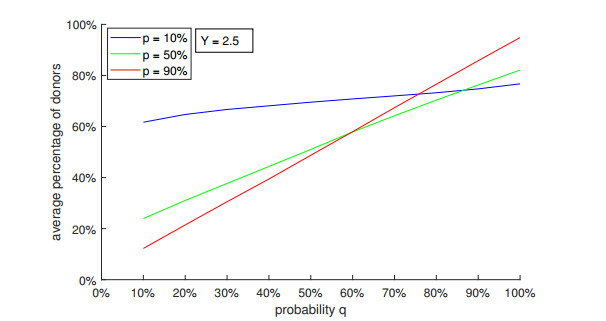
Figure 5 exhibits ˉδ in function of p for q for Y=2.5. In order to better understand this plot, two other figures were made: Figure 6 shows how ˉδ depends on p for Y=2.5 and q=0.1 (blue line), q=0.5 (green line), and q=0.9 (red line); and Figure 7 shows how ˉδ depends on q for Y=2.5 and p=0.1 (blue line), p=0.5 (green line), and p=0.9 (red line). Figures 5-7 confirm that ˉδ increases with q, but it can decrease or increase with p, depending on the value of q, as observed in Figures 2 and 3.
As already stated above, ˉδ does not vary with Y. For instance, by taking N=4096 and the other parameter values used in Figure 1, then ˉδ=0.51±0.02 for Y∈[0.5,5.0]. The simulations also show that values of ˉδ and Δ are not notably affected by changing the population size N. For instance, by taking N=1024 (instead of 4096) and the other parameter values used in Figure 1, the long-term percentage of donors is 0.52±0.02 (instead of 0.51±0.02).
These numerical results suggest that ˉδ can be analytically written in terms of p and q as:
In this expression, the first term is the average percentage of I-donors and the second term is an approximation for the average percentage of E-donors. Notice that the probability of an E-individual playing G is supposed to be given by pqH(p,q). Thus, this probability is null for p=0 or q=0, as mentioned in Section 2. The fitting function H(p,q) is here written as H(p,q)=∑Uu=0∑Vv=0αuvpuqv, in which U and V determine the order of this polynomial function and αuv are constants. The values of the constants αuv can be computed by using a least-squares method [59]. For instance, take U=2 and V=1. From the three plots shown in Figure 6, then H(p,q)=60−51q−136p+66pq+76p2. For p=0.5 and q=0.5, then H(0.5,0.5)=2 and, from Eq. (3.1), ˉδ(0.5,0.5)≃0.50, which is close to the average number of donors obtained in Figure 1.
4.
Discussion and conclusions
Common terms employed in studies on charitable attitudes are altruism, generosity, solidarity. Despite their differences, these terms are related to people making decisions that benefit strangers [10,28,60].
In the model proposed here, there is a fraction p of I-individuals that make heartfelt charity and a fraction 1−p of E-individuals that make self-interested charity. Also, I-individuals act according to a probabilistic rule and E-individuals act according to a deterministic rule. Hence, the higher the value of p, the lower the value of the standard deviation Δ.
Figures 2, 3, 5, and 6 show that for high values of q (that is, q>0.5), ˉδ increases with p (that is, with the proportion of I-individuals); for low values of q (that is, q<0.5), ˉδ decreases with p. Therefore, despite E-individuals making charitable donations for promoting themselves, their presence can increase ˉδ if the probability q of spontaneous donation for I-individuals is low. Thus, "impure" altruism can be as beneficial as "pure" altruism. Individuals who donate only for self-promotion can motivate others to making contributions for the same reason and, because of that, the number of donors increases.
Figures 4, 5, and 7 show that ˉδ increases with the probability q of I-individuals making donations. Thus, the pure altruism of I-individuals increases the number of donors, by stimulating E-individuals to engaging in charitable solicitations. Evidently, q=1 leads to the (optimal) scenario in which ˉδ is maximum (that is, ˉδ=1). In a real-world society, the value of q can be influenced by the current socioeconomic scenario (which impacts the financial situation of all individuals).
Figures 2–4 reveal that ˉδ is not significantly affected by the value of Y. The rationale behind this result is the following. I-individuals receive Y for donating; however, they do not donate for obtaining this payoff; E-individuals receive Y for simultaneous donations (by considering a neighbor); however, this is not the highest payoff available for them. Therefore, the payoff Y is either unimportant (for I-individuals) or unappealing (for E-individuals).
In short, despite E-individuals being motivated by self-interest, their behavior can positively affect the contributions to fundraising campaigns, especially when the chance of I-individuals making donations declines (which can occur, for instance, in times of economic crisis). By publicly acknowledging the donations of E-individuals, charitable foundations concurrently improve the reputation of these individuals and, more importantly, attract new donors.
Observe that Eq. (3.1) can be used to estimate the average number of donors Nˉδ in this simulated society from the values of p and q. The validity of this equation (and of the model itself) can be tested by using actual data. These data should also contain realistic values of the psychological payoffs, in order to derive an analytical expression for ˉδ(p,q) suitable for a real-world society. Such an expression could be used by charitable foundations to plan their activities.
The model proposed here is based on the assumptions that I-individuals randomize their choices and E-individuals inevitably copy the best neighbor. Variations of this model could consider that I-individuals follow a deterministic donation schedule and/or E-individuals are ruled by a probabilistic imitation dynamics. In fact, different profiles of donors can be taken into account in future studies.
Data availability
The data used to support the findings of this study are available from the first author upon request.
Acknowledgements
LHAM is partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) under the grant #302946/2022-5. This study was financed in part by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) - finance code 001.
Conflicts of interest
The authors declare that there are no conflicts of interest regarding the publication of this article.









 DownLoad:
DownLoad: