Analysis of the mechanisms of deformation of topocomposites by modeling of the indentation load-displacement curves

1.   Introduction

In order to calculate the hardness, elastic modulus, and a number of other mechanical characteristics in the surface layers of compact materials, instrumented indentation testing is widely used in tribological material science on the microscale and nanoscale levels ^[1].

The maximum insertion depth for a particular load, together with the slope of the unloading curve measured tangentially to the point of the maximum load, leads to the possibility of calculating both the hardness and the elastic modulus of the sample material. The authors of ^[2,3] proposed a method for analyzing the mechanics of the contact interaction of indenters having different shapes with the surface of an elastic perfectly plastic body, which allows one to calculate theoretically the load-displacement curves (indentation diagram) for a compact material, wherein the mechanical properties of both the sample and indenter are taken as input parameters. It is shown that in the case of an abrupt transition from elastic to plastic deformation, the loading phase of an instrumented indentation can be described by the following relationship

where s is the depth of indentation in the surface of the sample counted from the free surface, E^* is the combined elastic modulus, taking into account the elastic moduli of the material of the sample and that of the indenter, H is the hardness of the sample material, and α is the equivalent cone angle (70.3 degrees for a Berkovich indenter).

In the course of the unloading phase, the elastic recovery of the sample material is observed. The slope of the unloading curve at any point is called the contact stiffness. The contact stiffness in combination with the calculated area of real contact is used to determine the combined elastic modulus of the system ^[1], which includes the material under study and the indenter material.

Considering the contact of the indenter with a solid as an axially symmetric cone ^[3], the contact between the indenter and the elastic half-space can be described by the following expression

Here, just as under loading, there is a quadratic relationship between the load and the depth of indentation.

For topocomposites, measured hardness is the composite hardness that includes, to varying degrees, the hardnesses of the base and coating materials. To acquire intrinsic properties of thin films, it is necessary to know how mechanical properties of substrate affect the hardness measurement of thin films. The direct measurement of hardness of thin films is impossible by conventional micro-indentation because substrate participates in plastic deformation during an indentation process. In order to obtain "film-only" mechanical properties, a commonly used rule-of-thumb is to limit indentation depth to less than 10% of film thickness ^[3]. When the depth of indentation exceeds one-tenth of film thickness, the measured hardness H_c (composite hardness) includes the combined contribution of substrate and coating. To determine the true hardness of a film, it is necessary to separate these two contributions.

Common practice has transferred widely quoted rule-of-thumb has its basis in the determination of hardness testing is no real physical basis to the determination of elastic modulus for topocomposites ^[3]. The important result that measured elastic modulus E_c (effective modulus) by instrumented indentation testing, no matter how small the penetration depth, is a combined modulus of the film and substrate system. One approach to testing the effective modulus of elasticity is to determine the stiffness function of a heterogeneous material, which is found by solving the contact problem of introducing an axisymmetric stamp into a heterogeneous body. The result of this solution is to determine the relationship between the pressing force and the displacement of the indenter, or, more precisely, the value of the stiffness function as a derivation from them ^[4,5,6]. Another approach is to use a two-sided asymptotic method for solving the integral equation of the contact problem and splice the limiting expansions ^[7].

The author of ^[8] applied a two-sided asymptotic method for the equation of displacement of the surface of a two-layer half-space and splice obtained limiting expansions using the Pade two-point approximation method.

Such a methodical approach allowed us to obtain a mathematical model of the process of contact interaction of a rigid sphere with an elastic perfectly plastic two-layer half-space ^[9]. On the basis of the obtained mathematical model, it became possible to calculate the deformation-force parameters for a contact and a number of effective characteristics of a layered body in a wide range of coating thickness, the spherical indenter radius, and the elastic and plastic characteristics of materials that compose the layered body. In particular, an analytical relationship was obtained to determine the effective elastic modulus E_с and composite hardness H_c for the topocomposite surface through parameters characterizing the homogeneous elastic and plastic characteristics of substrate and coating:

where ${K_c} = \frac{1}{{{E_c}}}$ is the effective elastic characteristic (contact stiffness) of layered body; ${K_0} = \frac{{1 - \mu _0^2}}{{{E_0}}}$ and ${K_1} = \frac{{1 - \mu _1^2}}{{{E_1}}}$ are the elastic constants of substrate and coating materials, respectively; E₀, μ₀ and E₁, μ₁ are the elastic modulus and Poisson's ratio of substrate and coating materials, respectively; H₀ is the hardness of substrate; $\Phi$ and $\overline{\Phi}_{i}$ are the elastic-geometric and limit elastic-geometrical parameters, correspondingly.

The elastic-geometrical parameter $\Phi$ depends on geometrical ($h,s$) and elastic constants (K₀, K₁) of components of the topocomposite, where h is the thickness of coating, s is the penetration depth of pyramidal indenter, $K = \frac{{{K_1}}}{{{K_0}}}$. Parameter $\overline{\Phi}_{i}$ depends on geometrical ($h, s$), elastic constants (K₀, K₁) and hardness (${H_0}, {H_1}$) of components of the topocomposite, where H₀ and H₁ are the hardness of substrate and coating materials, respectively. The limit elastic-geometrical parameter $\overline{\Phi}_{i}$ are determined separately for three regions of existence of coating thickness, where i = Ⅰ, Ⅱ, Ⅲ. At small thickness $\overline{\Phi}_{\mathrm{I}} = (\Phi)^{3}$; at middle thickness $\overline{\Phi}_{\mathrm{II}} = \left(0.31 T_{k}^{-1}\right)^{2}(\Phi)^{3}$ and at big thickness $\overline{\Phi}_{\mathrm{III}} = (\Phi)^{3} \times Y^{2}$, where $Y = \frac{{{H_1}}}{{{H_0}}}$, ${T_k} = \frac{1}{2} \cdot \left[{\frac{3}{2} \cdot {{\left({1 + {{\bar h}^2}} \right)}^{ - 1}} - \left({1 + {\mu _0}} \right) \cdot \left({1 - \bar h \cdot arctg\left({\frac{1}{{\bar h}}} \right)} \right)} \right]$, $\bar h = \frac{h}{s}$, (see in more detail in ^[8,9]).

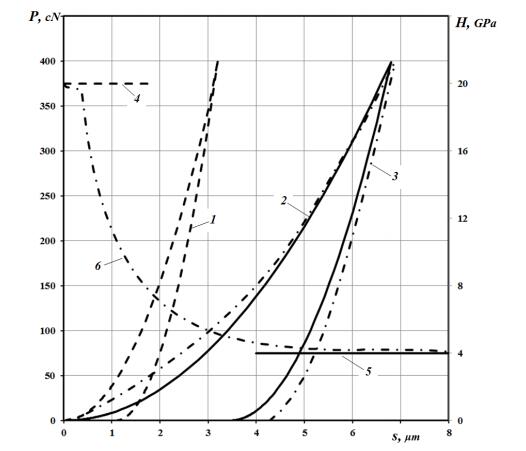
The analysis of the theoretical relationships obtained demonstrated that the hardness under indenting on the surface of the topocomposite over the entire depth of the surface layer with increasing penetration depth is characterized by the presence of three regions (Ⅰ, Ⅱ, Ⅲ) of the existence of the parameter investigated (Figure 1).

Figure 1.  Dependence of varying theoretical hardness of the two-layered elastic rigidly-plastically medium with parameters K = 0.5, Y = 3 on the implementation depth of the rigid four-sided pyramid and schematic representation of the character of the layered system deformation for some implementation depths.

DownLoad: Full-Size Img PowerPoint

The analysis of Eq 4 for changing the compositional hardness of the topocomposite showed that the first region (Ⅰ) characterizes the reaction to the indentation in the material of the surface layer (coating), the third region (Ⅲ) represents a reaction of the substrate material of the topocomposite, whereas the second region (Ⅱ) characterizes a complex reaction of the material coating and substrate material to the indentation. It is just the second region of the hardness depending on the depth of indentation that has been called "composite hardness" in the scientific literature and in the practice of studies of surfaces with thin coatings. Analysis of functional dependence of the hardness in the second sector from the implementation depth (Figure 1) shows that the hardness of the layered system is independence on the value of the plastic characteristic of the coating material, i.e., the hardness. Thus, the mechanism of deformation of the layered system in the second sector of the diagram of hardness is the elastic deformation of the coating material and plastic deformation of the substrate material. Equation 4 indicates that it describes a region Ⅱ of the diagram of hardness and may be reduced to the form

Theoretical indentation diagrams can serve as an effective tool for revealing deformation features inherent in real materials as a result of comparison between experimental indentation diagrams and indentation diagrams theoretically calculated according to experimentally determined mechanical properties. In developing surface hardening methods, especially in the preparation of surface coatings having a small thickness, but significantly different in the mechanical characteristics from the substrate material, an urgent problem consists in finding the analytical patterns of layered system deformation under instrumental indentation.

The aim of this work was a theoretical description of the diagram for instrumental indentation of materials with a topocomposite structure and analysis of the deformation processes into a layered body using knowledge about individual elastic and plastic characteristics of the materials as coating and so substrate.

2.   A solution of the problem

By using the above-mentioned Eqs 1, 3 and 4 (for the loading curve) and Eqs 2 and 3 (for the unloading curve), let us theoretically construct an indentation diagram for the case of indenting an ideal pyramidal indenter into an ideal single-layer topocomposite with known mechanical characteristics of the layered body components and with a known coating thickness. By an ideal single-layer topocomposite, we mean a surface-layered medium consisting of an elastic rigid-plastic coating coherently connected to an elastic rigid-plastic substrate. By an ideal pyramidal indenter, we mean a Berkovich rigid indenter with perfect shape with a sharp tip.

Using Eqs 1 and 2, let us theoretically construct indentation diagrams for the case of an ideal pyramidal indenter and compact materials such as a coating material and a substrate material, the mechanical characteristics of which correspond to those inherent in the topocomposite components.

Based on the analysis and comparison of energy consumption for the deformation of the topocomposite components and the topocomposite itself, let us determine the possibility of applying analytical expressions for the composite hardness (Eq 4) and the effective elastic modulus (Eq 3) of the topocomposite to derive analytical relationships describing the loading and unloading curves in the case of instrumental indentation in the topocomposite.

The loading curve of the topocomposite within region I can be constructed using Eq 1, wherein hardness parameter H takes the coating hardness values H₁, whereas parameter E^* uses the effective elastic modulus of topocomposite E_c, determined by Eq 3:

The loading curve of the topocomposite in region II can be constructed using Eq 1 as well, wherein the hardness parameter H possesses the values of the composite hardness H_с, determined by Eq 4, whereas as parameter E* uses the effective elastic modulus of topocomposite E_c, determined by Eq 3:

The coordinates of the inflection point are determined by the solving system of Eqs 6 and 7.

The unloading curve of the topocomposite can be constructed using Eq 2, wherein parameter E^* takes the effective elastic modulus of topocomposite E_c is used determined by Eq 3:

3.   Results and discussion

Let us take the following values of the parameters characterizing the conditions of theoretical instrumental indentation in an ideal topocomposite: the indenter is the ideal Berkovich pyramid; the coating material and substrate hardness is 4 GPa and 2 GPa, respectively; the elastic modulus of the coating material and the substrate is 500 GPa and 200 GPa, and the coating thickness is 5 μm. The first subscripts "c", "1" and "0" indicate the parameter belongs to the topocomposite, the coating material, and the substrate material, respectively. The second subscript indices "e" and "p" indicate the elastic and plastic deformation taken into account in the mentioned parameter, respectively.

Using Eqs 1–4, we construct the theoretical indentation load-displacement and hardness-displacement curves for the ideal coating material, substrate material, and the topocomposite (Figure 2).

Figure 2.  Indentation diagrams for coating (1), substrate (3) materials and topocomposite (2). Hardness-displacement curves (4, 5, 6) for substrate material, coating material, and topocomposite, respectively.

DownLoad: Full-Size Img PowerPoint

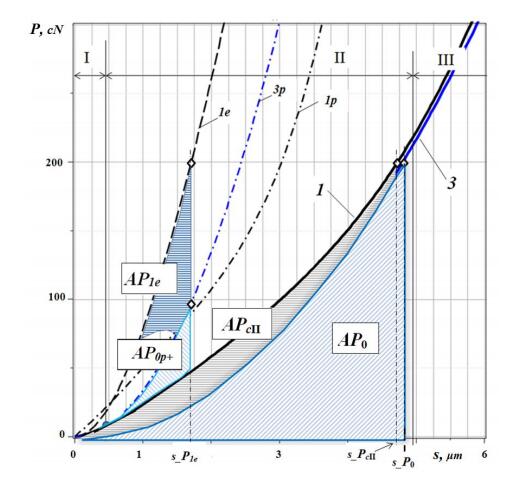
An important element of theoretical Eq 6 describing the loading curve for indentation in the topocomposite in region Ⅱ is the absence of the coating material hardness in the compositional hardness of the topocomposite H_c in region Ⅱ since the compositional hardness H_cII is calculated according to Eq 5. Using the method of comparing the work spent for the deformation of the topocomposite as a whole and the components of the topocomposite as individual compact materials; let us show that in the second region of topocomposite loading there is the elastoplastic deformation work for the substrate material and the elastic deformation work for the coating material (Figure 3)

Figure 3.  Elastoplastic deformation curves for a topocomposite and for the substrate (1, 3), elastic and plastic deformation curves for topocomposite (1е, 1р), and plastic deformation curves for the substrate (3р).

DownLoad: Full-Size Img PowerPoint

where АP_сII is the elastoplastic deformation work for the topocomposite in region Ⅱ, АP₀ is the elastoplastic deformation work for the substrate material, АP_1e is the elastic deformation work for the coating material, and АP_0p+ is the restraining plastic deformation work for the substrate material.

The calculation of the values of spent work under the indentation of the pyramid in the model topocomposite up to a load value of 200 cN and the estimate of the error in comparison with the total amount of energy spent for the deformation the of the layered system components have been carried out using the Maple 15 mathematical software package

The error does not exceed 3%.

The need to take into account the additional work of substrate material deformation, called here the work of restraint, arose from analyzing the results of studies given in ^[10] and connected with the calculations of the stress–strain state in solid materials under the indentation in blunt indenters having different shapes and of the deformation wave restraint around a stamp using a hard overlay. Restrained loading conditions lead to an increase in the intensity of deformation.

Returning to Eq 9 and considering the coating of the topocomposite as a surface rigid body, which restricts the plastic deformation of the substrate material of the topocomposite in the course of indentation, we can explain it by the occurrence of additional work within the course of instrumental indentation.

Thus, the proposed theoretical model of topocomposite deformation in the course of instrumental indentation in the second region describes reliably the physical picture of the topocomposite deformation in the second loading region, does not take into account the plastic properties of a coating and can serve as a methodological basis for analyzing the loading curve of the experimental indentation diagram.

4.   Conclusion

A technique is presented for obtaining theoretical analytical dependences describing the loading and unloading curves of instrumented indentation testing in surface-layered solid materials (topocomposites). A connection has been found between the theory of instrumental indentation in compact materials composing the topocomposite and the theoretical dependences proposed in this paper that describe the indentation diagram for topocomposites. The results obtained can be used to analyze experimental indentation diagrams obtained for hardened surfaces and surfaces with thin coatings. The phenomenon of additional plastic deformation of the base material of the topocomposite is established.

Acknowledgment

The research was supported by the Ministry of Education and Science, Project RFMEFI60717X0166 (Agreement No. 14.607.21.0166, dated 26.09.2017).

Conflict of interest

The author declares that there is no conflict of interests regarding the publication of this paper.