Two-dimensional implementation of the coarsening method for linear peridynamics

1.   Introduction

Peridynamics is a nonlocal continuum theory developed by Silling ^[1] with the objective of overcoming the shortcomings associated with the Classical Continuum theory particularly as it relates to the ability to model fracture and damage in materials. To achieve this objective, the equation of motion of the classical theory was cast in an integral form. This paved the way for the unification of the mathematical modelling of continuous media, fracture and particles in a single modelling framework. Thus, peridynamics provided a robust structure that can find application in situations involving evolution and propagation of discontinuities such as crack nucleation and growth using the same field equation as in the continuous case. Another feature of the Peridynamic formulation is that it is a nonlocal theory that incorporates the concept of long-range forces by allowing interaction of particles located at a finite distance from each other through a pairwise force field.

The peridynamic theory has extensively been investigated and is shown to have capabilities of modelling a wide range of engineering problems ^{[2,3,4,5,6,7,8,9,10]}. However, for certain problems, it suffers from the disadvantage of being computationally more expensive compared to the classical continuum theory which is attributable to its nonlocal formulation. In an effort to mitigate against this issue, researchers have proposed a number of multiscale modelling techniques. An adaptive refinement method was proposed in ^[11] for bond-based peridynamic problems involving a variable horizon. A peridynamic-based framework for hierarchical multiscale modelling was proposed in ^[12] that couples molecular dynamics and peridynamics. These techniques allow coupling of models at different scales for effective inter-scale information transfer. A coarsening method was also proposed in ^[13]. The key idea of the coarsening method is to obtain accurate results by solving a reduced order model. The reduction in the order of model is achieved by substituting a detailed model with a surrogate model with fewer degrees of freedom. The objective of this study is to extend the application of a coarsening method for linear peridynamics proposed in ^[13] for two-dimensional analysis. Moreover, the existing one-dimensional coarsening method was further explored by considering different micromodulus functions other than that considered in ^[14].

2.   Peridynamics

Recalling from the classical continuum theory, the equation of motion of a medium arising from conservation of momentum is as follows:

where ρ is the mass density of the medium, σ is the stress tensor, b is a vector of body force density, ü is the acceleration vector field of the material point x within the medium at time t. The key challenge in using Eq 1 to model discontinuous system behaviour is the presence of the divergence operator, which implies the existence of the spatial derivative of the stress field and consequently the displacement field within the domain of interest. However, since these field variables are not continuous over features such as crack tip and crack surfaces, the derivatives in such instance are undefined. In the peridynamic formulation, the equation of motion was casted such that the integral operators replaced the derivatives on the right hand side of Eq 1. A "bond-based" peridynamic equation of motion was originally proposed by Silling ^[1] as

where u is the displacement vector field, ${{\mathcal{H}} _\boldsymbol{x}}$ is the neighbourhood of the particle located at point x. f is the pairwise force function with a unit of force per unit volume squared that a particle located at point q exerts on a particle located at point x.

2.1.   Micromodulus function for linear peridynamics

If we assume a linear material behaviour, then the pairwise force function ^[1] takes the form

where C(ξ) is a tensor valued function called the micromodulus function given by

ξ = q-x is the relative position of the particles in the reference configuration, and η = u(q, t)-u(x, t) is their relative displacement. The peridynamic equation of motion (Eq 2) therefore specialises to

The micromodulus function C(ξ) is required to satisfy certain properties ^[1]. Moreover, the range of admissible functions that can be used is extensive ^[14]. However, only a few of them will be discussed here.

The first sets of examples of the micromodulus functions to be given belong to a class of materials called microelastic materials. A peridynamic material is said to be microelastic if the pairwise force function, f, is derived from a scalar micropotential, w:

The micropotential, w is the energy of a single bond and represents a local strain energy density ^[2] which is given by

where the stretch, s can be defined as

From Eqs 7 and 8, Eq 6 becomes

where $c\left({\left| \xi \right|} \right)$ is a function that is characteristic of the material and is called the bond constant. Differentiating Eq 9 with respect to η and assuming small displacements yields

for two-dimensional configurations. For one-dimensional configurations, Eq 10 specialises to

In order to determine the bond constants for microelastic materials, the strain energy density of a given point can be defined ^[2] as

2.2.1.   One-dimensional micromodulus

Let δ be the radius of the influence domain or horizon that is characteristic of the material. Then, using Eq 7 and assuming a one-dimensional problem, the peridynamic strain energy density of a material point becomes

If we assume $c\left({\left| \xi \right|} \right)$ to be independent of bond length, i.e., $c\left({\left| \xi \right|} \right) = {c_0}$, then Eq 13 can be written for constant stretch for all bonds as

For the same condition, the strain energy density from classical continuum theory can be written as

Equating Eqs 14 and 15 yields

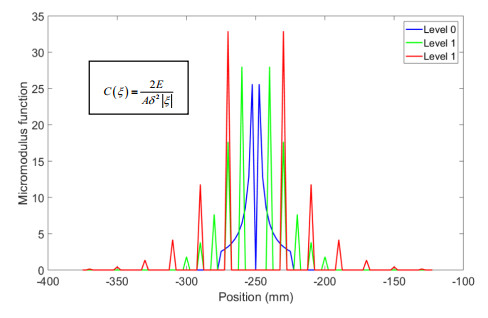
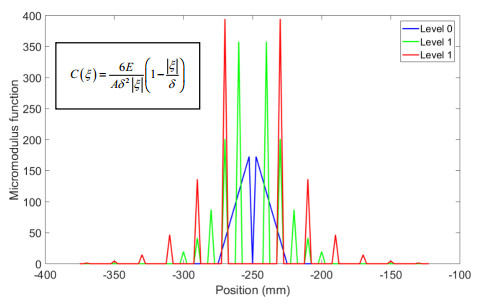
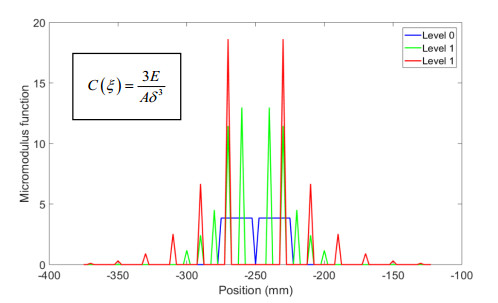
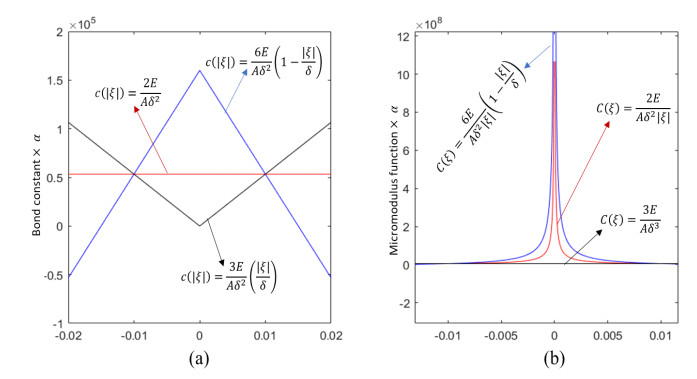
Hence, the micromodulus function for this material is

In the case where $c\left({\left| \xi \right|} \right)$ is dependent on the bond length and assumed to have a triangular profile, i.e., $c\left({\left| \xi \right|} \right) = {c_1}\left({1 - \frac{{\left| \xi \right|}}{\delta }} \right)$, then Eq 13 becomes

Equating Eq 18 with Eq 15 gives

The micromodulus function in this case is

In the case where the dependency of $c\left({\left| \xi \right|} \right)$ is in the form of an inverted triangular profile ^[3], in which case, bonds closer to the principal point are softer than bonds further away from it, such that, $c(|ξ|) = c_2 (|ξ|/δ)$ for bonds within the horizon. In this case, Eq 13 becomes

Equating Eq 21 with Eq 15 gives

The micromodulus function for this scenario then becomes

Notice that the micromodulus function in this case is a constant function. Figure 1a shows a plot of the three different bond constants as functions of α while Figure 1b is a plot of the corresponding micromodulus functions as functions of α, where $\alpha = E/6A$.

2.1.2.   Two-dimensional micromodulus

In the two-dimensional case, let δ be the radius of sphere ${\mathcal{H}}$ describing the horizon. Then, the two-dimensional equivalence of the micromodulus Eqs 17, 20 and 23 are respectively given as

Notice that Eq 26 unlike its one-dimensional counterpart is not a constant function.

3.   Coarsening method

The goal of the coarsening method is to provide a multiscale framework based on peridynamic theory that will predict macroscale response of a medium based on the underlying evolving microstructure, without necessarily resolving all microstructural details. This is achieved by a process of successive elimination of points from the medium called coarsening. Each successive coarsening results in a medium with a reduced material points as well as reduced level of geometrical detail. However, the properties of the coarsened medium are determined such that the effects of the excluded material points are implicitly included in the coarsened level simulation. The coarsening formulation presented here is adapted from ^[14] for the completeness of the paper.

3.1.   Peridynamic coarsening formulation

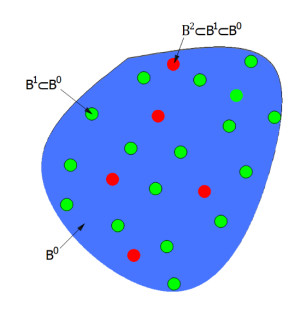
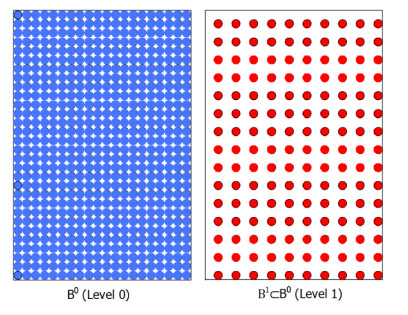
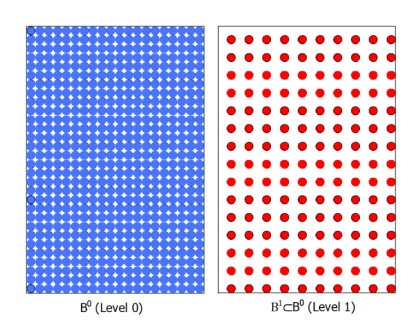
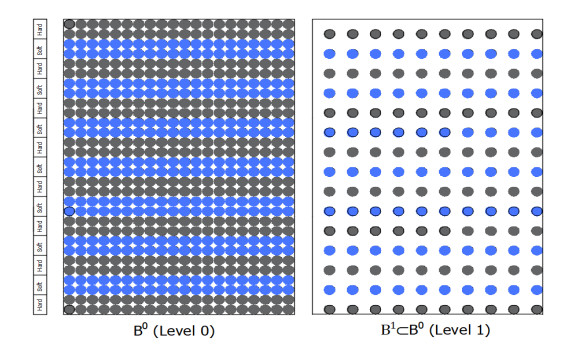
To coarsen a detailed model as proposed in ^[13], let ${\mathcal{B}}^0$ be a linear elastic peridynamic body as shown in Figure 2. Let ${\mathcal{A}}^0$ be the set of linear admissible displacement fields on ${\mathcal{B}}^0$, and let C⁰:${\mathcal{B}}^0$×${\mathcal{B}}^0$→$\ell$ be the micromodulus tensor associated with the material of the body where ${\mathcal{L}}$ is the set of all second order tensors. Assume r⁰ is a positive number that represents the maximum interaction distance for all points in ${\mathcal{B}}^0$, such that if

Let ${\mathcal{B}}^1$⊂${\mathcal{B}}^0$, and let ${\mathcal{A}}^1$ represent the set of admissible displacement fields on ${\mathcal{B}}^1$. ${\mathcal{B}}^0$ and ${\mathcal{B}}^1$ are called level 0 and level 1 body, respectively. The objective of this coarsening process is to express the internal forces acting on ${\mathcal{B}}^1$ in terms of its own displacements only while implicitly accounting for forces points in ${\mathcal{B}}^0$-${\mathcal{B}}^1$ exert on ${\mathcal{B}}^1$. To achieve this objective, let x be an arbitrary point in ${\mathcal{B}}^1$ and let δ¹ be a positive number. Let ${\mathcal{H}}_\bf{x}^1$ be the closed neighbourhood of x in ${\mathcal{B}}^0$ with radius r¹

Let ${\mathcal{R}}_\bf{x}^1$ = ${\mathcal{H}}_\bf{x}^1$∩${\mathcal{B}}^1$. Suppose u¹∈${\mathcal{A}}^1$ is given and let u⁰∈${\mathcal{A}}^0$ satisfy the compatibility condition

Outside of ${\mathcal{R}}_\bf{x}^1$, assume that u⁰ satisfies the equilibrium condition, neglecting interactions between ${\mathcal{H}}_\bf{x}^1$ and its exterior:

where

Also, assume that there is no body force density applied outside ${\mathcal{R}}_\bf{x}^1$

Further assume that for a given displacement field u¹ Eqs 29 and 30 have a unique solution u⁰ on ${\mathcal{H}}_\bf{x}^1$, and let S_x^{0, 1} be the resolvent kernel that generates this solution:

From Eqs 29 and 33, we can infer that

where $\mathbb{I}$ is the isotropic tensor and ∆ is the three dimensional Dirac delta function. For the special case where u⁰ represents a linear rigid translation of points in ${\mathcal{R}}_\bf{x}^1$ through an arbitrary displacement u, then all points in ${\mathcal{H}}_\bf{x}^1$-${\mathcal{R}}_\bf{x}^1$ will also translate by u. Therefore, from Eq 33, we see that

from which we can obtain the following identity

Subtracting u⁰(z) from both sides of Eq 33 and using the identity given in Eq 36, we can obtain

Substituting this result in Eq 31 yields

Reversing the order of integration and rearranging gives

Recalling that x is an arbitrary point in ${\mathcal{B}}^1$, if we denote the force density in any such choice of x by

Then, from Eqs 39 and 40 we can obtain

where the coarsened micromodulus in level 1 C¹: ${\mathcal{B}}^1$×${\mathcal{B}}^1$ is defined by

Similarly, for any level m in the coarsening process, the force density can be obtained from

where the coarsened micromodulus in level m, C^m: ${\mathcal{B}}^m$×${\mathcal{B}}^m$ is defined by

3.2.   Discretization of the coarsening method

To carry out the numerical implementation of the coarsening method described in the preceding section, ${\mathcal{B}}^0$ is discretised into nodes, which for simplicity are taken to have equal volume v. Let x_i be the position of node i in level m_i. For any nodes i and j, let

The coarsened micromodulus ${\bf{C}}_{_{\mathit{\boldsymbol{i, j}}}}^1$ is obtained by discretizing Eq 42 as

To evaluate Eq 46, the resolvent kernel ${\bf{S}}_{_{\mathit{\boldsymbol{k, j}}}}^{^{{\bf{0}},{\rm{ }}{\bf{1}}}}$ needs to be determined. A convenient means of obtaining the kernel function was proposed in ^[13]. Successive coarsening to higher levels can be achieved by following the same procedure as above, so that for any m≥1,

To compute the coarsened micromodulus at level m for node i, the resolvent kernel $\bf{S}_{k, j}^{m-1, m}$ must be determined. A method was suggested in ^[13] for determining the resolvent kernel. This method proceeds by creating and merging two sub-systems of equations into a global system of equations. To create such a system, two vectors {u⁰} representing the displacement field in the level 0 body and {u¹} representing the displacement field in level 1 body are defined. The relationship between these two displacement fields is formulated as follows:

The displacement fields u_i⁰ and u_i¹ for nodes in level 1 body are constrained to satisfy Eq 29:

The second system of equations is obtained by ensuring that the nodes complementary to nodes in level 1 body ${\mathcal{H}}_{x}^1$-${\mathcal{R}}_{x}^1$ satisfy Eqs 30, 31 and 32. Concatenation of these two systems of equations results in a global system of equations that has the following form in one dimension:

where R is the number of nodes in ${\mathcal{R}}_{x}^1$, N is the number of nodes in ${\mathcal{H}}_{x}^1$ and the diagonal elements P_i are given by

In shorthand notation, Eq 49 can be written as

where [A] is N×N square matrix in one-dimension and 2N×2N in two-dimensions. Let [A]^-1 be the inverse of [A], [S^{0, 1}] in one-dimension will be the leftmost R columns of [A]^-1. In two-dimensions, [S^{0, 1}] is the leftmost 2R columns of [A]^-1.

4.   Coarsening the micromodulus function

In this section, the coarsened form of various micromodulus functions will be presented. One-dimensional cases will be followed by a two dimensional case.

4.1.   Coarsening of one-dimensional micromodulus functions

The one-dimensional problem is a homogeneous bar with a length of 1 m. The elastic modulus of the material is assumed to be 200 GPa. Three scenarios will be investigated by considering the following micromodulus functions:

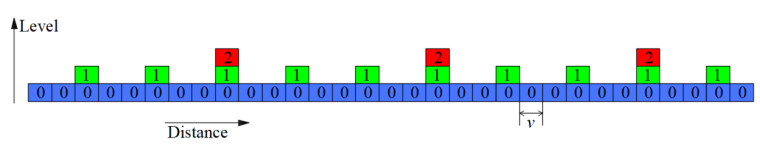
The level 0 horizon is specified as δ⁰ = 25 mm. Note that this same horizon will be used in the coarsened models. The bar is discretized into 400 nodes with spacing ∆x = 2.5 mm. Coarsening of the detailed model to the level 1 body is carried out by retaining every fourth node of the level 0 body. Similarly, coarsening of the level 1 body to the level 2 body proceeds by retaining every second node in the level 1 body. Figure 3 shows a schematic representation of the coarsening process. The micromodulus of the detailed model (level 0) C⁰ as well as the coarsened micromodulus C¹ and C² for the three scenarios are shown in Figures 4 to 6 These curves are characterized by sharp peaks consistent with the fact that the coarsened micromodulus functions are defined only at their respective coarsened regions.

4.2.   Coarsening of two-dimensional micromodulus function

The two-dimensional problem is a 500×500 mm square plate with a thickness of 50 mm. Let the elastic modulus of the plate to be 200 GPa and its micromodulus function is given by

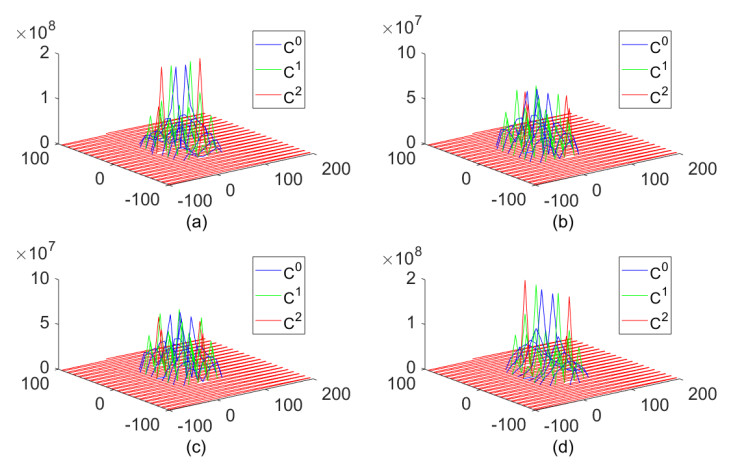
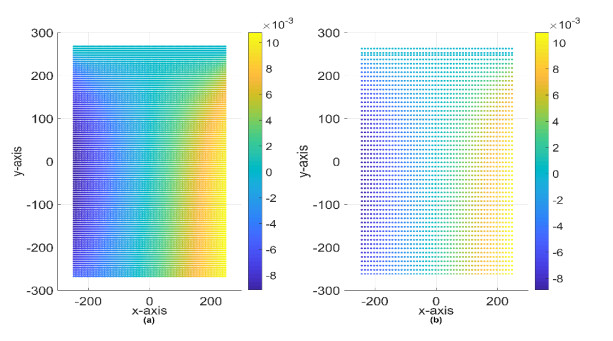
Coarsening is carried out as shown schematically in Figure 7. Every second node in every second row of the level 0 model is retained in the coarsened level 1 model. Similarly, every second node in the second row of level 1 is retained in level 2 body. Figure 8 shows the micromodulus function C⁰ of the level 0 model as well as the coarsened micromodulus C¹ of the level 1 model. It is noticed that the coarsened micromodulus C¹ is characterised by sharp peaks which is a reflection of the fact that it is only defined at the coarsened region. Figure 8a shows the response of the i-th material point in the x-direction for a displacement of the j-th point in the x-direction. Figure 8b shows the response of the i-th material point in the x-direction if the j-th point is displaced in the y-direction. Figure 8c shows the response in the y-direction of the i-th point when the j-th point displaces in the x-direction. Finally, Figure 8d shows the response of the i-th point in the y-direction when the j-th point is displaced in the y-direction.

5.   Numerical results

This section comprises five numerical experiments to illustrate the application of the coarsening method in solving solid mechanics problems. The systems are assumed to be in a state of static equilibrium and thus an implicit static solution scheme has been utilized. The first three examples focus a one-dimensional bar under tension loading cases for homogeneous and composite materials with and/or without defect. The last two examples demonstrate the capability of the coarsening approach for two dimensional plate problems for isotropic and composite materials.

5.1.   One-dimensional homogeneous bar under tension loading

This example is a numerical experiment aimed at illustrating the capability of the coarsening method in capturing the correct bulk behaviour of a system even with reduced degrees of freedom as opposed to if the degrees of freedom were to be reduced without the coarsening process. Consider a bar of length 1 m of material having a micromodulus function of the form:

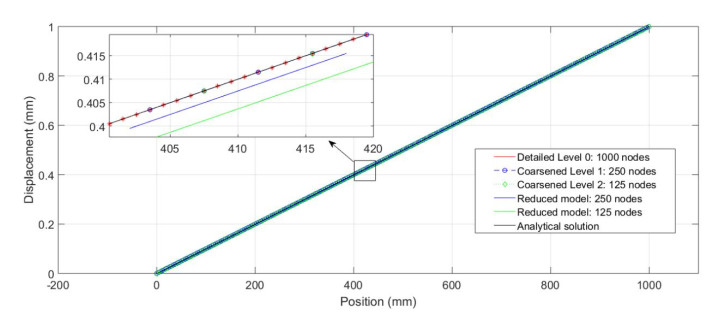
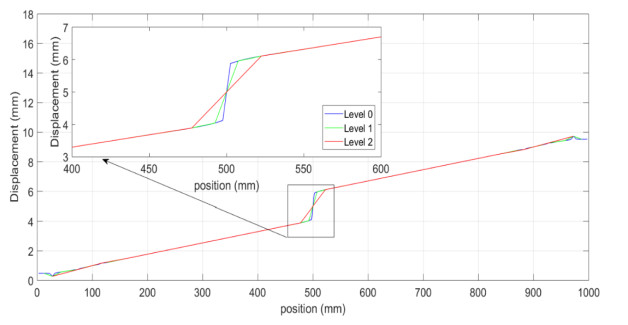
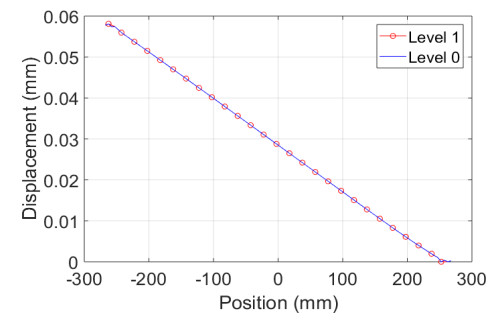
The maximum interaction distance δ = 10∆x, where ∆x is the length of a material point. The detailed model (level 0) is discretised into 1000 points, so that ∆x = 1 mm. The elastic modulus of the material is E = 200 GPa. Coarsening of the level 0 model to level 1 proceeds by retaining every fourth node in level 0. Level 2 model retains every second node in level 1 model as shown in Figure 3. A body force density of b = 200 $N/m{{m}^{3}}$ is applied to the rightmost level 2 node, while the third leftmost level 2 node is constrained to have zero displacement. The displacement field associated with the level 0 and coarsened levels 1 and 2 are shown in Figure 9. It is observed that even with reduced degrees of freedom as the detailed model is coarsened into level 1 and subsequently level 2, the displacement fields obtained from all these models are very similar to each other. This would not have been the case if the reduction in degrees of freedom were not achieved through the coarsening process.

The analytical solution based on the classical theory to the axial bar problem is of the form

where x is the distance from the support, u(x) is the displacement at point x, E is the elastic modulus, A is the cross sectional area, and F is the force applied at the free end of the bar. The result from the analytical model and those from the detail level 0 model as well as the results from coarsened levels 1 and 2 model are almost identical.

To illustrate the need for the coarsening process in achieving model order reduction, the number of nodes was reduced from 1000 to 250 and further to 125 without following the coarsening procedure. As shown in Figure 9, although the results from the coarsened models and the results from the models with reduced number of nodes are very close to each other, coarsened model results agree better with the analytical solution.

5.2.   One-dimensional composite bar under tension loading

In this example, a one-dimensional composite bar with a length of 1m and a cross-sectional area of 100 mm² is considered. The composite bar has a periodic microstructure consisting of alternating strips S_hard and S_soft of the hard and the soft materials, respectively. Each strip is 50 mm in length. The horizon for both hard and soft section is 50 mm. The micromodulus of the composite system has the form:

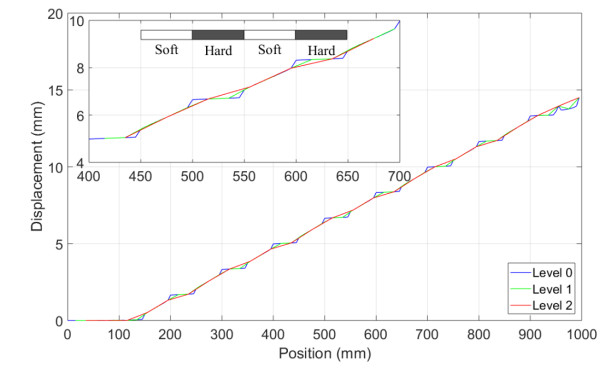
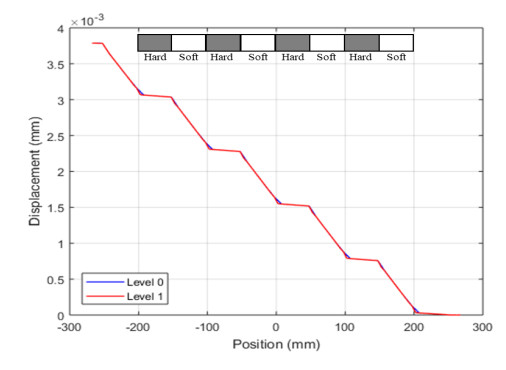
In other words, bonds with both ends in hard strip have hard properties while bonds with either ends in soft strip have soft properties. The elastic moduli of the hard and soft materials are E₁ = 200 GPa and E₂ = 9 GPa, respectively. The level 0 horizon is specified as δ⁰ = 10∆x. Coarsening from the level 0 to the level 1 body is carried out as shown in Figure 3 by retaining every fourth node of the level 0 body. Similarly, the level 1 body is coarsened to level 2 body by retaining every second node in the level 1 body.

A body force density of b = 0.001 $N/m{{m}^{3}}$ is applied to the three rightmost level 2 nodes, while the three leftmost level 2 nodes are constrained to have zero displacement. The computed displacements of coarsened level 0, 1 and 2 are shown in Figure 10. As expected, computation from the level 0 revealed the most detailed microstructural information. As the computational regions get coarsened, these microstructural details get smoothed out. However, both detailed and coarsened models have similar global stretch. This demonstrates the fact that the effective properties produced by the coarsening process accurately reflect the bulk properties of the composite.

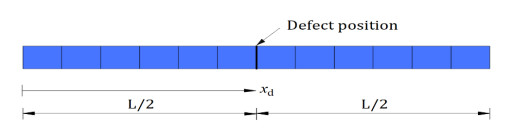
5.3.   One-dimensional homogeneous bar with a defect

This example considers a homogeneous bar with a defect. The bar has a length of 1 m. The constitutive model of the bar is given by

where φ is a degrading term given by

The horizon is specified as δ⁰ = 50 mm in the level 0 and the bar is discretised into 200 nodes. The defect is located at the center of the bar as shown in Figure 11. The level 1 contains every third node in the level 0 and similarly, the level 2 contains every third node of the level 1 as shown in Figure 12. Prescribed displacement boundary conditions are applied to the three leftmost and three rightmost level 2 nodes. The values of the prescribed displacements are given by $u_{i}^{0} = u_{i}^{1} = u_{i}^{2} = 0.01{{x}_{i}}$, where x_i is the coordinate of the node.

The displacement fields for the level 0 model as well as the coarsened level 1 and level 2 models near the defect are shown in Figure 13. The three levels give identical displacement profile except for close to the site of the defect. This reflects the fact that due to fewer nodes in the coarsened models, wider spacing exits between nodes.

5.4.   Two-dimensional homogeneous plate under tension loading

This example concerns a two-dimensional homogeneous plate under tension loading. The plate is a 500 mm×500 mm square plate. The micromodulus of the plate is chosen as

The horizon for the level 0 body is specied as δ⁰ = 3.015∆x. The plate is discretised into 200 points in both x and y-directions with every point having ∆x = ∆y = 2.5 mm. The thickness of the plate is ∆x. Coarsening of the detailed model is achieved by retaining every second point in the second row as shown schematically in Figure 14.

Two boundary layers each consisting of one grid of 100 points are created; one along the top edge and the other along the bottom edge. At the top boundary layer, every second point of the detailed model is constrained to have zero displacement. A body force density of 2000 $N/m{{m}^{3}}$ is applied to every second point in the bottom boundary layer in the detailed model.

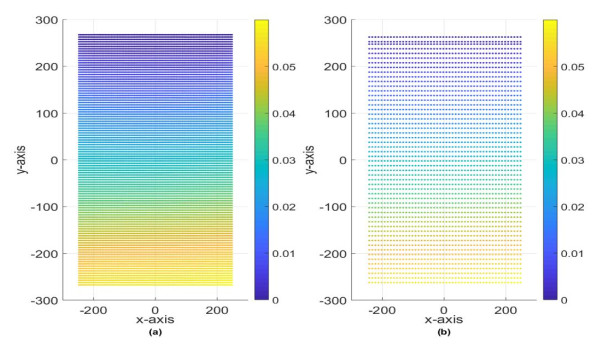
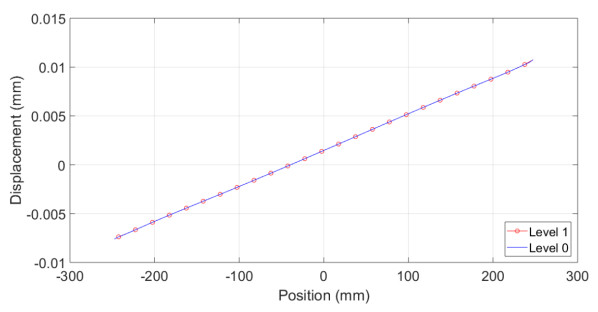
The displacement field obtained from solving both a detailed (level 0) and the coarsened model (level 1) are similar as can be seen from Figure 15 and Figure 16. The displacement profile of a specific grid of points along the y-axis and x-axis are plotted and shown in Figure 17 and Figure 18 respectively. It is observed that both models result in very similar displacement fields.

5.5.   Two-dimensional composite plate under tension loading

This example will consider a two-dimensional 500 mm×500 mm square plate with periodic microstructure consisting of alternative strips S_hard and S_soft of hard and soft materials, respectively as shown in Figure 19. Each strip is 50 mm in length. The horizon for both hard and soft sections is 50 mm. The micromodulus of the composite system is given by

The horizon is specified as δ⁰ = 3.015∆x. The plate is discretized into 200 points in both x and y-directions with every point having ∆x = ∆y = 2.5 mm. Coarsening of the detailed model and the applied boundary condition is same as that of previous example.

The computed displacement profile along the y-direction for the identical boundary condition for the detailed model (level 0) and the coarsened model (level 1) is shown in Figure 20. It is observed that because the detailed model included more material points, it has been able to resolve more microstructural details than the coarsened models. However, both models have the same global stretch thereby demonstrating that the effective properties obtained using this coarsening method is an accurate representation of the bulk properties of the composite.

6.   Computational cost

Determination of computational cost savings arising from coarsening a numerical model will follow from the idea suggested in ^[1]. Consider a body that is discretized into N₀ nodes in the level 0 model. Let $J = aN_{M}^{p}$ be the number of arithmetic operations used by a linear solver to solve the fully coarsened level M model, where a and p are constants (n = 3 for Gaussian elimination ^[1]), and N_M is the total number of nodes in level M model. Suppose each level has $1/\alpha$ as many nodes as the previous level, where α is a constant, such that

where D is the dimension of the problem (In the example on two dimensional homogeneous plate, α = 2 and D = 2).

The computational effort in determining material properties at level m+1 from level m is proportional to N_m since in doing so, the inverse of the matrix ${{A}_{{{N}_{m}}\times {{N}_{m}}}}$ has to be computed. Therefore, for some positive constant b, the total arithmetic operations that will be used to coarsen a numerical model and solve the fully coarsened level M model can be written as

It can be concluded from Eq 64 that the computational effort of coarsening up to level M in a linear solver for a boundary value problem is reduced by a factor of α^nDM over the computational effort needed to solve the detailed level 0 model. For a two-dimensional problem such as the example on two-dimensional homogeneous plate, this factor will be 2^3×2×M = 2^6M. The computational price paid to determine the coarsened properties of the model is less than $b{{N}_{0}}\alpha /\left(\alpha -1 \right)$ which is independent of M.

7.   Conclusions

The coarsening method developed in ^[13] extended for two-dimensional application in this work has demonstrated its robustness in modelling a range of problems. Moreover, several one-dimensional problems were considered to investigate the effect of different micromodulus functions other than considered in ^[14]. The examples solved in this work have demonstrated that this method is able to relate the bulk behaviour of materials to the details of their microstructure in two-dimensional problems. This allows us to reduce the order of the problem without losing accuracy in predicting the bulk response of the system. This translates to a reduction in computational time and storage required. Another advantage offered by the coarsening method is that the model retains its attributes such as boundary conditions and applied force density after the coarsening process. This is not the case if the model is reduced without going through the coarsening process. In this case, the boundary conditions and applied force density can no longer be identically applied as in the original model.

It is instructive to mention a number of caveats related to this method. This coarsening method is currently valid only for linear and static problems. This limitation is a consequence of assumption made in obtaining Eq 30.

Acknowledgments

The first author is supported by the government of the federal republic of Nigeria through the Petroleum Technology Development Fund (PTDF).

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this manuscript.