Citation: Kai Lu, Yinsheng Li. Fatigue crack growth calculations for two adjacent surface cracks using combination rules in fitness-for-service codes[J]. AIMS Materials Science, 2017, 4(2): 439-451. doi: 10.3934/matersci.2017.2.439
| [1] | Genshichiro Katsumata, Valéry Lacroix, Yinsheng Li . Effect of interaction of embedded crack and free surface on remaining fatigue life. AIMS Materials Science, 2016, 3(4): 1748-1758. doi: 10.3934/matersci.2016.4.1748 |
| [2] | Jian-Feng Wen, Yong Zhan, Shan-Tung Tu, Fu-Zhen Xuan . A combination rule for multiple surface cracks based on fatigue crack growth life. AIMS Materials Science, 2016, 3(4): 1649-1664. doi: 10.3934/matersci.2016.4.1649 |
| [3] | Masanori Kikuchi . Study on multiple surface crack growth and coalescence behaviors. AIMS Materials Science, 2016, 3(4): 1623-1631. doi: 10.3934/matersci.2016.4.1623 |
| [4] | Pierre Dulieu, Valéry Lacroix . Mutual interaction of stress concentration and stress intensity factor between semi-circular notch and crack. AIMS Materials Science, 2016, 3(4): 1520-1533. doi: 10.3934/matersci.2016.4.1520 |
| [5] | Mordechai Perl, Qin Ma, Cesar Levy . The influence of a non-aligned semi-elliptical surface crack on a quarter-circle corner crack in an infinitely large plate under uniaxial tension. AIMS Materials Science, 2016, 3(4): 1474-1492. doi: 10.3934/matersci.2016.4.1474 |
| [6] | Yanmei Zhang, Mu Fan, Zhongmin Xiao . Nonlinear elastic-plastic stress investigations on two interacting 3-D cracks in offshore pipelines subjected to different loadings. AIMS Materials Science, 2016, 3(4): 1321-1339. doi: 10.3934/matersci.2016.4.1321 |
| [7] | Pawan Kumar, B B Verma . Propagation of corrosion induced fatigue crack in aluminum alloy. AIMS Materials Science, 2022, 9(3): 512-521. doi: 10.3934/matersci.2022030 |
| [8] | R. Citarella, M. Lepore, M. Perrella, C. Calì . Multiple crack propagation by DBEM in a riveted lap-joint. AIMS Materials Science, 2016, 3(4): 1577-1586. doi: 10.3934/matersci.2016.4.1577 |
| [9] | Mordechai Perl, Tomer Saley . The cumulative detrimental impact of pressure and autofrettage on the fatigue life of an externally cracked modern tank gun barrel. AIMS Materials Science, 2019, 6(5): 833-851. doi: 10.3934/matersci.2019.5.833 |
| [10] | Bohdan Stasyuk . Interacting cracks 3D analysis using boundary integral equation method. AIMS Materials Science, 2016, 3(4): 1796-1810. doi: 10.3934/matersci.2016.4.1796 |
Cracks may occur during the manufacture or operation process of the structural components. In this situation, assessments are required to estimate the remaining life of the cracked component and to determine whether the cracks should be removed or the repair/replacement of the component is necessary. For crack assessments, the rules on crack evaluation are needed for industries, utilities and regulators. By now, several fitness-for-service (FFS) codes in various countries have been published to provide crack assessment rules for evaluation, and these rules have achieved a consensus by engineers. When crack assessments are performed in accordance with FFS codes, the quality assurance during production as well as the structural integrity of the degraded components during operation can be demonstrated. Therefore, FFS codes are known to be essential and important for structural integrity assessments of components in engineering.
If a single crack is found in a component, the stress intensity factor (SIF) tables provided in FFS codes are available for evaluation. However, in engineering applications, multiple cracks due to fatigue or stress corrosion cracking (SCC) are often detected in structural components including petrochemical stations, offshore platforms and nuclear power plants [1]. Because multiple cracks interact on each other, it is not easy to conduct the structural integrity assessments of the components containing multiple cracks. In the past years, although several studies related to multiple cracks have been carried out [2,3,4,5,6,7,8,9,10], it is known that SIF solutions for multiple cracks have not been developed systematically. In order to evaluate the component containing multiple cracks, an engineering simplification is given by the current FFS codes [11,12,13,14,15,16,17,18,19]. That is, combination rules are applied together with SIFs of the single crack. Although the concepts of the combination rules are similar, the specific criteria are quite different among various FFS codes. Thus, it is reasonable to expect that different remaining lives can be obtained if using different combination criteria.
The objective of this paper is to discuss the fatigue crack growth (FCG) calculation results for two adjacent surface cracks in a plate, and to determine whether the results can be affected by the different combination criteria provided in the current FFS codes. The SIF solutions in ASME Boiler and Pressure Vessel Code Section XI (ASME Code Sec. XI) [11] were used in calculations. From the calculation results, it is found that the FCG behaviors obtained by various codes are considerably different. In addition, the growths of crack depth and crack length, and the crack shape development are shown to be affected greatly by the combination behavior of the two cracks.
The current FFS codes [11,12,13,14,15,16,17,18,19] provide combination rules for multiple cracks. Figure 1 illustrates two adjacent surface cracks in accordance with the FFS codes. The crack depths are a1 and a2, crack lengths are λ1 and λ2, and the distance between the two cracks is S. Table 1 summarizes the combination rules for the two surface cracks prescribed in the available FFS codes [11,12,13,14,15,16,17,18,19]. It is clear that the specific criteria differ significantly among these codes.
| Groups | FFS codes | Combination criteria |
| (1) | ASME Code Sec. XI |
S = 0 for fatigue and SCC S ≤ 0.5 × max (a1, a2) for fracture |
| (2) | BS 7910 and FITNET |
S ≤ min (λ1, λ2) for a1/λ1 or a2/λ2 > 0.5 S ≤ 0.5 × max (a1, a2) for a1/λ1 or a2/λ2 ≤ 0.5 |
| (3) | FKM, SSM and GB/T 19624 | S ≤ min (λ1, λ2) |
| (4) | API 579, HPIS and A16 | S ≤ 0.5 × (λ1 + λ2) |
Group (1) represents the case of ASME Code Sec. XI [11]. In accordance with this code, the combination rules are applied for assessments at inspection, subcritical crack growths (such as fatigue and SCC growths) and fracture estimation. In the case of fatigue and SCC growths, the distance S = 0 means that the two cracks are combined into a single crack when the inner side points of the two cracks touch each other. In the case of fracture, the combination rule should be considered with the criterion of S ≤ 0.5 × max (a1, a2).
In Group (2), the British Standard (BS) 7910 [12] and European Project FITNET [13] Codes provide similar combination criteria for a fracture assessment, which depend on the initial crack aspect ratio. In addition, the BS 7910 and FITNET Codes indicate that it is not necessary to apply the combination criteria in a fatigue assessment. However, if there is any doubt, multiple cracks should be combined. Thus, the combination criteria in Group (2) are investigated in the present FCG calculations.
The FKM [14], SSM [15] and GB/T 19624 [16] Codes in Group (3) have the same combination criterion for multiple surface cracks, where S is compared with the minimum crack length of the two cracks. It should be noted that, the SSM and FKM Codes do not specify the applicable range of the combination criterion of S ≤ min (λ1, λ2), whereas the GB/T 19624 Code indicates that this criterion can be applied for both the fatigue and fracture assessments. For comparison, the criterion in Group (3) is also considered in the present calculations.
The API 579 [17], HPIS [18] and A16 [19] Codes in Group (4) also provide an identical combination criterion for multiple surface cracks. This criterion indicates that S should be compared with one half of the sum of crack lengths. Note that, the API 579 Code states that the combination criterion of S ≤ 0.5 × (λ1 + λ2) is applicable for the fatigue and fracture assessments. On the other hand, this criterion in the HPIS Code is applicable for a fatigue assessment and the applicability of this criterion in the A16 Code is not clear. In addition, for the case of two surface cracks with an identical length, this combination criterion in Group (4) is equivalent to that given by Group (3).
In order to clarify the FCG behaviors for multiple surface cracks using different combination criteria in codes, FCG calculations for two adjacent surface cracks in a flat plate were performed. The two surface cracks have the same size with the aspect ratio less than or equal to 0.5. Figure 2 shows two identical semi-elliptical surface cracks in a flat plate with its wall thickness of t = 11.0 mm.
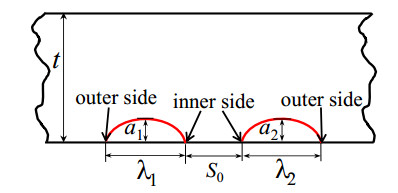 Figure 2. Two identical semi-elliptical surface cracks.
Figure 2. Two identical semi-elliptical surface cracks.Table 2 summarizes the crack size and location for each case. Three different aspect ratios were investigated and the crack size was set by referring to the allowable size in accordance with the acceptance standard in ASME Code Sec. XI. A nominal initial distance of S0 = 5 mm was considered.
| a1 = a2, mm | λ1 = λ2, mm | a1/λ1, a2/λ2 | S0, mm |
| 1.74 | 34.8 | 0.05 | 5 |
| 1.74 | 11.6 | 0.15 | |
| 1.74 | 3.48 | 0.5 |
The material considered in this study is austenitic stainless steel. A cyclic tensile loading was applied with a maximum stress of σmax = 123 MPa, which corresponds to the allowable design stress for stainless steel, and the minimum stress is σmin = 0 MPa [20]. Thus, the stress ratio is R = σmin/σmax = 0.
It is known that the SIFs are necessary for FCG evaluations. However, the current FFS codes only provide SIFs for a single crack but do not include the SIF solutions for multiple cracks. When performing FCG calculations for two adjacent surface cracks, code users have to calculate FCGs for each crack independently using the combination rule. When the distance S between the two cracks satisfies the combination rule, the two cracks are combined into one crack.
The SIF solutions for a surface crack in a flat plate provided in ASME Code Sec. XI were used for the present calculations, even though other FFS codes provide their own SIF tables, this was done so that the difference in the calculation results would arise only due to combination criteria. If using SIFs given by different FFS codes for the corresponding combination criteria, it may be difficult to understand whether the difference in the FCG results is caused by the combination criteria or SIFs.
In addition, the reference FCG rate provided in ASME Code Sec. XI was also used in this study. For austenitic stainless steels, the FCG rate is given by:
| dadN=C0(ΔKI)n | (1) |
where da/dN is the FCG rate in the units of mm/cycle, DKI indicates the range of SIF in MPa·m1/2, C0 and n are parameters depending on the material and environment. Based on ASME Code Sec. XI, C0 can be determined using the following equation and n is given as n = 3.3:
| C0=CS' | (2) |
where C is a scaling parameter to account for temperature given by:
| C=10(−8.714+1.34×10−3T−3.34×10−6T2+5.95×10−9T3) | (3) |
where T is the metal temperature, and S’ is a scaling parameter to account for the stress ratio R as given by Eq. (4). In this calculation, the scaling parameter S’ = 1.0 because of R = 0.
| S′={1.0whenR≤01.0+1.8Rwhen0<R<0.79−43.35+57.97Rwhen0.79<r<1.0 | (4) |
As described before, when calculating FCGs for two adjacent cracks, code users perform calculations for each crack independently and check their geometries including the crack depth, length and the distance between the two cracks. Note that both the SIF solutions at the deepest and surface points were calculated by considering that the SIF depends on the crack depth and aspect ratio. Figure 3 illustrates the FCG behaviors for two adjacent surface cracks. Cracks #1 and #2 grow independently and symmetrically. That is, crack growth amounts are the same for the inner and outer side surface points. Each crack is not considered to interact on the other.
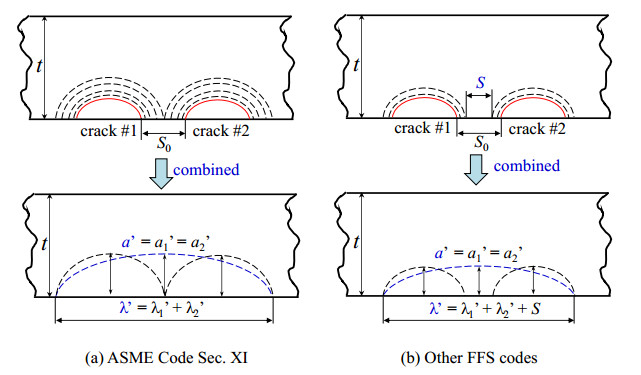 Figure 3. FCG behaviors in accordance with the FFS codes.
Figure 3. FCG behaviors in accordance with the FFS codes.In Figure 3(a), for ASME Code Sec. XI, the two cracks are combined into one crack when the inner side surface points of Crack #1 and Crack #2 touch each other. After combination, the crack length becomes λ’ = λ1’ + λ2’. Figure 3(b) depicts the FCG behaviors for other FFS codes (i.e., the codes in Groups (2), (3) and (4) in Table 1). Because two identical surface cracks are considered here, the combination criteria given by the codes in Groups (3) and (4) become equivalent as S ≤ λ1 (or λ2). When the distance between the two cracks satisfies the combination criteria, they are combined into one crack whose length is expressed as λ’ = λ1’ + λ2’ + S. The FCG behaviors after combination vary with the specific combination criteria, thus, it is expected that the calculation results may be different given by various FFS codes.
The FCG calculation results for two adjacent surface cracks in a flat plate are reported in this section. Note that, some finite element analyses have been performed previously for comparison, and the general tendency of X-FEM results are found to be similar to that by the code procedure [21]. In accordance with the allowable limit in ASME Code Sec. XI, the FCG calculations were terminated when the crack depth reached 75% of the wall thickness, t; i.e., a = 0.75t = 8.25 mm. The relationships of crack depth, a, and crack length, λ, versus number of cycles, N, for the codes in Groups (1)-(4) are shown in Figures 4-9. Note that, the results for Groups (3) and (4) are always the same because of the identical combination criterion. In addition, since the considered two cracks have the same crack size, only the results for one crack are plotted.
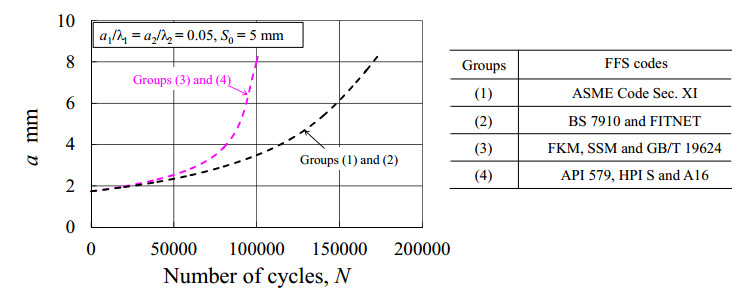 Figure 4. Results of a versus N for the case of a1/λ1 = a2/λ2 = 0.05 and S0 = 5 mm.
Figure 4. Results of a versus N for the case of a1/λ1 = a2/λ2 = 0.05 and S0 = 5 mm.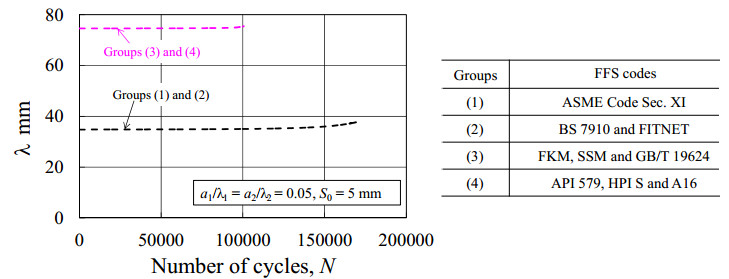 Figure 5. Results of λ versus N for the case of a1/λ1 = a2/λ2 = 0.05 and S0 = 5 mm.
Figure 5. Results of λ versus N for the case of a1/λ1 = a2/λ2 = 0.05 and S0 = 5 mm.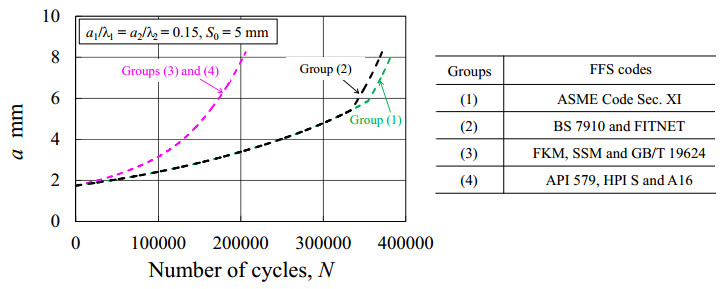 Figure 6. Results of a versus N for the case of a1/λ1 = a2/λ2 = 0.15 and S0 = 5 mm.
Figure 6. Results of a versus N for the case of a1/λ1 = a2/λ2 = 0.15 and S0 = 5 mm.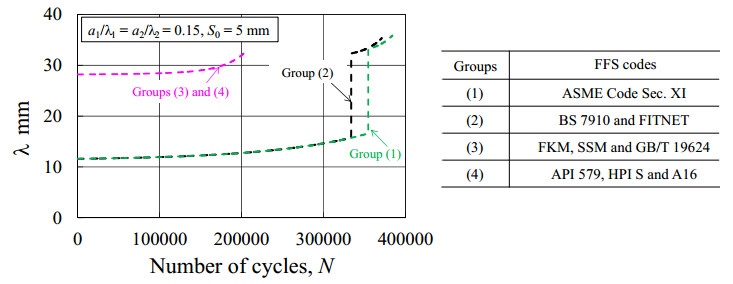 Figure 7. Results of λ versus N for the case of a1/λ1 = a2/λ2 = 0.15 and S0 = 5 mm.
Figure 7. Results of λ versus N for the case of a1/λ1 = a2/λ2 = 0.15 and S0 = 5 mm.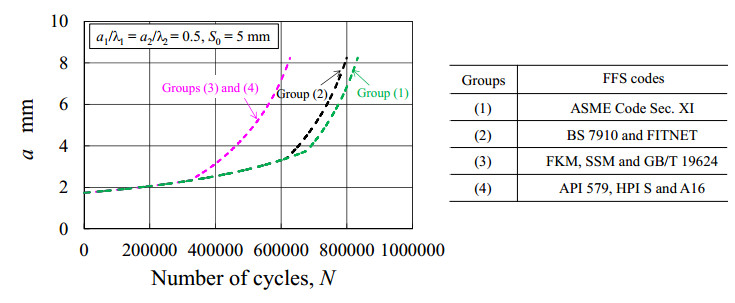 Figure 8. Results of a versus N for the case of a1/λ1 = a2/λ2 = 0.5 and S0 = 5 mm.
Figure 8. Results of a versus N for the case of a1/λ1 = a2/λ2 = 0.5 and S0 = 5 mm.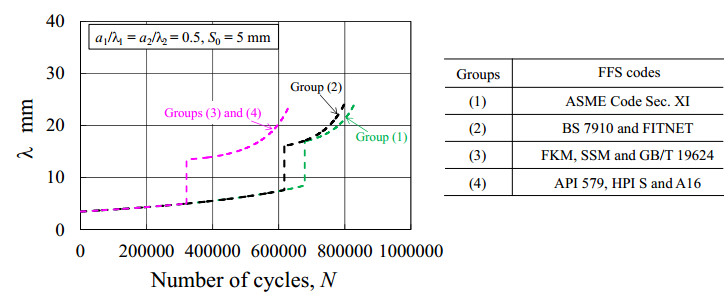 Figure 9. Results of l versus N for the case of a1/λ1 = a2/λ2 = 0.5 and S0 = 5 mm.
Figure 9. Results of l versus N for the case of a1/λ1 = a2/λ2 = 0.5 and S0 = 5 mm.Figure 4 shows the relationship between a and N for the case of a1/λ1 = a2/λ2 = 0.05. In accordance with Table 1, it is known that the combination criteria by the FFS codes are: S = 0 for ASME Code Sec. XI in Group (1), S = 0.87 mm for the codes in Group (2) and S = 34.8 mm for the codes in Groups (3) and (4). As seen in Figure 4, the same results are shown for Groups (1) and (2). That is, the two cracks are not combined even the crack depth a reaches 8.25 mm (i.e., a/t = 0.75). This is because the initial distance S0 = 5 mm is sufficiently large in comparison to S = 0 for ASME Code Sec. XI in Group (1) or S = 0.87 mm for the codes in Group (2). On the other hand, for Groups (3) and (4), the two cracks are combined at the beginning of calculations because S0 = 5 mm is smaller than S = 34.8 mm. The general tendency seen from Figure 4 is that, the growing behavior of crack depth obtained for Groups (1) and (2) are significantly different from that for Groups (3) and (4). Focusing on the remaining fatigue lives at a/t = 0.75, the relative difference among codes is found to be approximate 40% with N = 172,700 for the codes in Groups (1) and (2) and N = 100,600 for the codes in Groups (3) and (4). This difference results from the different combination criteria since other conditions were set to be identical in the FCG calculations.
In addition to the results of a versus N, the relationship between λ and N is also presented as shown in Figure 5. The codes in Groups (1) and (2) give the same results, i.e., the crack length grows monotonically from 34.8 mm to 38.2 mm at a/t = 0.75. For Groups (3) and (4), because the two cracks are already combined at the beginning, the initial crack length for the combined crack is 74.6 mm and it grows to 75.5 mm at a/t = 0.75. It is clear that the final crack length obtained by the codes in Groups (1) and (2) differs greatly from that obtained by the codes in Groups (3) and (4), and the difference is caused by the different combination criteria in various codes.
Figures 6 and 7 summarize the FCG calculation results for the case of a1/λ1 = a2/λ2 = 0.15, where the results of a versus N for Figure 6 and the results of λ versus N for Figure 7. The combination criteria given by various codes are: S = 0 for ASME Code Sec. XI in Group (1), S = 0.87 mm for codes in Group (2) and S = 11.6 mm for the codes in Groups (3) and (4). As seen in Figure 6, the crack depth increases gradually with increasing number of cycles during FCGs. The two cracks are combined into one crack at N = 354,600 for Group (1) and N = 333,700 for Group (2), where the discontinuities can be seen in Figure 6. After combination, the combined crack grows continuously until a/t = 0.75, and the remaining fatigue lives for Groups (1) and (2) show a small difference within 5%. For the codes in Groups (3) and (4), the two cracks are combined into one crack at the beginning, then the combined crack grows continuously until a/t = 0.75. The remaining fatigue life obtained for Groups (3) and (4) is N = 205,900, which shows a more than 80% difference from those obtained for Groups (1) and (2). The difference in the remaining fatigue lives comes from the different combination criteria in various codes.
Regarding the results of λ versus N in Figure 7, in the case of Groups (1), the crack length increases from the initial value of 11.6 mm to 16.6 mm before combination. When the two cracks are combined, a sudden increase of the crack length is seen and the combined crack length increases continuously to 35.9 mm at a/t = 0.75. A similar tendency can be seen in the growing crack length curve for Groups (2) and the final crack length is λ = 35.3 mm. For Groups (3) and (4), because the two cracks are combined at the beginning, the initial combined crack length becomes 28.2 mm and grows to 32.8 mm at a/t = 0.75. In addition, it is found from Figure 7 that, although the FCG behaviors obtained by various codes vary considerably, the difference in the final crack length at a/t = 0.75 is relatively small for all of the codes.
Figures 8 and 9 show the results for the case of a large aspect ratio of a1/λ1 = a2/λ2 = 0.5. The combination criteria given by various codes are: S = 0 for ASME Code Sec. XI in Group (1), S = 0.87 mm for the codes in Group (2) and S = 3.48 mm for codes in Groups (3) and (4). In Figure 8, the results of a versus N are plotted. It is seen that the two cracks grow slowly and are combined into one crack at the cycle numbers of N = 678,600 for Group (1), N = 616,900 for Group (2) and N = 320,600 for Groups (3) and (4). After combination, the combined crack grows continuously until a/t = 0.75. The remaining fatigue lives at a/t = 0.75 are N = 833,000 for Group (1), N = 799,700 for Group (2) and N = 627,400 for Groups (3) and (4). Again, it can be concluded that, the growing crack depth curve for Groups (1) is close to that for Group (2) but is significantly different from that for Groups (3) and (4), and the difference in the remaining fatigue lives results from the different combination criteria in various codes.
With regard to the results of λ versus N shown in Figure 9, for Group (1), it is found that the crack length grows from 3.48 mm to 8.48 mm before combination. When the two cracks are combined, a sudden increase of the crack length can be seen. After combination, the crack length increases continuously to 24.6 mm until a/t = 0.75. A similar tendency is obtained for Group (2), although a slight difference is found for the cycle number at combination. For Groups (3) and (4), the growing process of the crack length is similar to those for the other two codes except the growth behaviors after combination. The results in Figure 9 indicate that the final crack length at a/t = 0.75 shows a relatively small difference but the remaining fatigue lives are significantly different among the codes.
Besides the growing crack depth and crack length during FCGs, the past studies [5,22,23] indicated that the crack shape development was also important for the fatigue growth assessment. Here, the results of the aspect ratio, a/λ, versus the normalized crack depth, a/t, are plotted for discussion.
At first, the case of a single surface crack was investigated and the results of a/λ versus a/t are summarized as shown in Figure 10. Here, the calculation conditions such as the flat plate geometry, loading condition and FCG rate are the same as those described previously. Three different crack aspect ratios were investigated with a = 1.74 mm and λ = 3.48, 11.6 and 34.8 mm (i.e., a/λ = 0.5, 0.15 and 0.05). The FCG calculations were started from the initial crack depth of a/t = 1.74/11 ≈ 0.16 and were terminated at a/t = 0.75.
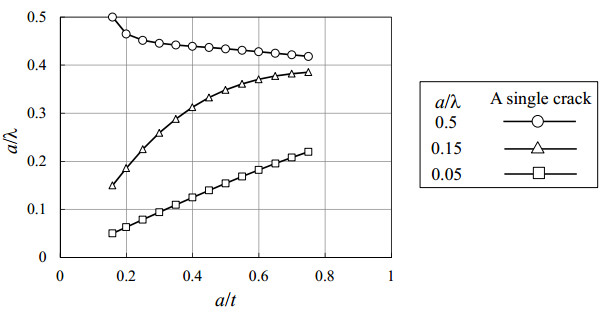 Figure 10. Results of a/λ versus a/t for a single surface crack with the initial a = 1.74 mm.
Figure 10. Results of a/λ versus a/t for a single surface crack with the initial a = 1.74 mm.As seen in Figure 10, for the initial aspect ratios, a/λ = 0.05 and 0.15, because the SIF at the deepest point is always higher than that at the surface point, the growth amount of the crack depth should be larger than that of the crack length. As a result, the aspect ratio a/λ increases monotonically with the normalized crack depth a/t. For the case of the initial a/λ = 0.5, since the SIF at the deepest point is lower than that at the surface point, a/λ decreases during the FCG which means the crack transforms from a semi-circular shape to a semi-elliptical shape.
Based on the FCG calculation results shown in Figures 4-9, the crack shape development for the case of two cracks is also plotted in Figure 11. Figures 11(a),(b), and (c) represent the calculated results using the combination criteria given by the codes in Group (1), Group (2), and Groups (3) and (4), respectively. As a general tendency, the crack shape development obtained by ASME Code Sec. XI in Group (1) is relatively close to that obtained by the codes in Group (2) but is remarkably different from that obtained by the codes in Groups (3) and (4).
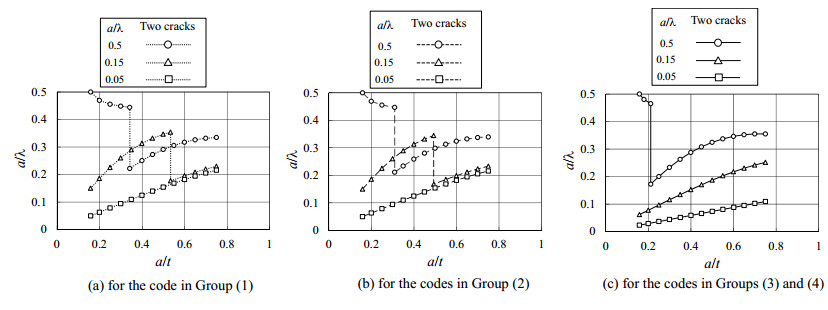 Figure 11. Comparison of a/λ versus a/t for a single crack and two cracks using combination rules in various FFS codes.
Figure 11. Comparison of a/λ versus a/t for a single crack and two cracks using combination rules in various FFS codes.In Figure 11(a), the results of a/λ versus a/t for ASME Code Sec. XI in Group (1) are summarized. For the case of a/λ = 0.05, since the two cracks are not combined even when a/t reaches 0.75, the crack shape development is the same as that for the single crack in Figure 10. For the case of a/λ = 0.15, a/λ increases from the initial value of 0.16 to a value of 0.35. After that, due to the combination, the combined crack aspect ratio a/λ suddenly drops to 0.17 and then increases continuously with the final a/λ = 0.23 at a/t = 0.75. For the case of a/λ = 0.5, a/λ decreases to a value of 0.44 at which the two cracks are combined. After combination, a/λ suddenly drops to a value of 0.22 and then increases continuously with the final a/λ = 0.33 at a/t = 0.75. In addition, comparing with the results for the single crack in Figure 10, it is found that the combination of two adjacent cracks significantly alters the crack propagation process and can lead to a sudden decrease of a/λ during FCGs.
Figure 11(b) shows the crack shape development obtained by the codes in Group (2). The overall tendency in Figure 11(b) is similar as that seen in Figure 11(a) for Group (1). However, a slight difference can still be noticed. That is, for both a/λ = 0.15 and 0.5, the crack shape development at combination is different.
In regard to the results for the codes in Groups (3) and (4) as shown in Figure 11(c), for the case of a/λ = 0.05, since the two cracks are combined into one crack at the beginning, the initial aspect ratio for the combined crack becomes 0.023 and increases gradually with a/t. For a/λ = 0.15, the similar tendency can be obtained as that for a/λ = 0.05. In particular, the aspect ratio for the combined crack is a/λ = 0.062 and increases up to 0.25 at a/t = 0.75. For the case of a/λ = 0.5, the results in Figure 11(c) show a similar tendency as those obtained in Figures 11(a) and (b), although the crack shape development at combination differs among the codes. Again, comparing with the results for the single crack in Figure 10, it is found that the combination of adjacent two cracks changes the crack propagation process significantly and induces a sudden decrease of a/λ during FCGs.
FCG calculations were conducted for two adjacent surface cracks with the same size using combination rules provided in the current FFS codes. Three different crack aspect ratios of a/λ = 0.05, 0.15 and 0.5 and a constant initial distance of S0 = 5 mm between the two cracks were considered. The calculation results using different combination criteria in various codes were compared. The conclusions drawn from the results are:
(1) The FCG behaviors are influenced by the combination criteria provided in various FFS codes. In particular, the results obtained by ASME Code Sec. XI are relatively close to those for the BS 7910 Code (or the FITNET Code) but are greatly different from those obtained by the other codes (i.e., the codes in Groups (3) and (4) in Table 1).
(2) For the case of a small aspect ratio with a/λ = 0.05, both the remaining fatigue lives and the crack lengths at a/t = 0.75 are different among various FFS codes. However, for the cases of a/λ = 0.15 and 0.5, it is found that the crack length at a/t = 0.75 shows a relatively small difference although the remaining fatigue lives are remarkably different for various FFS codes.
(3) The combination behavior of the two cracks can significantly affect the growths of crack depth and crack length as well as the crack shape development during FCGs.
The authors declare no conflicts of interest regarding this paper.
| [1] | Kamaya M, Miyokawa E, Kikuchi M (2011) Crack Growth Prediction Method Considering Interaction between Multiple Cracks. Bull Jpn Soc Mech Eng 77: 552–563. |
| [2] | Isida M (1970) Analysis of Stress Intensity Factors for Plates Containing Random Array of Cracks. Bull Jpn Soc Mech Eng 13: 635–642. |
| [3] |
Murakami Y, Nemat-Nasser S (1982) Interacting Dissimilar Semi-Elliptical Surface Flaws under Tension and Bending. Eng Fract Mech 16: 373–386. doi: 10.1016/0013-7944(82)90115-1

|
| [4] |
Murakami Y, Nemat-Nasser S (1983) Growth and Stability of Interacting Surface Flaws of Arbitrary Shape. Eng Fract Mech 17: 193–210. doi: 10.1016/0013-7944(83)90027-9

|
| [5] | Iida K (1983) Shapes and Coalescence of Surface Fatigue Cracks. Proceedings of ICF International Symposium on Fracture Mechanics, Beijing, China. |
| [6] | Iida K, Kuwahara M (1978) An Assessment of Fatigue Crack Growth from Adjacent Multiple Surface Flaws. Third International Symposium of Japan Welding Society, Tokyo, 325. |
| [7] |
Soboyejo WO, Kishimoto K, Smith RA, et al. (1989) A Study of the Interaction and Coalescence of Two Coplanar Fatigue Cracks in Bending. Fatigue Fract Eng M 12: 167–174. doi: 10.1111/j.1460-2695.1989.tb00524.x

|
| [8] |
Kishimoto K, Soboyejo WO, Smith RA, et al. (1989) A Numerical Investigation of the Interaction and Coalescence of Twin Coplanar Semi-Elliptical Fatigue Cracks. Int J Fatigue 11: 91–96. doi: 10.1016/0142-1123(89)90003-0

|
| [9] |
Bezensek B, Hancock JW (2004) The Re-Characterization of Complex Defects Part I: Fatigue and Ductile Tearing. Eng Fract Mech 71: 981–1000. doi: 10.1016/S0013-7944(03)00155-3

|
| [10] |
Bezensek B, Hancock JW (2004) The Re-Characterization of Complex Defects Part II: Cleavage. Eng Fract Mech 71: 1001–1019. doi: 10.1016/S0013-7944(03)00156-5

|
| [11] | American Society of Mechanical Engineers (2015) ASME B&PV Code Section XI, Rules for In-service Inspection of Nuclear Power Plant Components, ASME, New York, USA. |
| [12] | British Standard Institution (2005) BS 7910, Guide to Method for Assessing the Acceptability of Flaws in Metallic Structure, BSI, London, UK. |
| [13] | Kocak M, Hadley I, Szavai S, et al. (2008) FITNET fitness-for-service procedures, Vol. II., Joint Research Centre, GKSS Research Centre, Geesthacht, Germany. |
| [14] | Berger C, Maschinenbau FF (2009) Fracture Mechanics Proof of Strength for Engineering Components, FKM Guideline, 2nd Revised Edition. |
| [15] | Swedish Radiation Safety Authority (2008) A Combined Deterministic and Probabilistic Procedure for Safety Assessment of Components with Cracks-Handbook, SSM, Stockholm, Sweden. |
| [16] | Chinese Standard Committee (2004) GB/T 19624, Safety Assessment for In-Service Pressure Vessels Containing Defects, Beijing (in Chinese). |
| [17] | American Petroleum Institute (2007) Fitness-for-Service, API 579-1/ASME FFS-1. |
| [18] | High Pressure Institute of Japan (2008) Assessment Procedure for Crack-Like Flaws in Pressure Equipment, HPIS Z 101, Tokyo (in Japanese). |
| [19] | AFCEN (2010) Guide for Defect Assessment and Leak Before Break Analysis, A16, RCC-MRx, France. |
| [20] | Katsumata G, Li Y, Hasegawa K, et al. (2015) Fatigue Crack Growth Calculations for Pipes Considering Subsurface to Surface Flaw Proximity Rules. Proceedings of ASME 2015 Pressure Vessel and Piping Division Conference, American Society of Mechanical Engineers. |
| [21] |
Lu K, Li Y, Hasegawa K, et al. (2017) Remaining Fatigue Lives of Similar Surface Flaws in Accordance with Combination Rules. J Pressure Vessel Technol 139: 021407. doi: 10.1115/1.4035317

|
| [22] |
Soboyejo WO, Knott JF (1991) The Propagation of Non-Coplanar Semi-Elliptical Fatigue Cracks. Fatigue Fract Eng M 14: 37–49. doi: 10.1111/j.1460-2695.1991.tb00641.x

|
| [23] |
Tu ST, Dai SH (1994) An Engineering Assessment of Fatigue Crack Growth of Irregularly Oriented Multiple Cracks. Fatigue Fract Eng M 17: 1235–1246. doi: 10.1111/j.1460-2695.1994.tb01412.x

|
| 1. | Ivan Pidgurskyi, Mykola Stashkiv, Mykola Pidgurskyi, Yurii Rudyak, Yevgen Ripetskyi, Roman Ripetskyi, Valeriy Lazaryuk, Prediction of residual durability of structural elements with identical surface cracks taking into account the stage of their coalescence, 2022, 36, 24523216, 190, 10.1016/j.prostr.2022.01.023 |
| Groups | FFS codes | Combination criteria |
| (1) | ASME Code Sec. XI |
S = 0 for fatigue and SCC S ≤ 0.5 × max (a1, a2) for fracture |
| (2) | BS 7910 and FITNET |
S ≤ min (λ1, λ2) for a1/λ1 or a2/λ2 > 0.5 S ≤ 0.5 × max (a1, a2) for a1/λ1 or a2/λ2 ≤ 0.5 |
| (3) | FKM, SSM and GB/T 19624 | S ≤ min (λ1, λ2) |
| (4) | API 579, HPIS and A16 | S ≤ 0.5 × (λ1 + λ2) |
| a1 = a2, mm | λ1 = λ2, mm | a1/λ1, a2/λ2 | S0, mm |
| 1.74 | 34.8 | 0.05 | 5 |
| 1.74 | 11.6 | 0.15 | |
| 1.74 | 3.48 | 0.5 |
| Groups | FFS codes | Combination criteria |
| (1) | ASME Code Sec. XI |
S = 0 for fatigue and SCC S ≤ 0.5 × max (a1, a2) for fracture |
| (2) | BS 7910 and FITNET |
S ≤ min (λ1, λ2) for a1/λ1 or a2/λ2 > 0.5 S ≤ 0.5 × max (a1, a2) for a1/λ1 or a2/λ2 ≤ 0.5 |
| (3) | FKM, SSM and GB/T 19624 | S ≤ min (λ1, λ2) |
| (4) | API 579, HPIS and A16 | S ≤ 0.5 × (λ1 + λ2) |
| a1 = a2, mm | λ1 = λ2, mm | a1/λ1, a2/λ2 | S0, mm |
| 1.74 | 34.8 | 0.05 | 5 |
| 1.74 | 11.6 | 0.15 | |
| 1.74 | 3.48 | 0.5 |