1. Introduction

Magnetic vortices in thin ferromagnetic disks of sub-micron size offer an interesting system for the study of collective dynamics of fundamental excitations ^[1]. A single vortex centered in a circular disk can be the absolute minimum energy state or it can be metastable, separated from a nearby quasi-single-domain state by a weak energy barrier. A vortex experiences a restoring force $\textbf{F}=-k_F \textbf{R}$ dependent on its displacement $\textbf{R}=(X, Y)$ from the center, mostly caused by demagnetization effects from weak pole formation on the disk edges, where $k_F$ is a force constant ^[2]. The response to this force is the gyrotropic orbital vortex motion at a frequency $\omega_G$, which can be detected in resonance experiments ^[3]. The effective force constant also can be modified by using an applied field in the disk plane to displace the equilibrium vortex location.

While much work has been developed for disks with a circular boundary, less studied are disks with an elliptical boundary ^[4]. Quite generally in physical problems, deviation of a circular system into one with elliptical symmetry leads to interesting modifications, due to the breaking of the circular symmetry. We consider an elliptical edge characterized by semi-major radius $a$ along the $x$-axis and a semi-minor radius $b$ along the $y$-axis, for a disk of thickness $L$ with $L\ll a$. In a circular disk, the in-plane angle of local magnetization in a vortex state is determined by vorticity charge $q=\pm 1$, and a chirality or circulation charge $c=\pm 1$, via a relation

$\phi (x, y)=q{{\tan }^{-1}}\left( \frac{y-Y}{x-X} \right)+c\frac{\pi }{2}.$

(1)

The gyrotropic charge is $G=2\pi qp$, or gyrovector ${\bf G}=G\hat{z}$, where $p=\pm 1$ is the polarization direction (magnetization along $\pm z$) of the vortex core. Simulations show that the vortex structure itself is not squeezed along the narrow direction of the ellipse. Rather, the vortex retains close to a circular shape, but experiences a modified potential. When taken as an assumption, this is the rigid vortex approximation. In numerical simulations, it need not hold precisely. Regardless of that, the deviation of the disk edge from circular symmetry is found to introduce two non-equivalent force constants $k_x$ and $k_y$, corresponding to the principal axes of the ellipse. The force constants change with the shape of the disk ^[5], until reaching a high in-plane aspect ratio $b/a \ll 1$, where the vortex becomes unstable and a single- or multi- domain state emerges. a nearly uniform quasi-single-domain state or possibly a two-domain state emerges, similar to those found ^[6] in circular nanodisks. Here only the vortex state is considered.

With a magnetic field applied in the plane of the disk, the vortex equilibrium position will be displaced away from the disk center, perpendicular to the field in a direction depending on chirality $c$. In an elliptic disk, displacements along the two principal directions are non-equivalent. Buchanan et al. ^[7] have noted that a field $H_y^{\rm ext}$ applied along the shorter ($y$) axis, that shifts the vortex minimum position along the long ($x$) axis, results in an increase in its gyrotropic frequency. To the contrary, a field $H_x^{\rm ext}$ along the long axis, shifting the vortex minimum position along the short axis, does not significantly change the frequency. We confirm these results, showing how the vortex effective potential and force constants are modified by the displaced vortex equilibrium location. The gyrotropic resonant frequency is then seen to shift, without any modification of the gyrotropic charge or gyrovector $G$. If a field is applied instead perpendicular to the disk plane ($z$-axis), there will be two non-degenerate vortex gyrotropic modes, as has been seen in resonance experiments ^[8] and micromagnetics ^[9] for circular disks. Here further analysis of this effect is given, and we find how a perpendicular applied field modifies both the force constants and gyrotropic frequencies. The gyrovector is shifted with an out-of-plane applied field $H_z^{\rm ext}$, such that the resonant frequency changes nearly linearly with $H_z^{\rm ext}$. A field pointing out-of-plane in the same direction as the vortex core magnetization increases $\omega_G$.

In this article vortex motion in elliptic disks is considered, as obtained from two-dimensional micromagnetics simulations, and from analysis of the Thiele equation ^[10] for magnetization dynamics of a collective excitation such as a domain wall or vortex. The Thiele equation analysis depends directly on the force or the effective potential that the vortex moves in. This analysis is considered first for the zero temperature motion as obtained from Landau-Lifshitz-Gilbert (LLG) equations. The studies verify that the Thiele equation gives a good description of the motion and can predict the gyrotropic frequencies, based on the force constants, even in the presence of applied fields.

Quasi-static vortex structures and their energies can be used to estimate the force constants. The dynamic motion itself can also be used to estimate the force constants, especially for vortices displaced by an in-plane applied field. In the first set of studies presented here, some of the behaviors of the force constants and the gyrovector with disk geometry and applied field are discussed. Note that the gyrovector only changes significantly for an out-of-plane applied field. In a second set of studies, the stochastic effects due to finite temperature are included, by using the Langevin-LLG equations for the micromagnetics. The simulations can be compared with the vortex statistics expected from applying the principle of equipartition, not to the numerous spin degrees of freedom, but rather, to only the two degrees of freedom for the position of the vortex core. That is, good agreement is found for the vortex position statistics, based on a theory with only two degrees of freedom, when analyzing simulation data for the $2N$ degrees of freedom represented in the dynamics of $N$ micromagnetics cells for an elliptical nanodisk of magnetic material.

---

2. The System, Energetics and Dynamic Equations

The magnetic medium is assumed be of thickness $L$ along the $z$-axis and have an elliptical boundary in the $xy$-plane,

$\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1.$

(2)

The vortex magnetization structure is not strongly modified by the boundary, however, the vortex experiences a non-circular effective potential $U({\bf R})$ caused by the boundary. ${\bf R}=(X, Y)$ represents the vortex core location, measured from the disk center. For slight deviations from its equilibrium position, the potential experienced by a vortex is found to be of elliptical form,

$U(\mathbf{R})=U(X, Y)={{U}_{0}}+\frac{1}{2}\left( {{k}_{x}}{{X}^{2}}+{{k}_{y}}{{Y}^{2}} \right).$

(3)

The in-plane aspect ratio or ellipticity $b/a\le 1$ controls the properties of the potential in which the vortex moves, which is represented in terms of the force constants $k_x$ and $k_y$. When the ratio $b/a$ becomes too small, a vortex will be destabilized, and some other vortex-free state such as a quasi-single-domain state will be prefered. state such as a multi-domain state will be preferred.

The underlying dynamics is that of the local magnetization ${\bf M}({\bf r})=M_s {\bf m}({\bf r})$. Analyzed numerically in the micromagnetics approximation, the magnitude is fixed at the saturation value $M_s$ and only the direction ${\bf m}({\bf r})$ is changing. A continuum energy function for the system includes isotropic exchange, and demagnetization (${\bf H}^M$) and applied (${\bf H}^{\rm ext}$) fields:

$E[\mathbf{m}]=\int{d}V\left\{ {{A}_{\text{ex}}}\nabla \mathbf{m}\cdot \nabla \mathbf{m}-{{\mu }_{0}}\left( \frac{1}{2}{{\mathbf{H}}^{M}}+{{\mathbf{H}}^{\text{ext}}} \right)\cdot \mathbf{M} \right\}.$

(4)

The exchange is characterized by the exchange stiffness $A_{\rm ex}$ in units of J/m. Its competition with magnetostatic energy due to demagnetization effects leads to the exchange length, that sets a length scale for the problem:

${{\lambda }_{\text{ex}}}=\sqrt{\frac{2{{A}_{\text{ex}}}}{{{\mu }_{0}}M_{s}^{2}}}.$

(5)

The magnetization tends to preserve its direction over this length scale. Two-dimensional (2D) micromagnetics is based on the idea of using a 2D grid with cells not larger than this scale, so that the spatial variations in ${\bf m}$ can be correctly described. For Permalloy with $A_{\rm ex}\approx 13$ pJ/m and $M_s \approx 860$ kA/m, and $\mu_0 M_s \approx 1.08$ T, that gives $\lambda_{\rm ex} \approx 5.3$ nm. In these micromagnetics simulations we have used cells of size $a_{\rm cell}\times a_{\rm cell} \times L$, with $a_{\rm cell} = 2.0$ nm, so that weak changes in magnetization direction will be included. This 2D analysis is based on the assumption that there is little dependence of ${\bf m}$ on the $z$-coordinate, through the thickness of the disk. That should be true for thin disks. The numerical simulations keep track of cell magnetic dipoles $\vec{\mu}_i=\mu {\bf m}_i$ where $i$ labels the cells, and $\mu\equiv La_{\rm cell}^2 M_s$ is their fixed magnitude. Neighboring cells have an effective exchange constant, $J=2A_{\rm ex}L$. The demagnetization fields ${\bf H}^{M}_i$ are produced as a result of the current state of the ${\bf m}_i$. Their calculation is based on magnetostatics theory for an isolated thin 2D system, using effective Green's functions appropriate for the thin disk problem ^[11]. The calculations of ${\bf H}^{M}_i$ can be accelerated somewhat through the use of fast Fourier transforms applied to the defining convolution integrals.

For the discretized 2D system, the dynamic equations of motion resulting from (4), and including an additional damping term with dimensionless parameter $\alpha$, are the Landau-Lifshitz-Gilbert (LLG) torque equations,

$\frac{d{{{\vec{\mu }}}_{i}}}{dt}=\gamma {{\vec{\mu }}_{i}}\times {{\mathbf{B}}_{i}}-\frac{\alpha }{\mu }{{\vec{\mu }}_{i}}\times \left( \gamma {{{\vec{\mu }}}_{i}}\times {{\mathbf{B}}_{i}} \right).$

(6)

This includes the gyromagnetic ratio $\gamma$ and the effective local magnetic induction ${\bf B}_i$ acting on a cell,

${{\mathbf{B}}_{i}}={{\mu }_{0}}{{\mathbf{H}}_{i}}=-\frac{\delta E}{\delta {{{\vec{\mu }}}_{i}}}.$

(7)

Of course, there are contributions to ${\bf B}_i$ due to exchange fields, demagnetization fields, and the externally applied field. For numerics, we measure ${\bf B}_i$ in a basic unit $B_0 \equiv J/\mu= 2A_{\rm ex}/(a_{\rm cell}^2 M_s)$, defining dimensionless fields as ${\bf b}_i={\bf B}_i/B_0$. With cell size $a_{\rm cell}=2.0$ nm, this is $B_0 \approx 7.59$ T for the simulations described here using Permalloy parameters. Then the time is measured in units $t_0\equiv (\gamma B_0)^{-1}$, leading to dimensionless time variable $\tau=t/t_0$. Thus the dynamics follows the dimensionless equations,

$\frac{d{{\mathbf{m}}_{i}}}{d\tau }={{\mathbf{m}}_{i}}\times {{\mathbf{b}}_{i}}-\alpha {{\mathbf{m}}_{i}}\times \left( {{\mathbf{m}}_{i}}\times {{\mathbf{b}}_{i}} \right),$

(8)

For the numerical simulations, the magnetization unit vectors ${\bf m}_i(t)$ are evolved forward by some updating procedure. The method used depends on whether static or dynamic results are desired. Static or quasi-static vortex structures were used to get force constants, as an example. Dynamic simulation is necessary to obtain the gyrotropic frequencies.

---

3. Quasi-Static Vortex Properties

For finding quasi-static or relaxed structures, a local spin alignment relaxation scheme has been used, iteratively pointing each magnetic moment to align with its effective field, until some convergence is reached. The vortex energy (same as total system energy) was evaluated for different positions, which were enforced by a Lagrange constraint ^[12] on the vortex core, explained briefly here.The constraint is included by adding additional terms to the energy functional, creating the modified energy functional on the 2D grid with $N$ cells,

$\Lambda [\mathbf{m}]=E[\mathbf{m}]+\sum\limits_{i=1}^{N}{{{\alpha }_{i}}}(\mathbf{m}_{i}^{2}-{{m}^{2}})-\vec{\lambda }\cdot \sum\limits_{i=1}^{{{N}_{c}}}{{{\mathbf{m}}_{i}}}.$

(9)

Here the set of $\alpha_i$ at $N$ grid sites are Lagrange multipliers used to enforce ultimately a fixed length $m=1$ for the reduced magnetization vectors. The vector $\vec{\lambda}=(\lambda_x, \lambda_y)$ with only $xy$ components is a pair of Lagrange multipliers for enforcing the position constraint. $\vec{\lambda}$ is a fictitious field applied only to a limited set of grid sites $N_c=24$ symmetrically surrounding the vortex core. One can note that the in-plane magnetization structure of a vortex is highly symmetrical around its core, with the in-plane components of ${\bf m}$ pointing in opposite directions on opposing sides of the vortex. This is the reason for including the last term in the expression for $\Lambda$. The requirements that $\Lambda$ be an extremum with respect to variations in the set of $\alpha_i$ and $\lambda_x, \lambda_y$ leads to a set of equations that can be solved iteratively for the cell magnetizations ${\bf m}_i$ and the constraining field. This works for a desired core position exactly between four nearest grid cells. A slight modification to this scheme allows for securing the position offset arbitrarily from these symmetrical positions, see Ref. ^[12] for further details.

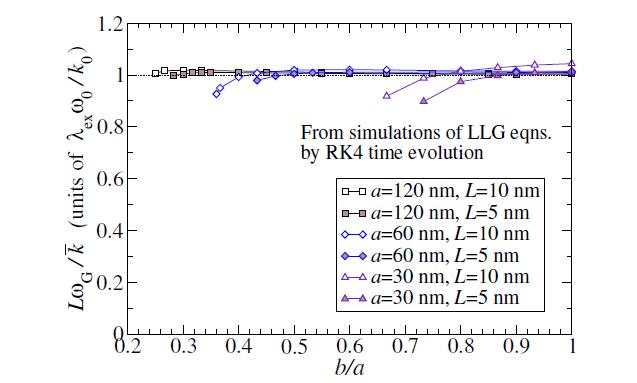
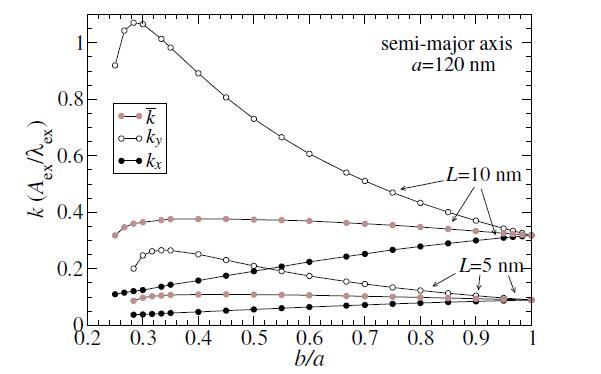
For elliptical nanodisks without applied fields, Figure 1 shows results for the vortex force constants obtained by this scheme, for vortices near the center of elliptical disks. The semi-major radius is $a=120$ nm, while the semi-minor radius $b$ takes on a range of values, corresponding to ellipses of different shapes. The force constants were estimated by using the energy change for a displacement of $\Delta X=4.0$ nm or $\Delta Y=4.0$ nm away from the disk center, where the vortex energy is the minimum value, $U_0$. Assuming the potential in Eq. (3), the force constants are obtained quasi-statically by expressions,

${{k}_{x}}=\frac{2\left[ U(\Delta X, 0)-{{U}_{0}} \right]}{{{(\Delta X)}^{2}}}, \quad {{k}_{y}}=\frac{2\left[ U(0, \Delta Y)-{{U}_{0}} \right]}{{{(\Delta Y)}^{2}}}.\text{ }$

(10)

The results in Figure 1 show some interesting features. First, the potential is stiffer for vortex motion along the shorter ($y$) direction. Thus, $k_y\ge k_x$, where the equality holds only in the circular limit. The vortex moves much more freely along the longer ($x$) axis. Secondly, for ellipses with a higher in-plane aspect ratio (i.e., smaller $b/a$), $k_x$ reduces slightly while $k_y$ increases more rapidly. At the same time, the geometric mean force constant $\bar{k}$ remains nearly constant. Eventually all of the force constants tend towards zero for small enough $b/a$, where the vortex is destabilized. Finally, also note that the force constants increase with the thickness of the disk, more than linearly with $L$. The disk with greater thickness have a much stronger demagnetization effect, which leads to a much stronger restoring force on the vortex.

---

3.1. About Finding the Vortex Location

The vortex core position ${\bf R}=(X, Y)$ can be determined with a precision much smaller than the numerical grid. This is done by first locating the set of four cells that surround the vorticity center or vortex core, among which the change in in-plane angle $\phi$ changes by $2\pi$ as expected from Eq. (1). Then, using a set of the cells within about 4 exchange lengths from that preliminary position estimate ${\bf r}_v$, an improved estimate is found from an average weighted by the squares of out-of-plane scaled magnetization components $m_i^z$. This uses the fact that the magnetization tilts out of the disk plane at the vortex center, with $m_i^z$ decaying away towards its boundary value over a distance on the order of the exchange length. We use an expression to estimate the position,

$\mathbf{R}=\frac{\sum\limits_{|{{\mathbf{r}}_{i}}-{{\mathbf{r}}_{v}}|<4{{\lambda }_{\text{ex}}}}{{{(m_{i}^{z})}^{2}}}{{\mathbf{r}}_{i}}}{\sum\limits_{|{{\mathbf{r}}_{i}}-{{\mathbf{r}}_{v}}|<4{{\lambda }_{\text{ex}}}}{{{(m_{i}^{z})}^{2}}}}.$

(11)

Each ${\bf r}_i$ is the center position of a cell, with the sum restricted to the core region. Especially for zero-temperature simulations this weighted location gives a very smoothly changing vortex position, even when following the dynamics. It is verified by comparison with the time-dependent plots of the magnetization as it evolves in the simulations. It is used below for the comparison of simulations with the Thiele theory for vortex core motion, and also in the study of vortex position statistics in Section 7.

---

4. Thiele Equation Analysis

The results found for vortex dynamics based on numerics can be analyzed in light of the Thiele collective coordinate equation for a localized magnetic excitation. If the effective force ${\bf F}=-\vec\nabla U({\bf R})$ is acting on the vortex core, then the Thiele equation for the core velocity ${\bf V}=\dot{\bf R}$ predicts the motion by

$\mathbf{F}+\mathbf{G}\times \mathbf{V}=0.$

(12)

This depends on the topological charge or gyrovector ${\bf G}$ of the vortex, which is determined by the vorticity charge $q=+1$ (antivorticity with $q=-1$ is not considered here), the out-of-plane core polarization $p=\pm 1$, and the magnetic dipole moment per unit area, $m_0=LM_s$,

$\mathbf{G}=G\mathbf{\hat{z}}=2\pi pq{{m}_{0}}{{\gamma }^{-1}}\mathbf{\hat{z}}.$

(13)

The potential in (3) is assumed, which depends on force constants $k_x$ and $k_y$. With the gyrovector having only an out-of-plane component, the equations of motion are equivalent to those of an elliptical oscillator, e.g.,

${{F}_{x}}=-{{k}_{x}}X=-{{(\mathbf{G}\times \mathbf{V})}_{x}}=G\dot{Y}$

(14)

${{F}_{y}}=-{{k}_{y}}Y=-{{(\mathbf{G}\times \mathbf{V})}_{y}}=-G\dot{X}$

(15)

Starting at location $(X_0, Y_0)$ at time $t=0$, the solution is that of elliptical motion,

$X(t)\text{ }={{X}_{0}}\cos {{\omega }_{G}}t+({{Y}_{0}}{{k}_{y}}/\bar{k})\sin {{\omega }_{G}}t$

(16)

$Y(t)={{Y}_{0}}\cos {{\omega }_{G}}t-({{X}_{0}}{{k}_{x}}/\bar{k})\sin {{\omega }_{G}}t$

(17)

$\bar{k}=\sqrt{{{k}_{x}}{{k}_{y}}},\qquad {{\omega }_{G}}=-\bar{k}/G.$

(18)

The geometric mean of the force constants, $\bar{k}$, determines the gyrotropic frequency $\omega_G$, which can also be taken as a vector perpendicular to the plane, $\vec\omega_G = \omega_G {\bf \hat{z}}$. The minus sign is included in (18) to indicate clockwise motion in the $xy$-plane when the gyrovector has a positive $z$-component. While the mean force constant determines $\omega_G$, the ratio of those force constants controls the shape of the orbit. Considering using $Y_0=0$, one gets the ratio of maximum displacements on the two axes (orbital ellipticity $e$, or ratio of semi-minor to semi-major axes) to be

$e\equiv \frac{{{Y}_{\mathbf{max}}}}{{{X}_{\text{max}}}}=\frac{{{k}_{x}}}{{\bar{k}}}=\sqrt{\frac{{{k}_{x}}}{{{k}_{y}}}}.$

(19)

Thus, the magnetic dynamics leads to vortex elliptical motion, whose ellipticity is directly related to the square root of the force constant ratio. Simulations of static vortex structure that lead to $k_x$ and $k_y$, such as in Figure 1, show that to a good approximation, $e\approx b/a$ for adequately large nanodisks.

For some analysis, a stretching of the coordinate system into a new variable is useful,

$\vec{\rho }\equiv (\sqrt{e}X,\frac{1}{\sqrt{e}}Y),$

(20)

because it returns the potential to a circular symmetry:

$U(\vec{\rho }\ )=\frac{1}{2}\bar{k}{{\vec{\rho }}^{\ 2}}.$

(21)

For the same reason, the vortex core motion then takes a simple form,

$\dot{\vec{\rho }}=({{\dot{\rho }}_{x}},{{\dot{\rho }}_{y}})={{\vec{\omega }}_{G}}\times \vec{\rho }.$

(22)

The variable, $\vec{\rho}$ and especially its magnitude is convenient for analysis of vortex position statistics.

---

4.1. Vortex Gyrotropic Frequencies

For zero temperature dynamics, fourth order Runge-Kutta (RK4) scheme has been used to get the time evolution. For finite temperature dynamics, additional stochastic fields are included into the equations (8), and the resulting Langevin-LLG equations (also known as the stochastic LLG equations) can be evolved forward in time using a second order Heun method. The chosen temperature $T$ determines the relative strength of the stochastic magnetic fields. See Refs. ^{[2, 5]} for further details.

At zero temperature, the validity of the Thiele analysis is confirmed by simulating vortices starting with a small displacement ($4.0$ nm) from the disk center, and evolving the undamped LLG equations forward in time with an RK4 scheme. The motion can be followed over 10 to 20 periods, from which the frequency is measured. The frequencies obtained dynamically are found to be directly proportional to the mean force constants $\bar{k}$ obtained from statics. Results versus disk ellipticity are summarized in a compact form in Figure 2. for two thicknesses $L=5$ nm, $10$ nm, and three semi-major axis lengths, $a=30$ nm, $60$ nm, $120$ nm. The frequencies follow closely the prediction (18) of the Thiele equation, which for $q=1$ can be transformed to a form:

$\frac{L{{\omega }_{G}}}{{\bar{k}}}=\frac{-p\gamma }{2\pi {{M}_{s}}}=-p{{\lambda }_{\text{ex}}}\left( \frac{{{\mu }_{0}}}{4\pi }\gamma {{M}_{s}} \right)\left( \frac{{{\lambda }_{\text{ex}}}}{{{A}_{\text{ex}}}} \right)$

(23)

The RHS contains $\lambda_{\rm ex}$ as length unit, a frequency unit $\omega_0\equiv \frac{\mu_0}{4\pi}\gamma M_s$, and the force constant unit $k_0\equiv A_{\rm ex}/\lambda_{\rm ex}$. Thus, the Thiele equation predicts in these units:

$\frac{(L/{{\lambda }_{\text{ex}}})({{\omega }_{G}}/{{\omega }_{0}})}{(\bar{k}/{{k}_{0}})}=-p.$

(24)

This is confirmed in the simulations for various disk geometries to within a few percent, except for small ellipticity, for which there is limited vortex stability, see Figure 2.

---

5. Vortex in an Out-of-plane Applied Field

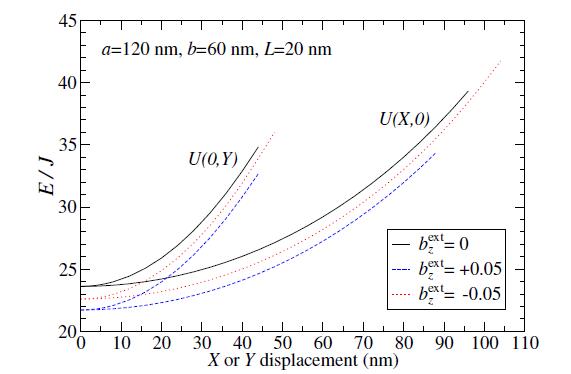
Next, consider an applied field $H_z^{\rm ext}$, or in dimensionless simulation units, include a nonzero field $b_z^{\rm ext}=\mu_0 H_z^{\rm ext}/B_0$. Circular magnetic disks with this field orientation have been considered by Loubens et al. ^[8] and more recently by Fried et al. ^[9], where it was found that the two opposite vortex polarizations become energy- and frequency-split by the field. Here we consider a vortex with $q=p=+1$, and positive (negative) values of $b_z^{\rm ext}$ correspond to the applied field pointing in the same (opposite) direction as the magnetization in the vortex core region. The effect on the vortex effective potential for a system with $b/a=0.5$ is shown in Figure 3, for applied fields $b_z^{\rm ext}=0, \pm 0.05$. The total system energy is plotted as a function of the vortex displacement from the disk center. Generally, the total energy is reduced with an applied field, and due to the symmetry, the disk center remains the location of the minimum. A positive field causes the larger reduction in total energy, as more of the magnetization is strongly aligned to the applied field.

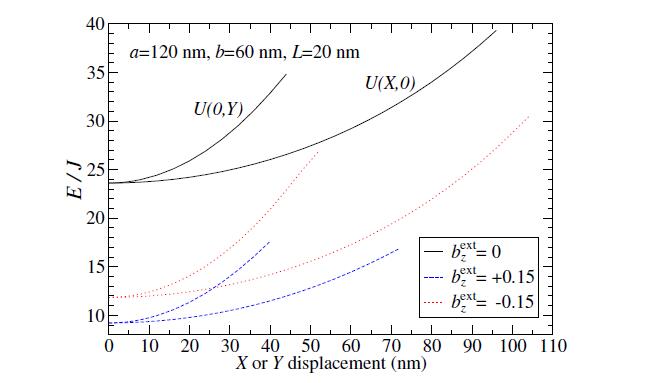
Another example for the same system, but with $b_z^{\rm ext}= \pm 0.15$, is shown in Figure 4. Obviously, an even greater field causes a larger downward energy shift. More importantly, the force constants are also modified by $b_z^{\rm ext}$, although this effect is difficult to see in the plots of $U({\bf R})$. Using Eq. (10), the results for $k_x, k_y$ and $\bar{k}$ are shown in Figure 5. This clearly shows how all of these are maximized at zero field, and tend towards $k_x=k_y=\bar{k}\rightarrow 0$ at an upper positive field limit, where the vortex is destabilized. Similarly, the vortex will be destabilized by a strong enough negative field, however, this takes place partly because the vortex core region in that case will acquire a very short radius (the core will be oppositely polarized to its surroundings). Note that the gyrotropic frequency $\omega_G=\bar{k}/G$ would be diminished by positive or negative $b_z^{\rm ext}$, if the gyrovector were constant. However, that is not the case, and the gyrotropic frequencies versus $b_z^{\rm ext}$ does not have the shape of the $\bar{k}$ curves.

Without applied fields, the dimensionless gyrovector $\gamma G/m_0=2\pi pq$ represents the total steradians of a unit sphere covered by the magnetization direction of the vortex, which is half of the unit sphere. $G$ is also given by a formula involving the out-of-plane reduced magnetization at the core, $m_z(0)=p$ and at infinite radius, $m_z(\infty)=0$,

$G={{G}_{0}}\left[ {{m}_{z}}(0)-{{m}_{z}}(\infty ) \right],$

(25)

where the scale is determined by the zero-field continuum gyrovector value,

${{G}_{0}}\equiv 2\pi qL{{M}_{s}}{{\gamma }^{-1}}.$

(26)

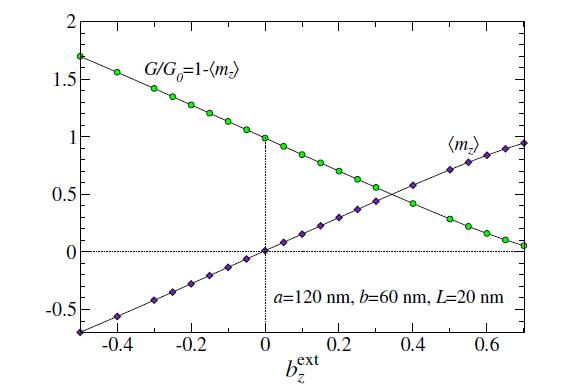
Once a field is applied along the $z$-axis, the boundary value $m_z(\infty)$ will be modified, which directly leads to a modification of $G$. Considering the case $p=+1$, $G$ is reduced (increased) for positive (negative) $b_z^{\rm ext}$, compared to its value at zero field. For a large enough system, the vortex core region is small compared to the rest of the area. Then an approximate expression for the value at large radius is to use the average over the whole system, $m_z(\infty)\approx \langle m_z \rangle$. This gives a rough estimate of the gyrovector,

$G\approx {{G}_{0}}\left[ p-\langle {{m}_{z}}\rangle \right].$

(27)

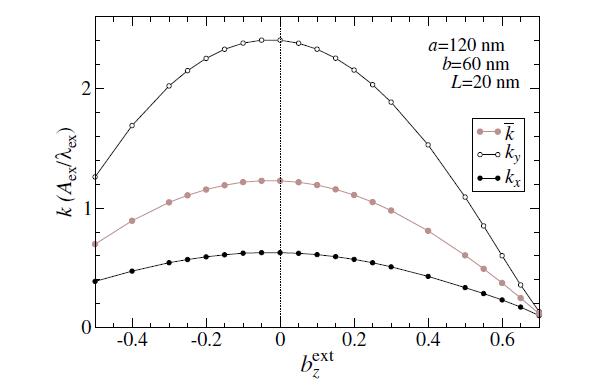
A plot showing the behaviors of $\langle m_z \rangle$ and the resulting $G$ for an elliptical system with $a=120$ nm, $b=60$ nm, is displayed in Figure 6. There results close to a linear dependence of $G$ on the out-of-plane field.

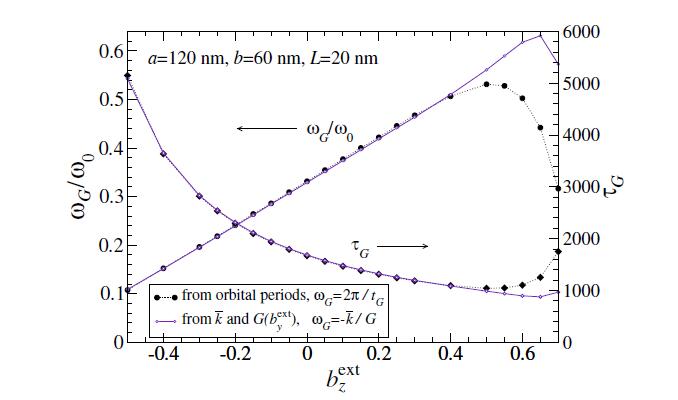
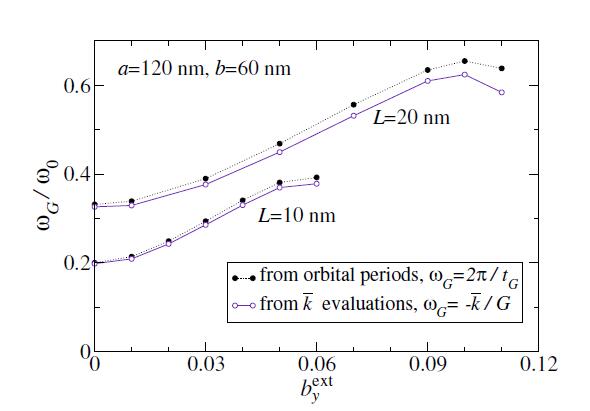
Using LLG simulations of vortex motions, starting from small displacements $X=4.0$ nm, many orbits can be followed, from which the periods $t_G$ can be determined, then leading to the gyrotropic frequencies $\omega_G=2\pi/t_G$. Note that in dimensionless units the period is $\tau_G=t_G/t_0$, where $t_0=(\gamma B_0)^{-1}$ is the simulation time unit. For the example system with $a=120$ nm, $b=60$ nm, $L=20$ nm, the resulting periods and frequencies are shown in Figure 7 over a range of out-of-plane applied field. There is very good agreement between the frequencies from the simulations, and those derived from the Thiele theory expression (18), , using the gyrovector $G$ that varies with field in Figure 6. One finds a rather strong effect of the field on $\omega_G$. The frequency exhibits a nearly linear dependence on $b_z^{\rm ext}$ at weaker fields, and even for negative fields, where there is little destabilization of the vortex. At the higher positive field values, the frequency deviates from the linear behavior, as the vortex becomes unstable. The weak-field linear behavior is consistent with that found by Loubens et al. ^[8], while the nonlinear dependence at higher field strength may be explained by core deformation, according to Fried et al. ^[9].

---

6. Effect of an In-plane Applied Field

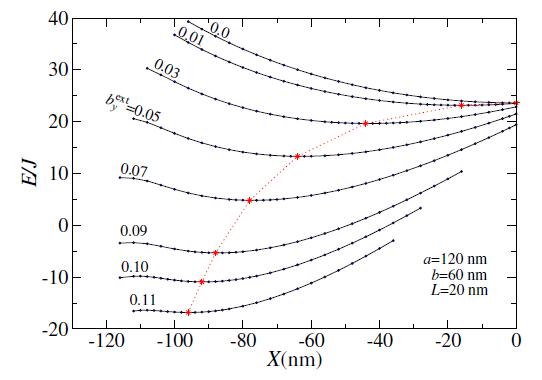
A magnetic field applied within the plane of the disk will displace the equilibrium vortex position away from the disk center, along a line perpendicular to that field; the direction depends on the vortex chirality $c$ or twist direction, Eq. (1). Doing simulations of the quasi-static vortex potentials, results such as those in Fig. 8 are found.

A field applied along the $y$ direction, for positive chirality $c$, displaces the vortex in the $-x$ direction, all the more so for stronger field. Similar potential curves were obtained by Buchanan et al. ^[7] using what they called a "static approach" in micromagnetics. A field applied on the whole system was used to move the vortex around to different equilibrium positions. Then the system energy for the vortex relaxed through micromagnetics at different equilibrium positions gives the potential curves. The Lagrange-constrained approach used here appears to give equivalent potential curves, and has the advantage that this iterative scheme is faster than running a micromagnetics relaxation for every desired point on the potential curve. However, one could argue that the scheme applied by Buchanan et al. is conceptually simpler and numerically more straightforward.

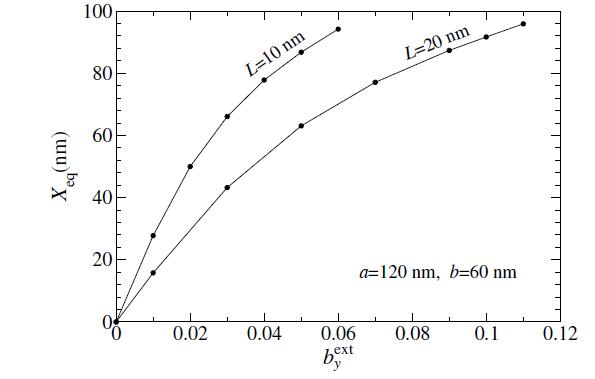
The asterisks in Figure 8 indicate the minima of the different potential curves. The resulting equilibrium vortex locations, as functions of the applied field, are those shown in Figure 9. The vortex appears to become unstable when reaching some edge region of the disk, which is about the same distance for the two disk thicknesses tested here.

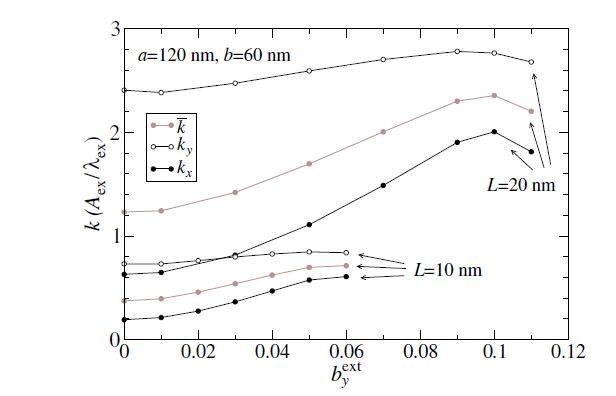
Buchanan et al. ^[7] have noticed further that in addition to this displacement, there is an upward shift in the gyrotropic frequency, resulting in close to a 100% increase, as long as the vortex has been shifted on the longer axis of the ellipse. Here we give further analysis to this effect; we find that the shifted location changes the force constants, but $\bar{k}$ still primarily determines $\omega_G$, because for the most part $G$ is unaffected by an in-plane field.

Initially a vortex is relaxed with damping, in the presence of an in-plane field, $b^{\rm ext}_y$ along the shorter ellipse axis. This produces some equilibrium location $(X_{\rm eq}, 0)$ away from the center, on the longer axis, and a corresponding minimum energy $E_{\rm eq}$. Then, another simulation is done without damping, starting from a nearby position, which results in gyrotropic motion around location $(X_{\rm eq}, 0)$, at some higher energy $E$, whose period $t_G$ is measured. The resulting orbital shape ($X(\tau)$, $Y(\tau)$) has a semi-major axis $A_{\rm path}$ and semi-minor axis $B_{\rm path}$. Fitting the energy difference $E-E_{\rm eq}$ to expression (3) for $U({\bf R})$, gives a dynamic evaluation of the force constants by

${{k}_{x}}=\frac{2(E-{{E}_{\text{eq}}})}{A_{\text{path}}^{2}},\quad {{k}_{y}}=\frac{2(E-{{E}_{\text{eq}}})}{B_{\text{path}}^{2}}.$

(28)

Some typical results for $k_x$, $k_y$, and the resulting $\bar{k}$ are indicated in Figure 10, for different disk thicknesses. At least at weaker field magnitude, the force constants increase with $b_y^{\rm ext}$. This is the primary cause of an increasing gyrotropic frequency. It appears that there is a greater tendency for $k_x$ to increase rather than $k_y$. As the vortex is pushed into the narrower end of the disk, it experiences stronger demagnetization fields and a resulting stiffer potential.

The gyrotropic frequency $\omega_G=2\pi/t_G$ then is compared with the Thiele prediction, $\omega_G=-\bar{k}/G$, using their geometric mean value $\bar{k}$, and assuming the zero-field gyrovector value, $G=G_0$. Results are shown in Figure 11, as functions of the dimensionless applied field $b_y^{\rm ext}$, up to a limit where the vortex is forced out the edge of the disk. The increase of $\omega_G$ with applied field is seen to be significant, consistent with the results of Buchanan et al. ^[7]. The largest frequency change takes place as the vortex is forced to move close to the disk edge. A weakening in the effect takes place near the limiting value of $b_y^{\rm ext}$, which is most simply explained by the reduction of $\bar{k}$ when the vortex is near the disk edge.

---

7. Thermally Induced Spontaneous Motion

It was pointed out by Machado et al. ^[13] and studied further by Wysin and Figueiredo ^[2] that gyrotropic motion can be spontaneously generated at finite temperature. The motion can self-generate even for a vortex initially at the disk center (no applied field is considered here). The amplitude of the motion is determined by equipartition, which can be analyzed under the assumption that the vortex core obeys the Thiele equation. This means that the vortex is considered to possess only two primary degrees of freedom, being the two Cartesian coordinates $(X, Y)$ of its core position. A short exercise shows that a Lagrangian that leads back to the Thiele equation with elliptic potential is ^[5]

$L=-\frac{1}{2}G(X\dot{Y}-Y\dot{X})-\frac{1}{2}\left( {{k}_{x}}{{X}^{2}}+{{k}_{y}}{{Y}^{2}} \right).$

(29)

Using the resulting canonical momentum ${\bf P}$, this implies a Hamiltonian that can be expressed as purely potential energy, $E= {\bf P}\cdot \dot{\bf R}-L=U(X, Y)=\frac{1}{2}\bar{k}\vec{\rho}^{\;2}$. Then assuming equipartition for only two degrees of freedom, each with average energy of $\frac{1}{2}k_B T$, with $k_B$ is Boltzmann's constant, the thermally averaged Hamiltonian takes the value, $\langle E \rangle = k_B T \equiv \beta^{-1}$. This gives a prediction for the distribution of vortex core radial position using the effective circular coordinate $\rho$ defined in (20) as

$p(\rho )=\beta \bar{k}\rho {{e}^{-\frac{1}{2}\beta \bar{k}{{\rho }^{2}}}}.$

(30)

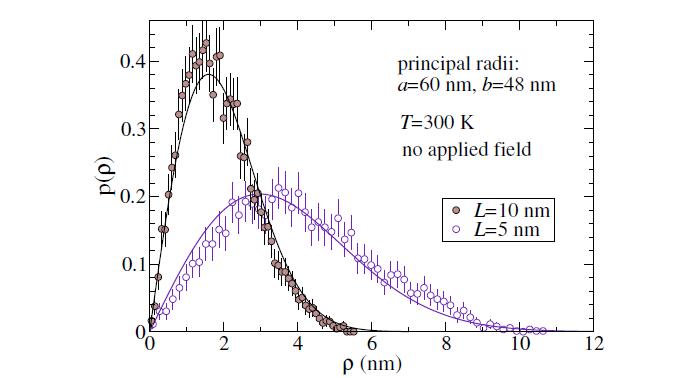
The most probable effective radius is given by $\rho_{\rm max}=(\beta\bar{k})^{-1/2}$, which demonstrates how weaker restoring force leads to a wider distribution. Simulations can be used to test these expectations, solving the Langevin-LLG equations by a second order Heun method ^[11]. The integration was done out to time $\tau=2.5\times 10^5$, with a weak damping constant $\alpha=0.02$, starting with a vortex at the disk center. The vortex motion initiates spontaneously due to thermal fluctuations, then proceeds in a noisy gyrotropic orbit for many periods, from which a histogram of $\rho$ can be calculated. Some typical results without an applied field are shown in Figure 12 for disks with $a=60$ nm, $b=48$ nm at $T=300$ K using Permalloy parameters. There is reasonable agreement between the simulation and the Thiele theory, however, averaging over at least 100 orbits is required. The distribution of vortex velocity can also be found to follow a Boltzmann form.

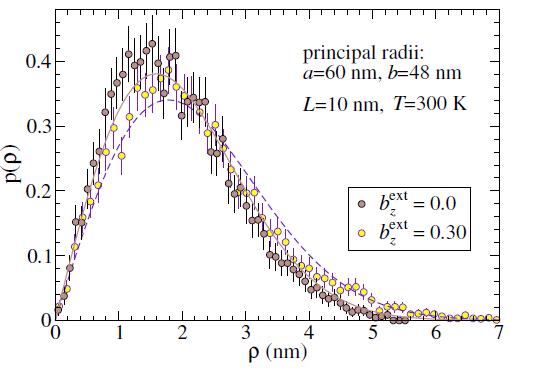
The application of an out-of-plane field can be seen to modify the thermally generated vortex radial distribution. For instance, for an elliptical Permalloy disk with $a=60$ nm, $b=48$ nm, $L=10$ nm, the zero-field mean force constant is $\bar{k}=1.632\times 10^{-3}$ N/m, as used in Figure 12. With the field $b_z^{\rm ext}=0.30$ applied, quasi-static vortex relaxation shows that the force constant is reduced to $\bar{k}=1.304\times 10^{-3}$ N/m. This is similar to the force constant reductions as displayed in Figure 5. A slight change in $p(\rho)$ results, as shown in Figure 13, where the zero-field and non-zero field cases are plotted. The slightly weaker potential in the presence of the field allows the vortex to explore a larger area of the disk, for fixed temperature. If a much stronger field were applied, it could be possible to weaken the potential sufficiently for the vortex to destabilize or exit the disk.

Some similar results should be expected for a vortex with an in-plane applied field in the presence of thermal fluctuations.

---

8. Conclusions

Magnetic vortex motion in thin elliptical nanometer scaled disks with applied fields has been considered here. The dynamics is controlled to a great extent by the effective potential and related force constants $k_x$, $k_y$, and their geometric mean value, $\bar{k}$. The gyrotropic resonant frequency is given by $\omega_G=-\bar{k}/G$, according to the Thiele equation analysis. The Thiele equation works well in describing magnetic vortex dynamics in elliptical nanodisks, even in the presence of applied fields, provided that the force constants and gyrovector are known. The force constants can be found from quasi-static vortex relaxation with a Lagrange constraint ^[12], however, it is also possible to infer their values from a simple analysis of the vortex orbital shape in simulations of the zero-temperature LLG equations. The gyrovector is fairly well estimated with Eq. (27), by assuming a core magnetization $m(0)=p$ and a far-field magnetization approximately equal to the system's mean value, $\langle m_z \rangle$. We do see a limit to the applicability of the Thiele equation when the vortex is exposed to strong enough fields that reduce its stability. For more moderate fields, an out-of-plane field increases (decreases) $\omega_G$ when parallel (antiparallel) to the vortex core magnetization, with close to a linear relationship between $b_z^{\rm ext}$ and $\omega_G$, see Figure 7. The simulations also have confirmed that an in-plane field along the shorter ($y$) disk axis both displaces the vortex equilibrium point along the long ($x$) axis, and increases its gyrotropic frequency, as found in Figure 11. These field effects on a vortex could be very useful in the design of new microwave oscillators and detectors.

---

Conflict of Interest

The author declares no conflict of interest in this paper.

---