Nomenclature
| 2ae | Crack height of the elliptical embedded crack |
| as | Crack depth of the semi-elliptical surface crack |
| a* | The effective crack height |
| 2be | The major axis length of the elliptical embedded crack |
| A0~A9 | Coefficients in Eq. (2) |
| 2bs | The major axis length of the semi-elliptical surface crack |
| CTOD_S | The CTOD value at the semi-elliptical surface crack tip |
| CTOD_L | The CTOD value at the left crack tip of the elliptical embedded crack |
| CTOD_R | The CTOD value at the right crack tip of the elliptical embedded crack |
| CTODin | The CTOD_S values from the case of two collinear cracks |
| CTODonly | The CTOD_S values from the case of a surface crack only |
| D | Outer diameter of pipeline |
| E | Young’s modulus |
| L | Length of pipeline segment adopted |
| n | Strain hardening coefficient |
| s | The distance between the surface crack tip and the left tip of embedded crack |
| t | Wall thickness of pipeline |
| γs | The interaction factor |
| εg | Global strain |
| ν | Poisson’s ratio |
| σU | Ultimate tensile strength of the material |
| σY | Yield tensile strength of the material |
1. Introduction
The study of multiple cracks in engineering structures such as pressure vessels and pipelines has become increasingly important due to many catastrophic failures of piping components. The fact is that under continuous loading conditions, small and rather closely distanced cracks can grow and coalesce into a large one which may subsequently pose a threat to the integrity and safety of the engineering structures [1,2,3]. To understand the influence of multiple cracks on integrity and safety of the pipelines is indeed desirable in engineering practice [1,4,5,6,7].
Multiple cracks have been observed in various cases of aging marine components. For example, the stress corrosion cracking in pipelines was reported by Leis and Mohan [8]. The piloted tests were conducted on the interaction effect between the coplanar cracks and irregular cracks for fatigue crack growth in 1990s [9,10,11]. Moreover, the fatigue growth of the interacting surface cracks in a steel plate [12,13,14,15] was investigated experimentally and numerically. In their studies, the relative spacing of cracks and the stress intensity factor were also discussed. For the thin-wall pipelines, a large crack interacting with one or several small cracks were numerically examined by Ouinas et al. [16]. In addition, the problem of nonplanar multiple cracks was also investigated. For instance, the relationship between the interaction factor of the multiple cracks and the crack’s aspect ratio was examined using finite element simulations [10,17]. Based on a series of FE analyses of both the nonaligned and aligned multiple cracks and the combination rules, a failure assessment diagram was proposed for multiple surface flaws subject to the limited loadings [14,18].
Although a lot of research works were performed on evaluating the interaction of multiple cracks on the fatigue crack growth and fracture behaviors, most of them were based on the elastic analyses and also constrained to crack size studies. There is a lack of information on nonlinear elastic-plastic analysis of fracture behaviors of ductile materials which are commonly used in pipelines. Moreover, in engineering practice, multiple cracks are generally treated as an equivalent large crack according to the existing codes, such as BS7910:2005 [19]. The simplified combination rules of multiple cracks results in conservative evaluations for applications such as in the offshore pipelines containing multiple cracks since the relatively simple elastic analyses are employed in these guidelines and codes. Therefore, a reasonable and accurate approach is highly required to evaluate the fracture response of offshore pipelines with multiple cracks subjected to large plastic deformation.
This study presents a systematic investigation on the fracture behaviors of two collinear 3-D cracks in the pipelines subjected to large plastic deformation. Nonlinear elastic-plastic FE analyses are carried out for the interaction of a semi-elliptical surface crack and an elliptical embedded crack. The influences of the cracks configuration, the separation distance and various loadings on the crack behaviors are investigated for these two collinear cracks. Based on the numerical results, the function of interaction factor is proposed for assessing the fracture behavior of the large surface crack affected by the interaction of two collinear cracks. Furthermore, the influence of the internal pressure on the fracture response (represented by CTOD value) is investigated for the flawed pipelines under tension or bending. Conclusions and a summary of the work presented in this study are given in the last section.
2. Materials and Method
2.1. Geometrical Configuration of the Pipeline with Two Collinear Cracks
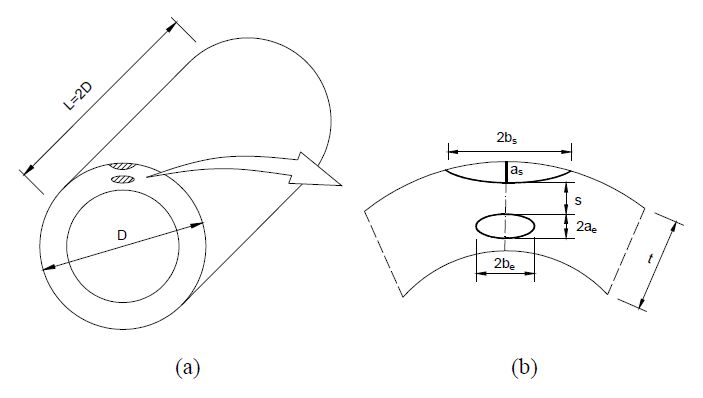
Some defects or flaws may be introduced in the manufacturing or installation process. These closely located flaws could be developed during service as a result of overloading, fatigue or harsh environmental conditions [20,21,22]. Thus, in this study nonlinear 3-D finite element analysis is conducted on circumferentially flawed pipeline with one semi-elliptical surface flaw and an elliptical embedded crack. The pipeline has an outer diameter D of 400 mm with wall thickness t of 20 mm.
The geometrical configuration of the pipeline with two coplanar cracks is shown in Figure 1. Considering that it is the clean pipeline used and also the two cracks are modeled in the axial section profile of the pipeline, the length of the pipeline segment L adopted in all analyses is twice of the outer diameter. It is sufficiently long for bending load without much change of results, as recommended in several references [23,24,25,26]. Figure 1(b) shows the details of thetwo cracks geometries considered. For a semi-elliptical surface crack, the crack depth is denoted by as and the major axis length of semi-ellipse is represented by 2bs. The value of as is adopted as 3, 5 and 7 mm which covers the range from a shallow to a deep surface crack. For each, three values of bs varying from 3 mm to 35 mm, are considered. Meanwhile, for an elliptical embedded crack, the crack height is denoted by 2ae. The major axis of elliptical embedded crack is 2be which is called the embedded crack length. As the wide variation of embedded crack geometry is not of primary concern in this study, only some values of the embedded crack size are considered for comparison purpose. In addition, the separation distance between the surface crack tip and the left crack tip of the embedded crack is denoted by s, varying from 3 mm to 9 mm.
2.2. Material Properties
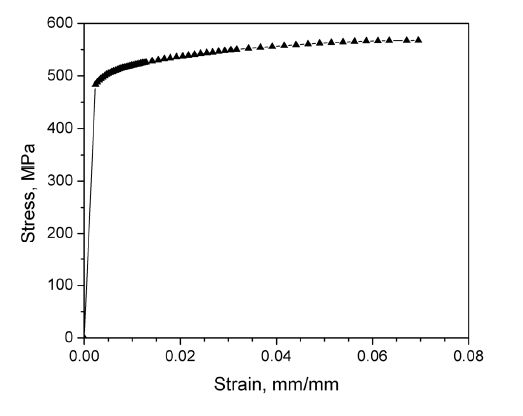
The material model used here is the carbon steel API X-65. The true stress-strain response for the pipeline material is shown in Figure 2. The values of the Young’s modulus E and Poisson’s ratio ν are assumed to be 207 GPa and 0.3, respectively. The yield stress (σY) of 484 MPa and hardening exponent of are obtained for isotropic hardening behavior based on the uniaxial tension tests. It should be noted that the ratio of the ultimate tensile strength to yield stress (σuts/σY) is roughly equal to 1.174.
2.3. FE Modelling
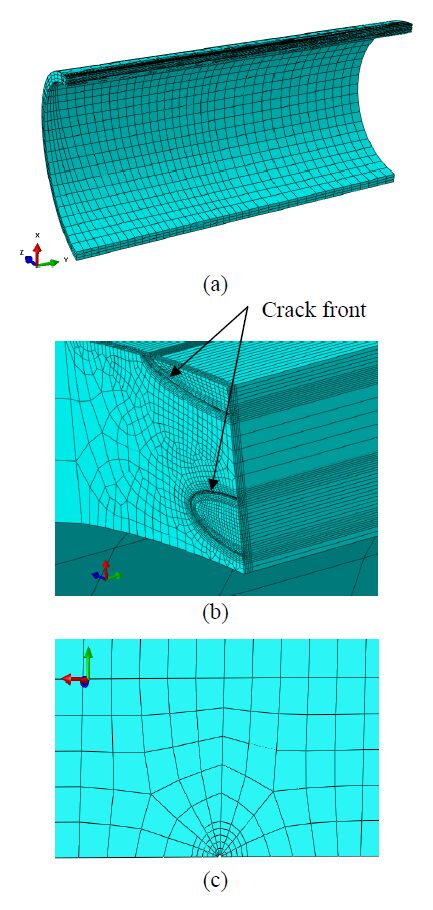
ABAQUS version 6.13 is utilized for nonlinear elastic-plastic analyses of the flawed pipelines. Due to symmetry of the proposed problem, only one-quarter of the pipeline model is built with C3D8R element.
Figure 3 shows a typical finite element meshes for the flawed pipeline model with the two cracks. Very similar mesh patterns are employed for the other crack geometry configurations. The blunt crack tip is adopted in order to avert the problem of stress singularity and also to accommodate the large plastic deformation induced by large plastic strains [27], although the sharp crack tip was used in other research works [28]. To implement it, a small hole with radius of 0.01 mm is assigned at each crack tip since it was suggested that blunt crack tip with a small hole of radius 0.5-1% crack length has no much influence on the numerical result and better promote the numerical convergence [29]. Meanwhile, focused spider web mesh is used for the blunt crack tip region, shown in Figure 3(c). It can be observed that the smallest element size is in the vicinity of the crack front, around 0.04 mm. In addition, over the wall thickness at the cracked section there is approximate 80 elements since the three crack tips are considered. Therefore, a typical FE model for the flawed pipe with two cracks has approximately 51, 000~62, 100 elements, depending on the crack size.
2.4. Loadings
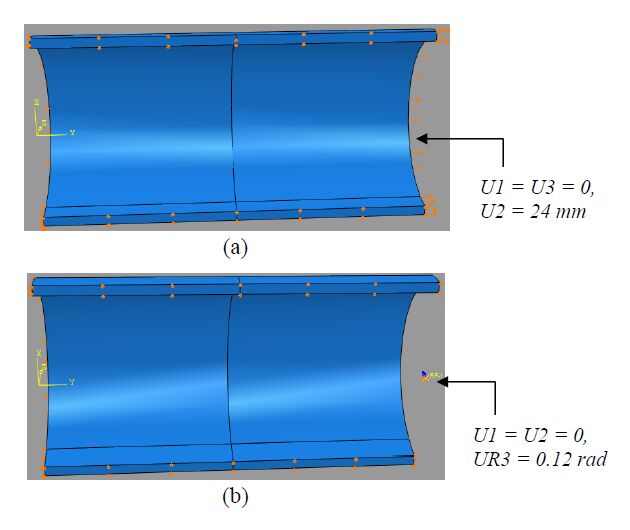
The tension and pure bending load are two primary loadings that most offshore pipelines experience, especially during the reeling installation [24,30]. The displacement-controlled tension is considered since it is widely recognized that the use of load-controlled tension is not suitable for the ductile materials with large plastic deformation in excess of yielding [31,32,33]. In our investigation, the tension loading is displacement-controlled, shown in Figure 4(a). For pure bending, it is implemented through a set of kinematic coupling constraint which is applied on the un-cracked section of pipeline, illustrated in Figure 4(b). The maximum global strain is assumed as 0.03 for both tension and pure bending cases.
For the case with biaxial loading, the internal pressure is taken into account due to its existence on the pipelines during service [34]. The two different biaxial loadings—tension combined with the internal pressure and bending combined with the internal pressure, are considered in this study. The biaxial loading is enforced through two steps: a constant internal pressure is applied first and then followed by tension or bending. This loading sequence is common in practice and can produce high value of fracture response which corresponds to the worst scenario. In order to investigate the effect of biaxial loading on the flawed pipeline with multiple cracks, the value of internal pressure varies from 10 MPa to 25 MPa, resulting in the ratio of the hoop stress to the yield stress of 0.2, 0.3 and 0.5, respectively. Hoop stress is expressed by σH=PD/2t, in which P is the internal pressure, D is the outer diameter of pipeline and t is the wall thickness.
3. Results and Discussion
3.1. Fracture Response of Pipelines with Two Collinear Cracks under Tension
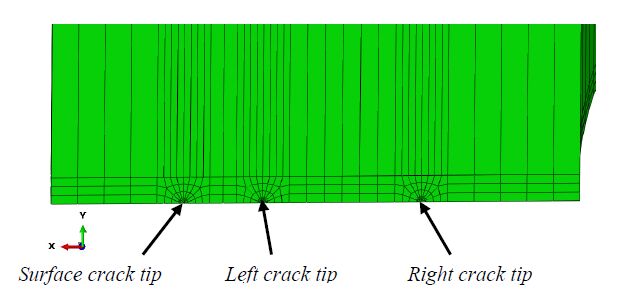
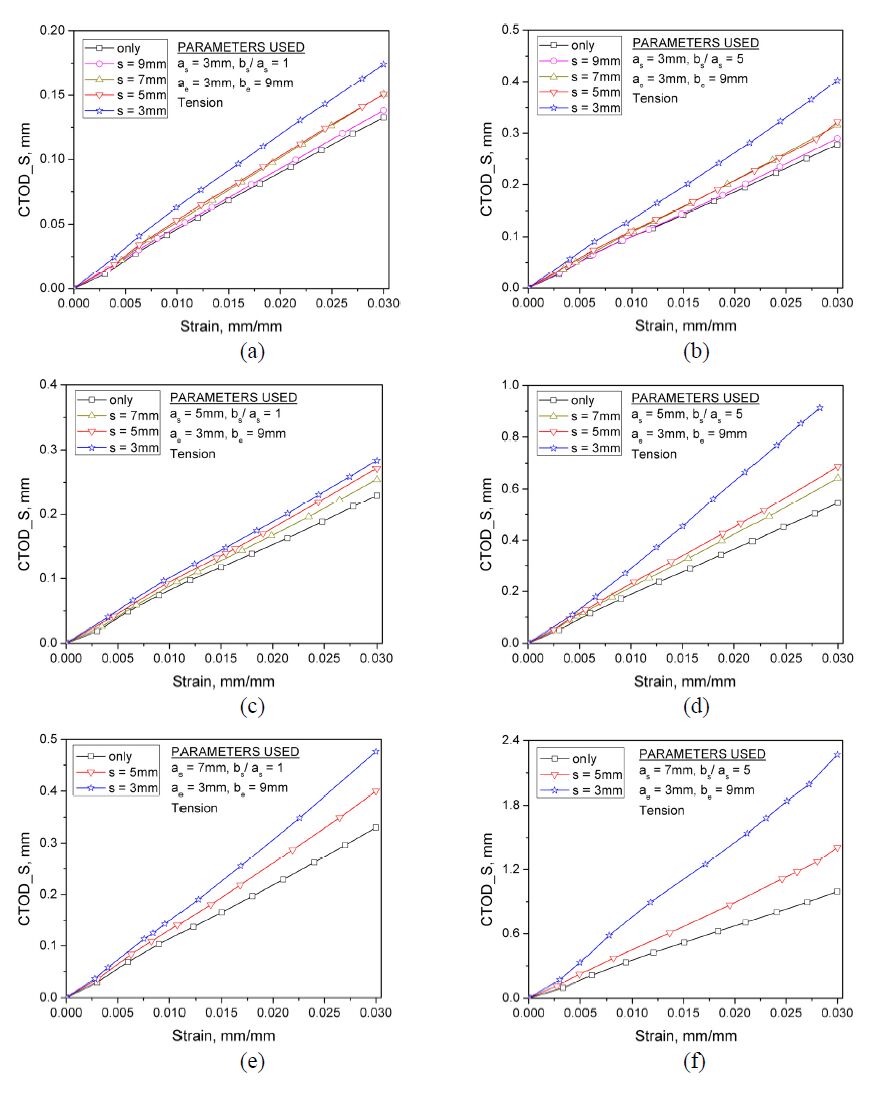
Nonlinear elastic-plastic simulations are carried out to investigate the fracture behaviors of the two interacting cracks located in the pipeline subjected to tension load. We use CTOD_S to represent the CTOD value of the surface crack tip. Similarly, for the embedded crack the CTOD values at the left and right crack tips are denoted by CTOD_L and CTOD_R, respectively. For better illustration and understanding, the three crack tips are presented in Figure 5. The influences of separation distance (s) between the surface crack and embedded crack, crack size and the combined loading on the fracture response are discussed in the following subsections.
The results obtained from the semi-elliptical surface crack are considered to investigate the interaction of these two cracks when the embedded crack size is kept constant as the crack height of ae=3 mm with be/ae=3. Figure 6 shows the CTOD_S-strain curves for different separation distances, given the certain surface crack. The results obtained from the cases with only one surface crack denoted by “only”, are also presented for comparisons. From Figure 6(a) and 6(b), it can be seen that for the case of as=3 mm, CTOD_S increases linearly with the strain for both bs=3 mm and bs=15 mm. Marginal difference between the case of “only” and the case of s=9 mm indicates that the effect of embedded crack on the fracture response of surface crack is minimal. It is consistent with the combination rule of effective crack by BS7910, in which no interaction is considered if the separation distance is greater than the summation of the crack heights of the two cracks. In other words, when the two cracks are separated by more than the critical interaction distance (s=as + ae), the two cracks can be regarded as isolated. While, as the separation distance s is reduced, greater CTOD_S value is obtained.
It can be observed in Figure 6 that when the separation distance s is smaller than the critical interaction distance, the curve of CTOD_S versus strain becomes steeper, compared to the case of “only”, indicating that the CTOD_S value starts to be affected by the crack interaction as a result of the shortened separation distance. Moreover, Figure 6(e) and 6(f) present the curves of CTOD_S versus strains for the deep surface crack (as=7 mm). It is observed that when the separation distance is further reduced, the cracks interaction becomes more pronounced, resulting in much higher CTOD_S values. These observations imply that for varying separation distance, the fracture response at relatively far distance is affected by the cracks interaction in a mild manner, whereas the nonlinear and rapid increases in the fracture response of deep surface crack are observed as the separation distance is reduced. Particularly, compared to the single crack cases, the CTOD_S values can be doubled or even more for the deeper surface crack due to the strong interaction of two closely adjacent cracks.
3.2. Fracture Response of Pipelines with Two Collinear Cracks under Bending
Under the bending load, the flawed pipelines with varying embedded crack sizes are also modeled for comparisons while the semi-elliptical surface crack remains unchanged.
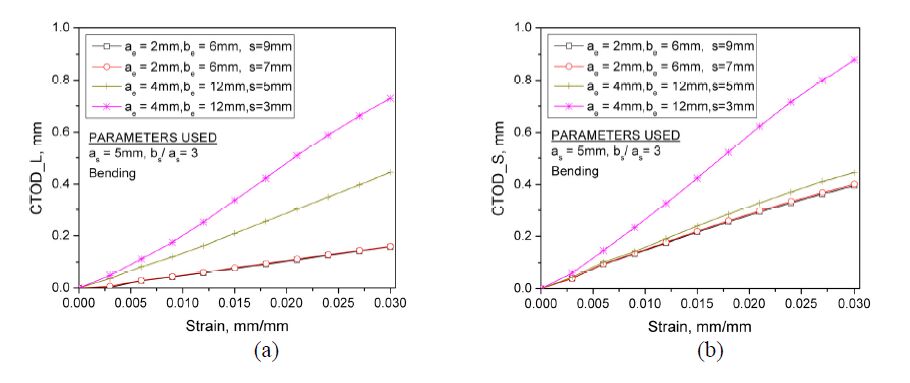
Firstly, the relationships of CTOD against strains for different separation distances are presented in Figure 7(a) and 7(b) for CTOD_L and CTOD_S, respectively. For the small embedded crack (ae=2 mm), the difference of CTOD_L evolutions between the case of s=7 mm and s=9 mm is marginal. While for a large embedded crack (ae=4 mm), the CTOD_L value increases significantly for both s=5 mm and s=3 mm. The similar trend for CTOD_S is also observed from Figure 7(b). It should be noticed that if the two cracks are located so far apart that the cracks can be considered isolated (i.e., s > as + ae), the overall fracture behavior of cracked pipeline is dominated by the relatively large surface crack alone, compared to the small embedded crack. However, it can be seen that in the case of ae=4 mm, the CTOD_S value increases by two times at any strain level when the separation distance s is reduced from 5 mm to 3 mm. It demonstrates that for a given crack configuration, the fracture responses of both cracks are significantly affected by the strong interaction when they are located closer to each other.
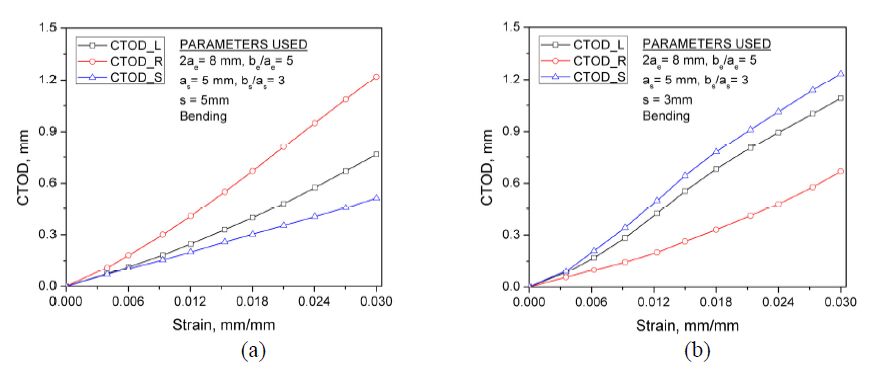
Secondly, the curves of CTOD values versus strains for the three crack tips are presented in Figure 8, where the separation distances of s=5 mm and s=3 mm are considered for the semi-elliptical surface crack of as=5 mm with bs/as=3 and the elliptical embedded crack of with be/ae=5.
In Figure 8(a), it can be seen that at any given strain level, the highest CTOD value is obtained from the right crack tip of the elliptical embedded crack. The possible reason could be explained by the followings: considering the two-crack configuration, the right crack tip is very close to the inner wall (the distance from the right crack tip to the inner wall of the pipeline is 2 mm), which in turn results in higher stress at the right crack tip than the other two crack tips due to the bending moment. In this case, the fracture response of the elliptical embedded crack plays a dominant role in the whole scenario.
On the other hand, in the case of s=3 mm shown in Figure 8(b), it is clearly shown that when the elliptical embedded crack moves closer to the surface crack, i.e., the separation distance is reduced from 5 mm to 3 mm, the value of CTOD_S is the highest while the CTOD_R value is the least at any given strain level. This scenario is quite different from the case of s=5 mm. Additionally, it is noticed that both the CTOD_S and CTOD_L values increases significantly as the strain increases. All these observations indicate that the reduced separation distance plays a significant role in determining the fracture response of multiple interacting cracks.
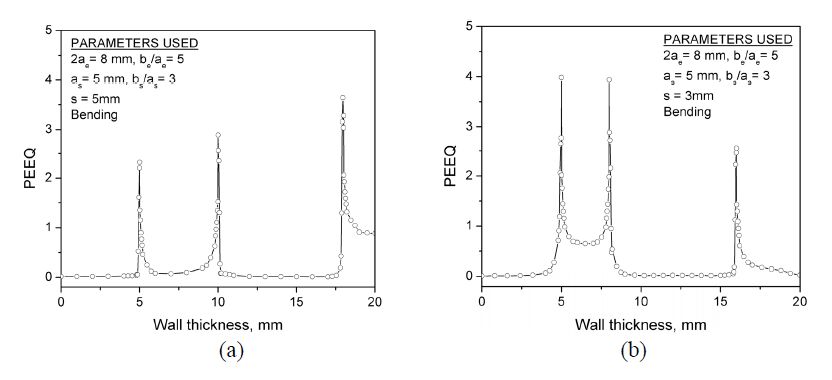
Furthermore, in order to explore the interaction of the semi-elliptical surface crack and the elliptical embedded crack, the variation of the equivalent plastic strain (PEEQ) along the wall thickness is analyzed when the global strain is considered as 0.03. Figure 9 shows the curves of PEEQ versus wall thickness for s=5 mm and s=3 mm, for the given two-crack configuration.
It should be noted that in the axis of abscissa, the value of“0”denotes the outer surface of pipeline along the section profile, and the value of“20”represents the inner surface of pipeline. In Figure 9 it can be observed that three peaks of PEEQ values are obtained at the place of the three crack tips. In the case of s=5 mm, the peak of PEEQ value occurs at the right crack tip of the elliptical embedded crack. However, the semi-elliptical surface crack tip produces the maximum value of PEEQ when the separation distance is reduced to 3 mm.
It is recognized that the higher PEEQ reflects the occurrence of larger plastic deformation. Thus the curves of PEEQ against wall thickness demonstrate that when the two collinear cracks move closer, i.e., the separation distance is shortened to 3 mm, the corresponding fracture behaviors are significantly affected by the strong interaction of the two collinear cracks.
3.3. Interaction Factor γs
To better understand the interaction of two collinear cracks, the interaction factoris introduced to quantify their interactions, defined as follows,
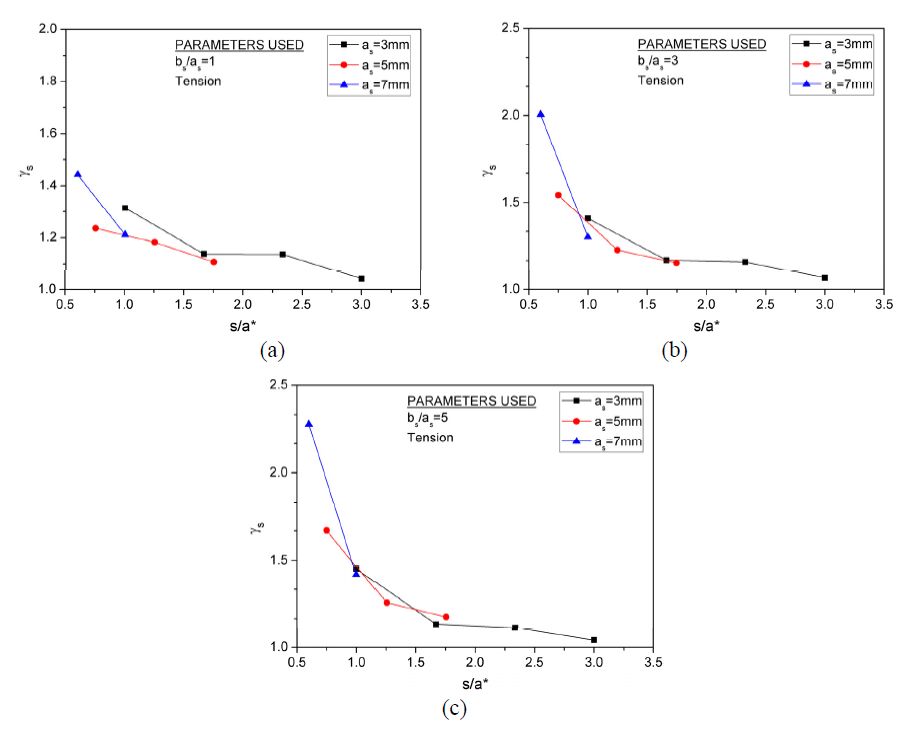
where CTODin and CTODonly are the CTOD_S values from the case of two collinear cracks and the case of a surface crack only, respectively. The effective crack height is defined as a*=(as + ae)/2, then s/a* is regarded as the dimensionless separation distance. When the global strain is assumed as 0.03, the variations of γs with s/a* for different surface crack aspect ratios are plotted in Figure 10. It can be observed that in the case of bs/as=1 shown in Figure 10(a), i.e., for the circular surface crack, most of γs values are less than 1.2 and the maximum one is roughly 1.4 for all the crack depth considered. It indicates that the interaction of two cracks has a little influence on the fracture response of the circular surface crack, although large global strain 3% is considered. As the aspect ratio of surface crack increases, the s/a* value increases significantly. In Figure 10(c) with bs/as=5, for s/a*≤1.0, a considerable increase in γs is observed as s/a* is shortened. The observation implies that the fracture response of the semi-elliptical surface crack is significantly enhanced by the cracks interaction, in particular, for the relatively large deep crack.
Considering the strong influence of the two cracks interaction on the fracture behavior of semi-elliptical surface crack, the function of γs in terms of the relative position of the interacting cracks is proposed for the preliminary fracture assessment of the surface crack affected by the multiple cracks interaction. It is difficult to describe the variation of γs with the dimensionless separation distance by using a low order function [10]. Therefore, by virtue of Least Squares Method, the three order polynomial is employed to fabricate the relationship between γs, s/a* and bs/as. The expression of γs function is given below,
|
γs=A9(s/a∗)3+A8(bs/as)3+A7(s/a∗)(bs/as)2+A6(s/a∗)2(bs/as)+A5(s/a∗)2+A4(bs/as)2+A3(s/a∗)(bs/as)+A2(s/a∗)+A1(bs/as)+A0
|
(2)
|
Where A0 : A9 are coefficients determined by Least Squares Method, based on the current FE results. The values for these coefficients are listed in Table 1.
Table 1.Values for the coefficients in Eq. (2).
| A0 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 |
| 2.475 | 0.001 | −2.329 | −0.350 | 0.150 | 1.446 | 0.071 | 0.006 | −0.019 | −0.268 |
The comparisons of the computational and the predicted γs for the tension and bending are presented in Table 2 and Table 3, respectively. From these two tables, it can be seen that most of the γs values obtained by Eq. (2) are in good agreement with the current numerical results within an error limit of 5%. It indicates that Eq. (2) can provide a reasonably accurate and reliable value of interaction factor γs for the pipelines with multiple cracks subjected to large plastic strain of 0.03.
Table 2.Comparisons of the computational and the predicted γs for tension.
| bs/as | s/a* | Computational γs | Predicted γs | Error |
| 1 | 0.75 | 1.2352 | 1.3417 | −8.63% |
| 1.00 | 1.1825 | 1.1823 | −0.02% |
| 1.25 | 1.1821 | 1.1120 | 5.93% |
| 1.67 | 1.1373 | 1.1248 | 1.10% |
| 2.33 | 1.1357 | 1.2254 | −7.89% |
| 3.00 | 1.0422 | 1.0082 | 3.26% |
| 3 | 0.75 | 1.5434 | 1.6440 | −6.52% |
| 1.00 | 1.4080 | 1.3841 | 1.70% |
| 1.25 | 1.2268 | 1.2309 | −0.33% |
| 1.67 | 1.1691 | 1.1448 | 2.08% |
| 2.33 | 1.1593 | 1.1890 | −2.57% |
| 3.00 | 1.0673 | 1.0408 | 2.48% |
| 5 | 0.75 | 1.6706 | 1.8247 | −9.22% |
| 1.00 | 1.4472 | 1.4771 | −2.07% |
| 1.25 | 1.2577 | 1.2539 | 0.30% |
| 1.67 | 1.1352 | 1.0902 | 3.96% |
| 2.33 | 1.1143 | 1.1122 | 0.19% |
| 3.00 | 1.0424 | 1.0670 | -2.36% |
Table 3.Comparisons of the computational and the predicted γs for bending.
| bs/as | s/a* | Computational γs | Predicted γs | Error |
| 1 | 0.75 | 1.2089 | 1.3417 | 10.99% |
| 1.00 | 1.1825 | 1.1823 | −0.02% |
| 1.25 | 1.2046 | 1.1120 | −7.69% |
| 1.67 | 1.1395 | 1.1248 | −1.29% |
| 2.33 | 1.2176 | 1.2254 | 0.64% |
| 3.00 | 1.0282 | 1.0082 | −1.95% |
| 3 | 0.75 | 1.5067 | 1.6440 | 9.11% |
| 1.00 | 1.4105 | 1.3841 | −1.87% |
| 1.25 | 1.1948 | 1.2309 | 3.02% |
| 1.67 | 1.1300 | 1.1448 | 1.31% |
| 2.33 | 1.1131 | 1.1890 | 6.82% |
| 3.00 | 1.0196 | 1.0408 | 2.08% |
| 5 | 0.75 | 1.8752 | 1.8247 | −2.69% |
| 1.00 | 1.4395 | 1.4771 | 2.61% |
| 1.25 | 1.2809 | 1.2539 | −2.11% |
| 1.67 | 1.1170 | 1.0902 | −2.40% |
| 2.33 | 1.1099 | 1.1122 | 0.21% |
| 3.00 | 1.0000 | 1.0670 | 6.70% |
3.4. Effect of Internal Pressure
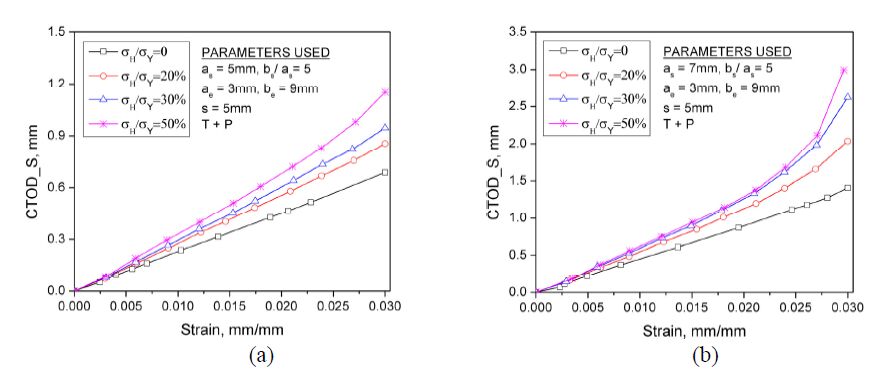
Internal pressure is one of the primary loadings experienced by offshore pipelines as well as ground pipelines in operation. For pipeline design, the effect of the internal pressure cannot be neglected, since it changes the effective axial force which is one of the dominating factors resulting in global buckling of pipelines [35]. In this section, the nonlinear elastic-plastic analyses focus on two circumferential cracks in the cracked pipeline subjected to combined loadings such as tensile loading combined with the internal pressure. The influence of the hoop stress (induced by internal pressure) on the CTOD_S evolutions is investigated in details.
Given the same separation distance of s=5 mm, the comparisons of CTOD_S values obtained from tension combined with different internal pressure cases are presented in Figure 11.“T+P”denotes the tension combined with internal pressure. Three different values of σH/σY are considered as 20%, 30% and 50% respectively, and σH/σY=0 represents pure tension loading (no internal pressure). In Figure 11(a), for surface crack of as=5 mm with bs/as=5, CTOD_S increases gradually as the hoop stress increases at the same global strain level. For surface crack of as=7 mm with bs/as=5 as shown in Figure 11(b), the linear increasing trend of all four CTOD_S—strain curves can be observed for εg < 0.02. However, the exponential increase of CTOD_S values is found for the high strain level εg≥0.02 under the combined loadings. For instance, at εg=0.03, CTOD_S value obtained from the case of σH/σY=50 % is two times greater than that from the tension loading only (σH/σY=0). This observation could perhaps be explained by the enhancement of the local deformation in the cracked pipeline. In other words, the local deformation can be enlarged by the combined loading to some extent as the plastic strain increases continuously, and subsequently, it leads to the crack opening largely.
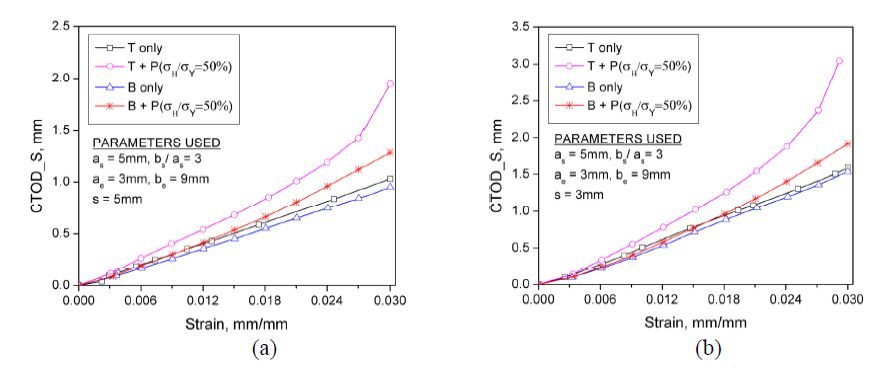
In order to further investigate the effect of the different combined loadings and the cracks interaction on the evolution of CTOD_S, the bending combined with internal pressure (“B+P”) is also considered for different separation distances.
For a given crack configuration, that is, surface crack of as=5 mm with bs/as=3 and embedded crack of ae=3 mm with be=3 mm, Figure 12(a) and 12(b) present the curves of the CTOD_S against strain for the four different loadings, corresponding to s=5 mm and s=3 mm, respectively.
When the internal pressure (σH/σY=50 %) is applied on the flawed pipeline, the CTOD_S values are significantly augmented for two combined loadings at the same strain level, which is similar to the investigation discussed for Figure 11. In addition, it is observed from both figures in Figure 12 that the slope of the CTOD_S-strain curve obtained from the tension only is slightly steeper than those from the bending only, implying that the more severe deformation can be introduced by the tension load rather than the pure bending.
Furthermore, it is also found that at any given strain level, the CTOD_S value from the tension load combined with the internal pressure (σH/σY=50 %) is much larger than that from the bending load combined with the internal pressure, indicating that the difference of CTOD_S between the two combined loadings is significantly amplified due to the additional internal pressure imposed. In addition, given the tension load combined with the internal pressure (σH/σY=50 %), comparison of two figures in Figure 12 reveals that when the two collinear cracks are moved closer to each other (s=3 mm), even higher CTOD_S values are produced due to the stronger interaction of the two closer cracks, compared to the case of s=5 mm in which interaction is less significant. In summary, all these observations demonstrate that the combined loadings can significantly affect the fracture response of the flawed pipelines, particularly at high global strain levels.
4. Conclusions
In this study, extensive 3-D finite element simulations are performed on the nonlinear elastic-plastic fracture behaviors of two interacting cracks contained in offshore pipelines. Different loading cases such as tension, pure bending and biaxial loadings are considered. The influences of the crack configurations, the separation distance, and the internal pressure on the fracture responses of the cracks are investigated in details. Some useful conclusions are drawn as follows.
1) A parametric study on the effect of different separation distances of the two interacting collinear cracks is performed.
2) The interaction factor is introduced to quantify the interaction of the two interacting cracks, and the proposed function for interaction factor can be useful for the preliminary fracture assessment of the surface crack affected by the interactions.
3) Four different loading conditions generally experienced by offshore pipelines are taken into account to investigate their corresponding fracture response. The results indicate that the most severe fracture response can be produced by the tension load combined with high internal pressure (σH/σY=50 %).
4) Given a certain separation distance, the parametric studies on the effect of the internal pressure show that under the combined loadings, the linear increasing trend for all CTOD_S-strain curves is observed when εg < 0.02, while the exponential increase of CTOD_S value is observed for the high strain level (εg≥0.02).
Conflict of Interest
The authors declare that there is no conflict of interest regarding the publication of this manuscript.









 DownLoad:
DownLoad: