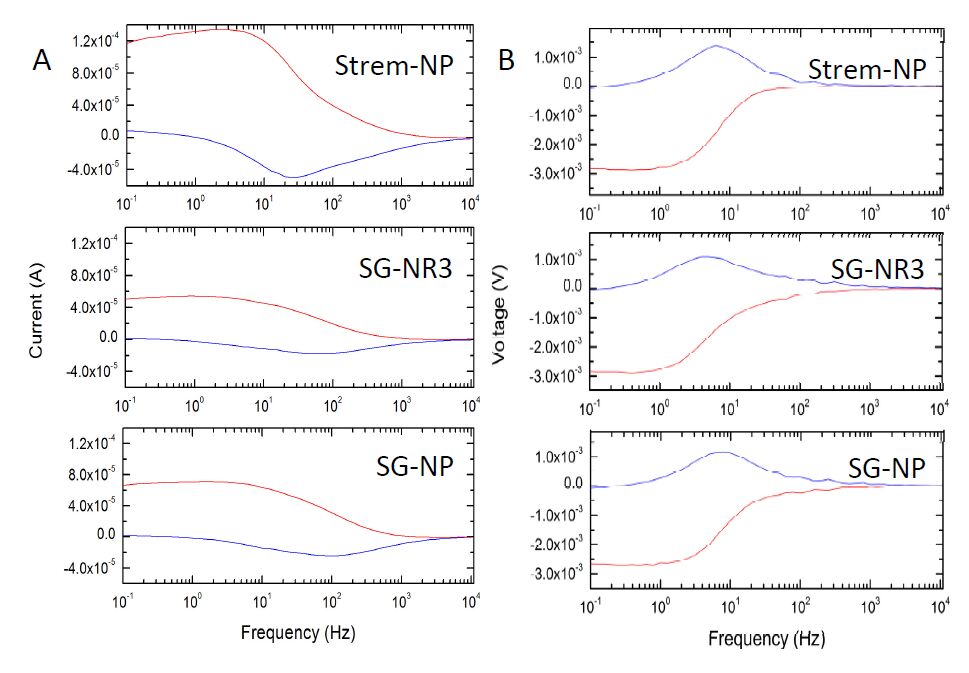
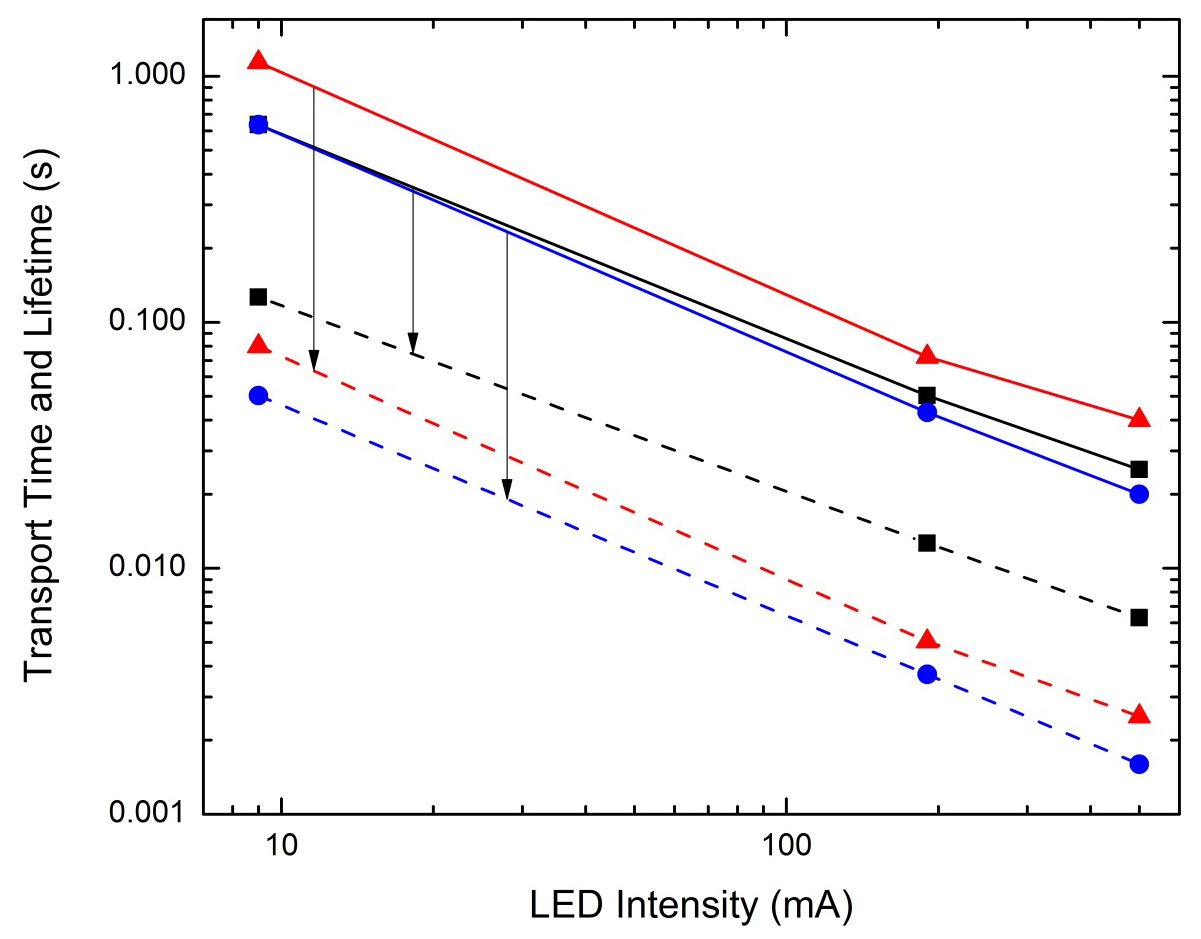
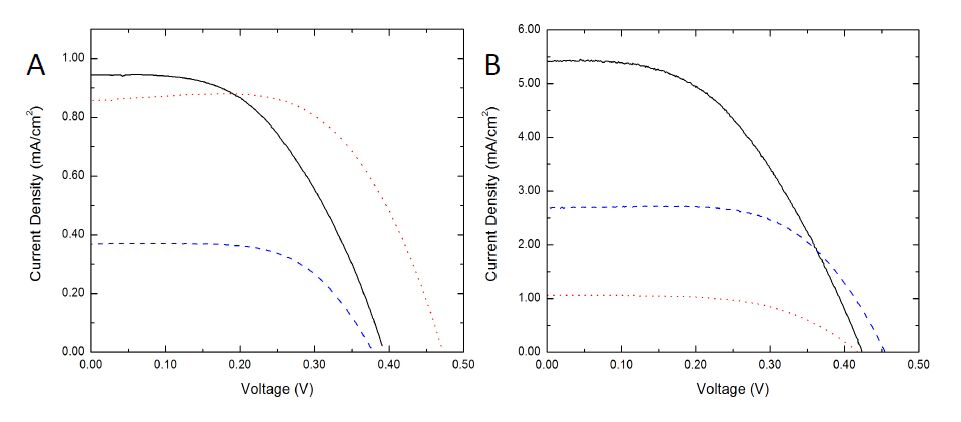
Owing to its high electron mobility, zinc oxide represents a promising alternative to titanium dioxide as the working electrode material in dye-sensitized solar cells (DSCs). When zinc oxide is grown into 1-D nanowire arrays and incorporated into the working electrode of DSCs, enhanced electron dynamics and even a decoupling of electron transport (τd) and electron lifetime (τn) have been observed. In this work, DSCs with working electrodes composed of solution-grown, unarrayed ZnO nanorods are investigated. In order to determine whether such devices give rise to similar decoupling, intensity modulated photocurrent and photovoltage spectroscopies are used to measure τd and τn, while varying the illumination intensity. In addition, ZnO nanorod-based DSCs are compared with ZnO nanoparticle-based DSCs and nanomaterial shape is shown to affect electron dynamics. Nanorod-based DSCs exhibit shorter electron transport times, longer electron lifetimes, and a higher τn/τd ratio than nanoparticle-based DSCs.
1.
Introduction
In this work, we are concerned with the following fractional boundary value problem
where $ 1 < \alpha\leq 2, \ D^{\alpha, \ \varphi}_{0^{+}} $ is the fractional derivative operator of order $ \alpha $ with respect to a certain strictly increasing function $ \varphi\in C^{2}[0, 1] $ with $ \varphi'(x) > 0 $ for all $ x\in [0, 1] $ and $ f, \varphi, \beta_{i}, \eta_{i}, \lambda $ satisfy:
$ (H_{1})\ f(t, u):[0, 1]\times R^{+}\rightarrow R^{+} $ is continuous and increasing in $ u $ for each $ t\in [0, 1], $ the function $ \varphi:[0, 1]\rightarrow R $ is a strictly increasing function such that $ \varphi\in C^{2}[0, 1], $ with $ \varphi'(x) > 0 $ for all $ x\in [0, 1] $;
$ (H_{2})\ 0\leq \beta_{i} < 1, \ 0 < \eta_{i} < 1\ (i = 1, 2, \cdot\cdot\cdot, m-2) $ satisfy $ 0\leq \sum\limits_{i = 1}^{m-2}\beta_{i} < 1, \ 0 < \eta_{1} < \eta_{2} < \cdot\cdot\cdot < \eta_{m-2} < 1, \lambda > 0 $ is a parameter.
The fractional calculus first began in 1965. After a long time, this subject was relevant only in pure mathematics, many mathematicians have studied these new fractional operators by presenting new definitions and studying their important properties, but in the last century, this subject showed its applications in the modeling of many phenomena in various fields of science and engineering, such as control theory, electric circuits, viscoelasticity, mechanics, physics, neural networks [1,2,3,4,5,6,7,8,9,10,11,12].
In all those definitions there is a special kind of a kernel dependency. Therefore, in order to analyze fractional differential equations in a generic way, a fractional derivative with respect to another function called $ \varphi $-Riemann-Liouville and $ \varphi $-Caputo derivative was proposed [15] and for particular choices of $ \varphi, $ we obtain some well known fractional derivative. For example, if we choose $ \varphi(t) = t, $ the $ \varphi $-Riemann-Liouville and $ \varphi $-Caputo fractional derivative are reduced to the Riemann-Liouville and Caputo derivative respectively in traditional sense. Alternatively, if we choose $ \varphi(t) = logt, $ where $ log(\cdot) = log_{e}(\cdot), $ the $ \varphi $-Riemann-Liouville and $ \varphi $-Caputo fractional derivative are reduced to the Hadamard and Hadamard-Caputo derivative respectively [13,14]. Therefore, problem (1.1), (1.2) generates many types and also mixed types of fractional differential equations with boundary conditions.
Let us mention some motivations for studying problem (1.1), (1.2). In the limit case $ \lambda = 1 $ and $ \beta_{i} = \beta, \eta_{i} = \eta, i = 1, 2, \cdot\cdot\cdot, $ (1.1), (1.2) reduces to
In [22], the authors studied the existence of positive solutions for the problem (1.3), (1.4). In [23], using the fixed point theorems of Banach and Schaefer, the authors studied the existence and uniqueness results of the boundary value problems for a fractional differential equation involving Caputo operator with respect to the new function $ \psi $ given by the form
where $ ^{C}D_{a^{+}}^{\alpha, \ \psi} $ is the $ \psi $-Caputo fractional derivative of order $ n-1 < \alpha\leq n\ (n = [\alpha]+1). $
Almeida et al. [24] studied the initial value problem of a fractional differential equation including $ \varphi $-Caputo fractional derivative
where $ ^{C}D_{a^{+}}^{\alpha, \ \varphi} $ is the $ \varphi $-Caputo fractional derivative of order $ n-1 < \alpha < n. $
On the other hand, most of the existing literature does not consider the properties of the solution. Well, here's the problem: How can we get the properties of the solutions when they are known to exist. So far, few papers can be found in the literature both on the existence and properties of solutions for fractional boundary value problem.
Zhai et al. [16] studied the following nonlinear fractional four-point boundary value problem with a parameter:
where $ D_{0^{+}}^{\alpha} $ is the Riemann-Liouville fractional derivative. Unfortunately, the fractional derivative in this paper is just the Caputo derivative in the traditional sense.
Inspired by the work in [16] and many known results, in this paper, we develop the existence and uniqueness of positive solutions to the fractional boundary value problems (1.1), (1.2). Using the fixed point theorems of concave operators in partial ordering Banach spaces, we not only show the existence of positive solution for the problem (1.1), (1.2), but also present some properties of positive solutions to the boundary value problem dependent on the parameter. Some definitions, lemmas and basic results about $ \varphi $-Riemann-Liouville derivative are presented in Section 2. The main results are given in section 3. Some illustrative examples are constructed in Section 4.
2.
The preliminary lemmas
Let $ \varphi $ be a function of $ C^{2}[a, b] $ with $ \varphi'(t) > 0 $ for all $ t\in [a, b]. $
Definition 2.1 [21] The $ \varphi $-Riemann-Liouville fractional integral of order $ \alpha > 0 $ of a function $ x:[a, b]\rightarrow R $ is given by
Definition 2.2 [21] The $ \varphi $-Riemann-Liouville fractional derivative of order $ \alpha $ of a function $ x $ is defined as
where $ n = [\alpha]+1. $
The $ \varphi $-Caputo fractional derivative of order $ \alpha $ of a function $ x $ is defined as
where $ x_{\varphi}^{[k]}(t): = \biggl(\frac{1}{\varphi'(t)}\frac{d}{dt}\bigamma)^{k}x(t). $
Theorem 2.1 [15] If $ x\in C^{n}[a, b], $ then
Theorem 2.2 [15] Let $ x: [a, b]\rightarrow R. $ Then
1. If $ x\in C[a, b], $ then $ ^{C}D^{\alpha, \ \varphi}_{a^{+}}I^{\alpha, \ \varphi}_{a^{+}}x(t) = x(t); $
2. If $ x\in C^{n-1}[a, b], $ then
In the following, we give some basic definitions in ordered Banach spaces and two fixed point theorems of concave operators which will be used later, all the materials can be found in [17,18,19,20]. We denote $ \theta $ the zero element of $ E. $
Definition 2.3 Let $ X $ be a semi-ordered real Banach space. The nonempty convex closed subset $ P $ of $ X $ is called a cone in $ X $ if $ ax\in P $ for all $ x\in P $ and $ a\geq 0 $ and $ x\in X $ and $ -x\in X $ imply $ x = \theta. $
Let the real Banach space $ E $ be partially ordered by a cone $ P $ of $ E, $ that is $ x\leq y $ if and only if $ y-x\in P. $ If $ x\leq y $ and $ x\neq y, $ then we denote $ x < y $ or $ y > x. $
Recall that cone $ P $ is said to be solid if the interior $ \mathring{P} $ is nonempty and we denote $ x > > 0 $ if $ x\in \mathring{P}. $ $ P $ is normal if there exists a positive constant $ N $ such that $ \theta\leq x\leq y $ implies $ \|x\|\leq N\|y\|, $ $ N $ is called the normal constant of $ P. $
Definition 2.4 Let $ D $ be a convex subset in $ E. $ An operator $ T:D\rightarrow E $ is a concave operator if
for all $ x, y\in D $ and $ t\in [0, 1]. $
Definition 2.5 Let $ P $ be a cone in real Banach space $ E $ and $ e\in P\backslash\{\theta\}. $ Set
and define
It is easy to see that $ E_{e} $ becomes a normed linear space under the norm $ \|\cdot\|_{e}. $ $ \|x\|_{e} $ is called the e-norm of the element $ x\in E_{e}. $
Lemma 2.3 [17] Suppose $ P $ is a normal cone. Then the following results hold:
(i) $ E_{e} $ is a Banach space with e-norm, and there exists a constant $ m > 0 $ such that $ \|x\|\leq m\|x\|_{e}, \ \ \ \forall x\in E_{e}; $
(ii) $ P_{e} = E_{e}\cap P $ is a normal solid cone of $ E_{e} $ and $ \mathring{P_{e}} = \{x\in E_{e}:\mbox{there exists}\ \delta = \delta(x) > 0\ \mbox{such that} \ x\geq \delta e\}. $
Lemma 2.4 [19] Suppose $ P $ is a normal solid cone and operator $ T:P\rightarrow P $ is a concave operator. Assume that $ T\theta > > \theta. $ Then the following results hold:
(ⅰ) there exists $ 0 < \lambda^{*}\leq \infty $ such that the equation
has a unique solution $ u(\lambda) $ in $ P $ for $ 0\leq \lambda < \lambda^{*}, $ when $ \lambda\geq \lambda^{*}, $ the operator equation (2.1) has no solution in $ P; $
(ⅱ) for any $ u_{0}\in P, $ let $ u_{0}(\lambda) = u_{0}, \ \ u_{n}(\lambda) = \lambda Tu_{n-1}(\lambda), \ n = 1, 2, 3, \cdot\cdot\cdot. $ Then for $ 0 < \lambda < \lambda^{*}, $ we have $ u_{n}(\lambda)\rightarrow u(\lambda) $ as $ n\rightarrow \infty; $
(ⅲ) $ u(\cdot):[0, \lambda^{*})\rightarrow P $ is continuous and strongly increasing $ (0\leq \lambda_{1} < \lambda_{2} < \lambda^{*}\Rightarrow u(\lambda_{1}) < < u(\lambda_{2})). $ Furthermore, $ u(t\lambda)\leq tu(\lambda) $ for $ 0\leq \lambda < \lambda^{*}, \ 0\leq t\leq 1. $
(ⅳ) $ \lambda\rightarrow\lambda^{*}-0 $ implies $ \|u(\lambda)\|\rightarrow \infty; $
(ⅴ) if there exist $ v_{0}\in P $ and $ \lambda_{0} > 0 $ such that $ \lambda_{0}Tv_{0}\leq v_{0}, $ then $ \lambda^{*} > \lambda_{0}. $
Lemma 2.5 [19] If $ T:P\rightarrow P $ is concave, then $ T $ is increasing.
Lemma 2.6 [20] Suppose $ P $ is a normal solid cone and operator $ T:\mathring{P}\rightarrow \mathring{P} $ is an increasing operator. We presume there exists a constant $ 0 < r < 1 $ such that
Let $ u_{\lambda} $ be the unique solution in $ \mathring{P} $ of the equation $ Tu = \lambda u(\lambda > 0). $ Then
(ⅰ) $ u_{\lambda} $ is strongly decreasing $ (0 < \lambda_{1} < \lambda_{2}\Rightarrow u_{\lambda_{1}} > > u_{\lambda_{2}}); $
(ⅱ) $ u_{\lambda} $ is continuous $ (\lambda\rightarrow \lambda_{0}(\lambda_{0} > 0)\Rightarrow \|u_{\lambda}-u_{\lambda_{0}}\|\rightarrow 0); $
(ⅲ) $ \lim_{\lambda\rightarrow +\infty}\|u_{\lambda}\| = 0, \ \ \ \lim_{\lambda\rightarrow 0^{+}}\|u_{\lambda}\| = +\infty. $
3.
Main results
Denote
Lemma 3.1 Assume that $ (H_{1}), (H_{2}) $ hold. Then the fractional boundary value problem (1.1), (1.2) is equivalent to the following integral equation
where
Here for the sake of convenience, we write $ \eta_{0} = 0, \eta_{m-1} = 1 $ and $ \sum\limits_{i = m_{1}}^{m_{2}}f_{i} = 0 $ for $ m_{2} < m_{1}. $
Proof. Use $ y(t) $ to replace $ f(t, u) $ in (1.1). Let
Then from Theorem 2.2, we have
Note that $ u(0) = 0 $ implies $ c_{2} = 0. $ Therefore, we obtain
In particular,
and
Note that $ u(1) = \sum_{i = 1}^{m-2}\beta_{i}u(\eta_{i}), $ and hence we obtain
As a result, from (3.4) we have
This completes the proof. Lemma 3.2 Assume that $ (H_{1}), (H_{2}) $ hold. Then the Green's function $ G(t, s) $ defined by (3.2) has the following properties:
(ⅰ) $ G(t, s) $ is a continuous function on $ [0, 1]\times [0, 1]; $
(ⅱ) $ G(t, s) > 0 $ for all $ (t, s)\in (0, 1); $
(ⅲ)
Proof. (ⅰ) From the expression of $ G(t, s), $ it is easy to get that $ G(t, s) $ is continuous.
(ⅱ) From $ (H_{1}), (H_{2}), $ we can get $ \mu > 0. $
For $ 0\leq t \leq 1, \ \eta_{i-1}\leq s\leq \min\{\eta_{i}, t\}, i = 1, 2, \cdot\cdot\cdot, m-1, $
Consider
Then we have
which implies that $ e(t) $ is decreasing for $ 0\leq t \leq 1, \ \eta_{i-1}\leq s\leq \min\{\eta_{i}, t\}, i = 1, 2, \cdot\cdot\cdot, m-1. $
Furthermore, we have
As we know,
consequently, we have $ e(1) > 0. $
As a result, $ G(t, s) > 0 $ for $ 0\leq t \leq 1, \ \eta_{i-1}\leq s\leq \min\{\eta_{i}, t\}, i = 1, 2, \cdot\cdot\cdot, m-1. $
For $ 0\leq t \leq 1, \ \max\{\eta_{i-1}, t\}\leq s\leq \eta_{i}, i = 1, 2, \cdot\cdot\cdot, m-1, $
Therefore, $ G(t, s) > 0 $ for all $ t, s\in (0, 1). $
(ⅲ) From $ (H_{1}), (H_{2}) $ and the expression of $ G(t, s), $ we can easily obtain this property. Let $ E = C[0, 1] $ be a Banach space equipped with the norm
Define the cone $ K\subset E $ by
then $ K $ is a normal solid cone of $ E. $ Let
From $ (H_{1}) $ and Lemma 3.2, we have $ g(t)\in E $ and $ g(t)\in K\setminus\{\theta\}. $
Let $ X = E_{e} = \{u\in E:\exists \tau > 0, \ \mbox{such that}\ -\tau g(t)\leq u(t)\leq \tau g(t), \ 0\leq t\leq 1\} $ be a Banach space equipped with the norm $ \|u\|_{X} = \inf\{\tau > 0: -\tau g(t)\leq u(t)\leq \tau g(t), \ \ 0\leq t\leq 1\}. $
Define $ \tilde{K} = X\cap K, $ then $ \tilde{K} $ is a normal solid cone of $ X $ and $ \mathring{\tilde{K}} = \{u\in X: \mbox{there exists}\ \delta > 0 \ \mbox{such that}\ u(t)\geq \delta g(t), \ \ 0\leq t\leq 1, \ \ \forall u\in X\}. $ Moreover, there exists a constant $ m > 0 $ such that $ \|u\|_{E}\leq m \|u\|_{X}. $
Theorem 3.3 Assume that $ (H_{1}), (H_{2}) $ hold. Furthermore, $ f(t, \cdot) $ is concave and there exist constants $ \chi > 0, \beta > 0 $ such that
Then the following results hold:
(ⅰ) there exists $ 0 < \lambda^{*}\leq \infty $ such that the fractional boundary value problem (1.1), (1.2) has a unique positive solution $ u_{\lambda} $ in $ \tilde{K} $ for $ 0 < \lambda < \lambda^{*}, $ the fractional boundary value problem(1.1), (1.2) has no positive solution in $ \tilde{K} $ for $ \lambda\geq \lambda^{*}; $
(ⅱ) for any $ u_{0}\in \tilde{K}, $ let
Then for $ 0 < \lambda < \lambda^{*}, $ we have
(ⅲ) if $ 0 < \lambda < \lambda^{*}, \ \max_{0\leq t\leq 1}|u_{\lambda}(t)- u_{\lambda_{0}}(t)|\rightarrow 0 \ \mbox{as} \ \lambda\rightarrow \lambda_{0} $ and if $ 0 < \lambda_{1} < \lambda_{2} < \lambda^{*}, $ then $ u_{\lambda_{1}}(t)\leq u_{\lambda_{2}}(t), \ \ 0\leq t\leq 1 $ and $ u_{\lambda_{1}}(t)\not\equiv u_{\lambda_{2}}(t); $
(ⅳ) $ u_{v\lambda}(t)\leq vu_{\lambda}(t) $ for $ 0 < \lambda < \lambda^{*}, \ \ 0\leq v\leq 1, \ \ 0\leq t\leq 1. $
(ⅴ) if $ \lim_{u\rightarrow \infty}\frac{f(t, u)}{u} = 0 $ uniformly on $ [0, 1], $ then $ \lambda^{*} = \infty. $
Proof. Define an operator $ T $ by
Thus we know that $ u $ is a solution of (1.1), (1.2) if and only if $ u = \lambda Tu. $ For $ u\in K, $ in view of $ (H_{1}), (H_{2}) $ and Lemma 3.2, we can get $ Tu\in K. $ Owing to the concavity of $ f(t, \cdot), $ for $ u > 1, $ we have
from (3.8), we obtain
So, for $ u\in K, $ we have
where $ N_{1} = \max_{0\leq t\leq 1}f(t, \|u\|_{E})\leq \max_{0\leq t\leq 1}f(t, \|u\|_{E}+1)\leq \beta (1+\|u\|_{E}), $ so, we have $ 0\leq (Tu)(t)\leq N_{1}g(t), $ which implies $ Tu\in X. $ Thus, $ Tu\in \tilde{K}, $ this means that $ T: \tilde{K}\rightarrow \tilde{K}. $ In view of the concavity of $ f(t, \cdot), $ we have the operator $ T $ is concave.
From (3.9), we have $ (T\theta)(t) = \int_{0}^{1}G(t, s)\varphi'(s)f(s, 0)ds\geq \chi g(t), \ 0\leq t\leq 1. $ So, $ T\theta\in \mathring{\tilde{K}}, $ this means that $ T\theta > > \theta. $ Then all the conditions of Lemma 2.4 are satisfied. Thus from Lemma 2.4, there exists $ 0 < \lambda^{*}\leq \infty $ such that the equation $ u = \lambda Tu $ has a unique positive solution $ u_{\lambda} $ in $ \tilde{K} $ for $ 0 < \lambda < \lambda^{*}, $ the equation $ u = \lambda Tu $ has no positive solution in $ \tilde{K} $ for $ \lambda\geq \lambda^{*}.; $
For any $ u_{0}\in \tilde{K}, $ let $ u_{n} = \lambda Tu_{n-1}, n = 1, 2, 3, \cdot\cdot\cdot, $ then we have $ u_{n}\rightarrow u_{\lambda}\ \mbox{as}\ \ n\rightarrow \infty $ for $ 0 < \lambda < \lambda^{*}, \ u_{\lambda}: (0, \lambda^{*})\rightarrow \tilde{K} $ is continuous and strongly increasing. Furthermore, $ u_{t\lambda}\leq tu_{\lambda} $ for $ 0\leq\lambda < \lambda^{*}, \ 0\leq t\leq 1;\ \lambda \rightarrow \lambda^{*}-0 $ implies $ \|u_{\lambda}\|_{X}\rightarrow \infty; $ if there exist $ v_{0}\in \tilde{K} $ and $ \lambda_{0} > 0 $ such that $ \lambda_{0}Tv_{0}\leq v_{0}, $ then $ \lambda^{*} > \lambda_{0}. $ From this results, we can get
(ⅰ) the fractional boundary value problem (1.1), (1.2) has a unique positive solution $ u_{\lambda} $ in $ \tilde{K} $ for $ 0 < \lambda < \lambda^{*}, $ the fractional boundary value problem (1.1), (1.2) has no positive solution in $ \tilde{K} $ for $ \lambda\geq \lambda^{*}; $
(ⅱ) for any $ u_{0}\in \tilde{K}, $ let
Then for $ 0 < \lambda < \lambda^{*}, $ we have
(ⅲ)$ \max_{0\leq t\leq 1}|u_{\lambda}(t)- u_{\lambda_{0}}(t)|\rightarrow 0 \ \mbox{as} \ \lambda\rightarrow \lambda_{0}, $ where $ 0 < \lambda_{0} < \lambda^{*} $ and if $ 0 < \lambda_{1} < \lambda_{2} < \lambda^{*}, $ then there exists $ \delta > 0 $ such that $ u_{\lambda_{2}}(t)- u_{\lambda_{1}}(t)\geq \delta g(t), \ \ 0\leq t\leq 1, $ this means that $ u_{\lambda_{1}}(t)\leq u_{\lambda_{2}}(t), \ 0\leq t\leq 1 $ and $ u_{\lambda_{1}}(t)\not\equiv u_{\lambda_{2}}(t); $
(ⅳ) for $ 0 < \lambda < \lambda^{*}, \ u_{\delta\lambda}(t)\leq \delta u_{\lambda}(t), \ \ 0\leq \delta\leq 1, \ \ 0\leq t\leq 1. $
(ⅴ) Denote $ \eta = \|g\|_{E}, $ for any given $ \lambda > 0, $ by $ \lim_{u\rightarrow \infty}\frac{f(t, u)}{u} = 0, $ there exists a large $ T > 0, $ such that $ f(t, T)\leq (\eta \lambda)^{-1}T, \ \ 0\leq t\leq 1. $ Let $ v_{0}(t) = \eta^{-1}T g(t), $ from Lemma 2.5, we have
where $ M_{2} = \sup_{0\leq t\leq 1}[\eta^{-1}T+\lambda f(s, T)]\leq \eta^{-1}T+\lambda \beta (T+1), $ this means that $ v_{0}(t)-\lambda Tv_{0}\in \tilde{K}. $ That is $ \lambda Tv_{0}\leq v_{0}. $ By Lemma 2.4 (v), we have $ \lambda^{*} > \lambda, $ because of the arbitrariness of $ \lambda, $ we can get $ \lambda^{*} = \infty. $ Theorem 3.4 Assume that $ (H_{1}), (H_{2}) $ hold. Furthermore, the following conditions hold:
(ⅰ) there exists a number $ 0 < r < 1 $ such that
(ⅱ) there exists a number $ \xi > 0 $ such that $ f(t, 1)\leq \xi; $
(ⅲ) $ \min_{0\leq t\leq 1}f(t, g(t)) > 0, $ where $ g(t) $ is given by (3.7).
Then the following results hold:
(ⅰ) for any given $ \lambda > 0, $ the fractional boundary value problem (1.1), (1.2) has a unique positive solution $ u_{\lambda} $ in $ \mathring{\tilde{K}}; $
(ⅱ) if $ 0 < \lambda_{1} < \lambda_{2}, $ then $ u_{\lambda_{1}}(t)\leq u_{\lambda_{2}}(t), \ 0\leq t\leq 1 $ and $ u_{\lambda_{1}}(t)\not\equiv u_{\lambda_{2}}(t); $
(ⅲ) $ \max_{0\leq t\leq 1}|u_{\lambda}(t)-u_{\lambda_{0}}(t)|\rightarrow 0 $ as $ \lambda\rightarrow \lambda_{0}; $
(ⅳ) $ \max_{0\leq t\leq 1}|u_{\lambda}(t)|\rightarrow +\infty $ as $ \lambda\rightarrow +\infty, \ \max_{0\leq t\leq 1}|u_{\lambda}(t)|\rightarrow 0 $ as $ \lambda\rightarrow 0^{+}. $
Proof. For $ u > 1, $ from the condition (ⅰ), we have
thus, we get
So, for $ u\in K, $ we have
where $ M_{3} = \max_{0\leq t\leq 1}f(t, \|u\|_{E})\leq \max_{0\leq t\leq 1}f(t, \|u\|_{E}+1)\leq \xi (1+\|u\|_{E})^{r}, $
Thus, $ 0\leq Tu(t)\leq M_{3}g(t), \ \ 0\leq t\leq 1, $ this means that $ T: \tilde{K}\rightarrow \tilde{K}. $
For $ u\in \mathring{\tilde{K}}, $ there exists $ \delta > 0 $ such that $ u(t)\geq \delta g(t)\geq 0, \ \ 0\leq t\leq 1. $ Let $ \omega\in (0, 1) $ such that $ \omega < \delta, $ we have
Set $ a = \min_{0\leq t\leq 1}f(t, g(t)), $ then $ a > 0 $ and $ (Tu)(t)\geq a\omega^{r}g(t), \ 0\leq t\leq 1, $ so $ T: \mathring{\tilde{K}}\rightarrow \mathring{\tilde{K}}. $ From $ f(t, \cdot) $ is increasing, we can get that $ T $ is increasing. Moreover, for $ u\in \mathring{\tilde{K}} $ and $ \omega\in (0, 1), $ we have
In the following, we consider the operator equation
Then all the conditions of Lemma 2.6 are satisfied. Thus, from Lemma 2.6, for any given $ \rho > 0, $ (3.10) has a unique solution $ u_{\rho} $ in $ \mathring{\tilde{K}}, $ $ u_{\rho} $ is strongly decreasing, $ u_{\rho} $ is continuous, this means that $ \|u_{\rho}-u_{\rho_{0}}\|\rightarrow 0 $ as $ \rho\rightarrow \rho_{0} $ and furthermore, $ \lim_{\rho\rightarrow +\infty}\|u_{\rho}\| = 0, \ \ \ \lim_{\rho\rightarrow 0^{+}}\|u_{\rho}\| = +\infty. $ Set $ \lambda = \frac{1}{\rho}, \ \lambda_{0} = \frac{1}{\rho_{0}}, \ \lambda_{1} = \frac{1}{\rho_{1}}, \ \lambda_{2} = \frac{1}{\rho_{2}}. $ Then (3.10) is equivalent to $ u(t) = \lambda (Tu)(t). $ As a result, we can get
(ⅰ) for any given $ \lambda > 0, $ the fractional boundary value problem (1.1), (1.2) has a unique positive solution $ u_{\lambda} $ in $ \mathring{\tilde{K}}; $
(ⅱ) if $ 0 < \lambda_{1} < \lambda_{2}, $ there exists $ \delta > 0 $ such that $ u_{\lambda_{2}}(t)-u_{\lambda_{1}}(t)\geq \delta g(t) $ which implies $ u_{\lambda_{1}}(t)\leq u_{\lambda_{2}}(t) $ and $ u_{\lambda_{1}}(t)\not\equiv u_{\lambda_{2}}(t), \ 0\leq t\leq 1; $
(ⅲ) $ \max_{0\leq t\leq 1}|u_{\lambda}(t)-u_{\lambda_{0}}(t)|\rightarrow 0 $ as $ \lambda\rightarrow \lambda_{0}; $
(ⅳ) $ \max_{0\leq t\leq 1}|u_{\lambda}(t)|\rightarrow +\infty $ as $ \lambda\rightarrow +\infty, \ \ \max_{0\leq t\leq 1}|u_{\lambda}(t)|\rightarrow 0 $ as $ \lambda\rightarrow 0^{+}. $
4.
Example
Example 4.1 Consider the fractional boundary value problem
We note that $ \alpha = \frac{3}{2}, \beta = \frac{1}{2}, \eta = \frac{1}{2}, \varphi(t) = \frac{t}{2}, f(t, u) = t^{2}+1+u^{\frac{1}{3}}. $ Thus, we have $ f(t, u):[0, 1]\times R^{+}\rightarrow R^{+} $ is continuous and increasing in $ u, f(t, u) $ is concave. We can check that conditions $ (H_{1}), (H_{2}) $ are satisfied. Choose $ \alpha = 1, \beta = 3 $ and $ f(t, u) $ satisfy
Then all the assumptions of Theorem 3.3 are satisfied. Thus from Theorem 3.3, we have $ \lambda^{*} = \infty, $ and the following conclusions hold:
(ⅰ) for $ \lambda > 0, $ the fractional boundary value problem (4.1), (4.2) has a unique positive solution $ u_{\lambda} $ in $ \tilde{K}; $
(ⅱ) for any $ u_{0}\in \tilde{K}, $ let
Then for $ \lambda > 0, $ we have
(ⅲ) $ \max_{0\leq t\leq 1}|u_{\lambda}(t)- u_{\lambda_{0}}(t)|\rightarrow 0 \ \mbox{as} \ \lambda\rightarrow \lambda_{0} $ and if $ 0 < \lambda_{1} < \lambda_{2} < +\infty, $ then $ u_{\lambda_{1}}(t)\leq u_{\lambda_{2}}(t), \ \ 0\leq t\leq 1 $ and $ u_{\lambda_{1}}(t)\not\equiv u_{\lambda_{2}}(t); $
(ⅳ) $ u_{v\lambda}(t)\leq vu_{\lambda}(t) $ for $ 0 < \lambda < +\infty, \ \ 0\leq v\leq 1, \ \ 0\leq t\leq 1. $
5.
Conclusions
In this paper, we discussed a class of fractional derivative with respect to another function called $ \varphi $-Riemann-Liouville fractional derivative. The new derivative herein generalizes the classical definitions of derivatives by choosing particular forms of $ \varphi(t). $ The main advantage of our paper is we not only develop the existence and uniqueness of positive solutions to the fractional boundary value problem, but also give some properties of positive solutions to the problem.
Acknowledgments
We express our sincere thanks to the anonymous reviewers for their valuable comments and suggestions. This work is supported by the Natural Science Foundation of Tianjin (No.(19JCYBJC30700)).
Conflict of interest
The authors declare no conflict of interest in this paper.















 DownLoad:
DownLoad: