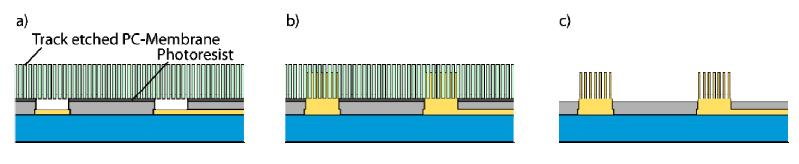
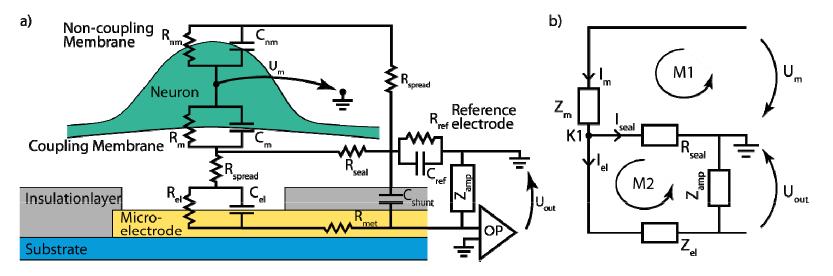
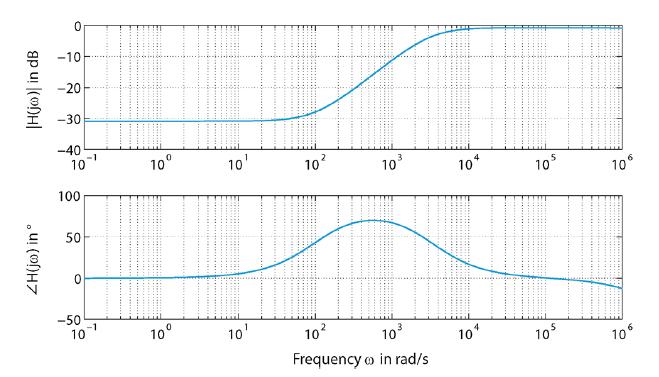
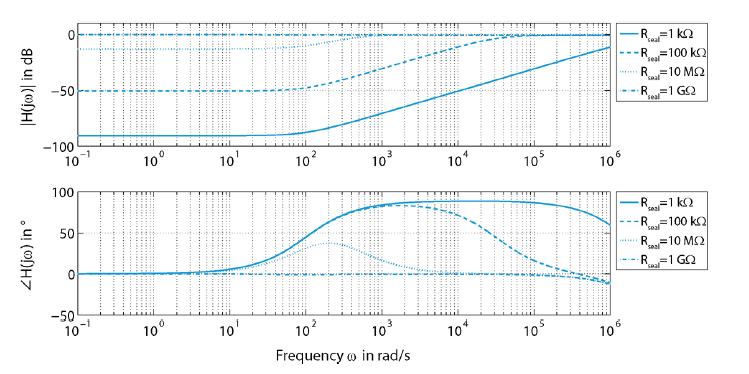
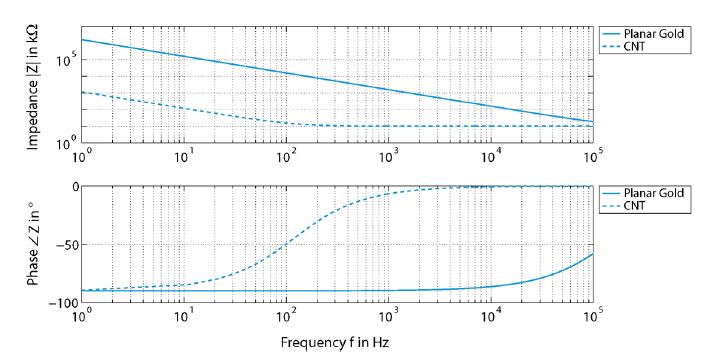
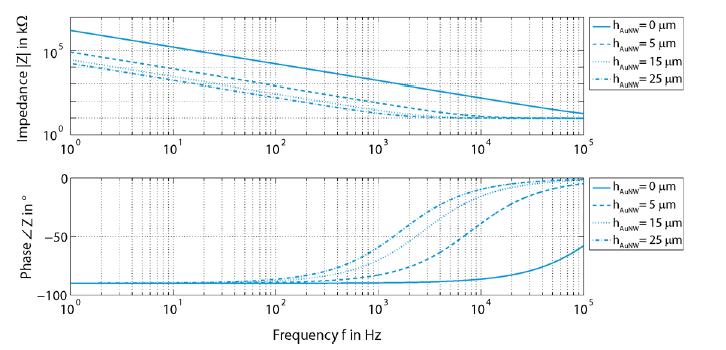
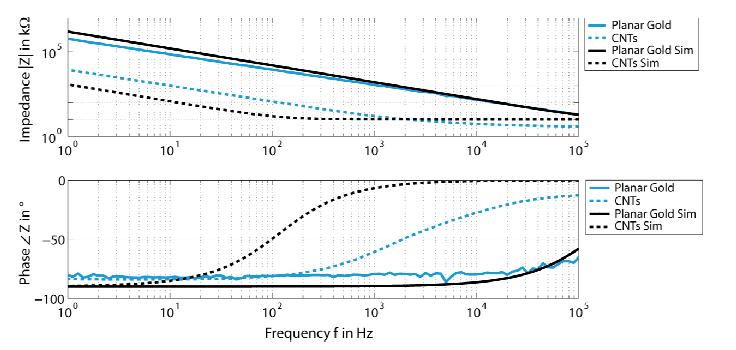
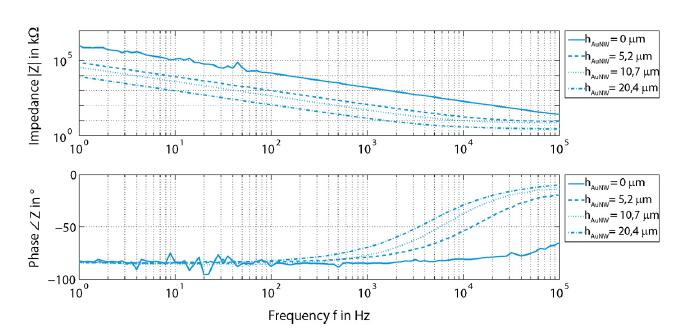
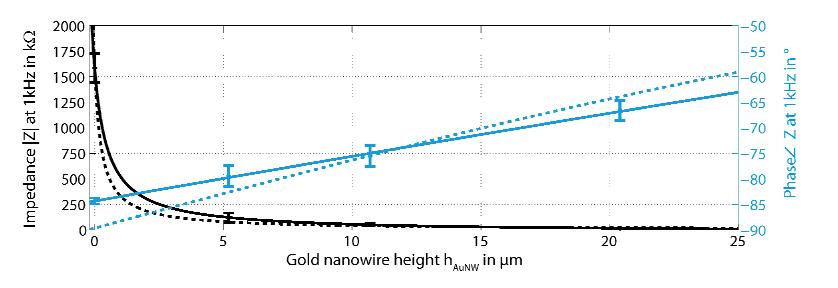
Improving the interface between electrodes and neurons has been the focus of research for the last decade. Neuroelectrodes should show small geometrical surface area and low impedance for measuring and high charge injection capacities for stimulation. Increasing the electrochemically active surface area by using nanoporous electrode material or by integrating nanostructures onto planar electrodes is a common approach to improve this interface. In this paper a simulation approach for neuro electrodes' characteristics with integrated high aspect ratio nano structures based on a point-contact-model is presented. The results are compared with experimental findings conducted with real nanostructured microelectrodes. In particular, effects of carbon nanotubes and gold nanowires integrated onto microelectrodes are described. Simulated and measured impedance properties are presented and its effects onto the transfer function between the neural membrane potential and the amplifier output signal are studied based on the point-contact-model. Simulations show, in good agreement with experimental results, that electrode impedances can be dramatically reduced by the integration of high aspect ratio nanostructures such as gold nanowires and carbon nanotubes. This lowers thermal noise and improves the signal-to-noise ratio for measuring electrodes. It also may increase the adhesion of cells to the substrate and thus increase measurable signal amplitudes.
1.
Introduction
Respiratory syncytial virus (RSV), although the leading cause of hospitalization of infants in developed countries, is still awaiting development of a safe and effective vaccine [1]. Infants typically contract RSV within the first two years of life [2], although there has been a recent suppression of RSV due to COVID-19 mitigation measures [3,4]. This has resulted in earlier and larger epidemics of RSV in many countries this year as COVID mitigation measures have been relaxed [5,6]. RSV can also cause serious illness and death in elderly adults [7]. While the severity of RSV in these two groups is thought to be in part due to a limited immune response [8], other factors might also play a role. A recent study by Felt et al. examined the role of defective viral genomes (DVGs) [9], finding that they might be an indicator of disease severity in RSV.
DVGs, are a feature of a number of viral infections besides RSV [10], including influenza [11,12,13], Sindbis virus [14], vesicular stomatitis virus [15,16], poliovirus [17,18,19], measles [20], SARS-CoV-2 [21], and parvovirus [22]. Defective genomes are thought to have a number of effects on the course of an infection. They interfere with production of fully competent infectious virus when they coinfect cells [11,23]. Interestingly, the within-cell interference can lead to persistence of the infection within the host [23,24,25]. More recently, studies have determined that DVGs also alter the immune response during an infection [9,26,27,28], with evidence suggesting that the presence of DVGs stimulates the innate immune response. Some DVGs are also being investigated as potential vaccines since they have the ability to also stimulate the adaptive immune response [29]. DVGs are also thought to play a role in the evolution of viruses providing increased genetic diversity during infections in a single host [30]. Thus there is a need to develop a better understanding of how the appearance of DVGs alters viral infections.
Mathematical modeling can help us develop an understanding of the role of DVGs in viral infections. There have already been a number of studies that examined models incorporating defective interfering particles (DIPs). DIPs occur when DVGs are packaged and exported out of the cell. DIPs can infect cells, but cannot produce new progeny virions on their own. They can, however, produce new DIPs when in a cell that is infected with both the DIP and a fully competent virus, since the full virus provides the missing components needed for replication, virion formation, and release [31,32]. For example, Liao et al. used a model to determine conditions under which current DIP quantification techniques resulted in correct estimates of the number of DIPs [11]. Shirogane et al. [19] examined how the DIPs competed with wild-type virus in a competitive coinfection model. Other within host models examined the possibility of using defective particles to treat viral infections [33,34,35]. More recent modeling efforts combined intracellular models with within host models in order to understand not only the effect of DIPs at the within host level, but to understand how DVGs might interfere with normal viral replication within the cell [36,37,38].
A limitation of all of these studies is that the models were developed based on assumptions of the effect of DIPs and the models were then used to examine possible outcomes of these assumptions. Unfortunately, many of the known effects of DVGs, such as their effect on the immune response [9,26,27,28,29], were not incorporated into these models, perhaps missing an important process that could alter the interplay between DVGs and fully competent virions. A recent study by Felt et al. [9] could allow for assessment of how DVGs alter the time course of a viral infection — information that can then be incorporated into future modeling efforts in order to produce more accurate mathematical models.
Here, we use mathematical models and the Felt at el. study to examine how DVGs alter the time course of viral load. Without directly incorporating DVGs, we fit a simple mathematical model to experimental data in order to identify differences in viral kinetics parameters under different infection conditions, such as infections with no DVGs and infections where DVGs appear. This type of approach has been used to quantify differences in viral kinetics parameters between wild-type and drug-resistant strains of influenza [39,40], quantify differences in aging animals with RSV [41,42] or SARS-CoV-2 [43], and examine the effect of an antiviral [44]. We find that the appearance of DVGs primarily changes the infection rate and the clearance rate of infections, but only when the DVGs appear late in the infection or are prolonged.
2.
Materials and methods
2.1. Mathematical model
We use a basic model of viral infection that does not include an eclipse phase and assumes that cells produce and release virus immediately upon infection [45],
In this model, $ T $, $ I $, and $ V $ are the variables of the model and $ \beta $, $ \delta $, $ c $, and $ p $ are the parameters. $ T $ represents the number of target cells infected with virus $ V $ at a rate $ \beta $. Once infected, the cells enter the infectious phase $ I $, in which they produce virus at a rate $ p $ and die at rate $ \delta $. Virus is cleared at rate $ c $. While this model excludes the eclipse phase — where the cell is infected, but not yet producing virus — inclusion of this phase would add an additional parameter that is known to not be identifiable from viral titer data alone [46].
2.2. Fitting experimental data
The experimental data used in this study was digitized from Felt et al. [9], which describes a challenge study of RSV infections in healthy adults. In this study, data was collected from nasal swabs taken from healthy adults challenged with RSV. 61 experimentally infected healthy non-smoking adults, aged 18-50 years old, were inoculated experimentally via intranasal drops. Nasal washes and blood samples were taken immediately before inoculation, daily for the first 10 days post infection, and again on days 14 and 28. For all patients, quantitative polymerase chain reaction with reverse transcription methods were used to estimate viral loads. Patients were separated into different groups based on the dynamics of DVGs during the infection and median viral titer curves were used to compare the different groups. One comparison was between patients who had no DVGs detected, those who had DVGs appear early (before 3, 5, or 6 days post infection), and those who had DVGs appear late (after 3, 5, or 6 days post infection). Another comparison was between patients who had no DVGs detected, those who had transient DVG detection (not detected after 6 dpi), and those who had prolonged DVG detection (detected at least once before 6 dpi and detected again after 6 dpi).
Data was extracted from figures using Webplotdigitizer (Webplotdigitizer.com). To fit the data and calculate the parameter estimates for data sets from this study, we used Python's built-in optimizing function $\texttt{scipy.optimize.minimize}$ and minimized the sum of squared residuals (SSR) using the Nelder-Mead algorithm. In addition to estimating the free parameters of the model ($ \beta $, $ p $, $ \delta $, $ c $), we use the estimates to calculate the basic reproductive number, $ R_0 = \frac{\beta p}{c\delta} $, which is the average number of secondary infections caused by a single infected cell, and the infecting time $ {t_{\mathrm{inf}}} = \sqrt{\frac{2}{p\beta}} $ [47], which is the average time between release of virus from one cell and infection of the next cell.
2.3. Bootstrapping and statistical analysis
Bootstrapping was used to estimate the distributions of the parameter estimates [48]. We shuffled the residuals at each time point using the numpy $\texttt{shuffle}$ function, which uses a Fisher-Yates shuffle. We then repeated the minimization process to produce another set of parameter estimates. After repeating this process 1000 times, we calculated the 95% confidence interval for each set of parameters.
To compare the parameter distributions, we performed Mann-Whitney U tests using Python's built-in $\texttt{mannwhitneyu}$ function to check if parameter distributions were distinct. The Mann-Whitney test is used since parameter distributions cannot all be assumed to be normal. $ p $ values less than 0.05 are considered statistically significant.
3.
Results
In the study by Felt et al. [9], infections are compared using two main features: the time at which DVGs are first detected, and the duration of DVG detection. In the first comparison, participants are divided into three groups: those where DVGs are not detected, those that have DVGs detected early and those that have DVGs detected late. Cutoffs to define early versus late start were set at 3, 5, or 6 days post-infection. The second comparison also consists of three groups: those who do not shed DVGs, those who shed DVGs transiently, and those who shed DVGs for a prolonged period of time. Prolonged DVG was defined as detection of DVGs on two or more days after 6 days post-infection. We perform our analysis using the same groupings.
3.1. Early vs. late appearance of DVGs
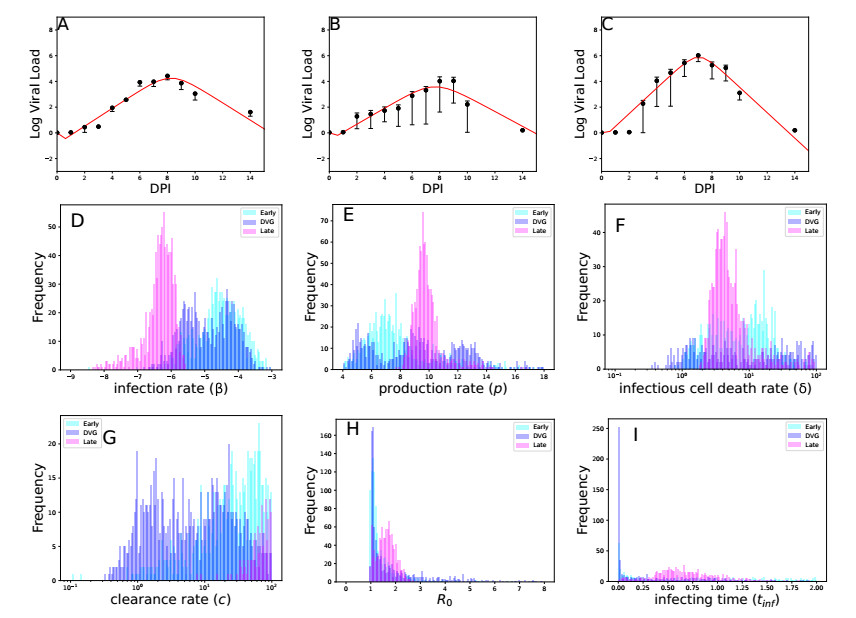
We show the viral load curves of Figure 5C in the Felt et al. manuscript and our best fit curves along with distributions for the parameter estimates in Figure 1. These viral load curves represent the mean viral load of people with no DVGs detected (A), early DVGs (B), and late DVGs (C) with the early/late cutoff set at 5 days post-infection. The best fit parameter values are given in Table 1. Distributions for the parameters of the viral kinetics model, $ \beta $, $ p $, $ c $, and $ \delta $, as well as distributions for the calculated values $ R_0 $ and $ {t_{\mathrm{inf}}} $, for all three groups are given in Figure 1 (bottom two rows). $ p $ values from the Mann-Whitney test are also presented in Table 1.
The model is able to fit the viral load curves quite well. The $ R_0 $ values are fairly low, just over the threshold needed to initiate an infection ($ R_0 = 1 $), which is smaller than other estimates found in literature [42,49], although those RSV infections were in animals other than humans. The infecting times range from about 6 minutes to 2 hours, which are more in line with previous estimates [42,49,50]. When comparing parameter estimates between the 3 groups, we note that parameter differences show up primarily in the infection rate, $ \beta $, and the clearance rate $ c $. When DVGs appear late, the infection rate appears to be lower and the clearance rate appears to be higher, than when DVGs appear early or not at all.
3.2. Effect of cutoff time
Since the cut-off of 5 days for early vs. late is arbitrary, two other cut-off times were tested. An earlier cut-off of 3 days is shown in Figure 2. In this case, the mean viral load in the early DVG group stayed below the threshold of detection, so we show only the viral time courses and best fit curves for no DVGs (A) and late DVGs (B). The best fit parameter values along with 95% confidence intervals are given in Table 2. Distributions for the parameters of the viral kinetics model, $ \beta $, $ p $, $ c $, and $ \delta $, as well as distributions for the calculated values $ R_0 $ and $ {t_{\mathrm{inf}}} $, for all three groups are given in Figure 2 (bottom two rows). $ p $ values from the Mann-Whitney test are also presented in Table 2.
The mean viral titer curve for the early DVG group remained below threshold for all time points, making it impossible to fit the model to this data. However, there were three patients in the early DVG group with the earliest cut-off of 3 days. This means that the early DVG patients were shedding very low amounts throughout the infection. For the remaining two groups, we see slightly higher basic reproduction numbers, although they are still fairly close to the threshold of 1. The infecting times are 45 minutes to 1 hour, which are similar to previous estimates [42,49,50]. We can only compare the no DVG and late DVG groups in this case, and we note that the only parameter that is statistically significantly different between the two groups is the infection rate.
A later cut-off date of 6 days was also tested. This is shown in Figure 3. The best fit parameter values along with 95% confidence intervals are given in Table 3. Distributions of the parameter estimates of the viral kinetics model for all three groups are given in Figure 3 (bottom two rows). $ p $ values from the Mann-Whitney test are also presented in Table 3.
As with the two previous assessments of the effect of time of appearance of DVGs, we see a statistically significant difference in the infection rates of early or no DVGs and late DVGs. We also see a statistically significant difference in the clearance rate between early or no DVGs and late DVGs. In this case, there is also a statistically significant difference between the clearance rates of early and no DVGs. So even when the cut-off day marking the difference between early and late DVGs is shifted, there is a consistent difference in infection rates between early or no DVGs and late DVGs. The differences in clearance rate appear to be more dependent on the chosen cut-off point.
3.3. Prolonged DVG shedding
We show the viral load curves of Figure 6C in the Felt et al. manuscript and our best fit curves along with distributions for the parameter estimates in Figure 4. These viral load curves represent the mean viral load of people shedding no DVGs (A), transient DVGs (B), and prolonged DVGs (C). The best fit parameter values are given in Table 4. Distributions for the parameters of the viral kinetics model, $ \beta $, $ p $, $ c $, and $ \delta $ as well as distributions for the calculated values $ R_0 $ and ${t_{\mathrm{inf}}}$, for all three groups are given in Figure 4 (bottom two rows). $ p $ values from the Mann-Whitney test are presented in Table 4.
The model, again, fits the viral load curves well. $ R_0 $ values are again just over the threshold for infection. The infecting times range from 3 to 48 minutes. The distribution for $ \beta $ estimates for prolonged DVGs is clearly lower than the $ \beta $ distributions for no DVGs or transient DVGs. This is reflected in the statistical tests, which show $ p $ values less than 0.05 for no DVG/prolonged DVGs and transient DVGs/prolonged DVGs comparisons of $ \beta $ estimates. We also see similar statistically significant differences in the estimates for the clearance rate $ c $ when comparing the prolonged DVGs to the other two groups.
4.
Discussion
In this manuscript, we fit a mathematical model of viral infections to data examining the appearance of DVGs in RSV infections. We found that the infection rate and the clearance rate are the parameters most affected by the presence of DVGs. Specifically, the infection rate is lower when DVGs appear later and are prolonged during the infection, while the clearance rate is higher in these two cases. In the case of the clearance rate, a possible mechanism is fairly straightforward. When DVGs occur late and are prolonged, they are essentially displacing fully competent virions, which then decrease more quickly than in infections that do not have DVGs or where DVGs are not present later in the infection. The link between later and longer DVGs and lower infection rate is less clear. Defective particles are known to interfere directly with intracellular replication of fully competent virus [51], but they can also interfere with infection dynamics by stimulating the immune response [52]. Since DVGs are known to stimulate the innate immune response in particular [9,26,27,28], this could be an indirect mechanism that reduces the infection rate since the innate immune response typically rises early and rapidly during infections [53]. It is also possible that a lower infection rate leads to a later appearance of DVGs. Since replication is slower in the case of low infection rates, replication of DVGs would presumably also be slower causing them to be detected later in the infection.
While our study could not quantify any differences in the viral time courses of early and no DVGs, the original study by Felt et al. noted that there was a marked difference in the clinical severity of the infection in these two cases. Specifically, they found that the appearance of DVGs early in the infection reduced the severity of the illness. Other recent studies have examined the correlation between viral load and clinical severity, with mixed results. Some studies have found no link between single viral load measures and severity [54,55] while others noted a correlation [56,57,58,59]. More detailed challenge studies note that there appears to be a time delay between rise of viral load and rise of symptoms [60,61], suggesting that there might be some intermediary steps linking viral load and symptoms.
There has been interest in using DVGs to potentially treat viral infections [51,52]. This treatment strategy has been tested in a number of animal models [62,63,64,65,66,67,68,69]. Our results indicate that the timing of treatment initiation could be an important factor since the timing of the appearance of DVGs is associated with different changes in viral kinetics parameters. Duration of production of the DVGs could also be an important factor in the efficacy of treatment since prolonged persistence of DVGs was associated with a lower infection rate and faster clearance of virus. While the idea is that a single injection of DVGs is sufficient because the DVGs should continue to replicate and will persist, this might not always happen since there were some patients in the Felt et al. study who had transient DVGs [9]. Transient DVGs showed no statistically significant difference in infection rate or clearance rate from no DVG patients in this study, suggesting that DVGs need to persist for some period of time in order to affect the time course of the infection.
This study used a very simple model of viral infection that neglects many details of the infection. Our understanding of how DVGs alter the time course of infections would be helped by fitting models that incorporate DVGs [11,33,34,36,37,38] to clinical data. In order to properly parameterize such a model, more data needs to be collected. In addition to viral time courses, we also need the time course of DVGs. A model that explicitly incorporates DVGs could provide insight into how late appearance of DVGs leads to lower infection rates, higher viral loads and more rapid clearance. The explicit inclusion of DVGs will also allow for estimation of parameters related to DVGs such as the DVG production rate, DVG infection rate, and DVG clearance rate.
Despite the simplicity of the model, we might not have found a global minimum and there was still difficulty in identifying all the parameters. It is known that for this simple model $ \delta $ and $ c $ are not both uniquely identifiable from viral titer data alone [46]. We note that some of the confidence intervals are fairly broad, so there is room for improvement on the identifiability of the parameters. In order to improve parameter estimates measurement of other quantities will be needed. For example, measuring both infectious virus and RNA copies can narrow the confidence intervals around parameters estimates [70], while measurement of infected cells in addition to viral measurements can help separate the effects of $ \delta $ and $ c $ [71].
In spite of these limitations, our application of a mathematical model to challenge infections of RSV found a robust link between the appearance and duration of DVGs and the infection rate. Further studies to refine both the model and the parameter estimates will lead to a better understanding of causal link between the appearance of DVGs and the infection rate.
Conflict of interest
The authors declare there is no conflict of interest.









 DownLoad:
DownLoad: