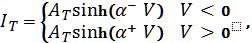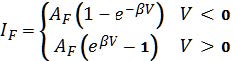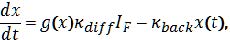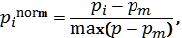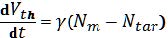1. Introduction
Regardless the tremendous success of digital computers over the last decades shortcomings are obvious when it comes to pattern recognition, unsupervised learning or cognitive tasks. Indeed machine learning has been a challenging task since the early beginning of serial, binary computation based on the von Neumann architecture. To some extend today’s super computers are able to mimic biological systems but on the cost of huge power dissipation and device overhead. Brains of humans, mammals and even simple forms of living species as invertebrates on contrary, are well adapted to permanently changing environments. The remarkable interaction performance between biological nerve system and their surroundings is a result of million years evolution explained by Darwinism [4]. It is not a surprise that scientists and engineers develop bio-inspired computing systems with the goal to realize so-called neuromorphic systems exhibiting benchmarks in pattern recognition, cognition and power efficiency as close as possible to their biological paradigms [5,6]. For these purposes roughly two pathways, software dominated Neuroinformatics [7,8] and analogue VLSI (Very Large Scale Integration) based on Si CMOS (Complementary Metal Oxide Semiconductor) technology [5,6] can be identified as major approaches. The latter gained new momentum with the advent of memristive devices.
In the simplest form a two terminal memristive device consists of a capacitor-like metal-insulator-metal layer sequence. In contrast to linear resistors, memristive devices are able to remember the history of applied electric potentials and therefore feature a device characteristic that cannot be emulated by one of the other basic two-terminal circuit elements (resistance, inductance, and capacitance). In this respect, recent investigations have recognized the analogue to the memristor [9], which has been theoretically predicted by Chua in 1971 [10]. In the memristor model the resistance (or memristance) M(x, V, t) of the device can be expressed by a state variable x(t), which itself depends on the applied voltage V(t) as
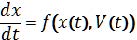 |
(1)
|
where
f is related in the most state-of-the-art memristive devices to ionic drift within the insulator. Actually memristive devices are considered as building blocks for future resistive random-access memories (RRAMs) which might show superior properties in comparison to charge based Flash technology
[11]. The system architecture and functionality of RRAMs will be very close to that used in common digital memories. Short non-volatile data storage, switching times in the ns range, long data retention times (10 years), a small device variability as well as good fatigue performance are a few essential design parameters for RRAM cells. The development of RRAMs may lead to a unified memory which is able to overcome the current bottleneck, i.e. the data transfer rate in digital computers known as memory-processor latency
[12].
In contrast, the possible benefits of memristive devices for bio-inspired neuromorphic circuits are not that obvious and hence have to be explored. The coactions of biological information processing from the molecular length scale up to the system level in the inch range are by far not understood. Although one can notify a tremendous progress in the understanding of biological nervous systems there is still a considerable lack to explore the whole principles of information pathways from the molecular length scale to the system level. In other words the “brain code” is not yet understood. Therefore, it is up to now practically impossible to develop neuromorphic systems which mimic the computing architecture of the entire brain. Instead trying to solve all problems at once, it is much more realistic and pragmatic to mimic specific feature of biological nerve systems by focusing on simpler and more visible goals. Indeed this strategy has been applied very successfully [13,14,15,16,17,18,19]. For example, the development of pattern recognition systems is an interesting approach which has many real world applications, such as autonomous robots and transportation, classifiers, front and speech recognition, and more general unsupervised learning strategies [20].
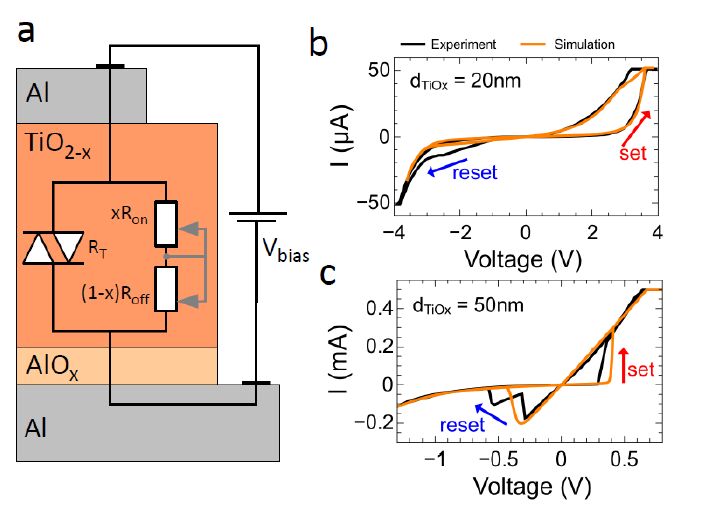
Here, we report on the development of TiO2-x-based memristive devices for bio-inspired neuromorphic systems and their performance in a bio-inspired network for pattern recognition by taking the characteristics from real devices in network level simulations. Therefore, devices consisting of 20 nm and 50 nm thick TiO2-x layers are fabricated, which are sandwiched in capacitor like structure between a metallic Al- (bottom and top) electrodes, an AlOx tunneling barrier. While for 50 nm thick TiO2-x devices, binary resistive switching was recorded, a reduction of the oxide thickness to 20 nm leads to a much more homogeneous resistance switching characteristics. A physical-based equivalent circuit model is employed to analyze the obtained switching characteristics in some more detail and to provide a realistic device model for network level simulations. Previously reported neural network-based computing paradigms have been used as guidelines for network simulations. [1,2,3] Here, a compact version of those networks is presented, which consists of ten output neurons, which are inhibitory linked within a winner-take-it-all architecture and a homeostasis-like rule for the spiking- neurons thresholds. On the basis of this pattern recognition system essential requirements for the development of optimal memristive device for neuromorphic circuits are discussed.
2. Materials and Method
2.1. Device Fabrication
The memristive devices were fabricated in a planar capacitor structure with the layer sequence Al/Al2O3/TiO2-x/Al as sketched in Figure 1(a). In particular, a 40 nm thick Nb layer was sputtered as the bottom electrode. Hereafter, 50 μm × 50 μm windows are defined using standard optical lithography. Afterwards, an 8 nm thick Al layer was sputtered, which was partially oxidized at 100 mbar in pure oxygen for 30 min. On top of the Al2O3 layer, respectively, 50 nm or 20 nm of TiO2-x are reactively sputtered in an Ar/O2 atmosphere, followed by a 32 nm Al-layer as the top electrode and a subsequent lift-off in acetone.
2.2. Electric Measurements
All measurements were performed using an Agilent E5260 source measurement unit. Current-voltage measurements (I-V curves) were obtained by sweeping the applied voltage and measuring the current simultaneously. For synaptic potentiation measurements, rectangular voltage pulses with different amplitudes, polarity, and pulse durations were applied to the devices. Positive voltage means positive voltage on the top layer and ground on the bottom layer.
3. Results and Discussion
3.1. Current-Voltage Characteristics and Device Model
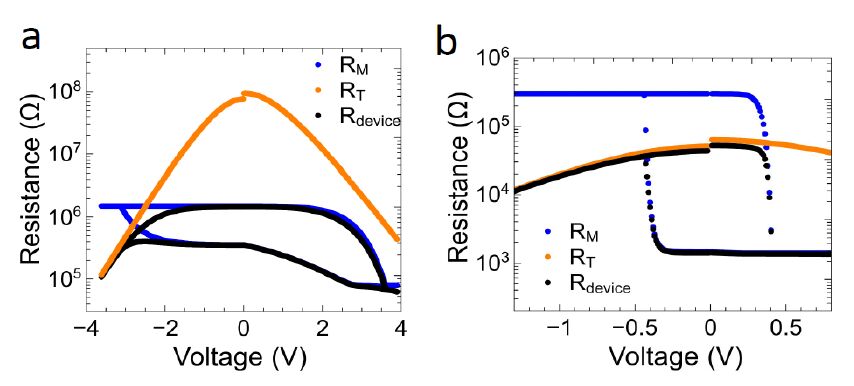
Two Al/Al2O3/TiO2-x/Al memristive devices with, respectively, 20 nm and 50 nm thick TiO2-x layers are compared in Figure 2(b) and (c). In particular, each sub-figure contains the I-V curve (black curve) and the simulated current-voltage characteristic (orange curve). In the following, characteristic features of both devices are described.
In Figure 2(b) a typical I-V curve obtained on devices with a TiO2-x layer thickness of 20 nm is shown. By sweeping the bias voltage between 2 V and -2 V the device resistance changes at positive voltages gradually and smoothly from the inertial high resistant state of 1 MΩ (HRS) to the low resistant state of 100 kΩ (LRS) and at negative voltages back to the inertial HRS. In order to avoid a device breakdown a current compliance of 50 μA was set. Devices with an increased layer thickness of 50 nm show binary resistance switching, as depicted in Figure 2(c). Therefore, at positive voltages the device resistance is changed from the HRS to the LRS at a set voltage of Vset = 0.3 V and vice versa by applying negative bias voltages lower than Vreset = -0.3 V. Thereby, the device resistance was decreased from 3 MΩ to 1 kΩ at Vset. Again a current compliance of ICC = 500 μA was used to avoid an irreversible breakdown of the device. Additionally, an electro-forming step was necessary for devices with TiO2-x layer thicknesses of 50 nm.
Table 1. Simulation parameters for the memristive device model.
|
dTiOx = 20 nm |
dTiOx = 50 nm |
| α+(α-) |
2.1 V-1 (2.6 V-1) |
2.1 V-1 (2.6 V-1) |
| β |
1.79 V-1 |
25.79 V-1 |
| AT |
1 10-8 A |
1.5 10-5 A |
| AF |
5 10-8 A |
5 10-8 A |
| κdiff |
4.82 105 A-1s-1 |
1.32 105 A-1s-1 |
| κback |
1 10-3 s-1 |
1 10-5 s-1 |
In order to study the device performance in bio-inspired computing schemes, the transition from a single device level to a multidimensional network level has to be explored. At this respect, a detailed device model is required, which reproduce the experimental recorded device characteristics as close as possible. Here, we modeled the experimental data within the framework of the simple voltage driven memristor model of Ref. [9] (cf. Equation 1). In addition, we used a physical motivated description for the ionic contributions within the TiO2-x layer under applied bias voltage. Therefore, we have assumed that mainly two transport mechanisms are involved in the charge transport process: Electronic transport through local conducting filaments and electron tunneling (respectively hopping) between TiO2-x defect states. Since both processes might occur simultaneously, it is proper to assume a parallel connection of both transport processes. A schematic sketch of the equivalent circuit model is superimposed to the device structure in Figure 1(a). Therefore, the electron tunneling between individual defect states was modeled as a constant mean tunneling current described by
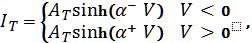 |
(2)
|
with
AT and α
+,- being positive constants. The oxygen ion diffusion under the applied bias voltage has been assumed to be the reason of a filament formation according to findings of Ref.
[21,22]. In the model the filamentary contribution to the overall device conductance has been taken into account using the diode equation
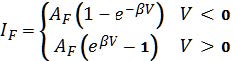 |
(3)
|
as proposed by Szot et al.
[21,22] to describe the filamentary behavior, where
AT and
β are positive parameters characterizing the filament. Moreover, back-diffusion of oxygen ions may additionally influence the dynamics of the resistance switching process, which has been recently recognized as essential factors with respect to the system dynamics at the network level
[13,23,24]. To take oxygen ion back-diffusion additionally into account, a memristive state depended back diffusion term is added, so that Equation 1 reads
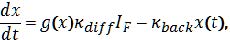 |
(4)
|
Here,
κdiff and
κback are the respective constants for the diffusion process, while g(x) is the in Ref.
[25] defined window function, which takes a reduced ion mobility at the boundaries of the TiO
2-x layer into account. Hence, the resistance of the filamentary branch can be therefore calculated by
RM =
xRLRS +
(1-x)RHRS, while the total device resistance is therewith given by R
device =
RM RT /(RM +RT). Here R
M, R
T are the filamentary and tunneling resistances respectively.
The calculated I-V characteristics are added as orange curves to our experimental recorded data, while the used simulation parameters are summarized in Table 1. In agreement to our experimental I-V curves a homogenous resistive switching characteristic could be obtained for a 20 nm TiO2-x thickness (cf. Figure 2(a)), while an increased thickness of 50 nm TiO2-x leads to a binary switching behavior. In order to model the experimental I-V curves within our device model the coefficient β of Equation 1 has been increased from 1.79 V-1 to 25.8 V-1 for an increase in the TiO2-x layer thickness from 20 nm to 50 nm. This in fact results in a much steeper rise in the TiO2-x filamentary diode characteristics according to Eq. 3, which points to a stronger filamentary electron transport characteristic and results in I-V curves exhibiting a sharp threshold voltage (see Figure 1(b)). This can be also seen by regarding the calculated resistances of both the tunneling and filamentary branch of our equivalent circuit model, as depicted in Figure 2. In particular, for the 20 nm thick TiO2-x device, the resistance RT (orange line in Figure 2(a)) is much higher compared those of the filamentary part (blue line in Figure 2(a)). Hence, RT did not feature significantly to the overall device resistance (black line in Figure 2(a)). In contrast to the 20 nm thick TiO2-x device for a 50 nm thick TiO2-x device the HRS is strongly dominated by the resistance RT, as it can be seen in Figure 2(b). Therefore, our simple model shows evidence of a fast filamentary driven switching process in case of thicker TiO2-x film and a much homogeneous oxygen diffusion for thinner oxide thicknesses with in agreement several investigations [21,26,27,28]. Therefore, we might assume that during the electric-forming step, which has been applied only to those devices consisting of a 50 nm thick TiO2-x, conducting filaments were created, where thereafter only local rearrangements of oxygen ions are responsible for resistance switching.
However, it is worth to mention that the presented simulation model covers only first order processes, which are involved in the switching mechanism. This might lead to some differences between simulation and measured I-V data. The most striking difference has been found for the 20 nm thick TiO2-x device at the negative voltage branch (cf. Figure 1(b)). While both simulation model and experiment show a gradual reset of the device resistance, the thresholds for the reset differs from each other. From our experimental investigation a gradual reset of the device resistance has been found below -2V, while the simulation model predicts a resetting of the device resistance starting from -1V. This might be based on ionic effects at the microscopic scale, which are not covered by the here presented device model. In order to describe the underlying physics at a microscopic level in more detail more sophisticated simulation models are required, which is, however, outside the scope of this investigation.
3.2. Synaptic Plasticity Measurements
In a theoretical work by Zamarreño-Ramos et al. [29] it has been shown that the synaptic weight ω between individual neurons can be related to the state variable x of memristive devices in the framework of the ideal voltage driven memristor model (cf. Equation 1). This in fact implies that the conductance of the memristive device is proportional to ω, in which biological plasticity mechanisms are emulated by changes in the device conductance under suitable voltage pulse trains. In this respect it is worth mentioning that biological computing schemes manifest in network behavior, where synaptic plasticity is a (local) cellular precondition. Therefore, binary resistive switching devices require different network topologies as continuous resistance switching devices. [30] However, in this investigation we study pattern recognition based on the simulation model proposed in Ref. [1,2], which require gradual resistance switching devices. For the following investigations it is therefore proper to focus on that device, which exhibits a gradual (homogeneous) switching behavior, i.e. the device of Figure 1(b) with a TiO2-x layer thickness of 20 nm.
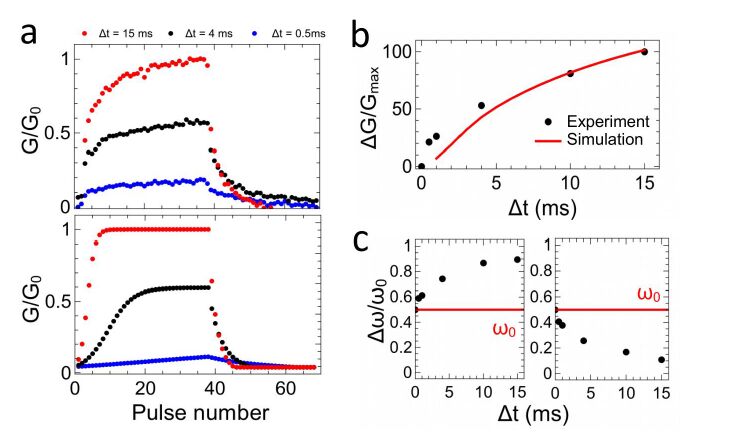
In order to study the capability of synaptic plasticity emulations with the memristive device exhibiting an analog switching mechanism (Figure 1(b)), voltage pulse trains consisting of a set of n equivalent positive voltage pulses (potentiation pulses) followed by n equivalent negative voltage pulses (depression pulses) were used. For resistance readout a positive read pulse (with voltage amplitude much lower than Vset to do not affect the device resistance) was applied after every potentiation and depression pulse. The obtained findings are presented in Figure 3(a) together with simulation potentiation/depression data (lower panel of Figure 3(a)). More precisely, pulse trains of 34 potentiation pulses and 34 depression pulses were applied, while the pulse duration was varied between 0.5 ms, 4 ms and 15 ms. As a result, a pulse time of 0.5 ms only weakly affects the resistance of the Al/Al2O3/TiO2-x/Al device (blue data points in Figure 3(a)), while an increased pulse time shows stronger changes in the device conductance. These experimental findings can be also reproduced by our numerical simulations (c.f. lower panel in Figure 3(a)).
A further important aspect of synaptic plasticity emulations for network computing schemes is that the change in the device conductance must be adjusted by the duration of single voltage pulses rather than by their pulse height. This implies that temporal differences in synaptic stimulations varying the synaptic coupling strength in a different manner, which is at the heart of spike-timing-depending plasticity (STDP) [31,32]. In Figure 3(b) experimental and simulated changes of the device conductance after application of 34 voltage pulses of 2 V with varying pulse lengths are compared. In result, a precise adjustment of the device conductance in dependence of the pulse width within the investigated interval of 0.5 ms to 15 ms is recorded, which has been also recaptured by our numerical simulation. Moreover, biological computing schemes at the network level require associativity, in which the potentiation of several synapses cause a decrease of other synapses leading to a comparative situation.[30,33] This in fact requires a balance of conductance increase versus conductance decrease under, respectively, positive and negative voltage pulses. In order to prove this requirement for the investigated device 34 potentiation or 34 depression pulses with different pulse times has been applied to the device, where initially a resistant state between the HRS and LRS of the device has been set. The obtained results are depicted in Figure 3(c). As a result, we notice a rather balanced behavior between potentiation and depression for the device under investigation. In particular, this means that 34 potentiation pulses affecting equally the device conductance, as 34 depression pulses with the same pulse times. For example 34 potentiation pulses with 10 ms pulse width leading to an increase of the device conductance of +36 %, while the same amount of depression pulses with 10 ms pulse times decrease the device conductance by -33 %.
3.3. Pattern Recognition
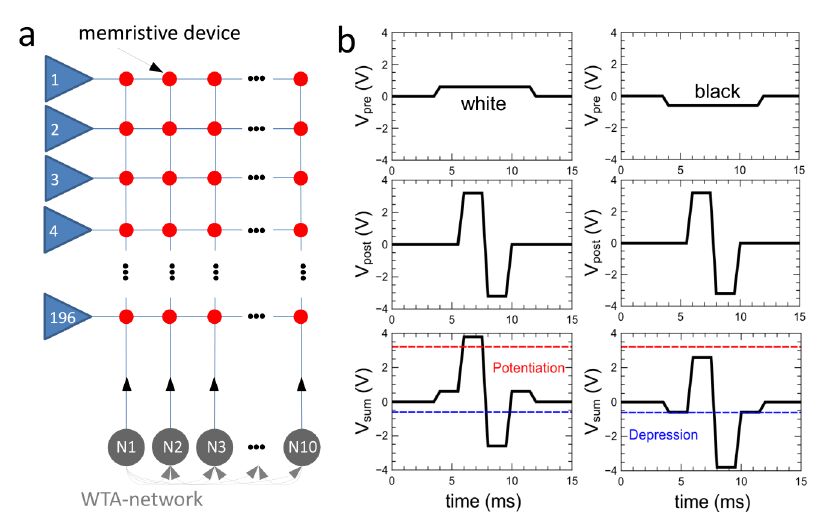
In order to explore the relation between the individual memristive characteristic and the overall system performance in a neural network, we used a compressed version of the network described in Refs. [1,2,3]. A schematic of the simulated neural network is shown in Figure 4. Therein, the memristive devices are arranged in a cross-bar array structure connected by input and output neurons, respectively, building a feed-forward neural network. Input pattern are applied to the network using positive and negative voltage pulses representing the individual pixel and their intensity values, as we will discuss it below. As output layer leaky integrate and fire neurons are used, which are laterally coupled within an inhibitory winner take it all network including adaptive thresholds for the spiking, as proposed in Ref. [1,2]. In particular, each of the output neuron receives input from the connecting memristive devices of the particular branch of the cross-bar array and changes therewith their activity in dependence of the resistance change of the particular connected devices. This enables unsupervised learning in such a way that every output neuron creates their specific receptive field during learning, while thereafter each of the output neuron will spike in accordance to the before learned pattern for a varying input pattern. In the following the different parts of the network are discussed in some more detail.
For performance studies of the network handwritten digits from the MNIST Database are used [34]. In total the MNIST Database consist of 60,000 handwritten digits from 250 different writers, while every digit is stored in a 256 grayscale image with 28 × 28 pixel. For this investigation we are using a subset of 9,000 images out of this database, in which 900 different images per digit are applied to the network. In order to reduce the overall amount of memristive devices in the network the original 28 × 28 pixel images was reduced to a 14 × 14 pixel, so that only 196 input neurons are needed (cf. Figure 4(a)). In fact, therefore the number of input neurons must be compromised by the accuracy of the learning results. At this respect, the use of every fourth pixel will lead to an acceptable compromise, as shown above. After learning the network is tested with 1000 unknown images, where every image are applied consecutively five times to the network. The pixels of the images are presented as voltage pulses of ±0.6 V. Moreover, it was necessary to use an additional threshold voltage, where only above (below) this threshold the device resistance is affected by the applied voltages. In particular, we found that the I-V nonlinearity of the here used device is not sufficient to define a distinct threshold for the switching process. Therefore, the need of selector devices, which provides clear threshold values, or memristive devices with a stronger I-V nonlinearity are required. As a threshold for the device resistance update +3.21 V and -0.61 V has been chosen, so that positive and negative input pulses of ±0.6 V are well below this threshold (cf. Figure 4(b)). The voltage pulse shape generated by the output neurons is shown in Figure 4(b). Therefore, the device resistance is affected the most in a situation where input and output pulse matches, as sketched in Figure 4(b). In particular, the superposition of a negative input pulse with an output neuron generated pulse will lead to a decreasing of the particular device resistance, while the superposition of a positive input pulse with a negative output pulse increases the resistance of the memristive devices connected to the specific neurons.
In order to guarantee the functionality of the investigated network, the presented images were coded as follows: In advance of an input voltage application each to the network presented pixel image is normalized to the interval -1 to 1. Following Ref. [1] the grayscale pi of each pixel are best normalized by
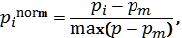 |
(5)
|
where p
m is the mean grayscale of all pixels of an individual image. After normalization the probability of an input spike generation was calculated by using a for each iteration step and pixel generated random number
r and the absolute value of the normalized pixel |p
inorm|. In particular, we are using the condition that r<|p
inorm| must be fulfilled so that, respectively, for a positive or negative p
inorm a positive or negative input spike is generated (cf.
Figure 4(b)).
For the output neurons leaky-integrate-and-fire neurons are used, which give the in Figure 4(b) presented voltage spike Vpost to the network whenever the threshold of the integration is reached. Further, all output neurons are arranged in a laterally coupled inhibitory network, in which the first spiking neurons resets the integration of all other output neurons. This in fact builds a winner-take-it all network architecture and guarantees that individual input patterns are learned by different neurons, which is at the heart of the unsupervised learning. Crucial for the learning is an adjustable neuron threshold, which guarantees that all output neurons are participating equivalently at the learning phase and which can be motivated regarding the process of homeostasis in biological systems. Therefore, the threshold of a neuron is increased whenever the spike number (activity) of a neuron is above the desired activity and decreased for the other way around. Following Ref. [1] this can be achieved by using
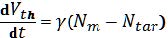 |
(6)
|
for the threshold voltage adaptation. Here,
γ,
Nm, and
Ntar are, respectively, a positive constant, the mean activity of an individual neuron, and the target activity.
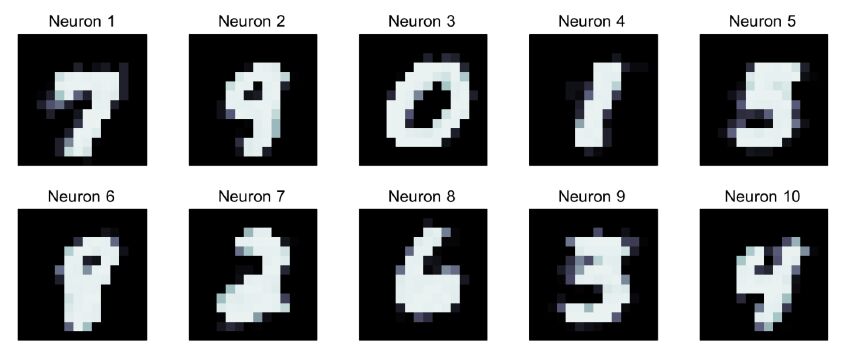
In Figure6(a) conductance maps (receptive fields) of the memristive devices at the specific site in the cross-bar-array assigned to each of their particular output neurons are shown. In particular, during learning each of the ten output neurons has unsupervised learned one of the input digits and is therewith capable to separate those digits thereafter. We like to point out that the network was able to learn all ten different digits by only presenting a subset of 9,000 digits out of the 60,000 MNIST pattern and by reducing also the resolution of the images from 784 pixels to 196 pixels. In particular, the network can clearly discriminate similar appearing digits like the nine (neuron 2 in Figure 5) and the four (neuron 10 in Figure 5) and all ten digits are clearly distinguishable within the receptive fields of the output neurons.
In order to estimate the recognition rate of the system we present 100 distinct digits to the network, which have not been shown to the network before. Following Ref. [1] the neuron, which spikes most frequently for one of the respectively presented input digit can be associated to them. Therefore, we compared the obtained spike intensities with the receptive fields of the output neurons (cf. Figure 5). As a result we obtain a recognition rate of 59.8%, which is in agreement to previous investigations [1,2,3]. However, as shown in Ref. [1], the recognition rate can be drastically increased by increasing the number of output neurons, since this allows to assign one digit to several output neurons. In order to qualitatively study the recognition rate dependence of an increased number of output neurons per input pattern in some more detail, we are presented only two different digits to the network by using five output neurons. In the first run we are using '0' and '7' as input pattern, since those digits are quite different. As a result we were able to reach a recognition rate of 97.5%. Thereafter, we are using quite similar digits, i.e. '4' and '9'. Here, the obtained recognition rate was still 61.5%. However, the aim of this investigation was to evaluate relevant device requirements and performing conditions of our fabricated TiOx-based memristive devices rather than improving previous investigations. At this respect, we can point out that memristive devices for this kind of applications should exhibits defined threshold voltages, a homogeneous resistive switching characteristic, and symmetric set and reset behavior.
4. Conclusion
In summary we compared two memristive devices exhibiting different I-V characteristics. Although based on the same Al/Al2O3/TiO2-x/Al (bottom to top) layer sequence, a 20 nm and 50 nm thick TiO2-x led to analog and digital I-V characteristics, respectively. This result means that even by using the same thin film technological procedure, qualitatively distinct I-V characteristics can be achieved. The experimental obtained devices characteristics was modeled in an equivalent circuit model, which relies on mobile oxygen ions by taking electronic transport through local conducting filaments and hopping between TiOx defect states into account. Moreover, to have a realistic model for network simulation at the hand a back diffusion of oxygen ions has been taken additionally into account.
As an example for a neural network application of the developed devices, we showed a pattern recognition system using the well accepted MNIST Database benchmark system. The recognition model system compromises memristive devices with gradual (homogenous) I-V characteristics, a cross-bar array with a feed-forward neural network, leaky-integrate-and-fire neurons including a winner-take it all strategy. As a result, we found that Al/Al2O3/TiO2-x/Al devices with an thin layer are suitable devices for pattern recognition in the presented network topology, since those devices exhibits an homogeneous resistive switching behavior as well as a symmetric set and reset behavior.
Acknowledgments
We would like to thank the Deutsche Forschungsgemeinschaft through FOR2093 for the financial support. MZ thanks Rolf Würtz (RU Bochum, Germany) for discussion.
Conflict of Interest
The authors of this publication have research support from German Research Society (DFG) and the government of the state Schleswig-Holstein, Germany. The terms of this arrangement have been reviewed and approved by the Christian-Albrecht University Kiel in accordance with its policy on objectivity in research.









 DownLoad:
DownLoad: