1. Introduction

The present work deals with the use of meso-scale coarse-grained molecular-dynamics simulations in order to assess shockwave-attenuation and -dispersion capacity of polyurea and identify the key molecular-level phenomena and processes responsible for this shockwave-mitigation ability (and possibly quantify their contribution). Hence, the main background topics overviewed in the remainder of this section include: (a) chemistry, synthesis, microstructure and properties of polyurea; (b) potential shockwave-mitigation mechanisms operating within this material; and (c) prior efforts dealing with the shockwave generation, propagation and interaction phenomena in polyurea.

1.1. Polyurea—Chemistry, synthesis, microstructure and properties

1.1.1. Synthesis

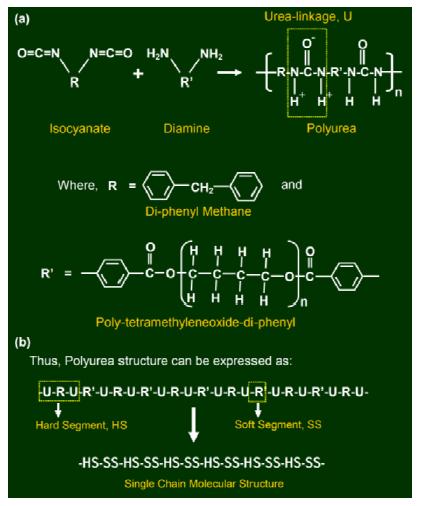
The co-polymerization reaction which results in the synthesis of polyurea is depicted schematically in Figure 1(a). It is seen that two monomers, one containing an isocyanate (-N=C=O) group, and the other containing an amine (-NH₂) group, participate in this co-polymerization reaction. There are two defining features of the polyurea synthesis reaction: (a) ease of occurrence over wide ranges of temperature and humidity conditions; and (b) high reaction rate.

Figure 1. Co-polymerization reaction resulting in the formation of polyurea consisting of alternating soft and hard segments. To simplify the schematic of the molecular structure, symbols SS (soft segment) and HS (hard segment) are used.

DownLoad: Full-Size ImgPowerPoint

1.1.2. Molecular-chain structure

For clarity, the following symbols are used in the molecular structure displayed in Figure 1 (a): (a) R for di-phenyl methane, an aromatic functional group; (b) R’ for poly-tetramethyleneoxide-diphenyl, an aromatic/aliphatic long chain functional group; and (c) U for a urea linkage. These symbols are used in Figure 1(b) to first define the soft and the hard segments within polyurea molecules and then to represent these molecules as a sequence of alternating hard and soft segments. For the two types of segments, the chemical composition and molecular structure can be defined as: (a) hard segment (HS)—a molecular assembly consisting of a diphenyl methane (C₆H₅-CH₂-C₆H₅) functional group sandwiched between two highly polar (i.e. containing centers/poles of negative and positive charge) urea linkages (-NH-CO-NH-); and (b) soft segment (SS)—a molecular assembly consisting of a series of aliphatic functional groups (C₆H₅-((CH₂)₄O)_n-C₆H₅).

1.1.3. Bulk-material microstructure

In Figure 2, the “ball-and-stick” representation is used to show a prototypical molecular-level microstructure within bulk polyurea. It is seen that the microstructure is meso-segregated into discrete hard domains and a continuous soft matrix. It is generally accepted that this meso-segregation process is mainly driven by: (a) strong inter-chain bidentate hydrogen bonds associated with urea linkages; and (b) Π-stacking of R-aromatic moieties. Since nitrogen atoms (represented as enlarged blue spheres) are only present within the urea linkages, hard domains can be readily identified in Figure 2. The hard domains are partly- or fully-crystalline, with a glass transition temperature above the ambient temperature. In sharp contrast, the soft matrix is amorphous, consists of a mixture of soft segments (the major component) and non-segregated hard segments (the minor component), and possesses a sub-ambient glass transition temperature.

Figure 2. Meso-segregated polyurea molecular-level microstructure showing the presence of an ellipsoidal-shaped discrete hard domain surrounded by a continuous soft matrix. To help identify the hard domain, nitrogen atoms residing within the hard domain are shown as (blue) enlarged spheres.

DownLoad: Full-Size ImgPowerPoint

Since inter-chain bonding is mainly based on the operation of hydrogen and P-bonds, polyurea is often considered as a thermo-plastically cross-linked elastomer. On the other hand, depending on the average functionality (i.e. the number of dangling bonds, which participate in the polymerization, in each mer) of the isocyanate precursor used for polyurea synthesis, polyurea may also possess some level of covalent cross-linking. As a result, average functionality of the isocyanate precursor can generally have a profound effect both on the polyurea meso-segregated bulk microstructure and its properties, e.g. [1,2]. In addition, polyurea microstructure and properties are found to be a sensitive function of the polyurea chemistry (e.g. the soft-segment molecular weight) and the synthesis route (e.g. curing temperature) [2,31,32,33,34,35,36].

1.1.4. Quasi-static and dynamic mechanical properties of polyurea

A comprehensive overview of the mechanical response of polyurea to various static and dynamic loading conditions can be found in our recent work [3,4,5,6]. The dominant features of the mechanical response of polyurea include: (a) a high extent of material constitutive non-linearity; (b) high sensitivity to thermo-mechanical loading conditions such as strain-rate, pressure and temperature; and (c) a high rate of hardening, particularly at large strains, strain-rates and (confining) pressures. This unique combination of properties of polyurea is clearly the result of its complex meso-scale microstructure and has been used to rationalize superior performance of this material in blast-/shockwave-mitigation applications.

1.2. Mechanisms for polyurea-induced ballistic-resistance/blast-mitigation enhancement

Polyurea is presently being used both in ballistic-protection and blast-/shock-wave mitigation applications. However, the phenomena and processes behind the superior ballistic-protection and blast-/shock-wave-mitigation capacities of polyurea appear to be different and, hence, they are overviewed separately in this sub-section.

1.2.1. Ballistic protection

Recent observations [7,8,37,38] suggest that: (a) the superior ballistic-protection capacity of polyurea is more related to its soft matrix than to its hard domains; (b) despite their dominant role in inter-chain bonding and in the formation of hard domains, hydrogen bonds do not appear to play a significant role in the ballistic-protection capacity of polyurea; and (c) the rubbery-to-glassy, second-order phase transition within the soft matrix of polyurea appears to make the dominant contribution to the superior ballistic-protection performance offered by polyurea coatings, linings or internal linings.

1.2.2. Shockwave mitigation

As for the shockwave attenuation and dispersion capability of polyurea, it is believed to be controlled mainly by the hard domains, and to a minor extent by the soft matrix [1,3,4,5,6,8,9,10,11,12,13,14,15,16]. However, presently there is no general consensus regarding the mechanism responsible for the superior shockwave-mitigation capacity of polyurea. The potential shockwave-mitigation mechanisms most frequently cited include shockwave-induced: (a) short-/long-range ordering within the hard domains [15]; (b) crystallization/densification within the hard domains [15]; (c) breakage of the existing and the formation of new, and more numerous, hydrogen bonds within the hard domains [13,14]; and (d) viscoelastic stress relaxation within the hard-domains/soft-matrix interfacial regions [16].

1.3. Molecular-/meso-scale modeling of shockwave phenomena in polyurea

A detailed literature review pertaining to the use of computational methods and tools for analyzing shockwave generation, propagation and interaction phenomena in polyurea, as reported in the open literature up to 2012, was presented and discussed in Ref. [1]. In the remainder of this section, only a brief overview of the most significant developments regarding the molecular-/meso-scale modeling of shockwave generation, propagation and interaction since 2012 is presented.

In Ref. [1], meso-scale coarse-grained molecular-dynamics simulations are used to help identify the operation of different shockwave attenuation/dispersion processes in meso-segregated polyurea as a function of polyurea chemistry (more specifically, the soft-segment molecular weight). The results obtained suggested that the chemistry-dependent extent of meso-scale phase segregation and of the degree of short-range order within the hard domains play an important role in the shockwave-mitigation ability of polyurea.

In Ref. [17], a multi-length-scale computational analysis is used to carry out the design of polyurea for maximum shockwave-mitigation performance. The computational analysis involves a combined all-atom/coarse-grained molecular-level investigation of shockwave-propagation within polyurea and a finite-element analysis of direct quantification of the shockwave-mitigation capacity of this material as a function of its chemistry (or, more specifically, of its soft-segment molecular weight). The results obtained suggest that the approach employed can correctly identify the optimal chemistry of polyurea and, thus, be of great benefit in the efforts to develop new highly-efficient blastwave-protective materials, in a cost-effective manner.

1.4. Main objectives

The main objective of the present work is to employ meso-scale coarse-grained molecular-level computational methods and tools in order to identify and characterize the phenomena and processes related to the effect of soft-segment molecular weight on: (a) the extent of meso-segregation and the resulting microstructure of polyurea; (b) the activation of various shockwave-attenuation and -dispersion processes within polyurea; and (c) the propagation kinetics of release waves and their ability to capture preceding shockwaves.

2. Materials and Methods

The present work utilizes the meso-scale coarse-grained molecular-level computational framework. Within this framework, the material under investigation is not treated as a continuum but rather as an assembly of discrete, interacting particles (referred to as “beads”, hereafter). Each bead represents a collection of atoms/ions and their bonds, and accounts for the collective degrees of freedom of the constituent particles. Adjacent beads residing within the same chain are bonded using “connectors” to form bead-based chains. Beads of the neighboring segments of different, or the same chain, are also allowed to interact in a van der Waals-like and/or Coulomb-like non-bond fashion. Due to the use of particles larger than atoms (that is, beads) within the meso-scale coarse-grained computational framework, relative to the ones (i.e. atoms/ions) used within the so-called all-atom computational framework, larger computational domains could be analyzed using the same number of particles, the treatment of which could be handled using the available computational and storage resources. Furthermore, since the high-frequency vibrations of the constituent atoms/ions are integrated out during the coarse-graining procedure, the system dynamics is controlled not by the stiff/hard, atom/atom interactions but rather by the compliant/soft, bead/bead interactions. Consequently, significantly longer time-steps (and, thus, simulation times) can be employed. This, in turn, enables direct simulation of the phenomena and processes such as: (a) meso-phase segregation and the formation of hard domains and soft matrix in polyurea [1]; and (b) the dynamics of larger microstructural constituents (e.g. polyurea-chain soft segments) [16]. In addition, due to the possibility for using larger computational domains, investigation of the propagation of medium-strength and weak shockwaves (associated with a relatively large wave-front width) becomes feasible. The ability to analyze intermediate-strength/weak shockwaves and to use longer simulation times was the main reason for choosing the coarse-grained computational framework over its all-atom counterpart. However, it should be noted that the two frameworks are fundamentally identical, since both treat materials as assemblies of interacting particles and use force-fields (a set of mathematical expressions describing various contributions to the potential energy function for the system of interacting particles) to quantify various bonding and non-bonding interactions between the constituent particles. The two main differences between the two methods are: (a) the nature, and size/mass, of the constituent (beads vs. atoms) particles; and (b) bead/bead interactions are generally quite more compliant (softer) than their atom/atom counterparts.

Typically, a complete formulation of a meso-scale coarse-grained molecular-simulation problem includes, at a minimum, the following four items: (a) a computational model consisting of one or more bead types; (b) a set of inter-bead force-field potentials which describe accurately various bonding and non-bonding bead/bead interaction forces; (c) a computational method(s) to be used in the simulations; and (d) formulation of the problem to be analyzed. These four items are discussed in greater detail in the remainder of this section.

2.1. Computational model(s)

2.1.1. Coarse-graining

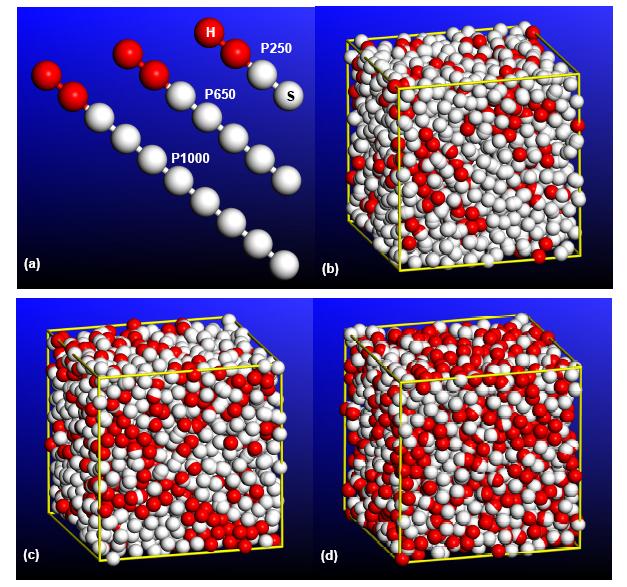
The polyurea grades analyzed in the present work are all based on an isocyanate consisting of diphenyl methane (R) functional group and a diamine consisting of poly-tetramethyleneoxide-diphenyl, PTMO (R’), functional group. Three renditions of polyurea (P1000, P650 and P250) were analyzed. They differ in the number of C₄H₈O units within the PTMO soft-segment (and thus in the soft-segment molecular weight). Specifically, P1000, P650 and P250 contain 14, 9 and 3 C₄H₈O units respectively. The numbers following P in the name of these polyurea renditions correspond approximately to the soft-segment molecular weight in a.m.u.

Since beads are hypothetical particles, the first step in the construction of coarse-grained computational model(s) involves specification of the number of bead types and the chemical makeup (and thus, the size/mass) of each bead. Adopting the coarse-graining procedure developed in [1], it is assumed here that for all the polyurea renditions analyzed in the present work, coarse-grained chains can be realistically represented by two bead types, H (hard) and S (soft). A single H-type bead consists of an assembly of one R functional group surrounded by two urea linkages and then by two phenyl groups, Figure 1(a). By requiring that the volumes of the H and S beads are comparable, the procedure developed in [1] established that the S-bead should be defined as an ensemble of two C₄H₈O functional groups. Once the chemical identity of the two bead types is established, their masses (needed in the coarse-grained molecular dynamics simulations) are determined as the sum of the masses of the constituent atoms. Consequently, the repeat units of the bead-based chains for P1000, P650 and P250 are approximated as H₂S₈, H₂S₅ and H₂S₂ respectively.

2.1.2. Computational cell

In order to analyze polyurea bulk behavior (i.e. the behavior of polyurea in the absence of free-surface effects) within the coarse-grained framework, a cube-shaped computational cell (with an edge length of 10 nm) was constructed and periodic boundary conditions applied to its faces. The three edges (a, b and c) of the cell are aligned respectively with the three coordinate axes (x, y and z). The repeat units along the bead-based chains within the three grades of polyurea are defined as: (a) H₂S₈ for P1000; (b) H₂S₅ for P650; and (c) H₂S₂ for P250. Bead configurations of these repeat units are displayed in Figure 3(a).

Figure 3. (a) Polyurea-chain coarse-grained repeat units consisting of H, hard, and S, soft, beads for the three (P1000, P650 and P250) polyurea grades analyzed in the present work (please see text for details); and examples of the initial coarse-grained computational cells containing fully-mixed bead-based chains for (b) P1000; (c) P650; and (d) P250.

DownLoad: Full-Size ImgPowerPoint

The repeat units are next replicated to generate the nearly equal-length chains for the three polyurea grades as: (H₂S₈)₄, (H₂S₅)₆ and (H₂S₂)₁₀. Subsequently, the Amorphous Cell program from Accelrys [18] was used to place (stochastically) the chains within the computational cell while ensuring (through minor adjustment to the cell-edge length) that the target mass-density is achieved. Lastly, the potential energy of the computational cell is minimized with respect to the spatial coordinates of the constituent beads. Examples of the resulting coarse-grained computational cells for P1000, P650 and P250 are displayed in Figures 3(b)-(d), respectively. It should be noted that polyurea chains initially residing within the computational cells, as displayed in Figures 3(b)-(d), are distributed randomly (i.e. no significant extent of meso-phase segregation is present). As will be discussed later, the computational cells depicted in Figures 3(b)-(d) are used to study the meso-segregation process and the resulting two-phase microstructure and properties of polyurea. In addition, as will be shown below, several adjacent computational cells aligned in the longitudinal (x-) direction will be combined to form a single extended computational cell to be used in the analysis of shockwave formation and propagation.

2.2. Force-fields

The meso-scale coarse-grained force-field used in the present work was constructed and parameterized in Ref. [1]. Since Ref. [1] contains all the details used to construct and parameterize the force-field, the same will not be repeated here. Instead, a brief overview of the main points used within the force-field construction/parameterization procedure will be given.

The meso-scale coarse-grained force-field used has the following features:

(a) it includes only two (functionally distinct) contributions to the system potential energy—(i) a bond-stretch term; and (ii) a non-bond van der Waals-type term;

(b) the bond-stretch term is represented using a harmonic-type potential-energy function, and includes three (H-H, H-S and S-S) types of connectors;

(c) to parameterize the bond-stretch force-field, all-atom molecular statics and dynamics calculations were carried out in conjunction with the so-called “Adaptive Biasing Force” (ABF) method. In these calculations, all-atom force-field COMPASS (Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies) [19,20] was used. However, to more accurately account for the effect of strong hydrogen bonding between urea linkages of the neighboring chain segments, additional quantum-mechanics-based calculations had to be carried out. Details of these calculations can be found in Ref. [21]. The results of these calculations are used to augment the original COMPASS force-field potential; and

(d) the non-bond van der Waals-type bead/bead interactions are accounted for through the use of either the 12-6 or the 9-6 Lennard-Jones types of functions, and also includes three (H-H, H-S and S-S) types of bead-pair interactions. Parameterization of this non-bond portion of the force-field was also accomplished in Ref. [1] through the use of the all-atom molecular-level calculations in conjunction with the ABF method. In addition, to smoothly reduce the non-bond interaction energy to zero at a predefined cutoff radius, a switching/scaling function was utilized.

2.3. Computational method(s)

The computational methods used in the portion of the present work dealing with the formation of meso-scale-segregated microstructure include molecular statics (i.e. potential-energy minimization) and (equilibrium) molecular dynamics (i.e. particle-trajectory analysis), as implemented in Discover (a general-purpose atomic simulation program) from Accelrys [24]. Within the molecular statics approach, the potential energy of the subject discrete-particle configuration is minimized with respect to the position of the particles/beads. On the other hand, within the molecular dynamics approach, gradient of the potential energy with respect to the particle positions is first used to generate forces acting on the particles and, then, the associated Newton’s equations of motion (for all particles) are integrated numerically in order to simulate the temporal evolution of the particle positions. In addition, within the equilibrium molecular-dynamics methods, the system under consideration is coupled to an (external) environment (a constant temperature reservoir, in the present case) which ensures that the system remains in thermodynamic equilibrium (i.e. the system does not experience fluxes of thermodynamic quantities). In the present work, an NVT (where N is the (fixed) number of atoms, V, the computational cell volume (also fixed, and set to an arbitrarily large value to provide for the isolated-beads interaction environment), and T (=300K) is the temperature) rendition of the molecular dynamics method is employed.

In addition to the methods listed above, the non-equilibrium molecular dynamics method was also employed in the portion of the coarse-grained molecular analysis dealing with the generation and propagation of shockwaves. Within non-equilibrium molecular dynamics, the system is subjected to large mechanical and/or thermal perturbations. As a consequence, the system experiences large fluxes of its thermodynamic quantities (e.g. mass, momentum and energy). Meso-scale shockwaves (or, more precisely, pairs of converging shockwaves, one pair per computational cell) are generated using a procedure which mimics the so-called “symmetric flyer-plate” shockwave-generation experiment and relies on a step-wise sequential contraction of the computational-cell longitudinal lattice parameter [25,39,40,41]. Contraction of the longitudinal lattice parameter, a, as a function of time, t, is carried out in accordance with the following relation:

a(t)=a(t=0)-2u_pt (1)

where u_p (=200-650 m/s) is the pre-selected “upstream” particle/bead velocity in the longitudinal direction. To mimic uniaxial-strain, planar-longitudinal-shockwave conditions typically encountered in blast-impact scenarios, transverse computational-cell parameters (b = c) are kept constant. The material swept by the shockwaves, advancing at a shockwave-strength-dependent speed U_s, undergoes abrupt and shockwave-strength-dependent increases in the mass density, internal energy density, stress, particle velocity, temperature and entropy density.

As will be shown below, combined application of the (equilibrium and non-equilibrium) molecular dynamics and molecular statics methods enables the investigation of: (a) the meso-scale segregation process; (b) characterization of the resulting two-phase microstructure and properties; and (c) phenomena associated with the generation, propagation and interaction of shockwaves within polyurea.

All the calculations in this portion of the work were carried out by coupling a user-defined coarse-grained force-field database with the Discover solver [24]. The aforementioned shockwave-generation procedure, including pre-shockwave thermal-equilibration of the meso-scale segregated polyurea, is implemented and linked with Discover through the use of an input file written in the BTCL script. This enabled precise control of all simulation tasks such as sequential contraction of the computational cell in the longitudinal direction, deactivation of the equilibrium molecular-dynamics algorithm implemented in Discover in order to perform non-equilibrium molecular-dynamics calculations, etc.

2.4. Problem formulation

The work carried out at the meso-scale coarse-grained molecular level involved three distinct efforts, all of which are carried out using Discover:

(a) generation of the meso-scale segregated state of polyurea using meso-scale coarse-grained equilibrium molecular dynamics method. Equilibrium molecular dynamics simulations are initially carried out for a sufficiently long time (ca. 50 ns), at high temperatures, to speed up the meso-scale segregation process. Subsequently, a multi-step temperature quench routine is applied in order to bring the system to room temperature. Based on the meso-scale coarse-grained force-field potentials used, it is assessed that the room temperature is higher than the T_g of the soft matrix and lower than the T_g of the hard-domain phase (which is fully consistent with the experimental calorimetric results for polyurea [2]). Equilibrium molecular dynamics simulations are then continued at room temperature, for sufficiently long time (ca. 50 ns), until the system reaches a state of “dynamic equilibrium,” defined as the state of the material in which changes in the pressure moving-average are smaller than a pre-defined upper bound. Since a similar and more complete effort of this type was reported in our recent work [22,23], no other details of this portion of the work will be presented here;

(b) characterization of the two-phase polyurea microstructure and properties through extensive post-processing analyses of the equilibrium molecular dynamics trajectory results. More details of the aspects of material microstructure and properties analyzed, and of the functional relations used, will be given in the next section; and

(c) the use of non-equilibrium molecular dynamics simulations to analyze shockwave generation and propagation through, and interactions with, the meso-segregated microstructure of polyurea and the resulting changes in the shockwave-front and material structures.

3. Results and Discussion

As mentioned earlier, the main objective of the present work is to obtain more insight into the effect of polyurea soft-segment molecular weight on: (i) the meso-scale segregation process resulting in the formation of a two-phase microstructure; (ii) mechanical properties of polyurea; and (iii) the shockwave-mitigation capacity of this material. It should be noted that, since P1000 is the most frequently used grade of polyurea, it is treated here as a reference material, while P650 and P250 are considered as the polyurea grades which enabled investigation of the effect of lower soft-segment molecular weight (relative to P1000). The key results obtained in the current meso-scale coarse-grained investigation are presented and discussed in the remainder of this section. Since some of the results were previously reported in Ref. [1], they will not be repeated here. However, they will be briefly overviewed in order to help clarify the final findings related to the role of polyurea soft-segment molecular weight on the shockwave-mitigation capacity of polyurea.

3.1. Microstructure characterization

3.1.1. Meso-scale phase segregation and hard-domain formation

Coarse-grained (meso-scale-segregated) material microstructures in P1000, P650 and P250 polyurea computational cells, after the application of the aforementioned prolonged high-temperature equilibration treatment and the subsequent multi-step temperature quench routine are depicted in Figures 4(a)-(c), respectively. For improved clarity: (a) hard beads are displayed as large (red) spheres while soft beads are displayed as substantially smaller (white) spheres; and (b) the chains’ backbone bonds are not shown.

Examination of the results displayed in Figures 4 (a)-(c) reveals that:

(a) discrete hard domains are formed only in P1000 and P650, Figures 4 (a)-(b), while in the case of P250, the meso-segregation process results in the formation of a fully-percolated hard-domain phase, Figure 4 (c). This finding is consistent with the fact that the volume fraction of the hard segments within the polyurea chains (i.e. the fraction of the hard beads) increases from 0.20 in P1000 to ~0.29 in P650 and then to 0.50 in P250;

Figure 4. Coarse-grained (meso-segregated) material microstructures in: (a) P1000; (b) P650; and (c) P250 polyurea computational cells, obtained after the application of a prolonged high-temperature equilibration treatment and subsequent multi-step temperature quench routine. Please see text for details.

DownLoad: Full-Size ImgPowerPoint

(b) by comparing Figures 4 (a)-(b), it is apparent that the hard domains in P1000 are smaller, present in a somewhat greater number density, and associated with a smaller volume fraction. Following the microstructure-characterization procedure (within which hard-domain particle-shape is idealized as being prolate spheroidal) described in Ref. [1], it is found that a reduction in the soft-segment molecular weight from ca. 1000 to ca. 650: (i) yields a 15-20% increase in the hard-domain particle major axis; and (ii) has relatively small (<2%) effect on the hard-domain particle ellipticity; and

(c) using the procedure described in Ref. [1], it is established that the extent of meso-phase segregation (defined as the fraction of hard beads residing within the hard domains) decreases in the order P1000 ® P650 ®P250. This finding is consistent with the fact that, as the molecular weight of the soft segments decreases, so does the soft-segment length, making the segment structurally/morphologically more rigid. This in turn results in increased energetic and entropic penalties associated with morphological changes of these segments (e.g. bending, twisting, etc.) accompanying the meso-segregation process and the formation of hard domains.

It should be noted that the observed differences in the coarse-grained meso-scale-segregated structure in the three polyurea renditions cannot be readily attributed to the effect of chain entanglement, since the polyurea chains analyzed in the present work are relatively short and of nearly identical length in the three grades of polyurea. However, chain entanglement may play a significant role in the meso-scale-segregation process of real polyureas [2]. These chain-entanglement effects, thus, were not captured in the present analysis.

3.1.2. Hard-domain bridging by soft segments

The work of Arman et al. [26] as well as our prior work [1] clearly established that hard-domain morphology, in general, and its connectivity, in particular, has a major effect on the way an advancing shockwave interacts with the polyurea medium. The results displayed in Figures 4 (a)-(c) already established that a reduction in the soft-segment molecular weight can have a profound effect on the hard-domain microstructure (changing it from a discrete-particle type in P1000 and P650 to a continuous-network type in P250). However, discrete hard domains are not generally isolated from their neighbors but rather connected with them via the polyurea-chain soft segments. This type of hard-domain connectivity has also been found to affect the details of the shockwave/material interactions [1,26]. Consequently, to properly quantify the extent of hard-domain connectivity in a given polyurea grade, one must also include the contribution of hard-domain bridging by the soft-segments. In the present work, it is found that in the case of P1000, the fraction of hard-domain-bridging soft segments is smaller than in P650 by ca. 20% (the extent of bridging by soft segments was not analyzed in P250 since this polyurea rendition already contains a continuous network of the hard-domain phase). This finding can be attributed to the fact that the soft-segments with a larger molecular weight are longer and, hence, more flexible, enabling polyurea chains to fold and adjacent hard segments to participate in the formation of the same hard-domain particle.

3.1.3. Hard-domain mass density and degree of order

As mentioned earlier, shockwave-induced hard-domain compaction and ordering is one of the identified shockwave-attenuation and dispersion mechanisms [15]. The extent of this blast-mitigation effect is generally expected to increase with an increase in the hard-domain volume fraction and with a decrease in the initial degree of order and mass density of the hard-domain phase, due to the accompanying increase in the (shockwave-induced ordering/densification) extent of shockwave-energy dissipation.

The effect of the polyurea soft-segment molecular weight on the volume fraction of the hard-domain phase was revealed in Figures 4 (a)-(c). In order to reveal the effect of the soft-segment molecular weight on the initial mass-density and the degree of order within the hard domains, the procedure developed in Ref. [1] was used to determine the H-H bead pair correlation (also known as radial distribution) function for each polyurea grade. This function can be viewed as a ratio of the probability per unit volume of finding a given bead-pair type with a given separation relative to the averaged probability per unit volume of finding the same bead-pair type. Furthermore, the Fourier transforms of the H-H bead pair correlation functions are directly related to scatter intensities that can be obtained experimentally through neutron scattering and small angle X-ray scattering (SAXS) techniques [2].

By applying the procedure described in Ref. [1], the H-H bead pair correlation functions are determined in the three polyurea renditions. This was done only for a relatively small inter-bead distance range, since the main purpose for computing these functions was the quantification of the extent of hard-bead clustering (including the local mass-density and the degree of ordering) within the hard domains. This procedure confirmed that as the soft-segment molecular weight is decreased from P1000 to P650 to P250: (a) the fraction of hard beads residing within the hard domains (i.e. the extent of meso-segregation) is reduced; (b) the average H-H bead nearest-neighbor distance is increased, resulting in a lower value of the local mass density; and (c) the breadth of the distribution of the H-H bead nearest-neighbor distances is increased, indicating a lower degree of local order. All these findings, as mentioned earlier, could be related to the increase in the soft-segment rigidity with a decrease in its molecular weight. In other words, the shorter and stiffer polyurea soft segments tend to interfere with both the meso-segregation process and with the process of packing and ordering of the hard beads within the hard domains.

3.2. Linear-response mechanical properties

Meso-scale coarse-grained equilibrium molecular dynamics simulations carried out in the present work yield the particle-trajectory (i.e. time-dependent position and velocity) results. As described in our prior work [1], results of this type can be used to determine the time-/frequency-dependent elastic and rheological properties of polyurea and their dependence on the soft-segment molecular weight. It should be recognized, however, that the application of the procedure described in Ref. [1] yields the so-called “linear response” material properties, i.e. the properties reflecting the material response under mechanical perturbations which place the material in a disturbed state relatively close to the stress-free reference state of the material. It should be recalled that one of the main objectives of the present work is to examine the interaction of propagating shockwaves with the polyurea medium and, under shockwave-loading conditions, mechanical (and thermal) perturbations are often substantial, displacing the material further away from its reference state. Under such conditions, the linear-response material properties, such as time-/frequency-dependent bulk and shear moduli and the Newtonian-type bulk and shear viscosities, are not expected to provide much insight into the response of the shockwave-loaded material. However, the utility of these properties is somewhat higher relative to predicting the material response to the propagation of a release-wave (the scenario which was also analyzed in the present work).

Since a detailed description of the computational procedure used to determine the linear-response material properties of polyurea and of the results obtained was given in Ref. [1], only the findings of relevance to the kinetics of propagation of release waves will be presented and analyzed in the remainder of this sub-section.

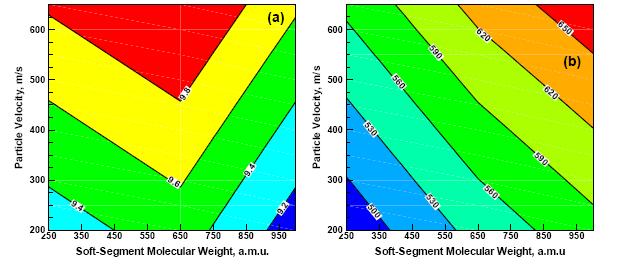
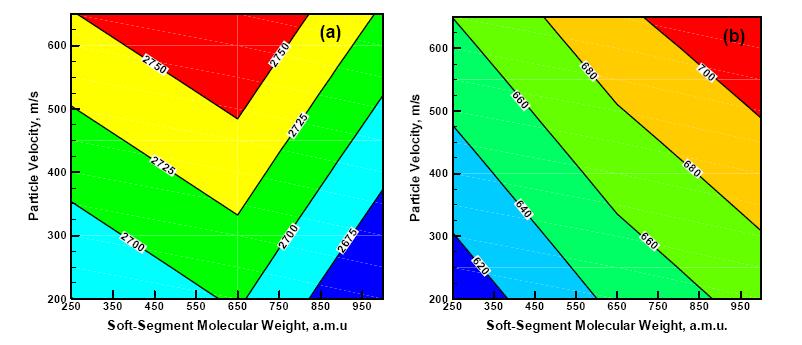
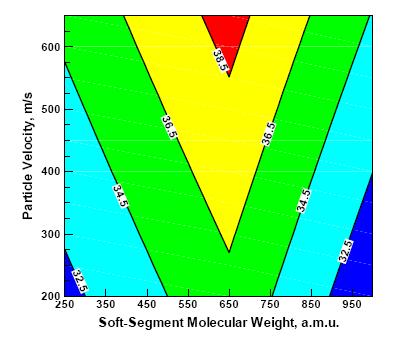
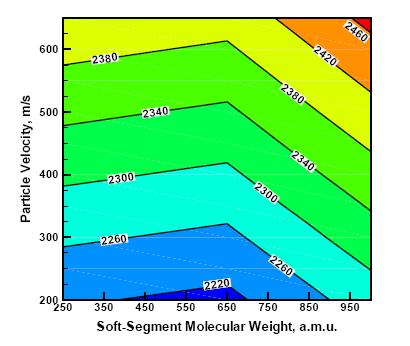
The effects of polyurea soft-segment molecular weight and the extent of the preludial shockwave loading (as quantified by the upstream average particle velocity) on the short-time (i.e. instantaneous) bulk and shear moduli are depicted in Figures 5 (a)-(b). Since unloading of the material swept by a release wave is of an elastic character, the instantaneous moduli depicted in Figures 5 (a)-(b), in conjunction with the corresponding (pre-shocked) material mass density, can be used to compute the corresponding release-wave speed using a standard relationship: wave speed = (elastic modulus / mass density)^0.5. The results of this procedure are depicted as a contour plot in Figures 6 (a)-(b). Of particular interest for the problem of TBI mitigation are the results displayed in Figure 6 (a), which show the effect of the polyurea soft-segment molecular weight and the extent of the preludial shockwave loading on the longitudinal release-wave speed. These results reveal that, for all extents of the shockwave loading, the longitudinal release-wave speed is the highest in the case of P650. This finding is very important since capture and neutralization of the preceding longitudinal shockwave by the trailing longitudinal release-wave is a very important shockwave-mitigation mechanism [27]. The results displayed in Figure 5 (a)-(b) and 6 (a)-(b) also can be used to explain commonly observed variability in the mechanical properties of polyurea of a constant nominal composition and processed under nominally identical conditions. That is, small local variations in the polyurea chemistry and processing conditions can alter, locally, the soft-segment molecular weight and thus, the mechanical properties.

Figure 5. Effect of poly-urea soft-segment molecular weight and the extent of the preludial shock-wave loading (as quantified by the upstream average particle velocity) on the short-time (i.e. instantaneous): (a) bulk modulus (in GPa); and (b) shear modulus (in MPa).

DownLoad: Full-Size ImgPowerPoint

Figure 6. Effect of poly-urea soft-segment molecular weight and the extent of the preludial shock-wave loading (as quantified by the upstream average particle velocity) on the release-wave: (a) longitudinalvelocity; and (b) transverse velocity (both in m/s).

DownLoad: Full-Size ImgPowerPoint

3.3. Fully-supported shockwave mitigation

In this section, key results pertaining to the propagation of (fully-supported) longitudinal shockwaves through, and their interactions with, the meso-segregated microstructures of the three polyurea renditions are presented and discussed. While many aspects of shockwave mechanics and shockwave/material interactions can be investigated, the present section focuses on those aspects which are most closely related to the ability of polyurea to attenuate and disperse shockwaves.

3.3.1. Longitudinal shockwave generation and propagation

The computational-cell contraction procedure described in Section 2.4 results in the formation of two fully-supported, converging, longitudinal shockwaves (within the computational cell). For clarity, the results presented in this section focus only on one (i.e. the right-propagating) shockwave. The term “fully-supported” simply implies that a sustained loading is applied to the end faces in order to support a continuous propagation of the shockwave.

An example of the typical results obtained in this portion of the work pertaining to the motion of the right-propagating shockwave through the meso-segregated microstructure of polyurea P650, and the accompanying changes in the positions of the H- and S-beads are shown in Figures 7 (a)-(d). The location of the shockwave front in Figures 7 (a)-(d) is defined by the region associated with the maximum changes in the average bead number-density. To help the reader, arrows are used in Figures 7 (a)-(d) to indicate the position of the shockwave front.

Figure 7. Typical results pertaining to the motion of the right-propagating shock-wave through the meso-segregated microstructure of polyureaP650, and the accompanying changes in the positions of the H- and S-beads. Approximate location of the shockwave- front is denoted by arrows.

DownLoad: Full-Size ImgPowerPoint

3.3.2. Shockwave-front profile and width

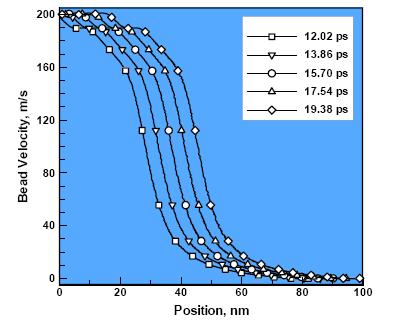
The ability of a material to mitigate fully-supported shockwaves (i.e. shockwaves which could not be attenuated) is often revealed by the shockwave front profile, or more specifically by its width. That is, in materials with a higher shockwave-mitigation capacity, the shockwave front is generally broader. Thus, the arrival of such a shockwave to a material boundary/interface is associated with a lower rate of momentum transfer (i.e. with lower loads). To determine the profile and the width of the longitudinal shockwaves generated in the present work, the procedure described in Ref. [1] was utilized. This procedure is based on the determination of the distribution of the locally-averaged beads’ longitudinal velocity, at different post-shockwave-initiation times, along the length of the computational cell. An example of the results obtained, for the case of P650, is displayed in Figure 8. This figure shows the resulting variation of the average particle velocity, u_p , along the length of the computational cell, at different post-shockwave-initiation times. The results are obtained under a continuously imposed unit-cell contraction rate (i.e. upstream particle/bead velocity) of 200 m/s.

Figure 8. Distribution of the locally-averaged beads’ longitudinal velocity, at different post-shock-initiation times, along the length of the computational cell for polyurea P650.

DownLoad: Full-Size ImgPowerPoint

Examination of the results displayed in Figure 8 shows: (a) formation of a fully-supported, right-propagating steady longitudinal shockwave; and(b) an apparent secondary trailing shockwave, the appearance of which could not be considered as unexpected, considering the heterogeneous meso-segregated nature of the material through which the shockwaves propagate [26].

The effects of polyurea soft-segment molecular weight and the shockwave-strength (as quantified by the upstream average particle velocity) on the shockwave-front width is depicted in Figure 9. The width of the shockwave-front is defined using the particle velocities corresponding to 0.1% and 99.9% of the imposed particle velocity. Examination of the results displayed in Figure 9

Figure 9. Effects of polyurea soft-segment molecular weight and the shockwave-strength (as quantified by the upstream average particle velocity) on the shockwave-front width (in nm).

DownLoad: Full-Size ImgPowerPoint

reveals that, at all shockwave-strengths analyzed, the wave-front is largest in the case of P650. This finding suggests that among the three polyurea renditions analyzed, P650 appears to have the highest mitigation potential with respect to the fully-supported longitudinal shockwaves.

3.3.3. Shockwave Lagrangian speed

The ability of a material to mitigate fully-supported shockwaves (i.e. shockwaves which could not be attenuated) is also revealed by the shockwave speed. That is, in materials with a higher shockwave-mitigation capacity, the shockwaves tend to propagate at a lower speed. Thus, the arrival of such a shockwave to a material boundary/interface is associated with a lower rate of momentum transfer (i.e. with lower loads).

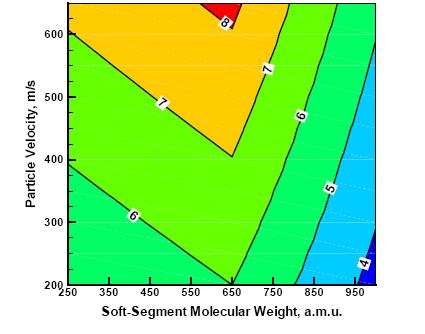
To compute the (average) Lagrangian shockwave speed at different imposed bead/particle upstream velocities, for the three polyurea grades investigated, the distance swept by the inflection point of the steady shockwave-front (like the one displayed in Figure 9) is divided by the corresponding post-shockwave-initiation time. The results of this procedure are shown in Figure 10, in which the effects of polyurea soft-segment molecular weight and the shockwave-strength on the shockwave Lagrangian speed are depicted.

Figure 10. Effects of polyurea soft-segment molecular weight and the shockwave-strength on the shockwave Lagrangian speed (in m/s).

DownLoad: Full-Size ImgPowerPoint

Examination of the results displayed in Figure 10 reveals that:

(a) overall, the polyurea soft-segment molecular weight appears to have a relatively small effect on the shockwave speed (at least in the bead-velocity and the soft-segment molecular weight ranges analyzed); and

(b) while the effect is relatively small, at each of the shockwave strengths examined, P650 appears to have the lowest shockwave longitudinal speed. This finding, in conjunction with the previously observed largest shockwave-front width found in P650, suggests that this rendition of polyurea appears to have the highest fully-supported shockwave-mitigation capacity. It should be noted that the results obtained in this portion of the work pertain to imposed upstream particle velocities in excess of 200 m/s. On the other hand, in the TBI-prevention applications of polyurea, upstream particle velocities of interest are in the ~20-50 m/s range. The use of these lower particle velocities would have resulted in wider shockwave fronts, requiring prohibitively larger computational domains and longer simulation times. Nevertheless, the nature of the results displayed in Figure 10 suggests that the behavior observed at the particle velocities in excess of 200 m/s can be extrapolated into the lower particle-velocity range of interest to the TBI-prevention problem. In other words, one could anticipate that even in the 20-50 m/s particle-velocity range, P650 would display superior fully-supported shockwave-mitigation capacity.

3.3.4. Hard-domain densification induced by shockwave loading

As mentioned earlier, hard domains may experience (permanent) compaction/densification and an increase in their degree of order when subjected to shockwave loading. Since these microstructural changes are associated with dissipation and absorption of shockwave kinetic energy, they are considered as potent shockwave-mitigation mechanisms. To quantify the extent of shockwave-induced permanent densification within the hard domains, average percent increase in the number density of H-beads within the hard domains of the three polyurea grades are determined after the passage of shockwaves of different strengths (and subsequent unloading in the three polyurea renditions). The results of this procedure are depicted in Figure 11.

Figure 11. Effects of polyurea soft-segment molecular weight and the shockwave-strength (as quantified by the upstream average particle velocity) on the average percent increase in the number density of H-beads within the hard domains after the passage of shockwaves of different strengths and subsequent unloading.

DownLoad: Full-Size ImgPowerPoint

Examination of the results displayed in Figure 11 reveals that: (a) for each of the three polyurea grades, the extent of hard-domain compaction increases with an increase in the shockwave strength; (b) at all shockwave strengths, the largest extent of hard-domain compaction is found in P650; and (c) since P650 was found to possess the highest fully-supported shockwave-mitigation capacity, it appears that this superior capacity is at least partly derived from the associated hard-domain densification process. That is, P650, due to its intermediate value of the soft-segment molecular weight, appears to be associated with an ideal combination of a large volume fraction of the hard domains and a low initial density of this phase of polyurea. In other words, soft segments in P650 appear not to be too stiff to interfere with the meso-segregation process, but stiff enough to initially prevent dense packing of hard beads within the hard domains.

Additional confirmation that permanent densification of hard domains by shockwave loading plays a major role in the mitigation of fully-supported shockwaves was obtained by analyzing the response of the three polyurea renditions, in their fully-mixed state, to the passage of the longitudinal shockwaves. It is found that in the case of hard-domain-free fully-mixed polyureas, the shockwave-front width is smaller by 5-10% while the Lagrangian shockwave-speed is larger by 5-10% relative to their meso-segregated polyurea counterparts.

3.4. Blast-induced shockwave mitigation

In the previous section, fully-supported shockwaves and their dispersion within polyurea was analyzed. Such shockwaves can be generated during: (i) impact of a polyurea-coated structure by a projectile; or (ii) during the collision of such a structure with another (typically stationary) structure. In the case when the polyurea-coated structure is the protective helmet, its impact by (blast-propelled) projectiles can result in the so-called secondary TBI while its collision with another structure can result in the so-called tertiary TBI [4]. However, the major concern is presently with the so-called primary TBI, which is caused by direct blast-loading of the protected helmet (and by the resulting generation, propagation and reflection of shockwaves, within the intracranial cavity).

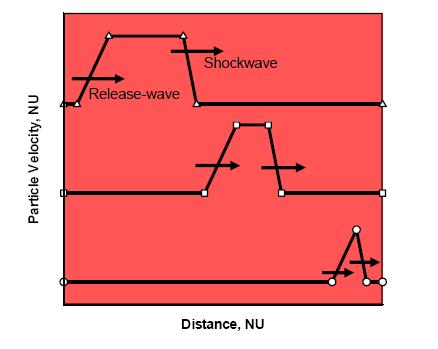
In the case of fully-supported shockwaves, the (imposed) loading was constant (i.e. time-invariant). In sharp contrast, loading by a (air-borne) blast-wave is initially associated with the largest magnitude and, as the time of loading increases, the extent of loading gradually decreases (and may ultimately change its sign/sense). This loading history is consistent with the so-called biphasic Friedlander equation for the temporal evolution of pressure at a point in air, following free-air detonation of a charge (at a stand-off location) e.g. [29,30]. The fact that loading continuously decreases suggests that the initial shockwave, produced by blast-loading of a structure, will be followed by a series of release waves. It is well established [27] that in the cases when the speed of the release waves is higher than the speed of the leading shockwave, the shockwave may be captured and attenuated by the trailing release waves. This process is generally considered as a highly potent shockwave-mitigation mechanism. Thus, when analyzing the blast-induced shockwave-mitigation potential of polyurea, one must account not only for the kinetics of the shockwaves but also for the kinetics of the trailing release waves. A schematic of the shockwave-mitigation process associated with the capture of a leading shockwave by a trailing and faster-moving release wave is provided in Figure 12.

Figure 12. A schematic of the shockwave-mitigation process associated with the capture of a leading shockwave by a trailing and faster-moving release-wave.

DownLoad: Full-Size ImgPowerPoint

To investigate the possibility for the aforementioned “shockwave-capture and neutralize” effect, the procedure used in the previous section to generate a fully-supported shockwave was modified in the following way:

(a) initial loading, as governed by the imposed upstream particle velocity, is applied, but only over a shorter period of time. This results in the formation of a fully-supported longitudinal planar shockwave (or more precisely, in the formation of two converging shockwaves);

(b) computational-cell contraction is then stopped. This causes the generation of a trailing release-wave (or more precisely, in the formation of two converging release-waves); and

(c) potential interactions between the leading shockwave(s) and the trailing release-wave(s) are then investigated.

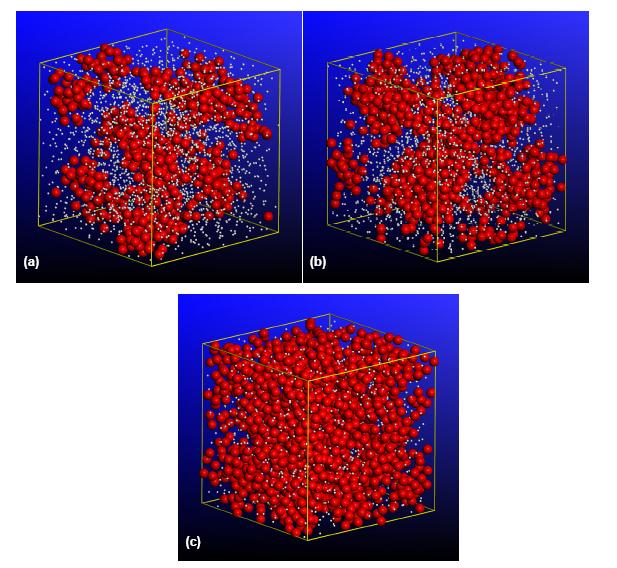
Examples of the prototypical results obtained, in this portion of the work, for the cases of polyurea grades P250, P650 and P1000 are displayed in Figures 13(a)-(c), respectively. It should be noted that for all three polyurea renditions, the results displayed in Figures 13(a)-(c) correspond to the same three post-shockwave-initiation times.

Examination of the results displayed in Figures 13(a)-(c) reveals that:

(a) a single release-wave is generated, as a result of stopping the computational-cell contraction, in all three polyurea grades;

(b) the release-wave propagates faster than the corresponding shockwave, in each of the three cases analyzed;

(c) within the available distance and time for the propagation of the shockwaves and release-waves, as offered by the present coarse-grained computational model, the trailing release wave has managed to significantly reduce its separation from the leading shockwave, in all three polyurea grades;

(d) in the cases of P250 and P650, Figures 13(a)-(b), the trailing release-wave has effectively captured the leading shockwave and has begun to neutralize it. On the other hand, in the P1000 case, Figure 13(c), the trailing release-wave has only approached the leading shockwave;

Figure 13. Demonstration of the “shock-wave capture and neutralize” effect (associated with a slower-propagating shockwave and a faster-propagating trailing release-wave) using the results pertaining to the distribution of the bead longitudinal velocity along the length of the computational domain, at different post-shockwave-initiation times, in the meso-segregated states of the three polyurea grades investigated: (a) P250; (b) P650; and (c) P1000.

DownLoad: Full-Size ImgPowerPoint

(e) reduction in the strength of the leading shockwave due to its interaction with the trailing release-wave appears to be largest in the case of P650, and practically absent in the case of P1000; and

(f) the maximum shockwave-attenuation effect (as measured by the reduction in the peak particle velocities) observed in P650, over the range of the shockwave-propagation distance (ca. 50 nm) is about 5-6 %. This shockwave-propagation distance is only a small fraction (ca. 5 × 10⁻⁷) of a prototypical 1 cm thickness of the helmet coating/lining. One expects that as the leading shockwave and the trailing release-wave continue to advance, the shockwave strength would reduce further. This finding is quite encouraging, suggesting that helmet coating/lining made of polyurea in general, and of P650 in particular, could provide good protection from blast-induced shockwaves.

The results obtained in this section again suggest that, even in the case of blast-induced shockwave mitigation and primary-TBI-prevention, P650 displays the highest potential among the three polyurea grades investigated. This finding could have been expected based on the previously discussed effect of the polyurea molecular weight on the release-wave speed and the shockwave speed. That is, in P650, the shockwave acquires the lowest speed due to the largest extent of hard-domain densification. At the same time, the corresponding release-wave acquires the highest speed since it propagates through the material containing highly-compacted, high-stiffness hard-domain phase. This combination of the shockwave and the release-wave speeds in P650 causes the shockwave capture by the trailing release-wave to occur after shorter shockwave-propagation distances.

To provide some confirmation for this explanation, additional simulations are carried out in order to determine the response of the three polyurea renditions, in their fully-mixed state, to the passage of the leading longitudinal shockwaves and the trailing release-waves. It is found that: (i) polyurea chemistry, as defined by its soft-segment molecular weight, only weakly affects its shockwave/release-wave behavior; and (ii) the velocity of the trailing release-waves is only slightly higher than that of the corresponding shockwaves (indicating that substantially higher propagation distances and post-shockwave-initiation times would be required for the onset of shockwave-capture and attenuation in the case of fully-mixed polyureas). This finding confirms that meso-segregation phenomena make an important contribution to the established shockwave-mitigation capacity of this material.

4. Conclusions

Based on the results obtained in the present work, the following summary remarks and main conclusions can be drawn:

1. Meso-scale coarse-grained molecular-level simulations, which employ energy minimization and equilibrium/non-equilibrium molecular dynamics, are used to investigate the effect of polyurea soft-segment molecular weight on: (i) the meso-segregation process which results in the formation of hard domains and soft matrix; (ii) the resulting microstructure and the linear-response mechanical properties; and (iii) the phenomena and processes related to the propagation of longitudinal shockwaves and the corresponding release-waves.

2. The results obtained are analyzed from the standpoint of inferring the intrinsic capacity of polyurea to mitigate both blast-induced shockwaves (as those encountered in the primary traumatic brain injury, TBI, problem) and fully-supported shockwaves (as the ones encountered in the secondary and tertiary TBI problems).

3. It is found that the soft-segment molecular weight can have a significant effect on the meso-scale segregation process, affecting: (i) the extent of segregation; (ii) the morphology of the resulting microstructure; (iii) the degree of compaction and ordering within the hard domains; and, in turn, (iv) the shockwave-mitigation potential of polyurea.

4. Of the three polyurea renditions analyzed, the one associated with an intermediate value of its soft-segment molecular weight was found to possess the highest shockwave-mitigation potential. This finding is rationalized in terms of the effect of the polyurea soft-segment molecular weight on the chain flexibility and, in turn, on the extents of the meso-segregation process, hard-domain packing and order.

Acknowledgments

The material presented in this paper is based on work supported by the Office of Naval Research (ONR) research contract entitled “Reactive-Moiety Functionalization of Polyurea for Increased Shock-Mitigation Performance, ” Contract Number N00014-14-1-0286. The authors would like to express their appreciation to Dr. Roshdy Barsoum, ONR, program sponsor, for many helpful discussions, guidance and continuing interest.

Conflict of Interest

The authors declare that there are no conflicts of interest related to this study.