Citation: Rahman Mashrur, Nigar Neema Meher. A GIS Based Integrated Approach to Measure the Spatial Equity of Community Facilities of Bangladesh[J]. AIMS Geosciences, 2015, 1(1): 21-40. doi: 10.3934/geosci.2015.1.21
| [1] | Sonia Malvica, Enrico Nicosia, Carmelo Maria Porto . Is the projected landscape also perceived? A proposed research plan on Etna Park's conflicting destination image. AIMS Geosciences, 2023, 9(4): 783-797. doi: 10.3934/geosci.2023042 |
| [2] | Wenqing Liu . A study on the spatial and temporal distribution of habitation sites in the Amur River Basin and its relationship with geographical environments. AIMS Geosciences, 2024, 10(1): 172-195. doi: 10.3934/geosci.2024010 |
| [3] | Matteo Bona . Comprehending the risk throughout a literary-geocritical approach. Rushdie's The Satanic Verses as evidence and an opportunity in investigating risk scenarios. AIMS Geosciences, 2024, 10(2): 419-435. doi: 10.3934/geosci.2024022 |
| [4] | Hamid Doost Mohammadian, Rasha Asim Gazzaz . A literary analysis of The Boy Who Harnessed the Wind: Creating Currents of Electricity and Hope (2009) towards sustainable development through i-Sustainability Plus theory. AIMS Geosciences, 2022, 8(4): 627-644. doi: 10.3934/geosci.2022034 |
| [5] | Zhongqiang Liu, Åse Marit Wist Amdal, Jean-Sébastien L'Heureux, Suzanne Lacasse, Farrokh Nadim, Xin Xie . Spatial variability of medium dense sand deposit. AIMS Geosciences, 2020, 6(1): 6-30. doi: 10.3934/geosci.2020002 |
| [6] | Giuseppe Borruso, Ginevra Balletto . Cities as innovation poles in the digital transition. The Italian case. AIMS Geosciences, 2024, 10(4): 918-938. doi: 10.3934/geosci.2024043 |
| [7] | Gary E. Bowman . Physics as Pilgrimage. AIMS Geosciences, 2016, 2(4): 391-400. doi: 10.3934/geosci.2016.4.391 |
| [8] | Giulia de Spuches, Francesca Sabatini, Gabriella Palermo, Emanuela Caravello . Risk narrations and perceptions in the COVID-19 time. A discourse analysis through the Italian press. AIMS Geosciences, 2020, 6(4): 504-514. doi: 10.3934/geosci.2020028 |
| [9] | Rafael Gotardo, Gustavo A. Piazza, Edson Torres, Vander Kaufmann, Adilson Pinheiro . Soil Loss Vulnerability in an Agricultural Catchment in the Atlantic Forest Biome in Southern Brazil. AIMS Geosciences, 2016, 2(4): 345-365. doi: 10.3934/geosci.2016.4.345 |
| [10] | Flavia Schiavo . Existential risks of an excluded community: Le mani sulle città by Franco Rosi. AIMS Geosciences, 2020, 6(4): 437-458. doi: 10.3934/geosci.2020024 |
During the last two decades, the issue of spatial equity has received much importance in literature [1,2,3]. Different studies have been carried out to develop a generic model concerning this issue. However, it has not been possible to give spatial equity a comprehensive evaluation till now [4]. Specifically, there is no reasonable mechanism available to measure the spatial equity of public facilities in an integrated manner for planning facilities throughout an area. Although some studies have been carried out, these were limited to single facilities. A considerable number of these studies have focused on the provision of parks [36,37,38,39] while others focused on the distribution of health care facilities [40,41,42]. Those studies found that there was a spatial disparity in the distribution of such facilities due to lack of accessibility. However, comparatively less research has been carried out analyzing the spatial equity of multiple facilities at a time [43].
In fact, each type of public facility has its own unique characteristics that satisfy particular needs of people. Hence, the preference and importance for different types of facilities are not the same. If a study concentrates on allocation of only a single type of public facility and ignores the relationship between other public facilities and their varied preferences, it will fail to analyze the overall equity status of an area.
Geographic scale is an integral component to be considered for spatial equity of public facilities. Lacking spatial data processing techniques and strong theoretical background, most of the previous empirical studies on spatial equity used aggregate indices considering larger spatial units [5,34,35]. In fact, equity of community level facilities in an integrated manner considering smaller geographical units was seldom been studied. To fill the gap, this paper proposes a GIS based integrated spatial equity index, considering spatial analytical perspectives, such as accessibility theories, and spatial association, and most importantly to indicate how these can be applied to examine whether and to what degree the distribution of public facilities is equitable. This paper focuses especially on the relevant factors for spatial equity as well as spatial patterns of equity of entire public services, based on the proposed index.
The general connotation of the term “spatial equity” refers to the equal distribution of services and facilities in space [15]. It also implies the equal distribution of facilities for people living in different places in relation to their needs and preferences. Although its definition and the way it is measured vary widely, the perception of accessibility occupies the central concept of spatial equity in the literature [6]. Most of the studies have explained spatial equity in terms of accessibility to facilities such as schools, markets, hospitals, health-care facilities etc. measured in terms of proximity or distance [2,3]. Of the many available means, accessibility indices have therefore been the most widely used for measuring spatial equity in context of planning public facilities.
The relative proximity of one place to another can be simply termed as accessibility. It can be defined as travel impedance (in terms of distance or time or both) to the desired facility location [7]. The further the distance, the more time it takes to reach the facility and the less likely the residents can reach and use that particular facility.
A considerable effort has been made to develop suitable accessibility indices in the past [8]. Existing literature on spatial accessibility measure can be categorized under three approaches: 1) container approach, 2) travel cost approach and 3) gravity based spatial interaction models [32]. A common approach is the container based method which takes the number of facilities in a specific geographic unit for measuring accessibility into account [33]. The travel cost approach simply measures accessibility based on average distance to the facilities or distance to the nearest facility. However both approaches have drawbacks. The container approach only takes the number of facilities into account, not how easily they can be reached by the people and the travel cost method never includes more than one facility for measuring accessibility. However, the travel cost approach has an advantage over the container based method as it takes into account the nearest distance not limited to a specific geographic unit because the nearest facility may be located in the neighboring unit as well. Therefore the most widely applied method is the gravity based spatial interaction method [9,10,45]. It overcomes the limitation of the above two approaches as it considers both the number of facilities and distance to the facilities as well. The general formula of gravity based spatial accessibility model can be expressed as following:
| Ai=∑jSjdβij |
Where Ai is the spatial accessibility of public facilities for the population living at i which may be the centroid of a geographical unit [30]; Sj is the service capacity of the given facility at location j, which can be expressed as the number of facilities at the location and their individual capacity; dij is the travel impedance, e.g. shortest network distance between points i and j; and β is a gravity decay coefficient, (it is sometimes referred to as the travel friction coefficient), representing level of impedance to travel created by distance .
Accessibility of a particular facility greatly depends on how near the facility is located. Proximity is the central concept of spatial analysis and the distance to the nearest facility from the demand point has been most widely used for measuring spatial proximity [22]. A particular area may have a sufficient number of facilities; however, if the distances to those facilities are beyond the service impact range, then accessibility will be reduced. There are different methods to measure distance. The physical distance to the closest facility is a good measure of spatial proximity [11,12,31]. The most common types of distance measure used for determining spatial accessibility in the literature are the Euclidean distance (more often known as straight line distance) and the distance along the transport network. Different studies have suggested that straight line distance is a good measure of spatial accessibility considering a wide analysis of numerous public facilities covering a large number of geographical units [13,22].
A facility may be well located, however the number of facilities may not be adequate to meet the demand of the residents and thereby the accessibility and spatial equity are affected. Apparicio et al. (2008) have used the number of facilities within a specified distance to measure spatial accessibility [14]. Talen and Anselin (1998) demonstrated that accessibility improves if either the number of facilities or the capacity at any facility provider increases [3].
Residents’ preferences for different types of facilities differ. For example, accessibility to the elementary school in a neighborhood may be more important than that of a college. For modeling spatial equity of different types of facilities in an integrated manner, such variations have to be considered. Tsou et al. (2005) have used an attitude scale (Likert scale) for assessing residents’ preferences and needs for different types of facilities [15].
Spatial patterns can be defined as the spatial arrangement pattern of features on a designated surface according to their location. Spatial statistics have been used in a range of accessibility studies. Both global and local patterns of spatial associations have been used for analyzing the pattern of spatial autocorrelation. In addition to analyzing global patterns, more emphasis has been recently put on analyzing local patterns of spatial association such as in [3,16,17].
The most widely used index to measure spatial autocorrelation is Moran’s I. The global spatial statistic Moran’s I measures global spatial autocorrelation based on feature geographic locations and associated attribute values [18]. Moran’s I measures the proximity of locations according to similar characteristics of their features. Moran’s global I statistic measures spatial autocorrelation without distinguishing between patterns of high or low values.
Given a set of features and an associated attribute, Moran’s global I statistic evaluates whether the pattern is clustered, dispersed, or random on a range from -1 to +1. The negative value indicates spatial dispersion while a positive value indicates spatial correlation [15,23].
In spatial analysis it is often required to know the degree of spatial association between variables. More recently additional models of spatial statistics, known as local spatial statistics have been developed to measure association between a single geographical area and its neighbors within a specified distance [19]. Local Indicator of Spatial Association (LISA) is a local spatial statistic which measures local spatial autocorrelation. It provides information on spatial clusters and spatial outliers [21,25]. Local Moran’s I developed by Anselin (1995) indicates the similarity of a geographical unit with respect to its neighboring units. A positive value for I indicates that the feature is surrounded by features with similar values. Such a feature is part of a cluster. A negative value for I indicates that the feature is surrounded by features with dissimilar values. Such a feature is an outlier. A limitation of this method is that the positive I value could be determined also for zones with low values if they are surrounded by other zones of low values [26,27,29]. Thus, Local Moran’s I usedto identify hot spots of zones can lead to ambiguous results.
Getis-Ord G-statistics (Gi and Gi*) is another way to measure the local spatial association introduced by Getis and Ord (1992). Gi calculates the effect of a target feature on neighboring features excluding the target itself [24]. It was later improved to Gi* (z-transformed form of Gi) in order to improve statistical testing which is known as the standardized Gi* statistic [28]. Unlike Gi it can include the value of the target features while measuring local spatial association. The Gi* statistic indicates whether features with high values or features with low values tend to cluster in a specified location: if a feature's value is high, and the values for all of its neighboring features are also high, it is a part of a hot spot; if a feature's value is low, and the values for all of its neighboring features are also low, it is a part of a cold spot. The Getis-Ord Gi* statistic is given as:
| G∗i=∑nj=1wijxj−ˉX∑nj=1wijs√[∑nj=1w2ij−(∑nj=1wij)2]n−1 |
Here, is the attribute value for the feature j; is the spatial weight between feature i and j and n is the total number of features.
| ˉX=∑nj=1xjn |
| S=√∑nj=1x2jn−(ˉX)2 |
The Gi* statistic returns for each feature in the dataset a z-score: for statistically significant positive z-scores, the larger the z score, the more intense the clustering of high values (hot spot); for statistically significant negative z-scores, the smaller the z-score, the more intense the clustering of low values (cold spot) [28]. As mentioned, Anselin’s Local Moran can only identify positive or negative spatial autocorrelation, that is, whether the zones are similar or dissimilar. Those zones with positive spatial autocorrelation could occur because of clustering of zones with high values or they could occur because of clustering of zones with low values. The Getis-Ord Gi* can distinguish between these two types [26,27,29].
Most of the indices developed so far have originated from the very fundamental equation based on gravity model [20]. However, it cannot state how disaggregated the measurement of accessibility is in terms of geographical units. For example, the distance of individual facilities can be considered on district level (from the centroid of individual districts), but not on the community level (centroid of unions). Hence, the measurement might not reflect the actual scenario of spatial equity of accessibility. This is also true while considering the number of facilities in each geographical unit. While the number of facilities in a particular district overall may be sufficient, some areas within the district may be over supplied while on other areas it may be lacking. Hence, while considering the spatial equity, the accessibility should be considered at the disaggregated level.
Again, although the accessibility of facilities is considered in an integrated manner, the range of service impact of these facilities are different. Some facilities are provided at community level like primary schools, high schools and family welfare centers. On the other hand, service impact ranges of some other facilities are beyond the community level like hospitals, colleges and growth centers. In this study six important public facilities have been considered; three at the union level and another three at the sub district level (Table 1).
| Public Facilities at Union Level | Public Facilities at Sub-district Level |
| Primary School | Growth Centers |
| High School | Hospital |
| Family Welfare Center | College |
DownLoad: CSVSpatial equity considering the facilities at the union level:
| Eij(k″)=∑Nn=1∑k″=3k″=1xn(k)×1dnj(k)N | (1) |
Eij(k″) is the value of spatial equity of the public facilities j(k”) in the sub district i, i = 1,2, . .., I; k” is the kth type of all public facilities at union level, k”= 3;
j(k”) is the jth public facility of the kth type of public facility, j = 1,2, . . ., J;
xn(k”) is the number of kth type of facility at union, n;
dnj is the nearest distance of kth facility from the centroid of the union;
N is the total number of unions in the sub district;
Spatial equity considering the facilities at the sub district level:
| Eij(k′)=k′=3∑k′=1xi(k′)×1dij | (2) |
Eij(k′) is the value of spatial equity of the public facilities j(k’) in the sub district i, i = 1,2, . .., I; k’ is the k th type of all public facilities at sub-district level, k’= 3;
j(k’) is the jth public facility of the kth type of public facility, j = 1,2, . . ., J;
xi(k’) is the number of kth type of facility sub district, i;
dij(k) is the nearest distance of kth facility from the centroid of the sub district;
Integrated Spatial Equity Index for Public Facilities:
| Eij(k)=wk[∑Nn=1∑k″=3k″=1xn(k)×1dnj(k)N+k′=3∑k′=1xi(k′)×1dij] | (3) |
Wk is the score of preferences for different types of facilities
AHP (Analytical Hierarchical Process) has been applied in this study to get the score of preference for different types of facilities. An effective way to determine the weights under AHP can be pair-wise comparison of the indicators. According to Satty (2008) a pair-wise comparison involves three tasks: (1) Developing a comparison matrix at each level of the hierarchy starting from the second level and working down, (2) Computing the relative weights for each element of the hierarchy and (3) Estimating the consistency ratio to check the consistency of the judgment [44]. Generally, the measurement scale of 1-9 is used to represent such relative importance, as shown in Table 2.
| Importance Intensity | Definition | X' compared with 'Y' |
| 1 | Equal importance | X is as equally important as Y |
| 3 | Moderate importance | X is moderately more important than Y |
| 5 | Strong importance | X is strongly more important than Y |
| 7 | Very strong importance | X is very strongly more important than Y |
| 9 | Extreme importance | X is extremely more important than Y |
| 2,4,6,8 | Intermediate values | X is compromise between two judgment of Y |
DownLoad: CSVFirst of all, a pair-wise comparison matrix is constructed. Then vector of weights, w = [w1, w2, …, wn], is computed on the basis of Satty’s eigenvector procedure. The computation of the weights involves two steps. First, the pair wise comparison matrix A = [aij]n×n is normalized by and then the weights are computed by the following equations.
| A=[aij]n×n[a11a12…a1na21a22…a2n…………an1an2…ann] |
| ¯aij=aij∑ni=1aij |
| wi=∑nj=1¯aijn |
To determine whether the level of consistency in the pair-wise comparison is ‘reasonable’ or not, a consistency checking is required. Therefore consistency ratio (CR) is to be calculated with the help of following formula.
| CR=CI(ConsistencyIndex)RI(RandomIndex) |
| CI=λmax−nn−1 |
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| RI | 0 | 0 | 0.58 | 0.9 | 0.12 | 1.24 | 1.32 | 1.41 | 1.46 | 1.49 |
If CR < 0.1, then the comparisons are acceptable. If, however, CR > 0.1, then the values of the ratio are indicative of inconsistent judgments.
In this study, GIS is used for the analysis for the following reasons: (1) to store and analyze the spatial distribution of each public facility; (2) to quantitatively process the spatial data and provide the proposed index; (3) to support the discovery and verification of spatial equity of public facility; and (4) to display the results of the index. ArcGIS 10.0 was used in this study for spatial data analysis. The process involved several steps mentioned below:
Step 1: First of all the centroid of the respective unions and sub districts was determined by transforming the polygon features into point features. It was assumed that, the population is concentrated at the central area of the unions and the sub-districts. Then the nearest distance of the public facilities from the centroid point was found through near analysis. In this case, Euclidean distance was considered for the reason mentioned earlier in this paper.
Step 2: The number of facilities in an area is a crucial determinant of spatial equity. The numbers of facilities for each unions and sub districts were counted through spatial join.
Step 3: Not all the facilities are equally important. Accessibility to some particular facilities is more important than others to the community people. Score of preferences for the facilities was determined through pair wise comparison according to Satty’s AHP method.
Step 4: After measuring the nearest distance of the facilities and their numbers, the spatial equity of the facilities provided at the union and sub-district level was determined from equation (1) and (2) respectively. Finally, using the score of preference for each six types of facilities, the integrated index for spatial equity was calculated for each sub districts of Bangladesh (equation 3).
Step 5: The global pattern of spatial association for the index was analyzed through spatial autocorrelation method. Moran’s I value was found for each facility indicating which one is more clustered or uniformly distributed across the space considering the accessibility of the facilities. For global Moran’s I, a threshold distance needs to be specified indicating the search radius within the neighborhood. In this study the minimum distance required to ensure that each geographical unit has at least one neighbor (27.19 km) was chosen as the threshold distance [26].
Step 6: The local pattern of spatial association indicates which regions are advantageous region and which ones are in a underprivileged condition. The Getis-Ord Gi* statistic (hot-spot analysis), a local spatial statistics was preferred over local Moran’s I for assessing local spatial patterns. Unlike local Moran’s I, a high value of Gi* indicates a cluster of features (sub-districts) with high attribute values and a low value of Gi* indicates the cluster of features (sub-districts) with low attribute values which was required to identify the advantaged and disadvantaged regions considering the accessibility of facilities. For Getis-Ord Gi*, the same threshold distance (27.19 km) was chosen as in global Moran’s I for showing clusters of high and low values.
Score of preference indicates the weights of different types of facilities. Expert opinion has been considered for the pair wise comparison method. The consistency ratio of the given score was checked. CR in this analysis has been found 0.0163 which is less than 0.1. Hence the scoring of weights is acceptable. The score of preferences in this study for different types of facilities are shown in table 3.
| Types of Facilities | Score of Preferences |
| Primary School | 0.35 |
| High School | 0.10 |
| Family Welfare Center | 0.27 |
| Growth Center | 0.14 |
| Hospital | 0.10 |
| College | 0.04 |
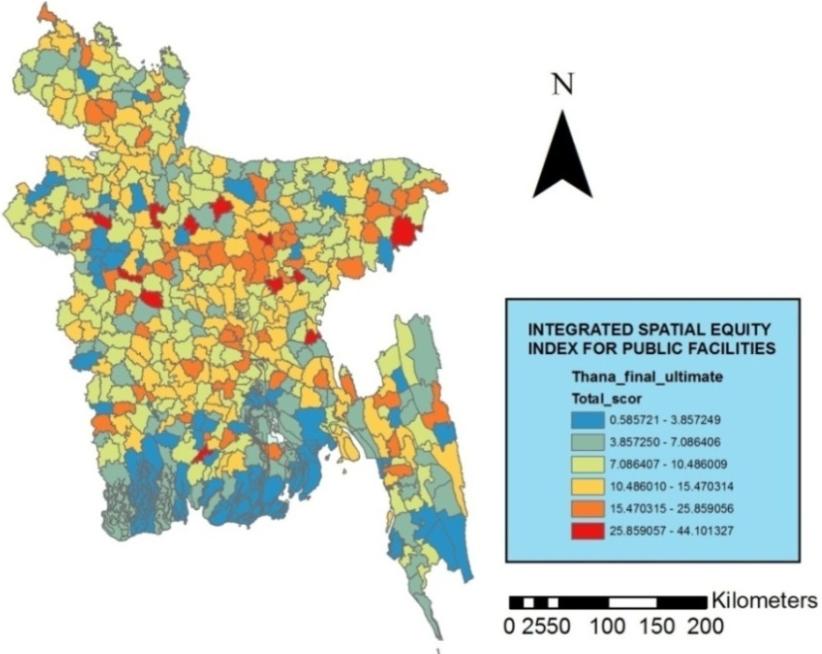
DownLoad: CSVFinally, the proposed index value was calculated. The index integrates the accessibility of six different types of public facilities. The value ranges from 0.59 to 44.10. The index values are shown in figure 1 and in the appendix.
The value of Moran’s I for all public facilities are positive. It means the index values of the facilities are spatially clustered in some areas (Table 4). Some areas are advantaged while other areas are in disadvantaged locations.
| Facilities | Moran's I |
| Primary School | 0.19154 |
| High School | 0.231979 |
| Family Welfare Center | 0.116283 |
| Growth Center | 0.073146 |
| Hospital | 0.038351 |
| College | 0.154822 |
| Aggregate for all facilities | 0.13333 |
| S.N: P < 0.001 | |
DownLoad: CSVMoran’s I values for educational facilities are greater than the other facilities. It implies that there is more spatial inequality regarding the accessibility to the educational institutions in Bangladesh.
The index value is lower for hospitals and growth centers. It implies that the distribution is random and spatially uniform for these facilities.
The aggregate value is 0.13. It implies that there may be uniform distribution of facilities considering some particular facilities like hospitals and growth centers; but considering all of the selected facilities, there is spatial clustering.
Figure 1. Integrated Spatial Equity Index for Public Facilities in Different Sub Districts of Bangladesh.
Accessibility to primary schools is more concentrated in central and North Eastern region of Bangladesh (Figure 2). The sub-districts of Dhaka division are in more advantageous locations than others considering primary schools. On the other hand, the cold spots suggest that the coastal areas of Bangladesh (Barisal and Chittagong division) are in more vulnerable positions than others.
Figure 2. Local spatial autocorrelation pattern: Primary School.
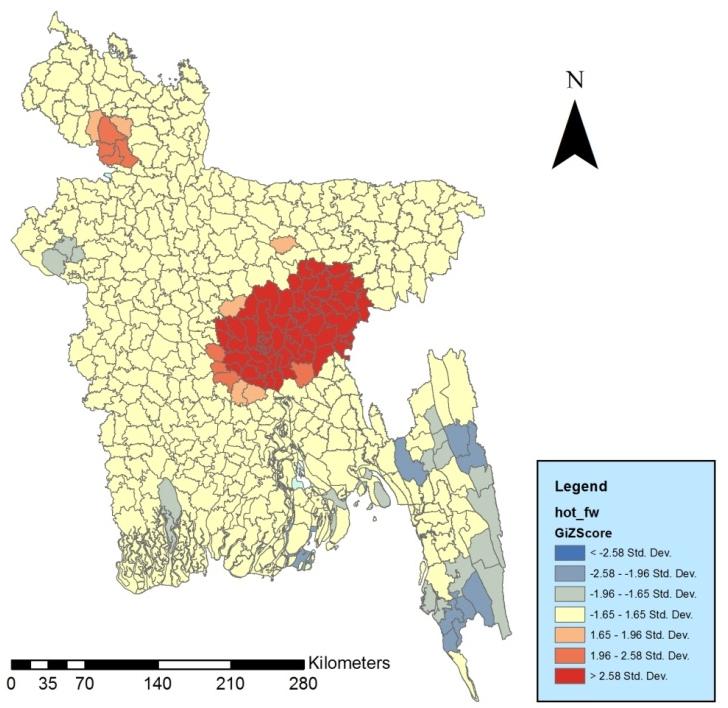
Like primary schools, accessibility to high school is also concentrated in central and south central region of Bangladesh. However, along with the coastal region, sub-districts of North Eastern region (Netrokona, Kishoreganj, Shunamganj districts) are more in disadvantaged locations (Figure 3).
Figure 3. Local spatial autocorrelation pattern: High School.
Figure 4. Local spatial autocorrelation patterns: Growth Center.
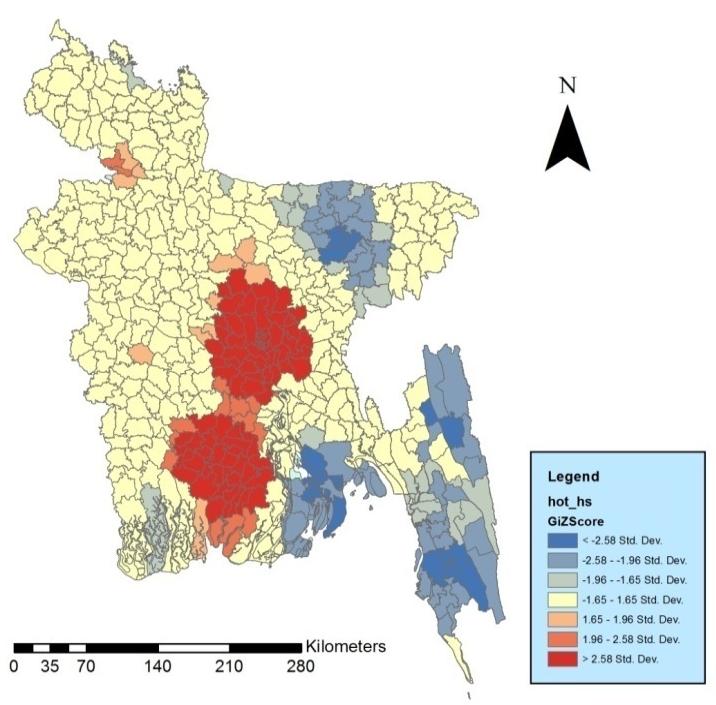
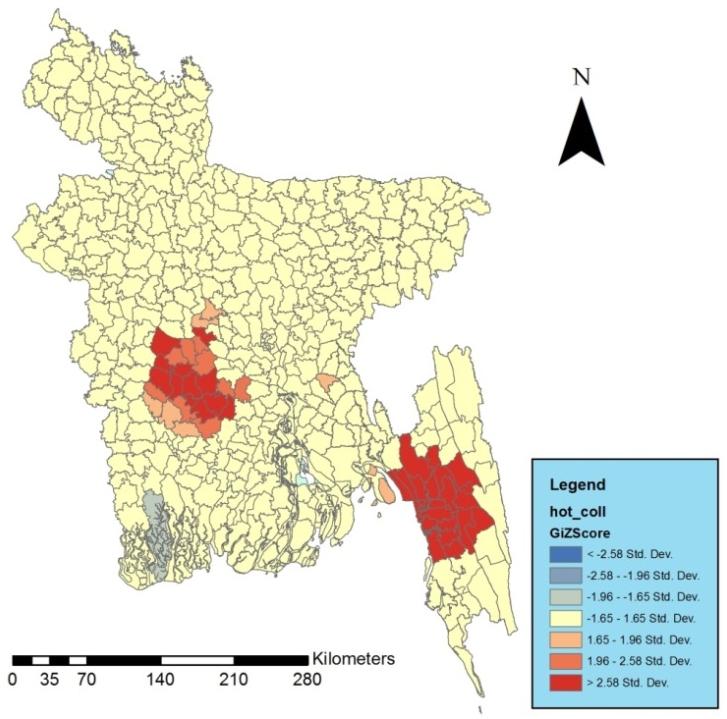
In case of family welfare facility, areas of Chittagong hill tracts are in disadvantaged locations while the areas of central region surrounding the capital are in advantageous position (Figure 5).
Figure 5. Local spatial autocorrelation pattern: Family Welfare Center.
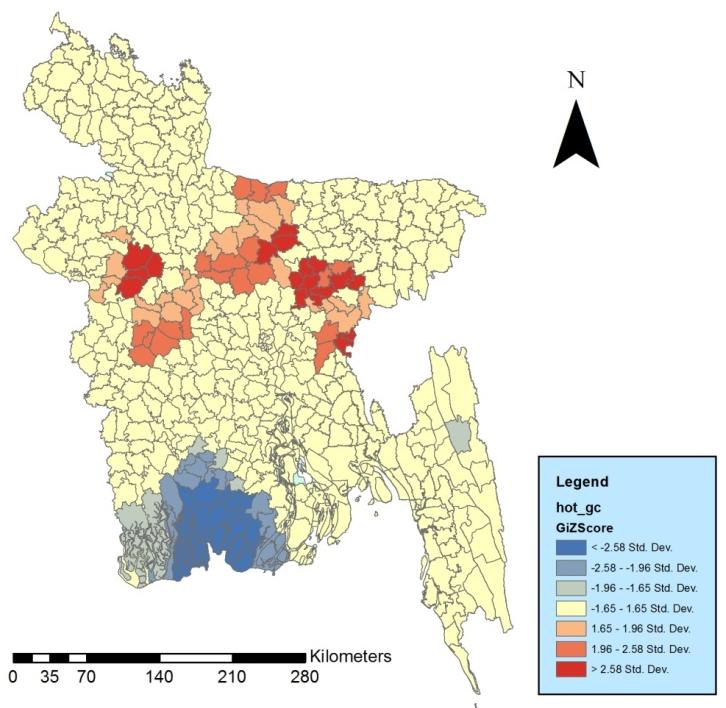
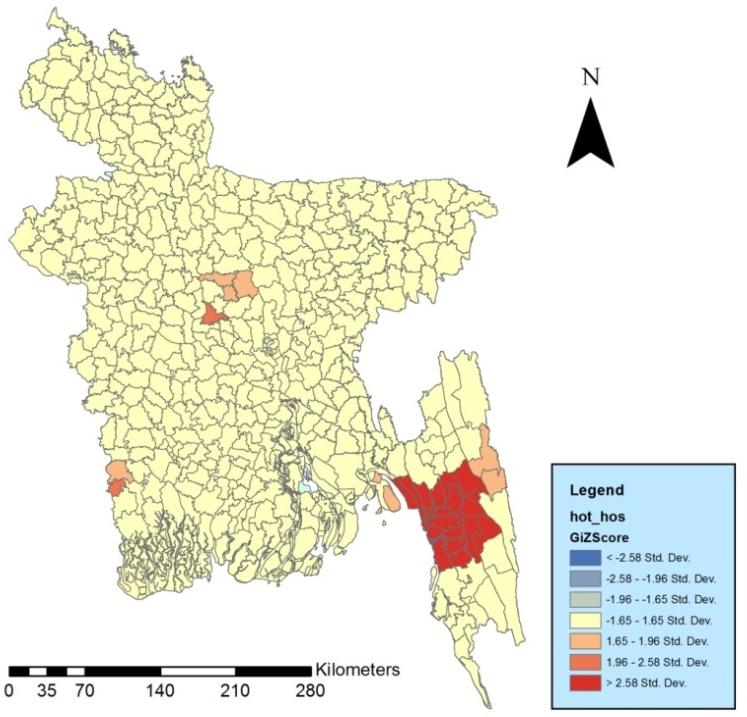
Unlike primary school, high school and family welfare center, accessibility to growth center, college and hospital is not concentrated in the central region of Bangladesh (Figure 4,6,7). As the spatial autocorrelation is not high for hospital and growth center (value of global Moran’s I is 0.038 and 0.073 respectively), only few areas are in advantageous position than others compared to other facilities.
Figure 6. Local spatial autocorrelation patterns Hospital.
Figure 7. Local spatial autocorrelation patterns College.
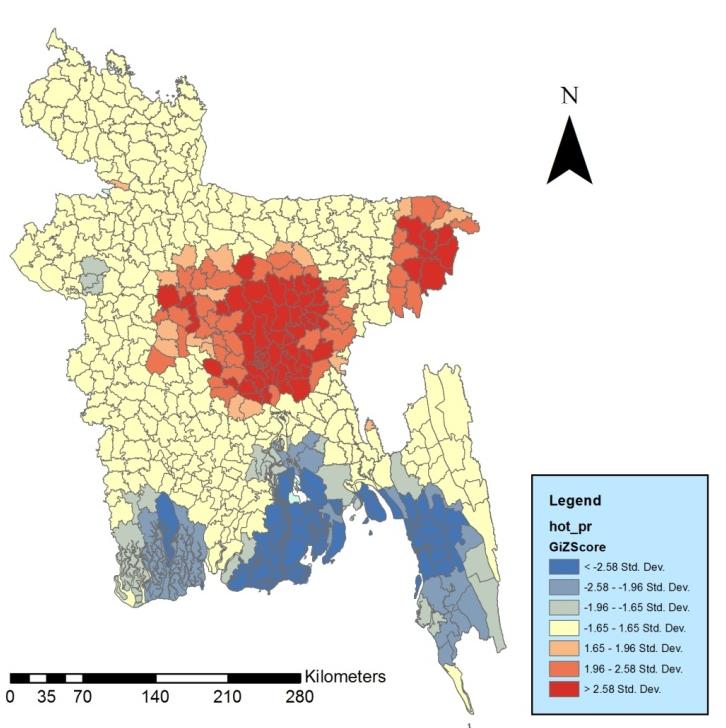
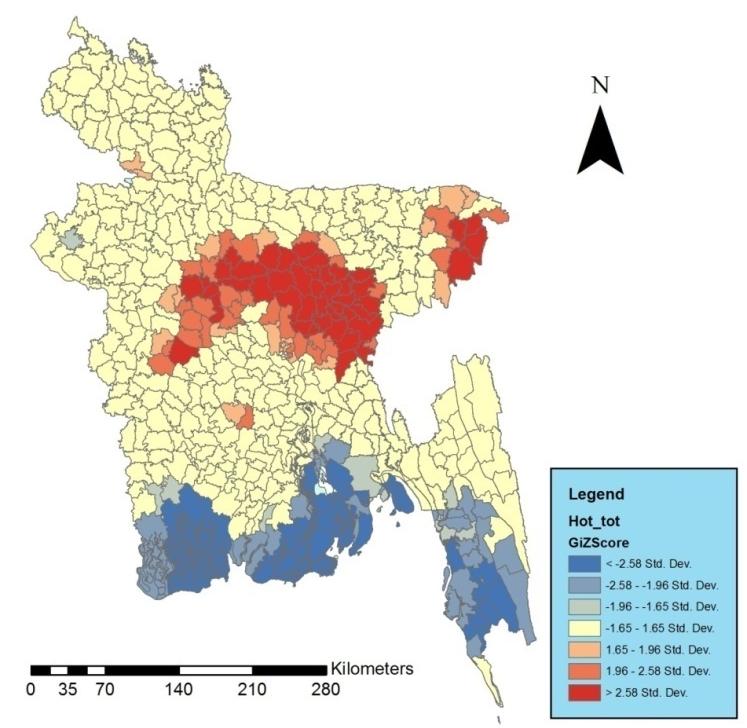
In aggregate level, considering all the selected facilities, it is clear from the hot spots that the central region of the country surrounding the capital Dhaka receives more accessibility for the public facilities than any other regions of Bangladesh. However, the southern coastal hill tracts region (Barisal, Patuakhali, Bhola, Barguna, Satkhira, Noakhali, Feni, Chandpur, Bandarban, Khagrachari, Rangamati) are in disadvantaged locations (Figure 8).
Figure 8. Local spatial autocorrelation patterns of public facilities (aggregated level).
In recent years, spatial equity of public facility planning has become a critical issue in many countries. As the research concerning public facilities involves dealing with complex characteristics of different types of facilities with varied preferences and importance, existing indices fail to meet this need. To solve the problem, this paper has proposed a GIS based integrated spatial equity index as a set of integrated indices to measure spatial equity based on accessibility. Here, the accessibility to the facilities has been considered at the community level and both in aggregate and disaggregated level for different types of facilities. GIS and spatial analysis techniques, offer an easily and intuitively interpreted summary of the data. Future studies can integrate more types of facilities according to the proposed method. Moreover, travel time, travel cost and population demand can also be considered in a more extensive level. By doing so, the spatial equity of public facilities at different levels can be better discerned.
All authors declare no conflicts of interest in this paper
| [1] | Jones K, Kirby A (1982) Provision and well being: an agenda for public resources research.Environment and Planning A 14: 297-310. |
| [2] | Smith DM (1994) Geog Social Justice.Blackwell, Oxford . |
| [3] | Talen E, Anselin L (1998) Assessing spatial equity: an evaluation of measures of accessibility to public playgrounds.Environment and Planning A 30: 595-613. |
| [4] | Kinman EL (1999) Evaluating health services equity at a primary care clinic in Chilimarca, Bolivia.Soc Sci Med 49: 663-678. |
| [5] | Yan C, Han R (1999) Cytoskeleton-associated protein tyrosine phosphorylation involved in induction of differentiation in mouse melanoma cells.Chin Sci Bull 335-340. |
| [6] | Kunzmann, K R (1998) Planning for spatial equity in Europe.Int Plan Stud 3: 101-121. |
| [7] | Guagliardo, M F (2004) Spatial accessibility of primary care: concepts, methods and challenges.Int J Health Geog 3: 1-13. |
| [8] | Pooler J (1987) Measuring geographical accessibility: a review of current approaches and problems in the use of population potentials.Geoforum 18: 269-289. |
| [9] | Pacione M (1989) Access to urban services — the case of secondary schools in Glasgow.Scott Geogr Mag 105: 12-18. |
| [10] | Talen E (1998) Visualizing fairness: Equity maps for planners.J Am Plan Assoc 64: 22-38. |
| [11] | Fryer, G EJ, Drisko J, et al. (1999) Multi-method assessment of access to primary medical care in rural Colourado.J Rural Health 15: 113-121. |
| [12] | Fortney J, Rost K, Warren J (2000) Comparing alternative methods of measuring geographic access to health services.Health Serv Outcomes Res Method 1: 173-184. |
| [13] | Doriwala HV, Shah NC (2010) GIS- Based Analysis of Facility Provision Accessible to Different Socio-Economic Groups in Surat City.World App Sc J 9: 740-745. |
| [14] | Apparicio P, et al. (2008) Comparing alternative approaches to measuring the geographical accessibility of urban health services: Distance types and aggregation-error issues.Int J Health Geog, 7: 1-14. |
| [15] | Tsou KW, Hung YT, Chang YL (2005) An accessibility-based integrated measure of relative spatial equity in urban public facilities.Cities 22: 424-435. |
| [16] | Apparicio P, et al. (2007) The case of Montreal's missing food deserts: evaluation of accessibility to food supermarkets.Inter J Health Geog 6: 4. |
| [17] | Algert SJ, Agrawal A, Lewis DS (2006) Disparities in access to fresh produce in low-income neighborhoods in Los Angeles.Am J Prev Med 30: 365-370. |
| [18] | Moran PAP (1950) Notes on Continuous Stochastic Phenomena.Biometrika 37: 17-23. |
| [19] | Getis A, Ord JK (1996) Local spatial statistics: an overview in Longley P. & Batty M (1996).Spatial Analysis: Mod in a GIS Environment. Cambridge: Geoinformation International . |
| [20] | Stewart JQ and Warntz W (1958) Physics of population distribution.J Reg Sc 1: 99-123. |
| [21] | Anselin L (1995) Local indicators of spatial association-LISA.Geog Analysis 27: 93-115. |
| [22] | Miller HJ (2004) Tobler’s first law and spatial analysis.Ann Assoc Am Geog 284-289. |
| [23] | Moran PAP (1948) The interpretation of statistical maps.J Royal Stat Soc 10: 243-251. |
| [24] | Getis A, Ord J (1992) The analysis of spatial association by distance statistics.Geographical Analysis 24: 189-206. |
| [25] | Murgante B, Borruso G (2012) Analyzing Migration Phenomena with Spatial Autocorrelation Techniques.Lect Notes Comput Sci 7334: 670-685. |
| [26] | Serra-Sogas N, et al. (2008) Exploratory spatial analysis of illegal oil discharges detected off Canada’s Pacific Coast.Lect Notes Comp Sc, 5072: 81-95. |
| [27] | Anselin L (1995) Local Indicator of Spatial Autocorrelation- LISA.Geog Analysis 27: 93-115. |
| [28] | Ord JK, Getis A (1995) Local Spatial Autocorrelation Statistics: Distributional Issues and an Application.Geog Analysis 27: 286-306. |
| [29] | Wolff M, Asche H (2009) Geovisualization Approaches for Spatio-Temporal Crime Scene Analysis - Towards 4D Crime Mapping.Lect Notes Comp Sc 5718: 78-89. |
| [30] | Geertman SCM, Ritsema VE (1995) GIS and models of accessibility potential: an application in planning.Inter J Geog Inf Sys 9: 67-80. |
| [31] | Hodgart RL (1978) Optimizing access to public services.Progress in Human Geography 2: 17-48. |
| [32] | Zhang X, Lu H, Holt JB (2011) Modeling spatial accessibility to parks: a national study.Int J Health Geog 10. |
| [33] | Talen E, Anselin L (1998) Assessing spatial equity: an evaluation of measures of accessibility to public playgrounds.Environment and Planning 30: 595-613. |
| [34] | Openshaw S, Rao L (1995) Algorithms for re-engineering 1991 census geography.Environment and Planning 27: 425-446. |
| [35] | Wrigley N, et al. (1996) Analyzing, modeling, and resolving the ecological fallacy. In P. Longley & M. Batty (Eds.).Spatial analysis Modeling in a GIS environment, Cambridge: Geoinformation International 25-40. |
| [36] | Moore LV, et al. (2008) Availability of recreational resources in minority and low socioeconomic status areas.Am J Prev Med 16-22. |
| [37] | Lotfi SM, Koohsari J (2009) Measuring objective accessibility to neighborhood facilities in the city (A case study: Zone 6 in Tehran, Iran).Cities 26: 133-140. |
| [38] | Smoyer Tomic KE, Hewko JN Hodgson MJ (2004) Spatial accessibility and equity of playgrounds in Edmonton, Canada.Canadian Geographer/Le Géographe canadien 48: 287-302. |
| [39] | Comber A, Brunsdon C, Green E (2008) Using a GIS-based network analysis to determine urban greenspace accessibility for different ethnic and religious groups.Landscape and Urban Planning 86: 103-114. |
| [40] | Seymour J, et al. (2006) Geographical access to imaging facilities for stroke patients in Scotland.Health & Place 12: 617-630. |
| [41] | Hare TS, Barcus HR (2007) Geographical accessibility and Kentucky's heart-related hospital services.Applied Geography 27: 181-205. |
| [42] | Ohta K, et al. (2007) Analysis of the geographical accessibility of neurosurgical emergency hospitals in Sapporo city using GIS and AHP.Inter J Geog Inf Sc, 21: 687-698. |
| [43] | Zhao L. (2011) Spatial equity analysis in the Atlanta 10-county region.Unpublished Thesis for the degree of Master of Geography in the Department of Geography in the Graduate School of The University of Alabama . |
| [44] | Saaty TL (2008) Decision making with the analytical hierarchy process.Inter J Serv Sc 1: 83-98. |
| [45] | Crecine JP (1964) A Time-Oriented Metropolitan Model For Spatial Location.Technical Bulletin No. 6. CONSAD Res. Corp., Pittsburgh, Pennsylvania . |
| 1. | Renbin Pan, Shuangyan Zhang, Hongtai Yang, Kun Xie, Yi Wen, 2019, Analysis of Spatial Equity in Taxi Services: A Case Study of New York City*, 978-1-5386-7024-8, 2659, 10.1109/ITSC.2019.8917258 | |
| 2. | Niaz Mahmud Zafri, Ishrar Sameen, Anurima Jahangir, Nawshin Tabassum, Md. Musleh Uddin Hasan, A multi-criteria decision-making approach for quantification of accessibility to market facilities in rural areas: an application in Bangladesh, 2020, 0343-2521, 10.1007/s10708-020-10161-z | |
| 3. | Jingyuan Chen, Yuqi Bai, Pei Zhang, Jingyuan Qiu, Yichun Hu, Tianhao Wang, Chengzhong Xu, Peng Gong, A Spatial Distribution Equilibrium Evaluation of Health Service Resources at Community Grid Scale in Yichang, China, 2019, 12, 2071-1050, 52, 10.3390/su12010052 | |
| 4. | Mohammad Azmoodeh, Farshidreza Haghighi, Hamid Motieyan, Proposing an integrated accessibility-based measure to evaluate spatial equity among different social classes, 2021, 2399-8083, 239980832199154, 10.1177/2399808321991543 | |
| 5. | Does the Difference in Urban Public Facility Allocation Cause Spatial Inequality in Housing Prices? Evidence from Chongqing, China, 2019, 11, 2071-1050, 6096, 10.3390/su11216096 | |
| 6. | Fajle Rabbi Ashik, Sadia Alam Mim, Meher Nigar Neema, Towards vertical spatial equity of urban facilities: An integration of spatial and aspatial accessibility, 2020, 9, 22265856, 77, 10.1016/j.jum.2019.11.004 | |
| 7. | Shuju Hu, Wei Song, Chenggu Li, Jia Lu, The Spatial Equity of Nursing Homes in Changchun: A Multi-Trip Modes Analysis, 2019, 8, 2220-9964, 223, 10.3390/ijgi8050223 | |
| 8. | Wenting Cheng, Jiahui Wu, William Moen, Lingzi Hong, Assessing the spatial accessibility and spatial equity of public libraries' physical locations, 2021, 07408188, 101089, 10.1016/j.lisr.2021.101089 | |
| 9. | Guijun Li, Tanxiaosi Luo, Yanqiu Song, Spatial equity analysis of urban public services for electric vehicle charging—Implications of Chinese cities, 2022, 76, 22106707, 103519, 10.1016/j.scs.2021.103519 | |
| 10. | Ninglong You, Srinivas Goli, Assessing equity of the spatial distribution of primary health care facilities in Fuzhou City, China: A comprehensive method, 2021, 16, 1932-6203, e0261256, 10.1371/journal.pone.0261256 | |
| 11. | Md Hamidur Rahman, Fajle Rabbi Ashik, Mamata Jafrin Mouli, Investigating spatial accessibility to urban facility outcome of transit-oriented development in Dhaka, 2022, 14, 25901982, 100607, 10.1016/j.trip.2022.100607 | |
| 12. | Sanghee Jung, Jaewon Han, Sugie Lee, Analysis of Supply Characteristics and Spatial Equity of Children's Playgrounds in Seoul, Korea : Focusing on Accessibility Disparities by Housing Type, 2023, 58, 1226-7147, 48, 10.17208/jkpa.2023.02.58.1.48 | |
| 13. | Abdelhalim Bendib, GIS-Based Multi-criteria Decision Analysis for the Optimal Location of Public Facility in Batna City, Algeria, 2024, 52, 0255-660X, 1073, 10.1007/s12524-024-01858-6 | |
| 14. | Fajle Rabbi Ashik, Md Saiful Islam, Md Saiful Alam, Nusrat Jahan Tabassum, Kevin Manaugh, Dynamic equity in urban amenities distribution: An accessibility-driven assessment, 2024, 164, 01436228, 103199, 10.1016/j.apgeog.2024.103199 | |
| 15. | Arnob Chakrabarty, Mohammad Rahman, Equity in Public Facilities Provision in an Urban Area: A Spatial Analysis of Rajshahi City Corporation , 2024, 9, 2575-1697, 96, 10.11648/j.urp.20240903.14 | |
| 16. | Xiatong Hao, Xiaojian Hu, Ke Zhang, Qian Chen, Assess Spatial Equity Considering the Similarity Between GIS-Based Supply and Demand Maps: A New Framework with Case Study in Beijing, 2025, 14, 2220-9964, 157, 10.3390/ijgi14040157 |
Figures(8) / Tables(4)
Rahman Mashrur, Nigar Neema Meher. A GIS Based Integrated Approach to Measure the Spatial Equity of Community Facilities of Bangladesh[J]. AIMS Geosciences, 2015, 1(1): 21-40. doi: 10.3934/geosci.2015.1.21
| Public Facilities at Union Level | Public Facilities at Sub-district Level |
| Primary School | Growth Centers |
| High School | Hospital |
| Family Welfare Center | College |
DownLoad: CSV| Importance Intensity | Definition | X' compared with 'Y' |
| 1 | Equal importance | X is as equally important as Y |
| 3 | Moderate importance | X is moderately more important than Y |
| 5 | Strong importance | X is strongly more important than Y |
| 7 | Very strong importance | X is very strongly more important than Y |
| 9 | Extreme importance | X is extremely more important than Y |
| 2,4,6,8 | Intermediate values | X is compromise between two judgment of Y |
DownLoad: CSV| Types of Facilities | Score of Preferences |
| Primary School | 0.35 |
| High School | 0.10 |
| Family Welfare Center | 0.27 |
| Growth Center | 0.14 |
| Hospital | 0.10 |
| College | 0.04 |
DownLoad: CSV| Facilities | Moran's I |
| Primary School | 0.19154 |
| High School | 0.231979 |
| Family Welfare Center | 0.116283 |
| Growth Center | 0.073146 |
| Hospital | 0.038351 |
| College | 0.154822 |
| Aggregate for all facilities | 0.13333 |
| S.N: P < 0.001 | |
DownLoad: CSV| Public Facilities at Union Level | Public Facilities at Sub-district Level |
| Primary School | Growth Centers |
| High School | Hospital |
| Family Welfare Center | College |
| Importance Intensity | Definition | X' compared with 'Y' |
| 1 | Equal importance | X is as equally important as Y |
| 3 | Moderate importance | X is moderately more important than Y |
| 5 | Strong importance | X is strongly more important than Y |
| 7 | Very strong importance | X is very strongly more important than Y |
| 9 | Extreme importance | X is extremely more important than Y |
| 2,4,6,8 | Intermediate values | X is compromise between two judgment of Y |
| Types of Facilities | Score of Preferences |
| Primary School | 0.35 |
| High School | 0.10 |
| Family Welfare Center | 0.27 |
| Growth Center | 0.14 |
| Hospital | 0.10 |
| College | 0.04 |
| Facilities | Moran's I |
| Primary School | 0.19154 |
| High School | 0.231979 |
| Family Welfare Center | 0.116283 |
| Growth Center | 0.073146 |
| Hospital | 0.038351 |
| College | 0.154822 |
| Aggregate for all facilities | 0.13333 |
| S.N: P < 0.001 | |
