1. Introduction
The study of alpine valleys and glacial landscapes requires interdisciplinary knowledge, including geology, geography, tectonics, and geomorphology [1,2,3,4,5,6] Understanding them helps give clues to pastclimates, plate movement, mountain landforms, bedrock geology and more. Those alpine valleys have been created by a combination of tectonic and erosional processes. The erosive capability of fluvial and glacial systems has been an area of intense research [7,8,9,10,11,12]. Alpine regions dominated by fluvial activity typically have concave long profiles and V-shaped cross-sections through the valley. The comparatively steady flow of a river down-cuts the valley at its lowest point, leaving a cross-section with near constant slopes [13] or possibly terraces where substantial changes in stream flow have occurred at times to modify the valley [14]. On the other hand, alpine areas that have been subject to glacial activity also have concave upward long profiles, but those occur at the lower reach of the valley and exhibit a more knobby profile at the headwaters [15]. This occurs because glaciers generally develop in cirques at the upper reach of a valley until they break through or flow over the barrier walls. The ice then travels down the valley and forms moraines at possibly several termini. Glacial valleys also typically have a U-shaped cross section [13]. In a temperate glacial system where the ice moves down the valley on a thin layer of water, it primarily erodes the bed of the valley. However, because of the size, relative amount, and internal flow of the ice, the sides of the valley are also eroded [16]. The river systems are generally considered to be less erosive than glacial ice; however, some evidence indicates the fluvial systems are at least as erosive, if not more in some cases [11].
Historically, the influence of glaciers on valley formation, if present at all, has been primarily determined by field investigations searching for residual evidence, and by analysis of geologic and topographic maps [17]. Quantitatively representing them, however, has been a large struggle and has been the focus of research in the recent past [13,18,19,20,21,22]. Swanson [18] attempted to quantitatively study the morphology of a glaciated valley by investigating the slope, curvature, and elevation distribution of both glaciated and non-glaciated basins. He used these quantitative measures in developing various plots (e.g. frequency distribution or box and whisker) to illustrate the differences between glaciated, partially glaciated and fluvial landscapes. Swanson also graphed the area distribution compared to the elevation, which explores how land mass is distributed through a basin. Swanson’s work presented several quantitative parameters of basins to compare glaciated and non-glaciated landscapes, highlighting their differences. But those comparisons were only based on the graphs and their shapes, and he did not present a method or model to predict whether a separate, unknown basin would have been modified by glacial erosion. Bonk [20] also utilized measurable parameters of mountain valleys, including slope angle, slope aspect and curvature, but used them to identify and define terrain-form objects.
Similarly, Amerson et al. [19] compared the morphometry of glaciated and fluvial valleys by studying their valley relief, width and cross-sectional area, and relating those to the drainage basins of each valley. They developed power-law regression equations for the three parameters based on the basin areas and concluded that the valley relief, width, and cross-sectional area in fact scale with the drainage areas differently between glacial and fluvial basins. The authors compared the glacial and fluvial valleys and quantitatively proved a difference. However, they also did not offer a model or algorithm for glaciation prediction.
Sternai et al. [13] used the hypsometric curve (i.e. frequency distribution of elevations) to describe how glacial erosion influences elevation distributions in alpine valleys and to help characterize fluvial and glaciated landscapes. They defined a new parameter called the hypsokyrtome that compares the gradient of the hypsometric curve to a reference value. They found that the hypsokyrtome and the hypsometric integral (area under the curve) are useful parameters to indicate geographic areas where glacial erosion was present.
To the best of our knowledge, a method that has not been explored with or linked to the quantitative morphological studies of glacial valleys is data mining, or knowledge discovery from data (KDD). This is a relatively new technique that combs through large data sets to find patterns in the data that can be used for associations or correlations, classification or prediction, and a host of other analyses [23,24]. Closely related to data mining is machine learning, of which the goal is to generalize a set of observed data for use with new, unobserved data [25]. Of importance to this project is the classification of data, a technique for predicting a group or category for some event based on a set of attributes and an input model [26].
The specific goal of this research is to develop and test a quantitative model that depicts the extent to which alpine valleys have been glaciated based on previously studied basins that have been categorized as glacial or non-glacial (i.e. whether glaciers have significantly modified the basin). The model will be based primarily on the form and statistics of the hypsometric curve (area-elevation curve, details below) for each valley and will be created by using various data mining techniques. The model will ultimately be utilized to predict the extent to which a valley was glaciated based on the same attributes, which can be easily obtained from digital elevation model (DEM) data.
2. Study area, data, and basin delineation
2.1. Study area
The study area consists of 6 mountainous regions where the extent of glaciation have previously been studied and published. The first region included is from the eastern Sierra Nevada range in east-central California. The area consists mainly of homogenous Cretaceous granodiorites and quartz monzonites and has a uniform uplift rate of approximately 0.2mm/yr predominantly due to strike/slip motion in the Owen’s Valley Fault to the east [8]. Also included is a portion of the Sangre de Cristo Range in southern Colorado with Paleozoic sedimentary units and Precambrian metamorphic rocks and faulting slip rates of approximately 0.1-0.2mm/yr [17]. The third region is along the eastern side of the Ben Ohau Range in New Zealand. It is predominantly composed of greywacke and argillaceous metasediments with some schist and localized volcanic rock; uplift rates are near 0.8mm/yr [17]. The degree of glaciation ranges from non- to fully-glaciated with varying intermediate designations and was determined by investigating geologic maps, aerial photographs, topographic maps and independent field observations [17]. The Bitterroot Mountains in western Montana have a metamorphic core complex with metasedimentary rocks to the north and granite to the south (54) and the uplift from the fault slip rate is approximately 0.14mm/yr [27]. In northwest Washington State, the Olympic mountain complex consists mainly of clastic sediments in three units, primarily composed of turbidite sandstones with pillow basalts [1,28]. The range has basins that were previously classified from analysis of geologic maps as glaciated, partially glaciated or unglaciated [29]. Lastly, a portion of the Sawtooth Mountains in south-central Idaho were included as study sites, which had been classified as either glaciated or fluvial based on analysis of geologic maps, digital elevation models (DEMs) and aerial photographs along with field reconnaissance studies [19]. The area consists mostly of Cretaceous biotite granodiorite, biotite granite, and rhyolitic to andesitic dikes [19].
Given that the focus of this research was mainly methodological in terms of defining a classification model, the focus was not on the climate or tectonics of each of the study areas, although they were noted. In gathering the data, the study areas were collected from varying geographic regions in order to establish a more robust model. And it is believed that the varying climate and tectonics of the areas should actually make the model more powerful in that it is based on data from different regions and settings. Furthermore, these sites were selected because in most of the selected ranges, the degree of glaciation was spatially variable, there is no pattern of glaciation through the range that is immediately apparent. The two exceptions are the Bitteroot site where the north and south facing slopes are either glaciated or non-glaciated, respectively, and the Sawtooth Mountains where the glaciation is longitudinally variable with the glaciated basins falling entirely to the east of the non-glaciated basins. The spatially variable arrangement is useful because it eliminates the necessity for geographically weighted variables, possibly making the hypsometric parameters included herein more apparent. Another reason for selecting the sites used in this study is that none of them were dominated by either glaciated or non-glaciated basins, the count for each type is approximately equal. This makes for a larger bank of basins of both types to base the classification model on.
2.2. Data and basin delineation
Morphometric analysis for this study was performed using ArcGIS and MATLAB software, and was based on 30-meter DEMs obtained from the United States Geologic Survey (USGS) National Elevation Dataset and EarthExplorer databases. The basins were defined using the projected DEMs by first filling any anomalous low points with the “Fill” function in ArcGIS. The flow direction and flow accumulation grids were calculated using their respective functions. In order to create basins at the correct size, all cells above some threshold were selected from the flow accumulation grid to define streams and the cells flowing into numerous streams were grouped to form different watersheds. For the purposes of this research, the flow accumulation threshold was chosen so that the derived watersheds closely matched the basins previously defined. To further assure that the delineated watersheds closely match those from previous studies, outlet points and, in some cases, manual editing were used.
There were a total of 190 basins described above and 75 of them have been designated as Fully-glaciated (“full”), 46 with minor, moderate, or significant glaciation (“intermediate”), and 69 as Non-glaciated (“none”). For this study we concentrated on the extreme cases, i.e., the “full” and “none” cases, giving a sample size of 144 basins to consider.
3. Quantitative parameters
3.1. Hypsometric attributes
Hypsometric analysis is the comparison between elevation and area encapsulated by that elevation [30]. The curve takes the form of a cumulative graph with elevation on the vertical axis and area on the horizontal. Both of these are normalized by dividing the measured values by the maximum of the basin, making the range of possible values of the elevation and area 0 to 1. This allows the different basins from different regions to be compared easily [31]. The curve can be described as a cumulative probability distribution based on the elevation and area of the basin, resulting in an s-shaped curved that can be represented by a polynomial function [32,33].
The area under the curve is the hypsometric integral (HI). It is a quantitative measure of the development stage or age of a drainage basin in terms of the drainage maturity and ranges between 0 and 1 on the normalized graph. For example, an HI near 1 is indicative of a youthful stage and the curve is commonly convex in shape [33]. This implies that the HI is at least partially representative of the stage of development and that it can be utilized to compare landscapes of varying origin or modification. HI can be calculated as (1) where x is the relative area and f(x) is related to the relative height.
However, curves with very different shapes could have similar HI values [34,35]. Harlin [34] developed 4 other parameters to supplement the HI that are derived by treating the hypsometric curve as a cumulative probability distribution and calculating the statistical moments. These parameters are the skewness (SK), kurtosis (KU), density skewness (DSK), and density kurtosis (DKU) (refer to [34] for complete derivation). In statistics, skewness is representative of the asymmetry of a distribution about the mean, being either positive (skew to the right) or negative (skew to the left) [25]. Kurtosis is a measure of the “flatness” or “peakedness” of a function compared to the normal distribution [25].
The density skewness and density kurtosis are the skewness and kurtosis of hypsometric density function, being the first derivative of the hypsometric curve [36]. The attributes defined (HI, SK, KU, DSK, DKU) describe different aspects of the shape of the curve, and they also portray certain properties of the basin. For example, the HI is indicative of the amount of material remaining after surface erosion [30], the skewness represents the amount of headward erosion in the upper reach, density skewness is indicative of slope change, kurtosis reflects the erosion in the upper and lower reaches and density kurtosis signifies the amount of midbasin slope [34]. For this study, the derived watershed boundaries as described above were used to clip the DEM for deriving each basin’s hypsometric curve and related attributes using the GIS extension CalHypso [33].
3.2. Hypsometrical basin equilibrium elevation (HBEE)
In addition to the hypsometric attributes attained with the CalHypso tool, a fifth parameter is herein introduced that is theoretically based on the equilibrium line altitude (ELA) of a valley glacier and is termed the hypothetical basin equilibrium elevation (HBEE). The ELA is the elevation within the valley where the deposition of glacier-forming snow is equal to the ablation [21]. Above the ELA there is a net gain of snow and below it there is a net loss of snow. The ELA is directly related to the temperature, topography and climate of the region [21] and is therefore dynamic both seasonally and over longer time periods. In the valley, the region at or near the ELA is also the area where maximum erosion occurs. Here, the ice is thickest, leading to increased sliding velocity, and increasing the potential to scour or pluck more material from the valley floor [37]. Current and reconstructed glaciers typically have more accumulation area than ablation area, and ratio of accumulation area to the total glacial area (accumulation area ratio, AAR) has a typical range of 0.5-0.8 [15,38].
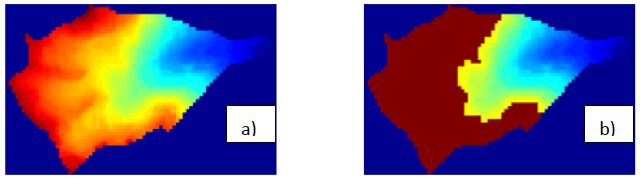
The concept of ELA is defined relative to the surface of glacial ice, which is difficult to obtain for past glaciers. Our HBEE is conceptually similar to ELA but defined relative to present day topography, which is readily available. Since present day topography is a result of erosion from past erosional processes, including glaciers, the HBEE offers a quantitative measure to link present topography to possible past glacial activities. The HBEE can be derived automatically using a program. The program (written in MatLab) starts with an initial elevation at the bottom of the basin and finds the ratio of the area of the watershed that lies above this initial elevation to the total area of the watershed (i.e., the AAR). It then examines if the AAR is at the desired value (e.g., 0.57, [39]). If not, the elevation is increased a small increment and the process is repeated. The process stops when the AAR is at or just above the desired value; the elevation at which the ratio is satisfied (i.e., the desired AAR) is the HBEE for that watershed. One example is shown in Figure 1. The program is automated to process all the watersheds in this study, one watershed at a time.
Similar to the ELA, the HBEE will not only vary between basins, but also from region to region because it is affected and dictated by the climate and environment. This makes it impractical to use the measured HBEE elevation directly in any analysis. To make it comparable between regions, we normalize the HBEE by creating a ratio of the calculated HBEE for each basin of a region to the median HBEE for that region. This creates a standardized HBEE for each basin that can be compared with other basins. This is useful because the HBEE of each basin in a particular range can be compared against that in other, separate regions that show varying degrees of glaciation. We also considered creating a ratio with the minimum, maximum and average values over each range but excluded them because they were not as effective as predictors or the possible range of values was too large and not comparable with the other regions.
4. Data mining analysis
We use a popular data mining software, Orange, developed by the Bioinformatics Laboratory at the University of Ljubljana, Slovenia, as our tool for the data mining analysis. It has a visual programming component that allows for easy data-input and manipulation through widgets that can be assembled to create and test several classifier routines and models concurrently [23,40].
For this research, we compiled four separate classifiers that simultaneously create separate functions to predict the extent of a basin’s glaciation based on the hypsometric variables and HBEE. Those classifiers are classification trees (CT), random forest (RF), naïve Bayes (NB), and k-nearest neighbors (kNN).
·Classification tree: This type of classifier algorithm works by recursively splitting independent variables into branches through several iterations until a data sub-set is accomplished that includes only instances of the same class and another split is either not possible or it is not beneficial to the model [41]. A “tree” is formed in that the model starts with a root variable and splits it into 2 subsets, and the process is repeated with other independent variables, creating “branches” and “leaves” with the optimum outcome. The optimum split and pruning rules are controlled by heuristics to create small but accurate trees that don’t over-fit the data [41].
·Random Forest: As the name implies, the random forest classifier is a collection of classification trees classifiers that are constructed from independent but identically distributed random vectors and then each tree casts a vote for the most popular classification of the dependent variable [42]. This approach aims to correct the problems of over-fitting the training data to make a tree too complex and pruning a fully grown tree that may increase the generalizations on the training data [43].
·Naïve Bayes: The Naïve Bayes classifier uses conditional and unconditional probabilities based on the training dataset to predict the class a sample would belong to. It is one of the most basic and accurate predictive methods available. The unconditional probability comes from the number of instances for each class in the training set divided by the total number training samples [41,44]. The conditional probability is created by multiplying the prior unconditional probability by the probabilities of the attributes to some outcome (i.e. the probability of an outcome is based on the product of the prior probability and the probability that an attribute contributes to the outcome) [41].
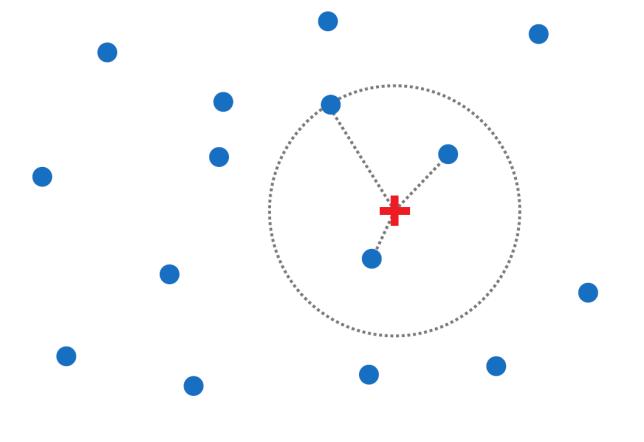
·K-Nearest Neighbor: the kNN approach predicts the outcome of an unknown dataset based on similar instances from a training set with the same parameters and uses the trainer’s most prominent classification to assign a predictive class for the unknown [41]. In other words, the reference points from the training set are plotted in a d-dimensional space and a point to be classified (or query point) is located. The distances from the query point to the reference points are calculated and the class of the k-nearest ones are used to classify the query point (Figure 2) [45].
5. Results
Using the ArcGIS software and CalHypso extension, we obtained the values of HI, SK, KU, DSK, and DKU for the 144 basins. We expected the average values related to each of the parameters to be significantly different between fully-glaciated and non-glaciated basins; however, the averages for some of the groups are surprisingly similar. For example, the average HI value for the non-glaciated basins is 0.506 while the value for the fully-glaciated basins is 0.497, and the results are similar for the kurtosis and density kurtosis.
Since some of the averages were similar, we ran regression analysis on the assigned glaciation designation against all of the hypsometric attributes and the HBEE to help identify the parameters that contribute more to the model. The result showed that, based on the t-statistics (overall R2 = 0.43), the HI, SK, KU, and HBEE are all statistically significant at a 95% confidence level, whereas the DSK and DKU were not. In other words, the model is significantly influenced by 4 of the 6 parameters.
With the Orange software, we can specify which variables should be used to build the model, how many samples are to be used to train the model and how many samples are to be used to test the model result and derive accuracy. For variables, we used all of the hypsometric attributes (HI, SK, KU, DSK, DKU, & HBEE) and during a second version of the model only those that were found to be significant in regression analysis (HI, SK, KU & HBEE). For samples, three scenarios were presented. First, all 144 samples were used to train and build the model and the resultant model was applied back to classify the samples and derive accuracy. This approach usually results in overfitting of the model and overestimate of accuracy [25], with kNN method producing 100% accuracy (Table 1). Second, 80% of the samples (115 basins) were used to train the classifiers and the resultant model was applied to test the separate, remaining 20% of the samples (29 basins), which did not participate in the training, and were used to derive the model accuracy. This approach usually produces more reliable accuracy estimate [25] and as shown in Table 1,the model correctly classifies up to 90% of the testing subset, with the kNN analysis being the most successful. The dual-set training and testing model building method (using 80% and 20% in our case) is an accepted way to create a classification model. A similar 3-way approach (using training, calibration and testing) was not implemented because the Orange software we chose to use does not explicitly allow for a calibration step and seems to handle that internally with the training step. Third, a cross-validation approach is used, in which all but one sample were used to train the model and that one sample used for validation. This process is repeated, each time with a different sample left out [46]. This approach also produces a reasonable accuracy estimate, comparable to that of the second scenario (Table 1). Ultimately, the results show that kNN model is the best, with overall accuracy reaching 90%, a conclusion that is further supported by the user and producer accuracies of the model (Table 2).
Table 1. Overall classification accuracy of the predictor model for 4 classifiers
|
100% training, 100%test |
80% training, 20% test |
Cross-validation |
|
HI, SK, KU, HBEE, DSK, DKU |
HI, SK, KU, HBEE |
HI, SK, KU, HBEE, DSK, DKU |
HI, SK, KU, HBEE |
HI, SK, KU, HBEE |
| NB |
76% |
78% |
76% |
76% |
72% |
| RF |
92% |
92% |
86% |
83% |
78% |
| CT |
96% |
97% |
72% |
69% |
76% |
| kNN |
100% |
99% |
90% |
86% |
81% |
| (NB=Naïve Bayes, RF=Random Forest, CT=Classification Tree, kNN=k-nearest neighbors). Values represent percentage of test data accurately classified with prediction model |
Table 2. User and producer accuracy of the predictor model for 4 classifiers
| HI, SK, KU, HBEE, DSK, DKU |
|
100% training, 100% Test |
80% training, 20% Test |
|
User |
Producer |
User |
Producer |
|
None |
Full |
None |
Full |
None |
Full |
None |
Full |
| NB |
73% |
79% |
84% |
67% |
79% |
73% |
73% |
79% |
| RF |
93% |
91% |
92% |
93% |
87% |
86% |
87% |
86% |
| CT |
95% |
92% |
96% |
90% |
82% |
67% |
60% |
86% |
| KNN |
100% |
100% |
100% |
100% |
93% |
87% |
87% |
93% |
| HI, SK, KU, HBEE, DSK, DKU |
|
100% training, 100% Test |
80% training, 20% Test |
|
User |
Producer |
User |
Producer |
|
None |
Full |
None |
Full |
None |
Full |
None |
Full |
| NB |
76% |
80% |
84% |
71% |
72% |
82% |
87% |
79% |
| RF |
93% |
91% |
92% |
93% |
78% |
91% |
93% |
86% |
| CT |
96% |
97% |
97% |
96% |
69% |
69% |
73% |
86% |
| KNN |
100% |
99% |
99% |
100% |
87% |
86% |
87% |
93% |
6. Discussion
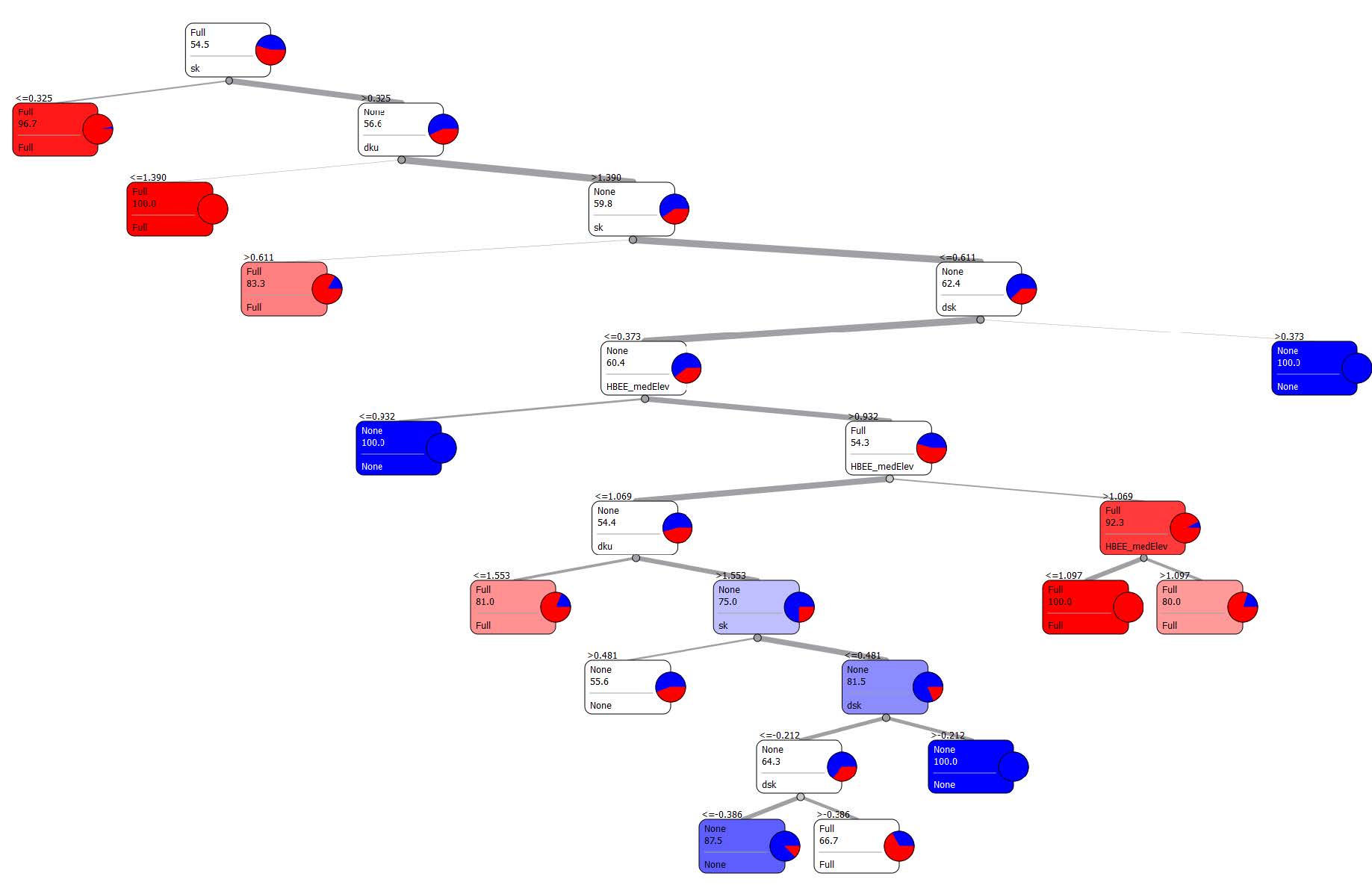
The results presented above show that the hypsometric attributes and the derived HBEE can reliably predict the existence of glaciation in a mountain valley with up to 90% accuracy. In all cases, the kNN model performed the best, showing that a predictive model that works on a case-by-case basis outperforms the ones that try to generalize the data and create a set of equations of if-then scenarios to guide the user towards a prediction. However, that is also one of the disadvantages of the kNN model, there is no output for the user to follow or apply to other datasets. On the other hand, the other three classifier methods have a visual or methodical output to follow. For example, the classification tree and random forest classifier can be graphically depicted as a set of nodes and edges, or leaves and branches (Figure 3). The classifier systematically splits the variables at a natural break point of the independent variables (HI, SK, KU, DSK, DKU and HBEE for this model) and classifies them as glacial or non-glacial. From Figure 3,the top node (or the root) initially uses the SK variable and splits it at 0.325 so that those basins with a value less than or equal to 0.325 are classified as fully-glaciated and those greater than that value are non-glaciated; this is the most basic classification. The nodes or variables continue to be split until a reasonable solution is no longer possible or the maximum number of branches is reached [26]. At the twelfth and final node, the class decision is:
If the SK is greater than 0.325 and DKU greater than 1.390, and SK less than or equal to 0.611, and DSK less than or equal to 0.373, and HBEE between 0.932 and 1.069, and DKU greater than 1.553, and SK less than or equal to 0.481, and DSK less than -0.212 and less than -0.386, then the basin falls under the non-glaciated class.
This example may be a case of the data being overfit, especially given the small range listed for the HBEE [42,47,48]. In any case, there are several possible splits, nodes and solutions to the class prediction between the first and seventh node, and the classification tree gives the user an easy interface and simple solution for the prediction.
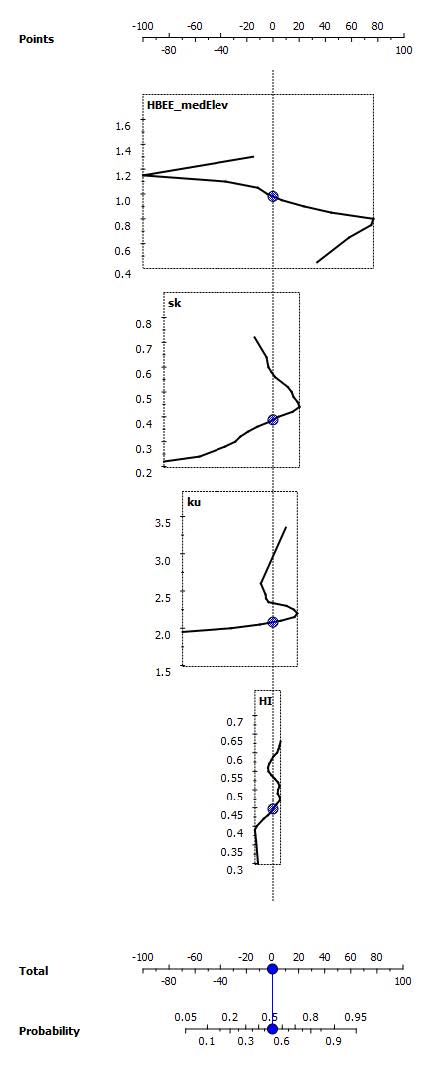
Like the classification tree, a nomogram is another method to visually represent the class solution. Associated with the naïve Bayes classifier, nomogroms graphically depict the quantitative relationships of two or more parameters and were originally designed for physicians to use as a diagnosis probability tool [49]. The nomogram for this basin classification is shown in Figure 4. The range of possible values for each attribute are plotted on the y-axes. The attributes share an x-axis, designated by a scale ranging from -100 to ﹢100 along the top of the graph, which reports a point value that measures the contribution of each attribute to the model. The light dotted line which extends through all of the single graphs is aligned at 0 and only signifies where the points break between positive and negative. As the user selects a value for one of the attributes by moving along the y-axis, the point value corresponding to that value is reported from the x-axis. The points move independently for the separate attributes, and are summed in the bottom scale with the same range. This means that as one attribute increases the total points with a positive move, another attribute could decrease the total with negative points. The summed points are linked to the probability scale, which ranges from 0 to 1.0. It indicates the likelihood of the measured feature being a member of a selected group or target class (e.g., non-glaciated in this case) (see [49] for a detailed discussion of the algorithm relating the points and probability). The nomogram in Figure 4 (i.e. the probability scale at the bottom) reports the likelihood of a basin belonging to the non-glacial class. In some cases, there is not a constant or direct relationship between the attribute value and the point value (i.e., as the attribute value moves from the minimum to maximum, the associated points may vary in a non-linear fashion, or even switch between positive and negative). For example, for the SK variable, based on Figure 4,from approximately 0.22 to 0.44, the points increase with the SK, but above 0.44, the probability begins to decrease. The nomogram from Figure 4 is also sorted in the order of variable influence with the most influential (HBEE) at the top and having the greatest width. Therefore, a small change in the value of the HBEE causes a large change in the points and probability whereas the opposite is true for the HI. While it’s not expected that the HI be the least influential in the model, it is a reasonable conclusion because it has been shown that the HI as a single variable has given mixed results as a predictor [35].
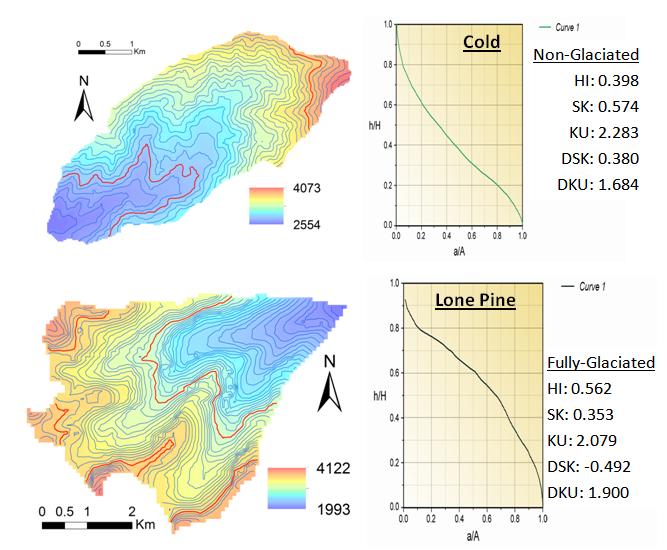
Regarding the SK, as the value is increased, the likelihood that the basin is non-glacial also increases. (This is generally true, although at the highest values of SK the probability actually decreases, but not by a significant amount.) This is further exhibited by comparing the SK values of two typical hypsometric graphs shown in Figure 5; the non-glaciated graph has a very different shape and a considerably larger SK value. Recall that SK shows the asymmetry of the graph, and it is apparent that the graph of a non-glaciated basin is more skewed than the glaciated graph. The same amount of change in relative elevation near the top (y-axis) corresponds to a smaller change in relative area (x-axis) for the non-glacial basin than that for a glaciated basin. The area-elevation or slope comparison for non-glaciated basin in Figure 5 is consistent with a typical basin with fluvial origins, the slope at the top of the basin is fairly large and then gradually decreases towards the bottom as the size of the stream increases and stabilizes (Horton 1945) [50]. The red highlighted contour lines in Figure 6 correspond to approximate breakpoints on the hypsometric graph. In the non-glaciated basin, the contours are 3750and 2850, which correspond to 0.8 and 0.2 elevation ratios, respectively. The contours between the highlighted lines show a gradually decrease in steepness with a decrease in elevation, similar to the slope of the hypsometric graph. In the glaciated basin highlighted the contours are 3700 and 3050, which correspond to 0.8 and 0.5, respectively. There is no significant change in the steepness of the basin as depicted by the spacing of the contours between the highlighted contours. However, the change in the area between the highlighted contours is evident, showing the relationship between the area and elevation.
The shape of the hypsometric graph from the glaciated basin reflects a process of mass removed from the top of the basin (possibly via cirque formation), and the mass being transported towards the bottom of the basin, with an extreme amount of erosion occurring with the glacier. That mass is probably not completely transported out of the basin though, as it may be deposited as moraines mid-basin, where the glacier ceased moving further down. The result is steeper slopes at higher elevations of the basin and gentler slopes at mid-basin elevations. This phenomenon is reflected in the large values of SK, which signify more erosion at the upper reaches of the basin [34,35].
The KU is a more difficult parameter to use as a predictive variable and is less significant to the model than the HBEE and SK, as indicated in the nomogram of Figure 4. The kurtosis of a graph measures its "peakedness", at least for a normal bell curve. Therefore, if the hypsometric graph is viewed as only one half of said normal graph, we might expect and actually see that the KU value is larger for the non-glaciated basin because the graph is generally steeper (i.e. a sharp peak) (see graphs of Figure 5). On the other hand, for the glaciated case the graph has only a very small “peak” towards the top and has a convex shape otherwise. The shape of the curve is characterized by a larger change in relative area for each unit change in relative height in the mid-basin region. This is consistent with the fact that a large amount of mass is eroded and moved from the top of the basin during glaciation, and possibly being deposited as moraines downstream. This is also a reflection of the relatively less erosive power of a stream at lower elevations than that of a glacier at higher elevations.
The AAR remains one of the best estimators of the ELA. However, it is sometimes difficult to determine where the ablation area is. It is possible to determine the AAR from oblique or aerial photos [52]. By locating the short term location of the snowline during the ablation season, Meier and Post [52] were able to determine the final AAR of a mountain range. However, in order to do that, knowledge of the approximate ablation period is necessary, along with an estimate of the snowline retreat rate and apparent snowpack thickness. These measures may require field study and/or first hand knowledge of the region that may only come with prolonged study. Furthermore, like the ELA, the AAR is extremely variable, both seasonally and over long periods of time. And because of continued geomorphological processes, the present day ELA is not consistent with that from the last glacial maximum. Some research has even found that the AAR is dependent on the valley shape and size. Kern and László [53] suggest that a range of AAR be utilized, either 0.44,0.54, or 0.64, based on whether a glacier is less than 1 km2,1-4 km2, or greater than 4 km2, respectively. The average area of the basins utilized in this study ranged from approximately 1 km2 (Bitterroot) to approximately 17 km2 (eastern Sierra Nevada). Our global estimate of 0.57 is therefore reasonable since that value falls within the presented ranges.
One of the limitations to using the HBEE is that it is only similar to and not exactly analogous to the ELA. The ELA is relative to the surface of glacial ice, comparing the accumulation and ablation area. Since our study includes basins that were non-glaciated, no ELA would be calculated for them. The HBEE on the other hand, is calculated based on the topography of the entire basin. Therefore, the HBEE of a glaciated basin would not match the ELA. However, the HBEE can be calculated for both glaciated and non-glaciated basins and does appear to be a satisfactory determinant for differentiating between glacial and non-glacial basins.
Because the hypsometry is a function of both the elevation and the area of the basin, the calculated hypsometric attributes are quite sensitive to the basin shape. For example, many of the basins used for this research are valleys along mountain ridges that empty into common, larger valleys. And depending on the ridge configuration, the individual basins may have a drainage system that creates a long “tail” to the valley. That “tail” can affect the hypsometry of the individual basin because it generally has a slope that is comparatively much smaller than the rest of the basin above it, which adds undue area to the lower elevations considered in the hypsometric calculations and possibly altering the results. We have mitigated these undesirable effect by having the watersheds automatically delineated by the GIS software and for the small number of resulting basins with long “tails”, by specifying the outlet point of the watershed which allows the routine to correctly delineate proper basin boundaries consistent with previous work [17] for our hypsometric analysis.
This research focuses on the ideal cases at the extremes of valley erosion, being shaped by either a glacier flowing down valley or a river cutting it down. However, it is recognized that an interplay exists between the two mechanisms. A valley where the initial incision is caused by water and later occupied with glaciers is exactly the case the model should detect, given that the valley should have clear evidence of glacial erosion. Yet, given the elapsed time since glaciation of some of the ranges included in the study, we must account for the opposite where a glaciated valley has been subject to fluvial erosion since it was carved out. In that case, the glacial valley would most likely have been partially infilled with regolith or sediment. Once the up-valley meltwater or precipitation fed river began to flow through, it would most likely cut a small v-shaped incision into the sediment or basal rock. During times of large flow such as floods, the valley may fill, spreading fluvial sediment over the valley. When the process of down-cutting and flooding in repeated, benches or steps are created across the valley.
The model presented should be unaffected by this post-glacial, fluvial scenario since the model is based primarily on mass removal rather than basin shape. Unless the basin was completely filled after the glacier retreated, the volume of mass moved by the glacier would probably still be more than what the fluvial system could move. Also, the sediment that remains after the glacier is gone would be less condensed and more easily transported than the bedrock that the river might otherwise be cutting into.
7. Conclusion
Alpine glacial processes are important for understanding past climates, plate movement, mountain landforms, bedrock geology and more. The study of alpine glacial processes starts with identifying glacial landforms. This has traditionally been accomplished by conducting field work and analyzing topographic maps, which is time consuming and impractical for hard to access areas. With ready availability of digital geospatial data and advancement of data mining techniques, it is possible and desirable to identify glacial landforms automatically and quantitatively.
This paper represents such an attempt. The point of this research is to create statistical models based on measured geospatial data. Furthermore, to quantify the morphology of alpine valleys at watershed basin scale, we utilized six parameters derived from digital elevation model (DEM) data, including five hypsometric attributes of the basins calculated from the elevation-area plots and one other variable, termed the HBEE, which is based on the ELA of a glaciated basin. These quantitative parameters were obtained for 144 glaciated and non-glaciated basins, whose origin have been determined from previous studies, in various regions. Based on these sample data, four classification algorithms from data mining were then used to build a model using the Orange software and various scenarios of training and test samples. The model is capable of predicting the outcome of either a glaciated or non-glaciated valley with up to a 90% accuracy based on the kNN classifying method, although other methods have lower predictive accuracies. The model can be applied to determine the extent of glaciation in places that is difficult to access for field work, but where DEMs can be obtained remotely, including extra-terrestrial locations such as Mars [51]. Additionally, users of these methods should understand the advantages of hypsometric data, the importance of a basin’s ELA (herein modelled by the HBEE) and the robust modelling power of data mining techniques to tease out patterns within data.
This work is different from previous studies in that it offers a model that is based on measured, quantifiable attributes of an alpine basin. The model is also intended to predict where glaciers were present. Previous research [13,15,18] has been influential by outlining aspects of alpine basins that can be used as predictive attributes, thereby laying a base for a model such as the one presented in this research. Some of those aspects were considered or included in this model, but our model takes the next step towards being able to investigate regions or landscapes that have limited or no accessibility. This model offers a tool for researchers struggling to understand Earth’s past environment, especially amid intense climate change discussions.
Acknowledgement
The authors greatly appreciate the comments and suggestions of two anonymous reviewers which helped improve the quality of the paper.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: