This study intends to investigate the performance of boosted regression tree (BRT) and frequency ratio (FR) models in groundwater potential mapping. For this purpose, location of the springs was determined in the western parts of the Mashhad Plain using national reports and field surveys. In addition, thirteen groundwater conditioning factors were prepared and mapped for the modelling process. Those factor maps are: slope degree, slope aspect, altitude, plan curvature, profile curvature, slope length, topographic wetness index, distance from faults, distance from rivers, river density, fault density, land use, and lithology. Then, frequency ratio and boosted regression tree models were applied and groundwater potential maps (GPMs) were produced. In the last step, validation of the models was carried out implementing receiver operating characteristics (ROC) curve. According to the results, BRT had area under curve of ROC (AUC-ROC) of 87.2%, while it was seen that FR had AUC-ROC of 83.2% that implies acceptable operation of the models. According to the results of this study, topographic wetness index was the most important factor, followed by altitude, and distance from rivers. On the other hand, aspect, and plan curvature were seen to be the least important factors. The methodology implemented in this study could be used for other basins with similar conditions to cope with water resources problem.
Citation: Seyed Mohsen Mousavi, Ali Golkarian, Seyed Amir Naghibi, Bahareh Kalantar, Biswajeet Pradhan. GIS-based Groundwater Spring Potential Mapping Using Data Mining Boosted Regression Tree and Probabilistic Frequency Ratio Models in Iran[J]. AIMS Geosciences, 2017, 3(1): 91-115. doi: 10.3934/geosci.2017.1.91
| [1] | Eric Ariel L. Salas, Sakthi Subburayalu Kumaran, Robert Bennett, Leeoria P. Willis, Kayla Mitchell . Machine Learning-Based Classification of Small-Sized Wetlands Using Sentinel-2 Images. AIMS Geosciences, 2024, 10(1): 62-79. doi: 10.3934/geosci.2024005 |
| [2] | Nudthawud Homtong, Wisaroot Pringproh, Kankanon Sakmongkoljit, Sattha Srikarom, Rungtiwa Yapun, Ben Wongsaijai . Remote sensing-based groundwater potential evaluation in a fractured-bedrock mountainous area. AIMS Geosciences, 2024, 10(2): 242-262. doi: 10.3934/geosci.2024014 |
| [3] | Watcharin Phoemphon, Bantita Terakulsatit . Assessment of groundwater potential zones and mapping using GIS/RS techniques and analytic hierarchy process: A case study on saline soil area, Nakhon Ratchasima, Thailand. AIMS Geosciences, 2023, 9(1): 49-67. doi: 10.3934/geosci.2023004 |
| [4] | Nicola Gabellieri, Ettore Sarzotti . Forest planning, rural practices, and woodland cover in an 18th-century Alpine Valley (Val di Fiemme, Italy): A geohistorical and GIS-based approach to the history of environmental resources. AIMS Geosciences, 2024, 10(4): 767-791. doi: 10.3934/geosci.2024038 |
| [5] | Gianni Petino, Gaetano Chinnici, Donatella Privitera . Heritage and carob trees: Where the monumental and landscape intersect. AIMS Geosciences, 2024, 10(3): 623-640. doi: 10.3934/geosci.2024032 |
| [6] | Maurizio Barbieri, Tiziano Boschetti, Giuseppe Sappa, Francesca Andrei . Hydrogeochemistry and groundwater quality assessment in a municipal solid waste landfill (central Italy). AIMS Geosciences, 2022, 8(3): 467-487. doi: 10.3934/geosci.2022026 |
| [7] | Francesca Romana Lugeri, Barbara Aldighieri, Piero Farabollini, Fabrizio Bendia, Alberto Cardillo . Territorial knowledge and cartographic evolution. AIMS Geosciences, 2022, 8(3): 452-466. doi: 10.3934/geosci.2022025 |
| [8] | Maria C. Mariani, Hector Gonzalez-Huizar, Masum Md Al Bhuiyan, Osei K. Tweneboah . Using Dynamic Fourier Analysis to Discriminate Between Seismic Signals from Natural Earthquakes and Mining Explosions. AIMS Geosciences, 2017, 3(3): 438-449. doi: 10.3934/geosci.2017.3.438 |
| [9] | Rosazlin Abdullah, Firuza Begham Mustafa, Subha Bhassu, Nur Aziaty Amirah Azhar, Benjamin Ezekiel Bwadi, Nur Syabeera Begum Nasir Ahmad, Aaronn Avit Ajeng . Evaluation of water and soil qualities for giant freshwater prawn farming site suitability by using the AHP and GIS approaches in Jelebu, Negeri Sembilan, Malaysia. AIMS Geosciences, 2021, 7(3): 507-528. doi: 10.3934/geosci.2021029 |
| [10] | Alexander Fekete . Urban and Rural Landslide Hazard and Exposure Mapping Using Landsat and Corona Satellite Imagery for Tehran and the Alborz Mountains, Iran. AIMS Geosciences, 2017, 3(1): 37-66. doi: 10.3934/geosci.2017.1.37 |
This study intends to investigate the performance of boosted regression tree (BRT) and frequency ratio (FR) models in groundwater potential mapping. For this purpose, location of the springs was determined in the western parts of the Mashhad Plain using national reports and field surveys. In addition, thirteen groundwater conditioning factors were prepared and mapped for the modelling process. Those factor maps are: slope degree, slope aspect, altitude, plan curvature, profile curvature, slope length, topographic wetness index, distance from faults, distance from rivers, river density, fault density, land use, and lithology. Then, frequency ratio and boosted regression tree models were applied and groundwater potential maps (GPMs) were produced. In the last step, validation of the models was carried out implementing receiver operating characteristics (ROC) curve. According to the results, BRT had area under curve of ROC (AUC-ROC) of 87.2%, while it was seen that FR had AUC-ROC of 83.2% that implies acceptable operation of the models. According to the results of this study, topographic wetness index was the most important factor, followed by altitude, and distance from rivers. On the other hand, aspect, and plan curvature were seen to be the least important factors. The methodology implemented in this study could be used for other basins with similar conditions to cope with water resources problem.
Groundwater problems have been identified as the most important challenges of the 21st century in the world [1,2]. Considering the increase of demand for fresh water resources, two appropriate tools are being used by the engineers and planners for an efficient management and production of groundwater resources [3]. Geographic information system (GIS) can be used in the decision making process in water resource management as it is a powerful tool [4]. Several researchers have applied a combination of GIS and remote sensing (RS) tools for evaluation of groundwater potential mapping in medium to regional scale [3,4,5]. With the progresses of the RS and GIS techniques and software, mapping of groundwater potential has become an easy and efficient procedure [5]. However, in developing and threshold countries like Iran, there is a severe lack of precise and complete dataset, for that reason, remote sensing data is necessary for understanding the groundwater condition and subsequently its management. In this respect, many researchers have used different models and methods, for example, Oh et al. [3], Ozdemir [6,7], Manap et al. [8], Pourtaghi and Pourghasemi [9], Naghibi et al. [10] used FR model. Other statistical models such as, weights-of-evidence [7,9], logistic regression [6], evidential belief function [11,12,13] models have been implemented for groundwater assessment. More recently, some researchers used data mining algorithms such as boosted regression trees (BRT), classification and regression trees, random forests, k nearest neighbor (KNN), linear discriminant analysis (LDA), quadric discriminant analysis (QDA), and multivariate adaptive regression splines (MARS), support vector machine (SVM), artificial neural network (ANN), flexible discriminant analysis, penalized discriminant analysis models in ground water potential mapping [14,15,16,17]. Data mining as a group of applied artificial intelligence can be clarified as the extraction of information from a dataset and relate the input and output variables [18]. Data mining models are able to deal with non-linear issues such as landslide and groundwater studies [14,19]. These models can be used for classification, regression and in some cases for survival studies. In this study BRT model was used for a two-condition classification problem which was existence or non-existence of the springs in the study area. In addition, it is worth mentioning that in the literature, some physically-based models are used to address the incidence of springs in massifs of crystalline rocks and at catchment scale, and have contributed to clarify the role of rock structure and flow circuits in the incidence of springs [20,21].
Recently, data mining approaches are getting extremely popular because of their high performance and strong features. Investigation of the literature shows that FR as a probabilistic model has been used in different studies for groundwater potential mapping. These studies have reported the results of this model acceptable. BRT, on the other hand, has been used in lower number of studies. This research aims to compare the performance of FR and BRT as probability based and data mining based approaches to determine which one of these approaches can provide better results. A thorough literature review reveals that several researchers have reported different importance and contribution of the GCFs in groundwater modelling. For example, some studies have reported high importance of altitude, plan curvature, and profile curvature [17], while other studies have depicted high contribution of altitude, TWI, slope angle, and fault density [15]. Thus, it can be seen that there are some differences between these two studies which could be related to different characteristics of the watersheds, and the modelling procedure implemented in the mentioned studies. Therefore, this research intends to (ⅰ) investigate and compare the performance of data mining based BRT and probabilistic based FR models, (ⅱ) investigate the relationship among the thirteen conditioning factors, and (ⅲ) determine the contribution of the conditioning factors.
The study area is situated in the western parts of the Mashhad Plain which consists of Torghabeh and Shandiz residential areas located between 36° 04′ 17″ and 36° 30′ 36″ latitudes, and 59° 02′ 32″ and 59° 33′ 48″ longitudes. The study area covers approximately 1, 268 km2(Figure 1). The altitude of the study area varies from 1, 045 to 2, 944 m (average = 1, 615 m). Four land use classes can be seen in the study area such as agriculture, orchard, rangeland, and residential area. Among these land use classes, rangeland covers the most part of the area. In this region, people exploit groundwater resources by well, spring and qanat, and use water resources in different sections such as farming, drinking water, and livestock.
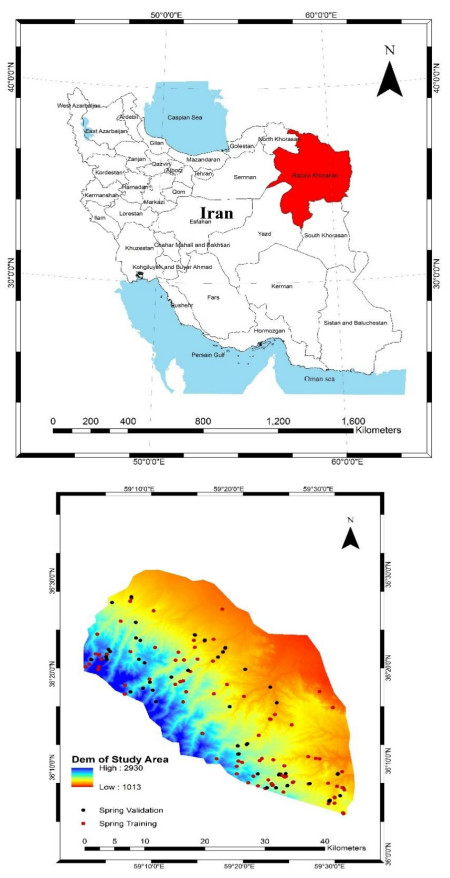 Figure 1. Location of the study area in Iran showing the DEM with training and validation data of the springs
Figure 1. Location of the study area in Iran showing the DEM with training and validation data of the springsIn the study area, 155 springs were detected and mapped at 1: 50, 000-scale by field surveys and national reports by Iranian Department of Water Resources Management [22] (Figure 1). Then, the reported spring data were randomly grouped [3,6,7] into two classes of 109 (70%), and 46 (30%). These two groups were employed in modelling and evaluating of the groundwater potential maps (GPM). Discharge of the springs ranges between 0.1 and 60 lit/s with an average of 3.6 lit/s. The pH of the water in springs changes from 5.2 to 8.4 with an average of 7.3. From 155 springs in the study area, 12 springs are seasonal and other springs are permanent. Water of these springs is used in different sections such as agriculture, drinking water, and livestock.
The main factors affecting groundwater potential were selected based on literature review [3,6,7]. However, other researchers [20,21] have mentioned that a few factors influence groundwater potential such as geological parameters (i.e. length of fractures, the stress field orientation and the deformational regimes) and recharge system. These factors are slope degree, slope aspect, altitude, plan curvature, profile curvature, slope length, topographic wetness index, distance from rivers and faults, river density, fault density, land use, and lithology. A DEM having 30×30 m grid size was derived from the 1: 50, 000-scale topographic maps of the studied area. This layer was employed to produce slope degree, slope aspect, altitude, slope length (LS), topographic wetness index (TWI), profile and plan curvature factors. Classification of the conditioning factors was arranged based on the methods encountered in the literature review [10,15,17].
Slope degree was produced and categorized into four classes with 0, 5, 15, and 30 as separators (Figure 2a). Slope aspect map was prepared and classified into nine classes (Figure 2b). Altitude map was prepared based on the 30-m DEM and categorized into 5 groups of ( < 1, 400, 1, 401-1, 800, 1, 801-2, 200, 2, 201-2, 400, and > 2, 400) (Figure 2c).
 Figure 2. (a) slope degree, (b) slope aspect, (c) altitude, (d) plan curvature, (e) profile curvature, (f) slope length (LS), (g) topographic wetness index (TWI), (h) distance from river, (i) distance from fault, (j) river density, (k) fault density, (l) land use, and (m) lithology
Figure 2. (a) slope degree, (b) slope aspect, (c) altitude, (d) plan curvature, (e) profile curvature, (f) slope length (LS), (g) topographic wetness index (TWI), (h) distance from river, (i) distance from fault, (j) river density, (k) fault density, (l) land use, and (m) lithologyIn addition, two curvature maps including plan and profile curvature maps which has been reported as important conditioning factors on groundwater potential were used. A contour line which is created at the crossing between the horizontal plane and terrain surface is called plan curvature (Figure 2d) [23,24,25]. Profile curvature is defined as curvature of the flow (Figure 2e) [23,25,26]. These layers were calculated in the system for automated geoscientific analyses (SAGA) software and were used in this study as conditioning factors.
In addition, two other DEM-derived factors of LS and TWI were produced using the SAGA software and used in the modelling process. The equation for calculating LS factor was defined by Moore and Burch [27] and used in this study (Figure 2f). Pourghasemi et al. [28] mentioned that there is a direct relationship between LS and the water that gathers at the bottom of the region. TWI was calculated using the equation defined by Moore et al. [29] and was classified and used in the current study (Figure 2g).
River and fault related factors were reported to have influence on the spring occurrence as well as the groundwater potentiality [10]. In this case, four factors were prepared and used such as distance layers of rivers and faults and density layers of the rivers and fault. One hundred, and two hundred and fifty meter intervals were considered in classifying two distance layers of river and fault (Figure 2h-i). In the case of river density and fault density, since there is jump in density layers, natural break classification scheme was implemented to classify them [30,31] (Figure 2j-k).
In order to create the land use map of the western parts of the Mashhad Plain, maximum likelihood, a supervised classification algorithm and Landsat satellite images of the year 2014 were implemented by Iranian forest, rangeland and watershed management organization [32]. Land use layer comprises four different classes of agriculture, orchard, rangeland and residential areas (Figure 2l).
A 1:100, 000-scale geological map was employed for preparing the lithology layer of the western parts of the Mashhad Plain [33]. The lithology layer includes thirteen groups that are represented in Figure. 2m, and Table 1.
| Class | Lithological characteristics |
| Group 1 | Claystone, sandstone |
| Group 2 | Granite-aplite |
| Group 3 | Gravel fan |
| Group 4 | Interbedded radiolarite slate and ultrabasic rocks |
| Group 5 | Leucogranite |
| Group 6 | Limestone recrystallized dolomitic |
| Group 7 | Marl, red-brown, gypsiferous |
| Group 8 | Quartz conglomerate |
| Group 9 | Recent alluvium |
| Group 10 | Sandstone, shale, conglomerate |
| Group 11 | Sandstone, slate crystalized limestone |
| Group 12 | Shale, phyletic, dark grey |
| Group 13 | Terraces |
Figure 3 displays the methodological flowchart of the current research.
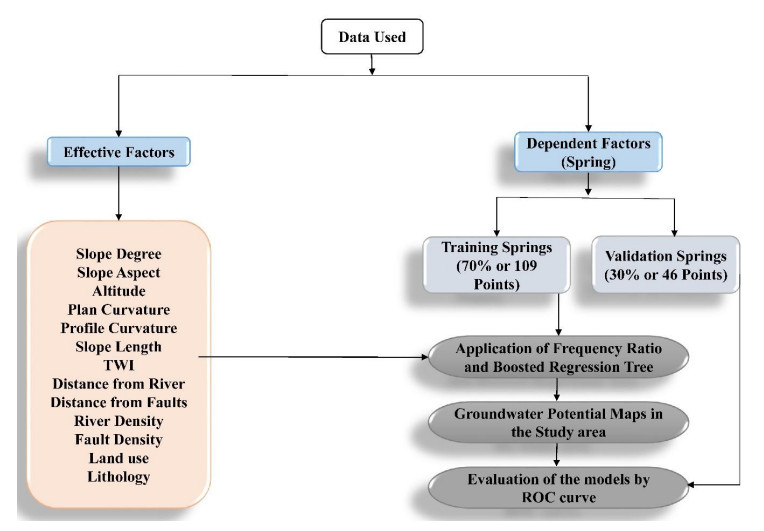 Figure 3. Flowchart of the methodology implemented in this study including selection of the conditioning factors, dependent factor classification, modelling process, and evaluation method in this study
Figure 3. Flowchart of the methodology implemented in this study including selection of the conditioning factors, dependent factor classification, modelling process, and evaluation method in this studyMulticollinearity denotes the non-independence of GCFs which can be seen in datasets due to their high correlation [34]. For analyzing the multicollinearity issue, two indices such as variance inflation factor (VIF) and tolerance were computed for GCFs. VIFs greater than 10 or tolerance less than 0.1 show that there is multicollinearity and the factor should be removed from next steps of the modelling process [35,36].
FR model can be used to compute the relationship among the input and output factors of the model which in this study are conditioning factors and spring location [3]. The results of this model can be understood easily and application of this model is simple [37,38]. To compute the FR for classes of each input factor, number of springs in each class and area related to each class was determined by ArcGIS 9.3. In the next stage, the FR equation can be used as below [39]:
| Frequency Ratio=S╱TSP╱TP | (1) |
Where, S depicts the number of springs in each class, TS shows the total number of springs, P represents the number of pixels in each class, and TP depicts the total number of pixels. At last, FR values for all of the factors will be summed and a final GPM will be produced by Equation 2:
| FR = FRslopedegree + FRslopeaspect + FRaltitude + FRplancurvature + FRprofilecurvature + FRslopelength + FRTWI + FRdistabcefromfaults + FRdistancefromrivers + FRriverdensity + FRfaultdensity + FRlanduse + FRlithology | (2) |
A FR value of 1 depicts an average value, while a greater value than 1 shows higher correlation and potential of each class [40].
Another relatively new data mining model which was used for groundwater potentiality modelling in this study is boosted regression trees. BRT uses two powerful techniques such as gradient boosting and classification and regression tree (CART) [41,42], and was introduced by Friedman [43]. Boosting is used to improve model accuracy by averaging many rules as an alternative of obtaining a single one with higher accuracy [44]. Decision trees include two types of classification and regression. In regression trees, the target or output variable can have continuous values. The rules are decision rules which could be different decision rules in tree-based models based on the relationship between the output and input factors and the modelling procedure as well. Boosting gradient technique employs a weighted average of results gained from prediction of various samples [45]. In BRT, three parameters require to be optimized including number of trees or number of boosting iterations, interaction depth or max tree depth, and shrinkage [46]. The shrinkage shows the contribution of the trees in the grown model [47]. The size of the individual trees is determined by a parameter called the interaction depth [48].
For tuning BRT, a grid of these parameters was employed and a 10-fold cross validation method was implemented. This grid contains interaction depths of 1, 5, and 9, shrinkages of 0.001, 0.005, 0.01, 0.05, and 0.1, and number of trees of 100 to 1, 000 with 100 intervals. BRT also determines the importance of the conditioning factors in the modelling process. This is done by measuring the final (tree) performances associated to the use of the given covariate and then normalizing with respect to the highest contributor [49]. In this study, BRT was optimized employing caret and generalized boosted regression models scripts in the R statistical software, and caret and gbm packages [46,50,51]. Considering the above mentioned grid, the model runs on data and the accuracy index will be calculated as shown in Figure 6. Finally, the CARET (Classification and Regression Training) package selects the best combination of the three mentioned parameters in BRT, and this final model will be employed in the prediction step. The CARET is a package which provides different models and algorithms for classification and regression issues [46]. In this package, two indices of accuracy and Kappa are calculated for the training procedure and selection of the best parameters for the final model. Accuracy, and Cohen's Kappa index, can be computed as below [52]:
| Accuracy=TP+TNTP+TN+FP+FN | (3) |
| Kappa=Pobs−Pexp1−Pobs | (4) |
| Pobs=TP+TN/n | (5) |
| Pexp=(TP+FN)(TP+FP)+(FP+TN)(FN+TN)/√N | (6) |
where, n is a proportion of pixels from the total number of training pixels that is accurately categorized. FP denotes false positive, TP shows true positive, TN represents true negative, and FN denotes false negative.
In the modeling procedure, one of the most important steps to achieve scientific significance is validation process. In many studies, ROC curve has been used to assess the efficiency of the groundwater potential mapping [4,9,53]. This curve is known as a common index for predication of accuracy of the models in classification problems [54]. Area under the mentioned curve illustrates the capability of the method to foresee whether a phenomenon happens or not [55]. In this study, ROC and AUC values were plotted and calculated using SPSS 20. For calculating ROC, a dataset including validations spring locations and non-spring locations were used. For ROC analysis, proportion of the springs and non-springs need to be determined. The researchers are arguing about the best proportion of presence and absence to use for validation process which is called cutoff value [56]. A cutoff of 0.5 is used when springs and non-springs have the same number in the validation step [56]. Lombardo et al. [57] suggested a balance proportion, while Heckman et al. [58] suggested an imbalance proportion relating the cutoff to the data. In fact, the selection of the proportion between spring and non-spring cases extremely impacts any classification algorithm. Considering the literature review and suggestion of Lombardo et al. [57], a validation dataset consisting of 46 springs and 46 non-springs with the same size as other layers (i.e. 30 m) was selected. In BRT which determines the probability of spring occurrence, a value greater than 0.5 shows high potential of the groundwater, while in frequency ratio, a high value of FR shows higher potential of the groundwater. This needs to be mentioned that non spring locations were determined by Hawth's tools extension in ArcGIS 9.3 based on a random algorithm. The results of this curve are represented in Figure 4. Based on the results, BRT had AUC of ROC value of 87.2%, while it was seen that FR had AUC of ROC value of 83.2% which shows higher capability of the BRT model than FR in this research.
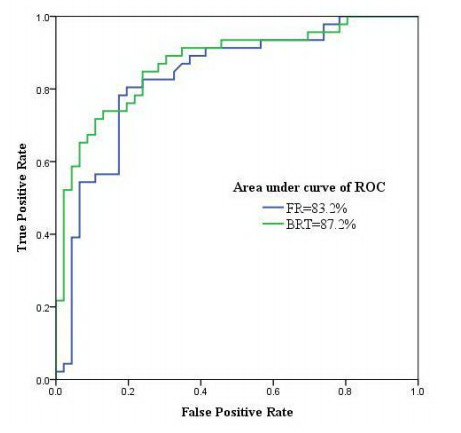 Figure 4. Receiver operating characteristics (ROC) curve and area under curve calculated for FR and BRT models; a higher area under curve shows better performance of the model
Figure 4. Receiver operating characteristics (ROC) curve and area under curve calculated for FR and BRT models; a higher area under curve shows better performance of the modelThe results of multicollinearity are presented in Table 2. According to the results, it can be seen that VIF values are less than 10 and tolerance values are greater than 0.1; thus, it can be evident that there is no multicollinearity problem in this study.
| GCFs | Collinearity statistics | |
| Tolerance | Variance inflation factor (VIF) | |
| Altitude | 0.517 | 1.934 |
| Slope aspect | 0.844 | 1.185 |
| Fault density | 0.326 | 3.063 |
| Distance from faults | 0.362 | 2.761 |
| Land use | 0.753 | 1.328 |
| Lithology | 0.705 | 1.418 |
| LS | 0.427 | 2.341 |
| Plan curvature | 0.609 | 1.641 |
| Profile curvature | 0.743 | 1.346 |
| River density | 0.453 | 2.209 |
| Distance from rivers | 0.452 | 2.213 |
| Slope angle | 0.356 | 2.811 |
| TWI | 0.392 | 2.552 |
Table 3 displays the result of the frequency ratio for different factors employed as input. A higher FR, in this case, shows higher probability of spring occurrence and groundwater potentiality [4,47]. Results implied that slope degree class (5-15) has a high FR value, slope aspect classes (east, and south) have the highest values, altitude class (1, 800-2, 200) has the highest values of 1.25, plan curvature class (concave) had the highest value of 1.34, profile curvature class ( < -0.001) showed the highest value of 1.45, slope length class ( > 60) have the highest value of 1.49, TWI class ( > 12) has the highest value of 2.64, distance from rivers class (100-200) has the highest value of 2.56, distance from faults class (250-500, and < 250) have the highest values of 1.68, and 1.67, respectively, river density class ( < 0.31) has the highest value of 1.59, fault density class (8.37-15.70) has the highest value of 1.31, land use class (rangeland) has the highest value 1.17, and lithology class (6 and 8) have the highest values of 11.45, and 6.11, respectively. Overall, the results of the FR model exhibit a relatively reverse relationship between spring occurrence and groundwater conditioning factors such as altitude and river density in the study area. Lower altitudes include lower slope areas with more developed drainage system which could be a reason for the observed reverse relationship between altitude and spring occurrence. In the respect of river density, higher river densities show higher concentration of the water flow and subsequently higher amount of infiltration. On the other hand, a direct relationship was seen between TWI and groundwater potentiality. TWI shows the water intent to gather at any point of the watershed, therefore a higher TWI could be referred to a higher amount of infiltration. The findings of this study also showed a reverse relationship between distance from faults and spring occurrence which could be the result of the influence of the faults on the fracture springs. In the GPM produced by FR, classes range and area percentage of each class are shown in Figure 5a and Table 5. According to Table 5, low, moderate, high, and very high classes cover 30.40, 19.44, 19.17, and 0.98 % of the study region, respectively.
| Conditioning factor and class | No. of Pixels | % of Pixels | No. of Springs | % of Springs | Frequency Ratio (FR) |
| Slope Degree | |||||
| 0-5 | 313126 | 22.22 | 23 | 21.10 | 0.95 |
| 5-15 | 536896 | 38.10 | 61 | 55.96 | 1.47 |
| 15-30 | 453814 | 32.20 | 21 | 19.27 | 0.60 |
| > 30 | 105306 | 7.47 | 4 | 3.67 | 0.49 |
| Slope aspect | |||||
| Flat | 772 | 0.05 | 0 | 0.00 | 0.00 |
| North | 223581 | 15.87 | 15 | 13.76 | 0.87 |
| Northeast | 226364 | 16.06 | 15 | 13.76 | 0.86 |
| East | 229760 | 16.30 | 24 | 22.02 | 1.35 |
| Southeast | 198182 | 14.06 | 15 | 13.76 | 0.98 |
| South | 144804 | 10.28 | 14 | 12.84 | 1.25 |
| Southwest | 92496 | 6.56 | 4 | 3.67 | 0.56 |
| West | 114300 | 8.11 | 7 | 6.42 | 0.79 |
| Northwest | 178883 | 12.69 | 15 | 13.76 | 1.08 |
| Altitude (m) | |||||
| < 1400 | 110085 | 7.81 | 1 | 0.92 | 0.12 |
| 1400-1800 | 709457 | 50.35 | 60 | 55.05 | 1.09 |
| 1800-2200 | 354494 | 25.16 | 34 | 31.19 | 1.24 |
| 2200-2400 | 182685 | 12.96 | 11 | 10.09 | 0.78 |
| > 2400 | 52421 | 3.72 | 3 | 2.75 | 0.74 |
| Plan curvature (100/m) | |||||
| Concave | 451969 | 32.07 | 47 | 43.12 | 1.34 |
| Flat | 542376 | 38.49 | 48 | 44.04 | 1.14 |
| Convex | 414797 | 29.44 | 14 | 12.84 | 0.44 |
| Profile curvature (100\m) | |||||
| < (-0.001) | 639818 | 45.40 | 72 | 66.06 | 1.45 |
| (-0.001)-(-0.001) | 203673 | 14.45 | 15 | 13.76 | 0.95 |
| > (0.001) | 565651 | 40.14 | 22 | 20.18 | 0.50 |
| Slope length (LS) (m) | |||||
| 0-20 | 537886 | 38.17 | 26 | 23.85 | 0.62 |
| 20-40 | 266643 | 18.92 | 23 | 21.10 | 1.12 |
| 40-60 | 188324 | 13.36 | 12 | 11.01 | 0.82 |
| > 60 | 416289 | 29.54 | 48 | 44.04 | 1.49 |
| Topographic wetness index (TWI) | |||||
| < 8 | 71347 | 5.06 | 2 | 1.83 | 0.36 |
| 8_12 | 1137227 | 80.70 | 66 | 60.55 | 0.75 |
| > 12 | 200568 | 14.23 | 41 | 37.61 | 2.64 |
| Distance from rivers (m) | |||||
| < 100 | 76011 | 5.39 | 10 | 9.17 | 1.70 |
| 100-200 | 65759 | 4.67 | 13 | 11.93 | 2.56 |
| 200-300 | 72512 | 5.15 | 9 | 8.26 | 1.60 |
| 300-400 | 62611 | 4.44 | 3 | 2.75 | 0.62 |
| > 400 | 1132249 | 80.35 | 74 | 67.89 | 0.84 |
| Distance from faults (m) | |||||
| < 250 | 94430 | 6.70 | 12 | 11.01 | 1.64 |
| 250-500 | 92160 | 6.54 | 12 | 11.01 | 1.68 |
| 500-750 | 90281 | 6.41 | 3 | 2.75 | 0.43 |
| 75-1000 | 90736 | 6.44 | 2 | 1.83 | 0.28 |
| > 1000 | 1041535 | 73.91 | 80 | 73.39 | 0.99 |
| River density (Km/Km 2) | |||||
| < 0.31 | 300817 | 21.35 | 37 | 33.94 | 1.59 |
| 0.31-0.78 | 466377 | 33.10 | 39 | 35.78 | 1.08 |
| 0.78-1.27 | 438029 | 31.08 | 22 | 20.18 | 0.65 |
| 1.27-2.51 | 203919 | 14.47 | 11 | 10.09 | 0.70 |
| Fault density (Km/Km 2) | |||||
| < 2.72 | 377803 | 26.81 | 29 | 26.61 | 0.99 |
| 2.72-8.37 | 639444 | 45.38 | 44 | 40.37 | 0.89 |
| 8.37-15.70 | 216981 | 15.40 | 22 | 20.18 | 1.31 |
| 15.70-26.80 | 174914 | 12.41 | 14 | 12.84 | 1.03 |
| Land use | |||||
| Agriculture | 91627 | 6.50 | 0 | 0.00 | 0.00 |
| Orchard | 325287 | 23.08 | 19 | 17.43 | 0.76 |
| Rangeland | 990485 | 70.29 | 90 | 82.57 | 1.17 |
| Residential area | 1743 | 0.12 | 0 | 0.00 | 0.00 |
| Lithology | |||||
| Group1 | 451 | 0.03 | 0 | 0.00 | 0.00 |
| Group2 | 1058 | 0.08 | 0 | 0.00 | 0.00 |
| Group3 | 132749 | 9.42 | 2 | 1.83 | 0.19 |
| Group4 | 32272 | 2.29 | 1 | 0.92 | 0.40 |
| Group5 | 16504 | 1.17 | 0 | 0.00 | 0.00 |
| Group6 | 10164 | 0.72 | 9 | 8.26 | 11.45 |
| Group7 | 6740 | 0.48 | 0 | 0.00 | 0.00 |
| Group8 | 12703 | 0.90 | 6 | 5.50 | 6.11 |
| Group9 | 72799 | 5.17 | 11 | 10.09 | 1.95 |
| Group10 | 64056 | 4.55 | 8 | 7.34 | 1.61 |
| Group11 | 43328 | 3.07 | 1 | 0.92 | 0.30 |
| Group12 | 846210 | 60.05 | 65 | 59.63 | 0.99 |
| Group13 | 170108 | 12.07 | 6 | 5.50 | 0.46 |
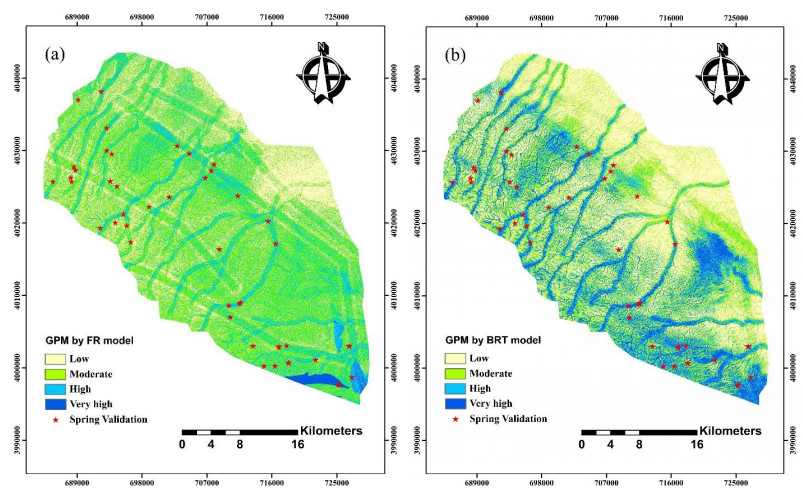 Figure 5. GPMs produced by (a) FR and (b) BRT models classified into four classes of low, moderate, high, and very high, and distribution of the validation springs in different classes
Figure 5. GPMs produced by (a) FR and (b) BRT models classified into four classes of low, moderate, high, and very high, and distribution of the validation springs in different classesThe results of the BRT model showed that the final BRT model included number of trees (Boosting iterations) of 500, interaction depth of 5, and shrinkage of 0.005 (Figure 6). The final BRT model had accuracy and kappa values of 0.73, and 0.47, respectively. In addition, the importance of the conditioning factors was determined using BRT model (Table 4). The results of BRT model showed that TWI, and altitude were the most important factors, while aspect and plan curvature had the lowest importance in groundwater potential modelling. Also, it was seen that lithology had not any effect on the modelling process in the current study. Figure 5b shows the final GPM produced by BRT model indicating that low, moderate, high, and very high classes cover 36.83, 29.57, 19.79, and 13.81 % of the study region, respectively (Table 5).
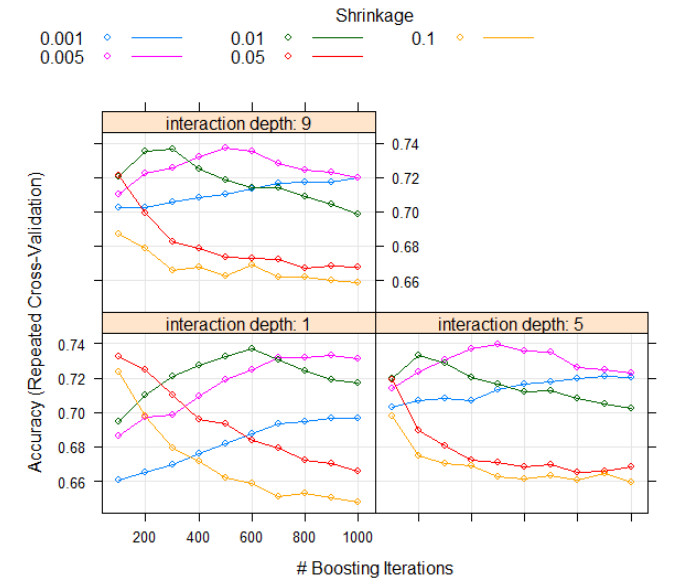 Figure 6. The results of the BRT model training for selecting its best parameters of shrinkage, interaction depth, and boosting iterations for applying the final model
Figure 6. The results of the BRT model training for selecting its best parameters of shrinkage, interaction depth, and boosting iterations for applying the final model| Factor | Importance |
| TWI | 100 |
| Altitude | 89.65 |
| Distance from rivers | 48.70 |
| Rivers density | 28.85 |
| Distance from faults | 18.21 |
| Faults density | 16.11 |
| Slope degree | 12.57 |
| Profile curvature | 11.70 |
| LS | 9.61 |
| Land use | 7.51 |
| Plan curvature | 5.19 |
| Aspect | 1.16 |
| Lithology | 0 |
| Class/Model | FR | BRT | ||
| Range | Area (%) | Range | Area (%) | |
| Low | 6.72-12.02 | 30.40 | 0-0.25 | 36.83 |
| Moderate | 12.02-14.18 | 19.44 | 0.25-0.43 | 29.57 |
| High | 14.18-19.30 | 19.17 | 0.43-0.64 | 19.79 |
| Very high | 19.30-29.73 | 0.98 | > 0.64 | 13.81 |
The findings of this study suggest that BRT and FR methods are appropriate tools for groundwater assessment. BRT had better performance than FR model, but their AUC of ROC values were both more than 80% which shows their acceptable performance in groundwater potential mapping. The BRT as a model that uses regression and gradient boosting algorithms [59] have some advantages and disadvantages. BRT is capable to select the conditioning factors, it can identify the interactions, and it is capable to fit an accurate function for classification [47]. In addition, one point which makes the BRT models robust is that it can remove predictor variable which have large number of missing values [60]. However, there are some disadvantage in the BRT model. For example, interpretation of the BRT model is difficult, and computation of the model can take a long time [60]. The results of the FR model showed that there is a relatively reverse relationship between spring occurrence and groundwater conditioning factors such as altitude and river density in the study area. On the other hand, a direct relationship was seen between TWI and groundwater potentiality. Moreover, this research attempted to define the importance of different groundwater conditioning factors in groundwater modelling. According to the results of this study, TWI was the most important factor, followed by altitude, and distance from rivers. On the other hand, aspect, and plan curvature were seen to be the least important factors. In addition, the results showed that lithology had not any effect on groundwater modelling using the BRT model. Naghibi and Pourghasemi [12] reported that altitude, distance from faults, SPI, and fault density represented the highest contribution to groundwater potential assessment. In another research, Naghibi et al [17] stated that altitude, slope, plan curvature, and profile curvature were the most important influencing factors. Comparing the results of the current research and the two above mentioned studies, it can be seen that only altitude was seen as an important factor, while other factors have different ranks and importance in different studies. This fact can be related to different hydro-geological, climatic, and topographical features of the watersheds. Furthermore, different algorithms and techniques employed in the implemented models could lead to these variations.
In order to obtain the objectives of this study, at first, a dataset of spring locations and groundwater conditioning factors was provided. Springs were classified into two groups of training and validation and groundwater conditioning factors are slope degree, slope aspect, altitude, plan curvature, profile curvature, slope length, topographic wetness index, distance from river, distance from fault, river density, fault density, land use, and lithology. Utilizing the training springs and groundwater conditioning factors, BRT and FR models were applied and GPMs were produced. At last, ROC and AUC were employed to appraise the capability of the methods in groundwater modelling. The results of this research showed that BRT and FR models are good tools for groundwater assessment. BRT had better performance than FR model, but their AUC of ROC values were both more than 80% which shows their acceptable performance. The results also showed that TWI was the most important factor, followed by altitude, and distance from rivers, while aspect, and plan curvature factors were seen to be the least important factors. In addition, the results showed that lithology had not any effect on groundwater modelling using the BRT model. The methodology produced in this study could be used for groundwater exploitation plans to decrease the costs and time needed for these projects in watersheds having similar conditions.
All authors declare no conflicts of interest in this paper.
| [1] | Altenburger R, Ait-Aissa S, Antczak P, et al. (2015) Future water quality monitoring—adapting tools to deal with mixtures of pollutants in water resource management. Sci Total Environ 512: 540-551. |
| [2] | Chezgi J, Pourghasemi HR, Naghibi SA, et al. (2015) Assessment of a spatial multi-criteria evaluation to site selection underground dams in the Alborz Province, Iran. Geocarto Int 31: 628-646. |
| [3] | Oh HJ, Kim YS, Choi JK, et al. (2011) GIS mapping of regional probabilistic groundwater potential in the area of Pohang City, Korea. J Hydrol 399: 158-172. |
| [4] | Nampak H, Pradhan B, Manap MA (2014) Application of GIS based data driven evidential belief function model to predict groundwater potential zonation. J Hydrol 513: 283-300. |
| [5] | Tweed SO, Leblanc M, Webb JA, et al. (2007) Remote sensing and GIS for mapping groundwater recharge and discharge areas in salinity prone catchments, southeastern Australia. Hydrogeol J 15: 75-96. |
| [6] | Ozdemir A (2011a) Using a binary logistic regression method and GIS for evaluating and mapping the groundwater spring potential in the Sultan Mountains (Aksehir, Turkey). J Hydrol 405: 123-136. |
| [7] | Ozdemir A (2011b) GIS-based groundwater spring potential mapping in the Sultan Mountains (Konya, Turkey) using frequency ratio, weights of evidence and logistic regression methods and their comparison. J Hydrol 411: 290-308. |
| [8] | Manap MA, Nampak H, Pradhan B, et al. (2014) Application of probabilistic-based frequency ratio model in groundwater potential mapping using remote sensing data and GIS. Arabian J Geosci 7: 711-724. |
| [9] | Pourtaghi ZS and Pourghasemi HR (2014) GIS-based groundwater spring potential assessment and mapping in the Birjand Township, southern Khorasan Province, Iran. Hydrogeology J 22:643-662. |
| [10] | Naghibi SA, Pourghasemi HR, Pourtaghi ZS, et al. (2015) Groundwater qanat potential mapping using frequency ratio and Shannon's entropy models in the Moghan watershed, Iran. Earth Sci Inform 8: 171-186. |
| [11] | Pourghasemi HR, Beheshtirad M (2015) Assessment of a data-driven evidential belief function model and GIS for groundwater potential mapping in the Koohrang Watershed, Iran. Geocarto Int 30: 662-685. |
| [12] | Naghibi SA, Pourghasemi HR (2015) A comparative assessment between three machine learning models and their performance comparison by bivariate and multivariate statistical methods in groundwater potential mapping. Water Res Manage 29: 5217-5236. |
| [13] | Al-Abadi A, M Pradhan B, Shahid S (2015) Prediction of groundwater flowing well zone at An-Najif Province, central Iraq using evidential belief functions model and GIS. Environ Monit Assess 188:549. |
| [14] | Naghibi SA, Pourghasemi HR, Dixon B (2016) GIS-based groundwater potential mapping using boosted regression tree, classification and regression tree, and random forest machine learning models in Iran. Environ Monit Assess 188: 1-27. |
| [15] | Naghibi S A, Dashtpagerdi MM (2016) Evaluation of four supervised learning methods for groundwater spring potential mapping in Khalkhal region (Iran) using GIS-based features. Hydrogeol J 1-21. |
| [16] | Zabihi M, Pourghasemi, HR, Pourtaghi ZS, et al. (2016) GIS-based multivariate adaptive regression spline and random forest models for groundwater potential mapping in Iran. Environ Earth Sci 75: 1-19. |
| [17] | Naghibi SA, Pourghasemi HR. , Abbaspour K (2017). A comparison between ten advanced and soft computing models for groundwater qanat potential assessment in Iran using R and GIS. Theoretical and Applied Climatology. |
| [18] | Mennis J and Guo D (2009) Spatial data mining and geographic knowledge discovery—an introduction. Comput Environ Urban Syst 33:403-408. |
| [19] | Tien Bui D, Le K-T, Nguyen V (2016a) Tropical forest fire susceptibility mapping at the Cat Ba National Park Area, Hai Phong City, Vietnam, using GIS-based Kernel logistic regression. Remote Sens 8: 347. |
| [20] | Pacheco, Fernando, Ana Alencoão (2002) "Occurrence of springs in massifs of crystalline rocks, northern Portugal." Hydrogeol J 10.2: 239-253. |
| [21] | Pacheco FAL and Vander Weijden CH (2014). Modeling rock weathering in small watersheds. J Hydrol 513C 13-27. |
| [22] | Iranian Department of Water Resources Management (2014) weather and climate report, Tehran province. Available from: http://www.thrw.ir/. |
| [23] | Dehnavi A, Aghdam IN, Pradhan B, et al. (2015) A new hybrid model using step-wise weight assessment ratio analysis (SWARA) technique and adaptive neuro-fuzzy inference system (ANFIS) for regional landslide hazard assessment in Iran. Catena 135: 122-148. |
| [24] | Conforti M, Pascale S, Robustelli G, et al. (2014) Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the Turbolo River catchment (northern Calabria, Italy). Catena 113: 236-250. |
| [25] | Oh H-J and Pradhan B (2011) Application of a neuro-fuzzy model to landslide-susceptibility mapping for shallow landslides in a tropical hilly area. Comput Geosci 37: 1264-1276. |
| [26] | Wilson JP and Gallant JG (2000) Terrain Analysis Principles and Applications. John Wiley and Sons, Inc. , New-York, 479. |
| [27] | Moore ID and Burch GJ (1986) Sediment Transport Capacity of Sheet and Rill Flow: Application of Unit Stream Power Theory. Water Resour Res 22: 1350-1360. |
| [28] | Pourghasemi H, Pradhan B, Gokceoglu C, et al. (2013) A comparative assessment of prediction capabilities of Dempster-Shafer and weights-of-evidence models in landslide susceptibility mapping using GIS. Geomatics Nat Hazards Risk 4: 93-118. |
| [29] | Moore ID, Grayson RB, Ladson AR (1991) Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol Process 5: 3-30. |
| [30] | Ayalew L and Yamagishi H (2005) The application of GIS-based logistic regression for land-slide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphol 65: 15-31. |
| [31] | Pradhan B, Abokharima MH, Jebur MN, et al. (2014) Land subsidence susceptibility mapping at Kinta Valley (Malaysia) using the evidential belief function model in GIS. Nat Hazards. |
| [32] | Iranian forest, rangeland and watershed management organization. 2014. Available from: http://www.frw.org.ir/00/En/default.aspx. |
| [33] | Geology Survey of Iran (GSI) (1997) Geology map of the Chaharmahal-e-Bakhtiari Province. http://www.gsi.ir/Main/Lang_en/index.html.AccessedSeptember2000. |
| [34] | Dormann CF, Elith J, Bacher S, et al. (2013) Collinearity: a review of methods to deal with it and a simula-tion study evaluating their performance. Ecogr 36: 27-46 |
| [35] | Hair JF, Black WC, Babin BJ, et al. (2009) Multivariate data analysis. Prentice Hall, New York. |
| [36] | Keith TZ (2006) Multiple regressions and beyond. Pearson, Boston |
| [37] | Lee S and Talib JA (2005) Probabilistic landslide susceptibility and factor effect analysis. Environ Geol 47: 982-990 |
| [38] | Yilmaz I (2007) GIS based susceptibility mapping of karst depression in gypsum: a case study from Sivas basin (Turkey). Eng Geol 90: 89-103 |
| [39] | Bonham-Carter G (1994) Geographic information systems for geoscientists modelling with GIS. Pergamon. |
| [40] | Lee S and Pradhan B (2006) Probabilistic landslide hazards and riskmapping on Penang Island, Malaysia. Earth Sys Sci 115: 661-667 |
| [41] | Lombardo L, Cama M, Conoscenti C, et al. (2015) Binary logistic regression versus stochastic gradient boosted decision trees in assessing landslide susceptibility for multiple-occurring landslide events: application to the 2009 storm event in Messina (Sicily, southern Italy). Nat Hazards 79: 1621-1648. |
| [42] | Abeare SM (2009) Comparisons of boosted regression tree, glm and gam performance in the standardization of yellowfin tuna catch-rate data from the gulf of mexico lonline fishery. |
| [43] | Friedman J (2001) Greedy boosting approximation: a gradient boosting machine. Ann Stat 29: 1189-1232. |
| [44] | Schapire RE (2003) The boosting approach to machine learning: an overview. Nonlinear Est Class 171: 149-171. |
| [45] | Sutton CD (2005) 11-Classification and Regression Trees, Bagging, and Boosting. Handbook of statistics 24: 303-329 |
| [46] | Kuhn M, Wing J, Weston S, et al. (2015) Package "caret". Available from: http://caret.r-forge.r-project.org. |
| [47] | Elith J, Leathwick JR, Hastie T (2008) A working guide to boosted regression trees. J Animal Ecol 77: 802-813 |
| [48] | Leathwick JR, Elith J, Francis MP, et al. (2006). Variation in demersal fish species richness in the oceans surrounding New Zealand: An analysis using boosted regression trees. Mar Ecol Prog Ser 321: 267-281. |
| [49] | Schillaci C, Lombardo L, Saia S, et al. (2017) Modelling the topsoil carbon stock of agricultural lands with the Stochastic Gradient Treeboost in a semi-arid Mediterranean region. Geoderma 286: 35-45. |
| [50] | R Development Core Team (2006) R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0. Available from: http://www.R-project.org |
| [51] | Ridgeway G (2015) Package "gbm. " |
| [52] | Guzzetti F, Reichenbach P, Ardizzone F, et al. (2006) Estimating the quality of landslide susceptibility models. Geomorphol 81: 166-184 |
| [53] | Umar Z, Pradhan B, Ahmad A, et al. (2014) Earthquake induced landslide susceptibility mapping using an integrated ensemble frequency ratio and logistic regression models in West Sumatera Province, Indonesia. Catena 118: 124-135 |
| [54] | Swets JA (1988) Measuring the accuracy of diagnostic systems. Sci 240: 1285-1293 |
| [55] | Negnevitsky M (2005) Artificial Intelligence: a guide to intelligent systems. Inf & Comput Sci 48: 284-300. |
| [56] | Frattini P, Crosta G, Carrara A (2010). Techniques for evaluating the performance of landslide susceptibility models. Eng Geol 111: 62-72. |
| [57] | Lombardo L, Cama M, Maerker M., et al. (2014). A test of transferability for landslides susceptibility models under extreme climatic events: Application to the Messina 2009 disaster. Natural Hazards 74: 1951-1989. |
| [58] | Heckman T, Gegg K, Gegg A, et al. (2014) Sample size matters: investigating the effect of sample size on a logistic regression susceptibility model for debris flow. Nat. Hazards Earth Syst. Sci 14: 259-278. |
| [59] | Youssef AM, Pourghasemi HR, Pourtaghi ZS, et al. (2015) Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 1-18 |
| [60] | Carty DM (2011) An analysis of boosted regression trees to predict the strength properties of wood composites. Arch Oral Biol 60: 45-54. |
| 1. | Bahareh Kalantar, Biswajeet Pradhan, Seyed Amir Naghibi, Alireza Motevalli, Shattri Mansor, Assessment of the effects of training data selection on the landslide susceptibility mapping: a comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN), 2018, 9, 1947-5705, 49, 10.1080/19475705.2017.1407368 | |
| 2. | Alireza Arabameri, Wei Chen, Thomas Blaschke, John P. Tiefenbacher, Biswajeet Pradhan, Dieu Tien Bui, Gully Head-Cut Distribution Modeling Using Machine Learning Methods—A Case Study of N.W. Iran, 2019, 12, 2073-4441, 16, 10.3390/w12010016 | |
| 3. | Jeong-Cheol Kim, Hyung-Sup Jung, Saro Lee, Spatial Mapping of the Groundwater Potential of the Geum River Basin Using Ensemble Models Based on Remote Sensing Images, 2019, 11, 2072-4292, 2285, 10.3390/rs11192285 | |
| 4. | Phong Tung Nguyen, Duong Hai Ha, Mohammadtaghi Avand, Abolfazl Jaafari, Huu Duy Nguyen, Nadhir Al-Ansari, Tran Van Phong, Rohit Sharma, Raghvendra Kumar, Hiep Van Le, Lanh Si Ho, Indra Prakash, Binh Thai Pham, Soft Computing Ensemble Models Based on Logistic Regression for Groundwater Potential Mapping, 2020, 10, 2076-3417, 2469, 10.3390/app10072469 | |
| 5. | Sunmin Lee, Yunjung Hyun, Moung-Jin Lee, Groundwater Potential Mapping Using Data Mining Models of Big Data Analysis in Goyang-si, South Korea, 2019, 11, 2071-1050, 1678, 10.3390/su11061678 | |
| 6. | Jalal Shiri, Mohammad Zounemat‐Kermani, Ozgur Kisi, Sahar Mohsenzadeh Karimi, Comprehensive assessment of 12 soft computing approaches for modelling reference evapotranspiration in humid locations, 2020, 27, 1350-4827, 10.1002/met.1841 | |
| 7. | Ali Imanian, Vahideh Sheykhi, Kamran Zare, Mohammad Zare, Introducing the recharge–discharge relationship to evaluate the recharge coefficient of karstic aquifers: thematic and indexing approaches, 2020, 65, 0262-6667, 1385, 10.1080/02626667.2020.1739288 | |
| 8. | Mohsen Zabihi, Hamid Reza Pourghasemi, Alireza Motevalli, Mohamad Ali Zakeri, 2019, Chapter 1, 978-3-319-73382-1, 1, 10.1007/978-3-319-73383-8_1 | |
| 9. | Alireza Motevalli, Seyed Amir Naghibi, Hossein Hashemi, Ronny Berndtsson, Biswajeet Pradhan, Vahid Gholami, Inverse method using boosted regression tree and k-nearest neighbor to quantify effects of point and non-point source nitrate pollution in groundwater, 2019, 228, 09596526, 1248, 10.1016/j.jclepro.2019.04.293 | |
| 10. | Soumya S. Singha, Srinivas Pasupuleti, Sudhakar Singha, Rambabu Singh, A. S. Venkatesh, Analytic network process based approach for delineation of groundwater potential zones in Korba district, Central India using remote sensing and GIS, 2019, 1010-6049, 1, 10.1080/10106049.2019.1648566 | |
| 11. | Davoud Davoudi Moghaddam, Omid Rahmati, Mahdi Panahi, John Tiefenbacher, Hamid Darabi, Ali Haghizadeh, Ali Torabi Haghighi, Omid Asadi Nalivan, Dieu Tien Bui, The effect of sample size on different machine learning models for groundwater potential mapping in mountain bedrock aquifers, 2020, 187, 03418162, 104421, 10.1016/j.catena.2019.104421 | |
| 12. | Saro Lee, Chang-Wook Lee, Jeong-Cheon Kim, 2019, Chapter 69, 978-3-030-01439-1, 305, 10.1007/978-3-030-01440-7_69 | |
| 13. | Bahareh Kalantar, Naonori Ueda, Husam Abdulrasool Hammadeh Al-Najjar, Alfian Abdul Halin, Parisa Ahmadi, Mohamed Barakat A. Gibril , Karsten Schulz, Konstantinos G. Nikolakopoulos, Ulrich Michel, 2019, On the effects of different groundwater inventory scenarios for spring potential mapping in Haraz, northern Iran, 9781510630154, 38, 10.1117/12.2532685 | |
| 14. | Seyed Amir Naghibi, Hossein Hashemi, Ronny Berndtsson, Saro Lee, Application of extreme gradient boosting and parallel random forest algorithms for assessing groundwater spring potential using DEM-derived factors, 2020, 589, 00221694, 125197, 10.1016/j.jhydrol.2020.125197 | |
| 15. | Seyed Vahid Razavi-Termeh, Abolghasem Sadeghi-Niaraki, Soo-Mi Choi, Gully erosion susceptibility mapping using artificial intelligence and statistical models, 2020, 11, 1947-5705, 821, 10.1080/19475705.2020.1753824 | |
| 16. | A’kif Al-Fugara, Hamid Reza Pourghasemi, Abdel Rahman Al-Shabeeb, Maan Habib, Rida Al-Adamat, Hani Al-Amoush, Adrian L. Collins, A comparison of machine learning models for the mapping of groundwater spring potential, 2020, 79, 1866-6280, 10.1007/s12665-020-08944-1 | |
| 17. | Alaa M. Al-Abadi, Jassim J. Alsamaani, Spatial analysis of groundwater flowing artesian condition using machine learning techniques, 2020, 11, 2352801X, 100418, 10.1016/j.gsd.2020.100418 | |
| 18. | Ehsan Kamali Maskooni, Seyed Amir Naghibi, Hossein Hashemi, Ronny Berndtsson, Application of Advanced Machine Learning Algorithms to Assess Groundwater Potential Using Remote Sensing-Derived Data, 2020, 12, 2072-4292, 2742, 10.3390/rs12172742 | |
| 19. | Ionut Cristi Nicu, Andrei Asăndulesei, GIS-based evaluation of diagnostic areas in landslide susceptibility analysis of Bahluieț River Basin (Moldavian Plateau, NE Romania). Are Neolithic sites in danger?, 2018, 314, 0169555X, 27, 10.1016/j.geomorph.2018.04.010 | |
| 20. | Seyed Amir Naghibi, Mojtaba Dolatkordestani, Ashkan Rezaei, Payam Amouzegari, Mostafa Taheri Heravi, Bahareh Kalantar, Biswajeet Pradhan, Application of rotation forest with decision trees as base classifier and a novel ensemble model in spatial modeling of groundwater potential, 2019, 191, 0167-6369, 10.1007/s10661-019-7362-y | |
| 21. | Seyed Naghibi, Mehdi Vafakhah, Hossein Hashemi, Biswajeet Pradhan, Seyed Alavi, Groundwater Augmentation through the Site Selection of Floodwater Spreading Using a Data Mining Approach (Case study: Mashhad Plain, Iran), 2018, 10, 2073-4441, 1405, 10.3390/w10101405 | |
| 22. | Ali Golkarian, Seyed Amir Naghibi, Bahareh Kalantar, Biswajeet Pradhan, Groundwater potential mapping using C5.0, random forest, and multivariate adaptive regression spline models in GIS, 2018, 190, 0167-6369, 10.1007/s10661-018-6507-8 | |
| 23. | Jeong-Cheol Kim, Hyung-Sup Jung, Saro Lee, Groundwater productivity potential mapping using frequency ratio and evidential belief function and artificial neural network models: focus on topographic factors, 2018, 20, 1464-7141, 1436, 10.2166/hydro.2018.120 | |
| 24. | Sajjad Mirzaei, Mehdi Vafakhah, Biswajeet Pradhan, Seyed Jalil Alavi, Flood susceptibility assessment using extreme gradient boosting (EGB), Iran, 2021, 14, 1865-0473, 51, 10.1007/s12145-020-00530-0 | |
| 25. | Optimized Conditioning Factors Using Machine Learning Techniques for Groundwater Potential Mapping, 2019, 11, 2073-4441, 1909, 10.3390/w11091909 | |
| 26. | Mojtaba Dolat Kordestani, Seyed Amir Naghibi, Hossein Hashemi, Kourosh Ahmadi, Bahareh Kalantar, Biswajeet Pradhan, Groundwater potential mapping using a novel data-mining ensemble model, 2019, 27, 1431-2174, 211, 10.1007/s10040-018-1848-5 | |
| 27. | Abdelmadjid Boufekane, Hind Meddi, Mohamed Meddi, Delineation of groundwater recharge zones in the Mitidja plain, north Algeria, using multi-criteria analysis, 2020, 22, 1464-7141, 1468, 10.2166/hydro.2020.082 | |
| 28. | Swades Pal, Sonali Kundu, Susanta Mahato, Groundwater potential zones for sustainable management plans in a river basin of India and Bangladesh, 2020, 257, 09596526, 120311, 10.1016/j.jclepro.2020.120311 | |
| 29. | Bhumika Thapa, Ramesh Raj Pant, Sudeep Thakuri, Gregory Pond, Assessment of spring water quality in Jhimruk River Watershed, Lesser Himalaya, Nepal, 2020, 79, 1866-6280, 10.1007/s12665-020-09252-4 | |
| 30. | Javed Mallick, Swapan Talukdar, Majed Alsubih, Mohd. Ahmed, Abu Reza Md Towfiqul Islam, Nguyen Viet Thanh, Proposing receiver operating characteristic-based sensitivity analysis with introducing swarm optimized ensemble learning algorithms for groundwater potentiality modelling in Asir region, Saudi Arabia, 2021, 1010-6049, 1, 10.1080/10106049.2021.1878291 | |
| 31. | Seyed Amir Naghibi, Mehdi Vafakhah, Hossein Hashemi, Biswajeet Pradhan, Seyed Jalil Alavi, Water Resources Management Through Flood Spreading Project Suitability Mapping Using Frequency Ratio, k-nearest Neighbours, and Random Forest Algorithms, 2020, 29, 1520-7439, 1915, 10.1007/s11053-019-09530-4 | |
| 32. | Ishaku Bashir, Rachel Sallau, Abubakar Sheikh, Zuni Aminu, Shu’aib Hassan, GIS-based MCDA for Gully Vulnerability Mapping Using AHP Techniques, 2020, 4, 2582-1083, 45, 10.21523/gcj5.20040201 | |
| 33. | Alireza Arabameri, Saro Lee, John P. Tiefenbacher, Phuong Thao Thi Ngo, Novel Ensemble of MCDM-Artificial Intelligence Techniques for Groundwater-Potential Mapping in Arid and Semi-Arid Regions (Iran), 2020, 12, 2072-4292, 490, 10.3390/rs12030490 | |
| 34. | A'kif Al-Fugara, Mohammad Ahmadlou, Rania Shatnawi, Saad AlAyyash, Rida Al-Adamat, Abdel Al-Rahman Al-Shabeeb, Sangeeta Soni, Novel hybrid models combining meta-heuristic algorithms with support vector regression (SVR) for groundwater potential mapping, 2020, 1010-6049, 1, 10.1080/10106049.2020.1831622 | |
| 35. | Aliasghar Azma, Esmaeil Narreie, Abouzar Shojaaddini, Nima Kianfar, Ramin Kiyanfar, Seyed Mehdi Seyed Alizadeh, Afshin Davarpanah, Statistical Modeling for Spatial Groundwater Potential Map Based on GIS Technique, 2021, 13, 2071-1050, 3788, 10.3390/su13073788 | |
| 36. | Yunzhi Chen, Wei Chen, Subodh Chandra Pal, Asish Saha, Indrajit Chowdhuri, Behzad Adeli, Saeid Janizadeh, Adrienn A. Dineva, Xiaojing Wang, Amirhosein Mosavi, Evaluation Efficiency of Hybrid Deep Learning algorithms with Neural Network, Decision Tree and Boosting Methods for Predicting Groundwater Potential, 2021, 1010-6049, 1, 10.1080/10106049.2021.1920635 | |
| 37. | Nguyen Ngoc Thanh, Pongsathron Thunyawatcharakul, Nguyen Huu Ngu, Srilert Chotpantarat, Global review of groundwater potential models in the last decade: Parameters, model techniques, and validation, 2022, 614, 00221694, 128501, 10.1016/j.jhydrol.2022.128501 | |
| 38. | Javed Mallick, Swapan Talukdar, Majed Alsubih, Mohammed K. Almesfer, Hoang Thi Hang, Atiqur Rahman, Integration of statistical models and ensemble machine learning algorithms (MLAs) for developing the novel hybrid groundwater potentiality models: a case study of semi-arid watershed in Saudi Arabia, 2022, 37, 1010-6049, 6442, 10.1080/10106049.2021.1939439 | |
| 39. | Michael Makonyo, Michael M. Msabi, Identification of groundwater potential recharge zones using GIS-based multi-criteria decision analysis: A case study of semi-arid midlands Manyara fractured aquifer, North-Eastern Tanzania, 2021, 23, 23529385, 100544, 10.1016/j.rsase.2021.100544 | |
| 40. | Biman Ghosh, Spatial mapping of groundwater potential using data-driven evidential belief function, knowledge-based analytic hierarchy process and an ensemble approach, 2021, 80, 1866-6280, 10.1007/s12665-021-09921-y | |
| 41. | Chandrashekhar Azad Vishwakarma, Vikas Rena, Deepali Singh, Saumitra Mukherjee, 2021, 9781119709732, 364, 10.1002/9781119709732.ch18 | |
| 42. | Karikkathil C. Arun Kumar, Gangalakunta P. Obi Reddy, Palanisamy Masilamani, Pundoor Sandeep, Spatial modelling for identification of groundwater potential zones in semi-arid ecosystem of southern India using Sentinel-2 data, GIS and bivariate statistical models, 2021, 14, 1866-7511, 10.1007/s12517-021-07669-0 | |
| 43. | Javed Mallick, Swapan Talukdar, Nabil Ben Kahla, Mohd. Ahmed, Majed Alsubih, Mohammed K. Almesfer, Abu Reza Md. Towfiqul Islam, A Novel Hybrid Model for Developing Groundwater Potentiality Model Using High Resolution Digital Elevation Model (DEM) Derived Factors, 2021, 13, 2073-4441, 2632, 10.3390/w13192632 | |
| 44. | Hamid Darabi, Omid Rahmati, Seyed Amir Naghibi, Farnoush Mohammadi, Ebrahim Ahmadisharaf, Zahra Kalantari, Ali Torabi Haghighi, Seyed Masoud Soleimanpour, John P. Tiefenbacher, Dieu Tien Bui, Development of a novel hybrid multi-boosting neural network model for spatial prediction of urban flood, 2022, 37, 1010-6049, 5716, 10.1080/10106049.2021.1920629 | |
| 45. | Raju Das, Sunil Saha, Spatial mapping of groundwater potentiality applying ensemble of computational intelligence and machine learning approaches, 2022, 18, 2352801X, 100778, 10.1016/j.gsd.2022.100778 | |
| 46. | Massinissa Braham, Abdelmadjid Boufekane, Hamid Bourenane, Baya Nait Amara, Rabah Bensalem, El Hadi Oubaiche, Youcef Bouhadad, Identification of groundwater potential zones using remote sensing, GIS, machine learning and electrical resistivity tomography techniques in Guelma basin, northeastern Algeria, 2022, 37, 1010-6049, 12042, 10.1080/10106049.2022.2063408 | |
| 47. | Javed Mallick, Swapan Talukdar, Mohd. Ahmed, Combining high resolution input and stacking ensemble machine learning algorithms for developing robust groundwater potentiality models in Bisha watershed, Saudi Arabia, 2022, 12, 2190-5487, 10.1007/s13201-022-01599-2 | |
| 48. | Mohammadtaghi Avand, Maziar Mohammadi, Fahimeh Mirchooli, Ataollah Kavian, John P. Tiefenbacher, A New Approach for Smart Soil Erosion Modeling: Integration of Empirical and Machine-Learning Models, 2023, 28, 1420-2026, 145, 10.1007/s10666-022-09858-x | |
| 49. | Alireza Arabameri, M. Santosh, Hossein Moayedi, John P. Tiefenbacher, Subodh Chandra Pal, Omid Asadi Nalivan, Romulus Costache, Naser Ahmed, Muhammad Al-Amin Hoque, Rabin Chakrabortty, Artemi Cerda, Application of the novel state-of-the-art soft computing techniques for groundwater potential assessment, 2022, 15, 1866-7511, 10.1007/s12517-021-09005-y | |
| 50. | Rui Liu, Gulin Li, Liangshuai Wei, Yuan Xu, Xiaojuan Gou, Shubin Luo, Xin Yang, Spatial prediction of groundwater potentiality using machine learning methods with Grey Wolf and Sparrow Search Algorithms, 2022, 610, 00221694, 127977, 10.1016/j.jhydrol.2022.127977 | |
| 51. | Abinet Addis, Kartik Ariyur, GIS-Based Landslide Susceptibility Mapping Using Frequency Ratio and Shannon Entropy Models in Dejen District, Northwestern Ethiopia, 2023, 2023, 2314-4912, 1, 10.1155/2023/1062388 | |
| 52. | Sandeepa Pantha, Sachin Timilsina, Sandip Pantha, Shiv Kumar Manjan, Menuka Maharjan, Water quality index of springs in mid-hill of Nepal, 2022, 9, 26670100, 100658, 10.1016/j.envc.2022.100658 | |
| 53. | Sarmad Dashti Latif, Ali Najah Ahmed, A review of deep learning and machine learning techniques for hydrological inflow forecasting, 2023, 1387-585X, 10.1007/s10668-023-03131-1 | |
| 54. | Maryam Sadat Jafarzadeh, N Tahmasebipour, Ali Haghizadeh, Hamidreza Pourghasemi, Hamed Rouhani, The Effect of Observation Data Sampling Methods on Infiltration Areas by Maximum Entropy Model, 2020, 11, 2251-6174, 96, 10.52547/jwmr.11.22.96 | |
| 55. | Prem Ranjan, Pankaj Kumar Pandey, Vanita Pandey, Groundwater spring potential zonation using AHP and fuzzy-AHP in Eastern Himalayan region: Papum Pare district, Arunachal Pradesh, India, 2023, 1614-7499, 10.1007/s11356-023-26769-w | |
| 56. | Sandeepa Pantha, Sachin Timilsina, Shiv Kumar Manjan, Menuka Maharjan, Sandip Pantha, Seasonal Variation of Water Quality Index of Spring in Mid-Hill of Nepal, 2022, 1556-5068, 10.2139/ssrn.4188462 | |
| 57. | Ankit Tyagi, Reet Kamal Tiwari, Naveen James, Identification of the significant parameters in spatial prediction of landslide hazard, 2023, 82, 1435-9529, 10.1007/s10064-023-03334-w | |
| 58. | José Miguel Deformes, Jorge Núñez, Jerry P. Fairley, José Luis Arumí, Ricardo Oyarzún, Assessing Groundwater Potential in a Mid-Mountain Dryland Area of North-Central Chile through Geospatial Mapping, 2023, 15, 2073-4441, 3005, 10.3390/w15163005 | |
| 59. | Hanaa A. Megahed, Amira M. Abdo, Mohamed A. E. AbdelRahman, Antonio Scopa, Mohammed N. Hegazy, Frequency Ratio Model as Tools for Flood Susceptibility Mapping in Urbanized Areas: A Case Study from Egypt, 2023, 13, 2076-3417, 9445, 10.3390/app13169445 | |
| 60. | V Gholami, M R Khaleghi, M Teimouri, H Sahour, Prediction of annual groundwater depletion: An investigation of natural and anthropogenic influences, 2023, 132, 0973-774X, 10.1007/s12040-023-02184-0 | |
| 61. | Hanxiang Xiong, Xu Guo, Yuzhou Wang, Ruihan Xiong, Xiaofan Gui, Xiaojing Hu, Yonggang Li, Yang Qiu, Jiayao Tan, Chuanming Ma, Spatial prediction of groundwater potential by various novel boosting-based ensemble learning models in mountainous areas, 2023, 38, 1010-6049, 10.1080/10106049.2023.2274870 | |
| 62. | Yuwen Chen, AL MAHFOODH, GIS-statically-based modelling the groundwater quality assessment coupled with soil and terrain attributes data, 2023, 18, 1932-6203, e0292680, 10.1371/journal.pone.0292680 | |
| 63. | Dara Faeq Hamamin, Arsalan Ahmed Othman, Diary Ali Mohammed Amin Al-Manmi, Comparison of different statistical approaches to assess spring potential mapping in a multi-aquifer system: a case study of Kurdistan Region, Iraq, 2023, 82, 1866-6280, 10.1007/s12665-023-11250-1 | |
| 64. | Abinet Addis, Gang Mei, Landslide Susceptibility Mapping Using GIS and Bivariate Statistical Models in Chemoga Watershed, Ethiopia, 2024, 2024, 1687-8094, 1, 10.1155/2024/6616269 | |
| 65. | Lhoussaine El Mezouary, Abdessamad Hadri, Mohamed Hakim Kharrou, Younes Fakır, Abderrahman Elfarchouni, Lhoussaine Bouchaou, Abdelghani Chehbouni, Contribution to advancing aquifer geometric mapping using machine learning and deep learning techniques: a case study of the AL Haouz-Mejjate aquifer, Marrakech, Morocco, 2024, 14, 2190-5487, 10.1007/s13201-024-02162-x | |
| 66. | Amaya Adama, Ndjounguep Juscar, Ntoumbe Mama, Tchinda Tsoptie, Bendaoud Rachida, Kah Elvis, Delineation of groundwater potential zones using multi-criteria analysis (AHP), frequency ratios (RF), remote sensing and GIS: a case study of the Batcham municipality (west Cameroon), 2024, 4, 2730-647X, 10.1007/s43832-024-00108-7 | |
| 67. | Elham Rafiei-Sardooi, Ali Azareh, Hossein Ghazanfarpour, Eric Josef Ribeiro Parteli, Mohammad Faryabi, Saeed Barkhori, An integrated modeling framework for groundwater contamination risk assessment in arid, data-scarce environments, 2024, 1895-7455, 10.1007/s11600-024-01470-9 | |
| 68. | Abdul Gaffar Sheik, Arvind Kumar, Anandan Govindan Sharanya, Seshagiri Rao Amabati, Faizal Bux, Sheena Kumari, Machine learning-based monitoring and design of managed aquifer rechargers for sustainable groundwater management: scope and challenges, 2024, 1614-7499, 10.1007/s11356-024-35529-3 | |
| 69. | Deepak Patle, Manoj Kumar Awasthi, Shailesh Kumar Sharma, Yogesh Kishore Tiwari, A Geoinformatics-Based Comparative Study of Multi-Criteria Decision Making Approaches of Groundwater Potential Zoning in Ken Basin, India, 2024, 0255-660X, 10.1007/s12524-024-02062-2 | |
| 70. | Sumon Dey, Swarup Das, Swarm optimization based heterogeneous machine learning techniques for enhanced landslide susceptibility assessment with comprehensive uncertainty quantification, 2025, 18, 1865-0473, 10.1007/s12145-024-01617-8 | |
| 71. | Devanantham Abijith, Subbarayan Saravanan, K S S Parthasarathy, Nagireddy Masthan Reddy, Janardhanam Niraimathi, Ahmed Ali Bindajam, Javed Mallick, Maged Muteb Alharbi, Hazem Ghassan Abdo, Assessing the impact of climate and land use change on flood vulnerability: a machine learning approach in coastal region of Tamil Nadu, India, 2025, 12, 2196-4092, 10.1186/s40562-025-00377-7 |
| Class | Lithological characteristics |
| Group 1 | Claystone, sandstone |
| Group 2 | Granite-aplite |
| Group 3 | Gravel fan |
| Group 4 | Interbedded radiolarite slate and ultrabasic rocks |
| Group 5 | Leucogranite |
| Group 6 | Limestone recrystallized dolomitic |
| Group 7 | Marl, red-brown, gypsiferous |
| Group 8 | Quartz conglomerate |
| Group 9 | Recent alluvium |
| Group 10 | Sandstone, shale, conglomerate |
| Group 11 | Sandstone, slate crystalized limestone |
| Group 12 | Shale, phyletic, dark grey |
| Group 13 | Terraces |
| GCFs | Collinearity statistics | |
| Tolerance | Variance inflation factor (VIF) | |
| Altitude | 0.517 | 1.934 |
| Slope aspect | 0.844 | 1.185 |
| Fault density | 0.326 | 3.063 |
| Distance from faults | 0.362 | 2.761 |
| Land use | 0.753 | 1.328 |
| Lithology | 0.705 | 1.418 |
| LS | 0.427 | 2.341 |
| Plan curvature | 0.609 | 1.641 |
| Profile curvature | 0.743 | 1.346 |
| River density | 0.453 | 2.209 |
| Distance from rivers | 0.452 | 2.213 |
| Slope angle | 0.356 | 2.811 |
| TWI | 0.392 | 2.552 |
| Conditioning factor and class | No. of Pixels | % of Pixels | No. of Springs | % of Springs | Frequency Ratio (FR) |
| Slope Degree | |||||
| 0-5 | 313126 | 22.22 | 23 | 21.10 | 0.95 |
| 5-15 | 536896 | 38.10 | 61 | 55.96 | 1.47 |
| 15-30 | 453814 | 32.20 | 21 | 19.27 | 0.60 |
| > 30 | 105306 | 7.47 | 4 | 3.67 | 0.49 |
| Slope aspect | |||||
| Flat | 772 | 0.05 | 0 | 0.00 | 0.00 |
| North | 223581 | 15.87 | 15 | 13.76 | 0.87 |
| Northeast | 226364 | 16.06 | 15 | 13.76 | 0.86 |
| East | 229760 | 16.30 | 24 | 22.02 | 1.35 |
| Southeast | 198182 | 14.06 | 15 | 13.76 | 0.98 |
| South | 144804 | 10.28 | 14 | 12.84 | 1.25 |
| Southwest | 92496 | 6.56 | 4 | 3.67 | 0.56 |
| West | 114300 | 8.11 | 7 | 6.42 | 0.79 |
| Northwest | 178883 | 12.69 | 15 | 13.76 | 1.08 |
| Altitude (m) | |||||
| < 1400 | 110085 | 7.81 | 1 | 0.92 | 0.12 |
| 1400-1800 | 709457 | 50.35 | 60 | 55.05 | 1.09 |
| 1800-2200 | 354494 | 25.16 | 34 | 31.19 | 1.24 |
| 2200-2400 | 182685 | 12.96 | 11 | 10.09 | 0.78 |
| > 2400 | 52421 | 3.72 | 3 | 2.75 | 0.74 |
| Plan curvature (100/m) | |||||
| Concave | 451969 | 32.07 | 47 | 43.12 | 1.34 |
| Flat | 542376 | 38.49 | 48 | 44.04 | 1.14 |
| Convex | 414797 | 29.44 | 14 | 12.84 | 0.44 |
| Profile curvature (100\m) | |||||
| < (-0.001) | 639818 | 45.40 | 72 | 66.06 | 1.45 |
| (-0.001)-(-0.001) | 203673 | 14.45 | 15 | 13.76 | 0.95 |
| > (0.001) | 565651 | 40.14 | 22 | 20.18 | 0.50 |
| Slope length (LS) (m) | |||||
| 0-20 | 537886 | 38.17 | 26 | 23.85 | 0.62 |
| 20-40 | 266643 | 18.92 | 23 | 21.10 | 1.12 |
| 40-60 | 188324 | 13.36 | 12 | 11.01 | 0.82 |
| > 60 | 416289 | 29.54 | 48 | 44.04 | 1.49 |
| Topographic wetness index (TWI) | |||||
| < 8 | 71347 | 5.06 | 2 | 1.83 | 0.36 |
| 8_12 | 1137227 | 80.70 | 66 | 60.55 | 0.75 |
| > 12 | 200568 | 14.23 | 41 | 37.61 | 2.64 |
| Distance from rivers (m) | |||||
| < 100 | 76011 | 5.39 | 10 | 9.17 | 1.70 |
| 100-200 | 65759 | 4.67 | 13 | 11.93 | 2.56 |
| 200-300 | 72512 | 5.15 | 9 | 8.26 | 1.60 |
| 300-400 | 62611 | 4.44 | 3 | 2.75 | 0.62 |
| > 400 | 1132249 | 80.35 | 74 | 67.89 | 0.84 |
| Distance from faults (m) | |||||
| < 250 | 94430 | 6.70 | 12 | 11.01 | 1.64 |
| 250-500 | 92160 | 6.54 | 12 | 11.01 | 1.68 |
| 500-750 | 90281 | 6.41 | 3 | 2.75 | 0.43 |
| 75-1000 | 90736 | 6.44 | 2 | 1.83 | 0.28 |
| > 1000 | 1041535 | 73.91 | 80 | 73.39 | 0.99 |
| River density (Km/Km 2) | |||||
| < 0.31 | 300817 | 21.35 | 37 | 33.94 | 1.59 |
| 0.31-0.78 | 466377 | 33.10 | 39 | 35.78 | 1.08 |
| 0.78-1.27 | 438029 | 31.08 | 22 | 20.18 | 0.65 |
| 1.27-2.51 | 203919 | 14.47 | 11 | 10.09 | 0.70 |
| Fault density (Km/Km 2) | |||||
| < 2.72 | 377803 | 26.81 | 29 | 26.61 | 0.99 |
| 2.72-8.37 | 639444 | 45.38 | 44 | 40.37 | 0.89 |
| 8.37-15.70 | 216981 | 15.40 | 22 | 20.18 | 1.31 |
| 15.70-26.80 | 174914 | 12.41 | 14 | 12.84 | 1.03 |
| Land use | |||||
| Agriculture | 91627 | 6.50 | 0 | 0.00 | 0.00 |
| Orchard | 325287 | 23.08 | 19 | 17.43 | 0.76 |
| Rangeland | 990485 | 70.29 | 90 | 82.57 | 1.17 |
| Residential area | 1743 | 0.12 | 0 | 0.00 | 0.00 |
| Lithology | |||||
| Group1 | 451 | 0.03 | 0 | 0.00 | 0.00 |
| Group2 | 1058 | 0.08 | 0 | 0.00 | 0.00 |
| Group3 | 132749 | 9.42 | 2 | 1.83 | 0.19 |
| Group4 | 32272 | 2.29 | 1 | 0.92 | 0.40 |
| Group5 | 16504 | 1.17 | 0 | 0.00 | 0.00 |
| Group6 | 10164 | 0.72 | 9 | 8.26 | 11.45 |
| Group7 | 6740 | 0.48 | 0 | 0.00 | 0.00 |
| Group8 | 12703 | 0.90 | 6 | 5.50 | 6.11 |
| Group9 | 72799 | 5.17 | 11 | 10.09 | 1.95 |
| Group10 | 64056 | 4.55 | 8 | 7.34 | 1.61 |
| Group11 | 43328 | 3.07 | 1 | 0.92 | 0.30 |
| Group12 | 846210 | 60.05 | 65 | 59.63 | 0.99 |
| Group13 | 170108 | 12.07 | 6 | 5.50 | 0.46 |
| Factor | Importance |
| TWI | 100 |
| Altitude | 89.65 |
| Distance from rivers | 48.70 |
| Rivers density | 28.85 |
| Distance from faults | 18.21 |
| Faults density | 16.11 |
| Slope degree | 12.57 |
| Profile curvature | 11.70 |
| LS | 9.61 |
| Land use | 7.51 |
| Plan curvature | 5.19 |
| Aspect | 1.16 |
| Lithology | 0 |
| Class/Model | FR | BRT | ||
| Range | Area (%) | Range | Area (%) | |
| Low | 6.72-12.02 | 30.40 | 0-0.25 | 36.83 |
| Moderate | 12.02-14.18 | 19.44 | 0.25-0.43 | 29.57 |
| High | 14.18-19.30 | 19.17 | 0.43-0.64 | 19.79 |
| Very high | 19.30-29.73 | 0.98 | > 0.64 | 13.81 |
| Class | Lithological characteristics |
| Group 1 | Claystone, sandstone |
| Group 2 | Granite-aplite |
| Group 3 | Gravel fan |
| Group 4 | Interbedded radiolarite slate and ultrabasic rocks |
| Group 5 | Leucogranite |
| Group 6 | Limestone recrystallized dolomitic |
| Group 7 | Marl, red-brown, gypsiferous |
| Group 8 | Quartz conglomerate |
| Group 9 | Recent alluvium |
| Group 10 | Sandstone, shale, conglomerate |
| Group 11 | Sandstone, slate crystalized limestone |
| Group 12 | Shale, phyletic, dark grey |
| Group 13 | Terraces |
| GCFs | Collinearity statistics | |
| Tolerance | Variance inflation factor (VIF) | |
| Altitude | 0.517 | 1.934 |
| Slope aspect | 0.844 | 1.185 |
| Fault density | 0.326 | 3.063 |
| Distance from faults | 0.362 | 2.761 |
| Land use | 0.753 | 1.328 |
| Lithology | 0.705 | 1.418 |
| LS | 0.427 | 2.341 |
| Plan curvature | 0.609 | 1.641 |
| Profile curvature | 0.743 | 1.346 |
| River density | 0.453 | 2.209 |
| Distance from rivers | 0.452 | 2.213 |
| Slope angle | 0.356 | 2.811 |
| TWI | 0.392 | 2.552 |
| Conditioning factor and class | No. of Pixels | % of Pixels | No. of Springs | % of Springs | Frequency Ratio (FR) |
| Slope Degree | |||||
| 0-5 | 313126 | 22.22 | 23 | 21.10 | 0.95 |
| 5-15 | 536896 | 38.10 | 61 | 55.96 | 1.47 |
| 15-30 | 453814 | 32.20 | 21 | 19.27 | 0.60 |
| > 30 | 105306 | 7.47 | 4 | 3.67 | 0.49 |
| Slope aspect | |||||
| Flat | 772 | 0.05 | 0 | 0.00 | 0.00 |
| North | 223581 | 15.87 | 15 | 13.76 | 0.87 |
| Northeast | 226364 | 16.06 | 15 | 13.76 | 0.86 |
| East | 229760 | 16.30 | 24 | 22.02 | 1.35 |
| Southeast | 198182 | 14.06 | 15 | 13.76 | 0.98 |
| South | 144804 | 10.28 | 14 | 12.84 | 1.25 |
| Southwest | 92496 | 6.56 | 4 | 3.67 | 0.56 |
| West | 114300 | 8.11 | 7 | 6.42 | 0.79 |
| Northwest | 178883 | 12.69 | 15 | 13.76 | 1.08 |
| Altitude (m) | |||||
| < 1400 | 110085 | 7.81 | 1 | 0.92 | 0.12 |
| 1400-1800 | 709457 | 50.35 | 60 | 55.05 | 1.09 |
| 1800-2200 | 354494 | 25.16 | 34 | 31.19 | 1.24 |
| 2200-2400 | 182685 | 12.96 | 11 | 10.09 | 0.78 |
| > 2400 | 52421 | 3.72 | 3 | 2.75 | 0.74 |
| Plan curvature (100/m) | |||||
| Concave | 451969 | 32.07 | 47 | 43.12 | 1.34 |
| Flat | 542376 | 38.49 | 48 | 44.04 | 1.14 |
| Convex | 414797 | 29.44 | 14 | 12.84 | 0.44 |
| Profile curvature (100\m) | |||||
| < (-0.001) | 639818 | 45.40 | 72 | 66.06 | 1.45 |
| (-0.001)-(-0.001) | 203673 | 14.45 | 15 | 13.76 | 0.95 |
| > (0.001) | 565651 | 40.14 | 22 | 20.18 | 0.50 |
| Slope length (LS) (m) | |||||
| 0-20 | 537886 | 38.17 | 26 | 23.85 | 0.62 |
| 20-40 | 266643 | 18.92 | 23 | 21.10 | 1.12 |
| 40-60 | 188324 | 13.36 | 12 | 11.01 | 0.82 |
| > 60 | 416289 | 29.54 | 48 | 44.04 | 1.49 |
| Topographic wetness index (TWI) | |||||
| < 8 | 71347 | 5.06 | 2 | 1.83 | 0.36 |
| 8_12 | 1137227 | 80.70 | 66 | 60.55 | 0.75 |
| > 12 | 200568 | 14.23 | 41 | 37.61 | 2.64 |
| Distance from rivers (m) | |||||
| < 100 | 76011 | 5.39 | 10 | 9.17 | 1.70 |
| 100-200 | 65759 | 4.67 | 13 | 11.93 | 2.56 |
| 200-300 | 72512 | 5.15 | 9 | 8.26 | 1.60 |
| 300-400 | 62611 | 4.44 | 3 | 2.75 | 0.62 |
| > 400 | 1132249 | 80.35 | 74 | 67.89 | 0.84 |
| Distance from faults (m) | |||||
| < 250 | 94430 | 6.70 | 12 | 11.01 | 1.64 |
| 250-500 | 92160 | 6.54 | 12 | 11.01 | 1.68 |
| 500-750 | 90281 | 6.41 | 3 | 2.75 | 0.43 |
| 75-1000 | 90736 | 6.44 | 2 | 1.83 | 0.28 |
| > 1000 | 1041535 | 73.91 | 80 | 73.39 | 0.99 |
| River density (Km/Km 2) | |||||
| < 0.31 | 300817 | 21.35 | 37 | 33.94 | 1.59 |
| 0.31-0.78 | 466377 | 33.10 | 39 | 35.78 | 1.08 |
| 0.78-1.27 | 438029 | 31.08 | 22 | 20.18 | 0.65 |
| 1.27-2.51 | 203919 | 14.47 | 11 | 10.09 | 0.70 |
| Fault density (Km/Km 2) | |||||
| < 2.72 | 377803 | 26.81 | 29 | 26.61 | 0.99 |
| 2.72-8.37 | 639444 | 45.38 | 44 | 40.37 | 0.89 |
| 8.37-15.70 | 216981 | 15.40 | 22 | 20.18 | 1.31 |
| 15.70-26.80 | 174914 | 12.41 | 14 | 12.84 | 1.03 |
| Land use | |||||
| Agriculture | 91627 | 6.50 | 0 | 0.00 | 0.00 |
| Orchard | 325287 | 23.08 | 19 | 17.43 | 0.76 |
| Rangeland | 990485 | 70.29 | 90 | 82.57 | 1.17 |
| Residential area | 1743 | 0.12 | 0 | 0.00 | 0.00 |
| Lithology | |||||
| Group1 | 451 | 0.03 | 0 | 0.00 | 0.00 |
| Group2 | 1058 | 0.08 | 0 | 0.00 | 0.00 |
| Group3 | 132749 | 9.42 | 2 | 1.83 | 0.19 |
| Group4 | 32272 | 2.29 | 1 | 0.92 | 0.40 |
| Group5 | 16504 | 1.17 | 0 | 0.00 | 0.00 |
| Group6 | 10164 | 0.72 | 9 | 8.26 | 11.45 |
| Group7 | 6740 | 0.48 | 0 | 0.00 | 0.00 |
| Group8 | 12703 | 0.90 | 6 | 5.50 | 6.11 |
| Group9 | 72799 | 5.17 | 11 | 10.09 | 1.95 |
| Group10 | 64056 | 4.55 | 8 | 7.34 | 1.61 |
| Group11 | 43328 | 3.07 | 1 | 0.92 | 0.30 |
| Group12 | 846210 | 60.05 | 65 | 59.63 | 0.99 |
| Group13 | 170108 | 12.07 | 6 | 5.50 | 0.46 |
| Factor | Importance |
| TWI | 100 |
| Altitude | 89.65 |
| Distance from rivers | 48.70 |
| Rivers density | 28.85 |
| Distance from faults | 18.21 |
| Faults density | 16.11 |
| Slope degree | 12.57 |
| Profile curvature | 11.70 |
| LS | 9.61 |
| Land use | 7.51 |
| Plan curvature | 5.19 |
| Aspect | 1.16 |
| Lithology | 0 |
| Class/Model | FR | BRT | ||
| Range | Area (%) | Range | Area (%) | |
| Low | 6.72-12.02 | 30.40 | 0-0.25 | 36.83 |
| Moderate | 12.02-14.18 | 19.44 | 0.25-0.43 | 29.57 |
| High | 14.18-19.30 | 19.17 | 0.43-0.64 | 19.79 |
| Very high | 19.30-29.73 | 0.98 | > 0.64 | 13.81 |