Two classes of improved fifth-order weighted compact nonlinear schemes for compressible Euler equations

1.   Introduction

The compressible Euler equations, a fundamental system in fluid dynamics, have important research and application value in many fields and are expressed as

where

Here, $\rho$ denotes the fluid density, while $u$ and $v$ denote the speed components along the $x$- and $y$-axes, respectively. In Eq (3), $E$ represents the total energy per unit fluid volume, with $P$ indicating the fluid pressure, and $\gamma = 1.4$ representing the specific heat ratio. Due to the hyperbolic property of the compressible Euler equations, their solutions may contain shock waves, discontinuities, and other complex phenomena. Therefore, it is difficult to solve these equations by applying high-order linear methods, because these methods are prone to result in numerical oscillations around jump discontinuities.

The original weighted essentially non-oscillatory (WENO) scheme ^[1] is an ideal choice for solving Euler equations among many high-precision numerical schemes, due to its ability to maintain high accuracy in smooth flow regions while effectively suppressing oscillations near discontinuities. This scheme obtains the unknown variables using a nonlinear weighting of all the candidate stencil information. The fifth-order WENO-JS scheme developed by Jiang and Shu ^[2] introduced novel smoothness indicators for the sub-stencils. Based on that work, a large number of studies have focused on the improvement of the accuracy and computational efficiency of the WENO scheme. For instance, Henrick et al. ^[3] developed the WENO-M scheme by introducing a mapping weight function to modify JS-type nonlinear weights. Subsequently, Borges et al. ^[4] established the WENO-Z approach by creating a global smoothness indicator across the five-point stencil and formulating innovative non-oscillatory Z-type weights. By substituting polynomial interpolation with Hermite interpolation, Qiu and Shu ^[5,6] designed a fifth-order Hermite WENO (HWENO) scheme. Guo and Jung ^[7,8] presented a new WENO scheme by applying the radial basis function (RBF) reconstruction and designed a monotone polynomial interpolation method to identify non-smooth stencils, where the WENO-JS-type reconstruction was used to maintain non-oscillatory behavior. Building upon the framework of the RBF-WENO scheme established by Guo and Jung ^[8], researchers have developed several non-polynomial reconstruction approaches, such as the WENO-G ^[9], TENO-P ^[10], and HP-WENO ^[11] schemes. These approaches offer performance optimization through adjustable parameters, showcasing remarkable adaptability. Most recently, Zuo and Zhu ^[12,13] proposed an innovative high-order hybrid multi-resolution (HMR) WENO method with new troubled-cell indicators. Hu et al. ^[14] established the WENO-CU6 scheme by implementing an adaptive switching between central and upwind schemes. The WENO-ZQ scheme formulated by Zhu and Qiu ^[15] applied weighted combinations of polynomial reconstructions at different stencil scales. Building on this, Shen et al. ^[16] constructed a novel WENO-Z scheme (WENO-ZN) with adaptive weight modification, replacing the Z-type weight constant with a discontinuity-sensitive function. Li et al. ^[17] later verified that higher-order WENO-ZN variants outperform the WENO-JS and WENO-Z schemes of the same order.

The weighted compact nonlinear scheme (WCNS), a high-precision scheme that was proposed by Deng and Zhang ^[18], is widely used for solving Euler equations. Nonomura and Fujii ^[19] formulated a new WCNS scheme by mixing the numerical flux of grid nodes and midpoints to improve accuracy and stability. Liu et al. ^[20] demonstrated that the WCNS scheme has the same strong shock-capturing capability as the classical WENO scheme, with low dissipation and high resolution. To improve the resolution of the WCNS scheme, Yan et al. ^[21] proposed an adaptive Y-type nonlinear weight. The weight is similar to the function in the WENO-ZN scheme and approaches a small value near discontinuities. Wong and Lele ^[22] proposed a low-dissipative WCNS scheme by using a linear scheme in smooth regions and a hybrid scheme of linear interpolation and WENO-type nonlinear interpolation near discontinuities to improve numerical stability and reduce numerical dissipation while capturing shock waves. To improve computational efficiency, Jiang et al. ^[23] presented a semi-implicit WCNS formulation with high-order accuracy specifically designed for stiff Navier–Stokes problems, avoiding the limitation of Courant-Friedrichs-Lewy (CFL) conditions required by explicit versions. Jiang et al. ^[24] extended a fifth-order WCNS scheme with WENO-Z-type weights for solving Hamilton-Jacobi equations that are related to hyperbolic conservation laws. For this kind of equations, Huang et al. ^[25] formulated a perturbed WCNS scheme (WCNS-P) with a free parameter and boosted the local accuracy by optimizing the parameter in the perturbed linear interpolations constructed on the two-point-wide sub-stencils.

This paper develops two enhanced fifth-order WCNS schemes, namely the WCNS scheme with the modified ZN-type weights (WCNS-ZNM) and the perturbed WCNS scheme (WCNS-P), for Euler equations. The fifth-order WCNS-ZNM scheme incorporates the improvement on the WENO-ZN-type nonlinear interpolation originally proposed by Li and Shen et al. ^[17]. The fifth-order WCNS-P scheme is developed by incorporating perturbation terms containing a free parameter into linear interpolations obtained on three-point-wide sub-stencils, extending the WCNS-P approach of third-order accuracy ^[25]. Optimizing the free parameter in the WCNS-P scheme can minimize numerical errors in the smooth regions, enhancing local accuracy. A local monotone interpolation method is presented to detect non-smooth stencils, enabling automatic switching between the WCNS-P and WCNS-ZNM schemes according to the smoothness of the global stencils, thereby improving numerical stability. This paper is organized as follows: Sections 2 and 3 detail the formulations of WCNS-ZNM and WCNS-P schemes, respectively. Section 4 presents 1D and 2D numerical validations, with conclusions provided in Section 5.

2.   WCNS-ZNM scheme

The fifth-order WCNS-ZNM scheme for 1D Euler equations is derived in this section. Multidimensional extensions can be obtained through the dimension-by-dimension method. A uniform grid (spacing $h = (b-a)/N$) discretizes the domain $\Omega = \left[a, b\right]\ \ \ (b > a)$, with cell centers located at ${x}_{i} = a+ih(i = \mathrm{0, 1}, ..., N)$ and the total number of cells $N$.

2.1.   Central difference scheme

In classical fifth-order WCNS schemes, flux derivatives ${\boldsymbol{F}}_{i}^{'}$ at cell nodes ${x}_{i}$ are calculated by using a sixth-order hybrid difference scheme combining cell-node and cell-edge approximations.

where ${\tilde{\boldsymbol{F}}}_{i\pm 1/2}$ denote the approximations of the flux $\boldsymbol{F}$ at the cell edges ${x}_{i\pm 1/2}$, respectively. To guarantee numerical stability, the characteristic-wise interpolation technique is applied to compute the numerical fluxes at cell edges. The interpolation procedure for ${\tilde{\boldsymbol{F}}}_{i+1/2}$ in the local characteristic space involves these steps:

1) Estimate the average states at cell edges as ${\boldsymbol{U}}_{i+1/2} = \frac{1}{2}({\boldsymbol{U}}_{i}+{\boldsymbol{U}}_{i+1})$.

2) Obtain the Jacobian $\boldsymbol{A} = (\partial \boldsymbol{F}/\partial \boldsymbol{U}{)}_{i+1/2}$ and its right eigenvectors ${\boldsymbol{R}}_{i+1/2} = \boldsymbol{R}\left({\boldsymbol{U}}_{i+1/2}\right)$ and left eigenvectors ${\boldsymbol{L}}_{i+1/2} = \boldsymbol{L}\left({\boldsymbol{U}}_{i+1/2}\right)$, i.e., $\boldsymbol{A} = {\boldsymbol{R}}_{i+1/2}{\boldsymbol{\varLambda }}_{i+1/2}{\boldsymbol{L}}_{i+1/2}$, where ${\boldsymbol{\varLambda }}_{i+1/2}$ is the diagonal matrix and its diagonal elements are ${\lambda }_{1} = u-c, {\lambda }_{2} = u, {\lambda }_{3} = u+c$. Here, $u$ is the fluid speed in the x-direction, and $c = \sqrt{\gamma P/\rho }$ is the sound speed.

3) Apply the Lax–Friedrichs flux splitting, i.e., $\boldsymbol{F} = {\boldsymbol{F}}^{+}+{\boldsymbol{F}}^{-}$ with ${\boldsymbol{F}}^{\pm } = \frac{1}{2}\left(\boldsymbol{F}\pm {\alpha }_{x}\boldsymbol{U}\right)$ and ${\alpha }_{x} = \underset{k}{max}\left|{\lambda }_{k}\right|$. Transform the point values ${\boldsymbol{F}}_{i+m}^{\pm }$ to the characteristic space as ${\boldsymbol{Q}}_{i+m}^{\pm } = {\boldsymbol{L}}_{i+\frac{1}{2}}{\boldsymbol{F}}_{i+m}^{\pm }(m = -2, ..., 3)$.

4) Employ the WENO-ZN interpolation to calculate the left and right states $\tilde{\boldsymbol{Q}}{i+1/2}^{+}$ and $\tilde{\boldsymbol{Q}}{i+1/2}^{-}$ at cell edges in the characteristic space.

5) Transform the calculated quantities $\tilde{\boldsymbol{Q}}{i+1/2}^{\pm }$ from step 4 back to physical space and calculate the cell-edge numerical fluxes as ${\tilde{\boldsymbol{F}}}_{i+1/2} = {\boldsymbol{R}}_{i+1/2}(\tilde{\boldsymbol{Q}}{i+1/2}^{+}+\tilde{\boldsymbol{Q}}{i+1/2}^{-})$.

The WENO-ZN-type interpolation procedure of $\tilde{\boldsymbol{Q}}{i+1/2}^{+}$ is described in detail by a component-by-component manner and by omitting the superscript "+" for clarity. The calculation of $\tilde{\boldsymbol{Q}}{i+1/2}^{-}$ follows the same procedure.

2.2.   WENO-ZN-type interpolation

To achieve fifth-order accuracy for each component $\tilde{q}_{i+1/2}$ of $\tilde{\boldsymbol{Q}}{i+1/2}^{+}$, we employ a five-point-wide stencil$S = \left\{{x}_{i-2}, {x}_{i-1}, {x}_{i}, {x}_{i+1}, {x}_{i+2}\right\}$ composed of three-point-wide sub-stencils ${S}^{k} = \left\{{x}_{i+k-2}, {x}_{i+k-1}, {x}_{i+k}\right\}, k = 0, 1, 2$. Using the global stencil $S$, the linear interpolation of $\tilde{q}_{i+1/2}$ can be obtained as

This equation can alternatively be formulated as a linear weighting of third-order linear interpolations obtained from three sub-stencils ${S}^{k}$, denoted $\tilde{q}_{i+1/2}^{k}$, $k = \mathrm{0, 1}, 2$.

where the linear weights are ${\delta }_{0} = \frac{1}{16}, {\delta }_{1} = \frac{10}{16}, {\delta }_{2} = \frac{5}{16}$. The expressions of the three third-order interpolations are

The high-order linear interpolation (6) may lead to non-physical oscillations around solution discontinuities. To enhance stability and avoid this issue, nonlinear weighting is implemented using three third-order interpolations (7), and the linear weights ${\delta }_{k}$ in Eq (6) are replaced with the nonlinear weights ${\varpi }_{k}$ for computing $\tilde{q}_{i+1/2}$.

A series of nonlinear weights in the literature (e.g., JS-type ^[2], Z-type ^[4], and ZN-type ^[16,17]) are presented in the WENO versions. The WENO-ZN weights are verified to be superior to the WENO-JS and WCNS-Z weights, in terms of accuracy and resolution, and are expressed as ^[17]

where $\epsilon = {10}^{-12}$ prevents division by zero and the parameter $\theta$ is defined as

Here, $\theta$ is related to the local smoothness indicators of the sub-stencils ${S}^{k}$, denoted as ${\beta }_{k}$, and is easily affected by numerical disturbances. To resolve this issue, we replace it with a large positive constant. The local smoothness indicators are defined as ${\beta }_{k} = {\left(h{p}_{k}^{'}\right)}^{2}+{\left({h}^{2}{p}_{k}^{''}\right)}^{2}, k = 0, 1, 2,$ and the specific formulas are

Define ${\tau }_{8}$ as the global smoothness indicator for stencil $S$:

According to Eqs (7) and (8), the nonlinear weighting of the interpolations of $\tilde{q}_{i+1/2}$ yields

Notice that the WCNS-ZN scheme is composed of a sixth-order central difference scheme (4) for the spatial derivative ${\boldsymbol{F}}_{i}^{'}$ and a WENO-ZN-type interpolation (12) with the parameter (9) for the numerical fluxes at cell edges. The WCNS-ZNM scheme is designed by replacing the parameter (9) in the WCNS-ZN scheme with a large positive constant.

3.   WCNS-P scheme

Guo and Jung ^[7,8] proposed the RBF-WENO scheme by selecting multiple quadratic forms and Gaussian RBF with free parameters as the non-polynomial interpolation basis. The local interpolation errors can be controlled by adjusting these parameters. Building on the RBF-WENO concept, Huang et al. ^[25] established a third-order WCNS-P scheme for Hamilton-Jacobi problems. This work advances the framework to fifth-order accuracy using a five-point stencil $S$.

3.1.   Non-polynomial interpolation

We add perturbation terms with an adjustable parameter ${\varsigma }^{2}$ into Eq (7), thereby deriving the following non-polynomial interpolation formula for three-point-wide sub-stencils.

In Eq (13), the parameter ${\varsigma }^{2}$ and the constants ${a}_{l}, {b}_{l}, {c}_{l}\left(l = 1, 2, 3\right)$ are determined by Taylor series expansion. The flux at cell edges is then evaluated via linear combination of the resulting non-polynomial interpolations, i.e.,

We expand the right-hand terms of Eq (13) using the Taylor expansion and derive the following expressions:

In order to ensure that the non-polynomial interpolations (13) have at least third-order accuracy, all the higher-order terms in Eqs (15)–(17) must be neglected, and the value of the parameter ${\varsigma }^{2}$ is obtained as

Substituting the expression (18) into Eqs (15)–(17) yields

The derivatives ${q}_{i+1/2}^{'}$ and ${q}_{i+1/2}^{\left(3\right)}$ in Eq (18) are numerically approximated by employing the nodal values of stencil $S$.

Substituting Eqs (22) and (23) into expression (18) generates

According to Eqs (19)–(21) and (24), it follows that the constants ${a}_{l}, {b}_{l}, {c}_{l}\left(l = \mathrm{1, 2}, 3\right)$ satisfy the following conditions:

Solving the above-mentioned linear equations subject to inequality constraints, we have

Based on Eq (29), we plug Eq (13) into the scheme (14) and have

Eq (30) is expanded as a Taylor series, resulting in the truncation error as follows:

Therefore, the WCNS-P scheme composed of the sixth-order central difference scheme (4) for the spatial derivative ${\boldsymbol{F}}_{i}^{'}$ and the scheme (14) for cell-edge fluxes can attain fifth-order accuracy in smooth regions. If the global stencil $S$ includes discontinuity, the WCNS-P scheme will not maintain the non-oscillating property due to the fact that the estimation of the free parameter ${\varsigma }^{2}$ in Eq (24) is carried out based on the global stencil.

3.2.   Local monotone interpolation method

The WCNS-P scheme cannot keep the non-oscillating property in non-smooth regions. Thus, we must find out non-smooth solution regions in which the WCNS-ZNM scheme is employed to enhance stability. Several approaches are used in the literature to identify the discontinuity and then initiate the shock-capturing schemes. For instance, Zuo and Zhu ^[12,13] developed a series of parameter-independent troubled-cell indicators based on different stencil sizes to determine whether extreme points exist within the interval, thereby accurately assessing the smoothness of the stencil. In this work, we adopt the local monotonicity-preserving interpolation method proposed in ^[7]. Unlike previous works ^[12,13], this method does not require the construction of a fourth-degree polynomial for the five-point stencil. Instead, it only necessitates the construction of second-degree polynomials on the three-point sub-stencils. This methodology significantly simplifies the extreme-point detection process while maintaining effectiveness. This subsection will provide a detailed description of this methodology.

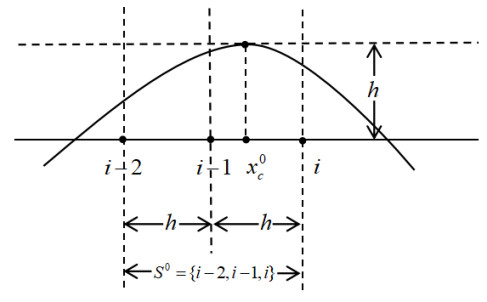
We reconstruct a quadratic polynomial on each sub-stencil. For example, the schematic diagram of the interpolating polynomial on the sub-stencil ${S}^{0}$, denoted by ${F}_{0}\left(x\right)$, is shown in Figure 1, where ${x}_{c}^{0}$ represents the critical point at which ${F}_{0}^{'}\left(x\right) = 0$. Notice that the critical point could be generated due to the Gibbs oscillations. Without loss of generality, let ${x}_{i-2} = 0, {x}_{i-1} = h, {x}_{i} = 2h.$ The polynomial ${F}_{0}\left(x\right)$ is formulated as

The coefficients ${a}_{0}, {b}_{0}, {c}_{0}$ are expressed as

The critical point ${x}_{c}^{0}$ is computed as

It is obvious that ${F}_{0}\left(x\right)$ is monotone if ${x}_{c}^{0}\le 0$ or ${x}_{c}^{0}\ge 2h$, while the derivative ${F}_{0}^{'}\left(x\right)$ changes its sign in the sub-stencil ${S}^{0}$, if ${x}_{c}^{0}$ is located in the interval. If ${F}_{0}\left(x\right)$ is not monotone, it could be oscillatory resulting from the Gibbs phenomenon.

Let ${x}_{c}^{k}$ represent the critical points of the quadratic polynomials ${F}_{k}\left(x\right)$ constructed on ${S}^{k}$, $k = 0, 1, 2$. If any of the three sub-stencils contains a critical point, the five-point-wide stencil $S$ is assumed to be non-smooth, and then the numerical fluxes obtained based on the information from the stencil $S$ are calculated using the WCNS-ZNM scheme. This discontinuity identification method realizes the adaptive switching between the two schemes in smooth regions and non-smooth regions, i.e.,

It follows that the designed WCNS-P scheme is essentially a hybrid scheme. Moreover, the proposed scheme naturally converts to the shock-capturing WCNS-ZNM scheme in non-smooth flow regions.

3.3.   Spectral properties

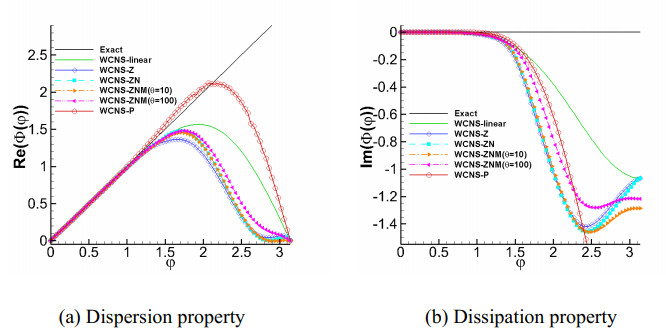
High-order shock-capturing schemes with low dissipation and dispersion can accurately simulate the flow field with complicated structures. We apply the approximate dispersion relation (ADR) ^[26] to analyze the spectral properties of the WCNS-ZN-type (i.e., WCNS-ZN and WCNS-ZNM) and WCNS-P schemes. For the WCNS-ZNM scheme, two different values of the parameter $\theta$ are taken into account, i.e., $\theta = 10$ and $100$. The reduced and modified wave numbers are denoted as $\phi$ and $\Phi$, respectively. For comparison, the spectral properties of the classical WCNS-Z scheme with the WENO-Z weights ^[4] are also presented. The spectral characteristics of these schemes are shown in Figure 2. From this figure, our analysis reveals that the WCNS-Z scheme exhibits the largest dissipation, while WCNS-P demonstrates superior dissipative/dispersive properties compared to both linear WCNS and nonlinear WCNS-Z-type (i.e., WCNS-Z, WCNS-ZN, and WCNS-ZNM) schemes across medium wave numbers. The spectral characteristics of the WCNS-ZNM scheme are affected by the choice of the parameter $\theta$, and the scheme with large $\theta$ has superior spectral characteristics as compared to the WCNS-ZN scheme. Although the WCNS-ZNM scheme with large $\theta$ produces lower numerical dissipation and dispersion, numerical oscillations around discontinuities are easily triggered. In view of spectral properties and numerical stability, parameter $\theta$ in WCNS-ZNM is set to be $\theta = 10$ for 1D cases and $\theta = 100$ for 2D cases.

4.   Numerical examples

Performance of WCNS-Z-type (including the fifth-order WCNS-Z, WCNS-ZN, and WCNS-ZNM) and WCNS-P schemes are tested by several 1D and 2D numerical examples governed by 1D and 2D Euler equations with different initial and boundary conditions, respectively. Time integration employs third-order TVD Runge-Kutta ^[2,15], with $\Delta t$ meeting CFL conditions, e.g., for 1D cases

We set the CFL number to 0.45, with $\Delta t\approx {h}^{5/3}$ for accuracy test cases. The numerical errors in the 1D accuracy test are calculated as

where ${\rho }_{i}, {\rho }_{i}^{exact}$ represent the numerical and exact densities at cell nodes ${x}_{i}$, respectively, while the numerical errors in the 2D accuracy test are measured in similar formulas.

Example 1. Accuracy tests

Consider the 1D Euler equations with initial data

given by the exact solutions

The computational domain is $\left[\mathrm{0, 2}\right]$ imposed by periodic boundary conditions. The numerical errors and convergence orders of the WCNS-ZN-type and WCNS-P schemes are calculated at time $t = 1$ using uniform grids with different numbers of cells. The results of the WCNS-ZN and WCNS-ZNM schemes are exactly the same. Therefore, only the results of WCNS-ZNM and WCNS-P schemes are presented. Table 1 clearly demonstrates that both schemes maintain fifth-order accuracy as expected, and the numerical errors obtained with the WCNS-P scheme are less than those obtained with the WCNS-ZNM scheme on the same grids.

Consider the 2D Euler equations with initial data

With periodic boundary conditions applied to the domain $[\mathrm{0, 2}{]}^{2}$, the computation runs until $t = 0.4$. Table 2 demonstrates the numerical errors and convergence orders of the WCNS-ZNM and WCNS-P schemes. From this table, it is also observed that the WCNS-ZNM/P maintains fifth-order accuracy, while the numerical errors produced by the WCNS-P scheme are smaller than those produced by the WCNS-ZNM scheme on the same grids.

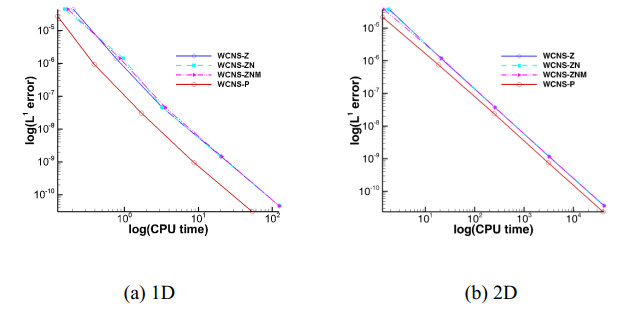
The relationships between ${L}^{1}$ errors and CPU time of the fifth-order WCNS-Z-type (i.e., WCNS-Z, WCNS-ZN, and WCNS-ZNM) and WCNS-P schemes are given in Figure 3. Evidently, for both 1D and 2D cases, the fifth-order WCNS-P scheme is computationally more efficient than the three classes of the fifth-order WCNS-Z-type schemes under the same conditions. The computational efficiency of the WCNS-ZN-type schemes is comparable to that of the WCNS-Z scheme.

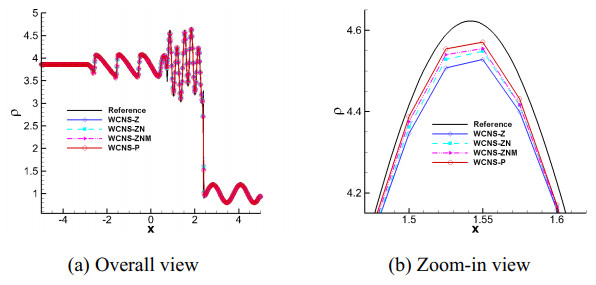
Example 2. 1D Lax problem

This problem is utilized to evaluate the shock-capturing performance of the presented schemes, with the following initial data

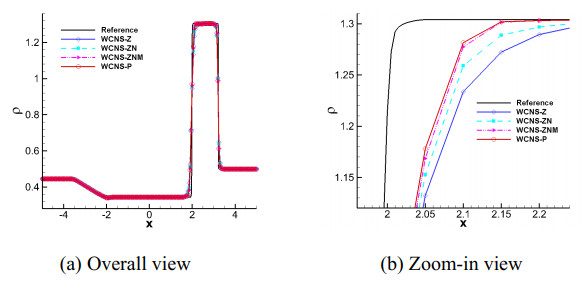
Here, the domain $[-\mathrm{5, 5}]$ is discretized into 200 cells, with computation terminating at $t = 1.3$. Four fifth-order schemes, WCNS-Z, WCNS-ZN, WCNS-ZNM, and WCNS-P, are selected for the calculation, with Figure 4 presenting numerical results of density distributions. A reference solution is obtained using the standard WCNS-Z scheme with 2000 grid cells. The results demonstrate that the WCNS-P scheme exhibits improvement over the WCNS-Z-type scheme, and the WCNS-ZNM scheme performs better than the WCNS-Z and WCNS-ZN schemes, with less numerical dissipation near the shock waves and stronger shock-capturing capability. Meanwhile, the WCNS-ZN scheme exhibits superior results compared to the WCNS-Z scheme, which agrees with the results in ^[17].

Example 3. 1D Sod problem

This problem is adopted to evaluate the stability of the presented schemes, with initial data

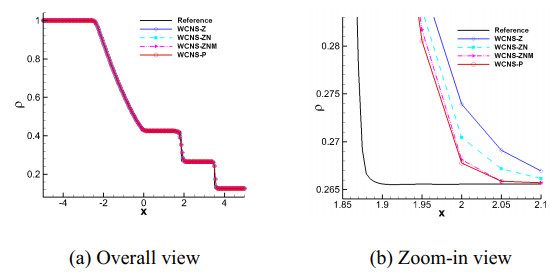
The computational domain is $[-\mathrm{5, 5}]$ discretized by 200 cells. Figure 5 demonstrates the numerical results obtained with four fifth-order schemes (WCNS-Z, WCNS-ZN, WCNS-ZNM, and WCNS-P) at time $t = 2$. We see that the numerical behaviors of the WCNS-P and WCNS-ZN schemes perform better than the other two schemes since the discontinuities are captured more sharply. Slightly better results can be achieved by the WCNS-P scheme in comparison to the WCNS-ZNM scheme.

Example 4. Osher-Shu problem

This problem expounds the interaction of a Mach 3 shock wave with a density wave, and the initial conditions are

Here, the domain $[-\mathrm{5, 5}]$ is discretized into 400 cells, with computation terminating at $t = 1.8$. Figure 6 illustrates numerical results obtained with four different schemes against a reference solution generated by the fifth-order WCNS-Z scheme using 4000 cells. We see that the WCNS-P and WCNS-ZN schemes exhibit better wave resolution than the WCNS-Z and WCNS-ZN schemes. Comparative analysis reveals the WCNS-P scheme as the least dissipative and the WCNS-Z scheme as the most dissipative among the fifth-order schemes.

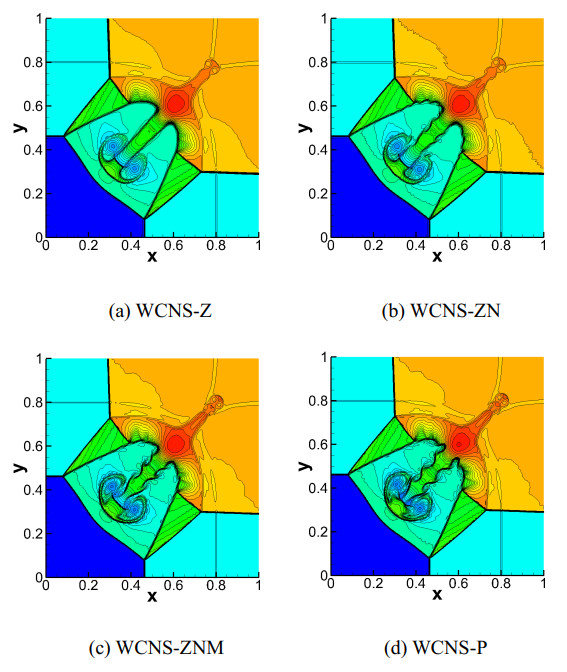
Example 5. 2D Riemann problem

This example represents a classical fluid dynamics problem that involves many complex fluid structures, with initial data described as

The domain $[\mathrm{0, 1}{]}^{2}$ with transmissive boundaries is divided into 400 × 400 cells. Four fifth-order schemes, WCNS-Z, WCNS-ZN, WCNS-ZNM, and WCNS-P, are applied for the computation. Figure 7 plots 35 density contours within the interval of $\left[\mathrm{0.14, 1.76}\right]$ at time $t = 0.8$. Numerical results show that fine-scale structures in the regions of strong velocity gradient are captured by the WCNS-ZNM and WCNS-P schemes more remarkably compared to the WCNS-Z and WCNS-ZN schemes. The WCNS-ZN scheme has a distinct advantage in resolution over the WCNS-Z scheme, which cannot resolve the Kelvin-Helmholtz (KH) instabilities due to the nonlinear shock-capturing mechanism. Compared to the WCNS-ZNM scheme, the WCNS-P scheme can capture much finer small-scale vortex structures incurred by the KH instabilities along the jet's neck and has obvious advantages in dissipation and resolution.

Example 6. 2D Rayleigh–Taylor instability problem

The example characterizes interfacial instability between density-stratified fluids under gravitational acceleration, widely adopted for assessing high-order schemes' dissipation and resolution capabilities. The initialization is defined as

In the above equations, the sound speed is $\alpha = \sqrt{\gamma P/\rho }$ with $\gamma = 5/3$ in this case. The domain $\left[\mathrm{0, 0.25}\right]\times \left[\mathrm{0, 1}\right]$ is divided into 240 × 960 cells, with Dirichlet boundary conditions $(\rho, u, v, P) = (2.0, 0.0, 0.0, 1.0)$ at the bottom and $(\rho, u, v, P) = (1.0, 0.0, 0.0, 2.5)$ at the top, and the left and right boundaries are set to reflective boundary conditions. The final time is $t = 1.95$. The fifth-order WCNS-Z, WCNS-ZN, WCNS-ZNM, and WCNS-P schemes are selected for the calculation, and 15 density contours, from 0.85 to 2.25, are shown in Figure 8. We see that the mushroom-cap shape spike is resolved by all of the four schemes. In comparison with the WCNS-Z scheme, the WCNS-ZN scheme has improved resolution but loses the symmetry incurred by the roundoff errors. The WCNS-ZNM and WCNS-P schemes outperform the two other schemes in resolution. Notably, the WCNS-P scheme captures finer curl structures and more small-scale vortices than the WCNS-ZNM scheme, with slightly lower numerical dissipation and better resolution.

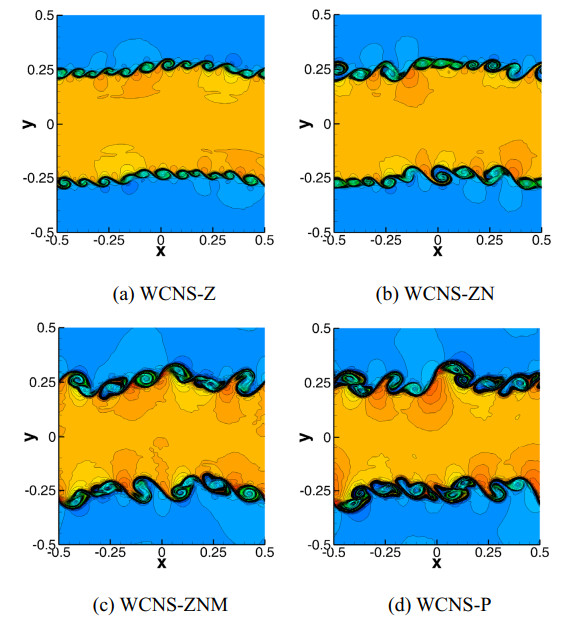
Example 7. 2D Kelvin–Helmholtz instability problem

This test case is commonly applied to validate the capability of high-order schemes in evolving small shear layers into 2D turbulence, expressed as:

We use 400 × 400 cells to discretize the domain $[-\mathrm{0.5, 0.5}{]}^{2}$ with periodic boundary conditions, simulating until $t = 1$. Density contour distributions (50 levels, from 0.8 to 2.26) are presented in Figure 9, which shows that all of the four fifth-order schemes (i.e., WCNS-Z, WCNS-ZN, WCNS-ZNM, and WCNS-P) are capable of capturing small-scale vortex structures caused by the KH instabilities, generating 2D turbulence with time. The size of vortices captured by the WCNS-ZNM and WCNS-P schemes is much bigger than that captured by the WCNS-Z and WCNS-ZN schemes. Among the four schemes, the WCNS-P scheme resolves vortices with the biggest size, exhibiting the best dissipation characteristics. Compared to the WCNS-Z scheme with the largest numerical dissipation, the WCNS-ZN scheme has better resolution, though still inferior to the WCNS-ZNM scheme.

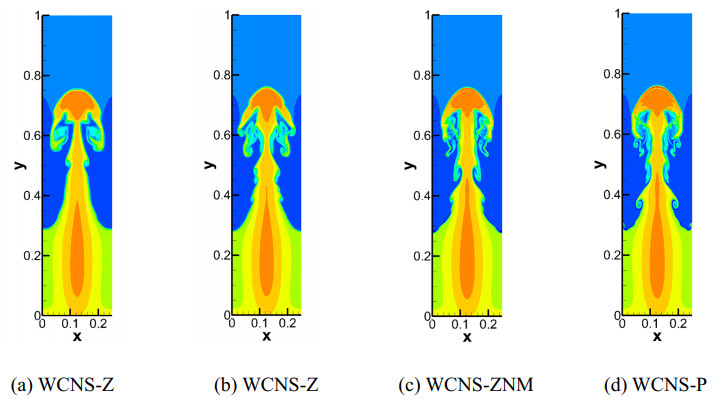
Example 8. 2D explosion problem

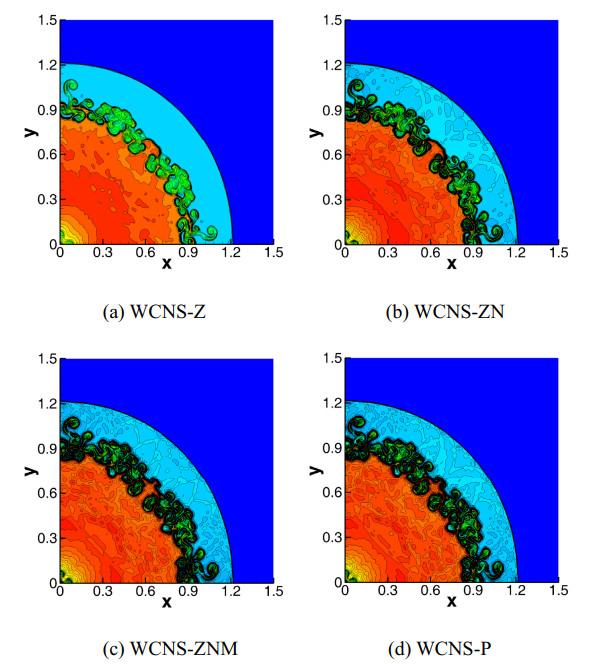
The explosion problem evaluates the stability of numerical methods to evolve unstable contacts, with cylindrically symmetric initial conditions

The domain $[\mathrm{0, 1.5}{]}^{2}$ is divided into 400 × 400 cells. Wall boundary conditions are imposed at the left and bottom boundaries; otherwise, free boundary conditions are imposed. Figure 10 shows the distribution results of 45 density contours in the interval $\left[\mathrm{0.1, 0.2}\right]$ at time $t = 3.2$. The numerical results indicate that the WCNS-ZNM and WCNS-P schemes behave better than the WCNS-Z and WCNS-ZN schemes, since they can capture the curly contact curve and small-scale vortex structures of finer scales. The WCNS-ZNM scheme has better resolution compared to the WCNS-ZN scheme. Among the four fifth-order schemes, the WCNS-Z scheme with excessive numerical dissipation resolves the narrowest mixing layer and the WCNS-P scheme resolves the curliest contact curve.

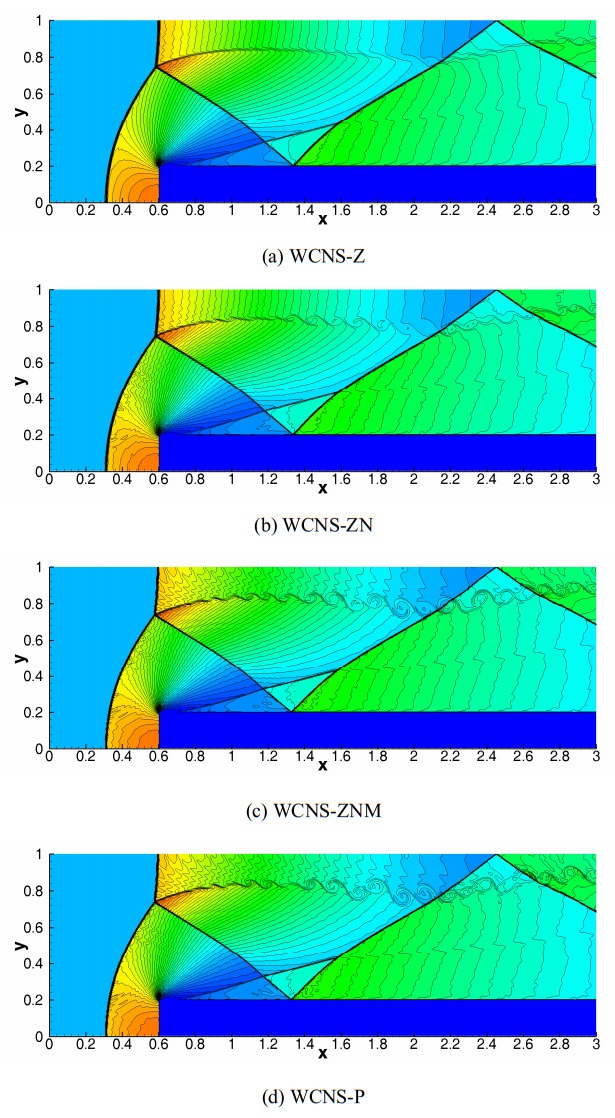
Example 9. 2D double Mach reflection problem

The shock wave structure in this example is extremely complex, including multiple reflected shock waves and density discontinuity lines. We use this case to test the performance of the presented schemes in capturing shocks and small-scale vortices. Initially, the pre- and post-shocked values are given by

The domain is $\left[\mathrm{0, 4}\right]\times \left[\mathrm{0, 1}\right]$ with 960 × 240 cells. Inflow/outflow conditions are set at left/right boundaries. The top boundary uses exact shock motion, while the bottom applies reflective (if $x > 1/6$) or transmissive conditions. We choose four schemes (i.e., WCNS-Z, WCNS-ZN, WCNS-ZNM, and WCNS-P) for calculation. Figure 11 displays the distribution results of 40 density contours in the interval $\left[\mathrm{1.5, 21.53}\right]$ at time $t = 0.2$. We observe that all schemes are capable of providing stable results and capturing the main flow features. The WCNS-ZNM and WCNS-P schemes better resolve the small-scale vortices induced by KH instabilities in the vortex rolling-up region, while they are partly dissipated by using the WCNS-Z scheme. The WCNS-ZN scheme outperforms the WCNS-Z scheme but underperforms compared to the WCNS-ZNM scheme. The WCNS-P scheme exhibits finer vortex detail at slip-line endpoints and in wall-jet zones compared to other fifth-order variants.

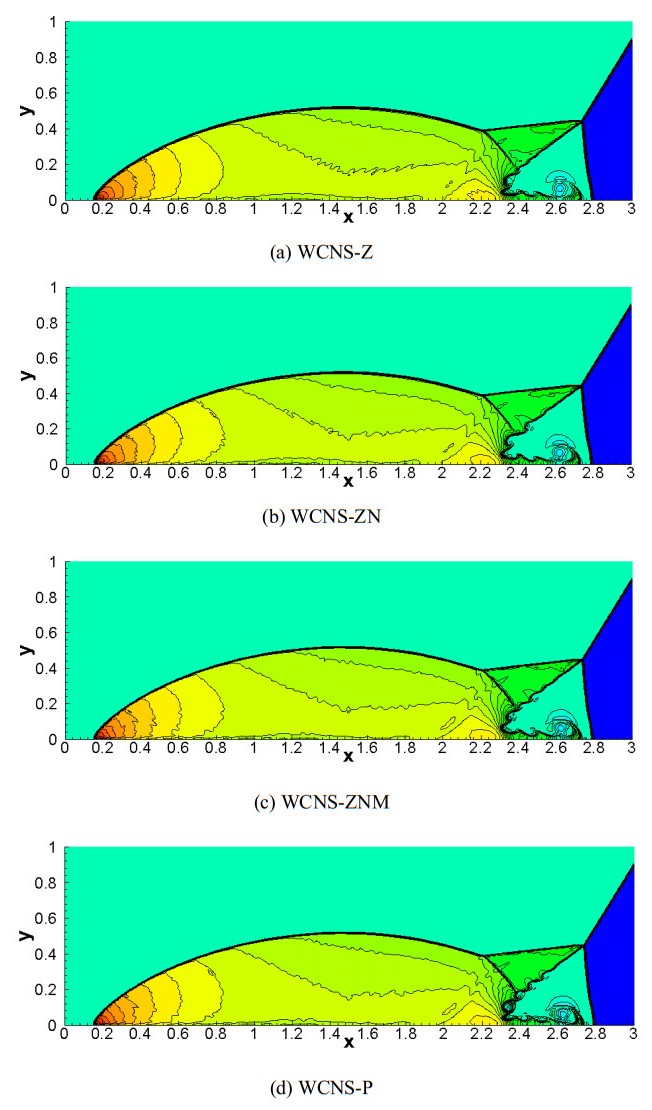
Example 10. 2D forward-facing step problem

This problem validates the resolution and stability of high-order schemes. The wind tunnel is set in the domain $\left[\mathrm{0, 0.6}\right]\times \left[\mathrm{0, 1}\right]\cup \left[\mathrm{0.6, 3}\right]\times \left[\mathrm{0.2, 1}\right]$. The left and right boundaries are treated as inflow and outflow conditions, respectively, while all other surfaces are treated as reflective walls. The initial conditions are given by $(\rho, u, v, P) = (\mathrm{1.4, 3}, \mathrm{0, 1})$. The domain is $\left[\mathrm{0, 3}\right]\times \left[\mathrm{0, 1}\right]$ with 900 × 300 cells. Density contour distributions (50 levels, from 0.3 to 6.68) are presented in Figure 12. From this figure, we can see that all of the four fifth-order schemes (i.e., WCNS-Z, WCNS-ZN, WCNS-ZNM, and WCNS-P) capture the shocks robustly. Among the four schemes, the WCNS-P scheme captures the most rolling-up structures of the vortex sheet emerging from the triple junction and triggered by the KH instabilities, with the least dissipation and the highest resolution. While WCNS-ZN outperforms WCNS-Z in resolution, it remains inferior to WCNS-ZNM.

5.   Conclusions

This study developed the enhanced WCNS-ZNM and WCNS-P schemes for the Euler equations. The WCNS-ZNM scheme is composed of the sixth-order hybrid central difference scheme for the flux derivatives and the modified characteristic-wise WENO-ZN-type interpolation technique for numerical fluxes at cell edges. The WCNS-P scheme was constructed by using a linear combination of three at least third-order non-polynomial interpolations with an adjustable parameter. By optimizing this parameter, the local numerical errors can be reduced, and thus, accuracy is improved. To maintain the non-oscillating property of the WCNS-P scheme, we apply the monotone polynomial interpolation approach to detect the non-smooth regions where the WCNS-ZNM scheme is initiated and accordingly realizes the adaptive switching between the two schemes in smooth and non-smooth regions. The ADR analysis indicates that the WCNS-P scheme has the best spectral properties, compared to the fifth-order WCNS-Z-type (i.e., WCNS-Z, WCNS-ZN, and WCNS-ZNM) schemes. Experimental results of accuracy tests show that the WCNS-ZNM and WCNS-P schemes are able to achieve the designed fifth-order accuracy in smooth regions, and the WCNS-P scheme has higher computational efficiency, compared to the three classes of WCNS-Z-type schemes of the same order. 1D and 2D numerical examples verify that the WCNS-ZN scheme shows clear improvement over the WCNS-Z scheme, and the WCNS-ZNM and WCNS-P schemes behave better than the WCNS-ZN scheme, as far as the resolution and shock-capturing capability are concerned. In general, the WCNS-P scheme provides improved numerical results and has better features with respect to high resolution in comparison to the WCNS-ZNM scheme.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare there is no conflict of interest.