Tidal time series are affected by a combination of astronomical, geological, meteorological, and anthropogenic factors, revealing non-stationary and multi-period features. The statistical features of non-stationary data vary over time, making it challenging for typical time series forecasting models to capture their dynamism. To solve this challenge, we designed memory factors, leveraging the fusion of statistical data at the channel dimension to enhance the model's prediction capacity for non-stationary data. On the other hand, traditional approaches have limitations in trend and cycle decomposition, making it difficult to detect complicated multi-period patterns and accurately separate the components. We combined integrated frequency domain optimization and multi-level, multi-scale convolutional kernel technologies. By employing Fourier-based methods and iterative recursive decomposition strategies, we effectively separated periodic and trend components. Then, the periodic multi-level wavelet block was applied to extract the periodic interaction features, aiming to deeply mine the latent information of periodic components and enhance the model's long-term prediction capabilities. In this paper, we used the Informer model as the foundational framework for further research and development. In comparative experiments, our proposed model outperformed LSTM, Informer, and MICN by 61.4%, 51.7%, and 23.8%, respectively. In multi-time-span prediction, the model's error remained stable as the prediction span increased from 48 to 96 steps (from 0.059 to 0.067). Under multi-site conditions, the model achieved varying degrees of improvement over the baseline in three key evaluation metrics, with average increases of 35.2%, 35.6%, and 61.2%, respectively. In this study, we focused on the extraction of short-period features from tidal data, providing an innovative and reliable solution for tidal height prediction. The results are significant for tidal assessments and protective engineering construction.
Citation: Peng Lu, Yuchen He, Wenhui Li, Yuze Chen, Ru Kong, Teng Wang. An Informer-based multi-scale model that fuses memory factors and wavelet denoising for tidal prediction[J]. Electronic Research Archive, 2025, 33(2): 697-724. doi: 10.3934/era.2025032
| [1] | Swarnava Biswas, Debajit Sen, Dinesh Bhatia, Pranjal Phukan, Moumita Mukherjee . Chest X-Ray image and pathological data based artificial intelligence enabled dual diagnostic method for multi-stage classification of COVID-19 patients. AIMS Biophysics, 2021, 8(4): 346-371. doi: 10.3934/biophy.2021028 |
| [2] | Soumyajit Podder, Somnath Bhattacharjee, Arijit Roy . An efficient method of detection of COVID-19 using Mask R-CNN on chest X-Ray images. AIMS Biophysics, 2021, 8(3): 281-290. doi: 10.3934/biophy.2021022 |
| [3] | Soumyajit Podder, Abhishek Mallick, Sudipta Das, Kartik Sau, Arijit Roy . Accurate diagnosis of liver diseases through the application of deep convolutional neural network on biopsy images. AIMS Biophysics, 2023, 10(4): 453-481. doi: 10.3934/biophy.2023026 |
| [4] | Manuel Bedrossian, Marwan El-Kholy, Daniel Neamati, Jay Nadeau . A machine learning algorithm for identifying and tracking bacteria in three dimensions using Digital Holographic Microscopy. AIMS Biophysics, 2018, 5(1): 36-49. doi: 10.3934/biophy.2018.1.36 |
| [5] | Muhammad Asif Zahoor Raja, Adeeba Haider, Kottakkaran Sooppy Nisar, Muhammad Shoaib . Intelligent computing knacks for infected media and time delay impacts on dynamical behaviors and control measures of rumor-spreading model. AIMS Biophysics, 2024, 11(1): 1-17. doi: 10.3934/biophy.2024001 |
| [6] | James C.L. Chow . Computer method and modeling: Medical biophysics applications in cancer therapy, medical imaging and drug delivery. AIMS Biophysics, 2021, 8(3): 233-235. doi: 10.3934/biophy.2021017 |
| [7] | Dinesh Bhatia, Tania Acharjee, Shruti Shukla, Monika Bhatia . Nano-technological advancements in multimodal diagnosis and treatment. AIMS Biophysics, 2024, 11(4): 464-507. doi: 10.3934/biophy.2024026 |
| [8] | Dina Falah Noori Al-Sabak, Leila Sadeghi, Gholamreza Dehghan . Predicting the correlation between neurological abnormalities and thyroid dysfunction using artificial neural networks. AIMS Biophysics, 2024, 11(4): 403-426. doi: 10.3934/biophy.2024022 |
| [9] | Bradley Vis, Jonathan J. Powell, Rachel E. Hewitt . Imaging flow cytometry methods for quantitative analysis of label-free crystalline silica particle interactions with immune cells. AIMS Biophysics, 2020, 7(3): 144-166. doi: 10.3934/biophy.2020012 |
| [10] | Francesca Ballarini, Mario P. Carante, Alessia Embriaco, Ricardo L. Ramos . Effects of ionizing radiation in biomolecules, cells and tissue/organs: basic mechanisms and applications for cancer therapy, medical imaging and radiation protection. AIMS Biophysics, 2022, 9(2): 108-112. doi: 10.3934/biophy.2022010 |
Tidal time series are affected by a combination of astronomical, geological, meteorological, and anthropogenic factors, revealing non-stationary and multi-period features. The statistical features of non-stationary data vary over time, making it challenging for typical time series forecasting models to capture their dynamism. To solve this challenge, we designed memory factors, leveraging the fusion of statistical data at the channel dimension to enhance the model's prediction capacity for non-stationary data. On the other hand, traditional approaches have limitations in trend and cycle decomposition, making it difficult to detect complicated multi-period patterns and accurately separate the components. We combined integrated frequency domain optimization and multi-level, multi-scale convolutional kernel technologies. By employing Fourier-based methods and iterative recursive decomposition strategies, we effectively separated periodic and trend components. Then, the periodic multi-level wavelet block was applied to extract the periodic interaction features, aiming to deeply mine the latent information of periodic components and enhance the model's long-term prediction capabilities. In this paper, we used the Informer model as the foundational framework for further research and development. In comparative experiments, our proposed model outperformed LSTM, Informer, and MICN by 61.4%, 51.7%, and 23.8%, respectively. In multi-time-span prediction, the model's error remained stable as the prediction span increased from 48 to 96 steps (from 0.059 to 0.067). Under multi-site conditions, the model achieved varying degrees of improvement over the baseline in three key evaluation metrics, with average increases of 35.2%, 35.6%, and 61.2%, respectively. In this study, we focused on the extraction of short-period features from tidal data, providing an innovative and reliable solution for tidal height prediction. The results are significant for tidal assessments and protective engineering construction.
Cellular membranes consist of lipid bilayers that separate the inside and outside of a cell. Surface receptors, among a multitude of membrane proteins incorporated in the bilayer, play a role in receiving signals from the environment outside. G-protein-coupled receptors are typical examples of the surface receptors, which receive chemical substances and commence signal transduction in the cell [1,2]. Yet another class of the surface receptors are ion channels, more than 400 of which are thought to be coded in the human genome [3]. The signals are typically chemical substances including hormones [4] and neurotransmitters [5]. For example, verapamil, a substance which belongs to phenylalkylamine class, inhibits the activity of L-type calcium channels in cardiomyocytes and thereby attenuates hypertension [6].
Yet another form of the signal, which affects the surface receptors, is the mechanical stimulus. Mechanosensitive ion channels (MS channels) change their conformation and function in response to mechanical stimuli, including pressure, shear stress, and osmolarity [7,8,9]. Function or malfunction of MS channels confer a vast range of biological processes, including tactile sensation [10], cell volume regulation [11], synapse formation [12], heart rate regulation [13], arrhythmia [14], pulmonary arterial hypertension [15], muscular dystrophy [16], polycystic kidney disease [17], and tumor progression [18]. Astonishingly enough, even the process of photoreception is suggested to be derived from MS channels in fly vision via membrane contraction evoked by light exposure [19]. Here, we discuss the role of MS channels in life activity at first, then the molecular structure, and the biophysical principle for their action (Figure 1).
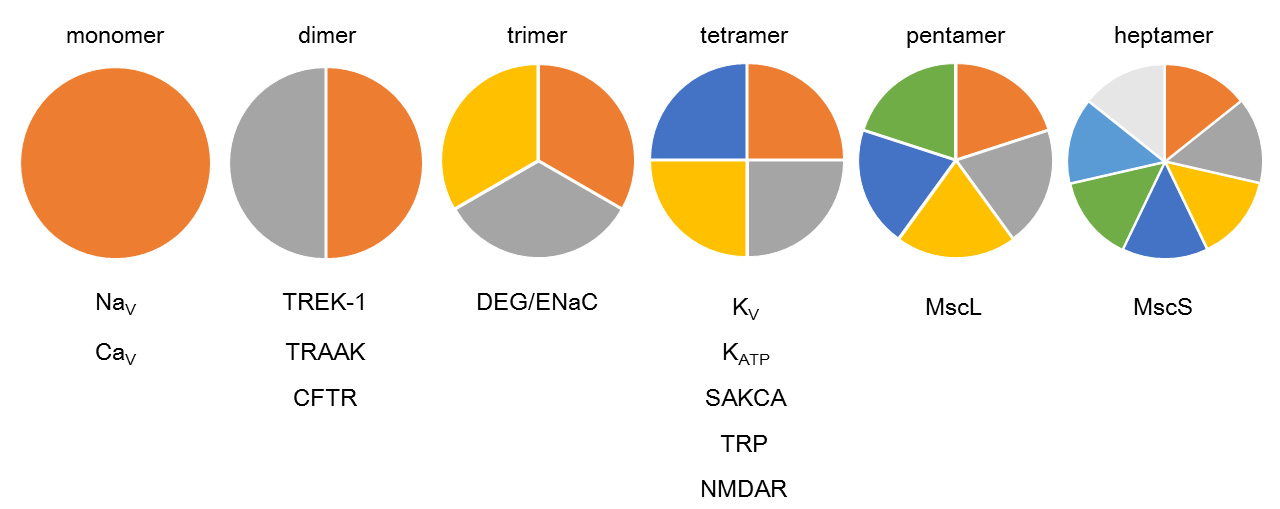 Figure 1. Number of pore forming subunits in mechanosensitive ion channels.
Figure 1. Number of pore forming subunits in mechanosensitive ion channels.
MS channels are expressed in a vast range of cells and involved in various biological functions [16,20,21,22,23,24,25,26]. Designations of MS channels and their location of expression are summarized in Table 1.
| Channels | Location | Ref. |
| Sodium channels | ||
| NaV1.5 | muscle, heart, gut | [43] |
| NaV1.6 | Neuron | [44] |
| DEG/ENaC | epithelial cells, distal nephrons, gastrointestinal tract, skin, mechanoreceptor neurons | [39,86] |
| Potassium channels | ||
| KV1 | [87] | |
| TREK-1 | Cardiomyocyte | [88,89] |
| TRAAK | neuron, retina | [74,78,90] |
| KATP | atrial myocyte | [91,92] |
| SAKCA | ventricular myocyte | [93] |
| KCNQ (KV7) | cochlear hair cells, peripheral nerve mechanoreceptor | [42] |
| Calcium channels | ||
| CaV1.2 | Cardiomyocyte, intestinal smooth muscle cell, knee joint neuron | [47,94] |
| Chloride channel | ||
| CFTR | epithelial cell, cardiomyocyte | [95,96] |
| atrial myocyte, SA node | ||
| Non-specific cation channels | ||
| TRPA1 | sensory neuron, inner ear hair cell, periodontal ligament cells, pancreatic beta cells | [20,27,28,29,31,97] |
| TRPC1 | cardiomyocyte, atrial volume receptor, spinal neuron | [32,33,34,98] |
| TRPC3 | sensory neuron, cochlear hair cell | [36] |
| TRPC6 | vascular smooth muscle cell, cardiomyocyte, sensory neuron, cochlear hair cell, podocyte | [36,37,99,100] |
| TRPM3 | nociceptive neuron, kidney, brain, retina, periodontal ligament cell | [101,102,103,104] |
| TRPM4 | Purkinje fiber, SA node, cerebral artery, fibroblast, endothelial cell, astrocyte | [105] |
| TRPM7 | atrial fibroblast, odontoblast, mesenchymal stem cell | [65,106] |
| TRPP1 | renal epithelial cells | |
| TRPP2 | renal epithelial cells, endocardial cell | [107] |
| TRPV1 | ||
| TRPV2 | cardiac muscle | |
| TRPV4 | atrial myocyte, atrial volume receptor, endocardial cell, cardiac fibroblast, osteoblast | [33,64,107,108] |
| NMDAR | Neuron | [109] |
The transient receptor potential (TRP) channels were first found in Drosophila and now 28 TRP subtypes are identified. TRPA1 (transient receptor potential cation channel, subfamily A, member 1) channel is widely expressed in tissues, including sensory neurons [27], inner ear hair cells [20], periodontal ligament cells [28], and pancreatic beta cells [29]. This channel was originally found as a cold sensor [30], but now it is also known as mechanosensor, for example, in the viscera [31].
TRPC1 (Transient receptor potential cation channel, subfamily C, member 1) channel is expressed in cardiomyocytes [32], sensory nerve ending of the atrial volume receptors [33], and spinal neurons [34]. TRPC1 regulates migration of renal epithelial cells by creating a calcium gradient, which determines the axis of cellular movement [35]. Considering embryonic development, migration can be described as a continuous process as cellular migration is a fundamental process in multicellular organisms, including humans. In the spinal axon, TRPC1 senses hardness of the surrounding environment and guides development of the axon [34]. TRPC3, together with TRPC6, is expressed in dorsal root ganglion neurons and is involved in touch sensation [36]. As later mentioned, TRPC1, 3, and 6 are expressed in the heart and involved in the development of cardiac hypertrophy. Besides, TRPC6 is also expressed in podocytes and is mechanically gated by membrane stretch [37]. Gain of function mutation of this protein causes nephrotic syndromes [38].
Blood vessels are sensing blood pressure and regulating their diameter to control blood flow appropriately. The epithelial sodium channel (ENaC) is expressed in epithelial cells, distal nephrons, gastrointestinal tract, skin, and cerebral arteries [39,40]. ENaC, together with transient receptor potential channels later mentioned, plays important roles in the pressure-induced myogenic response in cerebral arteries.
Hearing is one of the typical mechanosensitive processes. While TRPA1 is a well-known MS channel in the inner ear hair cells, response to auditory stimulus persists even after the knockdown of that protein [41]. On the other hand, KCNQ4, voltage-gated KQT-like subfamily Q member 4, is also expressed in the mechanosensitive hair cells of the inner ear and auditory neurons [42]. Mutation of this channel causes deafness (non-syndromic sensorineural deafness type 2). Intriguingly, KCNQ4 is also expressed in peripheral mechanoreceptors including hair follicle and Meissner corpuscle and is involved in tactile sensation. Other candidates for MS channels responsible for hearing are TRPC3/6. Co-expression of TRPC3 and TRPC6 is also observed in the cochlear hair cells, and double knockout of these genes shows impairment of hearing [36].
Several classes of voltage-gated cation channels are also regarded as mechanosensitive. For example, a voltage-gated sodium channel, NaV1.5, is expressed in electromechanical tissues, including the muscle, heart, and gut [43]. NaV1.6 channel is expressed in neurons [44]. A voltage-gated calcium channel, CaV1.2, is expressed in cardiomyocytes [45], intestinal smooth muscle cells [46], and knee joint afferents [47]. It is suggested that nociceptive mechanical stimuli to the knee joint evoke excitation of afferent nerve via CaV1.2 [47].
Mechanical stimuli affect the frequency of heartbeat. Stretch-activated ion channels are thought to play this role, and several MS channels are candidates for them. For example, TRPM4 channel is expressed in the heart and has a role in cardiac conduction [48]. Deletion of TRPM4 causes abnormality in cardiac electric conduction [49], and overexpression of the gene is the cause of progressive familial heart block type I [50]. Another candidate is TRPM7, which influences diastolic membrane depolarization and cardiac automaticity in the sinoatrial node [51]. This channel is expressed in atrial fibroblasts and plays a role in atrial fibrillation [52].
Cardiac hypertrophy is a consequence of long time exposure to pressure/volume overload. TRPC1/3/6 are candidates for the responsible channels for this mechanosensitive pathological process [53]. TRPC1 knockout mice lack maladaptive hypertrophic alteration in response to pressure overload [32]. In the patch clamp experiment using the TRPC1 knockout cardiomyocytes, TRPC-like current in response to mechanical stimulus was not observed [32]. On the other hand, blockade of TRPC3 and TRPC6 channels at the same time inhibit cardiac hypertrophy [54]. These channels are thought to form heterotetramers.
Of course the cellular mechanosensitivity does not serve only for pathological processes in the heart. TRPV4 (Transient receptor potential cation channel, subfamily V, member 4) and TRPP2 (Transient Receptor Potential Polycystic 2) channels are expressed in the endocardium and control development of cardiac valves via expression of Klf2a. In drosophila, TRPA channel is responsible for cardiac mechanosensitive response [55]. Thus, MS channels play indispensable roles for cardiac physiology and pathology.
Considering that bone is an organ, which bears loads due to gravity all the time, it is quite natural that this organ has specific contrivance for mechanosensitive response. Remodeling of bone is controlled both systemically and locally. Mechanical stress is a critical factor for bone mass regulation [56]. Unloading of mechanical stress causes severe decrease of bone mass. For example, when a tooth is lost, load to the root of the facing tooth will be lost and thereby the mass at nearby jawbone decreases. Other examples are bedridden patients and astronauts under microgravity [57].
The bone tissue is maintaining its physiological function due to the functions of osteoclasts, osteoblasts, lining cells (osteoblasts in a rest condition), and osteocytes (developed osteoblasts). These cells are maintaining homeostasis by sensing and transmitting mechanical stimuli. MS channels play a role in the bone mechanotransduction [58]. TRP [59] and BKCa [60]channels are thought to be mechanosensors in the bone.
Increase in DNA synthesis and decrease in ALP activity are observed in response to stretch stimulus in the osteoblast-like cells [61]. Among the factors, which induce bone formation, the calcium signaling pathway is thought to play an important role. There is a close relationship between MS channels and bone function. For example, mutation of TRPV4 gene causes skeletal dysplasias, including metatropic dysplasia and parastremmatic dysplasia [62]. Although unloading will usually cause bone loss, this mechanosensitive alteration is cancelled in TRPV4 deficient mice [63]. Besides, TRPV4 is involved in the flow-induced calcium signaling in osteoblasts [64]. Another TRP channel responsible for bone mechanosensitivity is TRPM7, which is expressed in human bone marrow mesenchymal stem cells and plays a pivotal role in osteogenesis [65].
Historically, many researches regarding MS channels have been done using bacterial mechanosensitive channel, especially MscL (mechanosensitive channel of large conductance), whose high-resolution three dimensional crystal structure was solved [66,67,68,69,70]. Using this structure, biophysical principles, which govern the dynamics of mechanosensitive conformational changes have been revealed by many groups steadily. Recently, high resolution three dimensional structures of eukaryote MS channels have been revealed eventually [71,72,73,74,75]. These structures will help us to reach a higher level of understanding cellular mechanosensitivity.
Whereas dedicated researches are still in progress, it seems that specific features responsible for the mechanosensitivity of ion channels are lacking at present. This is very different from the case of six transmembrane voltage-gated channels, which have well conserved amino acid sequence from bacteria to human, namely “voltage sensor”, at S4 transmembrane helix [76]. The structure of MS channels is very diverse. For example, the number of pore forming subunits ranges from two to seven (Fig.1). NaV and CaV channels have only one pore forming subunit which consists of four homologous domains. TREK-1 [77], TRAAK [78], and CFTR [73]channels have two pore forming subunits. Voltage gated (KV) and ATP-sensitive (KATP) potassium channels, SAKCA (stretch activated KCa) channels, TRP channels, and NMDAR (N-methyl-D-aspartate receptor) channels have four pore forming subunits. Some TRP channels form heterotetramers such as TRPC3/TRPC6. Bacterial mechanosensitive channels of large conductance (MscL) channel have five identical subunits, and mechanosensitive channels of small conductance (MscS) channel have seven identical subunits. So far any common or conserved “mechanosensor” domains have not been identified. Ion selectivity is also diverse; there are sodium, potassium, calcium, and chloride channels of various ion selectivity. Besides, most of the TRP channels are nonspecific cation channels. These facts imply that each MS channel has individual manner of conformational change in response to mechanical stimulus.
Interaction with other proteins is a critical factor, which determines the mechanosensitivity of the channel. For example, SAKCA channel has a pore-forming α-subunit and a regulatory β-subunit [79]. The α-subunit consists of four subunits and is regulated by the β-subunits in 1:1 stoichiometry (reviewed in [79]). The β-subunits significantly affect the kinetics of α-subunit. Recently, an intriguing fact regarding an MS channel and adhesome proteins was discovered. That is, TRPM4 channel is associated with cytoskeleton-related proteins such as filamin and vinculin, involved in disassembly of focal adhesions, thereby regulating cellular migration and contractility [80]. This finding will connect two areas hitherto individually treated MS channels and adhesomes together and deepen our understanding of cellular mechanosensitive response.
Every surface receptor, including MS channels, that resides in the cellular membrane that is composed of lipid bilayers. If an MS channel is to change its conformation in response to surrounding mechanical stimulus, it receives the stimulus from either or both of the following molecules: lipid and/or protein. The former case is called “bilayer mechanism”, in which the MS channel may receive energy for conformational change totally from the surrounding lipid bilayer and doesn’t require any associating proteins. Bacterial MscL and MscS are the typical examples of this mechanism. In eukaryotes, ENaC, TREK-1, TRAAK, TRPA1, TRPC1/6, TRPM3/4/7, NMDA receptor, and Piezo 1/2 channels are thought to work with the bilayer mechanism [81].
Phospholipids composed of lipid bilayers can be classified by several categories, including the length of acyl chain, the number of double bonds in acyl chain, the electric charge of lipid head groups, and the morphology of the lipid molecule in the membrane. These factors describe the lipid-channel interaction and determine the kinetics of the MS channel. For example, MscL channels are easy to open in lipids with shorter acyl chains [82]. Another factor, which is important for the MS channel activity, is curvature of the lipid bilayer. Some phospholipids (such as lysophosphatidylcholine, which have only one acyl chain) and amphipathic substance (such as chlorpromazine), bend the lipid bilayer locally and change the pressure profile in the bilayers [83]. With regard to the pressure profile, spider toxin GsMTx-4 is often used to block the activity of the “bilayer mechanism” channels because it interacts with membrane lipids and alters the profile.
Recently, more specific lipid-channel interactions were reported. In the case of TRAAK channel, an acyl chain extrudes into a small cavity of the TRAAK protein by blocking the hole in the resting state. Interestingly, however, this blockade is released along with the rotation of transmembrane helices in the conducting state [74].
While we discussed the “bilayer mechanism” so far, eukaryotic cells usually have solid cytoskeletal networks underneath the surface lipid bilayers, which prevent direct force transmission from the lipid bilayers to the MS channel. Some MS channels require binding to associating protein(s), such as cytoskeletal proteins and/or extracellular matrix proteins, for their activation in response to mechanical stimulus. This case is called “tethered mechanism”. ENaC [84] and TRP [85]channels are thought to work in this way. This mechanism is characterized in the touch receptor of Caenorhabditis elegans. For the touch receptor ENaC to open, MEC-7 (beta-tubulin) and MEC-12 (alpha-tubulin) are necessary. Mechanotransduction at the cochlear hair cells is thought to be a typical example of this “tethered mechanism”.
Mechanotransduction is fundamental to life activity. Cellular surface receptors reside at the border between inside and outside of the cell, and ion channels serve as the earliest messenger in the cellular signaling pathway. MS channels play indispensable roles in tissue development, cardiovascular regulation, and sensory signal transduction. Knowledge obtained from researches regarding MS channels will contribute to understand the physiology and pathology of life, and ultimately, to better our life.
This work was supported by a grant from JSPS KAKENHI (26220203).
The authors declare that there is no conflict of interests.
| [1] |
T. Bongarts Lebbe, H. Rey-Valette, É. Chaumillon, G. Camus, R. Almar, A. Cazenave, et al., Designing coastal adaptation strategies to tackle sea level rise, Front. Mar. Sci., 8 (2021), 740602. https://doi.org/10.3389/fmars.2021.740602 doi: 10.3389/fmars.2021.740602

|
| [2] |
G. Griggs, B. G. Reguero, Coastal adaptation to climate change and sea-level rise, Water, 13 (2021), 2151. https://doi.org/10.3390/w13162151 doi: 10.3390/w13162151

|
| [3] | A. T. Doodson, The analysis and predictions of tides in shallow water, Int. Hydrogr. Rev., 33 (1958), 85–126. |
| [4] |
R. E. Kalman, A new approach to linear filtering and prediction problems, J. Basic Eng., 82 (1960), 35–45. https://doi.org/10.1115/1.3662552 doi: 10.1115/1.3662552

|
| [5] |
G. Evensen, Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics, J. Geophys. Res., 99 (1994), 10143–10162. https://doi.org/10.1029/94JC00572 doi: 10.1029/94JC00572

|
| [6] |
Y. Yang, Y. Gao, Z. Wang, X. Li, H. Zhou, J. Wu, Multiscale-integrated deep learning approaches for short-term load forecasting, Int. J. Mach. Learn. Cybern., 15 (2024), 6061–6076. https://doi.org/10.1007/s13042-024-02302-4 doi: 10.1007/s13042-024-02302-4

|
| [7] |
S. Zhang, Z. Zhao, J. Wu, Y. Jin, D. S. Jeng, S. Li, et al., Solving the temporal lags in local significant wave height prediction with a new VMD-LSTM model, Ocean Eng., 313 (2024), 119385. https://doi.org/10.1016/j.oceaneng.2024.119385 doi: 10.1016/j.oceaneng.2024.119385

|
| [8] |
J. C. Yin, A. N. Perakis, N. Wang, An ensemble real-time tidal level prediction mechanism using multiresolution wavelet decomposition method, IEEE Trans. Geosci. Remote Sensing, 56 (2018), 4856–4865. https://doi.org/10.1109/TGRS.2018.2841204 doi: 10.1109/TGRS.2018.2841204

|
| [9] |
T. L. Lee, Back-propagation neural network for long-term tidal predictions, Ocean Eng., 31 (2004), 225–238. https://doi.org/10.1016/S0029-8018(03)00115-X doi: 10.1016/S0029-8018(03)00115-X

|
| [10] |
N. Portillo Juan, V. Negro Valdecantos, Review of the application of artificial neural networks in ocean engineering, Ocean Eng., 259 (2022), 111947. https://doi.org/10.1016/j.oceaneng.2022.111947 doi: 10.1016/j.oceaneng.2022.111947

|
| [11] |
C. L. Giles, G. M. Kuhn, R. J. Williams, Dynamic recurrent neural networks: Theory and applications, IEEE Trans. Neural Netw., 5 (1994), 153–156. https://doi.org/10.1109/TNN.1994.8753425 doi: 10.1109/TNN.1994.8753425

|
| [12] |
S. Fan, N. Xiao, S. Dong, A novel model to predict significant wave height based on long short-term memory network, Ocean Eng., 205 (2020), 107298. https://doi.org/10.1016/j.oceaneng.2020.107298 doi: 10.1016/j.oceaneng.2020.107298

|
| [13] |
L. H. Bai, H. Xu, Accurate estimation of tidal level using bidirectional long short-term memory recurrent neural network, Ocean Eng., 235 (2021), 108765. https://doi.org/10.1016/j.oceaneng.2021.108765 doi: 10.1016/j.oceaneng.2021.108765

|
| [14] |
Q. R. Luo, H. Xu, L. H. Bai, Prediction of significant wave height in hurricane area of the Atlantic Ocean using the Bi-LSTM with attention model, Ocean Eng., 266 (2022), 112747. https://doi.org/10.1016/j.oceaneng.2022.112747 doi: 10.1016/j.oceaneng.2022.112747

|
| [15] |
J. Oh, K. D. Suh, Real-time forecasting of wave heights using EOF-wavelet-neural network hybrid model, Ocean Eng., 150 (2018), 48–59. https://doi.org/10.1016/j.oceaneng.2017.12.044 doi: 10.1016/j.oceaneng.2017.12.044

|
| [16] |
H. H. H. Aly, Intelligent optimised deep learning hybrid models of neuro wavelet, Fourier series and recurrent Kalman filter for tidal currents constitutions forecasting, Ocean Eng., 218 (2020), 108254. https://doi.org/10.1016/j.oceaneng.2020.108254 doi: 10.1016/j.oceaneng.2020.108254

|
| [17] | A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, et al., Attention is all you need, in Advances in Neural Information Processing Systems, 30 (2017), 5998–6008. https://doi.org/10.48550/arXiv.1706.03762 |
| [18] |
S. Wang, Z. Huang, B. Zhang, X. Heng, Y. Jiang, X. Sun, Plot-aware Transformer for recommender systems, Electron. Res. Arch., 31 (2023), 3169–3186. https://doi.org/10.3934/era.2023160 doi: 10.3934/era.2023160

|
| [19] |
Y. Li, X. Wang, Y. Guo, CNN-Trans-SPP: A small Transformer with CNN for stock price prediction, Electron. Res. Arch., 32 (2024), 6717–6732. https://doi.org/10.3934/era.2024314 doi: 10.3934/era.2024314

|
| [20] |
J. Wan, N. Xia, Y. Yin, X. Pan, J. Hu, J. Yi, TCDformer: A transformer framework for non-stationary time series forecasting based on trend and change-point detection, Neural Netw., 173 (2024), 106196. https://doi.org/10.1016/j.neunet.2024.106196 doi: 10.1016/j.neunet.2024.106196

|
| [21] | H. Zhou, S. Zhang, J. Peng, S. Zhang, J. Li, H. Xiong, et al., Informer: Beyond efficient transformer for long sequence time-series forecasting, in Proceedings of the AAAI Conference on Artificial Intelligence, 35 (2021), 11106–11115. https://doi.org/10.48550/arXiv.2012.07436 |
| [22] |
H. Wu, J. Xu, J. Wang, M. Long, Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting, Adv. Neural Inf. Process. Syst., 34 (2021), 22419–22430. https://doi.org/10.48550/arXiv.2106.13008 doi: 10.48550/arXiv.2106.13008

|
| [23] |
T. Zhou, Z. Ma, Q. Wen, X. Wang, L. Sun, R. Jin, FEDformer: Frequency enhanced decomposed transformer for long-term series forecasting, J. Int. Law Policy, 3 (2022), 321–322. https://doi.org/10.48550/arXiv.2201.12740 doi: 10.48550/arXiv.2201.12740

|
| [24] | Y. Nie, N. H. Nguyen, P. Sinthong, J. Kalagnanam, A time series is worth 64 words: Long-term forecasting with transformers, in International Conference on Learning Representations, (2022). https://doi.org/10.48550/arXiv.2211.14730 |
| [25] | Y. Liu, H. Wu, J. Wang, M. Long, Non-stationary transformers: exploring the stationarity in time series forecasting, preprint, arXiv: 2205.14415. https://doi.org/10.48550/arXiv.2205.14415 |
| [26] |
Y. Liu, T. Hu, H. Zhang, H. Wu, S. Wang, L. Ma, M. Long, iTransformer: inverted transformers are effective for time series forecasting, J. Int. Law Policy, 3 (2023), 321–322. https://doi.org/10.48550/arXiv.2310.06625 doi: 10.48550/arXiv.2310.06625

|
| [27] | Y. H. H. Tsai, S. Bai, M. Yamada, L. P. Morency, R. Salakhutdinov, Transformer dissection: A unified understanding of transformer's attention via the lens of kernel, preprint, arXiv: 1908.11775. https://doi.org/10.48550/arXiv.1908.11775 |
| [28] |
S. G. Mallat, A theory for multiresolution signal decomposition: the wavelet representation, IEEE Trans. Pattern Anal. Mach. Intell., 11 (1989), 674–693. https://doi.org/10.1109/34.192463 doi: 10.1109/34.192463

|
| [29] |
S. G. Venkatesh, S. K. Ayyaswamy, S. Raja Balachandar, The Legendre wavelet method for solving initial value problems of Bratu-type, Comput. Math. Appl., 63 (2012), 1287–1295. https://doi.org/10.1016/j.camwa.2011.12.069 doi: 10.1016/j.camwa.2011.12.069

|
| [30] |
A. A. Abdulrahman, F. S. Tahir, Face recognition using enhancement discrete wavelet transform based on MATLAB, Int. J. Eng. Comput. Sci., 23 (2021), 1128–1136. https://doi.org/10.11591/ijeecs.v23.i2.pp1128-1136 doi: 10.11591/ijeecs.v23.i2.pp1128-1136

|
| [31] |
N. Zheng, H. Chai, Y. Ma, L. Chen, P. Chen, Hourly sea level height forecast based on GNSS-IR by using ARIMA model, Remote Sens., 43 (2022), 3387–3411. https://doi.org/10.1080/01431161.2022.2091965 doi: 10.1080/01431161.2022.2091965

|
| [32] |
D. Lee, S. Lee, J. Lee, Standardization in building an ANN-based mooring line top tension prediction system, Int. J. Nav. Archit. Ocean Eng., 14 (2022), 100421. https://doi.org/10.1016/j.ijnaoe.2021.11.004 doi: 10.1016/j.ijnaoe.2021.11.004

|
| [33] | J. Hu, L. Shen, G. Sun, Squeeze-and-excitation networks, in Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, (2018), 7132–7141. https://doi.org/10.1109/CVPR.2018.00745 |
| [34] |
H. Han, Z. Liu, M. Barrios, J. Li, Z. Zeng, N. Sarhan, et al., Time series forecasting model for non-stationary series pattern extraction using deep learning and GARCH modelling, J. Cloud Comput., 13 (2024), 2. https://doi.org/10.1186/s13677-023-00576-7 doi: 10.1186/s13677-023-00576-7

|
| [35] | I. Yanovitzky, A. VanLear, Time series analysis: Traditional and contemporary approaches, in The SAGE Sourcebook of Advanced Data Analysis Methods for Communication Research (eds. A. F. Hayes, M. D. Slater, L. B. Snyder), Sage Publications, (2008), 89–124. https://doi.org/10.4135/9781452272054.n4 |
| [36] | R. B. Cleveland, W. S. Cleveland, J. E. McRae, I. Terpenning, STL: A seasonal-trend decomposition procedure based on loess, J. Off. Stat., 6 (1990), 3–73. |
| [37] | C. Nontapa, C. Kesamoon, N. Kaewhawong, P. Intrapaiboon, A new time series forecasting using decomposition method with SARIMAX model, in Neural Information Processing, Communications in Computer and Information Science, 1333 (2020), 743–751. https://doi.org/10.1007/978-3-030-63823-8_84 |
| [38] |
T. Kim, B. R. King, Time series prediction using deep echo state networks, Neural Comput. Appl., 32 (2020), 17769–17787. https://doi.org/10.1007/s00521-020-04948-x doi: 10.1007/s00521-020-04948-x

|
| [39] | H. Wu, T. Hu, Y. Liu, H. Zhou, J. Wang, M. Long, TimesNet: Temporal 2D-variation modeling for general time series analysis, in International Conference on Learning Representations, (2022). https://doi.org/10.48550/arXiv.2210.02186 |
| [40] | A. R. Abdullah, N. M. Saad, A. Zuri, Power quality monitoring system utilizing periodogram and spectrogram analysis techniques, in Asean Virtual Instrumentation Applications Contest, (2007). https://doi.org/10.13140/2.1.3109.1841 |
| [41] | C. Samson, V. U. K. Sastry, A novel image encryption supported by compression using multilevel wavelet transform, Int. J. Adv. Comput. Sci. Appl., 3 (2012). https://doi.org/10.14569/IJACSA.2012.030926 |
| [42] | S. Liu, H. Yu, C. Liao, J. Li, W. Lin, A. X. Liu, et al., Pyraformer: low-complexity pyramidal attention for long-range time series modelling and forecasting, in Proceedings of the 10th International Conference on Learning Representations, 2022. Available from: https://openreview.net/forum?id = 0EXmFzUn5I. |
| [43] | H. Wang, J. Peng, F. Huang, J. Wang, J. Chen, Y. Xiao, MICN: Multi-scale local and global context modelling for long-term series forecasting, in International Conference on Learning Representations, 2023. Available from: https://openreview.net/forum?id = zt53IDUR1U. |
| [44] | M. Liu, A. Zeng, M. Chen, Z. Xu, Q. Lai, L. Ma, et al., SCINet: time series modelling and forecasting with sample convolution and interaction, in Advances in Neural Information Processing Systems, 35 (2022), 5816–5828. https://doi.org/10.48550/arXiv.2106.09305 |
| [45] | A. Zeng, M. Chen, L. Zhang, Q. Xu, Are transformers effective for time series forecasting?, in Proceedings of the AAAI Conference on Artificial Intelligence, 37 (2023), 11121–11128. https://doi.org/10.48550/arXiv.2205.13504 |
| 1. | Helmut Barz, Almut Schreiber, Ulrich Barz, Nerve impulse propagation: Mechanical wave model and HH model, 2020, 137, 03069877, 109540, 10.1016/j.mehy.2019.109540 | |
| 2. | Volha Liaudanskaya, Disha Sood, David L. Kaplan, 2019, 9780128098806, 391, 10.1016/B978-0-12-809880-6.00024-2 | |
| 3. | Benjamin Drukarch, Hanna A. Holland, Martin Velichkov, Jeroen J.G. Geurts, Pieter Voorn, Gerrit Glas, Henk W. de Regt, Thinking about the nerve impulse: A critical analysis of the electricity-centered conception of nerve excitability, 2018, 169, 03010082, 172, 10.1016/j.pneurobio.2018.06.009 | |
| 4. | Bernhard Schuster, Uwe B. Sleytr, 2020, Chapter 12, 978-1-4939-9868-5, 195, 10.1007/978-1-4939-9869-2_12 | |
| 5. | Andrew S. Johnson, William Winlow, The Soliton and the Action Potential – Primary Elements Underlying Sentience, 2018, 9, 1664-042X, 10.3389/fphys.2018.00779 | |
| 6. | Maryam Rahmati, Eduardo A. Silva, Janne E. Reseland, Catherine A. Heyward, Håvard J. Haugen, Biological responses to physicochemical properties of biomaterial surface, 2020, 49, 0306-0012, 5178, 10.1039/D0CS00103A | |
| 7. | Hui Yin Nam, Malliga Raman Murali, Raja Elina Ahmad, Belinda Pingguan-Murphy, Hanumantha Rao Balaji Raghavendran, Tunku Kamarul, Mechanical Strain-Mediated Tenogenic Differentiation of Mesenchymal Stromal Cells Is Regulated through Epithelial Sodium Channels, 2020, 2020, 1687-966X, 1, 10.1155/2020/5385960 | |
| 8. | Ken Takahashi, Mechanosensor, 2016, 128, 0030-1558, 61, 10.4044/joma.128.61 | |
| 9. | Neil Ibata, Eugene M. Terentjev, Why exercise builds muscles: titin mechanosensing controls skeletal muscle growth under load, 2021, 120, 00063495, 3649, 10.1016/j.bpj.2021.07.023 | |
| 10. | Fangtao Mao, Yuehua Yang, Hongyuan Jiang, Endocytosis and exocytosis protect cells against severe membrane tension variations, 2021, 120, 00063495, 5521, 10.1016/j.bpj.2021.11.019 | |
| 11. | Philippe Germain, Anthony Delalande, Chantal Pichon, Role of Muscle LIM Protein in Mechanotransduction Process, 2022, 23, 1422-0067, 9785, 10.3390/ijms23179785 | |
| 12. | Fangtao Mao, Yuehua Yang, Hongyuan Jiang, Electromechanical model for object roughness perception during finger sliding, 2022, 121, 00063495, 4740, 10.1016/j.bpj.2022.09.014 | |
| 13. | Chiara Dionisi, Marine Chazalon, Myriam Rai, Céline Keime, Virginie Imbault, David Communi, Hélène Puccio, Serge N Schiffmann, Massimo Pandolfo, Proprioceptors-enriched neuronal cultures from induced pluripotent stem cells from Friedreich ataxia patients show altered transcriptomic and proteomic profiles, abnormal neurite extension, and impaired electrophysiological properties, 2022, 5, 2632-1297, 10.1093/braincomms/fcad007 |
| Channels | Location | Ref. |
| Sodium channels | ||
| NaV1.5 | muscle, heart, gut | [43] |
| NaV1.6 | Neuron | [44] |
| DEG/ENaC | epithelial cells, distal nephrons, gastrointestinal tract, skin, mechanoreceptor neurons | [39,86] |
| Potassium channels | ||
| KV1 | [87] | |
| TREK-1 | Cardiomyocyte | [88,89] |
| TRAAK | neuron, retina | [74,78,90] |
| KATP | atrial myocyte | [91,92] |
| SAKCA | ventricular myocyte | [93] |
| KCNQ (KV7) | cochlear hair cells, peripheral nerve mechanoreceptor | [42] |
| Calcium channels | ||
| CaV1.2 | Cardiomyocyte, intestinal smooth muscle cell, knee joint neuron | [47,94] |
| Chloride channel | ||
| CFTR | epithelial cell, cardiomyocyte | [95,96] |
| atrial myocyte, SA node | ||
| Non-specific cation channels | ||
| TRPA1 | sensory neuron, inner ear hair cell, periodontal ligament cells, pancreatic beta cells | [20,27,28,29,31,97] |
| TRPC1 | cardiomyocyte, atrial volume receptor, spinal neuron | [32,33,34,98] |
| TRPC3 | sensory neuron, cochlear hair cell | [36] |
| TRPC6 | vascular smooth muscle cell, cardiomyocyte, sensory neuron, cochlear hair cell, podocyte | [36,37,99,100] |
| TRPM3 | nociceptive neuron, kidney, brain, retina, periodontal ligament cell | [101,102,103,104] |
| TRPM4 | Purkinje fiber, SA node, cerebral artery, fibroblast, endothelial cell, astrocyte | [105] |
| TRPM7 | atrial fibroblast, odontoblast, mesenchymal stem cell | [65,106] |
| TRPP1 | renal epithelial cells | |
| TRPP2 | renal epithelial cells, endocardial cell | [107] |
| TRPV1 | ||
| TRPV2 | cardiac muscle | |
| TRPV4 | atrial myocyte, atrial volume receptor, endocardial cell, cardiac fibroblast, osteoblast | [33,64,107,108] |
| NMDAR | Neuron | [109] |
| Channels | Location | Ref. |
| Sodium channels | ||
| NaV1.5 | muscle, heart, gut | [43] |
| NaV1.6 | Neuron | [44] |
| DEG/ENaC | epithelial cells, distal nephrons, gastrointestinal tract, skin, mechanoreceptor neurons | [39,86] |
| Potassium channels | ||
| KV1 | [87] | |
| TREK-1 | Cardiomyocyte | [88,89] |
| TRAAK | neuron, retina | [74,78,90] |
| KATP | atrial myocyte | [91,92] |
| SAKCA | ventricular myocyte | [93] |
| KCNQ (KV7) | cochlear hair cells, peripheral nerve mechanoreceptor | [42] |
| Calcium channels | ||
| CaV1.2 | Cardiomyocyte, intestinal smooth muscle cell, knee joint neuron | [47,94] |
| Chloride channel | ||
| CFTR | epithelial cell, cardiomyocyte | [95,96] |
| atrial myocyte, SA node | ||
| Non-specific cation channels | ||
| TRPA1 | sensory neuron, inner ear hair cell, periodontal ligament cells, pancreatic beta cells | [20,27,28,29,31,97] |
| TRPC1 | cardiomyocyte, atrial volume receptor, spinal neuron | [32,33,34,98] |
| TRPC3 | sensory neuron, cochlear hair cell | [36] |
| TRPC6 | vascular smooth muscle cell, cardiomyocyte, sensory neuron, cochlear hair cell, podocyte | [36,37,99,100] |
| TRPM3 | nociceptive neuron, kidney, brain, retina, periodontal ligament cell | [101,102,103,104] |
| TRPM4 | Purkinje fiber, SA node, cerebral artery, fibroblast, endothelial cell, astrocyte | [105] |
| TRPM7 | atrial fibroblast, odontoblast, mesenchymal stem cell | [65,106] |
| TRPP1 | renal epithelial cells | |
| TRPP2 | renal epithelial cells, endocardial cell | [107] |
| TRPV1 | ||
| TRPV2 | cardiac muscle | |
| TRPV4 | atrial myocyte, atrial volume receptor, endocardial cell, cardiac fibroblast, osteoblast | [33,64,107,108] |
| NMDAR | Neuron | [109] |