1. Introduction
Current techniques for observing bacterial motility are effectively two-dimensional because of the small depth of field provided by high numerical aperture objectives. Measurement of 3D trajectories is performed by approximating the third dimension from measured 2D trajectories, or by inferring the organisms' z positions as they travel into and out of focus. This severe limitation gives an incomplete image of the motility patterns observed. For example, a bacterium travelling vertically, parallel to the optical axis, will appear stationary using conventional techniques. A 2015 paper [1] calculated the systematic errors associated with observing bacterial motility when using conventional microscopic techniques and found that in addition to the effects of localization errors, 2D projection of the same volume introduce systematic errors in speed and turning angle measurements, compared to the correct speed and turning angle measurements found in 3D tracking. Similarly, observations obtained from 2D slicing are constrained to a thin focal plane thickness and ignore the vast majority of turning events; a bias against turning angles near 90° is also introduced. Finally, the boundaries of the sample chambers required for high-resolution imaging constrain motion in the z direction and affect the hydrodynamics of motility and the organisms' possible swimming ranges. Because of this, 2D methods do not capture the entire complexity of bacterial motility and shed doubt upon models of motility such as "run and tumble" or "flick" [2,3] the swimming patterns of most bacteria in an unconstrained 3D volume remain largely unknown.
Digital Holographic Microscopy (DHM) is based on the technique of holographic interferometry. In this technique, two physically separate beams of monochromatic and collimated light are used to create interference patterns at the digital detector when recombined at an angle. One beam passes through the sample of interest, which encodes its morphology and phase characteristics in the curvature of the transmitted light while the second beam remains undisturbed. This beam serves as a reference for the plane wave curvature before the light interacted with the sample. The digitally recorded hologram can then be reconstructed back into the original object wavefront using numerical methods [4].
The amplitude and phase distribution in the plane of the real image can be found from the hologram by the Fresnel-Kirchhoff integral [4,5]. If a plane wave illuminates the hologram located in the plane z=0, with an amplitude transmittance t(x,y), the Fresnel-Kirchhoff integral gives the complex wavefront, Γ(ξ,η), in the plane of the real image. The amplitude, A, in the real image can be calculated as the magnitude of the complex wavefront:
The phase information, ϕ, of the complex wavefront is obtained by:
Where ℑ(Γ) and ℜ(Γ) are the imaginary and real parts of the complex wavefront, respectively.
These methods allow for capture of an entire sample volume in a single hologram, followed by plane-by-plane reconstruction. This is ideal for sparse samples moving in three dimensions. Samples with multiple scatterers complicate the reconstruction; we have found that bacterial concentrations > 108 cells per ml are too dense for reconstruction using a Mach-Zehnder style DHM [6]. Reconstructed amplitude images correspond to brightfield images in ordinary light microscopy. Phase images have no direct counterpart and are an emerging field in and of themselves. Quantitative phase microscopic imaging has shown promise in diagnostics, label-free cell biology and more [7]. Because phase is recorded as modulo 2π, the problem of "unwrapping" multiples of 2π to calculate the true phase shift is one of the major challenges in this field.
DHM has been used to study distribution and swimming patterns of microorganisms on the scale of 10 µm: Algae in the laboratory [8] and plankton in the open ocean [9], to investigate dinoflagellate feeding behavior [10,11], to study the motility of algal zoospores [12] and to study cultured cells in the laboratory [13]. Nevertheless, papers on DHM imaging of micron-sized bacteria are few. We have constructed a DHM specifically for bacterial imaging, with sub-micron resolution, and have demonstrated its utility for detection of bacteria in extreme environments [14]. However, obtaining automated 3D tracks of bacterial cells with this instrument is still very challenging. Low contrast does not allow images to be thresholded and the presence of out-of-focus airy rings confuses detection algorithms. Amplitude images show a large amount of laser speckle noise, which is inherit to any imaging technique using coherent light sources. Some solutions have been presented in the literature. One paper successfully tracked bacteria using de-noising algorithms [2,15], but this approach is computationally intensive as well as labor-intensive. Holographic microscopy using incoherent light can eliminate speckle [16], but at the expense of depth of field, so that it is less useful for 3D tracking than coherent DHM. Synthetic aperture techniques can also improve resolution [17], but are used to improve images taken through low NA lenses. Operating at the diffraction limit makes such techniques difficult. Other super-resolution techniques, such as angular or wavelength multiplexing [18,19], require the sample to be stationary. Because studies of live bacteria require imaging at the order of the size of the wavelength of illumination light in a large volume, and because they move at tens to hundreds of microns per second, identifying and tracking them remains a challenge.
Phase images contain less speckle noise than amplitude images, but are subject to temporal phase noise, which results from the uncorrelated noise between the two beams of the interferometer. Most importantly, the contrast provided by bacterial cells is low. The contrast in phase images at a point (x,y) is provided by the spatially averaged phase difference Δϕ, which is related to the difference in indices of refraction between the medium (nm) and cell (nc) [20]:
|
Δϕ=2πλh(x,y)(nc(x,y)−nm)
|
(3)
|
Where λ is the wavelength of illuminating light and h is the thickness of the specimen at (x,y).
For bacteria, refractive indices differ from water only at the second decimal place (~1.38 vs. 1.33 for water) [21]. Thus, a typical phase shift for a 1 µm cell imaged at 405 nm is about π/4 or 45°, which can be difficult to resolve. The advantage to such small objects is that unwrapping is not required since phase shifts do not exceed 2π.
Automated particle tracking can generally be divided into two steps: Particle identification/detection (the spatial aspect), followed by particle tracking/linking (the temporal aspect). In 2014, Chenouard et al. [22] provided an objective comparative study of the most common particle tracking methods used in bioimaging. First, the authors identified three main factors that affect tracking performance: Dynamics (type of motion), density (number of particles per field of view), and signal-to-noise ratio (SNR). Second, they simulated a set of 2D and 3D image data based on these different factors. They then sent these image datasets to 14 teams who took up the challenge of identifying and tracking the particles using state-of-the-art methods. The teams then sent back their results, which showed that no one particle tracking method performed best for all data. The best identification methods were based on careful implementation and parameter tuning of any algorithm. The best tracking methods were the ones that used multiframe/multitrack optimization instead of the simpler nearest-neighbor linking. In addition, methods that made explicit use of the prior knowledge about the particle motion in each scenario were more successful than methods that did not.
In this work, a high precision machine-learning particle identification/detection algorithm based on linear logistic regression [23] is implemented for tracking of two test bacterial strains: Bacillus subtilis and Collwellia psychrerythraea. This algorithm is available in MATLAB as part of the Statistics and Machine Learning toolbox. This algorithm was used as a proof of concept; other machine learning algorithms such as decision tree model, support vector machine, or k-nearest neighbor classification model could also be implemented. The strains were chosen to represent relative extremes of prokaryotic size and motility. B. subtilis is large (5 µm long) and shows slow (~20 µm/s), undulating motility. C. psychrerythraea is a marine psychrophile that is very small (<1 µm) and swims at rapid speeds (over 40 µm/s even at subzero temperatures) [24].
The algorithm requires an expert user to identify bacteria from a training dataset, which is a small subset of the recorded data. Once trained using just a few examples, the algorithm is able to automatically detect organisms from the entire dataset. Performance is compared to manual tracking and found to give a precision of ≥ 91%. Once identified, bacteria may be tracked by the simple nearest-neighbor Hungarian linking algorithm [25]. This represents the first demonstration of an automated algorithm for tracking of bacteria using DHM. While much work on the subject remains to be done, this is a promising area of inquiry for anyone studying 3D bacterial motility.
2. Materials and methods
2.1. Design specifications of the Digital Holographic Microscope (DHM)
The DHM used in this study has been described elsewhere [14]. It is a twin-beam off-axis DHM, suitable for extreme environments in terms of mechanical and thermal stress. Specifications of this instrument are summarized in Table 1.
Table 1. Design specifications of the DHM instrument.
| Property |
Value |
Unit |
| Operating Wavelength |
405 |
nm |
| Objective focal length f0 |
7.6 |
mm |
| Objective Numerical Aperture |
0.30 |
|
| Relay lens focal length fr |
150 |
mm |
| System magnification |
19.7 |
|
| Lateral resolution |
0.7 |
µm |
| CCD pixel size |
3.45 × 3.45 |
µm × µm |
| Sample imaging volume |
360 × 360 × > 600 |
µm × µm × µm |
| Sampling Rate |
15 |
Frames per second |
| Instrument length |
400 |
mm |
2.2. Sample preparation
Bacillus subtilis was grown to mid-log phase in lysogeny broth (LB) in a shaking incubator at 30 ℃. Cultures were then diluted into motility medium (10 mM potassium phosphate, 10 mM NaCl, 0.1 mM EDTA, 0.1 mM glucose, pH 7.0) immediately before being inserted into the sample chamber and imaged using the DHM at room temperature.
Colwellia psychrerythraea was maintained in half-strength 2216 marine broth (Difco) at 6 ℃. Cultures were then diluted using the same Difco broth immediately before being inserted into the sample chamber and imaged using the DHM at room temperature.
The sample chamber consisted of high optical quality glass etalons separated by a PDMS gasket. Sample chamber depth was 800 µm with a total sample volume of 0.25 µL. Bacterial samples were pipetted into the chamber and videos were recorded using the commercial software KOALA (LynceeTec) [26] at maximum acquisition speed (7–15 frames per second).
Three separate datasets were acquired and analyzed. The first two consisted of either Bacillus subtilis or Colwellia psychrerythraea at low concentrations (on the order of 102 cells per mL), while the third consisted of Bacillus subtilis at a much higher concentration (on the order of 106 cells per mL). The two low concentration datasets were used to compare to "manually identified gold standard" tracks that were obtained by manually tracking each bacterium through (x,y,z,t) in order to quantify the level of error in the algorithm, while the high concentration data set was used to investigate its ability to track higher concentration samples. A summary of each dataset's properties are listed in Table 2.
Table 2. Properties of all three datasets acquired and analyzed.
| Property |
Dataset 1 |
Dataset 2 |
Dataset 3 |
| Sample Volume [µm3] |
360 × 360 × 252 |
360 × 360 × 392 |
360 × 360 × 500 |
| Bacteria Species |
Bacillus subtilis |
Colwellia psychrerythraea |
Bacillus subtilis |
| Concentration [cells per mL] |
≈ 102 |
≈ 102 |
≈ 106 |
| Object Volume and Shape |
≈ 8 µm3, elongated |
≈ 2 µm3, comma-shaped |
≈ 8 µm3, elongated |
| Number of z-planes |
201 |
157 |
201 |
| Number of time frames |
84 |
18 |
85 |
| Axial Resolution [µm] |
1.25 |
2.5 |
2.5 |
| Total Number of Bacteria in FOV |
8 |
6 |
149 |
2.3. Hologram reconstruction
KOALA (LynceeTec) was used for the holographic reconstruction of all datasets. The holograms of all datasets were numerically reconstructed into amplitude and phase images at a z spacing of 1.25 µm/slice and 2.50 µm/slice, respectively. Images were saved as 8-bit TIFF files. The phase reconstructions were used in the tracking of Dataset 1 and Dataset 2, while Dataset 3 was tracked by analyzing images obtained by the multiplication of the amplitude and phase reconstructions. By doing so, it was seen to increase contrast, which aids in the automated tracking of higher concentration datasets without introducing false positives.
2.4. Manual object identification
All analysis was performed on a custom built desktop computer, with an Intel Core i7-7800x CPU @ 3.50 GHz, 32.0 GB of Installed memory (RAM), running Windows 10 Pro and using MATLAB R2017b with the Image-Processing Toolbox and the Statistics and Machine Learning Toolbox installed.
Prior to the automated tracking of Datasets 1 and Datasets 2, manual tracks were compiled in order to quantify the performance of the automated tracking routine. Manual tracking was accomplished in two stages, both involving a human observer that would individually identify bacteria. In the first stage, raw holograms are analyzed by the observer. Because this is done before any numerical reconstruction, the raw holograms only provide (x,y,t) locations for a particular bacterium. The open source data visualization software FIJI (is just imageJ) was used with the "Manual Tracking" plugin [27]. Once these (x,y,t) coordinates are recorded, KOALA was used to numerically reconstruct the holograms at various focal planes. By knowing the (x,y,t) locations of bacteria, their respective z location can be found by cycling through the reconstructed focal planes and identifying the z-plane where a particular bacterium is in focus. With (x,y,z,t) coordinates for the bacteria in Datasets 1 and 2 compiled manually, quantifying the performance of the automated tracking routine is possible.
2.5. Validation metrics
To quantify the performance of the automated tracking algorithm, the manual tracks of Datasets 1 and 2 were used in order to calculate an Fβ score (F-score). The F-score is defined as:
Where β is a weighting factor, P is the statistical precision, and R is the statistical recall. Statistical precision is defined as:
And statistical recall is defined as:
Where Tp is the number of true positives, Fp is the number of false positives, and Fn is the number of false negatives.
The motivations that led to the development of this algorithm were to be able to extract statistically relevant motility characteristics of bacteria from a given dataset and not necessarily identify all bacteria present in the field of view. For this reason, precision is weighted higher than recall by defining β=0.5.
2.6. Automated particle identification and tracking
2.6.1. Pre-processing
All images that were analyzed with the automated tracking routine were subject to a pre-processing step in order to reduce noise in the image as well as normalize average pixel values from image to image. De-noising included calculating the mean image for a time sequence of images and subtracted that image from all images in that time sequence. By subtracting a temporally averaged image, all stationary artifacts of an image (e.g. speckle noise) are removed. Next, these mean subtracted images were band-pass filtered. This band-pass filtering was done by multiplying the Fourier Transform of an image with a binary mask matrix. The DHM used has been shown to operate at diffraction limited resolution, and so this absolute resolution limit was used as the upper cut-off frequency of the band pass filter, while the lower cut-off frequency was set to eliminate zero-frequency artifacts. For Dataset 3, the pre-processed amplitude and phase images were then multiplied together in order to further increase contrast.
2.6.2. Training
The linear logistic regression pixel classifier is a supervised learning algorithm that was implemented using MATLAB's Statistics and Machine Learning Toolbox. In order to train this classifier, a sample dataset is used to generate a classifier hw(x) as well as a pixel features matrix Xt. The pixel features that are used to construct Xt are summarized in Table 3.
Table 3. Pixel features used to train the classifier.
| Importance (descending order) |
Pixel Feature |
| 1 |
Absolute difference of pixel values |x−ˉx| |
| 2 |
Local image gradient |
| 3 |
Local standard deviation |
| 4 |
Absolute difference of pixel values (in z) |
| 5 |
Local neighborhood median value |
| 6 |
Total image standard deviation |
For a given sample dataset (x,y,z,t) coordinates are provided to the algorithm corresponding to the location of particles of interest. Pixel feature matrices are constructed near these coordinates along with a binary probability matrix ft, where ft∈{0,1}. Because absolute particle coordinates are known, this probability matrix contains zeros everywhere except for the pixels where a particle is located. Both the pixel feature matrix and the binary probability matrix are used to calculate the classifier, which is defined as:
Where wT is the transpose of a linear weighting matrix. There is no closed form solution for w and as a result a gradient descent iterative minimization approach is used such that:
|
wkm+1=wk−1m+αm∑i=1(ft,i−hk−1w(xi))xi
|
(8)
|
Where wkm+1 is the (m+1)th element of the kth iteration of the linear weighting matrix and α is gradient descent learning parameter. This learning parameter must be predefined and was chosen as α=−0.1.
2.6.3. Particle identification
With the classifier trained, arbitrary datasets can be used to construct pixel feature matrices (X). These matrices are then subsequently multiplied by the classifier to yield the probability matrix:
Where 0≤f≤1 the values of this matrix correspond to the probability that a particular pixel contains a particle of interest. A minimum probability threshold is then employed to decide whether or not a pixel is indeed a particle of interest.
2.6.4. Particle tracking
With (x,y,z,t) coordinates found for all particles of interest in the dataset, a "nearest neighbor" particle tracking algorithm is employed to identify identical particles across time sequences [25]. This algorithm requires inputs of spatial locations of particles at each time point to be analyzed. The tracking algorithm then operates in two stages. First, the algorithm compares the coordinates of particles in time point i to the coordinates in time point (i+1) and defines two coordinates as belonging to the same particle as the points with the smallest Euclidean distance between them across i and (i+1). The second step involves dealing with gaps. These gaps arise when a particle was not successfully identified in one or multiple frames, but reappears in subsequent frames. This stage is an iterative loop that identifies the location where trajectories end and searches subsequent time points for trajectories that begin near where the other ended. If the function is able to find a close enough pair of trajectories, then the two tracks become stitched together and the locations of the particle within the gap are calculated as a linear interpolation between the two known locations.
3. Results and discussion
With the manually tracked bacteria in Datasets 1 and 2, calculating an F-score was possible to quantify the performance of the automated tracking algorithm discussed in this work. For Dataset 1, the tracking algorithm yielded a precision of 98.9%, a recall of 57.1% and an F-score of 0.863. For Dataset 2, the tracking algorithm yielded a precision of 91.5%, a recall of 76.5% and an F-score of 0.880. The statistical performance of the automated tracking routine is summarized in Table 4.
Table 4. Performance statistics of automated tracking algorithm.
|
Dataset 1 |
Dataset 2 |
| Total number of points |
324 |
98 |
| Total number of points identified |
187 |
82 |
| True positives |
185 |
75 |
| False positives |
2 |
7 |
| False negatives |
139 |
23 |
| Precision |
98.8% |
91.5% |
| Recall |
57.1% |
76.5% |
| F-score |
0.863 |
0.880 |
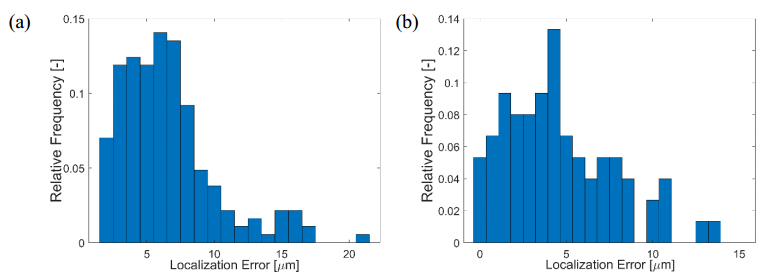
Of the bacteria that were identified in Datasets 1 and 2, the localization errors were quantified as the absolute Euclidean distance between the coordinates found by the algorithm and the coordinates obtained by manual tracking. The root-mean-squared (RMS) localization error of Dataset 1 was found to be 7 µm and 6 µm for Dataset 2. Figure 1 shows the histogram of localization errors from (a) Dataset 1 and (b) Dataset 2.
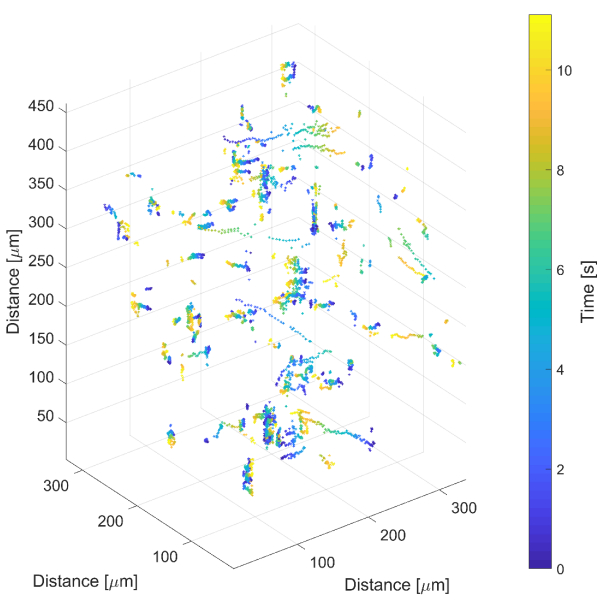
The tracking algorithm was also employed to track a dataset with a higher concentration of Bacillus subtilis (on the order of 106 cells per mL). At such a concentration, there are expected to be a range of 100 to 200 cells in the field of view of the DHM instrument at any one time. The tracking algorithm was able to identify 149 unique bacteria in this dataset, while a human observer was only able to identify 127 bacteria. The remaining 22 bacteria were noticed by the human observer only after they knew there were bacteria there. Figure 2 shows a three-dimensional plot of the trajectories extracted from the tracking algorithm of this dense sample. The trajectories are color coded with respect to time.
Swimming speeds of the tracked dataset were calculated as the root-sum-squared (RSS) of the x,y and z component velocities, such that:
|
vix(τ)=ΔxΔt=xi(τ+1)−xi(τ)t(τ+1)−t(τ)
|
(10A)
|
|
viy(τ)=ΔyΔt=yi(τ+1)−yi(τ)t(τ+1)−t(τ)
|
(10B)
|
|
viz(τ)=ΔzΔt=zi(τ+1)−zi(τ)t(τ+1)−t(τ)
|
(10C)
|
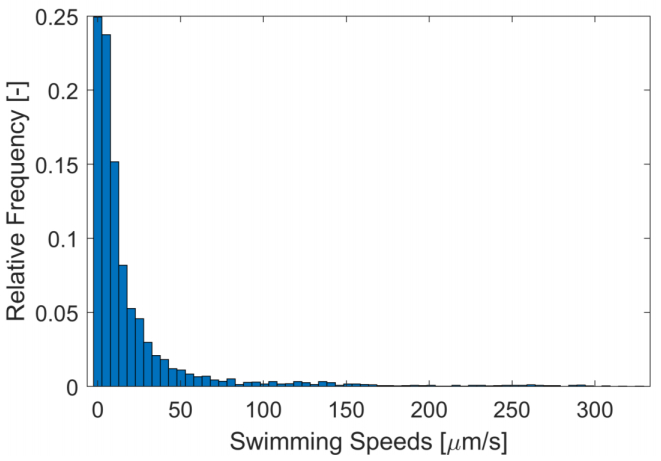
Where vij(τ) is the j-component velocity at time vij(τ) of the ith bacterium and |vi| is the absolute swimming speed of the ith bacterium. A histogram of the results is shown in Figure 3. The mean swimming speed was 23 ± 17 µm/s (standard deviation, n = 149) and the median swimming speed was 10 µm/s.
This shows that there were a considerable number of outliers, which is consistent with the experimental data. There were multiple very fast swimmers that shifted the mean. These values are in agreement with the literature on wild-type B. subtilis [28].
The motivations behind the development of this algorithm were to extract statistically significant motility characteristics of bacteria from a dataset in an automated manner. In doing so it was clear that statistical precision is more important than recall because in order to extract statistics from a dataset, not all bacteria need to necessarily be tracked, only a sufficient number of them to form an acceptable sample size. This reason justifies the relatively high number of false negatives in Datasets 1 and 2. Furthermore, although DHM allows three-dimensional imaging in real-time, it is susceptible to sources of noise that result in low signal to noise (SNR) ratios. The low SNR associated with DHM also helps explain the false negatives.
In the quantification of localization errors of this algorithm, it was found that there are RMS errors of 7 µm and 6 µm for Datasets 1 and 2, respectively. Because these errors were calculated relative to manual tracks, they are susceptible to human error as well. Any error in the centroid identification during manual tracking will affect the RMS error reported here.
Errors associated with Dataset 3 were not explicitly quantified, but rather are inferred upon by the error analysis conducted on the Dataset 1. This assumption is valid because Dataset 1 and 3 are identical other than the fact that Dataset 3 is at a higher bacterial concentration. It has been found that the average SNR obtained in DHM reconstructions is in fact a function of sample concentration, but the degradation of SNR from the concentration of Dataset 1 to Dataset 3 was found to be negligible [29].
A large hindrance of three-dimensional particle tracking is the data volumes associated with it. In the particular setup used in this work, 4 megapixel holograms (roughly 4 MB per hologram) were acquired at roughly 10 frames per second. Each hologram was then reconstructed into about 200 separate focal planes in both amplitude and phase. This results in a 400× increase in data size after numerical reconstruction (e.g. Dataset 3 was over 100 GB in size). Non-trivial software techniques must be employed in order to be able to analyze this volume of data with a modest computer. The algorithm described in this work employs these techniques in order to only occupy 8 GB of RAM at any one given time throughout the tracking process.
4. Conclusions
This work presents and validates a machine-learning identification algorithm based on linear logistic regressions that can identify microorganisms within DHM image reconstructions, with a precision of over 90% and localization error of roughly 7 µm. Identification was validated using two species of microorganisms of different sizes, without the use of any chemical contrast enhancement (e.g. fluorescent dyes).
The theoretical and mathematical foundation of this algorithm was introduced and discussed as well as the method in which it was implemented as a MATLAB routine.
A total of three datasets were analyzed using this algorithm consisting of Bacillus subtilis and Colwellia psychrerythraea. Two of the three datasets contained low concentrations of bacteria in order to allow for the quantization of error, while the third dataset contained a much higher concentration to illustrate its usefulness in practical biological imaging applications.
Although the data sizes associated with high spatial and temporal resolution three dimensional imaging are cumbersome, the algorithm developed in this work is able to track particles in arbitrarily large datasets (>100 GB) while only occupying 8 GB of RAM and modest CPU requirements. A fully annotated version of the software developed and used throughout this work is available for public use at: https://github.com/mbedross/MachineLearningObjectTracking.
Acknowledgments
The authors would like to acknowledge the Gordon and Betty Moore Foundation Grant Numbers 4037/4038 as the source of funding for this work, as well as the Keck Center at Caltech for hosting our collaborations.
Conflict of interest
The authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: