Reconstruction of initial heat distribution via Green function method

1.   Introduction

Many mathematical models of interest in the applications entail the coupling between a poroelastic medium and a fluid flowing in a hollow region outside of the matrix pores: It is the case, e.g., of the interaction between groundwater and surface waterbodies ^[34,49], between the blood-perfused cardiac tissue and the coronary flow ^[33,57], or between the interstitial Cerebrospinal Fluid (CSF) in the brain tissue and its flow in the hollow cerebral ventricles ^[12,25]. The latter is particularly relevant in the modeling of the waste clearance function played by CSF in the development of neurodegenerative diseases such as Alzheimer's ^[20,44]. Moreover, the CSF flow is strongly interconnected with the pulsatility of blood in the cerebral vasculature and capillaries ^[10,12], thus requiring for a Multiple-network Poroelasticity (MPE) model to account for the interstitial CSF and the blood flowing at different spatial scales in the porous tissue ^[29,43].

From the standpoint of finite element literature, interest has been paid to fluid-dynamics and poromechanics problems with the development and analysis of several methods, especially in the Discontinuous Galerkin (DG) class, including interior-penalty DG ^[8,51,52,63], staggered DG ^[27,48,69], and hybrid DG ^[3,16,19]. The coupling of the fluid and poroelastic systems yields a complex multi-physics problem, investigated in the numerical literature in the case of the Biot-Stokes model ^[2,11,54,68], also in the regime of large deformations ^[32], or for multilayered porous media coupled with Newtonian fluid flows ^[15,23]. However, almost no numerical analysis of the discretization of fluid-poromechanics equations with multiple porous compartments can be found in the literature, despite their relatively wide use in the applications ^[13,28,33]: The MPE system – without a coupled fluid problem – has been analyzed in ^[29,36,50], but the numerical analysis of the coupled MPE-Stokes problem can be found only in ^[40]. In the case of applications to brain function, the main challenges are the high complexity of the domain (encompassing intricate folds and tortuous channels) and the paramount role of stress and flow exchanges at the interface between the two physical domains. Therefore, a particularly suitable choice is the use of the Polytopal Discontinuous Galerkin (PolyDG) method. This method inherits many characteristics from "classical" DG methods, such as the natural support for local refinement, hanging nodes, and high-order polynomial degrees – that can guarantee low dispersion and dissipation errors – as well as the natural incorporation of interface conditions in the formulation, thanks to element-wise integration by parts. In addition to these, the PolyDG method also exhibits the following advantages:

● The use of general polytopal mesh elements enhances the geometrical flexibility of the method, particularly when the domain is geometrically complex and presents small-scale features: Using elements with a high number of edges/faces allows to attain geometrical accuracy without excessively increasing the number of mesh elements and thus the dimension of the discrete space;

● Element agglomeration is straightforwardly supported, and cost-effective agglomeration strategies have been developed to generate and employ polyhedral meshes ^[5,7,38]. This allows the construction of hierarchical meshes that can be used for multilevel iterative solvers and adaptive strategies (the latter, without the need of local remeshing);

● Very mild assumptions are made on the shape of the elements, thus improving the robustness of the method in practical applications with complex geometries, where it is difficult to ensure a good mesh quality ^[6].

Moreover, a polytopal mesh can be constructed by agglomeration starting from other grids, thus allowing to exploit several tools for the automatic generation of (possibly fine) simplicial/hexahedral mesh elements.

In this framework, the present work has four aims:

● Expanding and verifying the PolyDG method proposed in ^[40] in three-dimensional geometries;

● Assessing the computational advantage of employing a polytopal mesh instead of a classical hexahedral one, in the case of a 3D domain with small geometrical details;

● Extending the numerical method to include the physically-motivated Beavers-Joseph-Saffman (BJS) interface conditions and analyzing the stability and convergence of the resulting scheme. The BJS conditions play an essential role in practical applications, like in brain fluid mechanics or groundwater flows, because they take into account the friction and relative tangential velocity between the porous medium and the fluid in contact with it ^[25,61];

● Assessing the fluid-dynamics effects of modeling the CSF by either Stokes or Navier-Stokes equations, in the aforementioned multi-physics scenario and in the typical regime of brain waste clearance. Both fluid models have been used in the literature, but a direct quantitative comparison between the two is missing.

The paper is organized as follows. Section 2 describes the multiphysics mathematical model and its weak formulation, particularly discussing the imposition of interface conditions. The PolyDG space discretization method is introduced in Section 3 and its stability and convergence analysis is presented in Section 4. Time discretization is introduced in Section 5, while Section 6 reports some verification tests. Numerical results in an idealized geometry retaining the same topology of the brain and ventricles system, and set in a physiological physical regime, are discussed in Section 7, while Section 8 reports an assessment of the impact of the BJS condition and the advection term in Navier-Stokes equations on the fluid-dynamics of the system. A quantitative comparison between the polytopal-mesh-based discretization and a hexahedral one is reported in Section 9, in terms of the computational cost of solving a differential problem over a domain with small inclusions.

2.   The mathematical model

The modeling of multiphysics flow in the brain can entail complex mathematical equations, due to the softness of the cerebral tissue and the complexity of the interstitial space and the blood vessel network. However, to describe brain perfusion and CSF flow at the organ spatial scale and in the time frame of a heartbeat, the following assumptions are adopted in this work, in accordance with the literature ^{[25,28,40,64]}:

● Considering a small-deformation regime, the brain tissue is modeled by linear elastodynamics equations;

● Consistently, the equations and the boundary and interface conditions are formulated in the tissue's reference configuration;

● The interstitial space and the blood vessel network are homogenized over the whole organ, thus modeling the brain as a porous medium governed by Biot's equations;

● The fluids fully saturate the pores and capillary effects are negligible.

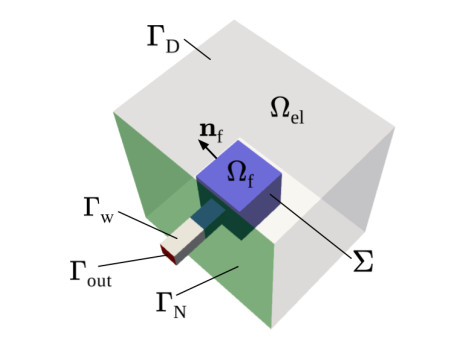
In this framework, we consider the coupling of a Multiple-Network Poroelasticity system and Navier-Stokes equations in a domain such as the one displayed in Figure 1.

The overall domain $\Omega\subset\mathbb R^d$ ($d = 2, 3$) is split into a poroelastic region $\Omega_ {{\text{el}}}$ and a fluid region $\Omega_ {{\text{f}}}$, separated by the interface $\Sigma = \overline{\Omega}_ {{\text{el}}}\cap\overline{\Omega}_ {{\text{f}}}$, which is assumed to be a piecewise smooth $(d-1)$-manifold. The poroelastic region is filled by an elastic solid body and $N_J$ fluid components, indicated by the elements of an index set $J$. Within this set, let us assume that only one component directly exchanges mass through $\Sigma$: We denote this component by ${{\text{E}}}\in J$. Considering a time interval $(0, T]$, the displacement of the solid matrix is denoted by ${\mathit{\boldsymbol{d}}}:\Omega_ {{\text{el}}}\times(0, T]\to\mathbb R^d$, its corresponding stress tensor is $\boldsymbol{\sigma}_ {{\text{el}}}({\mathit{\boldsymbol{{d}}}}) = 2\mu_ {{\text{el}}}\boldsymbol{\varepsilon}({\mathit{\boldsymbol{{d}}}})+\lambda(\nabla\cdot{\mathit{\boldsymbol{{d}}}})I,$ with $\boldsymbol{\varepsilon}({\mathit{\boldsymbol{{d}}}}) = \frac{1}{2}(\nabla{\mathit{\boldsymbol{{d}}}}+\nabla{\mathit{\boldsymbol{{d}}}}^T)$, and each of the fluid components is characterized by a pressure $p_ {{\text{j}}}:\Omega_ {{\text{el}}}\times(0, T]\to\mathbb R, {{\text{j}}}\in J$. For each compartment ${{\text{j}}}\in J$, we introduce the fluid's permeability and viscosity $k_ {{\text{j}}}, \mu_ {{\text{j}}}$, the specific storage coefficient $c_ {{\text{j}}}$ accounting for the fluid's inertia, the Biot-Willis coefficient $\alpha_ {{\text{j}}}$ relating the bulk moduli of the fluid and the solid matrix, and the external coupling coefficient $\beta_ {{\text{j}}}$ accounting for the effects of pressure deviation from its reference value. Moreover, for each pair $({{\text{j}}}, {{\text{k}}})\in J$ of compartments, the exchange of mass is related to a coupling transfer coefficient $\beta_{ {{\text{j}}} {{\text{k}}}}$. In the fluid domain $\Omega_ {{\text{f}}}$, velocity, pressure, and viscous stress are denoted by ${\mathit{\boldsymbol{{u}}}}$, $p$, and $\boldsymbol{\tau}_ {{\text{f}}}({\mathit{\boldsymbol{{u}}}}) = 2\mu_ {{\text{f}}}\boldsymbol{\varepsilon}({\mathit{\boldsymbol{{u}}}})$, respectively. The physical parameters in the above definitions and in the following are assumed to be constant.

In terms of boundary conditions on $\partial\Omega = (\partial\Omega_ {{\text{el}}}\cup\partial\Omega_ {{\text{f}}})\setminus\Sigma$, we consider a portion $\Gamma_\text{out}\subset(\partial\Omega_ {{\text{f}}}\setminus\Sigma)$ of the fluid domain boundary as an outlet and the remaining part $\Gamma_ {{\text{w}}} = \partial\Omega_ {{\text{f}}}\setminus(\Sigma\cup\Gamma_\text{out})$ as a solid wall, and also the poroelastic domain boundary $\partial\Omega_ {{\text{el}}}\setminus\Sigma$ is partitioned into a Dirichlet and a Neumann boundary, denoted by $\Gamma_\text{D}$ and $\Gamma_\text{N}$, respectively (see Figure 1).

In this framework, the coupled fluid-poroelastic system reads as follows:

with suitable definition of the source terms

of the boundary data $\overline{p}^\text{out}:\Gamma_\text{out}\times(0, T]\to\mathbb R$ representing the external normal stress at the outlet, and of the initial conditions ${\mathit{\boldsymbol{{d}}}}_0:\Omega_ {{\text{el}}}\to\mathbb R^d, \dot{{\mathit{\boldsymbol{{d}}}}}_0:\Omega_ {{\text{el}}}\to\mathbb R^d, {\mathit{\boldsymbol{{u}}}}_0:\Omega_ {{\text{f}}}\to\mathbb R^d, p_{ {{\text{j}}} 0}:\Omega_ {{\text{el}}}\to\mathbb R, {{\text{j}}}\in J$. Throughout the paper, these data are assumed to be sufficiently regular.

At the fluid-poroelastic interface $\Sigma$, the following conditions are imposed:

where $({\mathit{\boldsymbol{{\mathtt{v}}}}})_{\text{tg}} = {\mathit{\boldsymbol{{\mathtt{v}}}}}-({\mathit{\boldsymbol{{\mathtt{v}}}}}\cdot{\mathit{\boldsymbol{{n}}}}_ {{\text{f}}}){\mathit{\boldsymbol{{n}}}}_ {{\text{f}}}$ denotes the tangential component of a vector ${\mathit{\boldsymbol{{\mathtt{v}}}}}\in\mathbb R^d$ along $\Sigma$. Total stress balance is expressed by condition (2.2a), and the normal stress of the fluid at the pores is balanced only by the pressure of compartment ${{\text{E}}}$ (see (2.2b)).

Along the tangential direction, the shear stress is assumed to be proportional to the tangential velocity jump between the fluid and the poroelastic medium (see (2.2e)): This is the Beavers-Joseph-Saffman (BJS) condition, which accounts for the effects of the fluid velocity boundary layer that is created at a fluid-porous medium interface, due to viscous shear stress ^[14]. Notice that, although the condition is written in terms of the total stress in (2.2e), pressure does not actually play a role in the balance, since $({\mathit{\boldsymbol{{n}}}}_ {{\text{f}}})_\text{tg} = 0$. The BJS condition has been adopted in the literature to model CSF perfusion interfaces ^[25,35], and it can significantly affect the velocity profile near the interface, depending on the value of the slip rate parameter $\gamma$. To quantitatively assess these effects, in Section 7 we are going to compare the results obtained with the BJS condition against those obtained with the free-slip condition (corresponding to $\gamma = 0$) employed, e.g., in ^[40].

Remark 1 (Application to brain fluid-poromechanics). The mathematical system (2.1)-(2.2) considered here can be used to model fluid-poromechanics interaction in the brain ^[25,29,40], with the fluid domain corresponding to the brain ventricles filled with CSF and the cerebral tissue being the solid matrix perfused by blood and extracellular CSF. In the fluid compartments $J = \{\text{A}, \text{C}, \text{V}, {{\text{E}}}\}$, $\text{A}, \text{C}, \text{V}$ can represent the arterial, capillary, and venous blood networks, while the extracellular CSF (${{\text{E}}}\in J$) is the only compartment exchanging mass with the three-dimensional CSF (cf. (2.2c)-(2.2d)), due to the blood-brain barrier. In this context, the compartments represent separate pore networks at different space scales, and the exchange of mass among them is homogenized by the terms involving the coefficients $\beta_{ {{\text{j}}} {{\text{k}}}}$. Moreover, we consider the fluids to fully saturate the pores. In Sections 7 and 8, numerical experiments will be discussed in the framework of this brain fluid-poromechanics application.

The solution variables belong to the following functional spaces:

where the notation $L^2(0, T; H), H^k(0, T; H), k = 1, 2,$ denotes the time-dependent Bochner spaces associated to a Sobolev space $H$, and

where $H^1(\Omega)$ denotes the classical Sobolev space of order 1 over $L^2(\Omega)$.

The weak formulation of problem (2.1) reads as follows: Find $({\mathit{\boldsymbol{{d}}}}, \{p_ {{\text{j}}}\}_{ {{\text{j}}}\in J}, {\mathit{\boldsymbol{{u}}}}, p)\in \mathscr{D}\times\mathscr{P}\times\mathscr{V}\times\mathscr{Q}$ such that, for all $t\in(0, T]$,

for all $({\mathit{\boldsymbol{{w}}}}, \{q_ {{\text{j}}}\}_{ {{\text{j}}}\in J}, {\mathit{\boldsymbol{{v}}}}, q) \in \mathscr{D}\times\mathscr{P}\times\mathscr{V}\times\mathscr{Q}$, with ${\mathit{\boldsymbol{{d}}}}(0) = {\mathit{\boldsymbol{{d}}}}_0, \partial_t{\mathit{\boldsymbol{{d}}}}(0) = \dot{{\mathit{\boldsymbol{{d}}}}}_0, {\mathit{\boldsymbol{{u}}}}(0) = {\mathit{\boldsymbol{{u}}}}_0, p_ {{\text{j}}}(0) = p_{ {{\text{j}}}0}$ $\forall {{\text{j}}}\in J$. In (2.3), we denoted by $(\cdot, \cdot)_{\Omega}$ the $L^2$-product over $\Omega$ while the definitions of the bilinear and linear forms are reported in Appendix A.

We point out that, differently from the models studied in ^[29,40], here we consider the following additional terms: the trilinear form $N_ {{\text{f}}}$ and the interface form $\mathfrak G$, discussed in the following remarks.

Remark 2 (Skew-symmetry of the advection form $N_ {{\text{f}}}$). In the trilinear form

we include the additional term $\left(\frac{\rho_ {{\text{f}}}}{2}(\nabla\cdot{\mathit{\boldsymbol{{u}}}}'), {\mathit{\boldsymbol{{v}}}}\right)_{\Omega_ {{\text{f}}}}$, classically employed for Navier-Stokes problems ^[65] and considered in other works using a discontinuous Galerkin approach ^[70,71]. This term vanishes if ${\mathit{\boldsymbol{{u}}}}'$ is the fluid velocity ${\mathit{\boldsymbol{{u}}}}$ of (2.1), but it ensures that that $N_ {{\text{f}}}$ is skew-symmetric w.r.t. exchanging the second and third argument also if ${\mathit{\boldsymbol{{u}}}}'$ is such that $\nabla\cdot{\mathit{\boldsymbol{{u}}}}'\neq 0$, as it may occur after the discretization of the equations, as long as fully Dirichlet conditions are enforced on the whole boundary of $\Omega_ {{\text{f}}}$. In principle, if Neumann conditions are imposed on a portion of $\partial\Omega_ {{\text{f}}}$, boundary effects may arise; however, in all the numerical experiments discussed in the following sections, no such effect is observed (see Sections 6–8). A possible alternative skew-symmetric form is

which is equivalent to $N_ {{\text{f}}}$ when $\nabla\cdot{\mathit{\boldsymbol{{u}}}}' = 0$ and may avoid the boundary effects mentioned above.

Remark 3 (Derivation of the interface forms $\mathfrak J$ and $\mathfrak G$). The interface forms

naturally arise during the derivation of the weak form of problem (2.1). We test (2.1a)-(2.1b) against functions ${\mathit{\boldsymbol{{w}}}}\in{\mathit{\boldsymbol{{W}}}}$ and $q_ {{\text{j}}}\in Q_J$, with ${{\text{j}}}\in J$, over $\Omega_ {{\text{el}}}$, and (2.1c) against ${\mathit{\boldsymbol{{v}}}}\in {\mathit{\boldsymbol{{V}}}}$ over $\Omega_ {{\text{f}}}$. Then, integrating by parts and summing all the contributions yield the following boundary terms on the interface:

Using the interface conditions (2.2a), (2.2c) and then (2.2b), (2.2d), (2.2e), we can rewrite (2.4) as follows:

where we also used that ${\mathit{\boldsymbol{{a}}}}\otimes{\mathit{\boldsymbol{{b}}}}\colon I = {\mathit{\boldsymbol{{a}}}}\cdot{\mathit{\boldsymbol{{b}}}}$ for any ${\mathit{\boldsymbol{{a}}}}, {\mathit{\boldsymbol{{b}}}}\in \mathbb R^d$, and that ${\mathit{\boldsymbol{{n}}}}_ {{\text{f}}} = -{\mathit{\boldsymbol{{n}}}}_ {{\text{el}}}$ on $\Sigma$.

3.   Polytopal discontinuous Galerkin semi-discrete formulation

In this section, we introduce the space discretization of problem (2.3) by a discontinuous Finite Element method on polytopal grids.

Let $\mathscr T_{h, {{\text{el}}}}$, $\mathscr T_{h, {{\text{f}}}}$ be polytopal meshes discretizing the domains $\Omega_ {{\text{el}}}, \Omega_ {{\text{f}}}$, respectively. We define the faces of an element $K\in \mathscr T_{h, {{\text{el}}}}\cup\mathscr T_{h, {{\text{f}}}}$ as the $(d-1)$-dimensional entities constituting the intersection of $\partial K$ with either the boundary of a neighboring element or the domain boundary $\partial\Omega$. For $d = 2$ all faces are straight line segments, while for $d = 3$ they are generic polygons, in principle: We assume that each of these polygons can be further decomposed into triangles, and we define as face each of these triangles. We collect all faces in each physical domain into $\mathscr F_ {{\text{el}}}$ and $\mathscr F_ {{\text{f}}}$, and we partition these sets into internal faces $\mathscr F_ {{\text{el}}}^ {{\text{I}}}$, $\mathscr F_ {{\text{f}}}^ {{\text{I}}}$, Dirichlet/Neumann faces $\mathscr F_ {{\text{el}}}^ {{\text{D}}}/\mathscr F_ {{\text{el}}}^ {{\text{N}}}\subset\partial\Omega_ {{\text{el}}}\setminus\Sigma, \mathscr F_ {{\text{f}}}^ {{\text{D}}}/\mathscr F_ {{\text{f}}}^ {{\text{N}}}\subset\partial\Omega_ {{\text{f}}}\setminus\Sigma$ (as portions of the poroelastic and the fluid domain boundaries, respectively), and interface faces $\mathscr F^\Sigma\subset\Sigma$. We assume that the polytopal grids $\mathscr T_{h, {{\text{el}}}}$, $\mathscr T_{h, {{\text{f}}}}$ are geometrically conforming with $\Sigma$; yet, hanging nodes are admissible.

Over each mesh $\mathscr T_{h, \star}, \star\in\{ {{\text{el}}}, {{\text{f}}}\}$, we introduce the broken Sobolev spaces of order $s$, namely $H^s(\mathscr T_{h, \star}) = \{q\in L^2(\Omega_\star) \colon q|_K\in H^s(K)\quad\forall K\in\mathscr T_{h, \star}\}$. Moreover, we define the following piecewise polynomial spaces for a given integer $m\geq 1$:

The choice of the same polynomial degree $m$ for all the discrete spaces simplifies the notation and the proofs of the results discussed in the following. However, a smaller degree $m-1$ could be used for the fluid pressure space $Q^{{\text{DG}}}_h$: The results of Section 4 still hold in that case, and the convergence order of Theorem 2 is preserved.

To introduce the PolyDG discretization of (2.3), we define the symmetric outer product ${\mathit{\boldsymbol{{v}}}}\odot{\mathit{\boldsymbol{{n}}}} = \frac{1}{2}({\mathit{\boldsymbol{{v}}}}\otimes{\mathit{\boldsymbol{{n}}}}+{\mathit{\boldsymbol{{n}}}}\otimes{\mathit{\boldsymbol{{v}}}})$ and, for regular enough scalar-, vector- and tensor-valued functions $q, {\mathit{\boldsymbol{{v}}}}, \boldsymbol{\tau}$, we define the following average and jump operators.

● On each internal face $F\in\mathscr F^ {{\text{I}}} = \mathscr F_ {{\text{el}}}^ {{\text{I}}}\cup \mathscr F_ {{\text{f}}}^ {{\text{I}}}$ we set:

where ${\mathit{\boldsymbol{{n}}}}^+, {\mathit{\boldsymbol{{n}}}}^-$ are defined as in Figure 2 (left).

● On a Dirichlet face $F\in\mathscr F_ {{\text{el}}}^ {{\text{D}}}\cup\mathscr F_ {{\text{f}}}^ {{\text{D}}}$ we set:

where ${\mathit{\boldsymbol{{n}}}}$ is the unit normal vector pointing outward to the element $K$ to which the face $F$ belongs.

● On a face $F\in\mathscr F^\Sigma$ shared by two elements $K_ {{\text{el}}}\in\mathscr T_{h, {{\text{el}}}}$ and $K_ {{\text{f}}}\in\mathscr T_{h, {{\text{f}}}}$ we set:

where ${\mathit{\boldsymbol{{n}}}}_ {{\text{el}}}, {\mathit{\boldsymbol{{n}}}}_ {{\text{f}}}$ are defined as in Figure 2 (right). Notice that the definitions of the interface jump operators account for the different physics defined on each side of the interface.

By using the symmetric outer product $\odot$ in the definition of the jump operators, the DG stabilization terms introduced in the following will be smaller than they would if we had employed $\otimes$.

Based on the spaces and the trace operators defined above, the semidiscrete formulation of problem (2.3) reads as follows:

For any $t\in(0, T]$, find $({\mathit{\boldsymbol{{d}}}}_h, \{p_{ {{\text{j}}}, h}\}_{ {{\text{j}}}\in J}, {\mathit{\boldsymbol{{u}}}}_h, p_h)\in {\mathit{\boldsymbol{{W}}}}^{{\text{DG}}}_h\times [Q^{{\text{DG}}}_{J, h}]^{N_J} \times {\mathit{\boldsymbol{{V}}}}^{{\text{DG}}}_h \times Q^{{\text{DG}}}_h$ such that

with initial conditions defined in terms of the projections ${\mathit{\boldsymbol{{d}}}}_h(0), \dot{{\mathit{\boldsymbol{{d}}}}}_h(0), \{p_{ {{\text{j}}}, h}(0)\}_{ {{\text{j}}}\in J}, {\mathit{\boldsymbol{{u}}}}_h(0)$ of the initial data introduced in (2.1) onto the corresponding DG spaces. The forms and functionals appearing in (3.1) are the PolyDG version of those defined in (A.1) and their complete definitions can be found in Appendix A. Here we just report the definition of the interface terms, to show the role of the interface jump operators:

Moreover, we point out that the definitions of $\mathcal L_ {{\text{el}}}, \mathcal L_ {{\text{f}}}, \mathcal L_ {{\text{j}}}, {{\text{j}}}\in J,$ include stabilization terms with parameters that depend on the mesh element size (see Appendix A), that will be useful in the theoretical analysis of Section 4. However, these stabilization terms are defined only on internal faces and do not contribute to the interface terms.

4.   Stability and error analysis of the semidiscrete Stokes-MPE problem

In this section, we analyze the semidiscrete problem corresponding to a choice of the Stokes equations to model the CSF flow in $\Omega_ {{\text{f}}}$, namely we neglect the nonlinear advection term in the form $\mathcal L_ {{\text{f}}}$ of (3.1) (see form $\mathcal N_ {{\text{f}}}$ in (A.2c)). The following analysis holds for a generic set $J$ made of $N_J\in\mathbb N$ fluid compartments of the poroelastic model. For the sake of simplicity, we make the following assumptions.

Assumption 1. ● All the physical parameters of the model (cf. Table 1) are constant over the domain;

● All the physical parameters of the model (cf. Table 1) are piecewise constant over the aforementioned decomposition;

● The polytopal mesh $\mathscr T_h = \mathscr T_{h, {{\text{el}}}}\cup\mathscr T_{h, {{\text{f}}}}$ fulfills the regularity assumptions of the PolyDG framework, namely that $\mathscr T_h$ is $h$-uniformly polytopic-regular, a local bounded variation property holds, and there exists a suitable shape-regular simplicial covering of $\mathscr T_h$ ^[6,24].

In all the inequaslities appearing hereafter, the dependency on the model parameters and the finite element degree $m$ will be neglected: By $x\lesssim y$ we will indicate that $\exists C > 0:x\leq C y$, with $C$ independent of the space discretization parameters. The first assumption could be relaxed to the case of piecewise constant parameters over the polytopal mesh $\mathscr T_h$: If they are uniformly bounded, all the following results hold without substantial changes, by including the bounds in the constant $C$ defining the $\lesssim$ relation ^[6,24].

Following ^[8,29,40], we define the following broken norms:

and we introduce the following energy norms at time $t\in(0, T]$, based on those broken norms but also depending on the tangential velocity of the fluid and of the poroelastic structure along the interface $\Sigma$:

where

It can be shown that, for each $t\in(0, T]$, $|\mkern-1.5mu| {{({\mathit{\boldsymbol{{d}}}}, \{p_ {{\text{j}}}\}_{ {{\text{j}}}\in J}, {\mathit{\boldsymbol{{u}}}}, p)}} |\mkern-1.5mu|_{{\rm EN}, t}$ is only a semi-norm over $\mathscr{D}\times\mathscr{P}\times\mathscr{V}\times\mathscr{Q}$, but an actual norm over the semi-discrete space $H^2(0, t; {\mathit{\boldsymbol{{W}}}}^{{\text{DG}}}_h)\times H^1(0, t; Q^{{\text{DG}}}_{J, h})\times H^1(0, t; {\mathit{\boldsymbol{{V}}}}^{{\text{DG}}}_h)\times L^2(0, t; Q^{{\text{DG}}}_h)$ for any value of $\gamma\geq 0$, thanks to the element-wise regularity of polynomials. Consequently, the following stability result ensures the uniqueness of the semi-discrete solution of problem (3.1).

Theorem 1 (Stability estimate). Under Assumption 1 and assuming that sufficiently large values are chosen for the penalty constants (cf. (A.5)), the solution $({\mathit{\boldsymbol{{d}}}}_h, \{p_{ {{\text{j}}}, h}\}_{ {{\text{j}}}\in J}, {\mathit{\boldsymbol{{u}}}}_h, p_h)$ of the semidiscrete problem (3.1) fulfills the following inequality for each time $t\in(0, T]$:

where the first term depends on the initial conditions (2.1e)-(2.1f):

Proof. Choosing the test functions ${\mathit{\boldsymbol{{w}}}}_h = \partial_t{\mathit{\boldsymbol{{d}}}}_h(t), {\mathit{\boldsymbol{{v}}}}_h = {\mathit{\boldsymbol{{u}}}}_h(t), q_h = p_h(t), q_{ {{\text{j}}}, h} = p_{ {{\text{j}}}, h}(t)\ \forall {{\text{j}}}\in J$ in the semidiscrete problem (3.1) and following the arguments of [40, Theorem 4.1], we obtain the following inequality:

where $\text{RHS}$ denotes the right-hand side of (4.3). Observing that the term with the form $\mathcal G$ coincides with the definition of $| {{({\mathit{\boldsymbol{{u}}}}_h, \partial_t{\mathit{\boldsymbol{{d}}}}_h)}} |_{\text{tg}, t}^2$ concludes the proof. □

Remark 4. We point out that the semi-discrete problem (3.1) is stable in the Navier-Stokes case, too, since the advection form $N_ {{\text{f}}}$ is skew-symmetric and thus cancels out in the proof of Theorem 1. The error analysis reported in the following, instead, would require additional investigation to be extended to the Navier-Stokes equations, due to the nonlinearity of the advection form.

To derive an a-priori estimate for the space discretization error of the proposed PolyDG method, we rely on the following additional norms for non-discrete functions:

Moreover, we denote by $\mathscr E_K: H^s(\Omega)\to H^s(\mathbb R^d)$ the Stein extension operator from a Lipschitz domain $\Omega$ defined in ^[62], for which optimal interpolation results can be proven w.r.t. the norms defined above (cf. Appendix B). Combining the results above, we can prove the following optimal convergence estimate:

Theorem 2 (A priori error estimate). Let us assume that Assumption 1 holds and that the penalty parameters included in the discrete problem's formulation are sufficiently large (see (A.5)). If the solution of problem (2.3) is sufficiently regular, the following estimate holds for each $t\in (0, T]$:

where ${\mathit{\boldsymbol{{e}}}}^{\mathit{\boldsymbol{{d}}}} = {\mathit{\boldsymbol{{d}}}}-{\mathit{\boldsymbol{{d}}}}_h, e^{p_ {{\text{j}}}} = p_ {{\text{j}}}-p_{ {{\text{j}}}, h}\ \forall {{\text{j}}}\in J, {\mathit{\boldsymbol{{e}}}}^{\mathit{\boldsymbol{{u}}}} = {\mathit{\boldsymbol{{u}}}}-{\mathit{\boldsymbol{{u}}}}_h, e^{p} = p - p_h$, and $\widehat{K}\supseteq K$, for each $K\in\mathscr T_h$, are shape-regular simplexes covering $\mathscr T_h$, as in Assumption 1.

Proof. Considering the continuous displacement ${\mathit{\boldsymbol{{d}}}}$ and its semi-discrete counterpart ${\mathit{\boldsymbol{{d}}}}_h$, we introduce the error splitting ${\mathit{\boldsymbol{{d}}}}-{\mathit{\boldsymbol{{d}}}}_h = {\mathit{\boldsymbol{{e}}}}^{\mathit{\boldsymbol{{d}}}}_I-{\mathit{\boldsymbol{{e}}}}^{\mathit{\boldsymbol{{d}}}}_h$, with ${\mathit{\boldsymbol{{e}}}}^{\mathit{\boldsymbol{{d}}}}_I = {\mathit{\boldsymbol{{d}}}}-{\mathit{\boldsymbol{{d}}}}_I\in[H^{m+1}(\mathscr T_{h, {{\text{el}}}})]^d$ being the Stein interpolation error (cf. Appendix B and Lemma 1) and ${\mathit{\boldsymbol{{e}}}}^{\mathit{\boldsymbol{{d}}}}_h = {\mathit{\boldsymbol{{d}}}}_h-{\mathit{\boldsymbol{{d}}}}_I\in {\mathit{\boldsymbol{{W}}}}^{{\text{DG}}}_h$ being the approximation error. Analogous definitions are introduced for $e^{p_ {{\text{j}}}}\ \forall {{\text{j}}}\in J, {\mathit{\boldsymbol{{e}}}}^{\mathit{\boldsymbol{{u}}}}, e^{p}$. We subtract the continuous problem (2.3) from the semi-discrete problem (3.1), tested against $(\partial_t{\mathit{\boldsymbol{{e}}}}^{\mathit{\boldsymbol{{d}}}}_h, \{e^{p_{ {{\text{j}}}}}_h\}_{ {{\text{j}}}\in J}, {\mathit{\boldsymbol{{e}}}}^{\mathit{\boldsymbol{{u}}}}_h, e^{p}_h)$, we apply the coercivity of the bilinear forms $\mathcal{L}_ {{\text{el}}}, \mathcal{L}_ {{\text{f}}}, \mathcal{L}_ {{\text{j}}}, {{\text{j}}}\in J,$ and the continuity of these forms as well as of $\mathcal J$ (cf. [40, Lemmas 2 and 5]), and then we can follow the same steps of [40, Theorem 4.2] to arrive to the following inequality:

where $\text{RHS}$ is the right-hand side of the thesis (4.4). We have used the linearity of $\mathcal G$ and the fact that the squared energy norm defined in this work corresponds to that of ^[40] plus the tangential velocity squared seminorm $| {{({\mathit{\boldsymbol{{e}}}}^{\mathit{\boldsymbol{{u}}}}_h, \partial_t{\mathit{\boldsymbol{{e}}}}^{\mathit{\boldsymbol{{d}}}}_h)}} |_{\text{tg}, t}^2.$ Now, since the seminorm $| {{({\mathit{\boldsymbol{{e}}}}_I^{\mathit{\boldsymbol{{u}}}}, \partial_t{\mathit{\boldsymbol{{e}}}}_I^{\mathit{\boldsymbol{{d}}}})}} |_{\text{tg}, t}$ can be controlled by the corresponding broken $L^2$ norm over the interface faces $F\in\mathscr F^\Sigma$, we can employ Stein interpolation results and obtain the following (see Appendix B):

where $\widehat{K}\supseteq K$, for each $K\in\mathscr T_h$, are shape-regular simplexes covering $\mathscr T_h$, existing thanks to Assumption 1. Then, the application of Cauchy-Schwarz and Young inequalities on (4.5) concludes the proof. □

Remark 5. It is worth to point out that, in the proof of Theorem 2, the contribution of the interpolation error in the $| {{\cdot}} |_{\text{tg}, t}$ seminorm has a convergence order that is 1/2 greater than the other terms of the energy norm. This means that the treatment of the BJS condition in the proposed numerical method does not affect convergence.

5.   Fully discrete problem and implementation

Starting from the semi-discrete problem (3.1), we introduce a timestep $\Delta t$ and a corresponding time discretization over a uniform partition $\{t^n = n\Delta t\}_{n = 0}^N$ of the interval $(0, T]$. We use Newmark's $\beta$-method to discretize the terms tested against ${\mathit{\boldsymbol{{w}}}}_h$ in (3.1) (corresponding to the elastic momentum equation) and the Crank-Nicolson method for all the other terms. The nonlinear advection term is linearized by a semi-implicit approach, using a second-order extrapolation of the advecting velocity at time $t^{n+{}^{1}\!\!\diagup\!\!{}_{2}\; }$:

where the superscript $\cdot^n$ denotes the discrete variable approximating ${\mathit{\boldsymbol{{u}}}}$ at time $t^n$. A similar notation is used in the following for all the other variables.

In accordance with the above discretization methods, the algebraic form of the fully discrete problem reads as follows:

where

To employ Newmark's scheme, we have introduced two auxiliary vector variables ${\mathit{\boldsymbol{{Z}}}}^n, {\mathit{\boldsymbol{{A}}}}^n$ representing the first and second time derivatives of ${\mathit{\boldsymbol{{D}}}}^n$. The definition of the matrices $A_1({\mathit{\boldsymbol{{U}}}}^{n}, {\mathit{\boldsymbol{{U}}}}^{n-1}), A_2({\mathit{\boldsymbol{{U}}}}^{n}, {\mathit{\boldsymbol{{U}}}}^{n-1})$ can be obtained with slight changes from those reported in ^[40]. Specifically, the Navier-Stokes advection term encompasses a modification of the diagonal block corresponding to the fluid velocity ${\mathit{\boldsymbol{{U}}}}$, while the BJS condition yields the addition of the following matrix in the diagonal blocks corresponding to the solid and fluid velocities ${\mathit{\boldsymbol{{Z}}}}$ and ${\mathit{\boldsymbol{{U}}}}$, and their mutual coupling:

where the integrand is expressed in terms of the basis functions of the discrete spaces: ${\mathit{\boldsymbol{{W}}}}^{{\text{DG}}}_h = {\rm span}\{\boldsymbol{\varphi}_ {{\text{el}}}^i\}_{i = 0}^{N_ {{\text{el}}}}$, ${\mathit{\boldsymbol{{V}}}}^{{\text{DG}}}_h = {\rm span}\{{\boldsymbol{\varphi}_ {{\text{f}}}^i}\}_{i = 0}^{N_ {{\text{f}}}}$.

The resulting discrete scheme (5.2) is implemented in FEniCS – version 2019.1.0 1 ^[1,53], hinging upon the library multiphenics (https://github.com/multiphenics/multiphenics) to deal with the multiphysics nature of the problem. Although the method can be employed on general polyhedral meshes (as shown in 9), the construction of a three-dimensional polyhedral mesh of a generic domain with internal interfaces is a matter of active research, thus the meshes used to obtain the numerical results of Sections 6 to 8 are made of tetrahedral elements, generated by means of Gmsh ^[42] (https://gmsh.info/). Nevertheless, to assess the advantages of employing a polyhedral mesh w.r.t. more classical ones, in an in-house library we implemented a simplified single-physics problem, for which we could generate actually polyhedral meshes: The results of this assessment are reported in Section 9.

6.   Verification of convergence estimates

To verify the theoretical error estimates of Theorem 2 and the implemented solver, we report convergence tests on a simplified mesh made of two juxtaposed unit cubes $\Omega_ {{\text{f}}} = (0, 1)\times(0, 1)\times(-1, 0), \Omega_ {{\text{el}}} = (0, 1)^3$, where the interface is $\Sigma = \{{\mathit{\boldsymbol{{x}}}} = (x, y, z)\colon z = 0, (x, y)\in(0, 1)^2\}$. Considering only one fluid compartment in the poroelastic system, namely $J = \{ {{\text{E}}}\}$, and setting all physical coefficients of Table 1 to be equal to 1, except for $\alpha_ {{\text{E}}} = 0.5$, the following is an exact solution of problem (2.1)-(2.2) for suitable expressions of the source functions ${\mathit{\boldsymbol{{f}}}}_ {{\text{el}}}, g_ {{\text{E}}}, {\mathit{\boldsymbol{{f}}}}_ {{\text{f}}}$, the boundary data, and the initial conditions ${\mathit{\boldsymbol{{d}}}}_0, \dot{{\mathit{\boldsymbol{{d}}}}}_0, p_{ {{\text{E}}}0}, {\mathit{\boldsymbol{{u}}}}_0$:

In particular, we choose $M = 5$ and $\xi = 1$ and impose Neumann conditions (for the fluid problem) on $\Gamma_\text{N} = \{(x, y, z):z = -1, (x, y)\in(0, 1)^2\}$ and Dirichlet conditions for all variables on $\partial\Omega\setminus\Gamma_\text{N}$. We remark that we are solving the Navier-Stokes problem in the fluid domain, including the advection trilinear form $N_ {{\text{f}}}$ (cf. Section 3).

We simulate 5 time steps with step length $\Delta t = 10^{-7}$, chosen small enough to avoid spoiling convergence w.r.t. space discretization. In Figure 3, we report the computed errors in the energy norm (4.2). The results agree with the convergence order $h^m, m = 1, 2, 3$ predicted by Theorem 2.

7.   Application to brain fluid-poromechanics: physiological conditions in idealized geometry

In this section, we consider the CSF modeling by the Stokes equations (namely we neglect the nonlinear advection term in (2.1)) and we apply our multi-physics model to physiological settings, focusing on the CSF compartment. Specifically, we consider $J = \{ {{\text{E}}}\}$ and the values of the physical parameters reported in Table 1, with typical physiological values according to ^[25,46,66].

The only non-zero distributed source/sink term is $g_ {{\text{E}}}$, whereas ${\mathit{\boldsymbol{{f}}}}_ {{\text{el}}}, {\mathit{\boldsymbol{{f}}}}_ {{\text{f}}}$ are set to zero. This non-zero function is homogenous in space, and its dependence on time is $g_ {{\text{E}}}(t) = 0.2\pi\sin(2\pi t)$, corresponding to an overall inflow $Q_\text{in}(t) = |\Omega_ {{\text{el}}}|g_ {{\text{E}}}(t)$ which is in the range of the CSF generation rate in physiological conditions: cfr. ^[12,25].

The idealized geometry displayed in Figure 4, left, although not fully capturing the complex geometry of the actual brain and ventricle system, retains the same topology of the brain and CSF system: The porous tissue is contained in $\Omega_ {{\text{el}}}$, while the CSF can flow in the ventricle system $\Omega_ {{\text{f}}}$, including a duct connecting it to the spinal canal at $\Gamma_\text{out}$. The volumes of the poroelastic and fluid domains at rest are $|\Omega_ {{\text{el}}}| = {9.68\; }\mathrm{mL}$ and $|\Omega_ {{\text{f}}}| = {0.89\; }\mathrm{mL}$, respectively. and the cylindrical duct has a diameter of ${1\; }\mathrm{cm}$, which is in the physiological range 0.94–${1.72\; }\mathrm{cm}$ of the spinal canal ^[67]. The corresponding mesh is made of $N = {16834}{}$ elements with an average size $h = {1.6\; }\mathrm{mm}$. In terms of boundary conditions, on the outflow $\Gamma_\text{out}$ we prescribe the CSF pressure $\overline{p}^\text{out} = 0$ and on the outer wall $\Gamma_ {{\text{w}}}$ we impose no traction on the tissue and no flow of the extracellular CSF. To ensure that the periodic regime is attained, we simulate 3 periods of the source term $g_ {{\text{E}}}$, of duration $T = {1\; }\mathrm{s}$, using a time step $\Delta t = {10^{-3}\; }\mathrm{s}$. In the following, all results refer to the third period, with time $t = 0$ set at its beginning.

The displacement ${\mathit{\boldsymbol{{d}}}}_h$ and the interstitial CSF pressure $p_{ {{\text{E}}}, h}$ are reported in Figure 4, for selected time snapshots. The magnitude of ${\mathit{\boldsymbol{{d}}}}_h$, reaching its peak at $t = {0.5\; }\mathrm{s}$, never exceeds ${6.6\; }\mathrm{mm}$. This deformation, although non-negligible per se, corresponds to a volumetric change of 1.3%, thus justifying the choice of a linear elastic model for the cerebral tissue, at least as a first-order approximation. Moreover, the restriction of ${\mathit{\boldsymbol{{d}}}}_h$ on $\Sigma$ is always less than ${0.1\; }\mathrm{mm}$, confirming that neglecting the deformation of the fluid domain is an acceptable assumption in this regime. Regarding $p_{ {{\text{E}}}, h}$, at the same peak time $t = {0.5\; }\mathrm{s}$ we observe a maximum difference of ${4.4\; }\mathrm{mmHg}$ between the outer boundary $\Gamma_\text{out}$ and the interface $\Sigma$, which is comparable with analogous simulations in brain geometries ^[25,40]. We also observe that a slight phase displacement occurs in the late part of the period between $p_{ {{\text{E}}}, h}$ and the data $g_ {{\text{E}}}$, with a minimum of ${-1.9\; }\mathrm{mmHg}$ attained at $t = {0.94\; }\mathrm{s}$: This is due to the inertial properties of the system, which are going to be discussed in Section 8.

Regarding the CSF velocity ${\mathit{\boldsymbol{{u}}}}_h$ and pressure $p_h$ in the Stokes domain $\Omega_ {{\text{f}}}$, the results are reported in Figure 5. The pressure gradient is significantly smaller than in the poroelastic medium and the velocity magnitude is in the physiological range reported in clinical measurements and computational assessments in the cerebral aqueduct ^[12,25]. The positive and increasing pressure gradient observed in the final portion of the period (see Figure 5, $t = {1\; }\mathrm{s}$) is due to the aforementioned inertial effects, even more noticeable in the flowrate plots of Figure 6, where the output flowrate $Q_\text{out} = \int_{\Gamma_\text{out}}{\mathit{\boldsymbol{{u}}}}_h\cdot{\mathit{\boldsymbol{{n}}}}\, d\Gamma$ shows a phase delay of 0.11-0.12 w.r.t. the inflow $Q_\text{in} = \int_{\Omega_ {{\text{E}}}}g_ {{\text{E}}}\, d\Omega = |\Omega_ {{\text{E}}}|g_ {{\text{E}}}$ associated to the source term, while the period is equal to ${1}{}$ for both flowrates. This final observation holds true in all the cases compared in Section 8.

To conclude this section, we point out how the results presented here can vary if a fully detailed brain geometry were considered. Introducing the multi-chamber ventricle geometry would break the overall symmetry of the domain. In that case, relatively concentrated pressure gradients would appear in the small ducts connecting the chambers, and the partition of the ventricle interface into multiple regions (instead of the two considered here) could shed light on the heterogeneous distribution of fluid mass exchange between the tissue and the ventricles. Regarding the pial surface, instead, the computational modeling of the complex gyri and sulci structure and its mechanical interaction with the CSF in the subarachnoid space is still an open issue in the literature, due to the high computational demand involved in this task ^[25,64].

8.   Application to brain poro-mechanics: effects of BJS conditions and advection term

This section aims to assess the effects of the modeling choices for the advection term in the fluid part of system (2.1) – namely either Stokes or Navier-Stokes equations – and of the BJS condition (2.2e) at the interface – namely either $\gamma = 0$ or $\gamma = 1$. Since a semi-implicit treatment of the advection term is employed, as reported in (5.1), the problem to be solved at each time step is linear also in the Navier-Stokes case. Moreover, backflow stabilization is needed in the Navier-Stokes case for the latest portion of the period: The term $\int_{\Gamma_\text{out}}\frac{\rho_ {{\text{f}}}}{2}\min\left\{0, {\mathit{\boldsymbol{{u}}}}_h^n\cdot{\mathit{\boldsymbol{{n}}}}\right\}{\mathit{\boldsymbol{{u}}}}^{n+1}_h\cdot{\mathit{\boldsymbol{{v}}}}_h$ is added to the left-hand side of the fully discrete problem (5.2) ^[37].

8.1.   Effects of fluid inertia: Stokes vs. Navier-Stokes

Observing the outlet flowrate $Q_\text{out}$ and the interface flowrate $Q_\Sigma = \int_\Sigma{\mathit{\boldsymbol{{u}}}}_h\cdot{\mathit{\boldsymbol{{n}}}}_ {{\text{el}}}$ displayed in Figure 6, we can notice that the differences are negligible between the Stokes and Navier-Stokes case (for the same value of $\gamma$). Indeed, the outlet Reynolds number $\text{Re} = \frac{\rho_ {{\text{f}}} Q_\text{out}}{\mu_ {{\text{f}}} \pi D}$, $D$ being the diameter of the circular outlet section $\Gamma_\text{out}$, is in the range $(40, 50)$ for all cases.

However, some differences can be observed when focusing on the cylindrical duct. Indeed, denoting by $\Sigma_\text{can}$ the lateral surface of this canal, the flowrate $Q_{\Sigma_\text{can}} = \int_{\Sigma_\text{can}}{\mathit{\boldsymbol{{u}}}}_h\cdot{\mathit{\boldsymbol{{n}}}}_ {{\text{el}}}$ reported in Figure 6 displays significant amplitude differences and a phase difference (either positive or negative) of ${0.06}{}$ between the Stokes and Navier-Stokes cases. The same phase difference between the Stokes and Navier-Stokes model can also be appreciated in the interface-averaged pressure $P_\Sigma = \frac{1}{|\Sigma|}\int_\Sigma p_h$ reported in Figure 7, particularly in the case $\gamma = 1$ corresponding to BJS conditions: This difference can be ascribed to the additional inertia accounted for by the advection term in Navier-Stokes equations. The very same observation also holds if $P_{\Sigma_\text{can}} = \frac{1}{|\Sigma_\text{can}|}\int_{\Sigma_\text{can}} p_h$ is considered instead of $P_\Sigma$.

Overall, the results discussed here quantitatively show that the choice of the simpler Stokes model is enough to represent the general features of the flow in the regime of interest. The differences observed when focusing on the canal interface $\Sigma_\text{can}$ do not have a significant effect on the rest of the fluid domain, and these differences would be even less pronounced in the aqueduct of Sylvius of an actual brain geometry, which is characterized by an even smaller diameter ($\sim1$–${3\; }\mathrm{mm}$) and thus less inertial effects.

8.2.   Effects of BJS conditions

To assess the effects of the BJS condition (2.2e), we can compare the cases $\gamma = 0$ (no tangential stress at the pores) to the cases $\gamma = 1$ (BJS condition) in Figures 6 and 7. The approximately sinusoidal evolution of flowrates and pressure exhibits a smaller amplitude in the case $\gamma = 0$, particularly significant in the interface quantities $P_\Sigma$ and $Q_\Sigma$ and even more in the canal interface flowrate $Q_{\Sigma_\text{can}}$. An interpretation of this effect is that the friction in the tangential direction introduced by the BJS interface condition makes CSF velocity orient in the direction orthogonal to the interface, thus increasing the amount of CSF flowing through it at each given time. Due to the incompressibility of the fluid model, this increased flow corresponds to an increased pressure difference $P_\Sigma-\overline{p}_\text{out} = P_\Sigma$. This is confirmed by the results reported in Figure 8: When the BJS condition is applied, ${\mathit{\boldsymbol{{u}}}}_h$ is mostly normal to the interface in the upper region of $\Omega_ {{\text{f}}}$ (see the boxed panels in Figure 8), and an increased flowrate is observable in the vertical duct. Moreover, the friction introduced by the BJS condition yields a bell-shaped profile in the canal, in contrast with the flat profile of the case $\gamma = 0$. Such a profile better represents the actual CSF flow in the cerebral aqueduct and spinal canal ^[64]. To conclude this discussion, it is interesting to notice that, despite the significant differences in the pressure and velocity distribution, the outlet flowrate $Q_\text{out}$ shows little discrepancies between the different cases, since the outflow is mostly driven by conservation of mass.

9.   Computational advantages of employing polyhedral meshes

After the testing of the PolyDG method to solve the fluid-poromechanics problem of interest, discussed in the previous sections, we now want to assess the pros and cons of employing a polytopal mesh instead of a more standard tetrahedral/hexahedral one. In particular, we focus on the computational cost entailed by the two approaches on a simplified problem that retains some of the characteristics of the application of interest. Aiming to focus on the specifics of the numerical discretization method, we solve a Poisson problem in this domain, with an exact solution $u_\text{ex}(x, y, z) = \sin(\pi x)\sin(\pi y)\sin(\pi z),$ enforcing Dirichlet boundary conditions on the whole boundary. To assess the suitability of the methods on a domain with small geometrical details of characteristic size $\epsilon$, we consider the computational domain depicted in Figure 9, which contains 10 randomly placed inclusions of diameter $\epsilon$. In this domain, we generate a hexahedral mesh $\mathscr T_{26816}$ of 26816 elements by means of Gmsh ^[42]. Over there, we define a tensor-product DG space and quadrature formulas for any finite element polynomial degree $m$. From $\mathscr T_{26816}$, two polyhedral grids $\mathscr T_{45}, \mathscr T_{90}$ are generated by agglomeration via METIS ^[47], see Figure 9.

We remark that the hexahedral mesh needs to have a resolution proportional to the inclusion diameter $\epsilon$, at least close to the inclusions. On the other hand, the size of the polyhedral mesh elements is independent of $\epsilon$, thanks to the possibility of handling elements with many small faces. In addition to these meshes, we also include in the comparison a strongly graded hexahedral mesh $\widehat{\mathscr T}_{4256}$ (see Figure 9 bottom right), which has an element size that is comparable with that of the agglomerated polyhedral grids.

The complete DG discretization of the problem is reported in Appendix C: The same numerical scheme is applied to all meshes, and all the simulations discussed in this section were run on a single CPU.

To compare the polyhedral approach to the hexahedral ones in terms of both accuracy and computational efficiency, Figure 10 reports the results of convergence tests w.r.t. the polynomial degree $m$: For each of the meshes introduced above, we plot the convergence errors $E_{L^2} = \|u_\text{ex}-u_h\|_{L^2(\Omega)}, E_{H^1} = \|\nabla u_\text{ex}-\nabla_hu_h\|_{L^2(\Omega)}$ and the computational time of the simulations against the number of degrees of freedom (DOFs) entailed by each choice of $m$.

Observing the computed errors, we can notice that the polyhedral approach requires significantly fewer DOFs than the hexahedral one to attain a given level of accuracy. For example, an error $E_{L^2}$ of less than ${5 \cdot 10^{-4}}{}$ (marked by black squares in Figure 10) is achieved with either 3780 DOFs (with $m = 6$ over $\mathscr T_{45}$) or 5040 DOFs (with $m = 5$ over $\mathscr T_{90}$) using an agglomerated polyhedral mesh, while either 268160 DOFs ($m = 2$ over $\mathscr T_{26816}$) or 148960 ($m = 4$ over $\widehat{\mathscr T}_{4256}$) are required when using hexahedral meshes. Indeed, in the case of $\mathscr T_{26816}$, to capture the geometrical detail of the small inclusions, many hexahedral elements are required in some regions, leading to a large system without gaining in approximation; on the other hand, a single polyhedron with many small faces can preserve the same geometrical (and computational) accuracy. Using the strongly graded mesh $\widehat{\mathscr T}_{4256}$, the accuracy-to-DOFs ratio improves w.r.t. $\mathscr T_{26816}$, yet it remains far from the polyhedral cases. More ingenious strategies in mesh design could yield further enhancements in accuracy, but they could be significantly problem-specific and entail additional time for mesh generation, especially when the number of small geometrical details is relatively high as in the settings discussed here.

Regarding the results on $\widehat{\mathscr T}_{4256}$, we also point out that they show the robustness of the numerical method in dealing with highly anisotropic elements, at least in terms of $L^2$-error.

In terms of computational time, we discuss separately the times required to assemble the system and to solve it, both reported in Figure 10. We notice that solving the significantly smaller systems associated with the polyhedral meshes requires a much smaller computational time than in the hexahedral cases. Specifically, to attain the $L^2$-norm error of about ${5\cdot 10^{-4}}{}$ considered in the discussion above, the solution time for the hexahedral meshes is 2-3 orders of magnitude larger, and the use of the smaller graded mesh $\widehat{\mathscr T}_{4256}$ does not seem to be particularly efficient w.r.t. $\mathscr T_{26816}.$ Regarding the assembly phase, times seem comparable between the polyhedral and hexahedral approaches. Our current implementation of the 3D solver relies on a quadrature rule based on the sub-tessellation of each polyhedral element into hexahedra. Yet, the assembly could be made much more efficient by the quadrature-free strategy proposed in ^[4]: Two-dimensional tests in the open-source library $\texttt{lymph}$ showed more than 20% reduction in assembly time when using the quadrature-free strategy instead of sub-tessellation ^[5] (https://lymph.bitbucket.io/), and 3D implementations may yield even further reductions thanks to the recursive nature of this strategy ^[4].

To complete this discussion, we point out that agglomeration and setup of the PolyDG method over both $\mathscr T_{45}$ and $\mathscr T_{90}$ required less than 20 seconds in all cases, and the setup for the hexahedral solver was up to 50 seconds. Moreover, the PolyDG method can also be beneficial in terms of memory requirements, in the case of geometrically detailed domains. Indeed, the linear system to be assembled is smaller than in the hexahedral case, and it is still sparse with a limited bandwidth.

The results and discussion presented here can be extended to the more complex case of the fluid-poromechanics problem discussed in the rest of the manuscript: A realistic brain geometry would contain very fine geometrical details, and since the brain and CSF are not characterized by very large displacements or turbulent flows, the solution of problem (2.1) is relatively smooth. Moreover, all the conclusions on computational costs would extend to the larger systems solved on a parallel cluster: Mesh agglomeration entails a negligible computational effort w.r.t. assembly or solution of the linear system – and it needs to be performed only once, even in time-dependent problems – therefore it can be operated separately on the sub-mesh pertaining to each processor, resulting in negligible inter-process communication overhead.

10.   Conclusions

Motivated by the modeling of cerebrospinal fluid (CSF) flow in the brain, in this work we studied a coupled multi-domain system encompassing multiple-network poroelasticity and (Navier-)Stokes equations, with a particular focus on the interface conditions between the two physical domains. The polytopal discontinuous Galerkin method for space discretization introduced in ^[40] was extended to consider the nonlinear advection term of Navier-Stokes equations in the fluid domain and Beavers-Joseph-Saffman (BJS) interface conditions: An a priori analysis of the resulting method in the Stokes case proved it to be stable and optimally convergent. The method was numerically verified by means of convergence tests in three dimensions, and a quantitative comparison with a standard DG approach on a hexahedral mesh showed the advantages of the polyhedral approach. Considering an idealized geometry, representative of the main topological characteristics of the brain tissue and ventricular system, the method was employed to represent porous tissue dynamics and CSF flow in physiological settings, obtaining results in partial consistency with the literature. Analyzing the effects of the advection term in the fluid model, it was quantitatively observed that neglecting the advection term in the Navier-Stokes equations does not have a significant impact on the CSF velocity distribution (at least in physiological conditions), though it may yield a slightly inaccurate prediction of the pressure distribution. Finally, it was highlighted how the BJS condition strongly affects the CSF pressure and velocity distribution: The results obtained with the enforcement of this condition better represent the CSF flow in the brain, especially in terms of its profile in the canal.

To further develop the computational model proposed in this work, a crucial improvement would be to consider patient-specific geometries, including a detailed representation of the ventricle chambers, the interventricular foramina and aqueduct of Sylvius, and the folds of the brain cortex. This would allow to obtain physiologically accurate results, which are necessary for a comparison with clinical measurements, thus opening the way to data-driven and possibly personalized calibration of the model parameters. To build up a computational domain representing the complex brain geometry, image segmentation pipelines developed in the literature (see, e.g., ^[41,55]) should be combined with mesh generation and agglomeration algorithms for the construction of a polyhedral mesh ^[7,30,38]. The main challenge in this direction concerns the agglomeration algorithm and its application in the narrow channels connecting the brain ventricles. Indeed, although when meshing the tissue domain these geometrical features can be considered as small inclusions (as those discussed in Section 9 for a simpler problem), in the fluid domain they significantly change the local characteristic length of the domain itself. Therefore, an agglomeration algorithm not accounting for this geometric heterogeneity could yield a non-sufficient local number of degrees of freedom to accurately approximate the flow. To address this issue, the domain metric should be included in the agglomeration algorithm, or an hp-adaptive strategy should be combined with it.

Such a complex model would require further developments also in the computational solver, to make the numerical simulations affordable. The quantitative comparison between the PolyDG method and a standard DG method on a hexahedral mesh reported here provided a preliminary – yet indicative – assessment of the advantages of the polyhedral approach in handling fine geometric details, in terms of accuracy, memory requirements, and efficiency in the solution of the problem. Yet, to actually translate the method to a realistic geometry, some directions of further development must be followed. First, the assembly time of the PolyDG discretization, currently comparable with the standard DG one, could be further significantly improved by a quadrature-free strategy ^[4,5]. Then, a parallel solver could be attained with a suitable integration of the above-mentioned agglomeration algorithms, either as a pre-processing stage or by having each parallel process perform agglomeration on its own sub-mesh ^[7,38]. Finally, scalable preconditioners for multi-physics problems could be introduced, hinging upon either operator-based approaches or inexact factorization ^{[17,18,31,39,56]}.

In terms of model personalization, the multiple-network modeling of tissue perfusion could be exploited to assimilate clinical measurements of the blood flow in the cerebral vasculature directly into the model, without the need for a pre-processing phase to estimate CSF generation from such data, or to combine the system with more detailed computational models of the heart pulsation ^[21,45,59]. Finally, in terms of brain poromechanics modeling, extensions to account for more complex hyperelastic rheologies of the tissue and surface-tension effects could be envisaged, since both of these aspects are the subject of current investigation in biomechanics. Regarding the former, active experimental and theoretical research is addressing the characterization of the tissue's mechanical response ^[22,58,60]: Nonlinear effects in the large deformation regime need to be considered to describe impact-related injuries or brain shrinking due to aging and/or neurodegeneration, whereas the assessment of their relevance in the response to blood and respiration pulsatility is currently an open question. About surface effects, it is known that also in fluid-saturated porous media they may change the macroscopic mechanical properties of the medium – typically softening it if the pores constitute an open network – especially in the case of multiple interacting networks. However, the significance of these effects on organ-scale poromechanics of living tissues is still discussed ^[26]. In both perspectives, the devising of a robust and efficient computational method for the simulation of brain poromechanics would be far from trivial, requiring a careful treatment of nonlinearities, but it could help shed light on the role of the abovementioned mechanical features at the organ scale.

Use of Generative-AI tools declaration

The author declares he has not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The author would like to thank Nicola Parolini for the fruitful discussions on the topics of this work, and the anonymous reviewers for their insightful comments that contributed to improving the present work. The author has been supported by ICSC–Centro Nazionale di Ricerca in High Performance Computing, Big Data, and Quantum Computing funded by the European Union–NextGenerationEU. The present research is part of the activities of "Dipartimento di Eccellenza 2023–2027", Dipartimento di Matematica, Politecnico di Milano. The author is member of GNCS-INdAM and acknowledges the support of the GNCS project CUP E53C23001670001.

Conflict of interest

The author declares no conflict of interest.

Appendix

A.   Bilinear forms and functionals of the continuous and semi-discrete problem

The forms appearing in the continuous weak problem (2.3) are defined as follows:

The forms building up the semidiscrete problem (3.1) are defined as follows:

where

where $\nabla_h, \boldsymbol{\varepsilon}_h, {{\text{div}}}_h$ denote the element-wise gradient, symmetric gradient, and divergence operators, respectively, and the stress tensors $\boldsymbol{\sigma}_ {{\text{el}}}, \boldsymbol{\tau}_ {{\text{f}}}$ are implicitly defined in terms of these piecewise operators. The parameters $\eta, \zeta_ {{\text{j}}}, \gamma_{\mathit{\boldsymbol{{v}}}}, \gamma_p$ appearing in these forms are defined as follows ^[8,29]:

where $\{h\}_\text{H}$ denotes the harmonic average on $K^{\pm}$ (with $\{h\}_\text{H} = h_K$ on Dirichlet faces), $\overline{\mathbb C}_ {{\text{el}}}^K = \|\mathbb C_ {{\text{el}}}^{1/2}|_K\|_2^2$ and $\overline{k}_ {{\text{j}}}^K = \|k_ {{\text{j}}}^{1/2}|_K\|_2^2$ are the $L^2$-norms of the symmetric second-order tensors appearing in the elasticity and Darcy equations, for each $K\in\mathscr T_{h, {{\text{el}}}}$, and $\overline{\eta}, \overline{\zeta_ {{\text{j}}}}\ \forall {{\text{j}}}\in J, \overline{\gamma}_{\mathit{\boldsymbol{{v}}}}, \overline{\gamma}_p$ are penalty constants to be chosen large enough. In all the numerical tests of the present work, all these penalty constants are set to 10.

B.   Stein interpolation results

If $\Omega$ is a Lipschitz-regular domain, the following interpolation results hold for the Stein extension operator $\mathscr E_K: H^s(\Omega)\to H^s(\mathbb R^d)$ (cf. ^[9,40]):

Lemma 1. Under Assumption 1, the following estimates hold:

such that

where $\widehat{K}\supseteq K$, for each $K\in\mathscr T_h$, are shape-regular simplexes covering $\mathscr T_h$, thanks to 1.

C.   Discontinuous Galerkin method for the Poisson problem of 9

This section reports the Discontinuous Galerkin method applied to the Poisson problem

We introduce a generic mesh $\mathscr T_h$ of the domain $\Omega$, we collect the element faces in $\mathscr F$, and we employ an analogous notation to 3 for jump and average face operators. The discrete problem reads as follows:

Find $u_h\in X_h^\text{DG}$ such that

where $\overline\eta$ is a penalty coefficient and $\{h\}_\text{H}$ denotes the harmonic average of the element size across a face. For further details, we refer the reader to ^[6]. We point out that the same formulation can be employed on a standard simplicial or hexahedral mesh, or on a generic polyhedral one.