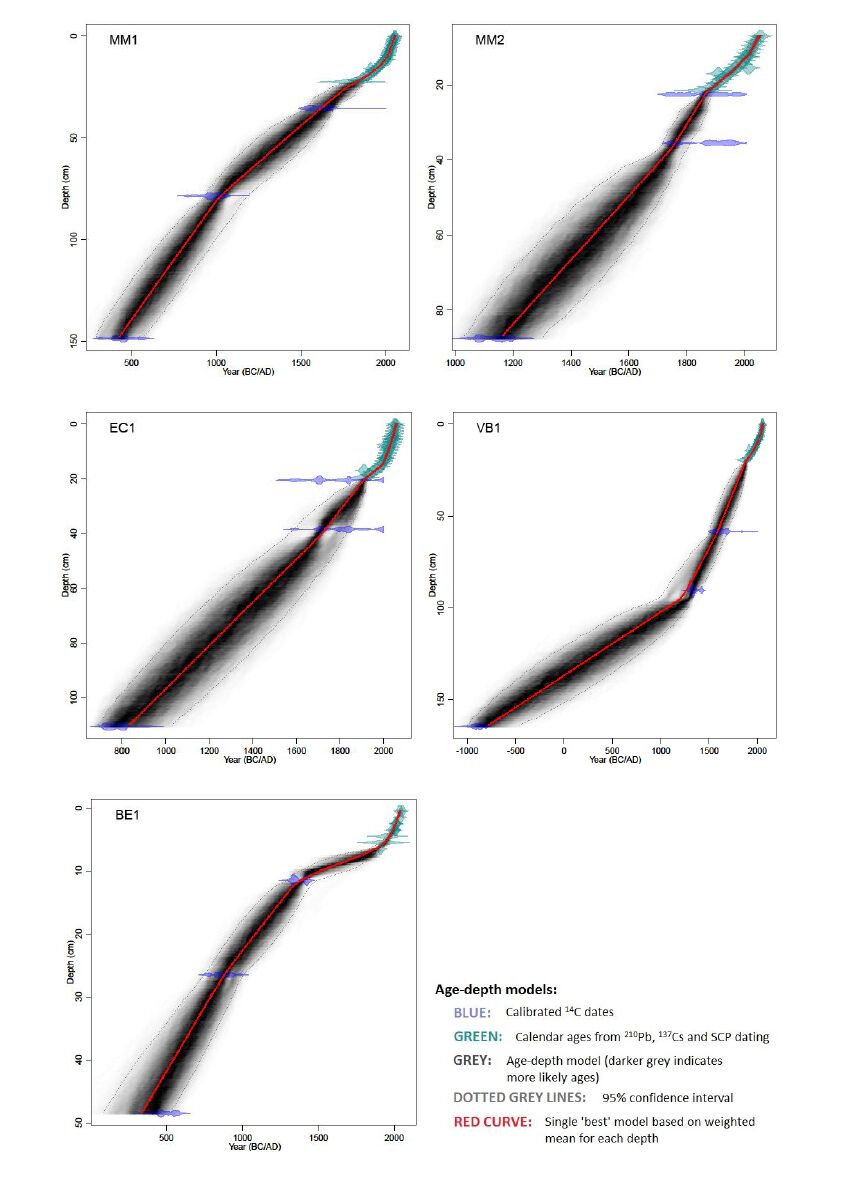
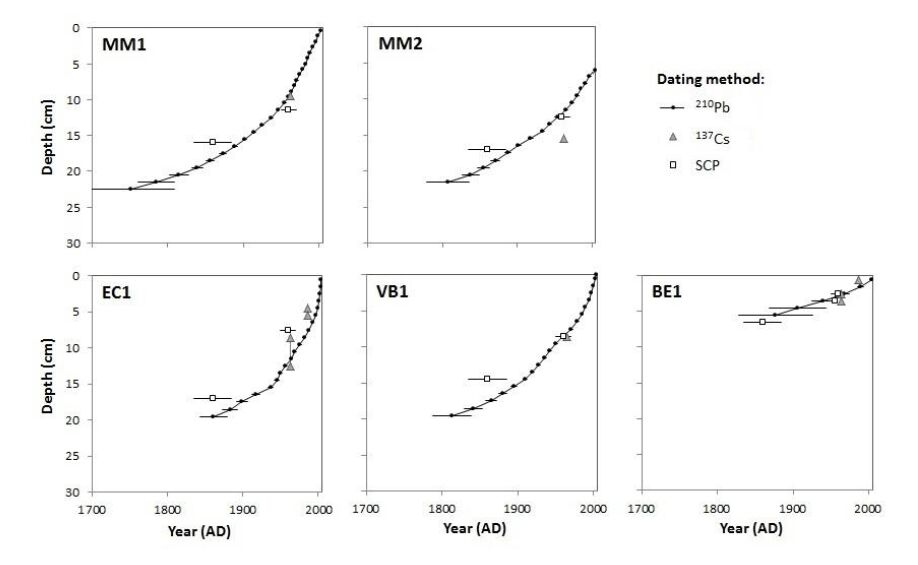
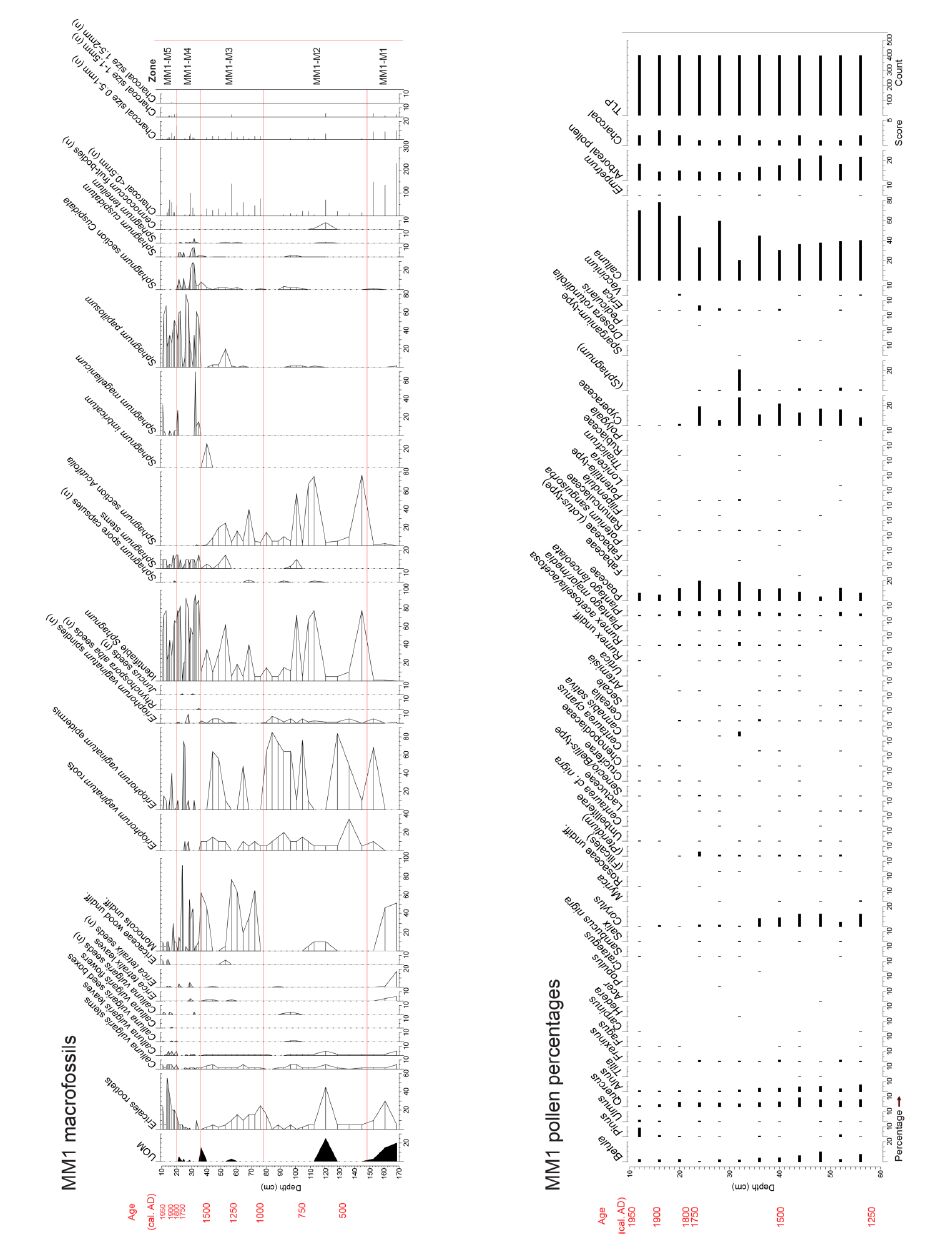
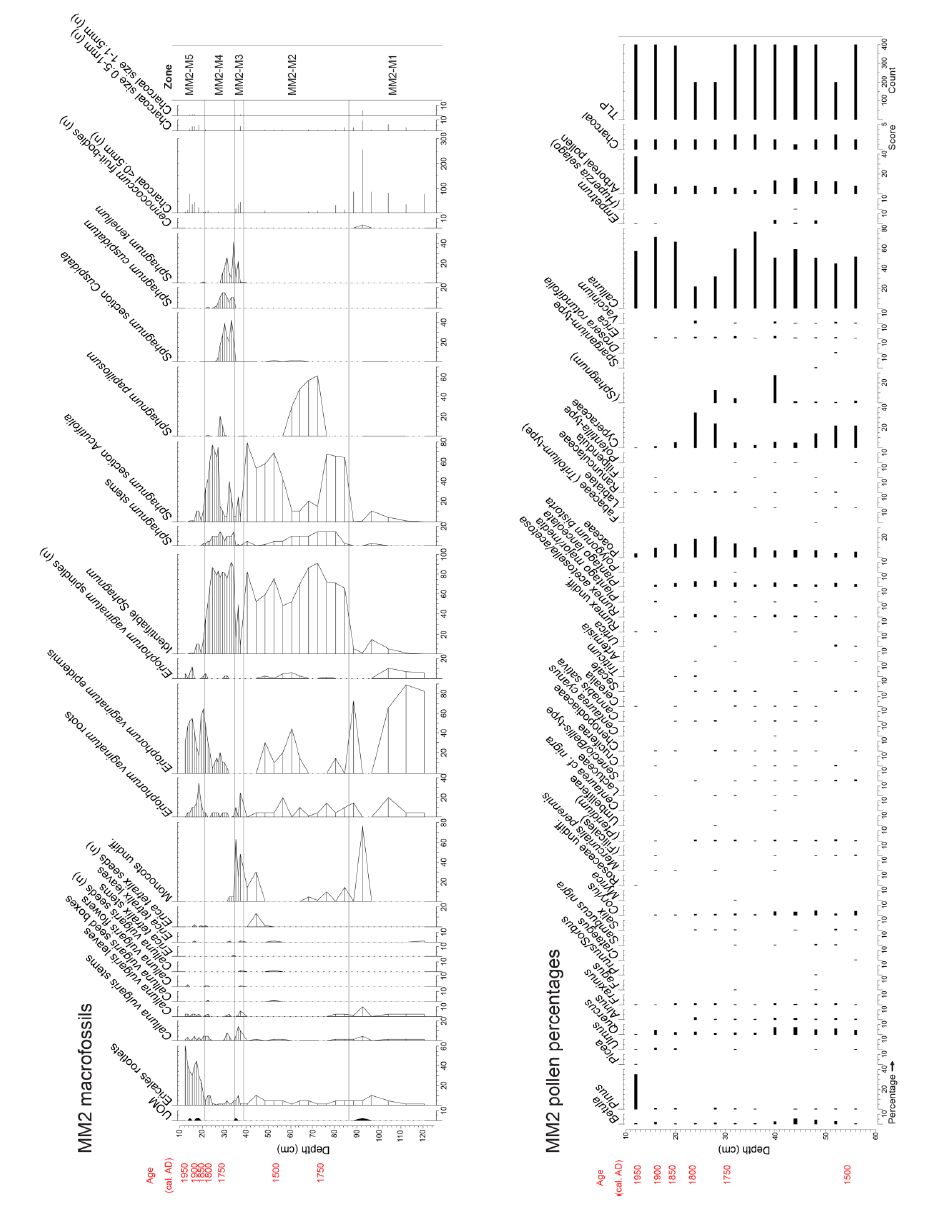
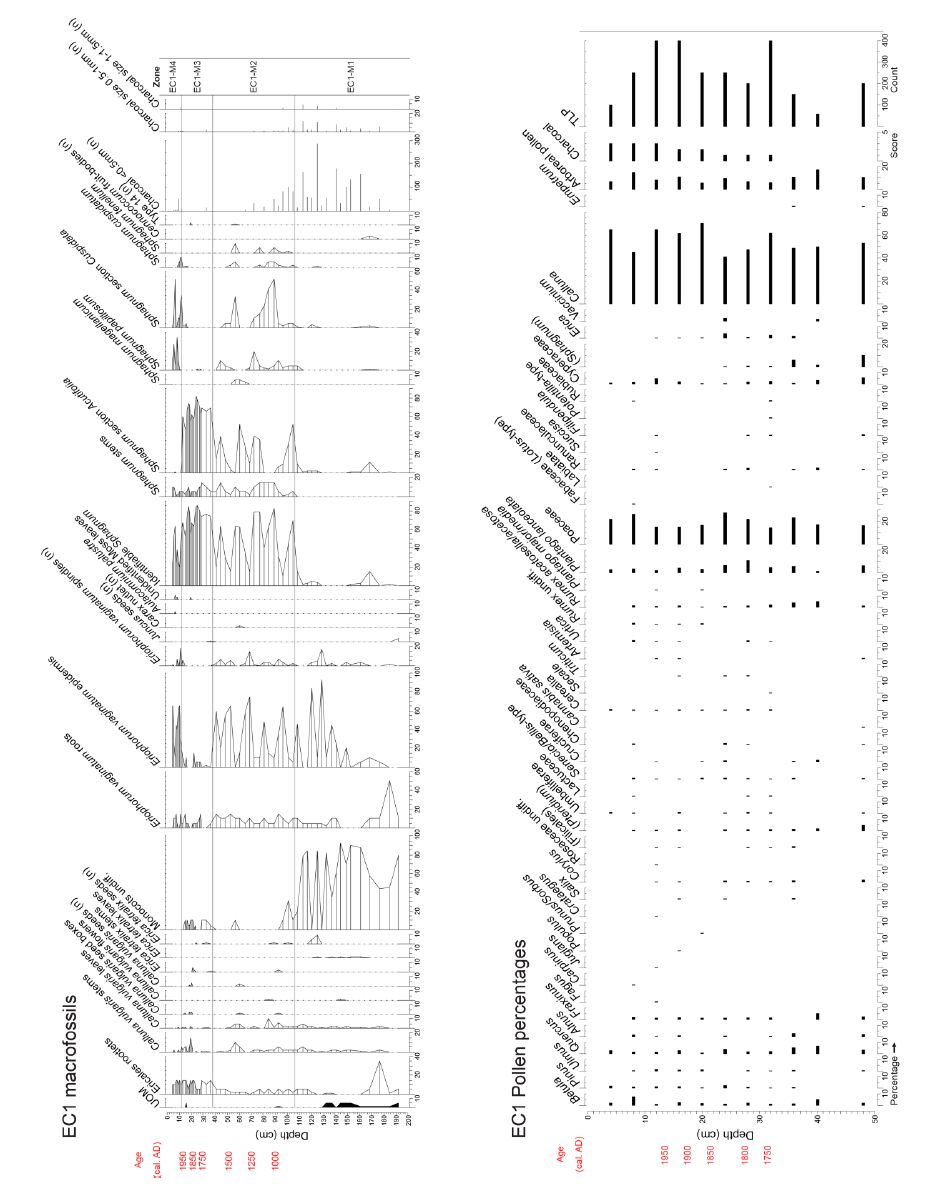
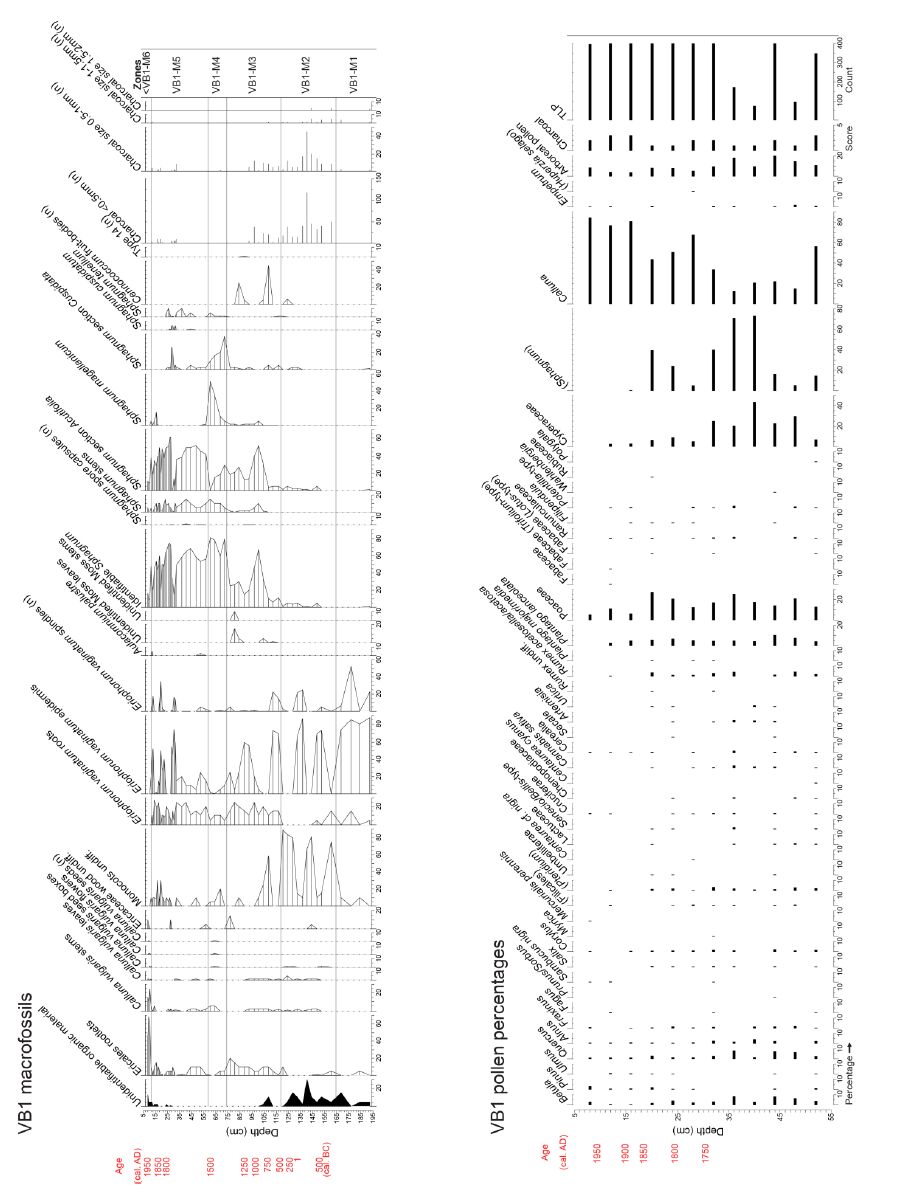
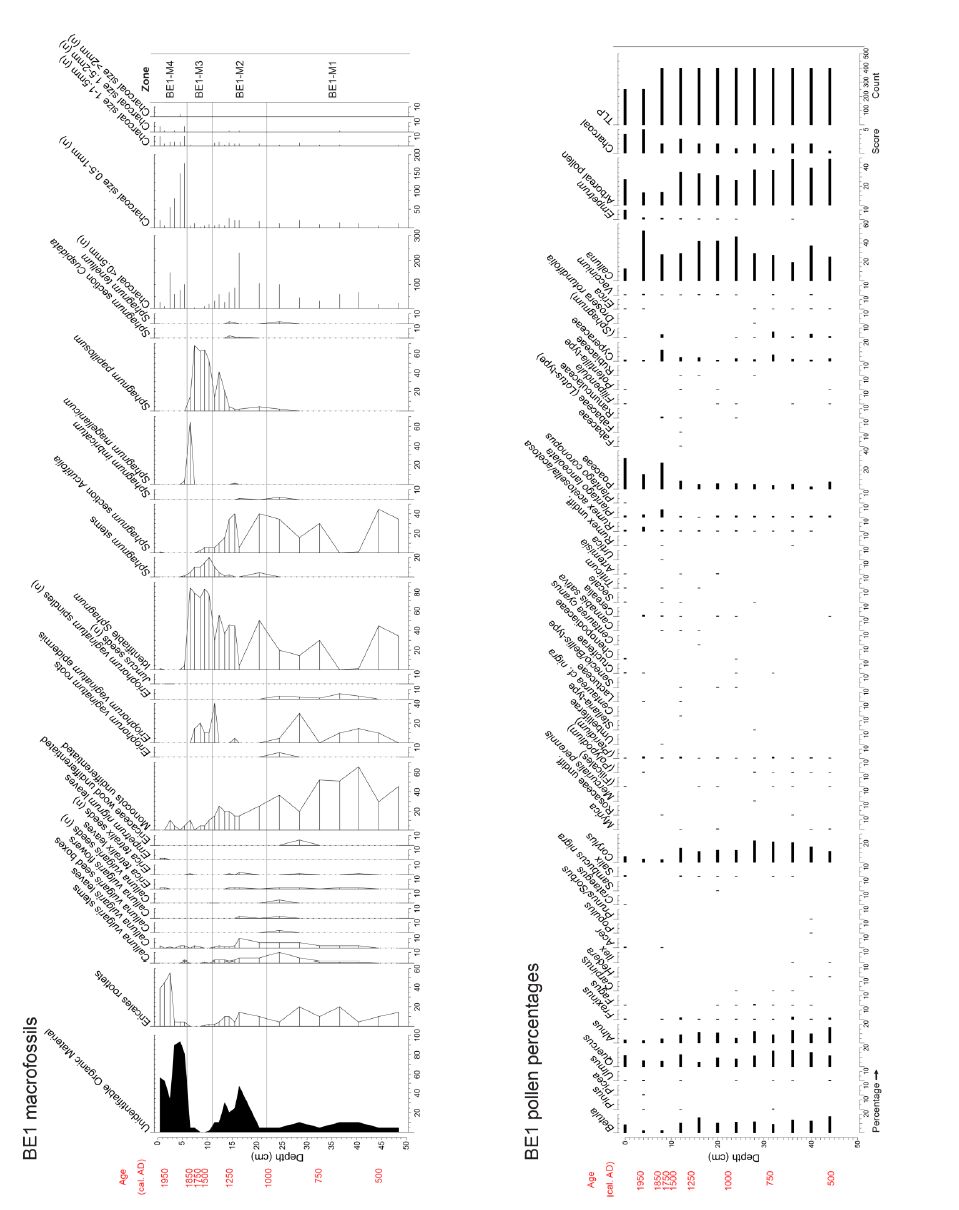
Large areas of upland mire and moorland in Northwest Europe are regarded as degraded, not actively peat-forming, and releasing carbon. Conservation agencies have short-term targets to restore such areas, but often have no clear knowledge of the timing and nature of degradation. It has been suggested that palaeoecology can be used to inform conservation management about past vegetation states, so as to help identify feasible restoration targets. Our research study in northern England, commissioned by the national statutory conservation agency, applied multiple palaeoecological techniques to establish the vegetation history of several mire and moorland sites, specifically to ascertain the nature and timing of degradation. Techniques applied included pollen analysis, plant macrofossil and charcoal analyses, determination of peat humification and mineral magnetic susceptibility, with ages ascertained using spheroidal carbonaceous particle analysis, 210Pb and 14C dating. Data are presented from case-study sites in the North York Moors, North- and South Pennines to illustrate how palaeoecology can extend long-term monitoring and guide conservation management. Palaeoecological data from a site within a National Nature Reserve, subject to exceptionally long-term (half-centennial) ecological monitoring, showed that this period does not include its pre-degradation state and that its current valued vegetation is novel and may have established after major fire. Overall, the studies suggest that the principal vegetation change at the sites took place after the start of the Industrial Revolution, and that the current landscape appearance not only has no long history, but that valued aspects, such as extensive heather moorland, feature only recently in the cultural landscape. These findings pose challenging questions for conservation management. We offer a non-specialist guide to the palaeoecological techniques that considers level of skill, cost, and comparability with ecological aspects of conservation and monitoring interest. We suggest palaeoecological data can provide valuable information and insights to aid practical conservation. While mires are particularly suitable, palaeoecological techniques could be applied in many other degraded landscapes internationally.
1.
Introduction
The convection-diffusion equation(CDE) governs the transmission of particles and energy caused by convection and diffusion. The CDE is given by
where ω denotes coefficient of viscosity and ϑ is the phase velocity respectively and both are positive. The Eq (1.1) is subject to the IC,
and the BCs,
where, ϕ, f0 and f1 are given smooth functions.
Numerous computational procedures have been developed in the literature for the CDE. Chawla et al. [1] developed extended one step time-integration schemes for the CDE. Daig et al. [2] discussed least-squares finite element method for the advection-diffusion equation(ADE). Mittal and Jain [3] revisited the cubic B-splines collocation procedure for the numerical treatment of the CDE. The characteristics method with cubic interpolation for ADE was presented by Tsai et al. [4]. Sari et al. [5] worked on high order finite difference schemes for solving the ADE. Taylor-Galerkin B-spline finite element method for the one-dimensional ADE was developed by Kadalbajoo and Arora [6]. Kara and Zhang [7] presented ADI method for unsteady CDE. Feng and Tian [8] found numerical solution of CDE using the alternating group explicit methods with exponential-type. Dehghan [9] used weighted finite difference techniques for the CDE. Further, Dehghan [10] developed a technique for the numerical solution of the three-dimensional advection-diffusion equation.
A second-order space and time nodal method for CDE was conducted by Rizwan [11]. Mohebbi and Dehghan [12] presented a high order compact solution of the one-dimensional heat equation and ADE. Karahan [13,14] worked on unconditional stable explicit and implicit finite difference technique for ADE using spreadsheets. Salkuyeh [15] used finite difference approximation to solve CDE. Cao et. al [16] developed a fourth-order compact finite difference scheme for solving the CDEs. The generalized trapezoidal formula is used by Chawla and Al-Zanaidi [17] to solve CDE. Restrictive Taylor approximation has been used by Ismail et al. [18] to solve CDE. A boundary element method for anisotropic-diffusion convection-reaction equation in quadratically graded media of incompressible flow was studied by Salam et al. [19]. Azis [20] obtained standard-BEM solutions o two types of anisotropic-diffusion convection reaction equations with variable coefficients. The principle inspiration of this investigation is that the introduced scheme offers the solution as a piecewise adequately smooth continuous function enabling us to discover a numerical solution at any point in the solution domain. Moreover, it is simple to implement and has incredibly diminished computational expense. The refinement of the scheme with new approximations has elevated the accuracy of the scheme. The methodology used by von Neumann is utilized to affirm that the introduced scheme is unconditionally stable. The scheme is implemented to various test problems and the results are contrasted with the ones revealed in [25,26,27]. For further related studies, the interested reader is referred to [28,29] and references therein.
The remaining part of the paper is organized in the following sequence. The numerical scheme is presented in section 2 which is based on the cubic B-spline collocation method. Section 3 deals with the Scheme's stability and convergence analysis. The comparison of our numerical results with the ones presented in [25,26,27] is also presented in this section. The study's finding is summed up in section 4.
2.
Materials and method
Derivation of the scheme
Define Δt=TN to be the time and h=d−cM the space step sizes for positive integers M and N. Let tn=nΔt,n=0,1,2,...,N, and zj=jh,j=0,1,2...M. The solution domain c≤z≤d is evenly divided by knots zj into M subintervals [zj,zj+1] of uniform length, where c=z0<z1<...<zn−1<zM=d. The scheme for solving (1.1) assumes approximate solution V(z,t) to the exact solution v(z,t) to be [23]
where Dj(t) are unknowns to be calculated and B3j(z) [23] are cubic B-spline basis functions given by
Here, just B3j−1(z),B3j(z) and B3j+1(z) are last on account of local support of the cubic B-splines so that the approximation vnj at the grid point (zj,tn) at nth time level is given as
The time dependent unknowns Dnj(t) are determined using the given initial and boundary conditions and the collocation conditions on B3j(z). Consequently, the approximations vnj and its required derivatives are found to be
where α1=16,α2=46,α3=12h,α4=0.
The new approximation [24] for (vnj)zz is given as
The problem (2.1) subject to the weighted θ-scheme takes the form
where hnj=ϑ(vnj)zz−ω(vnj)z and n=0,1,2,3,.... Now utilizing the formula, (vnj)t=vn+1j−vnjk in (2.6) and streamlining the terms, we obtain
Observe that θ=0, θ=12 and θ=1 in the system (2.7) correspond to an explicit, Crank-Nicolson and a fully implicit schemes respectively. We use the Crank-Nicolson approach so that (2.7) is evolved as
Subtituting (2.4) and (2.5) in (2.8) at the knot z0 returns
Substituting (2.4) and (2.5) in (2.8) produces
Subtituting (2.4) and (2.5) in (2.8) at the knot zM yields
From (2.9), (2.10) and (2.11), we acquire a system of (M+1) equations in (M+3) unknowns. To get a consistent system, two additional equations are obtained using the given boundary conditions. Consequently a system of dimension (M+3)×(M+3) is obtained which can be numerically solved using any numerical scheme based on Gaussian elimination.
Initial State: To begin iterative process, the initial vector D0 is required which can be obtained using the initial condition and the derivatives of initial condition as follows:
The system (2.12) produces an (M+3)×(M+3) matrix system of the form
where,
D0=[D0−1,D00,D01,...,D0M+1]T and b=[ϕ′(z0),ϕ(z0),...,ϕ(zM),ϕ′(zM)]T.
3.
Results
3.1. Stability analysis
The von Neumann stability technique is applied in this section to explore the stability of the given scheme. Consider the Fourier mode, Dnj=σneiβhj, where β is the mode number, h is the step size and i=√−1. Plug in the Fourier mode into equation (2.8) to obtain
where,
γ1=kϑ24h2,
γ2=α1−kωα32−kϑ3h2,
γ3=α2+kωα42+3kϑ4h2,
γ4=α1+kωα32−kϑ3h2,
γ5=α1+kωα32+kϑ3h2,
γ6=α2−kωα42−3kϑ4h2,
γ7=α1−kωα32+kϑ3h2.
Dividing equation (3.1) by σneiβjh and rearranging, we obtain
Using cos(βh)=eiβh+e−iβh2 and sin(βh)=eiβh−e−iβh2i in equation (3.2) and simplifying, we obtain
where, E1=α1+kϑ3h2,F1=kωα32,E2=α1−kϑ3h2,F2=kωα32.
Notice that β∈[−π,π]. Without loss of generality, we can assume that β=0, so that Eq (3.3) reduces to
which proves unconditional stability.
3.2. Convergence analysis
In this section, we present the convergence analysis of the proposed scheme. For this purpose, we need to recall the following Theorem [21,22]:
Theorem 1. Let v(z)∈C4[c,d] and c=z0<z1<...<zn−1<zM=d be the partition of [c,d] and V∗(z) be the unique B-spline function that interpolates v. Then there exist constants λi independent of h, such that
First, we assume the computed B-spline approximation to (2.1) as
To estimate the error, ‖v(z,t)−V(z,t)‖∞ we must estimate the errors ‖v(z,t)−V∗(z,t)‖∞ and ‖V∗(z,t)−V(z,t)‖∞ separately. For this purpose, we rewrite the equation (2.8) as:
where, v∗=vn+1j,(v∗)z=(vn+1j)z,(v∗)zz=(vn+1j)zz and r(z)=vnj−12kω(vnj)z+12kϑ(vnj)zz. Equation (3.4) can be written in matrix form as:
where, R=NDn+h and
,
h=[f0(tn+1),0,...0,f1(tn+1)]T, Dn=[Dn−1,Dn0,Dn1,...,DnM+1]T,
q1=α1−kωα32−7kϑ12h2,q2=α2+kωα42+11kϑ8h2,q3=α1+kωα32−7kϑ6h2,q4=7kϑ12h2,
q5=kϑ4h2,q6=kϑ24h2,q7=α1+kωα32+7kϑ12h2,q8=α2−kωα42−11kϑ8h2,
q9=α1−kωα32+7kϑ6h2,q10=α1−kωα32−7kϑ6h2,q11=α1+kωα32−7kϑ12h2,
q12=α1+kωα32+7kϑ6h2,q13=α1−kωα32+7kϑ12h2.
If we replace v∗ by V∗ in (3.4), then the resulting equation in matrix form becomes
Subtracting (3.6) from (3.5), we obtain
Now using (3.4), we have
From (3.8) and Theorem (1), we have
where M1=λ0h2+kω2λ1h+kϑ2λ2. It is obvious that the matrix A is diagonally dominant and thus nonsingular, so that
Now using (3.9), we obtain
Let aj,i denote the entries of A and ηj,0≤j≤M+2 is the summation of jth row of the matrix A, then we have
From the theory of matrices we have,
where a−1k,j are the elements of A−1. Therefore
Substituting (3.13) into (3.11) we see that
where M2=M1|ξl| is some finite constant.
Theorem 2. The cubic B-splines {B−1,B0,....BM+1} defined in relation (2.2) satisfy the inequality
Proof. Consider,
Now for z∈[zj+1,zj+2], we have
|B3j−2(z)|≤46
|B3j−1(z)|≤16,
|B3j(z)|≤46,
|B3j+1(z)|≤16.
Then, we have
as required.
Now, consider
Using (3.14) and Theorem 2, we obtain
Theorem 3. Let v(z) be the exact solution and let V(z) be the cubic collocation approximation to v(z) then the provided scheme has second order convergence in space and
Proof. From Theorem 1, we have
From (3.16) and (3.17), we obtain
where μ=λ0h2+53M2.
3.3. Applications of numerical scheme
In this section, some numerical calculations are performed to test the accuracy of the offered scheme. In all examples, we use the following error norms
The numerical order of convergence p is obtained by using the following formula:
where L∞(n) and L∞(2n) are the errors at number of partition n and 2n respectively.
Example 1. Consider the CDE,
with IC,
and the BCs,
The analytic solution of the given problem is v(z,t)=exp(5z−(0.25+0.01π2)t)sin(πz). To acquire the numerical results, the offered scheme is applied to Example 1. The absolute errors are compared with those obtained in [25] at various time stages in Table 1. In Table 2, absolute errors and error norms are presented at time stages t=5,10,100. Figure 1 displays the comparison that exists between exact and numerical solutions at various time stages. Figure 2 depicts the 2D and 3D error profiles at t=1. A 3D comparison between the exact and numerical solutions is presented to exhibit the exactness of the scheme in Figure 3.
The approximate solution when t=1,k=0.01 and M=20 for Example 1 is given by
Example 2. Consider the CDE,
with IC,
and the BCs,
The analytic solution is v(z,t)=exp(0.22z−(0.0242+0.5π2)t)sin(πz). The numerical results are obtained by utilizing the proposed scheme. In Table 3, the comparative analysis of absolute errors is given with that of [25]. Absolute errors and errors norms at time levels t=5,10,100 are computed in Table 4. Figure 4 shows a very close comparison between the exact and numerical solutions at various stages of time. Figure 5 plots 2D and 3D absolute errors at t=1. In Figure 6, a tremendous 3D contrast between the exact and approximate solutions is depicted.
The numerical solution when t=1,k=0.01 and M=20 for Example 2 is given by
Example 3. Consider the CDE,
with IC,
and the BCs,
The analytic solution is v(z,t)=exp(0.25z−(0.0125+0.2π2)t)sin(πz). By utilizing the proposed scheme the numerical results are acquired. An excellent comparison between absolute errors computed by our scheme and the scheme of [25] is discussed in Table 5. In Table 6, absolute errors and error norms are computed at different time stages. A close comparison between the exact and numerical solutions at different time stages is depicted in Figure 7. Figure 8 plots 2D and 3D absolute errors at t=1. Figure 9 deals with the 3D comparison that occurs between the exact and numerical solutions. The numerical solution when t=1,k=0.01 and M=20 for Example 3 is given by
Example 4. Consider the CDE,
with IC,
and the BCs,
The analytic solution of the given problem is v(z,t)=√2020+texp(−(z−2−0.8t)20.4(20+t)). In Table 7, a comparison between absolute errors calculated by our scheme and the scheme of [26] is presented. Absolute errors and errors norms at time levels t=5,10,100 are presented in Table 8. Figure 10 illustrates the behavior of numerical solutions at various time stages. Figure 11 depicts the 2D and 3D graphs of absolute errors. In Figure 12, an excellent 3D contrast between the exact and numerical solutions shows the enormous accuracy of the scheme.
The approximate solution when t=1,k=0.01 and M=20 for Example 4 is given by
Example 5. Consider the CDE,
with IC,
and the BCs,
The analytic solution of the given problem is v(z,t)=exp(1.17712434446770z−0.09t). The numerical outcomes are acquired by using the introduced scheme. The absolute errors and errors norms are computed in Tables 9 by applying the presented scheme on Example 5 and are compared with those obtained in [27]. In Table 10, absolute errors and error norms are presented at various time stages. Figure 13 plots the behavior of exact and numerical solutions at various time stages. Figure 14 depicts the 2D and 3D absolute error profiles at t=1. In Figure 15, a 3D contrast between the exact and numerical solutions is presented and all the graphs are in good agreement.
The approximate solution when t=1,k=0.01 and M=20 for Example 5 is given by
4.
Conclusions
This research uses a new approximation for second-order derivatives in the cubic B-spline collocation method to obtain the numerical solution of the CDE. The smooth piecewise cubic B-splines have been used to approximate derivatives in space whereas a usual finite difference has been used to discretize the time derivative. Special consideration is paid to the stability and convergence analysis of the scheme to ensure the errors do not amplify. The approximate solutions and error norms are contrasted with those reported previously in the literature. From this analysis, we can conclude that the estimated solutions are in perfect accord with the actual solutions. The scheme can be applied to a wide range of problems in science and engineering.
Acknowledgments
The authors are thankful to the worthy reviewers and editors for the useful and valuable suggestions for the improvement of this paper which led to a better presentation.
Conflict of interest
The authors have no conflict of interest.









 DownLoad:
DownLoad: